Abstract
The SyDPaCC framework for the Coq proof assistant is based on a transformational approach to develop verified efficient scalable parallel functional programs from specifications. These specifications are written as inefficient (potentially with a high computational complexity) sequential programs. We obtain efficient parallel programs implemented using algorithmic skeletons that are higher-order functions implemented in parallel on distributed data structures. The output programs are constructed step-by-step by applying transformation theorems. Leveraging Coq type classes, the application of transformation theorems is partly automated. The current version of the framework is presented and exemplified on the development of a parallel program for the maximum segment sum problem. This program is experimented on a parallel machine.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Our everyday activities generate extremely large volume of data. Big data analytics offer opportunities in a variety of domains [4, 13].
While there are many challenges in the design and implementation of big data analytics applications, we focus on the programming aspects. Due to the large scale, scalable parallel computing is a necessity. Most approaches either cite Bulk Synchronous Parallelism (BSP) [44] as an inspiration, that is the case of Pregel [32] and related frameworks such as Apache Giraph, or are related to, even if it is not often acknowledged, algorithmic skeletons [6]. This is the case of Hadoop MapReduce [9] and Spark [1].
Both BSP and algorithmic skeletons are structured and high-level approaches to parallelism which free the developers from tedious details of the implementation of parallel algorithms found for example in MPI programming, a de facto standard for writing HPC programs. While BSP is a general purpose parallel programming model, algorithmic skeletons approaches as well as the mentioned big data frameworks are limited to what is expressible by the building blocks they provide. This lack of generality is both a strength making them easier to use in the classes of applications they naturally cover, but also a weakness in that expressing one’s algorithm with these building blocks may become very convoluted or even impossible.
SyDPaCC [27, 28] is a framework for the Coq proof assistant to systematically develop correct and efficient parallel programs from specifications. Currently, SyDPaCC provides sequential program optimizations via transformations based on list homomorphism theorems [17] and the diffusion theorem [21]. It also provides automated parallelization via verified correspondences between sequential higher-order functions and algorithmic skeletons implemented using the parallel primitives of BSML [26] a library for scalable parallel programming with the multi-paradigm (including functional) programming language OCaml [24]. In this paper, we develop a new verified parallel algorithm for the maximum segment sum problem, which is for example a component of computer vision applications to detect the brightest area of an image.
The remaining of the paper is organized as follows. Functional bulk synchronous parallel programming with the BSML library is introduced in Sect. 2. Section 3 is devoted to an overview of the SyDPaCC framework. In Sect. 4, we develop a verified scalable Bulk Synchronous Parallel algorithm of the maximum segment sum problem and experiment (Sect. 5) on a parallel machine the extracted code from the Coq proof assistant. We compare our approach to related work in Sect. 6 and conclude in Sect. 7. The code presented in the paper is available in the SyDPaCC distribution version 0.5 at https://sydpacc.github.io.
2 Functional Bulk Synchronous Parallelism
In the Bulk Synchronous Parallel model, the BSP computer is seen as a homogeneous distributed memory machine with a point-to-point communication network and a global synchronization unit. It runs BSP programs which are sequences of so-called super-steps. A super-step is composed of three phases. The computation phase is concerned with each processor-memory pair computing using only the data available locally. In the communication phase, each processor may request data from other processors and send requested data to other processors. Finally, during the synchronization phase, the communication exchanges are finalized and the super-step ends with a global synchronization of all the processors.
BSML offers a set of constants (giving access to the parameters of the BSP machine as they are discussed in [40] but omitted here) including
 the number of processors in the BSP machine and a set of four functions which are expressive enough to express any BSP algorithm. BSML is implemented as a library for the multi-paradigm and functional language OCaml [24] ( [34] is a short introduction to OCaml and its qualities). BSML is purely functional but using on each processor the imperative features of OCaml, it is possible to implement an imperative programming library [26] in the style of the BSPlib for C [19]. In this paper we are interested in the pure functional aspects of BSML as it is only possible to write pure functions within Coq.
the number of processors in the BSP machine and a set of four functions which are expressive enough to express any BSP algorithm. BSML is implemented as a library for the multi-paradigm and functional language OCaml [24] ( [34] is a short introduction to OCaml and its qualities). BSML is purely functional but using on each processor the imperative features of OCaml, it is possible to implement an imperative programming library [26] in the style of the BSPlib for C [19]. In this paper we are interested in the pure functional aspects of BSML as it is only possible to write pure functions within Coq.
Given any type
 and a function
and a function
 from
from
 to
to
 (which is written
(which is written
 in OCaml), the BSML primitive
in OCaml), the BSML primitive
 (
(
 applied to
applied to
 , application in OCaml and many other functional languages is simply denoted by a space) creates a parallel vector of type
, application in OCaml and many other functional languages is simply denoted by a space) creates a parallel vector of type
 . Parallel vectors are therefore a polymorphic data-structure. In such a parallel vector, processor number i with
. Parallel vectors are therefore a polymorphic data-structure. In such a parallel vector, processor number i with

 , holds the value of
, holds the value of
 . For example,
. For example,
 is the parallel vector \(\langle 0,~\ldots ,~\mathtt {bsp\_p}-1\rangle \) of type
is the parallel vector \(\langle 0,~\ldots ,~\mathtt {bsp\_p}-1\rangle \) of type
 . In the following, this parallel vector is denoted by
. In the following, this parallel vector is denoted by
 . The function
. The function
 has type
has type
 and can be defined as:
and can be defined as:
 . In expression
. In expression
 , all the processors will contain the value of
, all the processors will contain the value of
 .
.
 is the partial application of addition seen in prefix notation, it is equivalent to
is the partial application of addition seen in prefix notation, it is equivalent to
 . Therefore
. Therefore
 is a parallel vector of functions and its type is
is a parallel vector of functions and its type is
 . A parallel vector of functions is not a function and cannot be applied directly. That is why BSML provides the primitive
. A parallel vector of functions is not a function and cannot be applied directly. That is why BSML provides the primitive
 that can apply a parallel vector of functions to a parallel vector of values. For example,
that can apply a parallel vector of functions to a parallel vector of values. For example,
 is the parallel vector \(\langle 1,~\ldots ,~\mathtt {bsp\_p}\rangle \). Using
is the parallel vector \(\langle 1,~\ldots ,~\mathtt {bsp\_p}\rangle \). Using
 and
and
 in such a way is common. The function
in such a way is common. The function
 is also part of the BSML standard library and is defined as:
is also part of the BSML standard library and is defined as:
 .
.
The primitive
 can be seen as a partial inverse of
can be seen as a partial inverse of
 , its type is
, its type is
 . However,
. However,
 is in general different from
is in general different from
 . Indeed
. Indeed
 may be defined on all the values of type
may be defined on all the values of type
 , but
, but
 is defined only on \(\{0,~\dots ,\mathtt {bsp\_p}-1\}\).
is defined only on \(\{0,~\dots ,\mathtt {bsp\_p}-1\}\).
To transform a parallel vector into a list, one can define
 as follows:
as follows:
 where
where
 has type
has type
 and contains the integers from 0 (included) to
and contains the integers from 0 (included) to
 (excluded).
(excluded).
While
 and
and
 do not require any communication or synchronization to run,
do not require any communication or synchronization to run,
 needs communications and a global synchronization. The value of each processor is sent to all the other processors (it is a total exchange). For a finer control over communications the primitive
needs communications and a global synchronization. The value of each processor is sent to all the other processors (it is a total exchange). For a finer control over communications the primitive
 should be used. It is the most complex operation of BSML and its type is
should be used. It is the most complex operation of BSML and its type is
 . The functions in the input vector contain the messages to be sent to other processors. The functions in the output vector contain the messages received from other processors. For example if the input vector contains function \(\textit{in}_i\) at processor i, then the value \(v = \textit{in}_i\ i'\) will be sent to processor \(i'\). After executing the
. The functions in the input vector contain the messages to be sent to other processors. The functions in the output vector contain the messages received from other processors. For example if the input vector contains function \(\textit{in}_i\) at processor i, then the value \(v = \textit{in}_i\ i'\) will be sent to processor \(i'\). After executing the
 , processor \(i'\) contains a function \(\textit{out}_{i'}\) such that \(\textit{out}_{i'}\ i = v\). Some OCaml values are considered to be empty messages so an application of
, processor \(i'\) contains a function \(\textit{out}_{i'}\) such that \(\textit{out}_{i'}\ i = v\). Some OCaml values are considered to be empty messages so an application of
 does mean that each processor communicates with every other processors. For the sake of conciseness we do not detail
does mean that each processor communicates with every other processors. For the sake of conciseness we do not detail
 further but we refer to [29].
further but we refer to [29].
As an example, we implement in Fig. 2 the set of algorithmic skeletons on a data-structure of distributed lists whose module type is shown in Fig. 1.
We implement the distributed list type as a record type: its content is a parallel vector of lists and it also possesses a field for the global size of the distributed list.
 is similar to
is similar to
 , however for distributed lists the size is given by the user while it is always
, however for distributed lists the size is given by the user while it is always
 for parallel vectors. We want the list to be distributed evenly: each processor contains
for parallel vectors. We want the list to be distributed evenly: each processor contains
 elements, or one more element than that.
elements, or one more element than that.
 is similar to the
is similar to the
 function on sequential lists: it applies a function
function on sequential lists: it applies a function
 to all the elements of the lists. Here each processor takes care of the sub-list it holds locally.
to all the elements of the lists. Here each processor takes care of the sub-list it holds locally.
 uses a predicate
uses a predicate
 to keep only the elements of
to keep only the elements of
 that satisfy this predicate. Our
that satisfy this predicate. Our
 skeleton does the same: the part about the content is easy to write. But we also need to update the global size of the distributed list and communications are required to do so. Note that after a filter, the distributed list may no longer be evenly distributed.
skeleton does the same: the part about the content is easy to write. But we also need to update the global size of the distributed list and communications are required to do so. Note that after a filter, the distributed list may no longer be evenly distributed.
3 An Overview of SyDPaCC
We present the use of SyDPaCC through a very simple example. In this case the specification is already quite efficient, but often the specification has a higher complexity than the optimized program. This is for example the case of the maximum prefix sum problem presented in [28] and the maximum segment sum problem presented in the next section. For a short introduction to Coq, see [2].
Our goal is to obtain a parallel algorithm for computing the average of a list of natural numbers. To do so, we use SyDPaCC to parallelize a function that sums the elements of a list and counts the number of elements of this list. This specification can be written as:

 is a recursive function defined by pattern matching on its list argument while
is a recursive function defined by pattern matching on its list argument while
 is just an alias for the pre-defined
is just an alias for the pre-defined
 function. The specification
function. The specification
 is defined as the tupling of these two functions.
is defined as the tupling of these two functions.
We then try to show that this function has some simple properties: it is leftwards, meaning it can be written as an application of
 , rightwards, meaning it can be written as an application of
, rightwards, meaning it can be written as an application of
 , and finally it has a right inverse, which is a weak form of inverse.
, and finally it has a right inverse, which is a weak form of inverse.
For a list
 , binary operations \(\oplus \) \(\otimes \), and values \(e_l\) \(e_r\), we have:
, binary operations \(\oplus \) \(\otimes \), and values \(e_l\) \(e_r\), we have:

 is indeed leftwards, rightwards and has a right inverse:
is indeed leftwards, rightwards and has a right inverse:

Each of these properties are expressed as instances of type-classes defined in SyDPaCC. Basically type-classes are just record types (in these cases with only one field that holds a proof of the property of interest) and the values of these types are called instances. The difference with record types is that instances are recorded in a database. Coq functions can have implicit arguments: when such arguments have a type that is a type-class, each time the function is applied, Coq searches for an instance that fits the implicit argument. Instances may have other instances as parameters. In this situation to build an instance the system first needs to build instances for the parameters. Such parametrized instances can be seen as Prolog rules while non-parametrized instances can be seen as Prolog facts. Coq searches for an instance with a Prolog-like resolution algorithm.
For the inverse, we need to build a list l such that for a sum s and a number of elements c, we have
 . One possible solution is to have
. One possible solution is to have
 . An application of function
. An application of function
 builds the list of zeros. If \(c=0\) then the list should be empty. The omitted proofs are short: from 3 to 9 lines with calls to a couple one-liner lemmas.
builds the list of zeros. If \(c=0\) then the list should be empty. The omitted proofs are short: from 3 to 9 lines with calls to a couple one-liner lemmas.
These instances are enough for the system to automatically parallelize the specification, as follows:

In this example,
 will produce a composition of a parallel
will produce a composition of a parallel
 and a parallel
and a parallel
 . The automated sequential optimization of
. The automated sequential optimization of
 , then the automated parallelization, are triggered by the call to
, then the automated parallelization, are triggered by the call to
 that has several implicit arguments whose types are type-classes.
that has several implicit arguments whose types are type-classes.
Two of them are notions of correspondence:
-
A type
 corresponds to a type
corresponds to a type
 if there exists a surjective function
if there exists a surjective function
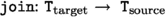 . We note
. We note
 \(\blacktriangleleft \)
\(\blacktriangleleft \)
 such a type correspondence. Intuitively, the
such a type correspondence. Intuitively, the
 function is surjective because we want the target type to have at least the same expressive power than the source type. If the source type is
function is surjective because we want the target type to have at least the same expressive power than the source type. If the source type is
 and target type is a distributed type such as
and target type is a distributed type such as
 , there are many ways a sequential list could be distributed into a parallel vector of lists.
, there are many ways a sequential list could be distributed into a parallel vector of lists. -
A function
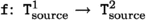 corresponds to
corresponds to
 if
if
 \(\blacktriangleleft \)
\(\blacktriangleleft \)
 and
and
 \(\blacktriangleleft \)
\(\blacktriangleleft \)
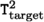 and the following property holds: $$\forall (x:\texttt{T}^1_\text {target}), \texttt{join}^2 ({\texttt{f}_\text {target}}\ x) = \texttt{f}_\text {source} (\texttt{join}^1\ x).$$
and the following property holds: $$\forall (x:\texttt{T}^1_\text {target}), \texttt{join}^2 ({\texttt{f}_\text {target}}\ x) = \texttt{f}_\text {source} (\texttt{join}^1\ x).$$
SyDPaCC provides type correspondences such as
 \(\blacktriangleleft \)
\(\blacktriangleleft \)
 as well as several function correspondences including
as well as several function correspondences including
 corresponds to
corresponds to
 . It also offers parametrized instances for the composition of functions with \(\circ \), \(\bigtriangleup \) and \(\times \) (pairing). Finally while looking for such instances, SyDPaCC also checks if there are optimized versions of functions, captured by instances of type
. It also offers parametrized instances for the composition of functions with \(\circ \), \(\bigtriangleup \) and \(\times \) (pairing). Finally while looking for such instances, SyDPaCC also checks if there are optimized versions of functions, captured by instances of type
 meaning
meaning
 is an optimized version of
is an optimized version of
 .
.
These optimizations are based on transformation theorems expressed as instances. SyDPaCC provides a variant of the third homomorphism theorem [17] that states that a function is a list homomorphism when it is leftwards, rightwards and has a right inverse. The first homomorphism theorem states that a list homomorphism can be implemented as a composition of
 and
and
 . The other transformation theorem available for lists is the diffusion theorem [21].
. The other transformation theorem available for lists is the diffusion theorem [21].
In the example,
 looks for a correspondence of
looks for a correspondence of
 that triggers the optimization of
that triggers the optimization of
 which is done thanks to the two homomorphism theorems mentioned above. At the end of the Prolog-like search, it is established (and verified) than
which is done thanks to the two homomorphism theorems mentioned above. At the end of the Prolog-like search, it is established (and verified) than
 corresponds to a composition of a parallel reduce and a parallel map.
corresponds to a composition of a parallel reduce and a parallel map.
To obtain a very efficient program, the user can try to simplify the binary operation and the function given respectively as arguments of the parallel reduce and the parallel map. Indeed, by default the former is:

and the latter is
 . To obtain optimized versions, one can use the type-classes
. To obtain optimized versions, one can use the type-classes
 and
and
 that only take as argument the specification. The optimized versions do not need to be known beforehand: they can be discovered while proving the instances. In our example, the operation is mostly the addition of the first components of the argument pairs (replaced by 0 if the second component is 0), and the function is
that only take as argument the specification. The optimized versions do not need to be known beforehand: they can be discovered while proving the instances. In our example, the operation is mostly the addition of the first components of the argument pairs (replaced by 0 if the second component is 0), and the function is
 .
.
Finally, the extractedFootnote 1 OCaml code (with calls to BSML functions in a module
 similar to the functions of Fig. 2) is given Fig. 3. Such a program can be compiled and run on (possibly massively) parallel machines. The SyDPaCC framework provided a guide towards the development of such a parallel program, but also the proof that this program is correct with respect to the initial specification.
similar to the functions of Fig. 2) is given Fig. 3. Such a program can be compiled and run on (possibly massively) parallel machines. The SyDPaCC framework provided a guide towards the development of such a parallel program, but also the proof that this program is correct with respect to the initial specification.
4 Verified Parallel Maximum Segment Sum
The goal of maximum segment sum problem is to obtain the maximum value among the sums of all segments (i.e. sub-structures) of a structure. We consider here lists, but algorithms are equivalent for 1D arrays.
Basically, the specification for this problem can be written as follows:

There are several derivations of parallel algorithms for the maximum segment sum problem. The first, informal one, was proposed by Cole [7]. Takeichi et al. [20] gave a formal account of this construction using a theory of tupling and fusion. Their theory may be expressed in Coq, but it is not simple as theorems are stated for an arbitrary number of mutually recursive functions which are tupled, hence it is necessary to deal with tuples of an arbitrary size. The algorithm they obtain (from a similar specification than the one above) is a list homomorphism and therefore SyDPaCC could automatically parallelized it. The GTA (generate-test-aggregate) approach [11] — which was implemented in Coq [12], but this implementation is not compatible with the current version of SyDPaCC — is also applicable. Both solutions are not well suited as we want to consider in the future the variant problem of maximum segment sum with a bound on the segment lengths. Thus, we based our contribution on the calculation proposed by Morihata [36].
Morihata only considered non-empty lists. There is support in SyDPaCC to deal with non-empty lists [28], but it requires for example to use different function compositions that transport facts about the non-emptyness of lists across function composition. For example,
 is the function that generates all the segments of a list, and it returns a non-empty list even if its argument is an empty list. The
is the function that generates all the segments of a list, and it returns a non-empty list even if its argument is an empty list. The
 function preserves non-emptiness. Finally, if
function preserves non-emptiness. Finally, if
 returns a number then it is defined only on non-empty lists.
returns a number then it is defined only on non-empty lists.
Here, we choose to deal with empty lists. Therefore, the function
 used in the specification has type
used in the specification has type
 where
where
 is an abstract type of numbers that possess the required algebraic properties, and
is an abstract type of numbers that possess the required algebraic properties, and
 is the Coq type:
is the Coq type:

which basically adds a value
 to the type given as argument to
to the type given as argument to
 . In the case of
. In the case of
 we interpret
we interpret
 as \(-\infty \). The definition of
as \(-\infty \). The definition of
 and
and
 follow:
follow:

 is a higher-order function that “sums” all the elements of a list using the binary operation given as first argument. We proved that is
is a higher-order function that “sums” all the elements of a list using the binary operation given as first argument. We proved that is
 is associative then
is associative then
 forms a monoid with the neutral element being
forms a monoid with the neutral element being
 .
.
During the transformations of
 , a version of
, a version of
 that deals with
that deals with
 values instead of
values instead of
 values is needed. The
values is needed. The
 function is:
function is:

If the original operation
 forms a monoid with neutral element
forms a monoid with neutral element
 , then the optionzed version forms a monoid with
, then the optionzed version forms a monoid with
 .
.
 is an absorbing element of
is an absorbing element of
 .
.
The function generating all the segments is defined in terms of
 and
and
 which are two functions already defined in SyDPaCC that respectively return the prefixes of a list and its suffixes (
which are two functions already defined in SyDPaCC that respectively return the prefixes of a list and its suffixes (
 is part of Coq ’s standard library and is list concatenation):
is part of Coq ’s standard library and is list concatenation):

We then prove the following instance of
 to give an equivalent but optimized version of
to give an equivalent but optimized version of
 :
:

The proof of this instance follows roughly the calculation of Morihata but for the treatment of empty lists. This proof is simple in term of structure: just a sequence of applications of rewriting steps, each step being the application of a transformation lemma. Most of the lemmas were already in Coq or SyDPaCC libraries but the definition of
 and related lemma (and instances omitted here):
and related lemma (and instances omitted here):

Morihata used this operator and a lemma based on a method first proposed by Smith [41].
The optimized version also uses
 which is linear on the length of its list argument. We implemented a tail recursive version of
which is linear on the length of its list argument. We implemented a tail recursive version of
 (as we do for all the function on lists that are supposed to be part of the final optimized code) and satisfies the following expected property for a
(as we do for all the function on lists that are supposed to be part of the final optimized code) and satisfies the following expected property for a
 :
:

The optimized version has a linear complexity in the length of its argument while the specification has a cubic one. The goal of the transformations was to remove the calls to
 and
and
 . These transformations are not automatic, but the support provided by SyDPaCC is a collection of already proved transformations.
. These transformations are not automatic, but the support provided by SyDPaCC is a collection of already proved transformations.
The last step is fully automatic and very simple as shown in Fig. 4. With the call to
 , SyDPaCC uses the instance
, SyDPaCC uses the instance
 as well as instances of types and functions correspondences that are part of the framework to generate a parallel version of
as well as instances of types and functions correspondences that are part of the framework to generate a parallel version of
 by replacing the list functions by their algorithmic skeletons counter-parts:
by replacing the list functions by their algorithmic skeletons counter-parts:
 ,
,
 and
and
 .
.
5 Experiments
The Coq proof assistant offers an extraction mechanism [25] able to generate compilable code from Coq definitions and proofs. In particular, it can generate OCaml code. Extracting the parametric module of Fig. 4 generates an OCaml functor (which is basically a parametric module). To be able to execute the function
 , we first need to apply this functor. For the number part, we just wrote a module using OCaml native integers of type
, we first need to apply this functor. For the number part, we just wrote a module using OCaml native integers of type
 for
for
 . For the parameter,
. For the parameter,
 we simply apply the actual parallel implementation of BSML primitives as provided by the BSML library for OCaml. This library is implemented on top of an API for parallel processing library in C named MPI [42] (several implementations of this API exist). For the moment, the
we simply apply the actual parallel implementation of BSML primitives as provided by the BSML library for OCaml. This library is implemented on top of an API for parallel processing library in C named MPI [42] (several implementations of this API exist). For the moment, the
 module of the BSML library cannot directly be given as argument to the
module of the BSML library cannot directly be given as argument to the
 functor. Indeed, processor identifiers are represented by mathematical natural numbers in Coq while they are encoded as OCaml bounded
functor. Indeed, processor identifiers are represented by mathematical natural numbers in Coq while they are encoded as OCaml bounded
 values. SyDPaCC features a wrapper module
values. SyDPaCC features a wrapper module
 that performs number conversions when needed.
that performs number conversions when needed.
The application of the verified extracted function and aspects such as input/output operations and command line argument management are not verified and written in plain OCaml. The final program was run on a shared memory parallel machine, but it could run on large scale distributed memory machines.
We ran the program on a machine having an Intel Xeon Gold 5218 processor with 32 cores. The operating system was Ubuntu 22.04. To compile we used OCaml 4.14.1. The MPI implementation was OpenMPI 4.1.2. We ran
 on a list of length \(64\cdot 10^6\) and measured the time required for this computation 30 times. The results for the relative speed-up are presented in Fig. 5 for an increasing number of cores. The speedup is fine but of course as the number of cores increases the relative impact of communication and synchronization time becomes bigger. The variance increases to reach a maximum for 4 cores then decreases again.
on a list of length \(64\cdot 10^6\) and measured the time required for this computation 30 times. The results for the relative speed-up are presented in Fig. 5 for an increasing number of cores. The speedup is fine but of course as the number of cores increases the relative impact of communication and synchronization time becomes bigger. The variance increases to reach a maximum for 4 cores then decreases again.
6 Related Work
The literature on constructive algorithmics, introduced by Bird [3], is extensive and includes studies on parallel programming [7, 10, 18, 22, 35]. While most of the work in this field has been done on paper, recent advancements have seen the use of interactive theorem proving, as demonstrated in works like [37]. However, interactive theorem proving has not been extensively explored in the context of parallel programming.
From a functional programming perspective, the study of frameworks such as Hadoop MapReduce [23, 33] and Apache Spark [1, 5] is relevant to our SyDPaCC framework, as we can adopt a similar approach to extract MapReduce or Spark programs from Coq. Ono et al. [39] employed Coq to verify MapReduce programs and extract Haskell code for Hadoop Streaming or directly write Java programs annotated with JML, utilizing Krakatoa [14] to generate Coq lemmas. However, their work is less systematic and automated than SyDPaCC.
There have been contributions that formalize certain aspects of parallel programming, but as far as we know, these approaches do not directly yield executable code like our SyDPaCC framework. Swierstra [43] formalized mutable arrays with explicit distributions in Agda, while BSP-Why [15] allows for deductive verification of imperative BSP programs, although they represent models of C BSPlib [19] programs rather than executable code. Another example is the formalization of the Data Parallel C programming language using Isabelle/HOL [8], where Isabelle/HOL expressions representing parallel programs were generated.
7 Conclusion
We developed a verified parallel implementation of a functional scalable parallel program for solving the maximum segment sum problem and studied its parallel performances. Experiments on a larger number of processors are planned.
Often in applications, the domain is 2D rather than 1D, and it may be interesting to consider segments of a given bounded size, for example in genomics. We therefore plan to systematically develop parallel algorithms for these problems starting from the work of Morihata [36].
The development of SyDPaCC started in 2015 while preparing a graduate course for a summer school, on the predecessor of SyDPaCC named SDPP. There are SDPP theories, namely BSP homomorphisms [16, 31] and generate, test, aggregate [11, 12] that have not been ported to SyDPaCC yet. We also plan to work on additional data-structures such as trees. For the moment, SyDPaCC only targets BSML+OCaml, but there is ongoing work to extend it to generate Scala [38] code with Apache Spark for parallel processing [30].
Notes
- 1.
The type annotations have been added manually and the argument renamed to increase readability.
References
Armbrust, M., et al.: Scaling spark in the real world: performance and usability. PVLDB 8(12), 1840–1851 (2015). http://www.vldb.org/pvldb/vol8/p1840-armbrust.pdf
Bertot, Y.: Coq in a hurry (2006). http://hal.inria.fr/inria-00001173
Bird, R.: An introduction to the theory of lists. In: Broy, M. (ed.) Logic of Programming and Calculi of Discrete Design. NATO ASI Series, vol. 36, pp. 5–42. Springer, Heidelberg (1987). https://doi.org/10.1007/978-3-642-87374-4_1
Cao, L.: Data science: a comprehensive overview. ACM Comput. Surv. 50(3), 1–42 (2017). https://doi.org/10.1145/3076253
Chen, Y.-F., Hong, C.-D., Lengál, O., Mu, S.-C., Sinha, N., Wang, B.-Y.: An executable sequential specification for spark aggregation. In: El Abbadi, A., Garbinato, B. (eds.) NETYS 2017. LNCS, vol. 10299, pp. 421–438. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-59647-1_31
Cole, M.: Algorithmic Skeletons: Structured Management of Parallel Computation. MIT Press, Cambridge (1989)
Cole, M.: Parallel programming, list homomorphisms and the maximum segment sum problem. In: Joubert, G.R., Trystram, D., Peters, F.J., Evans, D.J. (eds.) Parallel Computing: Trends and Applications, PARCO 1993, pp. 489–492. Elsevier (1994)
Daum, M.: Reasoning on Data-Parallel Programs in Isabelle/Hol. In: C/C++ Verification Workshop (2007). http://www.cse.unsw.edu.au/rhuuck/CV07/program.html
Dean, J., Ghemawat, S.: MapReduce: simplified data processing on large clusters. In: OSDI, pp. 137–150. USENIX Association (2004)
Dosch, W., Wiedemann, B.: List homomorphisms with accumulation and indexing. In: Michaelson, G., Trinder, P., Loidl, H.W. (eds.) Trends in Functional Programming, pp. 134–142. Intellect (2000)
Emoto, K., Fischer, S., Hu, Z.: Filter-embedding semiring fusion for programming with MapReduce. Formal Aspects Comput. 24(4–6), 623–645 (2012). https://doi.org/10.1007/s00165-012-0241-8
Emoto, K., Loulergue, F., Tesson, J.: A verified generate-test-aggregate Coq library for parallel programs extraction. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 258–274. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08970-6_17
Fang, R., Pouyanfar, S., Yang, Y., Chen, S.C., Iyengar, S.S.: Computational health informatics in the big data age: a survey. ACM Comput. Surv. 49(1), 1–36 (2016). https://doi.org/10.1145/2932707
Filliâtre, J.-C., Marché, C.: The why/Krakatoa/Caduceus platform for deductive program verification. In: Damm, W., Hermanns, H. (eds.) CAV 2007. LNCS, vol. 4590, pp. 173–177. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73368-3_21
Gava, F., Fortin, J., Guedj, M.: Deductive verification of state-space algorithms. In: Johnsen, E.B., Petre, L. (eds.) IFM 2013. LNCS, vol. 7940, pp. 124–138. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38613-8_9
Gesbert, L., Hu, Z., Loulergue, F., Matsuzaki, K., Tesson, J.: Systematic development of correct bulk synchronous parallel programs. In: Parallel and Distributed Computing, Applications and Technologies (PDCAT), pp. 334–340. IEEE (2010). https://doi.org/10.1109/PDCAT.2010.86
Gibbons, J.: The third homomorphism theorem. J. Funct. Program. 6(4), 657–665 (1996). https://doi.org/10.1017/S0956796800001908
Gorlatch, S., Bischof, H.: Formal derivation of divide-and-conquer programs: a case study in the multidimensional FFT’s. In: Mery, D. (ed.) Formal Methods for Parallel Programming: Theory and Applications, pp. 80–94 (1997)
Hill, J.M.D., et al.: BSPlib: the BSP programming library. Parallel Comput. 24, 1947–1980 (1998)
Hu, Z., Iwasaki, H., Takeichi, M.: Construction of list homomorphisms by tupling and fusion. In: Penczek, W., Szałas, A. (eds.) MFCS 1996. LNCS, vol. 1113, pp. 407–418. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61550-4_166
Hu, Z., Takeichi, M., Iwasaki, H.: Diffusion: calculating efficient parallel programs. In: ACM SIGPLAN Workshop on Partial Evaluation and Semantics-Based Program Manipulation (PEPM 1999), pp. 85–94. ACM (1999)
Hu, Z., Iwasaki, H., Takeichi, M.: Formal derivation of efficient parallel programs by construction of list homomorphisms. ACM Trans. Program. Lang. Syst. 19(3), 444–461 (1997). https://doi.org/10.1145/256167.256201
Lämmel, R.: Google’s MapReduce programming model - revisited. Sci. Comput. Program. 70(1), 1–30 (2008). https://doi.org/10.1016/j.scico.2007.07.001
Leroy, X., Doligez, D., Frisch, A., Garrigue, J., Rémy, D., Vouillon, J.: The OCaml system release 5.00 (2022). https://v2.ocaml.org/manual/
Letouzey, P.: Extraction in Coq: an overview. In: Beckmann, A., Dimitracopoulos, C., Löwe, B. (eds.) CiE 2008. LNCS, vol. 5028, pp. 359–369. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-69407-6_39
Loulergue, F.: A BSPlib-style API for bulk synchronous parallel ML. Scalable Comput. Pract. Experience 18, 261–274 (2017). https://doi.org/10.12694/scpe.v18i3.1306
Loulergue, F.: A verified accumulate algorithmic skeleton. In: Fifth International Symposium on Computing and Networking (CANDAR), pp. 420–426. IEEE, Aomori, Japan (2017). https://doi.org/10.1109/CANDAR.2017.108
Loulergue, F., Bousdira, W., Tesson, J.: Calculating parallel programs in Coq using list homomorphisms. Int. J. Parallel Prog. 45(2), 300–319 (2016). https://doi.org/10.1007/s10766-016-0415-8
Loulergue, F., Gava, F., Billiet, D.: Bulk synchronous parallel ML: modular implementation and performance prediction. In: Sunderam, V.S., van Albada, G.D., Sloot, P.M.A., Dongarra, J.J. (eds.) ICCS 2005. LNCS, vol. 3515, pp. 1046–1054. Springer, Heidelberg (2005). https://doi.org/10.1007/11428848_132
Loulergue, F., Philippe, J.: Towards verified scalable parallel computing with Coq and Spark. In: Proceedings of the 25th ACM International Workshop on Formal Techniques for Java-like Programs (FTfJP), pp. 11–17. ACM, New York, NY, USA (2023). https://doi.org/10.1145/3605156.3606450
Loulergue, F., Robillard, S., Tesson, J., Légaux, J., Hu, Z.: Formal derivation and extraction of a parallel program for the all nearest smaller values problem. In: ACM Symposium on Applied Computing (SAC), pp. 1577–1584. ACM, Gyeongju, Korea (2014). https://doi.org/10.1145/2554850.2554912
Malewicz, G., et al.: Pregel: a system for large-scale graph processing. In: SIGMOD, pp. 135–146. ACM (2010). https://doi.org/10.1145/1807167.1807184
Matsuzaki, K.: Functional models of hadoop mapreduce with application to scan. Int. J. Parallel Prog. 45(2), 362–381 (2016). https://doi.org/10.1007/s10766-016-0414-9
Minsky, Y.: OCaml for the masses. Commun. ACM 54(11), 53–58 (2011). https://doi.org/10.1145/2018396.2018413
Morihata, A., Matsuzaki, K., Hu, Z., Takeichi, M.: The third homomorphism theorem on trees: downward & upward lead to divide-and-conquer. In: Shao, Z., Pierce, B.C. (eds.) POPL 2009, pp. 177–185. ACM (2009). https://doi.org/10.1145/1480881.1480905
Morihata, A.: Calculational developments of new parallel algorithms for size-constrained maximum-sum segment problems. In: Schrijvers, T., Thiemann, P. (eds.) FLOPS 2012. LNCS, vol. 7294, pp. 213–227. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29822-6_18
Mu, S., Ko, H., Jansson, P.: Algebra of programming in Agda: dependent types for relational program derivation. J. Funct. Program. 19(5), 545–579 (2009). https://doi.org/10.1017/S0956796809007345
Odersky, M., Spoon, L., Venners, B.: Programming in Scala, 2nd edn. Artima, Walnut Creek (2010)
Ono, K., Hirai, Y., Tanabe, Y., Noda, N., Hagiya, M.: Using Coq in specification and program extraction of hadoop mapreduce applications. In: Barthe, G., Pardo, A., Schneider, G. (eds.) SEFM 2011. LNCS, vol. 7041, pp. 350–365. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24690-6_24
Skillicorn, D.B., Hill, J.M.D., McColl, W.F.: Questions and answers about BSP. Sci. Program. 6(3), 249–274 (1997)
Smith, D.R.: Applications of a strategy for designing divide-and-conquer algorithms. Sci. Comput. Program. 8(3), 213–229 (1987). https://doi.org/10.1016/0167-6423(87)90034-7
Snir, M., Gropp, W.: MPI the Complete Reference. MIT Press, Cambridge (1998)
Swierstra, W.: More dependent types for distributed arrays. Higher-Order Symbolic Comput. 23(4), 489–506 (2010). https://doi.org/10.1007/s10990-011-9075-y
Valiant, L.G.: A bridging model for parallel computation. Commun. ACM 33(8), 103 (1990). https://doi.org/10.1145/79173.79181
Acknowledgments
We wish to thank the reviewers for their suggestions and highlighting some typos.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Loulergue, F., Ed-Dbali, A. (2024). Verified High Performance Computing: The SyDPaCC Approach. In: Ben Hedia, B., Maleh, Y., Krichen, M. (eds) Verification and Evaluation of Computer and Communication Systems. VECoS 2023. Lecture Notes in Computer Science, vol 14368. Springer, Cham. https://doi.org/10.1007/978-3-031-49737-7_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-49737-7_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-49736-0
Online ISBN: 978-3-031-49737-7
eBook Packages: Computer ScienceComputer Science (R0)







 corresponds to a type
corresponds to a type
 if there exists a surjective function
if there exists a surjective function
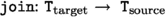 . We note
. We note

 such a type correspondence. Intuitively, the
such a type correspondence. Intuitively, the
 function is surjective because we want the target type to have at least the same expressive power than the source type. If the source type is
function is surjective because we want the target type to have at least the same expressive power than the source type. If the source type is
 and target type is a distributed type such as
and target type is a distributed type such as
 , there are many ways a sequential list could be distributed into a parallel vector of lists.
, there are many ways a sequential list could be distributed into a parallel vector of lists.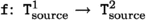 corresponds to
corresponds to
 if
if

 and
and

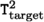 and the following property holds:
and the following property holds: 

