Strong Edge Coloring of Subquartic Graphs

Abstract

A strong k-edge coloring of a graph G is a mapping $c: E(G)\rightarrow \{1,2,3,...,k\}$ such that for any two edges e and $e'$ with distance at most two, $c(e)\ne c(e')$. The strong chromatic index of G, written $\chi '_s(G)$, is the smallest integer k such that G has a strong k-edge coloring. In this paper, using color exchange method and discharging method, we prove that for a subquartic graph G, $\chi _s'(G)\le 11$ if $mad(G)<\frac{8}{3}$, where $mad(G)=\max \{\frac{2|E(G)|}{|V(G)|},H\subseteq G\}$.

1 Introduction

To solve the Channel Assignment Problem in wireless communication networks, Fouquet and Jolivet [8] first introduced the notion of strong edge coloring in 1983. A strong k-edge coloring of a graph G is a mapping $c: E(G)\rightarrow \{1,2,3,\cdots ,k\}$ such that $c(e)\ne c(e')$ for any two edges e and $e'$ with distance at most two. The smallest integer k such that G has a strong k-edge coloring of G is called the strong chromatic index of G, written $\chi _s'(G)$. By greedy algorithm, it is easy to see that $2\varDelta ^{2}-2\varDelta +1$ is a trivial upper bound on $\chi _s'(G)$, where $\varDelta$ is the maximum degree of G. However, it is NP-complete to decide wether $\chi _s'(G)=k$ holds for a general graph G [14]. In 1989, Erdős and Nešetřil [7] proposed the following important conjecture while studying the strong edge coloring of graphs.

Conjecture 1

[7] For any graph G with maximum degree $\varDelta$, $\chi _{s}'(G)\le \frac{5}{4}\varDelta ^{2}$ if $\varDelta$ is even, $\chi _{s}'(G)\le \frac{5}{4}\varDelta ^{2}-\frac{1}{2}\varDelta +\frac{1}{4}$ if $\varDelta$ is odd.

In [7], Erdős and Nešetřil constructed two classes of graphs satisfying $\chi _{s}'(G)=\chi '(G)=|E(G)|$ while |E(G)| attains the upper bound in Conjecture 1. This illustrate that the upper bound is sharp if Conjecture 1 is true. Also, they asked a question: For a general graph G, is there any positive number $\varepsilon$ such that $\chi _{s}'(G)\le (2-\epsilon )\varDelta ^{2}$, where $\varDelta$ is the maximum degree of G. As yet, there are many research results on strong edge coloring. For a graph G with sufficient large $\varDelta$, Molloy and Reed [15] proved that $\chi _{s}'(G)\le 1.998\varDelta ^{2}$ using probabilistic methods. In the next decides, this result was improved to $1.93\varDelta ^{2}$ by Bruhn and Joos [4], $1.835\varDelta ^{2}$ by Bonamy, Perrett and Postle [3]. For graphs with small $\varDelta$, scholars also made a lot of research works. It is an obvious result that $\chi _{s}'(G)\le 5=\frac{5}{4}\varDelta ^{2}$ while $\varDelta =2$. For subcubic graphs, the above conjecture was verified by Andersen [1], and independently by Horák, Qing, Trotter [10]. For subquartic graphs, $\chi _{s}'(G)\le 22$ was proven by Cranston [6] using algorithms. Huang, Santana and Yu [11] reduced 22 to 21. For graphs with $\varDelta =5$, Zang [18] confirmed that $\chi _{s}'(G)\le 37$.

For graphs with maximum average degree restriction, there are also a mount of results. The maximum average degree of a graph G, written mad(G), is the largest average degree of its subgraph. In other words, $mad(G)=\max \{\frac{2|E(H)|}{|V(H)|}:H\subseteq G\}$. In 2013, Hocquard [9] studied the strong chromatic index of subcubic graphs with maximum average degree and obtained the following theorem.

Theorem 1

[9] Let G be a graph with $\varDelta (G)=3$.

• (1) If $mad(G)<\frac{7}{3}$, then $\chi '_{s}(G)\le 6$;

• (2) If $mad(G)<\frac{5}{2}$, then $\chi '_{s}(G)\le 7$;

• (3) If $mad(G)<\frac{8}{3}$, then $\chi '_{s}(G)\le 8$;

• (4) If $mad(G)<\frac{20}{7}$, then $\chi '_{s}(G)\le 9$.

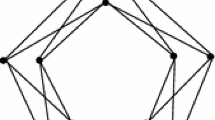
The given upper bound on mad(G) in Theorem 1(1)(2)(4) is optimal since there exist subcubic graphs with $mad(G)=\frac{7}{3}$ (or $mad(G)=\frac{5}{2}, \frac{20}{7}$) and $\chi _s'(G)>6$ (or $\chi _s'(G)>7,9$), see Fig. 1.

Fig. 1.

$mad(G)=\frac{7}{3}$ (or $\frac{5}{2}, \frac{20}{7}$) and  $\chi _s'(G)=7$ (or $\chi _s'(G)=8, 10$)

For subquartic graphs with bounded maximum average degree, Lv et al. [13] gave out the following theorem, which improved the corresponding upper bound on mad(G) due to Bensmail et al. [2].

Theorem 2

[13] Let G be a graph with $\varDelta (G)=4$.

• (1) If $mad(G)<\frac{61}{18}$, then $\chi _s'(G)\le 16$;

• (2) If $mad(G)<\frac{7}{2}$, then $\chi _s'(G)\le 17$;

• (3) If $mad(G)<\frac{18}{5}$, then $\chi _s'(G)\le 18$;

• (4) If $mad(G)<\frac{26}{7}$, then $\chi _s'(G)\le 19$;

• (5) If $mad(G)<\frac{51}{13}$, then $\chi _s'(G)\le 20$.

Ruksasakchai and Wang [17] studied the strong edge coloring of graphs with $\varDelta (G)\le 4$ and $mad(G)<3$ and obtained the following theorem.

Theorem 3

[17] If G is a graphs G with maximum degree $\varDelta \le 4$ and $mad(G)<3$, then $\chi _{s}'(G)\le 3\varDelta +1$.

For graphs with maximum degree 5 and bounded maximum average degree, Qin et al. [16] obtained the following theorem.

Theorem 4

[16] Let G be a graph with $\varDelta (G)=5$.

• (1) If $mad(G)<\frac{8}{3}$, then $\chi _s'(G)\le 13$;

• (2) If $mad(G)<\frac{14}{5}$, then $\chi _s'(G)\le 14$.

Additionally, Choi et al. [5] studied the strong edge coloring of graphs with maximum degree $\varDelta \ge 7$ and bounded maximum average degree. They obtained a theorem as follows.

Theorem 5

[5] Let G be a graph with maximum degree $\varDelta$.

• (1) If $\varDelta \ge 9$ and $mad(G)<\frac{8}{3}$, then $\chi _s'(G)\le 3\varDelta -3$;

• (2) If $\varDelta \ge 7$ and $mad(G)<3$, then $\chi _s'(G)\le 3\varDelta$.

Recently, Li et al. [12] studied the strong edge coloring of graphs with maximum degree $\varDelta \ge 6$ and bounded maximum average degree. The following theorem is given in [12].

Theorem 6

[12] Let G be a graph with maximum degree $\varDelta$.

• (1) If $\varDelta \ge 6$ and $mad(G)<\frac{23}{8}$, then $\chi _s'(G)\le 3\varDelta -1$;

• (2) If $\varDelta \ge 7$ and $mad(G)<\frac{26}{9}$, then $\chi _s'(G)\le 3\varDelta -1$.

In this paper, we further consider the strong edge coloring of subquartic graphs by using color exchange method and discharging method. We obtained the following theorem.

Theorem 7

If G is a graph with $\varDelta (G)=4$ and $mad(G)<\frac{8}{3}$, then $\chi '_{s}(G)\le 11$.

Fig. 2.

Subquartic graphs.

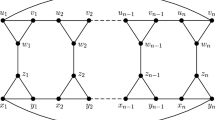
$G_1, G_2, G_3$ in Fig. 2 are subquartic graphs, where $mad(G_1)=\frac{8}{3}$, $\chi _s'(G_1)=10$; $mad(G_2)=\frac{20}{7}$, $\chi _s'(G_2)=11$ and $mad(G_3)=3$, $\chi _s'(G_3)=12$ (we can take the graph obtained from $G_1$ by deleting two 1-vertices, $G_2$ by deleting the 1-vertex and $G_3$ as subgraphs, respectively). We do not know whether the upper bound $mad(G)<\frac{8}{3}$ in Theorem 7 is optimal. However, due to the graph $G_3$ in Fig. 2, we know that there exists a graph G with $\varDelta (G)=4$, $mad(G)=3$ and $\chi '_{s}(G)=12$.

For the strong edge coloring of subquartic graphs, Theorem 2 gives out some sufficient conditions for $\chi '_{s}(G)\le 16$ (respectively 17,18,19,20). Theorem 3 indicates that any graph G with $\varDelta (G)=4$ and $mad(G)<3$ satisfies $\chi '_{s}(G)\le 13$. Therefore, Theorem 7 enriches the results of strong edge coloring for subquartic graphs.

2 Notations

All graphs considered here are finite undirected simple graphs. For a graph G, V(G), E(G), $\varDelta (G)$ and $\delta (G)$ denote its vertex set, edge set, maximum degree and minimum degree respectively. For $v\in V(G)$, $d_G(v)$ (abbreviated by d(v)) denotes the degree of v in G. v is a i (or $i^+$, $i^-$)-vertex if $d(v)=i$ (or $d(v)\ge i$, $d(v)\le i$). For a vertex v, a i-neighbor of v is a i-vertex in N(v). A $i_j$-vertex is a i-vertex adjacent to exactly j 2-vertices. A 2-vertex is bad if it is adjacent to a 2-vertex, semi-bad if it is adjacent to a $3_2$-vertex. A 2-vertex is good if it is neither bad nor semi-bad. For an edge e, F(e) denotes the set of forbidden colors for it.

3 Proof of Theorem 7

Suppose G is a counterexample with minimum $2^{+}$-vertices and then with minimum edges. Let H be the graph obtained from G by deleting all 1-vertices. Obviously, $H\subseteq G$ and then $mad(H)\le mad(G)<\frac{8}{3}$. In the following, we first illustrate some properties of H.

Lemma 1

H does not have vertices of degree 1.

Proof

Suppose v is a 1-vertex in H and $uv\in E(H)$. Since H is the graph obtained from obtained from G by deleting all 1-vertices, $d_G(v)>1$ and v has at least one 1-neighbor $v_1$ in G. Compared with G, $G-v_1$ has the same $2^{+}$-vertices but fewer edges. By the minimality of G, $\chi _s'(G-v_1)\le 11$. Note that in G, $|F(vv_1)|\le 6$. Thus, $vv_1$ can be colored, which leads to a contradiction.

Lemma 2

If $d_H(v)=2$, then $d_G(v)=2$.

Proof

Suppose $d_G(v)>2$. Then, v has at least one 1-neighbor $v_1$ in G. Compared with G, $G-v_1$ has fewer edges while the same $2^{+}$-vertices. By the minimality of G, $\chi _s'(G-v_1)\le 11$. Note that in G, $|F(vv_1)|\le 9$. Thus, $vv_1$ can be colored, which leads to a contradiction.

Lemma 3

If v is a $3_i$-vertex in H, where $i\ge 1$, then $d_G(v)=3$.

Proof

Suppose $d_G(v)>3$. Then, v has at least one 1-neighbor $v'$ in G. Let $v_1$ be a 2-neighbor of v in H, By Lemma 2, $d_G(v_1)=2$. Let $G'=G-v'$. Compared with G, $G'$ has the same $2^{+}$-vertices but fewer edges. By the minimality of G, $\chi _s'(G-v_1)\le 11$. Note that in G, $|F(vv')|\le 10$. Thus, $vv'$ can be colored, which leads to a contradiction.

Lemma 4

Every bad vertex in H is adjacent to a 4-vertex.

Proof

Suppose v is a bad vertex in H and it is adjacent to a 2-vertex u and a $3^{-}$-vertex w. By Lemma 2, $d_G(u)=d_G(v)=2$. Denote $N_G(u)=\{u_1,v\}$. Note that $2\le d_H(w)\le 3$. If $d_H(w)=2$, then $d_G(w)=2$ by Lemma 2. If $d_H(w)=3$, then by Lemma 3, $d_G(w)=3$ since $d_H(v)=2$. Let $G'=G-uv+ww_1$, where $ww_1$ is a pendent edge incident with w. Note that $3\le d_{G'}(w)\le 4$ and $G'$ has fewer $2^{+}$-vertices than G. By the definition of maximum average degree, $mad(G')<2$ if $mad(G)<2$ and $mad(G')\le mad(G)<\frac{8}{3}$ if $2\le mad(G)<\frac{8}{3}$. By the minimality of G, $\chi _s'(G')\le 11$. Let c be a strong 11-edge coloring of $G'$. Note that in G, $|F(uv)|\le 8$. If $c(uu_1)\ne c(vw)$, then uv can be colored, which is a contradiction. If $c(uu_1)=c(vw)$, then we first exchange the colors on pendant edges wv and $ww_1$ in $G'$. After that, uv can be colored, which leads to a contradiction.

Fig. 3.

.

Fig. 4.

.

Fig. 5.

.

Lemma 5

H does not have $3_3$-vertices.

Proof

Suppose v is a $3_3$-vertex in H and $N_H(v)=\{v_1,v_2,v_3\}$. By Lemma 2, $d_G(v_i)=2$, $i=1,2,3$. By Lemma 3, $d_G(v)=3$. Let $G'=G-v$. Note that $G'$ has fewer $2^{+}$-vertices than G. By the minimality of G, $\chi _s'(G')\le 11$. Note that in G, $|F(vv_i)|\le 6$, $i=1,2,3$, $vv_i$ can be colored, which is a contradiction.

Lemma 6

Every semi-bad vertex in H is adjacent to a 4-vertex.

Proof

Suppose v is a semi-bad vertex in H and it is adjacent to a $3_2$-vertex u and a $3^{-}$-vertex w. Let $N_H(u)=\{u_1,u_2,v\}$, where $d_H(u_1)=2$ (see Fig. 3). By Lemma 2, $d_G(u_1)=d_G(v)=2$. By Lemma 3, $d_G(u)=3$. Note that $2\le d_H(w)\le 3$ and $d_H(v)=2$, we have $d_G(w)=d_H(w)$ by Lemma 2 and Lemma 3. Let $G'=G-uv+ww_1$, where $ww_1$ is a pendant edge incident with w. Note that $G'$ has fewer $2^{+}$-vertices than G, by the definition of maximum average degree, $mad(G')<2$ if $mad(G)<2$ and $mad(G')\le mad(G)<\frac{8}{3}$ if $2\le mad(G)<\frac{8}{3}$. By the minimality of G, $\chi _s'(G')\le 11$. Let c be a strong 11-edge coloring of $G'$. Erase on color on $uu_1$. Note that in G, $|F(uu_1)|\le 9$, $|F(uv)|\le 9$. If $c(uu_2)\ne c(vw)$, then $uu_1, uv$ can be colored, which is a contradiction. If $c(uu_2)=c(vw)$, then we first exchange the colors on pendant edges wv and $ww_1$ in $G'$. After that, $uu_1$ and uv can be colored, which leads to a contradiction.

Lemma 7

Let v be a $4_i$-vertex in H, where $i\ge 3$. Then its 2-neighbors are all good vertices.

Proof

Suppose that $v_1, v_2, v_3$ are 2-neighbors of v and at least one of them is not good. Without loss of generality, we assume that $v_1$ is not a good vertex. This implies that $v_1$ is adjacent to a 2-vertex or a $3_2$-vertex.

If $v_1$ is adjacent to a 2-vertex u (see Fig. 4), then by Lemma 2, $d_G(v_i)=d_G(u)=2$, $i=1,2,3$. Let $G'=G-v_1$. Note that $G'$ has fewer $2^{+}$-vertices than G. By the minimality of G, $\chi _s'(G')\le 11$. Note that in G, $|F(uv_1)|\le 7$, $|F(vv_1)|\le 9$, $uv_1, vv_1$ can be colored, which is a contradiction.

If $v_1$ is adjacent to a $3_2$-vertex $v_1'$ and $u\ne v_1$ is the other 2-neighbor of $v_1'$ (see Fig. 5). By Lemma 2, $d_G(v_i)=d_G(u)=2$, $i=1,2,3$. By Lemma 3, $d_G(v_1')=3$. Let $G'=G-v_1$. Note that $G-v_1$ has fewer $2^{+}$-vertices than G. By the minimality of G, $\chi _s'(G')\le 11$. Note that in G, $|F(v_1v_1')|\le 9$, $|F(vv_1)|\le 10$. Thus, $vv_1, v_1v_1'$ can be colored in order, which is a contradiction.

Proof of Theorem 7:  We define weight function $w(v)=d(v)$ for each $v\in V(H)$ and we define five discharging rules R1-R5 as follows. Let $w'(v)$ be the final weight function while discharging finished. As we know, the sum weigh is fixed. However, we shall prove that $w'(v)\ge \frac{8}{3}$ for each $v\in V(H)$. This will lead to a contradiction as follow.

$$\frac{8}{3}|V(H)|\le \sum \limits _{v\in V(H)} w'(v) =\sum \limits _{v\in V(H)} w(v)\le mad(H)|V(H)|<\frac{8}{3}|V(H)|.$$

Discharging Rules:

R1 Each 4-vertex gives $\frac{2}{3}$ to each adjacent bad vertex.

R2 Each 4-vertex gives $\frac{1}{2}$ to each adjacent semi-bad vertex.

R3 Each 4-vertex gives $\frac{1}{3}$ to each adjacent good vertex.

R4 Each $3_2$-vertex gives $\frac{1}{6}$ to each adjacent semi-bad vertex.

R5 Each $3_1$-vertex gives $\frac{1}{3}$ to each adjacent good vertex.

In the following, we shall verify that $w'(v)\ge \frac{8}{3}$ for each $v\in V(H)$.

By Lemma 1, $\delta (H)\ge 2$.

• $d(v)=2$

If v is bad, then by Lemma 4, v is adjacent to a 4-vertex. By R1, $w'(v)=2+\frac{2}{3}=\frac{8}{3}$.

If v is semi-bad, then by Lemma 6, v is adjacent to a 4-vertex. By R2 and R4, $w'(v)=2+\frac{1}{2}+\frac{1}{6}=\frac{8}{3}$.

If v is good, then by the definition of good vertex and Lemma 5, each neighbor of v is either $3_1$-vertex or 4-vertex. By R3 and R5, $w'(v)=2+\frac{1}{3}\times 2=\frac{8}{3}$.

• $d(v)=3$

By Lemma 5, v is $3_i$-vertex, where $0\le i\le 2$.

If v is a $3_2$-vertex, then by R4, $w'(v)\ge 3-\frac{1}{6}\times 2=\frac{8}{3}$.

If v is a $3_1$-vertex, then by R5, $w'(v)\ge 3-\frac{1}{3}=\frac{8}{3}$.

If v is a $3_0$-vertex, then $w'(v)=w(v)=3$.

• $d(v)=4$

If v is a $4_i$-vertex, where $i\ge 3$, then by Lemma 7, the 2-neighbors of v are good. Thus, $w'(v)\ge 4-\frac{1}{3}\times 4=\frac{8}{3}$ by R3.

If v is a $4_i$-vertex, where $0\le i\le 2$, then by R1-R3, $w'(v)\ge 4-\frac{2}{3}\times 2=\frac{8}{3}$.

Therefore, for each $v\in V(H)$, $w'(v)\ge \frac{8}{3}$ and the proof of Theorem 7 is finished.   $\square$

4 Further Considered Problems

Theorem 7 illustrates that $\chi '_{s}(G)\le 11$ holds for any graph G with $\varDelta (G)=4$ and $mad(G)<\frac{8}{3}$. For the graph $G_3$ in Fig. 2, it satisfies that $\varDelta (G_3)=4$, $mad(G_3)=3$ and $\chi '_{s}(G_3)=12$. Then a question follows out naturally. What is the supremum M such that any graph G with $\varDelta (G)=4$ and $mad(G)< M$ satisfying $\chi '_{s}(G)\le 11$?