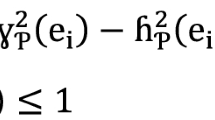Keywords

Mathematics Subject Classification

1 Introduction

Yager [1] proposed the fundamental theory of Pythagorean fuzzy sets (PyFS) to address the shortcoming of Intuitionistic (InFS) fuzzy sets [1, 2], i.e., when the sum of membership (MBV) Ψ value and non-membership (NMBV) π value is more than one, i.e., Ψ + π > 1 (0.7 + 0.6 > 1). MBV and NMBV in a Pythagorean fuzzy set satisfy the requirement Ψ2 + π2 ≤ 1. Since the PyFS membership value domain is larger than the InFS membership value domain, this impression has a wider range than InFS. It is a controlling mechanism to communicate confusing thoughts. Compared to other fuzzy models, it offers more flexibility in dealing with decision-making in the actual world. Yager [1, 2] and Yager and Abbasov [3] investigated the fundamental ideas behind PyFS and clarified the connection between PyFNs and complex numbers. After that, a variety of Pythagorean fuzzy aggregation operators, including PyFWAO, are also suggested. Zhang and Xu [4] then explained the fundamental mathematical procedures for PyFNs. For the selection of the location of distribution centres, a variety of models and approaches, including fuzzy logic, mathematical models, heuristic meta-heuristic methods, and the multi-criteria decision-making (MCDM) method, have recently been developed [5]. The selection difficulties, however, typically include a wide range of qualitative and quantitative factors. Applying MCDM approaches to create MCDM models is thus a workable solution to such issues. To help decision-makers choose the best distribution centre, a variety of MCDM techniques are available, including AHP, VIKOR, ELECTRE, PROMETHEE, ANP, DEMATEL, WASPAS, and TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution). The current market’s fierce competition has forced companies to concentrate on and increase their investments in logistics networks. As a result, researchers and practitioners are increasingly focused on finding ways to reduce logistics expenses and boost the effectiveness of logistics processes [6]. Distribution centres are important nodes in the logistics network that link all logistics-related activities [7]. Therefore, in order to effectively manage the logistics operations and develop the logistics network, it is crucial to handle the logistics distribution centre. The efficiency of a logistics distribution centre is influenced by various factors. One of them, the logistics distribution site, has the biggest impact on the enterprise’s overall management costs since it influences the optimization of the logistics distribution system. In order to reduce expenditures and increase profits in a logistics system, it is crucial to select an appropriate distribution centre location [8]. But there isn’t enough data to suggest a thorough distribution centre placement and selection model for the logistics sector. This study attempted to construct a hybrid model based on a novel Pythagorean fuzzy entropy measure and the TOPSIS approach to aid in the selection of a distribution centre site. Thus, an integrated entropy-TOPSIS approach is used to compute criterion weights and select the best location for the distribution centre. One of the key objectives of any site selection is to identify the most suitable location that could minimize the total costs. In their research, Agrebi et al. [9] employed the ELECTRE I approach in their study to examine the choice of distribution facilities.

Distribution centre location selection is a significant process in any business and should be done with care. The process of selecting a location for a distribution centre can involve a variety of criteria, such as proximity to customers, access to transportation networks, availability of resources, and cost. To effectively evaluate these factors, the decision-makers must have a comprehensive understanding of the method of decision-making. Accordingly, a literature review of the selection of distribution centre locations can provide useful insight into the various factors that must be considered.

The TOPSIS approach was first introduced by C.L. Hwang and K. Yoon in 1981. This approach successfully addresses the issue of ranking the alternatives. The TOPSIS approach and fuzzy set theory are thus frequently coupled to address problems involving multiple criteria decision-making (MCDM). Han et al. [10] modified the TOPSIS method using entropy and linguistically hesitant Pythagorean fuzzy sets to assess the contribution rates of WSoS- weapon system-of-systems. In order to evaluate the ranks and risk, Akram et al. [11] used the ELECTRE-I technique in a hesitant Pythagorean fuzzy setting. Ulutaş et al. [12] attempted to address the logistic centre location problem for Siva province in Turkey by applying the MCDM model with fuzzy SWARA and the CoCoSo method. Shafiee et al. [13] employed Pythagorean fuzzy sets with the DEMATEL method to analyse the risk of the consumable product supply chain network during the COVID-19 outbreak. Erdogan and Ayyildiz [14] applied novel AHP-integrated EDAS technology to evaluate pharmaceutical warehouse location selection to address pandemic conditions. Sagnak et al. [15] found transportation cost to be the most important criteria by applying fuzzy best-worst and TOPSIS methods, among several other criteria such as land cost, storage cost, energy cost, investment, etc., in the selection of sustainable collection centres. Yang et al. [16] applied the Pythagorean fuzzy MULTIMOORA method for determining complex criteria weights and selecting the electric vehicle power battery. Yin et al. [17] used IVPyFN to deal with the uncertainty concerning sustainability in rail transit photovoltaic power station site selection, and IVPyFN-TOPSIS was used to aggregate the decision matrix. The Stepwise Weight Assessment Ratio Analysis (SWARA)-TOPSIS in Pythagorean fuzzy environment approach, according to Saeidi et al. [18], is extremely successful and capable of handling the Sustainable Human Resource Management issue in manufacturing organizations. Based on an evaluation model based on Pythagorean fuzzy sets and the TOPSIS method, Li et al. [19] construct an evaluation index system with four aspects using the dispatching results of power systems with a high proportion of renewable energy under four different dispatching modes as the evaluation object. Ayyildiz [20] applied Pythagorean fuzzy SWARA and Pythagorean fuzzy CODAS to estimate the location of the charging station for an electric scooter. Using an integrated methodology based on entropy, Complex Proportional Assessment (COPRAS), and Step-wise Weight Assessment Ratio Analysis (SWARA) methodologies in a Pythagorean fuzzy environment, Alipour et al. [22] addressed supplier selection for fuel cells paired with hydrogen FCH. The supplier selection problem was solved by Yu et al. [23] using the extended fuzzy TOPSIS approach in an interval-valued Pythagorean setting. Parveen et al. [24, 25] applied the entropy-TOPSIS approach to the MCDM problem of selecting an online payment system and ranking the academic institute. Han et al. [26] solved the MCDM problem using TOPSIS based on entropy for Linguistic Pythagorean fuzzy soft sets. The research review indicates that PyFSs are better functionally equipped than InFSs to deal with uncertainty in difficult real-world decision-making situations. As a result, the standard TOPSIS technique that corresponds to the proposed entropy measure in PyFS was expanded in this article. This method is really straightforward and simple to comprehend. The traditional TOPSIS technique has been applied to a wider spectrum of issues. Although several MCDM approaches have been created under the PyFS environment, there have been few studies using PyFS entropy and the TOPSIS approach to evaluate the location of distribution centres. In order to solve this issue, this chapter provides the integrated entropy-TOPSIS technique, which may be used to examine the implicit uncertainty and ambiguity connected to the decision maker’s perspective. Here is a quick synopsis of this chapter:

  1. 1.

    A novel PyFS entropy metric is suggested, and it is contrasted with the existing ones.

  2. 2.

    The Integrated Entropy-TOPSIS approach combines Entropy and the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), two well-known MCDM techniques. While TOPSIS is used to rank the alternatives according to how well they perform on the criteria, entropy is used to assign weights to the criteria based on their relative importance.

  3. 3.

    Use the new Pythagorean entropy measure to determine the decision experts’ weights in PyFS.

  4. 4.

    Calculate the criteria weights using the suggested entropy.

  5. 5.

    A Pythagorean fuzzy-integrated entropy-TOPSIS model has been utilized to solve the multi-criteria decision-making problem of selecting the location of a sustainable distribution centre.

  6. 6.

    A comparison of the suggested method with the existing methodologies is provided to demonstrate the precision and practicality of the integrated PyF entropy-TOPSIS approach.

This chapter is divided into five sections: Section 1 is devoted to the introduction and literature review. Section 2 presents the fundamental principles and preliminary concepts in relation to Pythagorean fuzzy sets. Section 3 proposes the novel entropy measure and proves its validity. Further, Sect. 4 presents the Pythagorean fuzzy MCDM algorithm based on Entropy-TOPSIS and discusses its application to the problem of distribution centre location selection. Section 5 discusses the result and the conclusion.

2 Preliminaries

This section goes through the fundamental definitions of fuzzy sets, intuitionistic fuzzy sets, and Pythagorean fuzzy sets. Some of the PyFS features, operations, and existing entropy measures employed in this chapter are also discussed.

Definition 1

[21] An InFS ξ in C is defined as the following:

$$ \xi =\left\{\left\langle b\right.,{\mu}_{\textrm{p}}\left.(b),{\nu}_{\textrm{p}}(b)\right\rangle \left|b\in \textrm{C}\right.\right\} $$
(1)

where

$$ 0\le {\mu}_{\textrm{p}}(b)+{\nu}_{\textrm{p}}(b)\le 1\forall b\in \textrm{C} $$
(2)

and the functions μp(b) : C → [0, 1] denote the degree of membership and νp(b) : C → [0, 1] denote the degree of non-membership of b in C. The degree of indeterminacy of b in C indicated by λ and defined as

$$ {\lambda}_{\textrm{p}}(b)=1-\left\{{\mu}_{\textrm{p}}(b)+{\nu}_{\textrm{p}}(b)\ \right\} $$
(3)

Definition 2

A PyFS proposed by Yager [1] in finite universe of discourse C is an object having the Form

$$ \xi =\left\{\left\langle b\right.,{\mu}_{\textrm{p}}\left.(b),{\nu}_{\textrm{p}}(b)\right\rangle \left|b\in \textrm{C}\right.\right\} $$

where

$$ 0\le {\mu}_{\textrm{p}}^2(b)+{\nu}_{\textrm{p}}^2(b)\le 1\forall b\in \textrm{C} $$
(4)

and the functions μp(b) : C → [0, 1] denote the degree of membership and νp(b) : C → [0, 1] denote the degree of non-membership of b in C. The degree of indeterminacy of b in C is denoted by λ and defined as

$$ {\lambda}_{\textrm{p}}(b)=\sqrt{1-\left\{{\mu}_{\textrm{p}}^2(b)+{\nu}_{\textrm{p}}^2(b)\right\}} $$
(5)

Definition 3

[1, 4] Let P = (μp(b), νp(b) ) and Q = (μq(b), νq(b) ) be two PyFN, then

  1. (a)

    P ⊂ Q if ∀ b ∈ C μp(b) ≤ μq(b) and νp(b)≥ νq(b)

  2. (b)

    (P)b = {〈b, νp(b), μp(b)〉b ∈ C}

  3. (c)

    P = Q if P ⊂ Q and Q ⊂ P

  4. (d)

    \( P\bigcup \textrm{Q}=\left\{\left\langle \begin{array}{c}b,\max \left[\Big({\mu}_{\textrm{p}}(b),{\mu}_{\textrm{q}}(b)\right],\\ {}\ \min \left[{\nu}_{\textrm{p}}(b)\ge {\nu}_{\textrm{q}}(b)\right]\ \left|b\in \textrm{C}\right.\end{array}\right\rangle \right\} \)

  5. (e)

    \( P\cap \textrm{Q}=\left\{\left\langle \begin{array}{c}b,\min \left[\Big({\mu}_{\textrm{p}}(b),{\mu}_{\textrm{q}}(b)\right],\\ {}\ \max \left[{\nu}_{\textrm{p}}(b)\ge {\nu}_{\textrm{q}}(b)\right]\ \left|b\in \textrm{C}\right.\end{array}\right\rangle \right\} \)

  6. (f)

    \( P\oplus \textrm{Q}=\left\{\left\langle b,\sqrt{\mu_{\textrm{p}}^2(b)+{\mu}_{\textrm{q}}^2(b)-{\mu}_{\textrm{p}}^2(b){\mu}_{\textrm{q}}^2(b)},{\nu}_{\textrm{p}}(b){\nu}_{\textrm{q}}(b)|b\in \textrm{C}\right\rangle \right\} \)

  7. (g)

    \( P\otimes \textrm{Q}=\left\{\left\langle \textrm{c},{\mu}_{\textrm{p}}(b){\mu}_{\textrm{q}}(b),\sqrt{\nu_{\textrm{p}}^2(b)+{\nu}_{\textrm{q}}^2(b)-{\nu}_{\textrm{p}}^2(b){\nu}_{\textrm{q}}^2(b)}|b\in \textrm{C}\right\rangle \right\} \)

Definition 4

Zhang [27] defined the operators based on Yager’s [2] PyFWA and PyFWG for PyFNs \( {P}_j=\left({\mu}_{{\textrm{p}}_j},{\nu}_{{\textrm{p}}_j}\right) \) for (j = 1, 2, …. ., n) as follows:

PyFWA: Let \( {P}_j=\left({\mu}_{{\textrm{p}}_j},{\nu}_{{\textrm{p}}_j}\right) \) for (j = 1, 2, …. ., n) be a collection of PyFNs, then PyFWA operator is defined as:

$$ \textrm{PyFWA}\left({P}_1,{P}_1,\dots ..,{P}_1\right)={}_{j=1}{}^n\oplus \left({w}_j{P}_j\right)\\ =\left(\sqrt{1-\prod_{j=1}^n{\left(1-{\mu}_{{\textrm{p}}_j}^2\right)}^{w_j}},\prod_{j=1}^n{\left({\nu}_{{\textrm{p}}_j}\right)}^{w_j}\right) $$
(6)

PyFWG: Let \( {P}_j=\left({\mu}_{{\textrm{p}}_j},{\nu}_{{\textrm{p}}_j}\right) \) for (j = 1, 2, …. ., n) be a PyFNs collection, then PyFWG operator is as follows:

$$ PyFWG\left({P}_1,{P}_1,\dots ..,{P}_1\right)={}_{j=1}{}^n\otimes {\left({P}_j\right)}^{w_j}\\ =\left(\prod_{j=1}^n{\left({\mu}_{{\textrm{p}}_j}\right)}^{w_j},\sqrt{1-\prod_{j=1}^n{\left(1-{\nu}_{{\textrm{p}}_j}^2\right)}^{w_j}}\;\right) $$
(7)

Where wj indicates the weight of Pj, such as wj ≥ 0 for (j = 1, 2, …. ., n) & \( {\sum}_{j=1}^n{w}_j=1 \).

3 Novel Pythagorean Fuzzy Entropy Measure

Entropy is an essential tool for measuring uncertain information. Less entropy means less uncertainty. PyFS is a more powerful structure to represent an information where the existing structure fails. Therefore, establishing the measure of entropy for PyFS is significant in the present situation. The axiomatic formulation of the entropy measure of fuzzy sets was provided by De Luca and Termini [28]. Later, it was expanded to include InFS entropy by Szmidt and Kacprzyk [29]. As an extension of the entropy measure of Pythagorean fuzzy sets [1], we proposed a new concept of the fuzzy entropy measures of PyFS as follows:

Definition 5

For the Pythagorean fuzzy set ξ = {〈b, μp(b), νp(b)〉|b ∈ C}, the Pythagorean fuzzy entropy of ψ is defined as

$$ {E}_{\textrm{p}}\left(\xi \right)=\frac{1}{n}\sum_{i=1}^n\left[\sqrt{2}\cos \left\{\ \frac{1+\left|{\mu}_{\textrm{p}}^2(b)-{\nu}_{\textrm{p}}^2(b)\right|}{4}\right\}\pi \right] $$
(8)

Axioms for Pythagorean Fuzzy Entropy Measure

The relation Ep : PFS(C) → [0, 1] is stated as Pythagorean fuzzy entropy if it satisfies:

  1. (i)

    \( \mbox{\textsf{0}}\le {E}_{\textrm{p}}\left(\xi \right)\le 1 \)

  2. (ii)

    Ep(ξ) = 0, if and only if ψ is a crisp set

  3. (iii)

    Ep(ξ) = 1, if and only if μp(b) = νp(b), ∀ b ∈ C

  4. (iv)

    Ep(ξb) = Ep(ξ)

  5. (v)

    Ep(δ) ≤ Ep(ξ), if δ is less fuzzy than ψ, i.e., μp(δ) ≤ μp(ξ) and νp(δ) ≥ νp(ξ) for μp(ξ) ≤ νp(ξ), or, μδ(b) ≥ μξ(b) and νδ(b) ≤ νξ(b) for μξ(b) ≥ νξ(b) ∀ b ∈ C.

Theorem 1 Ep(ξ) is a Pythagorean fuzzy entropy

Proof. (E1) Since \( 0\le {\mu}_{\xi }(b),{\nu}_{\xi }(b)\le 1\Rightarrow 0\le {\mu}_{\xi}^2(b),{\nu}_{\xi}^2(b)\le 1 \) so that \( 0\le \left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|\le 1 \)

$$ \Rightarrow 1\le 1+\left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|\le 2 $$
$$ \Rightarrow \frac{\pi }{4}\le \frac{1+\left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|}{4}\le \frac{\pi }{2} $$
$$ \Rightarrow \frac{1}{\sqrt{2}}\le \cos \left\{\frac{1+\left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|}{4}\right\}\pi \le 0 $$
$$ \Rightarrow 0\le \sqrt{2}\cos \left\{\frac{1+\left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|}{4}\right\}\pi \le 1\kern0.75em i\Rightarrow 0\le {E}_{\textrm{p}}\left(\xi \right)\le 1. $$

(E2) If Ep(ξ) = 0 \( \Rightarrow \cos \left\{\frac{1+\left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|}{4}\right\}\pi =0 \)

$$ \Rightarrow \frac{1+\left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|}{4}=\frac{1}{2}\Rightarrow \left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|=1. $$

We have, μξ(b) = 0, νξ(b) = 1 or μξ(b) = 1, νξ(b) = 0. Hence ξ is a crisp set.

If ξ is a crisp set, then Ep(ξ) = 0.

(E3) If \( {\mu}_{\xi }(b)={\nu}_{\xi }(b)=\frac{1}{\sqrt{3}} \), then,

$$ \Rightarrow \sqrt{2}\cos \left\{\frac{1+\left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|}{4}\right\}\pi =1 $$
$$ \Rightarrow {E}_{\textrm{p}}\left(\xi \right)=1 $$

(E4) As \( {E}_{\textrm{p}}\left(\psi \right)=\sum_{i=1}^n\left[\sqrt{2}\cos \left\{\frac{1+\left|{\mu}_{\xi}^2(b)-{\nu}_{\xi}^2(b)\right|}{4}\right\}\pi \right] \)

$$ =\sum_{i=1}^n\left[\sqrt{2}\cos \left\{\frac{1+\left|{\nu}_{\xi}^2(b)-{\mu}_{\xi}^2(b)\right|}{4}\right\}\pi \right]={E}_{\textrm{p}}\left({\xi}^b\right) $$

(E5) To prove axiom, we construct a function

\( f\left(x,y\right)=\sqrt{2}\cos \left\{\frac{1+\left|{y}^2-{x}^2\right|}{4}\right\}\pi \), where x, y ϵ [0, 1]

Case I: When x ≤ y,then \( {f}_1\left(x,y\right)=\sqrt{2}\cos \left\{\frac{1+\left|{y}^2-{x}^2\right|}{4}\right\}\pi \)

Now we need to prove that f1(x, y) increases with x and decreases with y.

Therefore,

$$ \frac{\partial {f}_1}{\partial x}=\frac{2\times \pi \times x}{4}\sin \left\{\frac{1+\left|{y}^2-{x}^2\right|}{4}\right\}\pi =\frac{\pi x}{2}\sin \left\{\frac{1+\left|{y}^2-{x}^2\right|}{4}\right\}\pi; $$
$$ \frac{\partial {f}_1}{\partial y}=-\frac{2\times \pi \times y}{4}\sin \left\{\frac{1+\left|{y}^2-{x}^2\right|}{4}\right\}\pi =-\frac{\pi y}{2}\sin \left\{\frac{1+\left|{y}^2-{x}^2\right|}{4}\right\}\pi $$

Now, when x ≤ y, \( \frac{\partial {f}_1}{\partial x}>0 \) and \( \frac{\partial {f}_1}{\partial y}<0 \). Therefore, we can say that f1(x, y) increases with x and decreases with y. In other words, μδ(b) ≤ μξ(b) and νδ(b) ≥ νξ(b) for μξ(b) ≤ νξ(b)∀ b ∈ C, i.e., Ep(δ) ≤ Ep(ξ).

Case II: When x ≥ y,then \( {f}_2\left(x,y\right)=\sqrt{2}\cos \left\{\frac{1+\left|{x}^2-{y}^2\right|}{4}\right\}\pi \)

Now we need to prove that f2(x, y) decreases with x and increases with y.

Therefore,

$$ \frac{\partial {f}_2}{\partial x}=-\frac{2\times \pi \times x}{4}\sin \left\{\frac{1+\left|{x}^2-{y}^2\right|}{4}\right\}\pi =-\frac{\pi x}{2}\sin \left\{\frac{1+\left|{x}^2-{y}^2\right|}{4}\right\}\pi; $$
$$ \frac{\partial {f}_2}{\partial y}=\frac{2\times \pi \times y}{4}\sin \left\{\frac{1+\left|{x}^2-{y}^2\right|}{4}\right\}\pi =\frac{\pi y}{2}\sin \left\{\frac{1+\left|{x}^2-{y}^2\right|}{4}\right\}\pi; $$

Now, when x ≥ y, \( \frac{\partial {f}_1}{\partial x}<0 \) and \( \frac{\partial {f}_1}{\partial y}>0 \). Therefore, we can say that f2(x, y) decreases with x and increases with y. In other words, μδ(b) ≥ μξ(b) and νδ(b) ≤ νξ(b) for μξ(b) ≥ νξ(b) ∀ b ∈ C, i.e., Ep(δ) ≤ Ep(ξ).

4 Pythagorean Fuzzy MCDM Algorithm Based on Entropy-TOPSIS

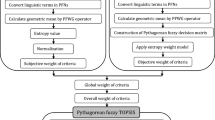
To estimate the weight of the criterion, TOPSIS is modified using the Pythagorean entropy metric in the proposed study. Zhang and Xu [6] applied the TOPSIS method to the Pythagorean fuzzy environment to solve the MCDM problem. The chosen alternative must be the furthest away from the NIdS and nearest to the PIdS to establish the TOPSIS method. In this technique, PIdS and NIdS are initially calculated in terms of PyFNs. Following that, the distances of PIdS and NIdS from each alternative are determined. Using the above distances, the closeness index of each alternative is determined. The rank is then determined using the closeness indices in descending order. The proposed framework uses linguistic variables to evaluate alternatives. To accommodate uncertainty, the PyFN counterparts of those options are then established using the Pythagorean fuzzy weighting scale, as shown in Table 3. Based on the inputs gathered from decision-makers in terms of linguistic factors, the Pythagorean fuzzy decision matrix of criteria is constructed.

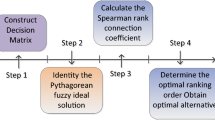
Let P = {P1, P2, ……. Pm} indicates the collection of m options from which decision-makers will select one using a set of criteria Z = {Z1, Z2, ……. Zn} consisting of n criteria. The various steps involved in the hybrid Pythagorean Entropy-TOPSIS method are described as follows.

Decision-Making Algorithm Using PyFS

  • Step 1: Estimate the Decision-Maker’s Weight

  • Using linguistic terms, Very Very Bad (ʪ1), Very Bad (ʪ2), Bad (ʪ3), Medium Bad (ʪ4), Fair (ʪ5), Good (ʪ6), Very Good (ʪ7), Very Very Good (ʪ8), Extremely Good (ʪ9), Exactly Equal (ʪ10), determines the significance of the ‘r’ decision-maker and are stated in Pythagorean fuzzy numbers. Let the PyFN to rate the uth decision-maker be θu=[μu, νu, πu]. So, the decision-maker’s weight is determined as follows:

    $$ {\Delta}_k=\frac{\left(\ {\mu}_u+{\pi}_u\left(\frac{\mu_u}{\mu_u+{\nu}_u}\ \right)\right)}{\sum_{u=1}^l\left(\ {\mu}_u+{\pi}_u\left(\frac{\mu_u}{\mu_u+{\nu}_u}\ \right)\right)} $$
    (9)

  • and \( \sum_{u=1}^l{\Delta}_u \) = 1

  • Step 2: Construct an aggregated PyFDM

  • Consider \( {P}^{(k)}={\left({p}_{ij}^{(k)}\right)}_{m\times n} \) to be a fuzzy Pythagorean decision matrix for each decision-maker. Where Δ = {Δ1, Δ2, ……Δl} represents the decision-maker’s weight and \( {\sum}_{k=1}^l{\Delta}_k=1,{\Delta}_k\in \left[0,1\right] \).

  • For aggregation, Zhang’s [27] PyFWA operator is utilized, P = (pij)m × n, where

    $$ P=\left[\begin{array}{ccc}{p}_{11}& {p}_{12}& \cdots \kern0.5em {p}_{1n}\\ {}{p}_{21}& {p}_{22}& \begin{array}{cc}\cdots & {p}_{2n}\end{array}\\ {}\begin{array}{c}\vdots \\ {}{p}_{m1}\end{array}& \begin{array}{c}\vdots \\ {}{p}_{m2}\end{array}& \begin{array}{cc}\begin{array}{c}\ddots \\ {}\cdots \end{array}& \begin{array}{c}\vdots \\ {}{p}_{mn}\end{array}\end{array}\end{array}\right] $$
    (10)

  • where, \( {p}_{ij}={\textrm{PFWA}}_{\Delta}\left({p}_{ij}^{(1)},{p}_{ij}^{(2)},\dots \dots \dots, {p}_{ij}^{(l)}\right) \)

    $$ =\left(\sqrt{1-\prod_{k=1}^l{\left(1-{\mu}_{ij}^2\right)}^{\Delta_k}},\prod_{k=1}^l{\left({\nu}_{ij}\right)}^{\Delta_k}\right) $$
    (11)

  • Here \( {p}_{ij}=\left({\mu}_{I_i}\left({z}_j\right)\bullet {\nu}_{I_i}\left({z}_j\right),{\pi}_{I_i}\left({z}_j\right)\right) \)

  • i = 1, 2, ……. . , m, and j = 1, 2, ……. . , n

  • Step 3: Evaluate Criteria Weight Utilizing Proposed Entropy Measure

  • Here, the weight vector W = (\( {\varpi}_1^e \), \( {\varpi}_2^e \), \( {\varpi}_3^e \),….,\( {\varpi}_n^e \)) is obtained using the Pythagorean fuzzy entropy measure Ep for criteria Cj (j = 1, 2,…, n) proposed in Eq. (8), where \( {\varpi}_j^e\ge 0 \) and \( \sum_{j=1}^n{\varpi}_j^e=1 \). The Pythagorean fuzzy entropy measure for each column of P is evaluated using Eqs. (8, 9, and 11), and thus to determine the weights \( {\varpi}_j^e \) of criteria Cj (j = 1, 2,…, n), the following expression is used:

    $$ {\varpi}_j^e=\frac{1-{E}_{\textrm{p}}\left({C}_j\right)}{n-{\sum}_{j=1}^n{E}_{\textrm{p}}\left({C}_j\right)} $$
    (12)

  • Step 4: Weighted Aggregated PyFDM

  • As a result, the weight vector W can be calculated and aggregated with the fuzzy Pythagorean decision matrix P [30] to create the weighted PyFDM, H.

    $$ \bar{H} = W^{\prime}\otimes\bar{P} = W^T \otimes\ \left[\bar{z}_{ij}\right]_{m\times n}=\left[\overset{=}{z}_{ij}\right]$$
    (13)

  • Where \( W=\left({\varpi}_1^e,\dots \dots {\varpi}_n^e\right) \) and \( \overset{=}{z}_{ij} = \langle\overset{=}{\mu}_{ij},\overset{=}{\nu}_{ij}\rangle = \langle 1-(1-\mu_{ij})^{\varpi_j^e},{\nu_{ij}^{\varpi_j^e}}\rangle \), wj > 0

  • Step 5: Evaluate PIdS and NIdS

  • Apply TOPSIS to the newly constructed aggregated PyFDM to resolve the MCDM problem. According to Zhang and Xu’s [4] definitions, the extrema score values are utilized to determine the Positive Ideal Solution (PIdS) and Negative Ideal Solution (NIdS).

    $$ {\textrm{PIS}}_j={\displaystyle \begin{array}{c}\max \\ {}i\end{array}}\left\{s\left({\alpha}_{ij}\right)\right\} $$
    (14)
    $$ {\textrm{NIS}}_j={\displaystyle \begin{array}{c}\min \\ {}i\end{array}}\left\{s\left({\alpha}_{ij}\right)\right\} $$
    (15)

  • Where s(αij) is PyFN’s score function

  • Step 6: Determine the Separation Measures

    $$ {\delta}_{PQ^{+}}=\frac{1}{n}{\sum}_{i=1}^n\max \left\{\left|{\mu_P}^2-{\mu_Q^{+}}^2\right|,\left|{\nu_P}^2-{\nu_Q^{+}}^2\right|\right\} $$
    (16)
    $$ {\delta}_{PQ^{-}}=\frac{1}{n}{\sum}_{i=1}^n\max \left\{\left|{\mu_P}^2-{\mu_Q^{-}}^2\right|,\left|{\nu_P}^2-{\nu_Q^{-}}^2\right|\right\} $$
    (17)

  • Step 7: Evaluate the Closeness Coefficient

  • The coefficient of closeness for each alternative is determined w.r.t. the Pythagorean fuzzy ideals using the following expression:

    $$ {C}_j=\frac{\delta_{PQ^{-}}}{\delta_{PQ^{+}}+{\delta}_{PQ^{-}}} $$
    (18)

  • Where 0 ≤ Cj ≤ 1 and j = 1, …. , m

  • Step 8: Ranking of Alternatives

  • Depending on their Cj value, the alternatives are ordered in descending order.

Application of the Entropy-TOPSIS Technique to Choose the Distribution Centre Location

Ten evaluation criteria and four alternatives were considered for the selection of distribution centre location based on a thorough literature review, which are as follows. Human resources availability (CHR), i.e., the availability of labourers to work at the distribution centre; i.e., the needed space must be suitable for a distribution facility. Ample surrounding space must also be available for future development. Distribution centres must have access to a variety of modes of transportation to enable easy and quick transit because transportation is one of the most crucial factors determining their success. Storage Convenience (CSTC): the proximity of the distribution centre to the location where storage services are offered is important. Distance to suppliers (CDS) has to do with suppliers’ closeness to the distribution centre. To reduce transit time and ensure supply, the distribution centre should be close to the suppliers. Distance to market (CDM) has to do with how close the marketplaces are to the distribution hub. Due to transportation considerations, distribution centres should be close to markets. Distance to airport (CDA) is the distribution centre’s close proximity to airports. Air transportation is appropriate for the delivery of urgent packages and precious cargo. As a result, the distribution centre should be near airports. Distance to other transport facilities (CDTF) is the distribution centre’s close access to roads, ports, and railways. Highways make it simple and quick for businesses to convey their goods. The issue of large shipments, particularly economical freight, may be solved by transportation by sea or interior waterways. Railways should be nearby since they are a reliable and affordable form of transportation. Land cost (CLC) refers to the amount of property wherever the distribution centre will be situated. The minimization criterion is the land cost because it influences the overall investment expenses. Logistics cost (CLGC) is the expense incurred to make the items available to the customers. This cost has an impact on the outcomes of corporate performance; hence, minimization is a requirement. Labour cost (CLBC) serves as the remuneration for the labourers who work in the distribution centre. Labour cost is the minimization criterion since it influences company performance outcomes.

  • Step 1: Estimate the Decision-Maker’s Weight

  • The Pythagorean fuzzy technique integrates the weights of each decision-maker using Eq. (9), and the decision-maker’s significance is evaluated. The linguistic terms used for rating decision makers are displayed in Tables 1 and 2 lists the resulting decision-makers’s weights.

Table 1 Linguistic terms
Full size table
Table 2 Weight of decision-makers
Full size table

  • Step 2: Construct Aggregated PyFDM

  • The aggregated Pythagorean fuzzy decision matrix is constructed using the linguistic terms shown in Table 3; the results of the decision-maker’s evaluation of each of the four distribution centre locations under consideration are displayed in Table 4. Based on the viewpoint of the typical decision-maker, Eq. (11) was utilized to generate the aggregated PyF decision matrix, which is shown in Table5.

Table 3 Linguistic terms
Full size table
Table 4 Weight of alternative’s based on criteria
Full size table
Table 5 Decision-maker’s evaluation in PyFNs in decision matrix
Full size table

  • Step 3: Evaluate Criteria Weight Utilizing Proposed Entropy Measure

  • In order to calculate the proposed entropy measure for PyFS using Eq. (8) and to estimate the weights for each criteria using Eq. (12), decision-makers calculated 10 independent criteria. The aggregated results of their assessments are shown in Table 6, along with the resulting entropy measure and weights.

Table 6 Evaluation of proposed entropy measure and criterion weights
Full size table

  • Step 4: Weighted Aggregated PyFDM

  • Using Eq. (13), a weighted aggregate PyFDM is constructed, and thus Table 7 is obtained.

Table 7 Aggregated weighted PyFDM
Full size table

  • Step 5: Evaluate PIdS and NIdS

  • Now, using Eqs. (14 and 15), PIdS and NIdS are estimated in accordance with Zhang and Xu’s [4] definitions, and the outcomes are displayed in Table 8.

Table 8 PIdS and NIdS for Pythagorean fuzzy set
Full size table

Step 6, 7, and 8

Calculate the separation measures of each alternative from the PIdS, NIdS, Closeness Coefficient, separation measure, and relative closeness. The coefficients are assessed using Eqs. (16)–(18), and the findings are shown in Table 9. The separation measure is calculated, and alternatives are thus ordered in decreasing order.

Table 9 Separation measure and ranking of alternative
Full size table

5 Result and Discussion

From the above table, alternative A2 was chosen as the best option based on the selected criteria, and alternative A4 is the least preferred distribution centre location as it received the worst rating from the four alternatives taken into consideration for the study. The rank obtained through the application of the proposed Entropy-TOPSIS method is compared with the few Pythagorean fuzzy entropy measures taken from the latest literature. The results thus obtained through the different entropy measures are shown in Table 10.

Table 10 Entropy comparison
Full size table

The following factors make the new PyFS-based entropy measures far more effective:

  • The new Pythagorean entropy measure is in perfect agreement with the axiomatic definition of entropy measures.

  • TOPSIS is defined using the information for PyFS.

  • A hybrid entropy-TOPSIS approach is applied to solve the multi-criteria decision-making problem.

  • The use of linguistic variables and PyFSs assures that this approach can better address the uncertainty in the decision-making method.

  • The suggested integrated methodology, which uses a newly defined Pythagorean entropy measure, is more appropriate and efficient for ranking alternatives than the current MCDM approaches.

6 Conclusion

Research pertaining to the selection of sustainable logistics centre locations has suggested that the application of the Pythagorean fuzzy entropy measure (PyFEM) can be advantageous. The use of PyFEM yields a set of weights, which are then used to evaluate the multiple criteria associated with the selection of a sustainable logistics centre location. This approach eliminates the need for subjective and time-consuming assessments, which may be prone to bias. Additionally, the application of PyFEM can help identify complex relationships between criteria and provide insights into the best location for a sustainable logistics centre. PyFS provides a tremendous ability to effectively regulate uncertainties and fuzziness. A hybrid entropy-TOPSIS model approach to solving the Pythagorean fuzzy MCDM problem is considered. The selection of a sustainable logistics centre location is used as an example, and Pythagorean fuzzy inputs in the form of linguistic data are used. A comparison of the existing entropy measures with the proposed measure reflects the efficiency of the proposed method. PyFS has the capability to handle the uncertainty in the system. The proposed methodology can be used to choose the best option when there are competing criteria in a variety of real-world decision-making situations in a fuzzy Pythagorean environment. The Pythagorean fuzzy set is a generalization for more effectively incorporating uncertainty in the data, and it is similar to other current fuzzy sets. In addition, a decision-making algorithm is applied to resolve decision-making complications when a group of experts is involved. The results of the case show the potential of the recommended entropy in the field of decision-making with linguistic data. The proposed measurement can be used as a component of new objective methods for setting attribute weights utilizing Pythagorean fuzzy sets in an upcoming analysis on multi-criteria decision-making. Future applications for the proposed Pythagorean fuzzy method are numerous. Additionally, the proposed measurement can be employed in subsequent studies by including various fuzzy systems into decision matrices and employing them to address various MCDM issues with unknown weights.