Abstract
Inconsistency in formal ontologies is usually addressed by computing repairs for the dataset. There are several strategies for selecting the repairs used to evaluate queries, with various levels of cautiousness and classes of computational complexity. This paper deals with inconsistent partially ordered lightweight ontologies. It introduces a new method that goes beyond the cautious strategies and that is tractable in the possibilistic setting, where uncertainty concerns only the data pieces. The proposed method, called C\(\pi \)-repair, proceeds as follows. It first interprets the partially ordered dataset as a family of totally ordered datasets. Then, it computes a single data repair for every totally ordered possibilistic ontology induced from the partially ordered possibilistic ontology. Next, it deductively closes each of these repairs in order to increase their productivity, without introducing conflicts or arbitrary data pieces. Finally, it intersects the closed repairs to obtain a single data repair for the initial ontology. The main contribution of this paper is an equivalent characterization that does not enumerate all the total orders, but also does not suffer from the additional computational cost naturally incurred by the deductive closure. We establish the tractability of our method by reformulating the problem using the notions of dominance and support. Intuitively, the valid conclusions are supported against conflicts by consistent inclusion-minimal subsets of the dataset that dominate all the conflicts. We also study the rationality properties of our method in terms of unconditional and conditional query-answering.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
The Ontology-Based Data Access (OBDA) paradigm relies on an ontology to provide a unified conceptual representation of some domain of interest, in order to improve access to data [27]. Lightweight fragments of description logics such as the DL-Lite family [1, 15] are commonly used to encode ontologies, since they allow for efficient query-answering. The conceptual knowledge of an ontology (i.e., the TBox) is usually assumed to be consistent. However, the dataset (i.e., the ABox) may potentially be inconsistent with respect to the TBox. In this case, reasoning with an inconsistent ontology amounts to evaluating queries over one or several of its data repairs (i.e., inclusion-maximal subsets of the ABox that are consistent with respect to the TBox). A variety of inconsistency-tolerant semantics have been proposed, with different levels of cautiousness and classes of computational complexity. These strategies select one or several repairs of an ABox in order to evaluate queries, with tractability achieved mostly for DL-Lite ontologies (see [3, 10] for a survey).
For instance, the well-known Intersection of ABox Repair (IAR) semantics [25] is a cautious strategy. Indeed, it avoids a random selection of the repairs since it evaluates queries over the intersection of all the repairs. It discards all the elements of the ABox that are involved in conflicts (i.e., inclusion-minimal subsets of the ABox that are inconsistent with respect to the TBox). Most notably, it is tractable in DL-Lite.
The Intersection of Closed ABox Repair (ICAR) semantics [25] applies the IAR semantics to the deductive closure of the ABox. This allows to derive more facts from the ABox, so ICAR is more productiveFootnote 1 than IAR, while it is likewise tractable in DL-Lite. However, ICAR may return undesirable conclusions. Consider a TBox with the concept inclusion axiom \(\textsf {Whale}\sqsubseteq \textsf {Mammal}\), and the concept disjointness axiom \(\textsf {Whale}\sqsubseteq \lnot \,\textsf {Shark}\). Say the ABox contains two facts \(\textsf {Whale}(\textsf {Humphrey})\) and \(\textsf {Shark}(\textsf {Humphrey})\), which are in conflict according to the disjointness axiom. ICAR returns \(\textsf {Mammal}(\textsf {Humphrey})\) as a valid conclusion, although it follows from \(\textsf {Whale}(\textsf {Humphrey})\), which is involved in a conflict.
For prioritized (or totally ordered) ontologies, computing repairs for the ABox is a challenging task. For instance, the Preferred Repair semantics [12] (based on the notion of preferred subtheories [13]) is coNP-complete in data complexity. The grounded repair [11] obtained from a Dung-style argumentation framework is tractable. However, the order relation only applies to the conflicts, so the ABox is assumed to be locally stratified (a similar order defined in propositional logic can be found in [8]). In contrast, three main tractable methods have been identified in [7] for totally ordered ABoxes. The non-defeated repair iteratively applies the IAR semantics to a cumulative sequence of strata of the ABox. The linear-based repair iteratively accumulates a sequence of strata of the ABox, by discarding any stratum that is inconsistent with respect to the TBox or that contradicts the preceding sequence of strata. The possibilistic repair leverages possibility theory, which supports inconsistent reasoning with incomplete, uncertain, qualitative and prioritized information [20, 23]. It infers all the facts that are strictly more certain than some inconsistency degree of the ABox, computed from the uncertainty degrees assigned to the elements of the ABox.
A few tractable methods have also been proposed for partially ordered ontologies. There is the Elect method [6] which generalizes both the IAR semantics and the non-defeated repair. There is also the possibilistic repair method defined for partially ordered ontologies [5]. Both Elect and the possibilistic repair method extend the partial order over the ABox into a family of total orders. This yields as many totally ordered ABoxes, for which repairs can be computed then intersected to obtain a single repair for the initial ABox. Such methods are interesting since they derive the conclusions that follow from all the totally ordered repairs. However, their productivity is hampered by their cautiousness.
A natural way for increasing productivity is to compute the deductive closure of the totally ordered repairs before intersecting them, in the spirit of the Intersection of Closed Repairs (ICR) semantics [9].Footnote 2 However, it is well-known that closing the repairs increases time complexity. For instance, for flat ontologies, inference with the IAR semantics and the ICAR semantics is tractable, but it is coNP-complete with the ICR semantics in data complexity [3, 9].
In this work, we undertake the difficult task of proposing a more productive, yet efficient method, in the case of partially ordered ontologies. We call the new method C\(\pi \)-repair and establish its tractability in the DL-Lite\(_{\mathcal {R}}\) fragment, using an interpretation of possibility theory as a strategy for computing the repair. We characterize C\(\pi \)-repair equivalently based on the notions of dominance and support. Intuitively, the valid conclusions are supported against conflicts by consistent inclusion-minimal subsets of the ABox that dominate all the conflicts.
We also study the rationality properties of C\(\pi \)-repair in terms of unconditional and conditional query-answering mechanisms. In particular, we show that the deductive closure preserves the satisfied properties of possibilistic query-answering from the intersection of the (unclosed) possibilistic repairs.
This paper is organised as follows. Section 2 recalls the basics of DL-Lite\(_{\mathcal {R}}\) and the possibilistic repair method. Section 3 defines the closure-based repair method C\(\pi \)-repair. Section 4 gives its tractable characterization. Section 5 studies its rationality properties, before concluding.
2 Preliminaries
We recall the underpinnings of the possibilistic repair for partially preordered ontologies [5] that are specified in the DL-Lite\(_{\mathcal {R}}\) fragment [15].
Flat (or Non-prioritized) Ontology: A DL-Lite\(_{\mathcal {R}}\) ontology is a knowledge base (KB) \({\mathcal {K}}= \langle \mathcal {T}, {\mathcal {A}} \rangle \), where \(\mathcal {T}\) is a TBox composed of axioms encoding domain knowledge, and \({\mathcal {A}}\) is an ABox composed of assertions (i.e., ground facts or data pieces). The axioms may be positive inclusions of concepts (e.g. \(B_1 \sqsubseteq B_2\)) or of roles (e.g. \(R_1 \sqsubseteq R_2\)), and they allow to derive new assertions from the ABox. The axioms may also be negative inclusions of concepts (e.g. \(B_1 \sqsubseteq \lnot \,B_2\)) or of roles (e.g. \(R_1 \sqsubseteq \lnot \,R_2\)), and they serve to exhibit the conflicts in the ABox.
Definition 1
(Conflict) Let \({\mathcal {K}}=\langle \mathcal {T},{\mathcal {A}} \rangle \) be a KB. A conflict is a subset \({\mathcal {C}}\subseteq {\mathcal {A}}\) such that \(\langle \mathcal {T},{\mathcal {C}} \rangle \) is inconsistent, and for all \(\varphi \in {\mathcal {C}}\), \(\langle \mathcal {T},{\mathcal {C}}\setminus \{\varphi \} \rangle \) is consistent. We denote by \(\textsf{Cf}({\mathcal {A}})\) the set of all the conflicts of \({\mathcal {A}}\), a.k.a. the conflict set.
Here, inconsistency means the absence of a model for the KB (we omit the semantics for space reasons). The conflict set \(\textsf{Cf}({\mathcal {A}})\) can be computed in polynomial time in the size of the ABox in DL-Lite\(_{\mathcal {R}}\) ontologies [15].
Totally Preordered Possibilistic Ontology: Possibilistic logic and possibility theory [4, 18, 19] are long-standing approaches for reasoning with uncertain information, and are closely related to ordinal conditional functions [29] and consonant belief functions [17, 22, 28]. Uncertainty can be represented either in extension using possibility distributions, or in a compact way using weighted logics or graphical models. Here, we opt for a qualitative representation of the preference relation induced over the ABox, where only the plausibility ordering between the assertions matters (see [5] for details and an overview of possibility theory).
Let \({\mathcal {K}}= \langle \mathcal {T}, {\mathcal {A}} \rangle \) be a KB, where the axioms in \(\mathcal {T}\) are fully certain and free of conflicts, while the elements of \({\mathcal {A}}\) may be uncertain and conflicting w.r.t. the axioms of \(\mathcal {T}\). Consider a total preorder \(\ge \) over \({\mathcal {A}}\)Footnote 3, and let > be the associated strict order, and let \(\equiv \) denote the associated equivalence relation. We denote the resulting ABox by  , and it can be represented as a well-ordered partition \(({\mathcal {S}}_1, \ldots , {\mathcal {S}}_n)\) such that:
, and it can be represented as a well-ordered partition \(({\mathcal {S}}_1, \ldots , {\mathcal {S}}_n)\) such that:
-
\({\mathcal {S}}_1 \cup \ldots \cup {\mathcal {S}}_n = {\mathcal {A}}\).
-
\({\mathcal {S}}_1 = \{\varphi _j \in {\mathcal {A}}:\) for all \(\varphi _k \in {\mathcal {A}}, \varphi _j \ge \varphi _k \}\).
-
\({\mathcal {S}}_i = \{\varphi _j \in {\mathcal {A}}\setminus {({\mathcal {S}}_1\cup \dots \cup {\mathcal {S}}_{i-1})}:\) for all \(\varphi _k \in {\mathcal {A}}\setminus {({\mathcal {S}}_1\cup \dots \cup {\mathcal {S}}_{i-1})}, \varphi _j \ge \varphi _k\}\), for \(i = 2, \ldots , n\).
The assertions in \({\mathcal {S}}_1\) (resp. \({\mathcal {S}}_n\)) are the most (resp. least) certain. Those in any \({\mathcal {S}}_i\) (\(i = 1, \ldots , n\)) are equally certain.
The totally preordered possibilistic repair [7], denoted  , can be computed tractably like so:
, can be computed tractably like so:
-
If \({\mathcal {K}}\) is consistent, then
 .
. -
Otherwise, if \(\langle \mathcal {T}, {\mathcal {S}}_1 \rangle \) is inconsistent, then
 .
. -
Otherwise, if for some i, \(1 \le i < n\), \(\langle \mathcal {T}, {\mathcal {S}}_1 \cup \ldots \cup {\mathcal {S}}_i \rangle \) is consistent, and \(\langle \mathcal {T}, {\mathcal {S}}_1 \cup \ldots \cup {\mathcal {S}}_{i+1} \rangle \) is inconsistent, then
 .
.
Partially Preordered Possibilistic Ontology: Consider a partial preorder \(\unrhd \) over \({\mathcal {A}}\)Footnote 4. Let \(\rhd \) be the associated strict order, and let \(\bowtie \)Footnote 5 denote incomparability. We denote the resulting ABox by  .
.
The partially preordered possibilistic repair [5], denoted  , relies on the notion of compatible bases. These are all the totally preordered ABoxes induced from
, relies on the notion of compatible bases. These are all the totally preordered ABoxes induced from  that preserve the ordering between its assertions. A totally preordered ABox \({\mathcal {A}}_\ge \) is compatible with
that preserve the ordering between its assertions. A totally preordered ABox \({\mathcal {A}}_\ge \) is compatible with  means that for all
means that for all  , for all
, for all  , if \(\varphi _j \unrhd \varphi _k\), then \(\varphi _j \ge \varphi _k\). This entails that \(\varphi _j \bowtie \varphi _k\) extends to three distinct cases: (i) \(\varphi _j > \varphi _k\), (ii) \(\varphi _k > \varphi _j\) or (iii) \(\varphi _j \equiv \varphi _k\). Thus,
, if \(\varphi _j \unrhd \varphi _k\), then \(\varphi _j \ge \varphi _k\). This entails that \(\varphi _j \bowtie \varphi _k\) extends to three distinct cases: (i) \(\varphi _j > \varphi _k\), (ii) \(\varphi _k > \varphi _j\) or (iii) \(\varphi _j \equiv \varphi _k\). Thus,  is obtained like so:
is obtained like so:
-
1.
First, extend the partial preorder \(\unrhd \) into a family of total preorders, each of which is denoted by \(\ge _i\), with \(1 \le i \le m\) and m is the number of extensions of \(\unrhd \). Each extension \(\ge _i\) defines an ABox
 that is compatible with
that is compatible with  .
. -
2.
Then for each compatible base
 , compute its totally preordered possibilistic repair
, compute its totally preordered possibilistic repair  as defined above.
as defined above. -
3.
Finally, intersect all the repairs
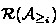 to obtain
to obtain  .
.
The repair  has been characterized tractably [5], without exhibiting all the extensions \(\ge _i\) of \(\unrhd \), using the notion of \(\pi \)-accepted assertions.
has been characterized tractably [5], without exhibiting all the extensions \(\ge _i\) of \(\unrhd \), using the notion of \(\pi \)-accepted assertions.
Definition 2
(\(\pi \)-accepted assertion) Let  be a partially preordered KB, and
be a partially preordered KB, and  its conflict set. An assertion
its conflict set. An assertion  is \(\pi \)-accepted if for all
is \(\pi \)-accepted if for all  , there is \(\varphi _k \in {\mathcal {C}}, \varphi _j \ne \varphi _k, \; s.t. \; \varphi _j \rhd \varphi _k\).
, there is \(\varphi _k \in {\mathcal {C}}, \varphi _j \ne \varphi _k, \; s.t. \; \varphi _j \rhd \varphi _k\).
The repair  is the set of all the \(\pi \)-accepted assertions, and it can be computed in polynomial time in the size of
is the set of all the \(\pi \)-accepted assertions, and it can be computed in polynomial time in the size of  in DL-Lite\(_{\mathcal {R}}\) ontologies [5].
in DL-Lite\(_{\mathcal {R}}\) ontologies [5].
We introduce a toy example of a sales company’s information security policy.
Example 1
We build a KB from the following mutually disjoint sets \(\mathsf {N_C}\), \(\mathsf {N_R}\) and \(\mathsf {N_I}\), containing respectively concept names, role names and individuals:
-
\(\mathsf {N_C}=\{\textsf {Reports}\), \(\textsf {HRfiles}\), \(\textsf {Manager}\), \(\textsf {Sales}\), \(\textsf {Staff}\), \(\textsf {HR}\}\), where \(\textsf {Reports}\), \(\textsf {HRfiles}\) are file categories and \(\textsf {Manager}\), \(\textsf {Sales}\), \(\textsf {Staff}\) and \(\textsf {HR}\) are employee positions.
-
\(\mathsf {N_R}=\{\textsf {Edit}\), \(\textsf {Sign}\), \(\textsf {Read}\}\), represent the privileges of an employee on a file.
-
\(\mathsf {N_I}=\{\textsf {Bob}\), \(\textsf {Alice}\), \(\textsf {F17}\), \(\textsf {F78}\}\), where \(\textsf {Bob}\), \(\textsf {Alice}\) are employees and \(\textsf {F17}, \textsf {F78}\) represent shared files.
Consider a partially preodered KB  depicted in Fig. 1.
depicted in Fig. 1.
According to \(\mathcal {T}\), a manager and a sales person are staff members. A manager (resp. a sales person) does not have editing (resp. signing) rights on files.
Applying Definition 2 to Fig. 1 (right), since \(\textsf {Reports}(\textsf {F78})\) is strictly preferred to at least one member of each conflict, we get  .
.
\(\square \)
3 The C\(\pi \)-Repair Method
In the literature, the notion of positive deductive closure is a natural way for obtaining more productive repairs. The idea is to apply the positive inclusion axioms of the TBox to the ABox in order to derive new assertions. However, this typically increases the computational cost. In this section, we propose a new method, called C\(\pi \)-repair, which produces a larger partially preordered possibilistic repair, while maintaining tractability in DL-Lite\(_{\mathcal {R}}\) and the satisfiability of the rationality properties. Moreover, the tractability of the proposed method is also applicable in fragments that are more expressive than DL-Lite\(_{\mathcal {R}}\).
Let us first recall the definition of the closure operator in the case of a flat KB [7, 15], which can be applied in the partially preordered case (we assume that the individuals included in the closure are limited to those present in the ABox):
Definition 3
(Closed ABox) Let \({\mathcal {K}}= \langle \mathcal {T}, {\mathcal {A}} \rangle \) be a DL-Lite\(_{\mathcal {R}}\) KB. Let \(\mathcal {T}_p\) denote the set of all the positive inclusion axioms of \(\mathcal {T}\). The deductive closure of \({\mathcal {A}}\) w.r.t. \(\mathcal {T}\) is defined as:
\(cl({\mathcal {A}}) = \{B(a) | \langle \mathcal {T}_{p}, {\mathcal {A}} \rangle \vDash B(a)\) s.t. B is a concept name in \(\mathcal {T}\), a is an individual in \({\mathcal {A}}\}\) \(\bigcup \) \(\{R(a,b) | \langle \mathcal {T}_{p}, {\mathcal {A}} \rangle \vDash R(a,b)\) s.t. R is a role name in \(\mathcal {T}\), a and b are individuals in \({\mathcal {A}}\}\), where \(\vDash \) is the standard DL-Lite\(_{\mathcal {R}}\) inference relation.
For partially preordered ABoxes, the deductive closure can be applied at two different levels to obtain a larger repair. The first option closes the initial ABox  (in the spirit of the ICAR semantics for flat ABoxes [25]). The second option closes each one of the possibilistic repairs
(in the spirit of the ICAR semantics for flat ABoxes [25]). The second option closes each one of the possibilistic repairs  associated with the compatible ABoxes
associated with the compatible ABoxes  (in the spirit of the ICR semantics for flat ABoxes [9]).
(in the spirit of the ICR semantics for flat ABoxes [9]).
In the first option, closing the ABox  before computing the repair may lead to undesirable conclusions. For instance, assume a DL-Lite\(_{\mathcal {R}}\) KB where \(\mathcal {T}=\{B \sqsubseteq E, A \sqsubseteq \lnot \,B\}\) and
before computing the repair may lead to undesirable conclusions. For instance, assume a DL-Lite\(_{\mathcal {R}}\) KB where \(\mathcal {T}=\{B \sqsubseteq E, A \sqsubseteq \lnot \,B\}\) and  . Then
. Then  and
and  . Assume that \(E(a) \rhd A(a) \rhd B(a)\). Using Definition 2, both E(a) and A(a) are \(\pi \)-accepted in
. Assume that \(E(a) \rhd A(a) \rhd B(a)\). Using Definition 2, both E(a) and A(a) are \(\pi \)-accepted in  . However, including E(a) in the repair is questionable, since it is supported by B(a) which conflicts with the \(\pi \)-accepted assertion A(a). Another issue with this approach concerns the reliability of the assertions that are inferred from incomparable elements. For instance, assume a DL-Lite\(_{\mathcal {R}}\) KB where \(\mathcal {T}= \{A \sqsubseteq E, B \sqsubseteq E\}\) and
. However, including E(a) in the repair is questionable, since it is supported by B(a) which conflicts with the \(\pi \)-accepted assertion A(a). Another issue with this approach concerns the reliability of the assertions that are inferred from incomparable elements. For instance, assume a DL-Lite\(_{\mathcal {R}}\) KB where \(\mathcal {T}= \{A \sqsubseteq E, B \sqsubseteq E\}\) and  , where \(A(b) \bowtie B(b)\). Then
, where \(A(b) \bowtie B(b)\). Then  and all the assertions are \(\pi \)-accepted (since the KB is consistent). The question is which certainty level should be assigned to E(b). The intuition is to consider E(b) to be at least as certain as A(b) and B(b), but this cannot be easily defined in a general way.
and all the assertions are \(\pi \)-accepted (since the KB is consistent). The question is which certainty level should be assigned to E(b). The intuition is to consider E(b) to be at least as certain as A(b) and B(b), but this cannot be easily defined in a general way.
In the second option, closing the possibilistic repairs  of the compatible ABoxes
of the compatible ABoxes  is more appropriate, such that a more productive repair for
is more appropriate, such that a more productive repair for  can be computed from the intersection of
can be computed from the intersection of  .
.
Definition 4
(C\(\pi \)-repair) Let  be a partially preordered ABox. Let
be a partially preordered ABox. Let  , with \(1 \le i \le m\), denote all its compatible bases and let
, with \(1 \le i \le m\), denote all its compatible bases and let  be the associated possibilistic repair. The closure-based partially preordered possibilistic repair of
be the associated possibilistic repair. The closure-based partially preordered possibilistic repair of  , denoted
, denoted  , is obtained as follows:
, is obtained as follows:

The closure-based repair  computed with this method is more productive than both the repair
computed with this method is more productive than both the repair  and its closure
and its closure  . Namely:
. Namely:

Figure 2 shows the C\(\pi \)-repair process of Definition 4.
-
First, extend the partially preordered ABox
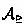 into a family of totally preordered ABoxes, denoted \(A_{\ge _1}, \ldots , A_{\ge _m}\) (“Extend” arc).
into a family of totally preordered ABoxes, denoted \(A_{\ge _1}, \ldots , A_{\ge _m}\) (“Extend” arc). -
Then, compute the repair \({\mathcal {R}}(A_{\ge _i})\) of each compatible base (“Repair” arc), and its deductive closure (“Close” arc).
-
Finally, intersect all the closed repairs \(cl({\mathcal {R}}(A_{\ge _i}))\) (“Intersect” arc) to obtain a single closure-based repair for the initial ABox
 .
.
Obviously, this method is naive and computationally expensive since enumerating all the compatible ABoxes may be exponential in the worst case.
Example 2
From Example 1, we have:  . Figure 1 illustrates
. Figure 1 illustrates  , its two conflicts and the relation \(\unrhd \). Recall that any compatible base
, its two conflicts and the relation \(\unrhd \). Recall that any compatible base  preserves the ordering between the assertions of
preserves the ordering between the assertions of  . Since \(\textsf {Reports}(\textsf {F78})\) is the most certain assertion in
. Since \(\textsf {Reports}(\textsf {F78})\) is the most certain assertion in  , it belongs to every
, it belongs to every  . Moreover, it is easy to check that each
. Moreover, it is easy to check that each  contains either \(\textsf {Manager}(\textsf {Bob})\) or \(\textsf {Sales}(\textsf {Bob})\). Using the axioms \(\textsf {Manager}\sqsubseteq \textsf {Staff}\) and \(\textsf {Sales}\sqsubseteq \textsf {Staff}\) of \(\mathcal {T}\), one can infer \(\textsf {Staff}(\textsf {Bob})\) from each closed repair
contains either \(\textsf {Manager}(\textsf {Bob})\) or \(\textsf {Sales}(\textsf {Bob})\). Using the axioms \(\textsf {Manager}\sqsubseteq \textsf {Staff}\) and \(\textsf {Sales}\sqsubseteq \textsf {Staff}\) of \(\mathcal {T}\), one can infer \(\textsf {Staff}(\textsf {Bob})\) from each closed repair  . Therefore,
. Therefore,  . So,
. So,  is larger than both
is larger than both  . \(\square \)
. \(\square \)
4 Characterization of C\(\pi \)-Repair
In this section, we propose an equivalent characterization of the closure-based repair introduced in Definition 4 without enumerating all the compatible bases. We first introduce two notions called support and dominance. The support (or an argument) of an assertion is an inclusion-minimal consistent subset of the ABox that allows to derive it. Formally:
Definition 5
(Support) Let \({\mathcal {K}}= \langle \mathcal {T},{\mathcal {A}} \rangle \) be a DL-Lite\(_{\mathcal {R}}\) KB. Let B be a concept name and R be a role name in \(\mathcal {T}\). Let a and b be individuals in \({\mathcal {A}}\). The subset \({\mathcal {B}}\subseteq {\mathcal {A}}\) is a support for B(a) (resp. R(a, b)) in \({\mathcal {A}}\) if:
-
\(\langle \mathcal {T},{\mathcal {B}} \rangle \) is consistent, and
-
\(\langle \mathcal {T},{\mathcal {B}} \rangle \vDash B(a)\), (resp. \(\langle \mathcal {T},{\mathcal {B}} \rangle \vDash R(a,b)\)), and
-
for all \({\mathcal {B}}' \subsetneq {\mathcal {B}}\), \(\langle \mathcal {T},{\mathcal {B}}' \rangle \nvDash B(a)\), (resp. \(\langle \mathcal {T},{\mathcal {B}}' \rangle \nvDash R(a,b)\)).
Where \(\vDash \) is the standard DL-Lite\(_{\mathcal {R}}\) inference relation.
Example 3
We continue Example 1. We have \(\{\textsf {Manager}(\textsf {Bob})\}\) supports \(\textsf {Staff}(\textsf {Bob})\) since \(\langle \mathcal {T},\{\textsf {Manager}(\textsf {Bob})\} \rangle \vDash \textsf {Staff}(\textsf {Bob})\), and it is minimal and consistent. \(\square \)
The dominance relation is a way for extending the partial preorder defined over an ABox into a partial preorder defined over the subsets of the ABox. Such extension allows to compare supports and conflicts. Intuitively, the dominance of a partially preordered subset over another requires that each element of the former be strictly more certain than at least one element of the latter. Formally:
Definition 6
(Dominance) Let  be a partially preordered KB equipped with \(\unrhd \). Let
be a partially preordered KB equipped with \(\unrhd \). Let  and
and  . We say that \({\mathcal {B}}_1\) dominates \({\mathcal {B}}_2\), denoted \({\mathcal {B}}_1 \, {\triangleright ^{dom}} \,{\mathcal {B}}_2\), if: for all \(\varphi _j \in {\mathcal {B}}_1\), there is \(\varphi _k \in {\mathcal {B}}_2\) s.t. \(\varphi _j \rhd \varphi _k\).
. We say that \({\mathcal {B}}_1\) dominates \({\mathcal {B}}_2\), denoted \({\mathcal {B}}_1 \, {\triangleright ^{dom}} \,{\mathcal {B}}_2\), if: for all \(\varphi _j \in {\mathcal {B}}_1\), there is \(\varphi _k \in {\mathcal {B}}_2\) s.t. \(\varphi _j \rhd \varphi _k\).
Example 4
Let \({\mathcal {B}}_1\), \({\mathcal {B}}_2\) and \({\mathcal {B}}_3\) be three subsets of  of Example 1, as illustrated by Fig. 3. \({\mathcal {B}}_1 \, {\triangleright ^{dom}} \,{\mathcal {B}}_2\) holds because \(\textsf {Reports}(\textsf {F78}) \rhd \textsf {Sales}(\textsf {Bob})\) and \(\textsf {Manager}(\textsf {Bob}) \rhd \textsf {Sign}(\textsf {Bob},\textsf {F78})\). \({\mathcal {B}}_1 \, {\triangleright ^{dom}} \,{\mathcal {B}}_3\) does not hold because \(\textsf {Manager}(\textsf {Bob}) \ntriangleright \textsf {Sales}(\textsf {Bob})\) and \(\textsf {Manager}(\textsf {Bob}) \ntriangleright \textsf {Edit}(\textsf {Bob},\textsf {F78})\).
of Example 1, as illustrated by Fig. 3. \({\mathcal {B}}_1 \, {\triangleright ^{dom}} \,{\mathcal {B}}_2\) holds because \(\textsf {Reports}(\textsf {F78}) \rhd \textsf {Sales}(\textsf {Bob})\) and \(\textsf {Manager}(\textsf {Bob}) \rhd \textsf {Sign}(\textsf {Bob},\textsf {F78})\). \({\mathcal {B}}_1 \, {\triangleright ^{dom}} \,{\mathcal {B}}_3\) does not hold because \(\textsf {Manager}(\textsf {Bob}) \ntriangleright \textsf {Sales}(\textsf {Bob})\) and \(\textsf {Manager}(\textsf {Bob}) \ntriangleright \textsf {Edit}(\textsf {Bob},\textsf {F78})\).
\(\square \)
Before characterizing C\(\pi \)-repair in general, we first discuss the special case where the ABox is consistent w.r.t. the TBox, i.e., the conflict set is empty. Hence, C\(\pi \)-repair simply amounts to applying standard DL-Lite\(_{\mathcal {R}}\) inference. Formally:
Lemma 1
Let  be a consistent, partially preordered KB, i.e.,
be a consistent, partially preordered KB, i.e.,  . Consider \(cl(\cdot )\) given by Definition 3. Let \(\varphi \) be an assertion. Then:
. Consider \(cl(\cdot )\) given by Definition 3. Let \(\varphi \) be an assertion. Then:  . Equivalently:
. Equivalently:  iff there is
iff there is  s.t. \(\langle \mathcal {T},{\mathcal {B}} \rangle \vDash \varphi \).
s.t. \(\langle \mathcal {T},{\mathcal {B}} \rangle \vDash \varphi \).
In the rest of this paper, we focus on the case where the ABox is inconsistent w.r.t. the TBox. Our goal is to use the notions of dominance and support (see Definitions 5 and 6) to characterize equivalently the assertions in the C\(\pi \)-repair. This allows to avoid enumerating all the totally preordered extensions of  . The idea is that an assertion \(\varphi \) belongs to C\(\pi \)-repair if and only if for every conflict \({\mathcal {C}}\) in the ABox, there is a support \({\mathcal {B}}\) of \(\varphi \) that dominates \({\mathcal {C}}\). We provide two propositions to confirm this intuitive characterization.
. The idea is that an assertion \(\varphi \) belongs to C\(\pi \)-repair if and only if for every conflict \({\mathcal {C}}\) in the ABox, there is a support \({\mathcal {B}}\) of \(\varphi \) that dominates \({\mathcal {C}}\). We provide two propositions to confirm this intuitive characterization.
Proposition 1
Let  be an inconsistent, partially preordered KB. Let
be an inconsistent, partially preordered KB. Let  be its conflict set and let \(\varphi \) be an assertion. If for all
be its conflict set and let \(\varphi \) be an assertion. If for all  , there is
, there is  s.t.:
s.t.:
-
1.
\({\mathcal {B}}\) supports \(\varphi \) (as per Definition 5), and
-
2.
\({\mathcal {B}}\, {\triangleright ^{dom}} \,{\mathcal {C}}\) (as per Definition 6),
then  .
.
We illustrate this result with our running example.
Example 5
Consider again Example 2. Let us use Proposition 1 to check that the assertion \(\textsf {Staff}(\textsf {Bob})\) is indeed in  . For each conflict in
. For each conflict in  , it suffices to exhibit a dominating support for \(\textsf {Staff}(\textsf {Bob})\), like so:
, it suffices to exhibit a dominating support for \(\textsf {Staff}(\textsf {Bob})\), like so:
-
For the conflict \({\mathcal {C}}_1=\{\textsf {Manager}(\textsf {Bob}),\textsf {Edit}(\textsf {Bob},\textsf {F78})\}\), \({\mathcal {B}}_1 = \{\textsf {Sales}(\textsf {Bob})\}\) supports \(\textsf {Staff}(\textsf {Bob})\) and \({\mathcal {B}}_1 \, {\triangleright ^{dom}} \,{\mathcal {C}}_1\) (since \(\textsf {Sales}(\textsf {Bob}) \rhd \textsf {Edit}(\textsf {Bob},\textsf {F78})\)).
-
For the conflict \({\mathcal {C}}_2=\{\textsf {Sales}(\textsf {Bob}),\textsf {Sign}(\textsf {Bob},\textsf {F78})\}\), \({\mathcal {B}}_2 = \{\textsf {Manager}(\textsf {Bob})\}\) supports \(\textsf {Staff}(\textsf {Bob})\) and \({\mathcal {B}}_2 \, {\triangleright ^{dom}} \,{\mathcal {C}}_2\) (since \(\textsf {Manager}(\textsf {Bob}) \rhd \textsf {Sign}(\textsf {Bob},\textsf {F78})\)).
\(\square \)
The other direction of Proposition 1, given in Proposition 2, is also true. In particular, if the characterization “for every conflict \({\mathcal {C}}\) in  , there is a support \({\mathcal {B}}\) of \(\varphi \) in
, there is a support \({\mathcal {B}}\) of \(\varphi \) in  that dominates \({\mathcal {C}}\)" is not true, then \(\varphi \) cannot belong to C\(\pi \)-repair. The proposition also covers the particular case of an assertion without a support, which cannot belong to C\(\pi \)-repair.
that dominates \({\mathcal {C}}\)" is not true, then \(\varphi \) cannot belong to C\(\pi \)-repair. The proposition also covers the particular case of an assertion without a support, which cannot belong to C\(\pi \)-repair.
Proposition 2
Let  be an inconsistent, partially preordered KB. Let
be an inconsistent, partially preordered KB. Let  be its conflict set and \(\varphi \) be an assertion.
be its conflict set and \(\varphi \) be an assertion.
If  , there is
, there is  s.t.:
s.t.:
-
1.
\({\mathcal {B}}\) supports \(\varphi \) (as per Definition 5), and
-
2.
\({\mathcal {B}}\, {\triangleright ^{dom}} \,{\mathcal {C}}\) (as per Definition 6).
We illustrate this result with our running example.
Example 6
Let  , where the TBox \(\mathcal {T}'\) is:
, where the TBox \(\mathcal {T}'\) is:
Thus, a manager (resp. a sales person) does not have editing (resp. signing) rights, and a sales person and a person with editing rights are staff members. The ABox  is the one of Example 1.
is the one of Example 1.
Consider \({\mathcal {A}}_{\ge _1}\) and \({\mathcal {A}}_{\ge _2}\) two ABoxes compatible with  , and their well-ordered partitions, \({\mathcal {A}}_{\ge _1} = ({\mathcal {S}}_1 \cup {\mathcal {S}}_2 \cup {\mathcal {S}}_3 \cup {\mathcal {S}}_4)\) and \({\mathcal {A}}_{\ge _2} = ({\mathcal {S}}_1 \cup {\mathcal {S}}_2 \cup {\mathcal {S}}'_3 \cup {\mathcal {S}}'_4)\) such that:
, and their well-ordered partitions, \({\mathcal {A}}_{\ge _1} = ({\mathcal {S}}_1 \cup {\mathcal {S}}_2 \cup {\mathcal {S}}_3 \cup {\mathcal {S}}_4)\) and \({\mathcal {A}}_{\ge _2} = ({\mathcal {S}}_1 \cup {\mathcal {S}}_2 \cup {\mathcal {S}}'_3 \cup {\mathcal {S}}'_4)\) such that:
\({\mathcal {S}}_1 = \{\textsf {Reports}(\textsf {F78})\}\), \({\mathcal {S}}_2 = \{\textsf {Manager}(\textsf {Bob})\}\), \({\mathcal {S}}_3 = \{\textsf {Sales}(\textsf {Bob})\}\), \({\mathcal {S}}'_3 = \{\textsf {Sales}(\textsf {Bob}),\) \(\textsf {Sign}(\textsf {Bob},\textsf {F78})\}\), \({\mathcal {S}}_4\) \( = \{\textsf {Sign}(\textsf {Bob},\textsf {F78}),\) \(\textsf {Edit}(\textsf {Bob},\textsf {F78})\}\), and \({\mathcal {S}}'_4 = \{\textsf {Edit}(\textsf {Bob},\textsf {F78})\}\).
Figure 4 illustrates  , \({\mathcal {A}}_{\ge _1}\) and \({\mathcal {A}}_{\ge _2}\) (recall that \(\equiv \) denotes equal certainty). It is easy to check that \({\mathcal {A}}_{\ge _1}\) and \({\mathcal {A}}_{\ge _2}\) are compatible with
, \({\mathcal {A}}_{\ge _1}\) and \({\mathcal {A}}_{\ge _2}\) (recall that \(\equiv \) denotes equal certainty). It is easy to check that \({\mathcal {A}}_{\ge _1}\) and \({\mathcal {A}}_{\ge _2}\) are compatible with  . Their associated repairs are: \({\mathcal {R}}({\mathcal {A}}_{\ge _1}) = \{\textsf {Reports}(\textsf {F78})\), \(\textsf {Manager}(\textsf {Bob})\), \(\textsf {Sales}(\textsf {Bob})\}\) and \({\mathcal {R}}({\mathcal {A}}_{\ge _2}) = \{\textsf {Reports}(\textsf {F78})\), \(\textsf {Manager}(\textsf {Bob})\}\).
. Their associated repairs are: \({\mathcal {R}}({\mathcal {A}}_{\ge _1}) = \{\textsf {Reports}(\textsf {F78})\), \(\textsf {Manager}(\textsf {Bob})\), \(\textsf {Sales}(\textsf {Bob})\}\) and \({\mathcal {R}}({\mathcal {A}}_{\ge _2}) = \{\textsf {Reports}(\textsf {F78})\), \(\textsf {Manager}(\textsf {Bob})\}\).
Consider the assertion \(\textsf {Staff}(\textsf {Bob})\) and its two supports, \({\mathcal {B}}_1=\{\textsf {Sales}(\textsf {Bob})\}\) and \({\mathcal {B}}_2 = \{\textsf {Edit}(\textsf {Bob},\textsf {F78})\}\). Notice that \({\mathcal {R}}({\mathcal {A}}_{\ge _1}) \vDash \textsf {Staff}(\textsf {Bob})\) but \({\mathcal {R}}({\mathcal {A}}_{\ge _2}) \not \vDash \textsf {Staff}(\textsf {Bob})\). Hence,  . Proposition 2 confirms this result, since neither \({\mathcal {B}}_1\) nor \({\mathcal {B}}_2\) dominates the conflict \(\{\textsf {Sales}(\textsf {Bob})\), \(\textsf {Sign}(\textsf {Bob},\textsf {F78})\}\).
. Proposition 2 confirms this result, since neither \({\mathcal {B}}_1\) nor \({\mathcal {B}}_2\) dominates the conflict \(\{\textsf {Sales}(\textsf {Bob})\), \(\textsf {Sign}(\textsf {Bob},\textsf {F78})\}\).
\(\square \)
Propositions 1 and 2 provide a full characterization for membership in  based on the notions of support and dominance. The next proposition states (as expected) that
based on the notions of support and dominance. The next proposition states (as expected) that  is consistent and more productive than
is consistent and more productive than  . Formally:
. Formally:
Proposition 3
-
1.
 is consistent.
is consistent. -
2.
 . The converse is false (i.e.,
. The converse is false (i.e.,  ).
).
Example 2 confirms that  .
.
The next proposition establishes the tractability of  . This follows from the characterization given in Propositions 1 and 2, i.e., using the notions of dominance and support. Indeed, computing the conflicts and the supports can be achieved in polynomial time [10]. Besides, it can be shown that the number of conflicts and supports is bounded by
. This follows from the characterization given in Propositions 1 and 2, i.e., using the notions of dominance and support. Indeed, computing the conflicts and the supports can be achieved in polynomial time [10]. Besides, it can be shown that the number of conflicts and supports is bounded by  (where \(cln(\mathcal {T})\) denotes the negative closure of the TBox \(\mathcal {T}\), i.e., all the negative axioms that can be inferred from it). Moreover, in the context of OBDA, the size of the TBox is often considered negligible compared to the size of the ABox, thus the main focus is on data complexity. Lastly, it is important to note that retrieving all the conflicts beforehand is not required. Instead, checking whether an assertion is in C\(\pi \)-repair can be performed by progressively examining the conflicts (an implementation is available at https://github.com/ahmedlaouar/py_reasoner). This incremental feature is particularly beneficial for evolving ABoxes.
(where \(cln(\mathcal {T})\) denotes the negative closure of the TBox \(\mathcal {T}\), i.e., all the negative axioms that can be inferred from it). Moreover, in the context of OBDA, the size of the TBox is often considered negligible compared to the size of the ABox, thus the main focus is on data complexity. Lastly, it is important to note that retrieving all the conflicts beforehand is not required. Instead, checking whether an assertion is in C\(\pi \)-repair can be performed by progressively examining the conflicts (an implementation is available at https://github.com/ahmedlaouar/py_reasoner). This incremental feature is particularly beneficial for evolving ABoxes.
Proposition 4
Let  be a partially preordered KB and \(\varphi \) be an assertion. Checking if
be a partially preordered KB and \(\varphi \) be an assertion. Checking if  is done in polynomial time in DL-Lite\(_{\mathcal {R}}\).
is done in polynomial time in DL-Lite\(_{\mathcal {R}}\).
5 Rationality Properties of \(\pi \)-Acceptance and C\(\pi \)-Repair
In this section, we study the rationality properties of query-answering using the possibilistic repair method and its closure-based version.
Let  be a partially preordered KB which may be inconsistent and let q be a query. Consider the KB’s possibilistic repairs
be a partially preordered KB which may be inconsistent and let q be a query. Consider the KB’s possibilistic repairs  (Definition 2) and
(Definition 2) and  (Definition 4).
(Definition 4).
Let us start with unconditional query-answering, which amounts to checking whether the query q follows from the repair  (resp.
(resp.  ), denoted with the symbol \(\vDash ^{\pi }\) (resp. \(\vDash ^{c\pi }\)), and \(\vDash \) denotes standard DL-Lite\(_{\mathcal {R}}\) inference. Formally:
), denoted with the symbol \(\vDash ^{\pi }\) (resp. \(\vDash ^{c\pi }\)), and \(\vDash \) denotes standard DL-Lite\(_{\mathcal {R}}\) inference. Formally:

The following result states that the unconditional inferences \(\vDash ^{\pi }\) and \(\vDash ^{c\pi }\) meet the rationality properties of unconditional inconsistency-tolerant semantics defined in [2]. Namely:
Proposition 5
The unconditional possibilistic inference relation \(\vDash ^{s}\) (with \(s \in \{\pi , c\pi \}\)) satisfies the following properties:
-
QCE (Query Conjunction Elimination) If
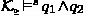 then
then  and
and  .
. -
QCI (Query Conjunction Introduction) If
 and
and  then
then  .
. -
Cons (Consistency) For any set of assertions \({\mathcal {B}}\), if
 then \(\langle \mathcal {T}, {\mathcal {B}} \rangle \) is consistent.
then \(\langle \mathcal {T}, {\mathcal {B}} \rangle \) is consistent. -
ConsC (Consistency of Conjunction) For any set of assertions \({\mathcal {B}}\), if for all \(\varphi \in {\mathcal {B}}\),
 , then \(\langle \mathcal {T}, {\mathcal {B}} \rangle \) is consistent.
, then \(\langle \mathcal {T}, {\mathcal {B}} \rangle \) is consistent. -
ConsS (Consistency of Support) For any set of assertions \({\mathcal {B}}\), if
 then there is a maximally consistent subset \({\mathcal {A}}'\) of
then there is a maximally consistent subset \({\mathcal {A}}'\) of  s.t. \(\langle \mathcal {T},{\mathcal {A}}' \rangle \vDash {\mathcal {B}}\).
s.t. \(\langle \mathcal {T},{\mathcal {A}}' \rangle \vDash {\mathcal {B}}\).
The proof of Proposition 5 is immediate since it is based on a direct application of standard DL-Lite entailment to the repairs  (resp.
(resp.  ).
).
We now focus on conditional query-answering, which amounts to querying a partially preordered KB under a given set of assertions considered fully reliable and consistent with respect to the TBox, called an observation or a fully observable set and denoted by \({\mathcal {O}}\). We write  to indicate that q follows from the KB
to indicate that q follows from the KB  , under the observation \({\mathcal {O}}\), using the inconsistency-tolerant semantics s (here \(s=\pi \) for the possibilistic repair and \(s=c\pi \) for its closure-based version). A standard way to proceed is to first add \({\mathcal {O}}\) to the ABox with the highest priority, then apply the possibilistic repair method (and its closure-based version) using Eq. 1 to unconditionally answer queries from the augmented KB.
, under the observation \({\mathcal {O}}\), using the inconsistency-tolerant semantics s (here \(s=\pi \) for the possibilistic repair and \(s=c\pi \) for its closure-based version). A standard way to proceed is to first add \({\mathcal {O}}\) to the ABox with the highest priority, then apply the possibilistic repair method (and its closure-based version) using Eq. 1 to unconditionally answer queries from the augmented KB.
Let us denote by \({\mathcal {K}}_{{\mathcal {O}}}=\langle \mathcal {T},{\mathcal {A}}_{\unrhd _{{\mathcal {O}}}} \rangle \) the augmented KB where  results from adding \({\mathcal {O}}\) to
results from adding \({\mathcal {O}}\) to  with the highest priority. Moreover, the partial preorder \(\unrhd _{{\mathcal {O}}}\) over
with the highest priority. Moreover, the partial preorder \(\unrhd _{{\mathcal {O}}}\) over  is obtained from \(\unrhd \) as follows:
is obtained from \(\unrhd \) as follows:
-
(i)
For all \(\varphi _1 \in {\mathcal {O}}\), for all \(\varphi _2 \in {\mathcal {O}}\): \(\varphi _1 \unrhd _{{\mathcal {O}}} \varphi _2\) and \(\varphi _2 \unrhd _{{\mathcal {O}}} \varphi _1\) (i.e., \(\varphi _1\) and \(\varphi _2\) are equally reliable).
-
(ii)
For all \(\varphi _1 \in {\mathcal {O}}\), for all
 : \(\varphi _1 \rhd _{{\mathcal {O}}} \varphi _2\) (i.e., every \(\varphi _1 \in {\mathcal {O}}\) is strictly more preferred than any
: \(\varphi _1 \rhd _{{\mathcal {O}}} \varphi _2\) (i.e., every \(\varphi _1 \in {\mathcal {O}}\) is strictly more preferred than any  . This serves to give priority to \({\mathcal {O}}\)).
. This serves to give priority to \({\mathcal {O}}\)). -
(iii)
For all
 , for all
, for all  : \(\varphi _1 \unrhd _{{\mathcal {O}}} \varphi _2\) iff \(\varphi _1 \unrhd \varphi _2\) (i.e., the relative ordering between the elements of
: \(\varphi _1 \unrhd _{{\mathcal {O}}} \varphi _2\) iff \(\varphi _1 \unrhd \varphi _2\) (i.e., the relative ordering between the elements of  that are not in \({\mathcal {O}}\) is preserved).
that are not in \({\mathcal {O}}\) is preserved).
Next, we define the partially preordered conditional query-answering relation.
Definition 7
(Conditional inference) Let  be a partially preordered KB, \({\mathcal {O}}\) an observation and q a query. Then q follows from
be a partially preordered KB, \({\mathcal {O}}\) an observation and q a query. Then q follows from  and \({\mathcal {O}}\), denoted
and \({\mathcal {O}}\), denoted  , if \({\mathcal {K}}_{{\mathcal {O}}} \vDash ^{s} q\) (with \(s\in \{\pi , c\pi \}\)), where \({\mathcal {K}}_{{\mathcal {O}}}=\langle \mathcal {T},{\mathcal {A}}_{\unrhd _{{\mathcal {O}}}} \rangle \) is the augmented KB and \(\unrhd _{{\mathcal {O}}}\) its associated partial preorder (described in (i), (ii), (iii)), and \(\vDash ^{s}\) is the unconditional query-answering relation given by Eq. 1.
, if \({\mathcal {K}}_{{\mathcal {O}}} \vDash ^{s} q\) (with \(s\in \{\pi , c\pi \}\)), where \({\mathcal {K}}_{{\mathcal {O}}}=\langle \mathcal {T},{\mathcal {A}}_{\unrhd _{{\mathcal {O}}}} \rangle \) is the augmented KB and \(\unrhd _{{\mathcal {O}}}\) its associated partial preorder (described in (i), (ii), (iii)), and \(\vDash ^{s}\) is the unconditional query-answering relation given by Eq. 1.
One can check that  is non-monotonic for both semantics (the possibilistic repair and its closure-based version). The well-known System P [24], originally defined in the context of propositional logic, has been adapted to DL-Lite\(_{\mathcal {R}}\) in [3] (see also [14, 21] for an adaptation to richer description logics).
is non-monotonic for both semantics (the possibilistic repair and its closure-based version). The well-known System P [24], originally defined in the context of propositional logic, has been adapted to DL-Lite\(_{\mathcal {R}}\) in [3] (see also [14, 21] for an adaptation to richer description logics).
The adaptation of System P’s rules is given below, where  is a KB, \({\mathcal {O}}_1\), \({\mathcal {O}}_2\), \({\mathcal {O}}_3\) are observations, s is an inconsistency-tolerant semantics with \(s\in \{\pi , c\pi \}\), \(\vDash \) and \(\equiv \) denote standard DL-Lite\(_{\mathcal {R}}\) inference and equivalence:
is a KB, \({\mathcal {O}}_1\), \({\mathcal {O}}_2\), \({\mathcal {O}}_3\) are observations, s is an inconsistency-tolerant semantics with \(s\in \{\pi , c\pi \}\), \(\vDash \) and \(\equiv \) denote standard DL-Lite\(_{\mathcal {R}}\) inference and equivalence:
-
R (Reflexivity)
 .
. -
LLE (Left Logical Equivalence) If \(\langle \mathcal {T},{\mathcal {O}}_{1} \rangle \! \equiv \! \langle \mathcal {T},{\mathcal {O}}_{2} \rangle \) and
 then
then  .
. -
RW (Right Weakening) If \(\langle \mathcal {T},{\mathcal {O}}_{1} \rangle \vDash \langle \mathcal {T},{\mathcal {O}}_{2} \rangle \) and
 , then
, then  .
. -
Cut If
 and
and  , then
, then  .
. -
CM (Cautious Monotony) If
 and
and  , then
, then  .
. -
And If
 and
and  then
then  .
.
In this paper, we propose to also consider two additional properties, originally defined in propositional logic, and which go beyond cautious monotony:
-
RM (Rational Monotony) If
 , then
, then  or
or  is inconsistent.
is inconsistent. -
Comp (Completeness) If
 , then either
, then either  or
or  is inconsistent.
is inconsistent.
Note that the adaptation of the last two properties that we propose uses the notion of inconsistency instead of negation in the original definition of rational monotony, and uses a disjunctive interpretation of RMFootnote 6. Here, RM states that given a new observation, we can continue to believe in the previous plausible consequences of the KB, or the new observation conflicts with the KB. The Comp ruleFootnote 7 is stronger than RM, and states that given a new observation \({\mathcal {O}}_2\), then either \({\mathcal {O}}_3\) continues to be derived from both \({\mathcal {O}}_1\) and \({\mathcal {O}}_2\), or \({\mathcal {O}}_2\) contradicts the whole KB (plus itself). Intuitively, this means that either we continue to believe in \({\mathcal {O}}_3\), or we should believe in its negation (there is no room for ignoring \({\mathcal {O}}_3\)).
The next proposition summarizes the results of the conditional properties:
Proposition 6
Let  be a partially preordered KB, \({\mathcal {O}}\) be an observation and q be a query. The query-answering relations
be a partially preordered KB, \({\mathcal {O}}\) be an observation and q be a query. The query-answering relations  and
and  satisfy the properties R, LLE, RW, Cut, CM and And. However, they fail to satisfy RM and Comp.
satisfy the properties R, LLE, RW, Cut, CM and And. However, they fail to satisfy RM and Comp.
6 Concluding Discussions
Developing tractable and safe methods for inconsistency management is a challenge and is crucial for dealing with inconsistent large-scale knowledge bases. This paper follows this research line where we tackled the issue of computing a productive repair for possibilistic partially preordered ontologies. We defined the C\(\pi \)-repair method which interprets a partial preorder into a family of compatible ABoxes, computes their possibilistic repairs, closes those repairs and intersects them to yield a more productive repair.
An important result of this paper is that we characterized this method equivalently using the notions of dominance and support, which ensures the tractable calculation of the repair. This characterization can be generalized easily to more expressive description languages (it suffices to replace the DL-Lite\(_{\mathcal {R}}\) inference relation in the support definition by that of a more expressive language). However, tractability is guaranteed only if the computation of the conflicts and supports is performed in polynomial time and their size remains polynomial in the ABoxe’s size (a detailed discussion is given below). A future work is to characterize the linear repair [26] and the Elect [6] methods to partially preordered ABoxes.
We conclude this paper with a few discussion points on the rational properties as well as on the possibility of generalizing our method to richer languages or other inconsistency-tolerant semantics.
On the Rational Properties: The two possibilistic semantics studied in this paper satisfy the unconditional properties (Proposition 5) and the rules of System P (Proposition 6). If these propositions seem natural, even minimal, they are not always satisfied by some inconsistency-tolerant semantics. For example, the so-called majority semantics (a query is valid if it is obtained from the majority of the repairs of an inconsistent ABox) does not satisfy these minimal properties. More precisely, in [3] it has been shown that majority-based inference does not satisfy Cut, Cautious Monotony, and And properties, even in DL-Lite\(_{\mathcal {R}}\). Another example where System P is not satisfied is existential inference, where a query is valid if it follows from one repair.
On the non-satisfaction of the rational monotony (RM) property, the result is expected if we draw a parallel with standard possibilistic propositional logic (LP) and with the properties of non-monotonic relations. Indeed, there is a representation theorem (KLM [24]) which shows that any non-monotonic relation which satisfies System P and RM is necessarily representable by a total order on the set of interpretations of propositional logic.
On the Extension to Richer Languages: From a semantic point of view, the definitions of C\(\pi \)-repair given in Sect. 3, that have been established within the framework of DL-Lite\(_{\mathcal {R}}\), remain valid for richer languages (provided that the notion of deductive closure of an ABox with respect to a TBox can be defined). Indeed, the general process given in Fig. 2 is not proper to DL-Lite\(_{\mathcal {R}}\) and easily applies to richer languages (e.g. Existential Rules). The challenge here is at the computational level, since we need first to find an equivalent characterization (like we did in this paper using support/dominance) and then show that it is tractable. For instance, in many description logics where conflicts may be composed of any number of assertions (unlike DL-Lite where conflicts consist of at most two assertions [16]), the extension of the support/dominance characterization is possible. However, even if the conflict set is computed in polynomial time, the size of this set itself can be exponential w.r.t. the size of the ABox. In this case, tractability cannot be preserved.
Furthermore, the main idea behind query-answering from inconsistent partially ordered knowledge bases is to extend the partial order into the set of its compatible total orders, then to apply a repair semantics to each one of them. The strategy we used in our approach (based on the possibilistic version of DL-Lite\(_{\mathcal {R}}\)) yields a single repair for each total order. However, in the general case, using a different strategy, each total order may return multiple repairs. Hence, a query needs to follow from all the repairs for all the compatible total orders.
On the Extension to Non-repair Based Semantics: We end this paper with a brief discussion on the applicability of inconsistency-tolerant semantics that are not directly based on repairs, such as paraconsistent multi-valued description logics, on partially ordered ABoxes. Let us first specify that an advantage of our approach is that once the possibilistic repair C\(\pi \)-repair is calculated, query-answering is done in a standard way. Within multi-valued semantics, the ABox remains unchanged, but the query-answering mechanisms need to be adapted and this can potentially generate an additional computational cost. Besides, from a semantic point of view, it is possible to redefine this work with multi-valued semantics. This can be done by first selecting a multi-valued semantics of DL-Lite\(_{\mathcal {R}}\) (for example the 4-valued semantics given in [30]). The next step consists in extending it to the possibilistic framework with a totally ordered ABox. This requires an adaptation of the existing work (for flat ABox) to define preferred 4-valued canonical models. The last step consists in taking all the extensions of the total orders and defining the 4-valued canonical models of the partial ABox as the union of the preferred 4-valued canonical model of each total ABox extension. However, having an equivalent characterization (without generating all the extensions of the partial order) to the one given in this paper (Propositions 1 and 2), is not obvious to achieve.
Notes
- 1.
Given two inconsistency-tolerant semantics \(s_1\) and \(s_2\). Then \(s_1\) is more productive than \(s_2\) if any conclusion derived with \(s_2\) can also be derived with \(s_1\).
- 2.
Note the difference between the ICR semantics which deductively closes the repairs of an ABox, and the ICAR semantics which computes the repairs for a closed ABox.
- 3.
A binary relation \(\ge \) over \({\mathcal {A}}\) is a total preorder if it is reflexive and transitive, and for all \(\varphi _j \in {\mathcal {A}}\), for all \(\varphi _k \in {\mathcal {A}}\), either \(\varphi _j \ge \varphi _k\) or \(\varphi _k \ge \varphi _j\).
- 4.
A binary relation \(\unrhd \) over \({\mathcal {A}}\) is a partial preorder if it is reflexive and transitive. Thus somes elements of \({\mathcal {A}}\) may be incomparable according to \(\unrhd \).
- 5.
Consider \(\varphi _j\) and \(\varphi _k\) in \({\mathcal {A}}\). \(\varphi _j \bowtie \varphi _k\) means that neither \(\varphi _j \unrhd \varphi _k\) nor \(\varphi _k \unrhd \varphi _j\) holds.
- 6.
In propositional logic (PL), RM is defined as: if \(\alpha \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \gamma \) and \(\alpha \,{\mid \!\not \sim }_{{\mathcal {K}}}^{}\, \lnot \beta \), then \(\alpha \wedge \beta \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \gamma \), where \(\alpha \), \(\beta \) and \(\gamma \) are PL formulas. Our adaptation consists first in rewriting RM equivalently in a disjunctive way: if \(\alpha \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \gamma \), then \(\alpha \wedge \beta \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \gamma \) or \(\alpha \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \lnot \beta \). Lastly, we replace \(\alpha \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \lnot \beta \) with \(\alpha \wedge \beta \) is inconsistent with the KB.
- 7.
In PL, Comp is defined as: if \(\alpha \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \gamma \), then either \(\alpha \wedge \beta \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \gamma \) or \(\alpha \wedge \beta \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \lnot \gamma \). Here, we simply replace \(\alpha \wedge \beta \,{\mid \!\sim }_{{\mathcal {K}}}^{}\, \lnot \gamma \) with \(\alpha \wedge \beta \wedge \gamma \) is inconsistent with the KB.
References
Artale, A., Calvanese, D., Kontchakov, R., Zakharyaschev, M.: The DL-Lite family and relations. J. Artif. Intell. Res. (JAIR) 36, 1–69 (2009). https://doi.org/10.1613/jair.2820
Baget, J., et al.: A general modifier-based framework for inconsistency-tolerant query answering. In: Principles of Knowledge Representation and Reasoning (KR), Cape Town, South Africa, pp. 513–516 (2016)
Baget, J.F., et al.: Inconsistency-tolerant query answering: rationality properties and computational complexity analysis. In: Michael, L., Kakas, A. (eds.) JELIA 2016. LNCS (LNAI), vol. 10021, pp. 64–80. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48758-8_5
Banerjee, M., Dubois, D., Godo, L., Prade, H.: On the relation between possibilistic logic and modal logics of belief and knowledge. J. Appl. Non-Classical Logics 27(3–4), 206–224 (2017)
Belabbes, S., Benferhat, S.: Computing a possibility theory repair for partially preordered inconsistent ontologies. IEEE Trans. Fuzzy Syst. 30, 3237–3246 (2021)
Belabbes, S., Benferhat, S., Chomicki, J.: Handling inconsistency in partially preordered ontologies: the Elect method. J. Log. Comput. 31(5), 1356–1388 (2021)
Benferhat, S., Bouraoui, Z., Tabia, K.: How to select one preferred assertional-based repair from inconsistent and prioritized DL-Lite knowledge bases? In: International Joint Conference on Artificial Intelligence (IJCAI), Buenos Aires, Argentina, pp. 1450–1456 (2015)
Benferhat, S., Garcia, L.: Handling locally stratified inconsistent knowledge bases. Stud. Logica. 70(1), 77–104 (2002)
Bienvenu, M.: On the complexity of consistent query answering in the presence of simple ontologies. In: Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, Toronto, Ontario, Canada (2012)
Bienvenu, M., Bourgaux, C.: Inconsistency-tolerant querying of description logic knowledge bases. In: Pan, J.Z., et al. (eds.) Reasoning Web 2016. LNCS, vol. 9885, pp. 156–202. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-49493-7_5
Bienvenu, M., Bourgaux, C.: Querying and repairing inconsistent prioritized knowledge bases: complexity analysis and links with abstract argumentation. In: Principles of Knowledge Representation and Reasoning (KR), Virtual Event, pp. 141–151 (2020)
Bienvenu, M., Bourgaux, C., Goasdoué, F.: Querying inconsistent description logic knowledge bases under preferred repair semantics. In: AAAI, pp. 996–1002 (2014)
Brewka, G.: Preferred subtheories: an extended logical framework for default reasoning. In: IJCAI, Detroit, USA, pp. 1043–1048 (1989)
Britz, K., Casini, G., Meyer, T., Moodley, K., Sattler, U., Varzinczak, I.: Principles of KLM-style defeasible description logics. ACM Trans. Comput. Log. 22(1), 1:1–1:46 (2021)
Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M., Rosati, R.: Tractable reasoning and efficient query answering in description logics: the DL-Lite family. J. Autom. Reason. 39(3), 385–429 (2007)
Calvanese, D., Kharlamov, E., Nutt, W., Zheleznyakov, D.: Evolution of DL-Lite knowledge bases. In: Patel-Schneider, P.F., et al. (eds.) ISWC 2010. LNCS, vol. 6496, pp. 112–128. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17746-0_8
Dempster, A.P.: Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 38, 325–339 (1967)
Dubois, D., Prade, H.: Possibilistic logic - an overview. Comput. Logic 9, 197–255 (2014)
Dubois, D., Prade, H.: A crash course on generalized possibilistic logic. In: Ciucci, D., Pasi, G., Vantaggi, B. (eds.) SUM 2018. LNCS (LNAI), vol. 11142, pp. 3–17. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00461-3_1
Dubois, D., Prade, H., Schockaert, S.: Generalized possibilistic logic: foundations and applications to qualitative reasoning about uncertainty. Artif. Intell. J. 252, 139–174 (2017)
Everett, L., Morris, E., Meyer, T.: Explanation for KLM-style defeasible reasoning. In: Jembere, E., Gerber, A.J., Viriri, S., Pillay, A. (eds.) SACAIR 2021. CCIS, vol. 1551, pp. 192–207. Springer, Cham (2022). https://doi.org/10.1007/978-3-030-95070-5_13
Fagin, R., Halpern, J.Y., Moses, Y., Vardi, M.Y.: Reasoning About Knowledge. MIT Press, Cambridge (2003)
Finger, M., Godo, L., Prade, H., Qi, G.: Advances in weighted logics for artificial intelligence. Int. J. Approximate Reasoning 88, 385–386 (2017)
Kraus, S., Lehmann, D., Magidor, M.: Nonmonotonic reasoning, preferential models and cumulative logics. Artif. Intell. J. 44(1–2), 167–207 (1990)
Lembo, D., Lenzerini, M., Rosati, R., Ruzzi, M., Savo, D.F.: Inconsistency-tolerant semantics for description logics. In: Hitzler, P., Lukasiewicz, T. (eds.) RR 2010. LNCS, vol. 6333, pp. 103–117. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15918-3_9
Nebel, B.: Base revision operations and schemes: semantics, representation and complexity. In: European Conference on Artificial Intelligence, pp. 341–345 (1994)
Poggi, A., Lembo, D., Calvanese, D., Giacomo, G.D., Lenzerini, M., Rosati, R.: Linking data to ontologies. J. Data Semant. 10, 133–173 (2008)
Shafer, G.: A Mathematical Theory of Evidence. Princeton University Press, Princeton (1976)
Spohn, W.: The Laws of Belief - Ranking Theory and Its Philosophical Applications. Oxford University Press, Oxford (2014)
Zhou, L., Huang, H., Qi, G., Ma, Y., Huang, Z., Qu, Y.: Paraconsistent query answering over DL-Lite ontologies. Web Intell. Agent Syst. Int. J. 10(1), 19–31 (2012)
Acknowledgements
This research has received support from the European Union’s Horizon research and innovation programme under the MSCA-SE (Marie Skłodowska-Curie Actions Staff Exchange) grant agreement 101086252; Call: HORIZON-MSCA-2021-SE-01; Project title: STARWARS (STormwAteR and WastewAteR networkS heterogeneous data AI-driven management).
This research has also received support from the French national project ANR (Agence Nationale de la Recherche) EXPIDA (EXplainable and parsimonious Preference models to get the most out of Inconsistent DAtabases), grant number ANR-22-CE23-0017 and from the ANR project Vivah (Vers une intelligence artificielle à visage humain), grant number ANR-20-THIA-0004.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Laouar, A., Belabbes, S., Benferhat, S. (2023). Tractable Closure-Based Possibilistic Repair for Partially Ordered DL-Lite Ontologies. In: Gaggl, S., Martinez, M.V., Ortiz, M. (eds) Logics in Artificial Intelligence. JELIA 2023. Lecture Notes in Computer Science(), vol 14281. Springer, Cham. https://doi.org/10.1007/978-3-031-43619-2_25
Download citation
DOI: https://doi.org/10.1007/978-3-031-43619-2_25
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43618-5
Online ISBN: 978-3-031-43619-2
eBook Packages: Computer ScienceComputer Science (R0)





 .
. .
. .
. that is compatible with
that is compatible with  .
. , compute its totally preordered possibilistic repair
, compute its totally preordered possibilistic repair  as defined above.
as defined above.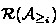 to obtain
to obtain  .
.
 . Right: The conflicts of
. Right: The conflicts of  (dashed lines) and the relation
(dashed lines) and the relation 
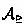 into a family of totally preordered ABoxes, denoted
into a family of totally preordered ABoxes, denoted  .
.

 is consistent.
is consistent. . The converse is false (i.e.,
. The converse is false (i.e.,  ).
).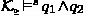 then
then  and
and  .
. and
and  then
then  .
. then
then  , then
, then  then there is a maximally consistent subset
then there is a maximally consistent subset  s.t.
s.t.  :
:  . This serves to give priority to
. This serves to give priority to  , for all
, for all  :
:  that are not in
that are not in  .
. then
then  .
. , then
, then  .
. and
and  , then
, then  .
. and
and  , then
, then  .
. and
and  then
then  .
. , then
, then  or
or  is inconsistent.
is inconsistent. , then either
, then either  or
or  is inconsistent.
is inconsistent.