Keywords

1 Introduction

A large number of works are devoted to the calculation of solid and composite plates [1,2,3,4,5,6,7,8,9]. This article presents the study of the coefficient K, which express the relation between the frequencies of natural vibrations and the maximum deflections of the plates.

The determination of static and dynamic characteristics leads to determining the deflections [10,11,12,13,14,15] and frequencies of system vibrations [16,17,18,19] in solving the relevant differential equations. The functional relationship between the maximum deflection and the frequency of the fundamental mode of free transverse vibrations of elastic isotropic plates was proved by V. I. Korobko [5].

2 Materials and Methods

The differential equation of the plate transverse deflection has the form:

$$ \frac{{\partial^{4} W}}{{\partial x^{4} }} + 2\frac{{\partial^{4} W}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} W}}{{\partial y^{4} }} = \frac{q}{D} $$
(1)

With the use of biharmonic operators, the equation takes the form:

$$ D\nabla^{2} \nabla^{2} W = \frac{q}{D}. $$
(2)

where W = W (x, y) is the deflection function of the plate at the transverse deflection; \(\nabla ^{2} \nabla ^{2}\)\({\nabla }^{2}{\nabla }^{2}\)—is a biharmonic operator; \({D=EH}^{3}/(12\left(1-{\upnu }^{2}\right))\) is cylindrical stiffness of the plate;

q(x, y) is the law of the lateral load change.

The differential equation of plate free vibrations:

$$ D\left( {\frac{{\partial^{4} W}}{{\partial x^{4} }} + 2\frac{{\partial^{4} W}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} W}}{{\partial y^{4} }}} \right) + m\frac{{\partial^{2} W}}{{\partial t^{2} }} = 0 $$
(3)
$$ D\nabla^{2} \nabla^{2} W + m\frac{{\partial^{2} W}}{{\partial t^{2} }} = 0. $$
(4)

where W = W (x, y, t) is the deflection function of a freely oscillating plate; m is the mass per unit area of the plate; E, ν are respectively the modulus of elasticity of the material and the Poisson’s ratio.

If the vibrations are harmonic

$$ W = W(x,y) \cdot \cos (\omega t), $$
(5)

then Eq. (1) can be transformed to the following form:

$$ D\nabla^{2} \nabla^{2} W - m\omega^{2} W = 0 $$

or

$$ D\nabla^{2} \nabla^{2} W - \beta^{2} W = 0, $$

where β2 = mω2/D is the eigenvalue of the differential equation of vibrations of the plates.

Let us represent the deflection function as a product of the maximum deflection W0 by the unit function f (x, y) and substitute it in the differential equations of transverse deflection and free vibrations of the plates:

$$ W(x,y) = W_{0} f(x,y) $$
(6)
$$ \left\{ \begin{gathered} D\nabla^{2} \nabla^{2} f - m\omega^{2} f = 0 \hfill \\ DW_{0} \nabla^{2} \nabla^{2} f - q(x,y) = 0 \hfill \\ \end{gathered} \right. $$

It should be noted that the precise solution of these differential equations is valid only in the frequent cases of plate forms and boundary conditions. Therefore, in practice, approximate methods of solution are mainly used.

If we assume that the plate is under a uniformly distributed load q, then having integrated Eq. (6) over the entire area of the region, and having performed the necessary transformations, we will get:

$$ W_{0} = \frac{q}{D}\frac{A}{{\iint\limits_{A} {\nabla^{2} \nabla^{2} fdA}}},\begin{array}{*{20}c} {} & {} \\ \end{array} \omega^{2} = \frac{D}{m}\frac{{\iint\limits_{A} {\nabla^{2} \nabla^{2} fdA}}}{{\iint\limits_{A} {fdA}}}. $$
(7)

The deflection function W(x, y) can approximately be put down in a one-parameter form in the polar coordinate system:

$$ W(x,y) = W_{0} f(x,y) = W_{0} g\left[ {\frac{t}{r(\phi )}} \right] = W_{0} g(\rho ) $$
(8)

where r = r(φ) is the equation of the contour of the plate in the polar coordinate system, t and φ are polar coordinates, ρ = t/r(φ) is the dimensionless polar coordinate.

This function describes a surface which level lines are similar to the region contour and are similarly located. The representation of the function of deflections in this form is justified by the fact that through it we can write down the exact solution to the problem of transverse deflection of a rigidly pinched elliptical plate under the action of a uniformly distributed load. Since just in a single case it is possible to represent the real deflection function in the form of a one-parameter function (8), further results are of an approximate nature.

We transform the integrals in (7), taking into account the deflection function in form (8).

$$ \iint\limits_{A} {fdA = \int\limits_{0}^{2\pi } {\int\limits_{0}^{r} {g(\rho )tdtd\phi .} } } $$
(9)

Multiplying and dividing the right-hand side by r2, we get after the transformations:

$$ \iint\limits_{A} {fdA = 2A\int\limits_{0}^{1} {g(\rho )\rho d\rho .} } $$
(10)

Completing the transformation of the integral of the biharmonic operator according to, we finally write:

$$ I = \left( {K_{f}^{2} \Phi _{{g1}} + K_{f} \Phi _{{g2}} } \right)/A = K_{f} \left( {K_{f} \Phi _{{g1}} + \Phi _{{g2}} } \right)/A $$
(11)

where

$$ \begin{gathered}\Phi_{g1}^{{}} = \frac{1}{2}\int\limits_{0}^{1} {\left( {g^{IV} \rho - 12g^{\prime\prime\prime} - 21g^{\prime\prime}\rho^{ - 1} - 3g^{\prime}\rho^{ - 2} } \right)d\rho } , \hfill \\ \Phi_{g2}^{{}} = \frac{\pi }{2}\int\limits_{0}^{1} {\left( {2g^{IV} \rho + 14g^{\prime\prime\prime} + 22g^{\prime\prime}\rho^{ - 1} + 3g^{\prime}\rho^{ - 2} } \right)d\rho } , \hfill \\ \end{gathered} $$
(12)

The sign of the approximate equality in (11) appeared under the transformation of integrals by means of the Bunyakovsky inequality. We substitute integrals (9) and (11) into expressions (6). After the necessary transformations, we get:

$$\left\{ \begin{gathered} W_{0} \approx \frac{{qA^{2} }}{D}\frac{1}{{K_{f} ^{2} \Phi _{{g1}} + K_{f} \Phi _{{g2}} }}, \hfill \\ \omega ^{2} \approx \frac{D}{{2A^{2} m}}\frac{{K_{f} ^{2} \Phi _{{g1}} + K_{f} \Phi _{{g2}} }}{{\int\limits_{0}^{1} {g\rho d\rho } }} \hfill \\ \end{gathered} \right. $$
(13)

Since all the values of the definite integrals occurring in the expressions (13) are constant numbers depending on the accuracy of the choice of function g (ρ), they can be represented as the proportionality coefficients Kw, Kω and B. Then

$$ W_{0} = K_{w} \frac{q}{D}\frac{{A^{2} }}{{K_{f}^{2} + BK_{f} }},\begin{array}{*{20}c} {} & {} \\ \end{array} \omega^{2} = K_{\omega } \frac{D}{m}\frac{{K_{f}^{2} + BK_{f} }}{{A^{2} }}. $$
(14)

where

$$K_{w} = {1 \mathord{\left/ {\vphantom {1 {\Phi _{{g1}} }}} \right. \kern-\nulldelimiterspace} {\Phi _{{g1}} }};\begin{array}{*{20}c} {} & {K_{\omega } = \frac{1}{2}{{\Phi _{{g1}} } \mathord{\left/ {\vphantom {{\Phi _{{g1}} } {\int\limits_{0}^{1} {g\rho d\rho } }}} \right. \kern-\nulldelimiterspace} {\int\limits_{0}^{1} {g\rho d\rho } }};} \\ \end{array} \begin{array}{*{20}c} {} & {B = {{\Phi _{{g2}} } \mathord{\left/ {\vphantom {{\Phi _{{g2}} } {\Phi _{{g1}} }}} \right. \kern-\nulldelimiterspace} {\Phi _{{g1}} }}} \\ \end{array} . $$
(15)

Strictly speaking, the signs of approximate equalities should be put in expressions (14), in view of (12) and the approximation of function g (ρ).

Let us multiply the expressions (14) to each other:

$$ W_{0} \omega^{2} = K_{w} K_{\omega } \frac{q}{m} = K\frac{q}{m}. $$
(16)

Taking into account that the coefficients Kw and Kω depend on the shape of the plate, the following regularity can be obtained from the expression (16): for elastic isotropic plates of identical shapes with homogeneous boundary conditions, the product of the maximum deflection W0 from the action of the uniformly distributed load q per square of their fundamental frequency of transverse vibrations in the unloaded state, ω2 with accuracy up to the dimensional factor q/m is a constant. Thus, it is mathematically and rigorously proved that for the whole set of plates with homogeneous boundary conditions the product W0⋅ω2 will be represented by a single curve. An important feature of the formulated regularity is the fact that the product W0⋅ω2, which is considered in it, does not depend on the flexural rigidity and dimensions of constructions.

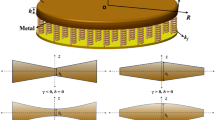
The design structure is a circular isotropic plate, the thickness of which varies in accordance with a parabola (Fig. 1). The thickness of the plate on the support is 5 cm, the thickness in the span varies according to the parabola with maximum value at the middle:

Fig. 1
A set of two illustrations. a. A circular isotropic plate in the shape of a parabola with varied thickness. b. A graph of T versus X depicts the thickness of the plate. The thickness is denoted by T 1, T 2, and T 3.

Circular plate with a linearly variable thickness (a—finite element scheme; b—plate thickness)

Full size image
$$t = 5 + k \cdot x^{{\frac{1}{2}}} (cm).$$
(17)

Numerical studies of the plates were carried out by the finite element method. The design schemes of composite plates are shown in Fig. 2. When calculating the plates, two support schemes were investigated: rigid pinching along the contour (Fig. 2a) and hinged support along the contour (Fig. 2b).

Fig. 2
A set of two illustrations depict the two support schemes of composite plates. a. It displays the rigid pinching along the contour. b. Hinged support along the contour. The plate diameter for two support schemes are noted as 6 meters.

Design diagrams of plates (a—with hinged support along the contour; b—with pinching along the contour)

Full size image

The plate with a diameter of 6 m is divided into 240 finite elements—24 elements in the annular direction and 10 finite elements in the radial direction (Fig. 1). The thickness of the plate on the support was taken constant 0.05 m; the thickness in the center was a variable parameter and varied from 0.05 m (plate of constant thickness) to 0.10 m with a step of 0.005 m. The plate was taken from steel of ordinary quality, volumetric weight 78.5 kN / m3. The modulus of elasticity is taken as E = 2.06 ⋅105 MPa according to the Building Code of Russian Federation SP 16.13330.2017 “Steel structures”. All studies were carried out under the assumption of the elastic work of the material. Uniformly distributed load was assumed to be q = 1 kN/m2 (Fig. 2). The support was carried out along the contour in the contour nodes of the plates. Two support schemes were provided—hinged support and fixing along the contour. To determine the natural frequencies of the transverse vibrations of the plates, concentrated masses from the empty weight of the plate were applied to the structural nodes in accordance with the load area of the nodes.

3 Results and Discussion

Determination of vibration and deflection frequencies was carried out using the SCAD software package [20]. The results of numerical studies of the plate are shown in Tables 1 and 2.

Table 1 Results of numerical studies of a circular plate, the thickness of which varies in accordance with a parabola, D = 6 m with hinged support
Full size table
Table 2 Results of numerical studies of a circular plate plate, the thickness of which varies in accordance with a parabola, d = 6 m when pinched along the contour
Full size table

According to the data of Tables 1 and 2, graphs of changes in the maximum deflections and vibration frequencies in the studied plates and the proportionality coefficient K are plotted. The deviation of the actual value of the coefficient K from the theoretical one was determined by the formula:

$$\Delta =\frac{{K}_{theor}-K}{{K}_{theor}}\cdot 100\%$$
(18)

Based on the results of the research, curves for the frequency of natural oscillations (Fig. 3), maximum deflections (Fig. 4) and the K coefficient (Fig. 5) are plotted.

Fig. 3
A graph depicts the change in maximum deflections and vibration frequencies for the two support schemes. It includes two plots. Pinched on the contour and hinged on the contour. The range of the pinched on the contour support plot is greater than that of the hinged support.

Change in free vibration frequencies depending on the thickness of the plate t2 in the center

Full size image
Fig. 4
A graph depicts the change in maximum deflections versus thickness of plate T 2 for the two support schemes. It includes two plots. Pinched on the contour and hinged on the contour. Hinged on the contour support plot has a higher range than the pinched contour support.

Change in deflections by static load depending on the thickness of the plate t2 in the center

Full size image
Fig. 5
A graph depicts the change in maximum coefficient versus thickness of plate T 2 for the two support schemes. It includes two plots. Pinched on the contour and hinged on the contour. Here the two plots are roughly similar. The pinched on the contour plot begins at negative 5 below the initial level.

Change in coefficient K depending on the thickness of the plate t2 in the center

Full size image

4 Conclusion

As a result of numerical studies, the maximum deflections and free vibration frequencies were determined for circular isotropic plates with a thickness varying in accordance with parabola with a thickening in the center. Studies showed that the coefficient K matches within 5% of the dependence of Professor V.I. Korobko only for the ratio of the thickness in the center to the thickness on the support t2 / t1 = 60/50 < 1.2 for both support schemes. This is due to the fact that formula (16) was derived for isotropic plates with constant thickness and the distribution of mass evenly over the entire area of the plate. This leads to a significant error already at the stage of a small difference between the thicknesses at the support and in the center. With a thickness ratio t2 / t1 = 100/50 = 2, the difference between the K coefficient and the analytical one is about 16%, and it should be expected that the difference will increase with increasing plate thickness in the center.