Geometrically Non-linear Free Vibrations of Simply Supported Rectangular Plates Connected to Two Distributions of Rotational Springs at Two Opposite Edges

Abstract

Although the dynamic behavior of rectangular plates has been the subject of much research for many decades, it remains of a crucial importance in various engineering fields and some edge conditions have not yet been treated, especially those involving edges connected to distributed rotational springs and non-linear vibrations. Also, in the practice of Modal Testing, theoretical models are needed for quantitatively estimating the flexibility of the real plate supports. A complementary work is presented here corresponding to plates connected to a distribution of rotational springs at two opposite edges vibrating in the geometrically non-linear regime occurring at large vibration amplitudes. To build the plate trial functions, defined as products of beam functions in the x and y directions, the mode shapes of simply supported beams connected to rotational springs are first calculated. Then, after exposing the general formulation of the non-linear problem, based on Hamilton’s principle and spectral analysis, the plate case is examined. Using the single mode approach, the backbone curves are determined, giving the non-linear frequency-amplitude dependence for plates having different combinations of stiffness and aspect ratios. It is noticed, as may be expected, that the obtained hardening non-linearity effect becomes more accentuated with increasing the rotational spring stiffness.

1 Introduction

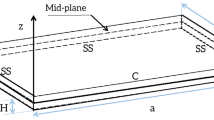
In spite of the amount of works performed on plate vibrations for many decades, only few papers deal with simply supported rectangular plates connected to two distributions of rotational springs at two opposite edges. Furthermore, to the knowledge of the authors, the geometrically nonlinear vibration of such elastically restrained plates has not been investigated, in spite of its theoretical and practical importance. On one hand, such edge conditions may be really encountered in practical situations. On the other hand, it should not be forgotten that the classical boundary conditions, i.e. simply supported and clamped, are practically impossible to achieve perfectly in real structures since the supports have always some flexibility. Consequently, it is of a crucial importance for designers to be able and quantitatively estimate how far do the plate real dynamic characteristics deviate from the theoretical ones, corresponding to rigid vertical supports and completely free rotations (simply supported case, denoted in what follows as SS), and to rigid vertical supports and completely prevented rotations (clamped case, denoted as C). From the point of view of modal analysis and testing, the availability of theoretical results corresponding to flexible supports with various stiffness values may be very useful in interpreting experimental data provided by modal testing and also for an accurate identification process.

The purpose of this paper is to present the formulation of the problem of non-linear vibrations of simply supported rectangular plates connected to two distributions of rotational springs at two opposite edges, in both the linear and non-linear cases. The Rayleigh-Ritz method is used in the linear case, with plate functions defined as products of beam functions, with appropriate end supports, in each direction. The extension of the Rayleigh-Ritz method to the nonlinear case, developed and applied to various non-linear problems by Benamar and his co-authors [1,2,3,4] is used here to investigate the large vibration amplitudes of the plates examined.

Consider the plate shown in Fig. 1. It is supposed to be simply supported at the four edges and to be in addition connected to distributed rotational springs at the edges y = 0 and y = b. As mentioned above, the Rayleigh-Ritz method is used to investigate the linear vibration case, with plate functions defined as products of appropriate beam functions in each direction. The next section is concerned with a brief presentation of how to determine the mode shapes of the beam shown in Fig. 2.

Fig. 1

SS Plate connected to distributed rotational springs at y = 0 and y = b

Fig. 2

SS beam, connected at the ends to rotational springs

2 Mode Shapes of a SS Beam Connected at the Ends to Rotational Springs

2.1 Theoretical Formulation

Consider the SS beam shown in Fig. 2, connected at the ends to two rotational springs of stiffness $K_{1Rot}$ and $K_{2Rot}$. The beam has the characteristics indicated in the figure. The governing equation of the beam transverse vibration is governed by the well known differential equation [5]:

$$ \frac{{{\text{d}}^{4} {\text{w}}}}{{{\text{dx}}^{4} }} +\upbeta^{4} .{\text{w}} = 0\quad {\text{with}}\quad\upbeta^{4} =\upomega^{2} .\frac{{\uprho.{\text{S}}}}{{{\text{E}}.{\text{I}}}} $$

(1)

The general solution of Eq. (1) can be written as:

$$ {\text{w}}_{\text{i}} \left( {\text{x}} \right) = {\text{C}}_{1} { \sin }\left( {\upbeta_{\text{i}} .{\text{x}}} \right) + {\text{C}}_{2} { \cos }\left( {\upbeta_{\text{i}} .{\text{x}}} \right) + {\text{C}}_{3} { \sinh }\left( {\upbeta_{\text{i}} .{\text{x}}} \right) + {\text{C}}_{4} { \cosh }\left( {\upbeta_{\text{i}} .{\text{x}}} \right) $$

(2)

The β_i’s are the beam mode shape parameters. C₁, C₂, C₃ and C₄ are determined by the end conditions:

$$ {\text{at}}\,{\text{x}} = 0:{\text{w}} = 0\quad {\text{and}}\quad M_{x} = {\text{E}}.{\text{I}}.{\text{w}}^{{\prime \prime }} = + K_{1Rot} .\frac{\partial w}{\partial x} $$

(3–4)

$$ {\text{at}}\,{\text{x}} = {\text{l}}:{\text{w}} = 0\quad {\text{and}}\quad M_{x} = {\text{E}}.{\text{I}}.{\text{w}}^{{{\prime \prime } '}} = - K_{2Rot} .\frac{\partial w}{\partial x} $$

(5–6)

$M_{x}$ is the bending moment. Equations 3–6 give a linear system with 4 equations and 4 unknowns. To avoid having only the trivial zero solution, the determinant of the system must vanish, which gives the frequency equation, leading to the frequencies and mode shapes of the vibrating beam connected to the rotational springs. The Newton–Raphson algorithm was used to find the roots $\upbeta_{1} .{\text{l}}$ of the transcendental frequency equation, corresponding to the first mode and to various values of the rotational spring stiffness C*. The solutions are summarized in Table 1 and compared to previous results.

Table 1 Beam fundamental frequency parameters $\upbeta_{1} .{\text{l }}$ for different values of the rotational stiffness ${\text{C}}^{ *} = \frac{{{\text{K}}_{{2{\text{Rot}}}} .{\text{l}}}}{{{\text{E}}.{\text{I}}}}$

3 Linear Vibration of SS Rectangular Plates Connected to Two Distributions of Rotational Springs at Two Opposite Edges

To examine the vibration of the plate shown in Fig. 1, the transverse displacement is assumed to be:

$$ {\text{W}}\left( {{\text{x}},{\text{y}},{\text{t}}} \right) = {\text{w}}\left( {{\text{x}},{\text{y}}} \right).{ \sin }\left( {\upomega{\text{t}}} \right) = {\text{a}}_{\text{i}} .{\text{w}}_{\text{i}} \left( {{\text{x}},{\text{y}}} \right){ \sin }\left( {\upomega{\text{t}}} \right) $$

(7)

In which the usual summation convention is used. The kinetic energy and the plate total strain energy V_T, which is the sum of the strain energy due to the bending V_b [6], plus the membrane strain energy due to the axial load induced by large deflections V_m [6], and the strain energy stored by the elastic edge restraints V_spring (V_T = V_b + V_m + V_spring) are given by Li [7]:

$$ \begin{aligned} {\text{T}} & = \frac{1}{2}\uprho{\text{H}}\int\limits_{\text{S}} {\left( {\frac{{\partial {\text{W}}}}{{\partial {\text{t}}}}} \right)^{2} .{\text{dS,}}} \\ {\text{V}}_{\text{b}} & = \frac{\text{D}}{2}\int\limits_{\text{S}} {\left[ {\left( {\frac{{\partial^{2} {\text{W}}}}{{\partial^{2} {\text{x}}}} + \frac{{\partial^{2} {\text{W}}}}{{\partial^{2} {\text{y}}}}} \right)^{2} + 2.\left( {1 -\upnu} \right).\left( {\left( {\frac{{\partial^{2} {\text{W}}}}{{\partial {\text{x}}\partial {\text{y}}}}} \right)^{2} - \frac{{\partial^{2} {\text{W}}}}{{\partial^{2} {\text{x}}}}.\frac{{\partial^{2} {\text{W}}}}{{\partial^{2} {\text{y}}}}} \right)} \right]{\text{dS}}} \\ \end{aligned} $$

(8–9)

$$ \begin{aligned} {\text{V}}_{\text{m}} & = \frac{{3.{\text{D}}}}{{2.{\text{H}}^{2} }}\int\limits_{\text{S}} {\left[ {\left( {\frac{{\partial {\text{W}}}}{{\partial {\text{x}}}}} \right)^{2} + \left( {\frac{{\partial {\text{W}}}}{{\partial {\text{y}}}}} \right)^{2} } \right]^{2} .{\text{dS}} } \\ {\text{V}}_{\text{Spring}} & = \frac{1}{2}\mathop \int \limits_{0}^{\text{a}} ({\text{K}}_{{1{\text{Rot}}}} .\left( {\frac{{\partial {\text{w}}\left( {{\text{x}},0} \right)}}{{\partial {\text{y}}}}} \right)^{2} + {\text{K}}_{{2{\text{Rot}}}} .\left( {\frac{{\partial {\text{w}}\left( {{\text{x}},{\text{b}}} \right)}}{{\partial {\text{y}}}}} \right)^{2} {\text{dx}} \\ \end{aligned} $$

(10–11)

The basic spatial plate functions (Eq. 7), are defined as [2] ${\text{w}}_{\text{i}} \left( {{\text{x}},{\text{y}}} \right) = {\text{P}}_{\text{I}} \left( {\text{x}} \right).{\text{Q}}_{\text{J}} \left( {\text{y}} \right)$, in which ${\text{P}}_{\text{I}} \left( {\text{x}} \right)$ and ${\text{Q}}_{\text{J}} \left( y \right)$ are beam functions with appropriate end conditions in each direction. The plate function index i is related to the indices I and J of the corresponding beam functions by: ${\text{i}} = {\text{N}}.\left( {{\text{I}} - 1} \right) + {\text{J}}$, where N is the number of beam functions used. One obtains after discretization of the energy expressions [2]:

$$ {\text{T }} = \frac{1}{2}\upomega^{2} {\text{a}}_{\text{i}} .{\text{a}}_{\text{j}} .{\text{M}}_{\text{ij}} .{ \cos }^{2} \left( {\upomega{\text{t}}} \right);\quad {\text{V}}_{\text{b}} = \frac{1}{2}{\text{a}}_{\text{i}} .{\text{a}}_{\text{j}} .{\text{K}}_{{{\text{ij}}_{{\_{\text{b}}}} }} .{ \sin }^{2} \left( {\upomega{\text{t}}} \right); $$

(11–12)

$$ {\text{V}}_{\text{m}} = \frac{1}{2}{\text{a}}_{\text{i}} .{\text{a}}_{\text{j}} .{\text{a}}_{\text{k}} .{\text{a}}_{\text{l}} .{\text{B}}_{\text{ijkl}} .{ \sin }^{4} \left( {\upomega{\text{t}}} \right),\quad {\text{V}}_{{{\text{spring}}}} = \frac{1}{2}{\text{a}}_{{\text{i}}} {{\text{a}}}_{{\text{j}}} {{\text{K}}}_{{{\text{ij}}_{\text{spring}} }} .{ \sin }^{2} \left( {\upomega{\text{t}}} \right). $$

(13–14)

In which M_ij, K_{ij_b}, ${\text{B}}_{\text{ijkl}}$ and K_{ij_spring} are the mass, linear and non-linear rigidity tensors, defined by:

$$ {\text{M}}_{\text{ij}} =\uprho{\text{H}}\int\limits_{\text{S}} {{\text{w}}_{\text{i}} .{\text{w}}_{\text{j}} .{\text{dS}}} $$

(15)

$$ \begin{aligned} {\text{K}}_{{{\text{ij}}\_{\text{b}}}} & = {\text{D}}\int\limits_{\text{S}} {\left[ {\left( {\frac{{\partial^{2} {\text{w}}_{\text{i}} }}{{\partial {\text{x}}^{2} }} + \frac{{\partial^{2} {\text{w}}_{\text{i}} }}{{\partial {\text{y}}^{2} }}} \right)\left( {\frac{{\partial^{2} {\text{w}}_{\text{j}} }}{{\partial {\text{x}}^{2} }} + \frac{{\partial^{2} {\text{w}}_{\text{j}} }}{{\partial {\text{y}}^{2} }}} \right)} \right.} \\ & \quad \left. { + 2.\left( {1 -\upnu} \right).\left( {\frac{{\partial^{{^{2} }} {\text{w}}_{\text{i}} }}{{\partial {\text{x}}\partial {\text{y}}}}.\frac{{\partial^{2} {\text{w}}_{\text{j}} }}{{\partial {\text{x}}\partial {\text{y}}}} - \frac{{\partial^{2} {\text{w}}_{\text{i}} }}{{\partial {\text{x}}^{2} }}.\frac{{\partial^{2} {\text{w}}_{\text{j}} }}{{\partial {\text{y}}^{2} }}} \right)} \right].{\text{dS}} \\ \end{aligned} $$

(16)

$$ {\text{B}}_{\text{ijkl}} = \frac{{3{\text{D}}}}{{2.{\text{H}}^{2} }}\int\limits_{\text{S}} {\left( {\frac{{\partial {\text{w}}_{\text{i}} }}{{\partial {\text{x}}}}.\frac{{\partial {\text{w}}_{\text{j}} }}{{\partial {\text{x}}}} + \frac{{\partial {\text{w}}_{\text{i}} }}{{\partial {\text{y}}}}.\frac{{\partial {\text{w}}_{\text{j}} }}{{\partial {\text{y}}}}} \right)\left( {\frac{{\partial {\text{w}}_{\text{k}} }}{{\partial {\text{x}}}}.\frac{{\partial {\text{w}}_{\text{l}} }}{{\partial {\text{x}}}} + \frac{{\partial {\text{w}}_{\text{k}} }}{{\partial {\text{y}}}}.\frac{{\partial {\text{w}}_{\text{l}} }}{{\partial {\text{y}}}}} \right).{\text{dS}}} $$

(17)

$$ {\text{K}}_{{{\text{ij}}\_{\text{Spring}}}} = \mathop \int \limits_{0}^{a} \left( {{\text{K}}_{{1{\text{Rot}}}} .\frac{{\partial {\text{w}}_{\text{i}} \left( {{\text{x}},0} \right)}}{{\partial {\text{y}}}}.\frac{{\partial {\text{w}}_{\text{j}} \left( {{\text{x}},0} \right)}}{{\partial {\text{y}}}} + {\text{K}}_{{2{\text{Rot}}}} .\frac{{\partial {\text{w}}_{\text{i}} \left( {{\text{x}},{\text{b}}} \right)}}{{\partial {\text{y}}}}.\frac{{\partial {\text{w}}_{\text{j}} \left( {{\text{x}},{\text{b}}} \right)}}{{\partial {\text{y}}}}} \right).{\text{dx}} $$

(18)

The indices i and j are summed over 1, 2 … n, n being the number of the plate functions used (n = N²).

A computer program has been written to calculate numerically the above parameters and solve the eigen value problem, corresponding to linear vibrations. To validate the program, a limit case, corresponding to C–SS–C–SS rectangular plates, for which the rotational spring stiffness tend to infinity, has been treated, for various plate aspect ratios α. The results obtained are summarized in Table 2 and compared to previously published results. Also, a comparison is made in Table 3 between the results obtained here and those given in [6], corresponding to the plate with elastic restraints shown in Fig. 1 (α = 0.4, 0.8, 1). 36 plate functions have been used in the Rayleigh-Ritz formulation for various values of the spring stiffness. It appears that the percentage difference remains reasonably small for small and high values of the stiffness, corresponding to the SS and C edge conditions, and does not exceed 6.65% in all cases.

Table 2 Non-dimensional frequency parameters, of a C–SS–C–SS rectangular plate, for various plate aspect ratios α (a) results obtained here (b) results obtained in Ref. [4] (c) results obtained in Ref. [10]

Table 3 Comparison of the frequency parameters $\frac{{{\varvec{\upomega}}^{2} .{\mathbf{a}}^{2} .{\mathbf{b}}^{2} .\varvec{\rho}}}{{{\varvec{\uppi}}^{4} .\varvec{D}}}$ (b) calculated here with (a) results given in [8] for different values of aspect ratio and different values of stiffness

4 Nonlinear Vibration of SS Rectangular Plates Connected to Two Distributions of Rotational Springs at Two Opposite Edges

To examine now the non-linear vibration of the rectangular plate examined, the membrane strain energy V_m induced by the large vibration amplitudes has to be taken into account in the application of Hamilton’s principle as follows:

$$ \delta \mathop \int \limits_{0}^{{\frac{2\omega }{\pi }}} \left( {T - (V_{b} + V_{spring} + V_{m} } \right).dt = 0 $$

(19)

After the integration of the time functions over the range $\left[ {0,\frac{2.\pi }{\omega }} \right]$, one gets a non-linear eigen value problem, written in a matrix form as [8]:

$$ 2.{\text{K}}.{\vec{\text{A}}} + 3.{\text{B}}\left( {{\vec{\text{A}}}} \right).{\vec{\text{A}}} =\upomega^{2} .{\text{M}}.{\vec{\text{A}}} $$

(20)

${\vec{\text{A}}}$ is the column vector of the basic function contribution coefficients. K and M are the classical rigidity and mass matrices, well known in linear vibration theory, and ${\text{B}}\left( {{\vec{\text{A}}}} \right)$ is the nonlinear geometrical rigidity tensor. Equation (20) is the Benamar’s adaptation of the Rayleigh-Ritz method to the nonlinear vibration problem, to be solved numerically, or explicitly. From Eq. (20), it is possible to calculate the frequency ω by pre-multiplying the two hand sides of the equation by ${\vec{\text{A}}}^{T}$ which gives:

$$ {\varvec{\upomega}}^{2} = \frac{{{\vec{\mathbf{A}}}^{{\mathbf{T}}} .{\mathbf{K}}.{\vec{\mathbf{A}}} + \frac{3}{2}.{\mathbf{A}}^{{\mathbf{T}}} .{\mathbf{B}}\left( {{\vec{\mathbf{A}}}} \right).{\vec{\mathbf{A}}}}}{{{\vec{\mathbf{A}}}^{{\mathbf{T}}} {\mathbf{M}}.{\vec{\mathbf{A}}}}} $$

(21)

The single mode approach (SMA), consists of neglecting all the basic functions except a single ‘‘resonant’’ mode. Thus, it reduces the multi-degree-of-freedom problem to a single dof. The single mode approach is often used in the literature [4] due to the great simplification it introduces in the theory on one hand, and on the other hand because the error it introduces in the estimation of the amplitude dependent nonlinear frequencies remains very small. Applying the SMA to Eq. (21) gives:

$$ \upomega^{2} = \frac{{{\text{K}}_{11} }}{{{\text{M}}_{11} }} + \frac{3}{2}\frac{{{\text{a}}^{2} .{\text{B}}_{1111} }}{{{\text{M}}_{11} }} $$

(22)

In which K₁₁, M₁₁ and B₁₁₁₁ are the parameters related to the single mode examined, which is in the present case the fundamental mode of the plate shown in Fig. 1. Figure 3 shows, for a validation purpose, a satisfactory comparison between the results obtained here and those given in [4], corresponding to CSSCSS plate. Figure 4 gives the backbone curves corresponding to various values of the stiffness of the rotational springs distributed at the edges y = 0 and y = b of the rectangular plate. A hardening type non-linearity, indicating an increase in the frequency with the vibration amplitude is noticed and appears to become, as may be expected, more pronounced with increasing the spring stiffness.

Fig. 3

Comparison between the present backbone curve and that of Ref. [4]. Aspect ratio = 0.66

Fig. 4

Backbone curves for the four plates: (1) a CC plate in the x direction and SS in the y direction (2) a CC plate in the x direction and SS in the y direction with distributed rotational springs of stiffness ${\text{C}}^{*} = 50\left( {\varvec{C}^{\varvec{*}} = \frac{{{\mathbf{K}}_{{\varvec{iRota}}} .{\mathbf{b}}}}{{\mathbf{D}}}} \right)$; (3) a CC plate in the x direction and SS in the y direction with distributed rotational springs of stiffness C* = 500; (4) a CC plate in the x direction and SS in the y direction

5 Conclusion

To investigate the vibration of the plate shown in Fig. 1, the Rayleigh-Ritz method has been used in the linear case, with plate functions defined as products of x and y beam functions, with appropriate end supports in each direction. The extension of the Rayleigh-Ritz method to the nonlinear case, developed and applied to various non-linear problems by Benamar and his co-authors, has been used here to investigate the plate large vibration amplitudes. The basic functions used are obtained as product of beam functions in the x and y directions corresponding respectively to SS and ER (elastically restrained) beam end conditions, the last case being first analytically treated and numerically validated. Analytical details have been given and the numerical results were compared to those available in literature. The backbone curves are given for plates having different combinations of stiffness and aspect ratios.