Abstract
This paper is an introduction to the space of arcs and the space of jets of an algebraic variety. We also introduce the Nash problem on arc families, which makes a bridge between the theory of the space of arcs and the theory of birational geometry. We then focus on applications of the space of arcs to the theory of birational geometry and show the recent results.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
3.1 Introduction
3.1.1 Overview
Roughly speaking, an arc is a very small portion of a curve on a scheme and an m-jet is the approximation up to degree m of an arc. The space of arcs is the set of all arcs on a scheme and the space of m-jets is the set of all m-jets on a scheme. These spaces have the natural scheme structures and reflect the properties of the base scheme. The space of arcs plays the following roles:
-
1.
a role to describe singularities of a variety (local problem);
-
2.
a role to describe the global structure of a variety (global problem) and
-
3.
the role as a differential algebra (algebraic problem).
These roles are based on understandings of the structure of the arc space, which is simultaneously developing with the study on 1–3. We should mention that these roles mutually interact and the works corresponding to them are not exclusively classified into one of the roles 1–3. We should also mention that the theory of the space of arcs/jets is still developing, so in the future, more roles will potentially appear.
The following is a brief history of the development of the space of arcs/jets whilst mentioning the roles 1–3 in each step.
3.1.2 Brief History
The space of arcs and the space of m-jets appeared for the first time in the short preprint in 1968 by John Forbes Nash. But according to an expert, Monique Lejeune-Jalabert, of Nash problem, the concepts, arcs and jets were already studied by Isaac Newton in seventeenth century. In his book “ La Méthode des Fluxions et des Suites Infinies” Newton shows the method to express the \(x,y\)-coordinates of a plane curve by one parameter series which is the origin of an arc. Actually it is a natural question how to describe a curve by one parameter and it is not so mysterious to find this question in old literature. But we should have waited till the twentieth century for the concept “moduli space” consisting of all such parametrization.
In 1968, John Forbes Nash wrote a short preprint “Arc structures of singularities” in which he introduced the space of arcs. The preprint was not published at the beginning, but circulated in the world and was read by many people.
In 1995, the paper was eventually published as [81] in the issue of celebration of Nobel laureate Nash in Duke Mathematical Journal. Twenty seven years have passed since the paper was written. In those years Nash had suffered from mental disease, but later recovered miraculously, about which the reader can see in the book “A Beautiful Mind” [80].
Coming back to mathematics, the paper by Nash also posed a problem, so called “the Nash Problem”. After the preprint was circulated around the world in 1968, the space of arcs in relation with the Nash problem is studied by many people, Bouvier, Gonzalez-Sprinberg, Hickel, Lejeune-Jalabert, Nobile, Reguera-Lopez and others (see, [12, 39, 44, 68,69,70, 82, 89]). The first direct answer to the Nash Problem is obtained by Ana Reguera ([89]) in 1995. This is an affirmative answer to the problem in the case of simple singularities on a surface. Then, by the contributions of many people, the problem was completely solved in 2013. It took 45 years after the problem was posed. [1, 10,11,12,13, 19, 20, 38, 39, 46, 54, 63, 70, 71, 74, 84,85,86,87,88,89,90, 92] The reader can see a more detailed history about the Nash Problem in Section 4. As a matter of fact, the problem is affirmatively solved for two-dimensional singularities by J.F.de Bobadilla and M.P.Pereira [11] and toric singularities of arbitrary dimension as well by S. Ishii and J. Kollár [46]. But otherwise, it was negatively solved by S. Ishii and Kollár for dimension greater than 3 and by T. De Fernex [19], J. Johnson and J. Kollár [63] for dimension 3. In spite of the fact that the answer is negative for many cases, the Nash Problem still holds great significance. The problem bridges the theory of arc space and the theory of birational geometry. So the Nash Problem plays an important role on (1) in a viewpoint of birational geometry.
A surprising step in this direction is made by M. Mustaţǎ in [77] at the beginning of the twenty-first century. He characterizes a locally complete intersection canonical singularity (a kind of singularity in birational geometry) by irreducibility of all the spaces of jets. After that there appear similar characterizations of singularities in birational geometry in terms of the space of arcs/jets (see Corollary 3.5.38). Some birational invariants (“mld” and “lct”) of singularities are also interpreted in terms of the arc space. By making use of the interpretations some important results in birational geometry are obtained. One important point about these invariant is that the interpretations by the space of arcs/jets also work for the base field of positive characteristic. Comparing with the case of characteristic 0, algebraic geometry of positive characteristic is difficult to study, because some convenient properties do not hold in positive characteristic [60]. In such a situation, the interpretations by the space of arcs are expected to play significant roles. These things will be explained in Section 5. Aside from the Nash Problem, a remarkable idea “motivic integration” on the space of arcs is introduced by Kontsevich [67] in 1995. He proved that birationally equivalent Calabi-Yau manifolds have the same Hodge numbers by making use of motivic integration. This is considered as the role (2) of the space of arcs. Unfortunately there is no written version of [67], however we can read the papers by J. Denef and F. Loeser [23,24,25,26,27] which describe their own developments of the theory of motivic integration including Kontsevich’s original idea. Motivic integration leads the people to “motivic zeta function” on the arc space [23, 24] and also Batyrev’s “stringy function” [7, 8]. These functions describe global and local structures of the variety, therefore these are considered as the roles (2) and also (1) of the space of arcs. Local theory of singularities in terms of zeta function is developed by Veys [93,94,95] and Veys and Zuniga-Galindo[96]. In this paper we do not step into motivic integration, since there are many good expository papers by A. Craw [17], W. Veys [97], F. Loeser [72].
The space of arcs/jets on an affine variety becomes an affine scheme and the coordinate ring of the space of arcs/jets has a canonical structure of differential algebra. From this viewpoint, the space of arcs/jets is studied by Arakawa and Moreau [4], Buium [15], and Kolchin [64]. These are the role (3) of the space of arcs.
Because of the limitation of the pages, the proofs are given only when the proof helps the understanding of new concepts. For statements for which we omit the proofs, we show the citations so that the reader can find the proofs.
3.1.3 The Goal of this Chapter
In this expository paper, we introduce the space of arcs/jets and show basic properties of the space of arcs/jets with a focus on (1) in a viewpoint of birational geometry.
For the reader not so familiar to birational geometry, we introduce basic notions in birational geometry in the fifth section.
The reader interested in the other roles is encouraged to see the references cited above.
Throughout this paper k is an algebraically closed field of arbitrary characteristic unless otherwise stated and a variety is an irreducile reduced separated scheme of finite type over k. The basic knowledge of algebraic geometry is based on [43] by Hartshorne.
3.2 Construction of the Space of Jets and the Space of Arcs
3.2.1 Construction of the Space of Jets
Definition 3.2.1
Let \( X \) be a scheme of finite type over \( k \) and \(K\supset k\) a field extension. For \( m\in \mathbf {N} \), a \( k \)-morphism \( \operatorname {Spec} K[t]/(t^{m+1})\to X \) is called an \( m \)-jet of \( X \) and a \( k \)-morphism \( \operatorname {Spec} K[[t]]\to X \) is called an arc of \( X \). We denote the unique point of \( {\operatorname {Spec} K[t]/(t^{m+1})} \) by \( 0 \), while the closed point of \( \operatorname {Spec} K[[t]] \) by \( 0 \) and the generic point by \( \eta \).
Theorem 3.2.2
Let \( X \) be a scheme of finite type over \( k \) . Let \( \mathcal {S}ch/k \) be the category of \( k \) -schemes and \( \mathcal {S}et \) the category of sets. Define a contravariant functor \( F^X_{m}: \mathcal {S}ch/k \to \mathcal {S}et \) by
for an object Z of \( \mathcal {S}ch/k \) . And for a morphism \(f: Z\to Z'\) in \( \mathcal {S}ch/k \) , define \(F^X_{m}(f):\)
by\(\alpha '\mapsto \alpha '\circ (f\times 1)\).
Then,\( F^X_{m} \)is representable by a scheme\( X_{m} \)of finite type over\( k \). This\( X_{m} \)is called thespace of\( m \)-jetsof\( X \)or the\( m \)-jet schemeof\( X \).
Here, “\( F^X_{m} \) is representable by \(X_m\)” means that the functor \( F^X_{m} \) is naturally isomorphic (i.e., there exists an invertible natural transformation) to the functor \( \operatorname {Hom} _{k}(Z, X_{m})\). In particular, for an object \(Z\in \mathcal {S}ch/k \) the following bijection holds:
The above theorem is proved in [14, p. 276]. In this paper, we prove this by a concrete construction of \(X_m\) for affine \( X \) and then patching them together for a general \( X \). For our proof, we need some preparatory discussions.
Note 3.2.3
Let \( X \) be a \( k \)-scheme. Assume that \( F_{m}^X \) is representable by \( X_{m} \) for every \( m\in \mathbf {N} \). Then, for \( m<m' \), the canonical surjection \( k[t]/(t^{m'+1}) \to k[t]/(t^{m+1}) \) induces a morphism
Indeed, the canonical surjection \( k[t]/(t^{m'+1})\to k[t]/(t^{m+1}) \) induces a morphism
for an arbitrary \( k \)-scheme \( Z \). Therefore we have a map
which gives the map by the bijection (3.1)
Take, in particular, \( X_{m'} \) as \( Z \),
then the image of \( id_{X_{m'}}\in \operatorname {Hom} (X_{m'},X_{m'}) \) by this map gives the required morphism.
This morphism \( \psi _{m',m} \) is called a truncation morphism. In particular for \( m=0 \), \( \psi _{m',0}:X_{m'}\to X \) is denoted by \( \pi _{m} \). When we need to specify the scheme \( X \), we denote it by \( \pi _{m}^X \).
Actually \( \psi _{m',m} \) “truncates” a power series in the following sense: A point \( \alpha \) of \( X_{m'} \) gives an \(m'\)-jet \( \alpha : \operatorname {Spec} K[t]/(t^{m'+1}) \to X \), which corresponds to a ring homomorphism \( \alpha ^*: A\to K[t]/(t^{m'+1}) \), where \( A \) is the affine coordinate ring of an affine neighborhood of the image of \( \alpha \). For every \( f\in A \), let
then
This fact can be seen by letting \( Z=\{\alpha \} \) in the above discussion.
As we did already in the above argument, we denote the point of \( X_{m} \) corresponding to \( \alpha : \operatorname {Spec} K[t]/(t^{m+1}) \to X \) by the same symbol \( \alpha \). Then, we should note that \( \pi _{m}(\alpha )=\alpha (0) \), where in the left hand side we regard \({\alpha }\) as a point of \(X_m\), while in the right hand side we regard it as a morphism \(\operatorname {Spec} K[t]/(t^{m+1}) \to X\).
3.2.2 Morphisms of the Spaces of Jets
Proposition 3.2.4
Let \( f:X\to Y \) be a morphism of \( k \) -schemes of finite type. Assume that the functors \( F_{m}^X \) and \( F_{m}^Y \) are representable by \( X_{m} \) and \( Y_{m} \) , respectively. Then for every \( m\in \mathbf {N} \) there is a canonical morphism \( f_{m}:X_{m}\to Y_{m} \) such that the following diagram is commutative:
Proof
Let \( X_{m}\times {\operatorname {Spec} k[t]/(t^{m+1})}\to X \) be the “universal family” of \( m \)-jets of \( X \), i.e., it corresponds to the identity map in \( \operatorname {Hom}_{k}(X_{m},X_{m}) \). By compositing this map and \( f:X\to Y \), we obtain a morphism
which gives a morphism \( X_{m}\to Y_{m} \). Pointwise, this morphism maps an \( m \)-jet \( \alpha \in X_{m} \) of \( X \) to the composite \( f\circ \alpha \) which is an \( m \)-jet of \( Y \). To see this, just take a point \( \alpha \in X_{m} \) and see the image of \( \{\alpha \}\times {\operatorname {Spec} k[t]/(t^{m+1})} \to Y \). The commutativity of the diagram follows from this description. □
Proposition 3.2.5
For\( k \)-schemes\( X \)and\( Y \), assume that the functor\( F_{m}^X \)and\( F_{m}^Y \)are representable by\( X_{m} \)and\( Y_{m} \), respectively. If\( f:X\to Y \)is an étale morphism, then\( X_{m}\simeq Y_{m}\times _{Y}X \), for every\(m\in \mathbf {N} \).
Proof
By the above proposition we have a commutative diagram:
It is sufficient to prove that for every commutative diagram:
there is a unique morphism \( Z\to X_{m} \) which is compatible with the projections to \( X \) and \( Y_{m} \). By definition of \(Y_m\), we are given the following commutative diagram:
As \( f \) is étale, there is a unique morphism \( Z\times _{\operatorname {Spec} k}\operatorname {Spec} k[t]/(t^{m+1})\to X \) which makes the two triangles commutative. This gives the required morphism:
□
As a corollary of this proposition, we obtain the following lemma:
Lemma 3.2.6
Let\( U\subset X \)be an open subset of a\( k \)-scheme\( X \). Assume the functors\( F^X_{m} \)and\( F^U_{m} \)are representable by\( X_{m} \)and\( U_{m} \), respectively. Then,\(U_{m}= (\pi _{m}^X)^{-1}(U) \).
Proof of Theorem 3.2.2
Since a \( k \)-scheme \( X \) is separated, the intersection of two affine open subsets is again affine. Therefore, for an affine covering \(\{U_i\}_i\) of a k-scheme X, if the functor \(F_m^{U_i}\) is representable by \((U_i)_m\) for every i, then we can patch \((U_i)_m\)’s together to obtain \(X_m\) by Lemma 3.2.6. Now, it is sufficient to prove the representability of \( F_{m}^X \) for affine \( X \). Let \( X \) be \( \operatorname {Spec} R \), where we denote \( R=k[x_{1},\ldots ,x_{n}]/(f_{1},..,f_{r}) \). It is sufficient to prove the representability for an affine variety \( Z=\operatorname {Spec} A \). Then, we obtain that
If we write \( \varphi (x_{j})= a_{j}^{(0)}+a_{j}^{(1)}t+a_{j}^{(2)}t^2+..+a_{j}^{(m)}t^m \) for \( a_{j}^{(l)}\in A \), it follows that
for polynomials \( F_{i}^{(s)} \) in \( a_{j}^{(l)} \)’s \((1\leq j \leq n, 0\leq l\leq s)\). Then the above set (3.2.2.1) is described as follows:
If we define \( X_{m}=\operatorname {Spec} k[x_{j},x_{j}^{(1)},.,x_{j}^{(m)}]/ ( F_{i}^{(s)}(x_{j}^{(l)})) \), the last set is bijective to
This completes the proof of Theorem 3.2.2. □
Remark 3.2.7
The functor \( F_{m}^X \) is also representable even for \( k \)-scheme of non-finite type over \( k \). The existence of the space of jets for wider class of schemes is presented in [98].
3.2.3 The Space of Arcs
Definition 3.2.8
The system \( \{\psi _{m', m}:X_{m'}\to X_{m}\}_{m< m'} \) is a projective system. Let \( X_{\infty }={ \mathop {\text{lim}} \limits _{\longleftarrow }} _{m}X_{m} \) and call it the space of arcs of \( X \) or arc space of \( X \). Note that \( X_{\infty } \) is not of finite type over k if \( \dim X>0 \).
Remark 3.2.9
The reader may be afraid that the projective limit of the schemes \( { \mathop {\text{lim}} \limits _{\longleftarrow }} _{m}X_{m} \) may not exist. But in our case we need not to worry, since for an affine scheme \( X =\operatorname {Spec} R\), the \( m \)-jet scheme \( X_{m}=\operatorname {Spec} R_{m} \) is affine for every \( m \in \mathbf {N}\). Here, the morphisms \( \psi ^*_{m',m}:R_{m}\to R_{m'} \) corresponding to \( \psi _{m',m} \) are direct system. It is well known that there is a direct limit \( R_{\infty }={ \mathop {\text{lim}} \limits _{\longrightarrow }}_{m}R_{m} \) in the category of \( k \)-algebras. The affine scheme \( \operatorname {Spec} R_{\infty } \) is our projective limit of \( X_{m} \). For a general \( k \)-scheme \( X \), we have only to patch affine pieces \( \operatorname {Spec} R_{\infty } \).
Using the representability of \( F_{m}^X \) we obtain the following universal property of \(X_{\infty }\):
Proposition 3.2.10
Let \( X \) be a scheme of finite type over \( k \) . Then for a k-algebra A we obtain:
Proof
In case X is affine k-scheme \(X=\operatorname {Spec} R\). Then by the representability of \( F_{m}^X \) we obtain an isomorphism of projective systems:
Then, we obtain an isomorphism of the projective limits:
which gives the required isomorphism for affine scheme X.
For a general X, see [9]. When we study singularities locally, we need only the affine case. □
Remark 3.2.11
Note that in general
Indeed, for example, for \( A=k[x] \), the ring \( A[[t]] \) contains \( \sum _{i=0}^\infty f_{i}(x)t^i \) such that \( \deg f_{i} \) are unbounded, while \( A\otimes _{k}k[[t]] \) does not contain such an element.
Now, consider the case \( A=K \) for an extension field \( K\supset k \), the bijection
shows that a \( K \)-valued point of \( X_{\infty } \) is an arc \( {\operatorname {Spec} K[[t]]}\to X \).
In [51, Proposition 2.13] the author sloppily stated Proposition 3.2.10 for every k-scheme Z instead of \(\operatorname {Spec} A\). But actually the correct statement proved at this moment is in the form as Proposition 3.2.10.
Definition 3.2.12
Denote the canonical projection \( X_{\infty }\to X_{m} \) induced from the surjection \( k[[t]]\to k[t]/(t^{m+1}) \) by \( \psi _{m} \) and the composite \( \pi _{m}\circ \psi _{m} \) by \( \pi \). When we need to specify the base space \( X \), we write it by \( \pi ^{X} \).
A point \( x \in X_{\infty } \) gives an arc \( \alpha _{x}:{\operatorname {Spec} K[[t]]} \to X \) and \( \pi (x)=\alpha _{x}(0) \), where \( K \) is the residue field at \( x \). In the same way as in the case of \( m \)-jets, we denote both \( x \in X_{\infty } \) and \( \alpha _x \) by the same symbol \( \alpha \).
For every \( m\in \mathbf {N} \), \( \psi _{m}(X_{\infty }) \) is a constructible set, since \( \psi _{m}(X_{\infty })=\psi _{m',m}(X_{m'}) \) for sufficiently big \( m' \) ([41]). We know that the image of a morphism of finite type is a constructible set.
Definition 3.2.13
Denote the canonical morphism \( X\to X_{m} \) induced from the inclusion \( k\hookrightarrow k[t]/(t^{m+1}) \)\( (m\in \mathbf {N}\cup \{\infty \}) \) by \( \sigma _{m} \). Here, we define \( k[t]/(t^{m+1})= k[[t]] \) for \( m=\infty \). As \( k\hookrightarrow k[t]/(t^{m+1}) \) is a section of the projection \( k[t]/(t^{m+1}) \to k\), our morphism \( \sigma _{m}:X\to X_{m} \) is a section of \( \pi _{m}:X_{m}\to X \).
Let \(x\in X\) be a point and \(m\in \mathbf {N}\cup \{\infty \}\). Then the fiber scheme \(\pi _m^{-1}(x)\) is denoted by \(X_m(x)\).
For a point \( x\in X \), let \( K \) be the residue field at \( x \), then define
as the \( m \)-jet that factors through \( \operatorname {Spec} K\to X \) whose image is \( x \). Therefore, \( \sigma _{m}(x) \) is the constant\( m \)-jet at \( x \), this is denoted my \( x_{m} \).
Example 3.2.14
Under the notation in the proof of Theorem 3.2.2, for \( X={\mathbf {A}}_{k}^n \), we have \((f_1,\ldots , f_r)=0\). Therefore, it follows \( X_{m}={\mathbf {A}}_{k}^{n(m+1)} \) and the truncation morphism \(\psi _{m',m}:X_{m'}\to X_m\) is the projection \({\mathbf {A}}_{k}^{n(m'+1)}={\mathbf {A}}_k^{n(m+1)}\times {\mathbf {A}}_k^{n(m'-m)}\to {\mathbf {A}}_{k}^{n(m+1)} \).
Example 3.2.15
Let X be a non-singular variety of dimension n. Then for every \(m\in \mathbf {N}\), the space of m-jets \(X_m\) is a non-singular variety of dimension \(n(m+1)\) and the truncation morphism \(\psi _{m',m}:X_{m'}\to X_m\) is a locally trivial fiber space with the fiber \({\mathbf {A}}_k^{(m'-m)n}\). Indeed, if X is non-singular, then at each point \(x\in X\) there is an open neighborhood \(U_x\) such that we have an étale morphism \(U_x\to \mathbf { A}_k^n\). By Proposition 3.2.5, it follows that \((U_x)_m\simeq U_x\times _{{\mathbf {A}}_k^n}{\mathbf {A}}_k^{n(m+1)}\simeq U_x\times _{\operatorname {Spec} k} {\mathbf {A}}_k^{mn}\). This shows that \(\pi _m: X_m\to X\) is a locally trivial fiber space with the fiber \({\mathbf {A}}_k^{mn}\). For \(m<m'\), we have\((U_x)_{m'}=(U_x)_m\times _{\operatorname {Spec} k} {\mathbf {A}}_k^{(m'-m)n}\) by the discussion above. Hence, \(\psi _{m',m}:X_{m'}\to X_m\) is a locally trivial fiber space with the fiber \({\mathbf {A}}_k^{(m'-m)n}\).
Example 3.2.16
Let \( X \) be the hypersurface in \( {\mathbf {A}}_{k}^3 \) defined by the equation \( f=xy+z^2=0 \). We leave the calculation of \(X_1\) to the reader and here we calculate \(X_2\). The space of 2-jets \( X_{2} \) is defined in \( {\mathbf {A}}_{k}^{9} \) by the equations \( xy+z^2=x^{(1)}y+xy^{(1)}+2zz^{(1)}=x^{(2)}y+x^{(1)}y^{(1)} +xy^{(2)} +z^{(1)}z^{(1)}+2zz^{(2)}=0 \). We can prove that \( X_{2} \) is irreducible and non-normal as follows: As an open subset \( X\setminus \{0\} \) is non-singular, \( \pi _{2}^{-1}(X \setminus \{0\}) \) is 6-dimensional non-singular variety. On the other hand \( \pi _{2}^{-1}(0) \) is a hypersurface in \( {\mathbf {A}}_k^6 \) defined by the equation \(x^{(1)}y^{(1)} +z^{(1)}z^{(1)}=0\), therefore its dimension is 5. As \( X_{2} \) is defined by three equations, every irreducible component of \( X_{2} \) has dimension greater than or equal to \(9-3=6\). By this \( \pi _{2}^{-1}(0) \) does not produce an irreducible component of \(X_2\). Hence, \( X_{2} \) is irreducible. On the other hand, by the Jacobian matrix, we can see that the singular locus of \( X_{2} \) is \( \pi _{2}^{-1}(0) \). This locus is of codimension 1 in \( X_{2} \), which yields that \( X_{2} \) is not normal. The origin is the unique singular point of X and is called an “\(A_1\)-singularity”. Later on, in Corollary 3.5.38, we will have that \(X_m\)\((m\in \mathbf {N})\) are all irreducible.
Example 3.2.17
Let \( X \) be the plane curve defined by \( x^2-y^2-x^3=0 \) Then \( \pi _{1}^{-1}(X\setminus \{0\})\to X\setminus \{0\} \) is a locally trivial fiber space over \(X\setminus \{0\}\) with the fiber \( {\mathbf {A}}_{k}^1 \), which shows that \( \pi _{1}^{-1}(X\setminus \{0\}) \) is of dimension 2. On the other hand, we have \(\pi _{1}^{-1}(0) \simeq {\mathbf {A}}_{k}^2 \). Therefore \( X_{1} \) consists of two irreducible components \( \overline {\pi _{1}^{-1}(X\setminus \{0\})} \) and \( \pi _{1}^{-1}(0) \).
Example 3.2.18
Consider the space of 1-jets for an arbitrary scheme X of finite type over k. For every closed point \( x\in X \), the set of closed points of \( \pi _{1}^{-1}(x) \) is the set of morphisms \( \operatorname {Spec} k[t]/(t^2)\to X \) with the image x. This set is nothing but the Zariski tangent space of \( X \) at \( x \). Therefore, \(\pi _1: X_{1}\to X \) is regarded as the “tangent bunlde” of \( X \).
Example 3.2.19
If \( X={\mathbf {A}}_{k}^n \), then \( X_{\infty }=\operatorname {Spec} k[x_{j},x_{j}^{(1)},x_{j}^{(2)}\ldots \mid j=1,\ldots , n] \) which is isomorphic to \( {\mathbf {A}}_{k}^{\infty }=\operatorname {Spec} k[x_{1},x_{2},\ldots , x_{i},\ldots ] \). Here, we note that the set of closed points of \( {\mathbf {A}}_{k}^{\infty } \) does not necessarily coincide with the set
(see the following theorem).
Theorem 3.2.20 ([48], Proposition 2.10, 2.11)
Every closed point of \( {\mathbf {A}}_{k}^{\infty } \) is a \( k \) -valued point if and only if \( k \) is an uncountable field.
3.2.4 Thin and Fat Arcs
The concept “thin” in the following is first introduced in [33].
Definition 3.2.21
Let \( X \) be a variety over \( k\). We say that an arc \( \alpha :{\operatorname {Spec} K[[t]]} \to X \) is thin if \( \alpha \) factors through a proper closed subvariety of \( X \). An arc which is not thin is called a fat arc.
An irreducible subset \( C \) in \( X_{\infty } \) is called a thin set if \( C \) is contained in \( Z_{\infty } \) for a proper closed subvariety \( Z\subset X \). An irreducible subset in \( X_{\infty } \) which is not thin is called a fat set.
In case an irreducible subset \( C \) has the generic point \( \gamma \in C \) (i.e., the closure \( \overline {\{\gamma \} }\) contains \( C \)), \( C \) is a fat set if and only if \( \gamma \) is a fat arc.
The following holds by the definition and the valuative criterion of properness:
Proposition 3.2.22 ([49] Proposition 2.5)
Let \( X \) be a variety over \( k\) and \( \alpha :{\operatorname {Spec} K[[t]]}\to X \) an arc. Then, the following hold:
-
(i)
\( \alpha \) is a fat arc if and only if the ring homomorphism \( \alpha ^*: {\mathcal O}_{X, \alpha (0)}\to K[[t]] \) induced from \( \alpha \) is injective;
-
(ii)
Assume that\( \alpha \)is fat. For an arbitrary proper birational morphism\( \varphi :Y\to X \), the arc\( \alpha \)is lifted to\( Y \).
Remark 3.2.23
A fat set in \( X_{\infty } \) for a variety \( X \) introduces a discrete valuation on the rational function field \( K(X) \) of \( X \) (see Definition 3.5.22).
A Nash component (see section 4) is a fat set and the Nash map (see section 4) is just the correspondence to associate a fat set to the valuation induced from the fat set ([49]).
Example 3.2.24
One of typical examples of fat sets is an irreducible cylinder (i.e., the pull back \( \psi _{m}^{-1}(S) \) of a constructible set \( S\subset X_{m} \)) for a non-singular \( X \). Actually, let C be an irreducible closed subset of \(X_m\) and take an \( m \)-jet \( \alpha _{m}:{\operatorname {Spec} k[t]/(t^{m+1})}\to X \) in \( C \), then, at a neighborhood of \( x=\alpha _{m}(0)=\pi _{m}(\alpha _{m}) \), \( X \) is étale over \( {\mathbf {A}}_{k}^n \). Therefore, we may assume that \( X={\mathbf {A}}_{k}^n \) and \( x=0 \). Assume that \( \psi _{m}^{-1}(\alpha _{m}) \) is thin, then it is contained in \( Z_{\infty } \) for some proper closed subset \( Z\subset X \). The \( m \)-jet \( \alpha _{m} \) corresponds to a ring homomorphism
Let \( x_{i}^{(j)} \) be an indeterminate for every \( i=1,\ldots ,n \) and \( j\geq m+1 \). Let
be an arc defined by
Let \( \alpha ^*(f)=F_{0}(a_{i}^{(j)},x_{i}^{(j)})+F_{1}(a_{i}^{(j)},x_{i}^{(j)})t+\cdots + F_{\ell }(a_{i}^{(j)},x_{i}^{(j)})t^{\ell }+\cdots \) for \( f\in I_{Z} \). Then, as \( x_{i}^{(j)} \)’s are indeterminates there is \( \ell \) such that \( F_{\ell }\neq 0 \). Hence, we obtain \( \alpha \in \psi _{m}^{-1}(C)\) such that \( \alpha \not \in Z_{\infty } \).
Example 3.2.25 ([21])
For a singular variety \( X \), an irreducible cylinder is not necessarily fat. Indeed, let \( X \) be the Whitney Umbrella that is a hypersurface defined by \( xy^2-z^2=0 \) in \( {\mathbf {A}}_{k}^3 \). For \( m\geq 1 \), let
be the \( m \)-jet defined by \( \alpha _{m}(x)=t, \alpha _{m}(y)=0, \alpha _{m}(z)=0 .\) Then, the cylinder \( \psi _m^{-1}(\alpha _{m}) \) is contained in \( \operatorname {Sing}(X)_{\infty } \), where \( \operatorname {Sing}(X)= (y=z=0) \). This is proved as follows: Let an arbitrary \( \alpha \in \psi _{m}^{-1}(\alpha _{m}) \) be induced from
with
where we note that \( a_{1}=1 \). Then, the condition \( \alpha ^*(xy^2-z^2)=0 \) implies that the initial term of \( \alpha ^*(xy^2) \) and that of \( \alpha ^*(z^2) \) cancel each other. If \( \alpha ^*(y)\neq 0 \), then the order of \( \alpha ^*(xy^2) \) is odd. On the other hand, if \( \alpha ^*(z)\neq 0 \), the order of \( \alpha ^*(z^2) \) is even. Hence if \( \alpha ^*(y)\neq 0 \) or \( \alpha ^*(z)\neq 0 \), then the initial term of \( \alpha ^*(xy^2) \) and that of \( \alpha ^*(z^2) \) do not cancel each other. Therefore, \( \alpha ^*(y)=\alpha ^*(z)=0 \), which shows that \( \psi _{m}^{-1}(\alpha _{m})\subset \operatorname {Sing}(X)_{\infty } \).
3.3 Properties of the Space of Arcs and the Space of Jets
3.3.1 Group Actions on the Space of Jets/Arcs
Note 3.3.1
Consider \( G={\mathbf {A}}_k^1\setminus \{0\}=\operatorname {Spec} k[s,s^{-1}] \) as a multiplicative group scheme. Usually this group scheme is denoted by \({\mathbf {G}}_m\), but this symbol would conflict with the space of m-jets. Therefore we do not use the usual symbol in this paper. For \( m\in \mathbf {N}\cup \{\infty \} \), the morphism \( {k[t]/(t^{m+1})} \to k[s,s^{-1}, t]/(t^{m+1}) \) defined by \( t\mapsto s\cdot t \) gives an action
of \( G \) on \( {\operatorname {Spec} k[t]/(t^{m+1})} \). Therefore, it gives an action
of \( G \) on \( X_{m} \). As \( \mu _{m} \) is extended to a morphism:
we obtain the extension
of \( \mu _{Xm} \).
Note that \( \overline {\mu }_{Xm}(\{0\}\times \alpha )=x_{m} \), where \( x_{m} \) is the trivial \( m \)-jet on \( x=\alpha (0)\in X \). Therefore, every orbit \( \mu _{Xm}(G\times \{\alpha \}) \) contains the trivial \( m \)-jet on \( \alpha (0) \) in its closure.
Proposition 3.3.2
For\( m\in \mathbf {N}\cup \{\infty \} \), let\( Z \subset X_{m}\)be a\( G \)-invariant closed subset. Then the image\( \pi _{m}(Z) \)is closed in\( X \). In particular the image\( \pi _{m}(Z) \)of an irreducible component of\( Z\subset X_{m} \)is closed in\( X \).
Proof
Let \( Z \subset X_{m}\) be a \( G \)-invariant closed subset. Then, we obtain:
On the other hand, \( \overline {\mu }_{Xm}(\{0\}\times Z)=\sigma _{m}\circ \pi _{m}(Z) \) by Note 3.3.1. Therefore, as \( Z \) is closed, it follows that
which yields \( \pi _{m}(Z)\supset \overline {\pi _{m}(Z)} \). □
Note 3.3.3
Let \( G:={\mathbf {A}}^1\setminus \{0\}=\operatorname {Spec} k[s,s^{-1}] \) be as above. As we have an action
of G on \( X_{m} \), we have the \({\mathcal O}_X\)-graded algebra \( \oplus _{i\geq 0} {\mathcal {R}}_i\) with \( {\mathcal {R}}_0={\mathcal O}_X\) such that
Indeed, we can define
Lemma 3.3.4 ([56])
For every \(m\in \mathbf {N}\) , the base scheme X is the categorical quotient of \(X_m\) by the action of G.
Here, the definition of the categorical quotient is found in [76, Definition 0.5].
3.3.2 Morphisms of the Space of Jets/Arcs
Proposition 3.3.5
Let \( f:X\to Y \) be a morphism of \( k \) -schemes of finite type. Then there is a canonical morphism \( f_{\infty }:X_{\infty }\to Y_{\infty } \) such that the following diagram is commutative:
Proof
The morphism \( f_{\infty } \) is induced as the projective limit of \( f_{m} \)\(( m\in \mathbf {N}) \) (see Proposition 3.2.4). □
Proposition 3.3.6
Let \( f:X\to Y \) be a proper birational morphism of \( k \) -schemes of finite type such that \( f|{ }_{X\setminus W}:X\setminus W\simeq Y\setminus V \) , where \( W\subset X \) and \( V\subset Y \) are closed. Then \( f_{\infty } \) gives a bijection
Proof
Let \( \alpha \in Y_{\infty }\setminus V_{\infty } \), then \( \alpha (\eta )\in X\setminus V \). As \( X\setminus W\simeq Y\setminus V \). We obtain the following commutative diagram:
Then, as \( f \) is a proper morphism, by the valuative criteria of properness, there is a unique morphism \( \tilde \alpha : {\operatorname {Spec} K[[t]]} \to Y \) such that \( f\circ \tilde \alpha =\alpha \). This shows the bijectivity as required. □
Remark 3.3.7
The bijection above is not isomorphic in general. Actually the following is an example that \(X_{\infty }\setminus W_{\infty } \to Y_{\infty }\setminus V_{\infty } \) is not isomorphic.
Let \((Y, y)\) be a germ of isolated singularity and \(f: X\to Y\) be a resolution of the singularity \((Y,y)\). Let \(W:=f^{-1}(y)\) and \(V:=\{y\}\). Take a k-valued arc \(\alpha \in (\pi ^Y)^{-1}(y)\setminus V_\infty \) and let \(\tilde \alpha \in X_\infty \) be the corresponding arc to \({\alpha }\) by the above bijective map. Then, by Grinberg and Kazhdan [42], the formal neighborhoods \(({X}_\infty )_{\tilde \alpha }\) of \(X_\infty \) at \(\tilde \alpha \) and \(({Y}_\infty )_\alpha \) of \(Y_\infty \) at \({\alpha }\) are described as follows:
where \(D=\mathrm {Spf} k[[x]]\) and \(Z_z\) is the formal neighborhood of a scheme Z of finite type over k at a k-valued point \(z\in Z\). In [28, Example], we can take Z singular at z, which implies that
The following is the version for \( m=\infty \) of Proposition 3.2.5:
Proposition 3.3.8
If \( f:X\to Y \) is an étale morphism, then
Proof
As \( { \mathop {\text{lim}} \limits _{\longleftarrow }}_{m}(Y_{m}\times _{Y}X)=({ \mathop {\text{lim}} \limits _{\longleftarrow }}_{m}Y_{m})\times _{Y}X \), the case \( m=\infty \) is reduced to the case \( m<\infty \) which is proved in Proposition 3.2.5. □
Proposition 3.3.9
There is a canonical isomorphism:
for every \( m \in \mathbf {N}\cup \{\infty \} \) . Here, \(\times _k\) means \(\times _{\operatorname {Spec} k}\) for avoiding the bulky notation.
Proof
For an arbitrary \( k \)-scheme \( Z \),
and the right hand side is isomorphic to
The case \( m=\infty \) follows from this. □
Proposition 3.3.10
Let\( f:X\to Y \)be an open immersion (resp. closed immersion) of\( k \)-schemes of finite type. Then the induced morphism\( f_{m}:X_{m}\to Y_{m} \)is also an open immersion (resp. closed immersion) for every\( m\in \mathbf {N}\cup \{\infty \} \).
Proof
The open case follows from Lemma 3.2.5 and Proposition 3.3.8. For the closed case, we may assume that \( Y \) is affine. If \( Y \) is defined by \( f_{i} \)\( (i=1,.,r) \) in an affine space, then \( X \) is defined by \( f_{i} \)\( (i=1,.,r,.,u) \) with \( r\leq u \) in the same affine space. Then, \( Y_{m} \) is defined by \( F^{(s)}_{i} \)\( (i=1,.,r,\ s\leq m) \) and \( X_{m} \) is defined by \( F^{(s)}_{i} \)\( (i=1,.,r,.,u,\ s\leq m) \) in the corresponding affine space. This shows that \( X_{m} \) is a closed subscheme of \( Y_{m} \). □
Remark 3.3.11
In the above proposition we see that the property open or closed immersion of the base spaces is inherited by the morphism of the space of jets and arcs. But some properties are not inherited. For example, surjectivity and closedness are not inherited.
Example 3.3.12
There is an example that \( f:X\to Y \) is surjective and closed but \( f_{\infty }:X_{\infty }\to Y_{\infty } \) is neither surjective nor closed. Let \( X={\mathbf {A}}_{\mathbf {C}}^2 \) and \( G=\langle \left ( \begin {array}{cc} \epsilon & 0\\ 0 & \epsilon ^{n-1}\\ \end {array}\right )\rangle \) be a finite cyclic subgroup in \( \operatorname {GL}(2, \mathbf {C}) \) acting on \( X \), where \( n\geq 2 \) and \( \epsilon \) is a primitive \( n \)-th root of unity. Let \( Y=X/G \) be the quotient of \( X \) by the action of \( G \). Then, it is well known that the singularity appeared in \( Y \) is \( A_{n-1} \)-singularity. Then the canonical projection \( f:X\to Y \) is closed and surjective. We will see that these two properties are not inherited by \( f_{\infty }:X_{\infty }\to Y_{\infty } \). Let \( p \) be the image \( f(0)\in Y \). Then, by the commutativity
we obtain \( (\pi ^{X})^{-1}(0)=f_{\infty }^{-1}\circ (\pi ^{Y})^{-1}(p) \). Here, \( (\pi ^{X})^{-1}(0) \) is irreducible, since \( X \) is non-singular. On the other hand \( (\pi ^{Y})^{-1}(p) \) has \( (n-1) \) irreducible components by Petrov [81] and Ishii and Kollár [46]. Therefore the morphism \( f_{\infty } \) is not surjective for \( n\geq 3 \). As \( X\setminus \{0\}\to Y\setminus \{p\} \) is étale, The morphism
is also étale by Proposition 3.3.8. Since \( Y_{\infty } \) is irreducible by Corollary 3.5.38, \( f_{\infty } \) is dominant. Therefore, \( f_{\infty } \) is not closed.
Next we think of the irreducibility of the arc space or jet schemes. The following is proved in [64]. In [47] we gave another proof by using [46, Lemma 2.12] and a resolution of the singularities. Here we show a proof without a resolution.
3.3.3 The Structure of the Space of Jets/Arcs
Theorem 3.3.13 ([47, 64])
If characteristic of \( k \) is zero, then the space of arcs of a variety \( X \) is irreducible.
Proof
By Ishii and J. Kollár [46, Lemma 2.12] we obtain the following:
-
(1)
Given any arc \(\phi :\operatorname {Spec} k'[[s]]\to X\), we construct an arc \(\varPhi : \operatorname {Spec} K[[s]]\to X\) such that \(\phi \in \overline {\{\varPhi \}}\) and \(\varPhi (\tilde 0)=\varPhi (\tilde \eta )=\phi (\eta )\), where \(\eta \) and \(\tilde \eta \) are the generic points of \(\operatorname {Spec} k'[[s]]\) and \(\operatorname {Spec} K[[s]]\), respectively, while \(\tilde 0\) is the closed point of \(\operatorname {Spec} K[[s]]\).
-
(2)
We construct an arc \(\varPsi \) such that \(\varPhi \in \overline {\{\varPsi \}}\) and \(\varPsi (\tilde \eta )\in X\setminus \operatorname {Sing} X\).
Now for this \(\varPsi \) we apply the procedure (1) again, then we obtain a new arc
such that \(\varPsi \in \overline {\{\varPsi '\}}\) and \(\varPsi '(\tilde 0')=\varPsi '(\tilde \eta ')=\varPsi (\tilde \eta )\in X\setminus \operatorname {Sing} X\), where \(\tilde 0'\) (resp. \(\tilde \eta '\)) is the closed point (resp. the generic point) of \(\operatorname {Spec} K'[[s]]\). If we denote \(\pi (\varPsi ')=\varPsi '(\tilde 0')=\lambda \), then as \(\lambda \in X\setminus \operatorname {Sing} X\), it follows that
where the set of the right hand side is irreducible. This yields
hence \(X_\infty =\phi \in \overline {\pi ^{-1}(X\setminus \operatorname {Sing} X)}\) which is irreducible. □
Example 3.3.14 ([46], Example 2.13)
If the characteristic of \( k \) is \( p>0 \), \( X_{\infty } \) is not necessarily irreducible. For example, the hypersurface \( X \) defined by \( x^p-y^pz=0 \) has an irreducible component in \( (\operatorname {Sing} X)_{\infty } \) which is not in the closure of \( X_{\infty }\setminus (\operatorname {Sing} X)_{\infty } \).
Note that if the characteristic of k is 0, then every arc in \((\operatorname {Sing} X)_\infty \) lies in the closure of \(X_\infty \setminus (\operatorname {Sing} X)_\infty \). But in our case \(char k=p>0\), an arc \((x(t),0,0)\in (\operatorname {Sing} X)_\infty \cap \pi ^{-1}((0,0,0)) \) belongs to \(\overline {X_\infty \setminus (\operatorname {Sing} X)_\infty }\) if and only if \(x(t)\) has the form \(x(t)=\sum _{j=1}^\infty a_{jp}t^{jp}\)>
Example 3.3.15 ([48])
Let \( X \) be a toric variety over an algebraically closed field of arbitrary characteristic. Then, \( X_{\infty } \) is irreducible.
Next let us think of the space of \( m \)-jets. The space of \( m \)-jets of a variety is not necessarily irreducible even if the characteristic of \( k \) is zero (see Example 3.2.17).
The geometric structures of X and the space of arcs/jets affect each other.
Proposition 3.3.16 ([55])
If X is smooth, then \(X_m\) is also smooth for every \(m\in \mathbf {N}\) . Conversely, if there is \(m\in \mathbf {N}\) , such that \(X_m\) is smooth, then X is smooth.
Generally speaking, if \(X_m\) has property (P) for some \(m\in \mathbf {N}\), then X has property (P) for many properties (P).
As the k-scheme X is the categorical quotient of \(X_m\) for every \(m\in \mathbf {N}\) by the action of G (Lemma 3.3.4), we obtain by Mumford et al. [76] the following:
Proposition 3.3.17 ([56])
The following is a list of the statements of the form \(X_m\) has (P) for an \(m\in \mathbf {N}\) , then X has (P).
Example 3.3.18
The converse of (i) does not hold in general. We give here an example in [40]. Let X be defined by \(xy=0\) in \({\mathbf {A}}_{\mathbf {C}}^2\). Then, X itself is reduced but \(X_m\) is not reduced for any \(m\in \mathbf {N}\). Indeed, let \(I_m\) be the defining ideal of \(X_m\) in \(({\mathbf {A}}_{\mathbf {C}}^2)_m\). Then \(I_m\) is a homogeneous ideal of \( \mathbf {C}[x^{(0)},y^{(0)},x^{(1)},y^{(1)},\ldots , x^{(m)}, y^{(m)}]\). The degree 0 part of \(I_m\) is generated by
and the part of degree 1 is generated by
as \(\mathbf {C}[x^{(0)},y^{(0)}]\)-modules. Then, \(f:=x^{(0)}y^{(1)}\not \in I_m\), but \(f^2\in I_m.\)
The paper [40] shows more general statement. Let I be a reduced monomial ideal on \({\mathbf {A}}_{{\mathbf {C}}^n}\), then \(I_m\) is not a monomial ideal in general but \(\sqrt {I_m}\) is a monomial ideal for every \(m\in \mathbf {N}\)
Remark 3.3.19
About (ii), we have the converse statement: If X is connected, then \(X_m\) is connected for every \(m\in \mathbf {N}\). This can be seen as follows: Let \(P\in X_m\) be any point and let \(x=\pi _m(P)\). Then, the orbit \(O_G(P)\) of P by the action of G is irreducible and the closure \(\overline {O_G(P)}\) contains \(\sigma _m(x)\). Thus, every point of \(X_m\) is connected to the section \(\sigma _m(X)\) by an irreducible curve. Since \(\sigma _m(X)\simeq X\) is connected, \(X_m\) is connected.
Example 3.3.20
The converse of (iii) or the converse of (iv) do not hold in general. For example, let \(X\subset {\mathbf {A}}_{\mathbf {C}}^3\) be a curve defined by \(x^3-y^2=x^2-z^3=0\). Then, the main component \(\overline {\pi _m^{-1}(X_{reg})}\) of \(X_m\) has dimension \(m+1\). Here, \(X_{reg} \) is the open subset consisting of non-singular points of X. On the other hand, since \(\pi _m^{-1}(0)\) is defined in \((\pi _{{{\mathbf {A}}^3}m})^{-1}(0)={\mathbf {A}}_{\mathbf {C}}^{3m}\) by \(2m-2\) equations, it follows that \(\dim \pi _m^{-1}(0)\geq m+2\). This shows that \(X_m\) is not irreducible for any \(m\in \mathbf {N}\). As \(X_m\) is connected, it also shows that \(X_m\) is not locally integral for \(m\in \mathbf {N}\).
Example 3.3.21
The converse of (v) does not hold in general. For example, let X be a normal surface defined by \(x^2+y^2+z^2=0\) in \({\mathbf {A}}_{\mathbf {C}}^3\). It has an \(A_1\)-singularity at the origin. Then, \(X_m\) is irreducible by Mustaţǎ [77] but not normal for any \(m\in \mathbf {N}\). Indeed, it is known that \(X_m\) is of dimension \(2(m+1)\) for every \(m\in \mathbf {N}\). On the other hand, we can see that \(\dim \operatorname {Sing}(X_m)=\dim \pi _m^{-1}(0)=2m+1\), which shows that \(X_m\) is not normal.
Next we will think of further properties.
Theorem 3.3.22 ([56])
If \(X_m\) is locally a complete intersection for an \(m\in \mathbf {N}\) , then X is also locally a complete intersection.
Example 3.3.23
If X is locally a complete intersection, then \(X_m\) is not necessarily locally a complete intersection. Example 3.3.20 shows such an example.
Definition 3.3.24
Let X be a normal variety defined over k.
-
(i)
If for a Weil divisor D on X there exists \(r \in \mathbf {N}\) such that rD is a Cartier divisor, we call D a \(\mathbf {Q}\)-Cartier divisor on X.
-
(ii)
If every Weil divisor on X is \(\mathbf {Q}\)-Cartier divisor, we say that X is \(\mathbf {Q}\)-factorial.
-
(iii)
If for a canonical divisor \(K_X\) of X there exists \(r\in \mathbf {N}\) such that \(rK_X\) is a Cartier divisor, then we call X a \(\mathbf {Q}\)-Gorenstein variety and the minimal such \(r\in \mathbf {N}\) the index of X.
Remark 3.3.25
The property \(\mathbf {Q}\)-Gorenstein plays an important role in birational geometry. Indeed, sometimes one needs to compare the canonical divisors \(K_X\) and \(K_Y\) of the varieties X and Y , respectively, in the situation that there exists a birational morphism \(\varphi :Y\to X\). But the problem is how to compare them, because \(K_X\) and \(K_Y\) are on the different varieties and there is no canonical way to compare two divisors on different varieties. Here, if \(K_X\) is a Cartier divisor, then one can pull it back directly to get a Cartier divisor \(\varphi ^*K_X\) on Y and compare \(K_Y\) and \(\varphi ^*K_X\). A variety with \(\mathbf {Q}\)-Cartier divisor \(K_X\) is called a \(\mathbf {Q}\)-Gorenstein variety and studied in the Section 3.5.
Definition 3.3.26
Let D be a \(\mathbf {Q}\)-Cartier Weil divisor on a normal variety X defined over k. Let \(\varphi : Y \to X\) be a birational morphism. Let \(r\in \mathbf {N}\) be such that rD is a Cartier divisor. Define \(\varphi ^* D\in \mathbf {Q}\otimes _{\mathbf {Z}}\mathrm {Div}(Y)\) as follows:
where note that \(\varphi ^*(rD)\) is well defined, as rD is a Cartier divisor. The \(\mathbf {Q}\)-Cartier divisor \(\varphi ^* D\) is called the pull-back of D.
Theorem 3.3.27 ([56])
If \(X_m\) is \(\mathbf {Q}\) -factorial for an \(m\in \mathbf {N}\) , then X is \(\mathbf {Q}\) -factorial
Theorem 3.3.28 ([56])
If\(X_m\)is\(\mathbf {Q}\)-Gorenstein of index r for an\(m\in \mathbf {N}\), then X is\(\mathbf {Q}\)-Gorenstein of index\(\leq r(m+1)\).
In the following we show some results about singularities canonical, log-canonical, terminal, and log-terminal on the jet schemes. These notions will be introduced in Definition 3.5.2.
Theorem 3.3.29 ([56])
Assume \(char k=0\) . If \(X_m\) has at worst canonical (resp. terminal, log-terminal) singularities for an \(m\in \mathbf {N}\) , then X has at worst canonical (resp. terminal, log-terminal) singularities.
Theorem 3.3.30 ([56])
Assume \(char k=0\) . If \(X_m\) has at worst log-canonical singularities for an \(m\in \mathbf {N}\) , then X has at worst log-terminal singularities.
Theorem 3.3.31 ([56])
Let \(f:X \to Y\) be a morphism of k-schemes. If the induced morphism \(f_m:X_m\to Y_m\) is flat for some \(m\in \mathbf {N}\) , then f is flat.
Example 3.3.32
The converse of the theorem does not hold. Let \(X\subset {\mathbf {A}}_{\mathbf {C}}^3\) be defined by the equation \(t^d+x^d+y^d=0, \) with \(d\geq 3\), then it is a normal surface with the singularity at the origin \({0}=(0,0,0)\). Let \(f:X\to Y={\mathbf {A}}_{\mathbf {C}}^1\) be the first projection \((t,x,y)\mapsto t\). Then, as f is a surjective morphism from a reduced scheme to a non-singular curve, it is flat. However, for every \(m\geq 2\) the induced morphism \(f_m:X_m\to Y_m\) is non-flat. This is shown as follows: For every \(m\in \mathbf {N}\), consider the commutative diagram:
As \(\pi _{m}^Y\) is smooth, it is sufficient to prove that \(f\circ \pi _m^X\) is not flat for \(m\geq 2\). Note that \((\pi _{m}^X)^{-1}(X\setminus \{ 0\})\) is irreducible and of dimension \(2(m+1)\).
For \(m<d\), \((\pi _{m}^X)^{-1}(0)=(\pi _{m}^{{\mathbf {A}}^3})^{-1}( 0)={\mathbf {A}}^{3m}\). For \(m\geq d\), as \((\pi _{m}^X)^{-1}( 0)\) is defined by \(m+1-d\) equations in \({\mathbf {A}}^{3m}\), it follows that
If we assume that \(m\geq 2\), in both cases above we have
where \(0\neq t\in Y\). This yields that \(f\circ \pi _{m}^X\) is not flat.
The structures of the space of arcs and the space of jets are determined by the base scheme. So, it is natural to ask whether the converse holds, i.e., whether the space of arcs/jets determine the base scheme. This problem can be divided into the global case and the local case. First we discuss the global problem. This is again divided into two cases. The first one is posed under the additional assumption of existence of certain morphisms:
Proposition 3.3.33
Let X and Y be two schemes over k and G as in Note3.3.3. If there exists a G-equivariant isomorphism\(X_m\stackrel {\sim }\longrightarrow Y_m\)of m-jet schemes for some\(m\in \mathbf {N}\cup \{\infty \}\), then there is an isomorphism\(X\stackrel {\sim }\longrightarrow Y\).
Proof
As X and Y are the categorical quotients of \(X_m\) and \(Y_m\), respectively by the action of G (Lemma 3.3.4), the G-equivariant isomorphism of \(X_m\) and \(Y_m\) provides with the isomorphism of the categorical quotients. □
If there is a morphism \(f:X\to Y\), the induced morphism \(f_m:X_m \to Y_m\) is G-equivariant. Therefore, by the previous proposition and the universality of the categorical quotient, we obtain the following:
Corollary 3.3.34
Let \(f:X\to Y\) be a morphism of schemes over k. If the induced morphism \(f_m:X_m\to Y_m\) is an isomorphism for some \(m\in \mathbf {N}\cup \{\infty \}\) , then the morphism f is an isomorphism.
Remark 3.3.35
This corollary can be proved directly by using the fact that the morphism of the base spaces induces the morphism of the sections in the jet-schemes.
Now for the second case of global version, let us be just given an isomorphism of m-jet schemes and consider if it induces an isomorphism of base schemes. The following is a counterexample for this problem. We use the counterexample of the cancellation problem called Danielewski’s example.
Theorem 3.3.36 ([53])
Let X and Y be hypersurfaces in\({\mathbf {A}}_{\mathbf {C}}^3\)defined by\( xz-y^2+1=0 \)and\(x^2z-y^2+1=0\), respectively. Then,\(X\not \simeq Y\)but\(X_m\simeq Y_m\)for every\(m\in \mathbf {N}\cup \{\infty \}\).
Now let us turn to the local problem. The following is the affirmative answer to the local problem assuming the existence of a morphism between the base schemes. Here, we note that the notation \(X_m(x)\) in the following is defined in Definition 3.2.13.
Theorem 3.3.37 ([73])
Let \(f: (X,x)\to (Y,y)\) be a morphism of germs of a varieties. Assume that f induces isomorphisms \(f_m: X_m(x)\simeq Y_m(y)\) for all \(m\in \mathbf {N}\cup \{\infty \}\) , then f is an isomorphism.
Remark 3.3.38
Unlike the global version, only one isomorphism \(f_m: X_m\simeq Y_m\) does not guarantee that f is isomorphic. Actually, for example the isomorphism \(f_1: X_1(x)\simeq Y_1(y)\) gives just that the Zariski tangent spaces of these singularities are isomorphic. One can see an example with isomorphic \(f_1\) but not isomorphic f in the following:
Let \(X\subset {\mathbf {A}}_{\mathbf {C}}^2\) be the closed subvariety defined by \(x^2-y^2+x^3=0\). Then, the inclusion morphism \(X\hookrightarrow {\mathbf {A}}_{\mathbf {C}}^2=:Y\) is not an isomorphism. But the induced morphism of the Zariski tangent spaces is an isomorphism.
The following is a modified version of local isomorphism problem.
Theorem 3.3.39 ([22, Proposition 4.12])
Let \(f: (X,x)\to (Y,y)\) be a morphism of germs of a varieties. Assume that f induces bijective morphisms \(f_m: X_m(x) \to Y_m(y) \) for all \(m\in \mathbf {N}\cup \{\infty \}\) (equivalently, \(f_m\) induces bijection \(|X_m(x) | \to | Y_m(y) |\) of underlying spaces), then it follows that:
-
(i)
The morphism f is a closed immersion;
-
(ii)
Let \(X\hookrightarrow A\) be a closed immersion to a smooth variety A and let \(I_X\) and \(I_Y\) be the defining ideals of X and Y , respectively, in A. Then, \(I_X\supset I_Y\) holds and \(I_X\) is integral over \(I_Y\) . Here, we note that by the isomorphism \(f_1:X_1(x)\simeq Y_1(y)\) , which is viewed as an isomorphism of the Zariski tangent spaces, we can identify the ambient spaces of X and of Y .
Conversely, let\(X\subset Y\subset A\)be closed subschemes with smooth A and\(0\in X\)a point. Assume that the defining ideal\(I_X\)of X is integral over the defining ideal\(I_Y\)of Y around 0. Then, we obtain the equalities\( | X_m(0) | = | Y_m(0) |\)of underlying spaces for every\(m\in \mathbf {N}\cup \{\infty \}\).
At the end of this section, we show a mysterious theorem by Grinberg and Kazhdan [42] about the formal neighborhood of a point of the arc space. This result is reproved in [28] in a simple way. This theorem is also used to construct the example in Remark 3.3.7 in this chapter.
Theorem 3.3.40 ([28, 41])
Let X be a scheme of finite type over a filed k, and \(\operatorname {Sing} X\) the singular locus. Let \(\gamma \in X_\infty \setminus (\operatorname {Sing} X)_\infty \) be a k-valued point and \((X_\infty )_\gamma \) the formal neighborhood of \(\gamma \) . Denote the formal disk \({\operatorname {Spf}}(k[[t]])\) by D and the product of countably many copies of D by \(D^\infty \) . Then, there exists a scheme \(Y=Y(\gamma )\) of finite type over k and a k-valued point \(y\in Y\) , such that
where \(Y_y\) is the formal neighborhood of y in Y .
It is a very interesting problem to find the relationship between the singularity of \((Y,y)\) and \((X, \gamma (0))\). Some people started to study this problem.
3.4 Introduction to the Nash Problem
In this section, we introduce the Nash problem. The author introduced the problem in the expository paper [51] in 2007. After that researches on this problem developed remarkably, so it seems a good timing to introduce the problem again and show the progress after 2007. In this section, we assume the existence of resolutions of singularities. It is sufficient to assume that the characteristic of \( k \) is zero.
3.4.1 Basics for the Statement for the Nash Problem
One of the most mysterious and fascinating problem in arc spaces is the Nash problem which was posed by Nash in his preprint in 1968. It is a question about the Nash components and the essential divisors. First we introduce the concept of essential divisors.
Definition 3.4.1
Let X be a variety, \( g:X_1 \to X \) a proper birational morphism from a normal variety \( X_{1} \) and \(E\subset X_1\) an irreducible divisor. Let \( f:X_2 \to X \) be another proper birational morphism from a normal variety \( X_{2} \). The birational map  is defined on a (nonempty) open subset \(E^0\) of E because, by Zariski’s main theorem, the “fundamental locus” of a birational map between normal varieties is a closed subset of codimension \( \geq 2 \). The closure of \((f^{-1}\circ g)(E^0)\) is called the center of E on \(X_2\).
is defined on a (nonempty) open subset \(E^0\) of E because, by Zariski’s main theorem, the “fundamental locus” of a birational map between normal varieties is a closed subset of codimension \( \geq 2 \). The closure of \((f^{-1}\circ g)(E^0)\) is called the center of E on \(X_2\).
We say that \( E \)appears in \( f \) (or in \( X_2 \)), if the center of E on \(X_2\) is also a divisor. In this case the birational map  is a local isomorphism at the generic point of \( E \) and we denote the birational transform of \( E \) on \( X_2 \) again by \( E \). For our purposes \(E\subset X_1\) is identified with \(E\subset X_2\). Such an equivalence class is called a prime divisor overX.
is a local isomorphism at the generic point of \( E \) and we denote the birational transform of \( E \) on \( X_2 \) again by \( E \). For our purposes \(E\subset X_1\) is identified with \(E\subset X_2\). Such an equivalence class is called a prime divisor overX.
Let a prime divisor E over X appear on \(g:X_1\to X\). If g is not an isomorphism at the generic point of E, then we call E an exceptional divisor over X.
Definition 3.4.2
Let \( X \) be a variety over \( k \) and let \( \operatorname {Sing} X \) be the singular locus of \( X \). In this paper, by a resolution of the singularities of \( X \) we mean a proper, birational morphism \( f:Y\to X \) with \( Y \) non-singular such that the restriction \(Y\setminus f^{-1}(\operatorname {Sing} X)\to X\setminus \operatorname {Sing} X\) of \( f \) is an isomorphism.
A resolution \( f:Y\to X \) whose fiber \(f^{-1}(\operatorname {Sing} X)\) is of pure codimension one is called a divisorial resolution.
Definition 3.4.3
An exceptional divisor \( E \) over \( X \) is called an essential divisor over \( X \) if for every resolution \( f:Y\to X \) the center of \( E \) on \( Y \) is an irreducible component of \( f^{-1}(\operatorname {Sing} X) \).
For a given resolution \( f:Y\to X \), the center of an essential divisor is called an essential component on \( Y \).
Proposition 3.4.4
Let \( f:Y\to X \) be a resolution of the singularities of a variety \( X \) . The set
corresponds bijectively to the set of all essential divisors over\( X \).
In particular, the set of essential divisors over \( X \) is a finite set.
Proof
The map
is surjective by the definition of essential components. To prove the injectivity, take an essential component \( C \) and the blow up \( Y'\to Y \) with the center \( C \). Then, there is a unique divisor \( E\subset Y' \) dominating \( C \). Let \( Y''\to Y' \) be a resolution of the singularities of \( Y' \). Then, \( E \) is the unique exceptional divisor on \( Y'' \) that dominates \( C \). Therefore, every exceptional divisor over \( X \) with the center \( C\subset Y \) has the center contained in \( E \) on a resolution \( Y'' \) of the singularities of \( X \). Therefore, by the definition of essential divisor, this \( E \) is the unique essential divisor whose center on \( Y \) is \( C \). □
C. Bouvier and G. Gonzalez-Sprinberg also introduce “essential divisors” and “essential components” in [12] and [13], but we should note that the definitions are different from ours. Nash problem is about our essential divisors and not about their “essential divisors”. In order to avoid a confusion, we give different names to their “essential divisors” and “essential components” and clarify different points among them.
Definition 3.4.5 ([12, 13])
An exceptional divisor \( E \) over \( X \) is called a BGS-essential divisor over \( X \) if \( E \) appears in every resolution. An exceptional divisor \( E \) over \( X \) is called a BGS-essential component over \( X \) if the center of \( E \) on every resolution \( f \) of the singularity of \( X \) is an irreducible component of \( f^{-1}(E') \), where \( E' \) is the center of \( E \) on \( X \).
We will see how different they are from our essential divisors and essential components. First we see that they coincide for 2-dimensional case. To show this we need to introduce the concept minimal resolution.
Definition 3.4.6
A resolution \( f:Y\to X \) of the singularities of \( X \) is called the minimal resolution if for any resolution \( g:Y'\to X \), there is a unique morphism \( Y'\to Y \) over X.
It is known that for a surface \( X \) the minimal resolution \( f:Y\to X \) exists. It is characterized by the fact that \( Y \) has no exceptional curve of the first kind over \( X \).
For higher dimensional variety \( X \), the minimal resolution does not necessarily exist. For example, \( X=\{xy-zw=0\}\subset {\mathbf {A}}^4 \) has two resolutions neither of which dominates the other. These two resolutions are obtained as follows: First take a blow-up \( f:\widetilde Y \to X \) at the origin of \( X \) which has the unique singular point at the origin. Then, \( f \) is a resolution of the singularity of \( X \) and the exceptional divisor \( E \) of \( f \) is isomorphic to \( {\mathbf {P}}^1\times {\mathbf {P}}^1 \). Here we have two contractions \( g_{1}:\widetilde Y\to Y_{1} \), \( g_{2}:\widetilde Y \to Y_2\) whose restrictions on E are the first projection \( p_{1}:E={\mathbf {P}}^1\times {\mathbf {P}}^1 \to {\mathbf {P}}^1\) and the second projection \( p_{2}:E={\mathbf {P}}^1\times {\mathbf {P}}^1 \to {\mathbf {P}}^1\), respectively. Then both \( Y_{i} \)’s are non-singular, therefore \( f_{i}:Y_i\to X \)\((i=1,2)\) are resolutions of the singularity of \( X \). It is clear that there is no morphism between \( Y_{1} \) and \( Y_{2} \) over \( X \).
Proposition 3.4.7
If \( X \) is a surface, then each of the set of “essential divisors”, “BGS-essential divisors” and “BGS-essential components” are bijective to the set of the components of the fiber \( f^{-1}(\operatorname {Sing} X) \) , where \( f:Y\to X \) is the minimal resolution. These are also essential components on the minimal resolution.
Remark 3.4.8
Four concepts “essential divisor”, “essential component”, “BGS-essential divisor” and “BGS-essential component” are mutually different in general.
First, our essential component is different from the others, because it is a closed subset on a specific resolution and the others are all equivalence classes of irreducible divisors.
Next, a BGS-essential divisor is different from a BGS-essential component or an essential divisor. Indeed, for \( X=(xy-zw=0)\subset {\mathbf {A}}_{k}^4 \), the exceptional divisor obtained by a blow-up at the origin is the unique essential divisor and also the unique BGS-essential component, while there is no BGS-essential divisor, since \( X \) has a resolution whose exceptional set is \( {\mathbf {P}}_{k}^1 \), which is not a divisor.
Finally a BGS-essential component and an essential component are different. Indeed, consider a cone generated by \( (0,0,1),(2,0,1),(1,1,1), \)\((0,1,1) \) in \( {\mathbf {R}}^3 \). It is well known that a cone generated by integer points in a real Euclidean space defines an affine toric variety (see [36, 83] for basic notion of toric varieties). Let \( X \) be the affine toric variety defined by this cone. Then the canonical subdivision adding a one dimensional cone \( {\mathbf {R}}_{\geq 0}(1,0,1) \) is a resolution of \( X \). As the singular locus of \( X \) is of dimension one, there is no small resolution. Therefore, the divisor \( D_{(1,0,1)} \) is the unique essential divisor, while \( D_{(1,1,2)} \) and \( D_{(2,1,2)} \) are BGS-essential components by the criterion [12, Theorem 2.3].
Definition 3.4.9
Let \( X \) be a variety and \( \pi :X_{\infty }\to X \) the canonical projection. An irreducible component \( C \) of \( \pi ^{-1}(\operatorname {Sing} X) \) is called a Nash component if it contains an arc \( \alpha \) such that \( \alpha (\eta )\not \in \operatorname {Sing} X \). This is equivalent to saying that \( C \not \subset (\operatorname {Sing} X)_{\infty } \).
The following lemma is already quoted for the irreducibility of the space of arcs (Theorem 3.3.13).
Lemma 3.4.10 ([46])
If the characteristic of the base field \( k \) is zero, then every irreducible component of \( \pi ^{-1}(\operatorname {Sing} X) \) is a Nash component.
We note that for the positive characteristic case this lemma does not hold. Indeed, Example 3.3.14 is an example that \( \pi ^{-1}(\operatorname {Sing} X) \) has an irreducible component which is not a Nash component.
Let \( f:Y\to X \) be a resolution of the singularities of \( X \) and \( E_{l} \)\( (l=1,..,r) \) the irreducible components of \( f^{-1}(\operatorname {Sing} X) \). Now we are going to introduce a map \( \mathcal {N} \) which is called the Nash map
Note 3.4.11 (Construction of the Nash Map)
The resolution \( f:Y\to X \) induces a morphism \( f_{\infty }:Y_{\infty }\to X_{\infty } \) of schemes. Let \( \pi ^{Y}:Y_{\infty } \to Y \) be the canonical projection. As \( Y \) is non-singular, \( (\pi ^{Y})^{-1}(E_{l}) \) is irreducible for every \( l \). Denote by \( (\pi ^{Y})^{-1}(E_{l})^o \) the open subset of \( (\pi ^{Y})^{-1}(E_{l}) \) consisting of the points corresponding to arcs \( \beta :\operatorname {Spec} K[[t]]\to Y \) such that \( \beta (\eta )\not \in f^{-1}(\operatorname {Sing} X) \). Let \( C_{i} \)\( (i\in I )\) be the Nash components of \( X \). Denote by \( C_{i}^o \) the open subset of \( C_{i} \) consisting of the points corresponding to arcs \( \alpha :\operatorname {Spec} K[[t]]\to X\) such that \( \alpha (\eta )\not \in \operatorname {Sing} X \). As \( C_{i} \) is a Nash component, we have \( C_{i}^o \neq \emptyset \). The restriction of \( f_{\infty } \) gives
By Proposition 3.3.6, \( f^{\prime }_{\infty } \) is surjective. Hence, for each \( i\in I \) there is a unique \( l_{i} \) such that \( 1\leq l_{i}\leq r \) and the generic point \( \beta _{l_{i}} \) of \( (\pi ^{Y})^{-1}(E_{l_{i}})^o \) is mapped to the generic point \( \alpha _{i} \) of \( C_{i}^o \). By this correspondence \( C_{i}\mapsto E_{l_{i}} \) we obtain a map
Lemma 3.4.12
The map\( \mathcal {N} \)is an injective map to the subset consisting of the essential components on\( Y \).
Proof
Let \( \mathcal {N}(C_{i})= E_{l_{i}} \). Denote the generic point of \( C_{i} \) by \( \alpha _{i} \) and the generic point of \( (\pi ^{Y})^{-1}(E_{l}) \) by \( \beta _{l} \). If \( E_{l_{i}}=E_{l_{j}} \) for \( i\neq j \), then \( \alpha _{i}=f^{\prime }_{\infty }(\beta _{l_{i}})= f^{\prime }_{\infty }(\beta _{l_{j}})= \alpha _{j}\), a contradiction. This gives the injectivity of \(\mathcal N\)
To prove that the \( \{E_{l_{i}}: i\in I\} \) are essential components on \( Y \), let \( Y'\to X \) be another resolution and \( \tilde Y \to X \) a divisorial resolution which factors through both \( Y \) and \( Y' \). Let \( E^{\prime }_{l_{i}}\subset Y' \) and \( \tilde E_{l_{i}}\subset \tilde Y \) be the irreducible components of the exceptional sets corresponding to \( C_{i} \). Then, we can see that \( E_{l_{i}} \) and \( E^{\prime }_{l_{i}} \) are the image of \( \tilde E_{l_{i}} \). This shows that \( \tilde E_{l_{i}} \) is an essential divisor over \( X \) and therefore \( E_{l_{i}} \) is an essential component on \( Y \). □
Problem 3.4.13
Is the Nash map
bijective?
3.4.2 History of the Nash Problem
Here we will see the results for this problem according to time line. The first affirmative result for the Nash problem was given by Nash himself.
Theorem 3.4.14 ([81])
The Nash problem is affirmatively answered for an\( A_{n} \)-singularity\( (n\in \mathbf {N}) \), where an\( A_{n} \)-singularity is the hypersurface singularity defined by\( xy-z^{n+1}=0 \)in\( {\mathbf {A}}_{k}^3 \).
It is difficult to realize the essential divisors for higher dimensional case, but for two-dimensional case the essential divisors are just the exceptional divisors on the minimal resolution. So, the people thought that surface case is the easiest for the problem and many people studied the problem for surface case. The first concrete result after Nash’s paper is the following:
Theorem 3.4.15 ([89])
The Nash problem is affirmatively answered for a minimal surface singularity. Here, a minimal surface singularity means a rational surface singularity with the reduced fundamental cycle. (A rational singularity is defined in Definition 3.5.6 in the next section.) The fundamental cycle is introduced by M. Artin (see [ 5 ] for the definition).
Theorem 3.4.16 ( [70, 88, 90])
The Nash problem is affirmatively answered for a sandwiched surface singularity and \(D_n\) -singularity for \(n>4\) . Here, a sandwiched surface singularity means the formal neighborhood of a singular point on a surface obtained by blowing up a complete ideal in the local ring of a closed point on a non-singular algebraic surface. A complete ideal is defined by O. Zariski and Samuel (see [ 99 ], Vol II, Appendix 4 ), but the idea of a sandwiched singularity is that it is a singularity which is birationally sandwiched by non-singular surfaces.
These are results on rational surface singularities, the following gives affirmative answer for some non-rational surface singularities:
Theorem 3.4.17 ([86])
The Nash problem is affirmatively answered for a normal surface singularities with the reduced fiber\( E \)of the singular point on the minimal resolution such that\( E\cdot E_{i}<0 \)for every irreducible component\( E_{i} \)of\( E \).
This result is generalized to a wider class of surface singularities in [74]. We omit the statement, since it is not simple.
The following results are for arbitrary dimension.
Theorem 3.4.18 ([46])
The Nash problem is affirmatively answered for a toric singularity of arbitrary dimension.
When we say just“toric variety”, we always assume normality of the variety. There is a notion “not-necessarily normal toric variety” and an even wider class “pretoric variety” that now we define.
Definition 3.4.19
A variety \( X \) is called a pretoric variety if
-
(1)
there are a toric variety \( Z \) with the torus \( T' \) and a finite morphism \( \rho :X\to Z \) étale on \( T' \),
-
(2)
for the normalization \( \nu :\overline {X} \to X \), \( \overline {X} \) is a toric variety with the torus \( T \) and the composite \( \rho \circ \nu :\overline {X}\to Z \) is the equivariant quotient morphism by the group \( N'/N \), where \( N \) and \( N' \) are the lattice on which the fans of \( \overline {X} \) and \( Z \), respectively, are defined, and
-
(3)
the subset \( \nu ^{-1}(\operatorname {Sing} X) \) is an invariant closed set on \( \overline {X} \).
We will see two typical examples of a pretoric variety.
Note 3.4.20 ([37])
Here, we introduce a not-necessarily normal affine toric variety. A not-necessarily normal affine toric variety is of the form \( X_{ \varGamma }= \operatorname {Spec} \mathbf {C}[ \varGamma ] \), where \( \varGamma \subset M= {\mathbf {Z}}^n\) is a finitely generated semigroup with \( 0 \) and \( \varGamma \) generates the abelian group \( M \). Then, the torus \( T=\operatorname {Spec} \mathbf {C}[M] \) acts on \( X_{ \varGamma } \). Denote by \( K( \varGamma )\subset M_{\mathbf {R}} \), the convex cone which is the convex hull of \( \varGamma \) and by \( \overline { \varGamma } \) the intersection \( K(\varGamma )\cap M \). Then, \( X_{\overline { \varGamma }} \) is a normal toric variety and the inclusion \( \mathbf {C}[ \varGamma ]\hookrightarrow \mathbf {C}[\overline { \varGamma }] \) induces the equivariant normalization \( X_{\overline { \varGamma }}\to X_{ \varGamma } \).
Example 3.4.21
A not-necessarily normal toric variety is a pretoric variety. This is proved as follows: Let \( X=\operatorname {Spec} \mathbf {C}[\varGamma ] \) be a not-necessarily normal toric variety of dimension \( n \). Let \(\sigma \subset N_{\mathbf {R}}\) be the cone such that \(\sigma ^{\vee }=K(\varGamma )\) under the notation as above. Let \( \overline {X}=\operatorname {Spec} \mathbf {C}[\sigma ^{\vee }\cap M] \) be the normalization of \( X \). Subdivide \( \sigma ^{\vee } \) into simplicial cones without adding any 1-dimensional cones. Let \( \tau _{1}, \tau _{2},.., \tau _{s} \) be the \( n \)-dimensional simplicial cones which are obtained by this subdivision. We can take generators \( e_{1}^{(i)},..,e_{n}^{(i)} \) of \( \tau _{i} \) in \( \varGamma \). Define \( M_{i}=\oplus _{j=1}^n\mathbf {Z} e_{j}^{(i)} \), then \( M_{i} \) is a subgroup of \( M \) of finite index. Let \( M' \) be the intersection \( \bigcap _{i=1}^s M_{i} \). Then, \( M' \) is a subgroup of \( M \) of finite index. It follows that \( \sigma ^{\vee }\cap M' \subset \varGamma \). Indeed, an arbitrary element \( u\in \sigma ^{\vee }\cap M' \) is contained in \( \tau _{i}\cap M_{i} \) for some \( i \). Then, by the definition of \( M_{i} \), we have that \( u=\sum _{j=1}^n a_{j}e_{j}^{(i)} \) with \( a_{j}\in {\mathbf {Z}}_{\geq 0} \). As \( e_{j}^{(i)} \)’s are in \( \varGamma \), it follows that \( u\in \varGamma \). By this inclusion \( \sigma ^{\vee }\cap M' \subset \varGamma \) we obtain a finite morphism \( \rho : X\to Z=\operatorname {Spec} \mathbf {C}[\sigma ^{\vee }\cap M'] \). The other conditions for a pretoric variety follow immediately.
The following is an example of a pretoric variety without a toric action.
Example 3.4.22
Let \( \overline {X} \) be \( \operatorname {Spec} \mathbf {C}[x,y] \) and \( X \) be \( \operatorname {Spec} \mathbf {C}[x,y^3, y^4] \), then \( X \) is a non-normal toric variety with the normalization \( \nu :\overline {X}\to X \). Therefore we have a diagram \( \overline {X}\stackrel {\nu }\longrightarrow X \stackrel {\rho }\longrightarrow Z \) as in Definition 3.4.19. Here, \(Z=\operatorname {Spec} \mathbf {C}[x, y^{12}]\) is constructed according to the previous example. Let \( X_{0} \) be \( \operatorname {Spec} \mathbf {C}[x, y+y^2, y^3, y^4] \), then \( X_{0} \) is a pretoric variety with the diagram: \( \overline {X}\to X_{0}\to Z \). By the definition, \( X_{0} \) does not admit a toric action.
Theorem 3.4.23 ([49])
The Nash problem is affirmatively answered for a pretoric variety of arbitrary dimension.
Theorem 3.4.24 ([1])
The Nash problem is affirmatively answered for non-rational quasi-rational hypersurface singularities of arbitrary dimension.
We have a notion of the local Nash problem which is a slight modification of the Nash problem ([50]).
Theorem 3.4.25 ([50])
The local Nash problem hold true for quasi-ordinary singularities. Here, a quasi-ordinary singularity is a hypersurface singularity which is a finite cover over a non-singular variety with the normal crossing branch locus. We note that a quasi-ordinary singularity is not necessarily normal and its normalization is toric.
The paper [87] by Plénat and Popescu-Pampu gives the affirmative answer to the Nash problem for a certain class of higher dimensional non-toric singularities.
So far we have seen the affirmative answers. But there are negative examples given in [46] by Ishii and Kollár .
Example 3.4.26 ([46])
Let \( X \) be a hypersurface defined by \( x_{1}^3+ x_{2}^3+x_{3}^3+x_{4}^3+x_{5}^6=0 \) in \( {\mathbf {A}}_{\mathbf {C}}^5 \). Then the number of the Nash components is one, while the number of the essential divisors is two. Therefore the Nash map is not bijective.
By the above example we can construct counter examples to the Nash problem for any dimension greater than 3 by making the product with \({\mathbf {A}}_k^n\) for \(n\geq 1\). Therefore at that moment of the paper, the unsolved case for Nash problem was only 2- and 3-dimensional cases. Then, J. F. Bobadilla and M.P.Pereira proved the affirmative answer for 2-dimensional case.
Theorem 3.4.27 ([11])
The Nash problem is affirmatively answered for surfaces.
This result is based on the topological observation by Bobadilla as follows:
Proposition 3.4.28 ([10])
Nash problem for surface singularities depends only on the topological type.
Later on, algebraic proof of the Nash problem for surface is given by De Fernex and Docampo as a corollary of their main theorem:
Theorem 3.4.29 ([20])
Let \(\varphi : Y\to X\) is a terminal model which means proper birational morphism from Y with at worst terminal singularities and \(\varphi \) -nef canonical divisor of Y . Then, the irreducible exceptional divisors on Y are in the images of the Nash map. In particular, irreducible exceptional curves on the minimal resolution of a surface are in the image of the Nash map.
Here, we should note that the minimal resolution of a surface singularity is the terminal model.
The first 3-dimensional negative example for the Nash problem is given by De Fernex.
Example 3.4.30 ([19])
The singularity of 3-dimensional hypersurface in \({\mathbf {A}}_{\mathbf {C}}^4\) defined by
has one Nash component and has two essential divisors. Thus the Nash map is not bijective.
The following is a bit more systematic example for the negative answer to the Nash problem for threefolds obtained by Johnson and Kollár:
Example 3.4.31 ([63])
For the singularities on \(X(m):=(xy-z^2+u^m=0)\subset {\mathbf {A}}_{\mathbf {C}}^4\) the Nash map is not surjective for odd \(m\geq 5\) but surjective for even m and \(m=3\). Thus the simplest example where the Nash map is not bijective is
Now we can formulate a new version of the Nash problem:
Problem 3.4.32
-
(i)
Characterize the image of the Nash map.
-
(ii)
Characterize the singularities for which the Nash problem is affirmative.
Related to these problems, we have one characterization of the image of the Nash map given by Reguera [91]. To formulate her result, we introduce the concept “wedge” which is also used in [11].
Definition 3.4.33
Let X be a k-scheme. Let \( K\supset k \) be a field extension. A \( K \)-wedge of \( X \) is a \( k \)-morphism \( \gamma :\operatorname {Spec} K[[\lambda , t]]\to X \). A \( K \)-wedge \( \gamma \) can be identified to a \( K[[\lambda ]] \)-point on \( X_{\infty } \). Denote by 0 and \(\eta \) the closed point and the generic point of \( \operatorname {Spec} K[[\lambda ]] \), respectively. We call the image \( \gamma (0)\in X_{\infty } \) the special arc of \( \gamma \) and call the image\(\gamma (\eta )\in X_{\infty } \) the generic arc of \( \gamma \).
Theorem 3.4.34 ([91])
Let \( E \) be an essential divisor over \( X \) and \( f:Y\to X \) a resolution of the singularities of \( X \) on which \( E \) appears. Let \( \alpha \in X_{\infty } \) be the generic point of \( f_{\infty }(\pi ^{Y})^{-1}(E) \) and \( k(\alpha ) \) the residue field of \( \alpha \) . Then the following conditions are equivalent:
-
(i)
\( E \) belongs to the image of the Nash map;
-
(ii)
For any resolution of the singularities\( g:Y'\to X \)and for any field extension\( K \)of\( k({\alpha }) \), any\( K \)-wedge\( \gamma \)on\( X \)whose special arc is\( \alpha \)and whose generic arc belongs to\( (\pi ^{X})^{-1}(\operatorname {Sing} X) \), lifts to\( Y' \);
-
(iii)
There exists a resolution of the singularities \( g:Y'\to X \) satisfying condition (ii).
As an application of this theorem, we obtain Theorem 3.4.16.
There are some notions “the Nash problem for a pair \( (X, Z) \)” consisting of a variety \( X \) and a closed subset \( Z \) (see [38, 85]).
3.5 Applications to Birational Geometry
3.5.1 Overview of Birational Geometry in Connection with the Space of Arcs
Birational geometry is the study properties of varieties which do not change under birational maps. In this viewpoint we identify varieties which are birationally equivalent each other. In each equivalence class, is there a “good” representative? We think that smaller variety is better, where we say X is smaller than Y if there is a proper birational morphism \(Y\to X\).
“Find a minimal variety (called a minimal model) in the equivalence class.”
This is one of the most important problems in birational geometry so called “Minimal Model Problem”. In dimension one and two, it is classically well known that there are smooth minimal models in an equivalence class. But in higher dimensional case, it is known that we cannot have such a model by the example following Definition 3.4.6. So we need to reformulate the Minimal Model Problem allowing mild singularities. In this way, mild singularities (terminal, log terminal, canonical, log canonical, see Definition 3.5.2 below) allowable in minimal models appeared around 1980. Minimal Model Problem was solved in dimension three in the most basic form by S. Mori [75]. Then, the problem is generalized to several variants. By the work [6], a large part of the problems for arbitrary dimensional case in characteristic 0 is solved. However in its most general setting the problem is still open and the main point of the problem is reduced to certain behaviors of “the minimal log discrepancy”, an invariant of a singularity. The research of this direction is still going on and the author thinks that it is good for the reader to know what is known and what is not.
In this section, we discuss about the expression of this invariant by the space of arcs and obtain one of the required behavior for Minimal Model Problem for a special case. We also obtain the characterization of the mild singularities by the space of jets.
3.5.2 Basics in Birational Geometry
Henceforth, we always assume that X is normal and \(\mathbf {Q}\)-Gorenstein variety (see Definition 3.3.24). The reader who would like to study this direction closely, please refer to [35] or [65]. A typical example of \(\mathbf {Q}\)-Gorenstein variety is a variety of locally a complete intersection. Here, the condition that X is “locally a complete intersection” means that at each point of X there is an affine open neighborhood embedded into a smooth affine variety with codimension c and defined by exactly c equations in the smooth variety. In particular, a hypersurface is an example of locally a complete intersection.
First we define the log discrepancy for a pair \((X, {\mathfrak {a}}^e)\) consisting of a normal \(\mathbf {Q}\)-Gorenstein variety X and a coherent multi-ideal sheaf \({\mathfrak {a}}\subset {\mathcal O}_X\) with a real exponent e, which means
where \({\mathfrak {a}}_i\subset {\mathcal O}_X\) are non-zero coherent ideal sheaves.
As we assume that X is \(\mathbf {Q}\)-Gorenstein, for a morphism
the pull-back \(\varphi ^*K_X\) is always defined and becomes a \(\mathbf {Q}\)-Cartier divisor on Y again (see, Definition 3.3.26).
Definition 3.5.1
Let E be a prime divisor over a normal \(\mathbf {Q}\)-Gorenstein variety X. Then we define log discrepancy\(k_E+1\in \mathbf {Z}\) of X at E as follows:
where \(\varphi :Y\to X\) is a birational morphism such that Y is normal, E appears on Y and \(\operatorname {ord}_E\) means the coefficient of the divisor at E.
Log discrepancy of a pair\((X,{\mathfrak {a}}^e)\) consisting of a normal \(\mathbf {Q}\)-Gorenstein variety X and multi-ideal sheaf \({\mathfrak {a}}^e\) with a real exponent at E is defined as follows:
where \(v_E\) is the valuation defined by E.
Definition 3.5.2
We say that a pair \((X,{\mathfrak {a}}^e)\) is terminal / canonical / log terminal / log canonical at a point \(x\in X\) if
respectively.
We say that X has terminal / canonical / log terminal / log canonical singularities, if \((X, {\mathcal O}_X)\) is terminal / canonical / log terminal / log canonical, respectively, at every point of X.
By the definition, the following implications are clear:
terminal \(\Rightarrow \) canonical \(\Rightarrow \) log terminal \(\Rightarrow \) log canonical.
One can see that if X is smooth and \({\mathfrak {a}}={\mathcal O}_X\), then for every exceptional prime divisor E over X, we have \(a(E; X,{\mathcal O}_X)\geq N:=\dim X\). Therefore we also obtain
According to the definition, in order to decide whether the pair is terminal or so one should check all prime divisors with the center containing x. However, if there is a “log resolution” for the pair, then we can decide by checking only finite number of exceptional prime divisors.
Definition 3.5.3
Let \((X, {\mathfrak {a}}^e)\) be as above. A morphism \(\varphi : Y \to X\) is called a log resolution of \((X, {\mathfrak {a}}^e)\), if the following hold:
-
(i)
\(\varphi \) is a proper birational morphism from a non-singular variety Y ;
-
(ii)
the ideals \({\mathfrak {a}}_i\cdot {\mathcal O}_Y\) are all locally principal on Y ;
-
(iii)
the union of all exceptional sets and the divisors defined by \({\mathfrak {a}}_i\cdot {\mathcal O}_Y\) is set theoretically a divisor with normal crossings.
Proposition 3.5.4 ([32, Proposition 7.2])
Let X be a normal and locally a complete intersection variety defined over an algebraically closed field k of arbitrary characteristic. Assume there exists a log resolution\(\varphi : Y\to X\)of a pair\((X,{\mathfrak {a}}^e)\).
If \(a(E_i; X,{\mathfrak {a}}^e)> 1 \ /\ \geq 1\ /\ > 0\ /\ \geq 0,\) for every exceptional divisor \(E_i\) on Y with the center containing x, then \((X,{\mathfrak {a}}^e)\) is terminal / canonical / log terminal / log canonical at x, respectively.
Remark 3.5.5
At present, existence of log resolutions is known when the base field k is of characteristic 0 (by Hironaka [45], see also [66]) or \(\dim X\leq 3\) (by Abhyankar [2, 3] and Cossart-Piltant [16]).
By using a resolution of the singularities \(\varphi :Y\to X\) we have another important and popular notion of a singularity.
Definition 3.5.6
We say that a variety X has rational singularity at \(x\in X\) if the following hold:
-
(i)
X is normal;
-
(ii)
X has a resolution of the singularities \(\varphi :Y\to X\) and the vanishing \(R^j\varphi _*{\mathcal O}_Y=0\) holds for every \(j\geq 1\) in a neighborhood of x.
Rational singularities do not affect the cohomologies between X and the smooth variety Y . So, a rational singularity is considered as a singularity close to a smooth point. It is well known that the singularities appearing on a toric variety are rational. It is natural to ask the relation of a rational singularity and the other classes of singularities defined above.
Proposition 3.5.7 ([34, 62])
Assume the base field k is of characteristic 0. If \((X, {\mathfrak {a}}^e)\) is log terminal at \(x\in X\) , then the singularity \((X,x)\) is rational.
Definition 3.5.8
The minimal log discrepancy for a pair \((X,{\mathfrak {a}}^e)\) at a point \(x\in X\) and at a proper closed subset \(W\subset X\) is defined as follows:
-
(i)
When \(\dim X\geq 2\),
$$\displaystyle \begin{aligned} {\mathrm{mld}} (x; X, {\mathfrak{a}}^e) =\inf\{ a(E;X, {\mathfrak{a}}^e) \mid E :\ {\operatorname { prime\ divisor \ with \ the\ center\ at }}\ x \},\end{aligned}$$$$\displaystyle \begin{aligned} {\mathrm{mld}} (W; X, {\mathfrak{a}}^e) =\inf\{ a(E;X, {\mathfrak{a}}^e) \mid E :\ {\operatorname { prime\ divisor \ with \ the\ center\ in }}\ W \}.\end{aligned}$$ -
(ii)
When \(\dim X=1\), define \({\mathrm {mld}} (x; X,{\mathfrak {a}}^e)\) and \({\mathrm {mld}}(W; X,{\mathfrak {a}}^e)\) by the same definitions as above if the right hand sides of the above definition are non-negative and otherwise define \({\mathrm {mld}}(W; X, {\mathfrak {a}}^e)= -\infty \).
Here, we remark that either \({\mathrm {mld}}(x; X, {\mathfrak {a}}^e)\geq 0\) or \({\mathrm {mld}}(x; X, {\mathfrak {a}}^e)=-\infty \) holds in any dimension.
Proposition 3.5.9
Let \((X,{\mathfrak {a}}^e)\) be a pair as above and \(x\in X\) a point. If the pair is terminal / canonical / log terminal / log canonical at x, then
Conversely, if \({\mathrm {mld}}(x; X,{\mathfrak {a}}^e) \geq 0\) , then the pair is log canonical at x. But for the other cases the converse does not hold in general.
Example 3.5.10
Let \(X={\mathbf {A}}_k^3\), \(\{x,y,z\}\) a coordinate system on \({\mathbf {A}}_k^3\) and \({\mathfrak {a}}:=(x\cdot y)\). Then,
but \((X, {\mathfrak {a}})\) is not log terminal at the origin 0 because the exceptional divisor E obtained by the blow up by the prime ideal \((x, y)\) has the log discrepancy
A modified pair \((X, {\mathfrak {a}}^e)\)\((1/2 < e < 1)\) from the above gives an example that has
but \((X, {\mathfrak {a}}^e)\) is not terminal because for a prime divisor E as above has the log discrepancy
Definition 3.5.11
Let E be a prime divisor over X with the center at x. We say that Ecomputes\({\mathrm {mld}}(x;X,{\mathfrak {a}}^e)\) if
Remark 3.5.12
If there exists a log resolution factored through the blow up at x, then there exists a prime divisor computing \({\mathrm {mld}}\) for the pair. Therefore, if \(char k=0\), then such a prime divisor always exists.
If all \(e_i\) are rational numbers, then the set of log discrepancies is discrete, which implies the infimum is minimum or \(-\infty \) and therefore there exists a prime divisor computing mld.
Definition 3.5.13
For a pair \((X,{\mathfrak {a}}^e)\) we define the log canonical threshold at \(x\in X\) as follows:
where \({\mathfrak {a}}^{ec}={\mathfrak {a}}_1^{e_1c}\cdots {\mathfrak {a}}_s^{e_sc}\)
Remark 3.5.14
For a pair \((X,{\mathfrak {a}}^e)\) and a point \(x\in X\) the \({\mathrm {lct}}_x(X, {\mathfrak {a}}^e)\) is obtained as follows:
-
(i)
\({{\mathrm {lct}}_x(X, {\mathfrak {a}}^e)=\inf \left \{ \frac {k_E+1}{\sum e_i\cdot v_E({\mathfrak {a}}_i)}\ \middle | \begin {array}{l} E : \mbox{prime}\ \mbox{divisor}\ \mbox{with}\ \\ \mbox{the }\ \mbox{center }\ \mbox{containing}\ x \\ \end {array} \right \}}.\)
-
(ii)
If \(\varphi :Y\to X\) is a log resolution of \((X, {\mathfrak {a}}^e)\) and \(E_j\)\((j=1,\ldots , m)\) are prime divisors on Y with the center containing x, which are either exceptional or in the support of \({\mathfrak {a}}_i\cdot {\mathcal O}_Y\)’s. Then it follows that:
$$\displaystyle \begin{aligned} {\mathrm{lct}}_x(X, {\mathfrak{a}}^e)=\min_{j=1,\ldots,m}\left\{ \frac{k_{E_j}+1}{\sum e_i\cdot v_{E_j}({\mathfrak{a}}_i)} \right\}.\end{aligned}$$
Note 3.5.15
Roughly speaking, a generalized MMP is in the form as follows:
“In the birational equivalence class of pairs \((X, {\mathfrak {a}}^e)\) with singularities of type (P), does there exist a minimal model \((X_0, {\mathfrak {a}}_0^e)\) with the singularities of the same type?”
Here, (P) is the representative of “terminal”, “log terminal”, “canonical”, “log canonical”. Note that in MMP singularities are studied under a general setting but in this paper we restrict our attention to locally complete intersection case,
In order to get a minimal model, one strategy, called Minimal Model Program, is established around 1990 and the successful cases of the problem so far all follow from this program.
This program to get a minimal model, roughly speaking, goes as follows:
-
(i)
If a pair with the singularities of type (P) is a minimal model, then there is nothing to do anymore.
-
(ii)
If a pair is not a minimal model, then we do
-
(C)
contract of extremal ray, which is to construct a certain proper birational morphism \(X\to X'\) to obtain a new pair \((X',{{\mathfrak {a}}'}^e)\).
Assume the new pair has the singularities of the same type. If the new pair \((X',{{\mathfrak {a}}'}^e)\) is a minimal model, we stop. Otherwise continue the process;i.e., go to (1) above and follow the instruction.
Assume the new pair \((X',{{\mathfrak {a}}'}^e)\) does not have singularities of the same type, then we do the following:
-
(F)
make a birational map called a flip
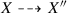 to get a new pair \((X'', {{\mathfrak {a}}''}^e)\) instead of the contraction.
to get a new pair \((X'', {{\mathfrak {a}}''}^e)\) instead of the contraction.Assume the new pair \((X'', {{\mathfrak {a}}''}^e)\) is a minimal model, then we stop.
Otherwise continue the process: i.e., go to (1) above and follow the instruction. In this way we carry out: step (C) or step (F). If the procedure stops at some stage, then it means that we get a minimal model. It is known that the possible number of steps (C) is limited, but that of (F) is not obvious. V. Shokurov proved that if the following two conjectures (ACC Conjecture and LSC Conjecture) hold, then the possible number of steps (F) is finite.
-
(C)
See [35] for more detailed information about Minimal Model Program.
Conjecture 3.5.16 (ACC Conjecture)
Let \(J\subset {\mathbf {R}}_{\geq 0}\) be a DCC set. (I.e., there is no infinite strictly decreasing sequence in J). Then the following set satisfies ACC (i.e., there is no infinite strictly increasing sequence).
Conjecture 3.5.17 (LSC Conjecture)
For a pair \((X,{\mathfrak {a}}^e)\) the following map is lower semi continuous (LSC):
i.e., for every \(r\in {\mathbf {R}}_{\geq 0}\) the set \(\{ x\in X \mid {\mathrm {mld}}(x;X,{\mathfrak {a}}^e)>r\}\) is an open subset of X.
Conjecture 3.5.18 (MN Conjecture)
For N and e, there exists a number \(\ell _{N,e}\) which depends on N and e, such that for every pair \((X, {\mathfrak {a}}^e)\) and a point \(x\in X\) (\(\dim X=N\)) there exists a prime divisor E computing \({\mathrm {mld}}(x;X,{\mathfrak {a}}^e)\) and satisfying \(k_E\leq \ell _{N,e}\).
MN Conjecture is Mustaţǎ-Nakamura’s conjecture posed by them in [79] and proved for special cases (surfaces and monomial ideals on arbitrary dimensional affine space).
They prove the relation of the conjecture and ACC Conjecture as follows:
Theorem 3.5.19 (Theorem 1.5, [79])
Fix a point \(x\in X\) on a variety X with “mild” singularities such that the assertion in MN Conjecture holds for \((X, x)\) . Then, for every fixed DCC set J, the following set satisfies ACC:
For the precise meaning of “mild singularities”, the reader can see in [79].
Remark 3.5.20
In ACC Conjecture and also in MN Conjecture, X and x may vary. But even for fixed \(x\in X\), the problem is not easy. These conjectures appeared motivated by MMP, but the problems themselves are interesting from the point of view of singularity theory. So these are studied under various conditions and in such a situation the space of arcs contributed quite a bit. We will see it in the following subsection.
3.5.3 Log Discrepancies via the Spaces of Arcs
Let E be a prime divisor over a normal locally complete intersection variety X. In this subsection we will express the log discrepancy \(k_E+1\) of X at E in terms of the space of arcs of X. We assume that X is just a variety over k unless otherwise stated. First we prepare the notion of the contact loci of an ideal in the space of arcs.
Definition 3.5.21 ([33])
For an affine variety \( X \) and an ideal \( {\mathfrak {a}}\subset {\mathcal O}_X \), we define
and
where the order \(\operatorname {ord}_\alpha \) is defined by \(\alpha \in X_\infty \) as follows:
Here, \(\alpha ^*: {\mathcal O}_X \to k[[t]]\) is the ring homomorphism corresponding to \({\alpha }\).
These subsets are called contact loci of the ideal \( {\mathfrak {a}} \). The subset \( \mathrm {{Cont}}^{\geq m}({\mathfrak {a}} ) \) is closed and \( \mathrm {{Cont}}^m({\mathfrak {a}} ) \) is locally closed. Indeed, let \(Z\subset X\) be the closed subscheme defined by the ideal \({\mathfrak {a}}\subset {\mathcal O}_X\), then, by the definitions we have;
which implies that the former subset is closed and the latter subset is locally closed. One can also see that both are cylinders.
In Definition 3.2.21, we introduced the concepts “thin” and “fat” for an arc and also for an irreducible subset on the space of arcs.
Definition 3.5.22
Let \( \alpha :{\operatorname {Spec} K[[t]]}\to X \) be a fat arc of a variety \( X \) and \( \alpha ^*: {\mathcal O}_{X, \alpha (0)}\to K[[t]] \) the local homomorphism induced from \( \alpha \). Here, \(\alpha (0)\in X\) is the image of the closed point \(0\in \operatorname {Spec} K[[t]]\) by \({\alpha }\). By the definition of a fat arc, \(\alpha ^*\) is injective, therefore it is extended to the homomorphism of fields \( \alpha ^*:K(X)\to K((t)) \), where \( K(X) \) is the rational function field of \( X \). Define a function \(v_{\alpha }: K(X)\setminus \{0\}\to \mathbf {Z} \) by
Then, \( v_{\alpha } \) is a discrete valuation of \( K(X) \). We call it the valuation corresponding to\( \alpha \).
Definition 3.5.23
A valuation \( v \) on the rational function field \( K(X) \) of a variety \( X \) is called a divisorial valuation over \( X \) if \( v=q \cdot v_{E} \) for some \( q\in \mathbf {N} \) and a divisor \( E \) over \( X \). The center of a divisor \( E \) is called the center of the valuation \( v=q\cdot v_{E} \). A fat arc \( \alpha \) of \( X \) is called a divisorial arc if \( v_{\alpha } \) is a divisorial valuation over \( X \). A fat set is called a divisorial set if the generic point is a divisorial arc.
Proposition 3.5.24 ([21], [60, Corollary 3.26])
Let \(\alpha \in X_\infty \) be the generic point of an irreducible fat component of a contact locus \(\mathrm {{Cont}} ^{ m}({\mathfrak {a}})\) or of a cylinder \(\psi _m^{-1}(S)\) ( \(S\subset X_m\) locally closed). Then \({\alpha }\) is a divisorial arc.
We will think of the converse implication.
Definition 3.5.25 ([52])
For a divisorial valuation \( v \) over a variety \( X \), define the maximal divisorial set corresponding to \( v \) as follows:
where  is the Zariski closure in \( X_{\infty } \).
is the Zariski closure in \( X_{\infty } \).
Proposition 3.5.26
Let E be a prime divisor over X and \(\varphi :Y\to X\) a birational morphism on which E appears. Let \(\eta \in E\) be the generic point. Let \(\tilde \alpha \in Y_\infty \) be the generic point of \((\pi ^Y)^{-1}(\eta )\) , where \(\pi ^Y: Y_\infty \to Y\) is the canonical projection. Then,
More generally for \(q\in \mathbf {N}\) , let \(\eta _{q-1}\in E_{q-1}\) be the generic point of the space of \((q-1)\) -jets of E. Let \(\tilde \alpha _{q-1}\) be the generic point of \((\psi _{q-1}^Y)^{-1}(\eta _{q-1})\) Then,
Proof
The statements of the proposition follows from
where \(E_0\subset E\) is the open dense subset consisting of points \(p\in E\) such that E and Y are both smooth at p ([52, Proposition 3.4]). □
The following is a kind of converse of Proposition 3.5.24:
Proposition 3.5.27 ([21, 60])
Let X be a variety over an algebraically closed field of arbitrary characteristic. For every divisorial valuation v over X the maximal divisorial set is an irreducible fat component of a contact locus and, in particular, of a cylinder.
As the arc space \(X_\infty \) of a variety X of dimension \(>0\) is a scheme of infinite dimension over k, codimension of a closed subscheme of \(X_\infty \) is not defined in general. But for subscheme of special type we can define the codimension whose important role is describing invariants of singularities on X.
Let X be an arbitrary variety over an algebraically closed field k, and let \(n = \dim X\). Let \({\mathcal {J}}_X \subset {\mathcal O}_X\) be the Jacobian ideal sheaf of X. In a local affine chart this ideal is defined as follows:
Restrict X to an affine chart, and embed it in some \({\mathbf {A}}_k^d\), so that it is defined by a set of equations
Then \({\mathcal {J}}_X\) is locally defined, in this chart, by the \(d-n\) minors of the Jacobian matrix \((\partial f_j/\partial u_i)\). Let \(S \subset X\) be subscheme defined by \({\mathcal {J}}_X\). Note that S is supported exactly over the singular locus of X.
We decompose
and let \(X_{m,\infty } := \psi _m(X_\infty )\) and \(X_{m,\infty }^e := \psi _m(X_\infty ^e)\), where \(\psi _m \colon X_\infty \to X_m\) is the truncation map. Also, let
We will need the following geometric lemma on the fibers of the truncation maps. A weaker version of this property was proven by Denef and Loeser in [24, Lemma 4.1]; the sharper stated here is taken from [32, Proposition 4.1].
Lemma 3.5.28 ([24, 32, 60])
For\(m \ge e\), the morphism\(X_{m+1,\infty }^e \to X_{m,\infty }^e\)is a piecewise trivial fibration with fibers isomorphic to\({\mathbf {A}}^n\).
Proposition 3.5.29 ([21, 60])
For an irreducible component C of a cylinder in \(X_\infty \) such that \(C\not \subset \operatorname {Sing}(X)_\infty \) , then there exists e such that
is a nonempty open subset of\(\psi _m(C)\)and the codimension of\({C}_m^{\le e}\)inside\(X_{m,\infty }^{\le e}\)stabilizes for\(m\gg e\).
Then we define
Remark 3.5.30
The codimension of defined above is not the codimension in the usual sense. Let C be as above and \(s=\operatorname {codim} (C, X_\infty )\) the codimension as defined above. Let r be the maximal length of a sequence \(C=C_0\subset C_1\subset \cdots \subset C_r=X_\infty \) of strictly increasing irreducible closed subsets of \(X_\infty \), then we have the inequality
The inequality can be seen as follows: from the strictly increasing sequence,
of irreducible closed subsets of \(X_\infty \), we have the sequence
for \(m\gg 0\), since \(C_i={ \mathop {\text{lim}} \limits _{\longleftarrow }}\overline {\psi _m(C_i)}\).
The inequality \(s\leq r\) can be a strict inequality, see for instance [59, Example 2.8]. The published version of the paper [21] contains a wrong statement
in Remark 3.3. The corrected remark is contained in the uploaded version arXiv:math/0701867.
Definition 3.5.31
Let E be a prime divisor over X, then the Mather discrepancy\({\hat {k}}_E \in {\mathbf {Z}}_{\geq 0}\) and the Jacobian discrepancy\(j_E\in \mathbf { Z}_{\geq 0}\) are defined as follows:
Let \(\varphi : Y \to X\) be a proper birational morphism from a normal variety Y such that \( E\) appears on Y . Then, there is a canonical \({\mathcal O}_Y\)-homomorphism
on the smooth locus of Y , where n is the dimension of X. Denote the image of the homomorphism above by \(Im\subset {\mathcal O}_Y(K_Y)\). Then
for an ideal sheaf \(\mathcal I\) in a neighborhood of the generic point \(\eta \in E\), because \(\eta \in Y\) is a smooth point and therefore \({\mathcal O}_Y(K_Y)\) is invertible. Define
We call \({\hat {k}}_E-j_E\) the Mather-Jacobian discrepancy of X at the prime divisor E.
If X is non-singular, then \(\wedge ^n\varOmega _X={\mathcal O}_X(K_X),\) and \(Im=\varphi ^*{\mathcal O}_X(K_X)\). Therefore by Definition 3.5.1, we obtain
for every prime divisor E over X.
Proposition 3.5.32
Let E be a prime divisor over X. If X is locally a complete intersection, then
In particular, if X is smooth, then\(k_E={\hat {k}}_E\).
Proof
As X is locally a complete intersection, we have
(See for example, Proposition 9.1 in [32]). Therefore, by pulling back of this equality onto a normal Y by the birational morphism \(\varphi :Y\to X\) where the exceptional prime divisor E appears, we obtain
which yields the required equality. □
There are some researches studying singularities in terms of invariants, say Mather discrepancy or Mather-Jacobian discrepancy, which are involving \({\hat {k}}_E\) or \({\hat {k}}_E-j_E\) (see for example [18, 29, 53, 58]). The infimum of these is well described in terms of the space of arcs, and because of that we have “Inversion of Adjunction” for these invariants. However, there have some differences from \(k_E\) for general \(\mathbf {Q}\)-Gorenstein variety which we do not step into in this paper. For a variety of locally a complete intersection, by virtue of Proposition 3.5.32, we have a description of infimum of log discrepancies in terms of the space of arcs (see Theorem 3.5.34).
Proposition 3.5.33 ([21, 60])
Let E be a prime divisor over a variety X defined over an algebraically closed field k of arbitrary characteristic and \(q\in \mathbf {N}\) , then for the divisorial valuation \(q\cdot v_E\) we have
By making use of this description, we obtain the interpretation of mld and lct by the space of arcs. In following discussions we will denote the symbol
Similarly, denote
Here, \(w=(w_1,\ldots ,w_s)\).
Theorem 3.5.34 ([30, 32, 60])
Let k be an algebraically closed field of arbitrary characteristic. Let X be a normal and locally complete intersection variety defined over k and \({\mathfrak {a}}^e={\mathfrak {a}}_1^{e_1}\cdots {\mathfrak {a}}_s^{e_s}\) a multi-ideal with real exponents \(e=(e_1,\ldots , e_s)\) . For a pair \((X, {\mathfrak {a}}^e)\) the \({\mathrm {mld}}\) is described in terms of the arc space as follows:
In particular, if X is smooth, then we have the following:
We have the same expression of \({\mathrm {mld}}(W; X, {\mathfrak {a}}^e)\) for a proper closed subset \(W\subset X\) with replacing \(\pi ^{-1}(x)\) by \(\pi ^{-1}(W)\) in the right hand sides of the equalities above.
Theorem 3.5.35 ([78, 100])
Let X be a smooth variety defined over k and \({\mathfrak {a}}^e\) a multi-ideal on X with real exponents e. For a point \(x\in X\) and a cylinder \(C\subset X_\infty \) , we define
For a pair \((X, {\mathfrak {a}}^e)\) the \({\mathrm {lct}}\) is described in terms of the arc space as follows:
Proof
These formulae are essentially proved in [78] in characteristic 0 and in [100] in positive characteristic. However in these papers it is formulated under the condition that \({\mathfrak {a}}\) is a single ideal and \(e=1\) and we do not find the proof for this general form in any references. So we write down the proof here. It will also suggest the proof of Theorem 3.5.34.
For the first equality in the statement, it is sufficient to show the following equality:
by Remark 3.5.14. First show \(\geq \) of the above equality. Take a prime divisor E over X with the center at x and define \(w_i:=v_E({\mathfrak {a}}_i)\) for every i and \(w:=(w_1,\ldots ,w_s)\). Then, we have
As the center of E is x, we obtain \(x\in \overline {\pi (C_X(v_E))}\). Therefore it follows that
This gives the required inequality
For the opposite inequality, take any \(w=(w_1,\ldots , w_s)\) and take an irreducible component \(T\subset \mathrm {{Cont}}^w({\mathfrak {a}})\) such that \(x\in \overline {\pi (T)}\) and \(\operatorname {codim}(T,X_\infty )=\operatorname {codim} _x(\mathrm {{Cont}} ^{w}({\mathfrak {a}}),X_\infty )\). The generic point of the cylinder T gives a divisorial valuation \(v_T=q\cdot v_E\) for some \(q\in \mathbf {N}\) and a prime divisor E. Note that the center of E on X contains x. By the definition of the valuation, we have
As \(q\cdot v_E({\mathfrak {a}}_i)=w_i\), we have
as required.
About the second equality in the statement, the inequality \(\geq \) is obvious, since \(\mathrm {{Cont}}^w({\mathfrak {a}})\subset \mathrm {{Cont}}^{\geq w}({\mathfrak {a}})\). For the opposite inequality, it is sufficient to show that for every \(w=(w_1,\ldots , w_s)\in {\mathbf {Z}}_{\geq 0}^s\) there exists \(w'=(w^{\prime }_1,\ldots , w^{\prime }_s)\in {\mathbf {Z}}_{\geq 0}^s\) such that
To show this, take an irreducible component \(T\subset \mathrm {{Cont}}^{\geq w}({\mathfrak {a}})\) such that \(x\in \overline {\pi (T)}\) and \(\operatorname {codim}(T,X_\infty )=\operatorname {codim} _x(\mathrm {{Cont}} ^{\geq w}({\mathfrak {a}}),X_\infty )\). Let \(v_T\) be the divisorial valuation defined by the generic point of T. Then \(w^{\prime }_i:=v_T({\mathfrak {a}}_i)\geq w_i\) and \(T\subset \mathrm {{Cont}}^{w'}({\mathfrak {a}})\). Hence, we obtain
and \(\sum _i e_i w^{\prime }_i\geq \sum _i e_iw_i\), which yield the required inequality. □
The following shows the relation of the mld between smooth variety A and a closed subscheme X on A. It is called “Inversion of Adjunction”.
Theorem 3.5.36 ([30, 32, 60])
Let k be an algebraically closed field of arbitrary characteristic. Let A be a smooth variety over k and \(X\subset A\) a closed subscheme of locally complete intersections with codimension c. Let \({\widetilde {{\mathfrak {a}}}}^e={\widetilde {{\mathfrak {a}}}}_1^{e_1}\cdots {\widetilde {{\mathfrak {a}}}}_s^{e_s}\) be a multi-ideal on A with exponents in \({\mathbf {R}}_{\geq 0}\) such that \({\mathfrak {a}}_i:={\widetilde {{\mathfrak {a}}}}_i{\mathcal O}_X\neq 0\) for every i. Let \(I_X\) be the defining ideal of X in A. Then for a point \(x\in X\) the following equality holds:
For a proper closed subset \(W\subset X\) the following holds:
Corollary 3.5.37
Let k be an algebraically closed field of arbitrary characteristic. Let X be a normal variety of locally complete intersections with dimension d. Let \(x\in X\) be a point and \(W\subset X\) a proper closed subset. Then, we have the equalities:
The following corollaries are proved in [30, 77] for the base field of characteristic 0 in different ways from the following proof. The proof below is based on the expression in Corollary 3.5.37 and it works for the base filed of arbitrary characteristic. In [61, Corollary 10.2.9] one can find more general statements and the proofs for them.
Corollary 3.5.38
Let X be a normal local complete intersection variety defined over algebraically closed field k of arbitrary characteristic. Then the following hold:
-
(i)
X has log canonical singularities if and only if\(X_m\)is locally a complete intersection for every\(m\in \mathbf {N}\),
-
(ii)
X has canonical singularities if and only if\(X_m\)is irreducible for every\(m\in \mathbf {N}\),
-
(iii)
X has terminal singularities if and only if\(X_m\)is normal for every\(m\in \mathbf {N}\).
Proof
Let \(d=\dim X\). As X is locally a complete intersection, X is locally defined by \(c:=N-d\) equations in a non-singular variety A of dimension N. Then, \(X_m\) is locally defined by \((m+1)c\) equations in a non-singular variety \(A_m\) of dimension \((m+1)N\) (cf. the construction of \(X_m\)). Therefore, we have
where the equality holds if and only if \(X_m\) is locally a complete intersection.
First we show the equivalence in (i). We know that the restriction
of \(\pi _m\) is a smooth morphism of relative dimension md. Therefore, by the formula in Corollary 3.5.37, X has log canonical singularities if and only if for every \(m\in \mathbf {N}\), the following inequality holds:
where W is the singular locus \(X_{\mathrm {sing}}\) of X. This is equivalent to the equality in (3.5.38 (i)).
For the both implications of (ii), we may assume that \(X_m\) is locally a complete intersection of dimension \((m+1)d\) by the result (i). Actually, if we assume that X has canonical singularities, then by (i) we obtain that \(X_m\) is locally a complete intersection for every \(m\in \mathbf {N}\). If we assume that \(X_m\) is irreducible, then it has dimension \((m+1)d\), because it contains an open dense subset \(\pi _m^{-1}(X_{reg})\) which has dimension \((m+1)d\). As \(X_m\) is locally defined by \((m+1)(N-d)\) equations in a smooth variety \(A_m\) of dimension \((m+1)N\), the subscheme \(X_m\) is locally a complete intersection.
Now, again by the formula in Corollary 3.5.37, X has canonical singularities if and only if for every \(m\in \mathbf {N}\) and the singular locus \(W\subset X\), the following inequality holds:
which yields \(\dim {X_m(W)}< (m+1)d\). This is equivalent to the fact that none of the irreducible components of \(X_m(W)\) can be an irreducible component of \(X_m\), since \(X_m\) is of pure dimension \((m+1)d\). This holds if and only if \(X_m\) is irreducible for every \(m\in \mathbf {N}\).
For the proof of (iii), we may assume that \(X_m\) is irreducible and locally a complete intersection of dimension \((m+1)d\) by the same reason as in the proof of (ii). We know that a local complete intersection variety is Gorenstein, in particular, it satisfies Serre’s condition \(S_2\). Thus \(X_m\) has the property \(S_2\). Now, X has terminal singularities if and only if for every \(m\in \mathbf {N}\) and the singular locus \(W\subset X\), the following inequality holds:
which yields \(\dim {X_m(W)}\leq (m+1)d-2\). Here we note that the singular locus of \(X_m\) is just \(X_m(W)\). Indeed, it is obvious that the singular locus of \(X_m\) is contained in \(X_m(W)\), as the compliment \({\pi _m}^{-1}(X_{\mathrm {reg}})\) of \(X_m(W)\) is non-singular. To show the opposite inclusion, denote the local Jacobian matrix of the embedding \(X_m\subset A_m\) by J and the Jacobian matrix of the embedding \(X\subset A\) by \(J_0\). Then J has the following form:
As we may assume that \(X_m\subset A_m\) is a complete intersection, \(X_m\) is non-singular at a point p if and only if the Jacobian matrix J has full rank at p. Here, if \(p\in X_m(W)\), then \(J_0\) does not have full rank, therefore J cannot have full rank.
Hence, the inequality \(\dim {X_m(W)}\leq (m+1)d-2\) is equivalent to the fact that \(X_m\) is normal by the Serre’s criteria for normality. □
The LSC Conjecture holds for a normal local complete intersection variety. It is proved in [31] for characteristic 0 by making use of Inversion of Adjunction (Theorem 3.5.36) and the description of mld in terms of the arc space (Theorem 3.5.34).
Theorem 3.5.39 ([31])
Let X is be a normal, local complete intersection variety over an algebraically closed field k of arbitrary characteristic. Let\({\mathfrak {a}}^e\)be a multi ideal on X. Then the function\(x\mapsto {\mathrm {mld}} (x;X,{\mathfrak {a}}^e)\), \(x\in X\), is lower semicontinuous.
Remark 3.5.40
By these theorems we can see the equivalence of a geometric property of X and a somehow weaker geometric property of \(X_m\). So it is natural to ask for a condition on \(X_m\) such that it forces X to be smooth. One candidate for such a mild condition is that \(X_m\) has at worst rational singularities for every \(m\in \mathbf {N}\cup \{\infty \}\) (By Proposition 3.3.16 we know that the existence of m such that \(X_m\) is smooth implies the smoothness of X, but we require a weaker condition for \(X_m\).)
The following is a negative answer to the expectation:
Example 3.5.41 ([57])
Let k be a field of characteristic 0. Let X be a hypersurface in \({\mathbf {A}}_k^N\) defined by the polynomial \(f=x_1^d+x_2^d+\cdots +x_N^d\). If \(d>1\), then it is clear that \((X, 0)\) is not smooth, and if \(d^2< N\), then the jet scheme \(X_m\) has at worst rational singularities for every \(m\in \mathbf {N}\).
The study of singularities by making use of the space of arcs is still developing. The author hopes to write a paper including the new results in future.
References
M. Leyton-Alvarez, Résolution du problème des arcs de Nash pour une famille d’hypersurfaces quasi-rationnelles, Annales de La Faculté des Sciences de Toulouse Math., Sér. 6, 20 no. 3 (2011) 613–667.
S. Abhyankar, Local uniformization on algebraic surfaces over ground fields of characteristic\(p\neq 0\), Annals of Mathematics, Second Series, 63 (3) (1956) 491–526.
S. Abhyankar, Resolution of singularities of embedded algebraic surfaces, Springer Monographs in Mathematics, Acad. Press (1966).
T. Arakawa and A. Moreau, Arc spaces and vertex algebras, Springer Monograph, April 17, (2021) 170 pages.
M. Artin, On isolated rational singularities of surfaces, Amer. J. Math. 88 (1966) 129–136.
C. Birkar, P. Cascini, C. D. Hacon and J. McKernan, Existence of minimal models for varieties of log general type, J. Amer. Math. 23 (2010) 405-468.
V. Batyrev, Stringy Hodge numbers of varieties with Gorenstein canonical singularities, Proc. Taniguchi Symposium 1997, In ’Integrable Systems and Algebraic Geometry, Kobe/ Kyoto 1997’, World Sci. Publ., (1999), 1–32.
V. Batyrev, Non-Archimedian integrals and stringy Euler numbers of log terminal pairs, J. Europ. Math. Soc., 1 (1999), 5–33.
B. Bhatt, Algebraization and Tannaka duality, Cambridge Journal of Mathematics 4 (2016) 403–461.
J. F. Bobadilla, Nash problem for surface singularities is a topological problem, Advances in Mathematics 230 (1) (2012) 131–176.
J. F. Bobadilla and M. P. Pereira, The Nash problem for surfaces, Annals of Math. 176 (2012) 2003–2029.
C. Bouvier, Diviseurs essentiels, composantes essentielles des variétés toriques singulières, Duke Math. J. 91 (1998) 609–620.
C. Bouvier and G. Gonzalez-Sprinberg, Système générateur minimal, diviseurs essentiels et G-désingularisations de variétés toriques, Tohoku Math. J. 47, (1995) 125–149.
S. Bosch, W. Lütkebohmert and M. Raynaud, Néron Models, Ergebnisse der Mathematik und ihrer Grenzgebiete, 21 (1990) Springer-Verlag.
A. Buium, Differential algebra and Diophantine geometry, Actualités Math.39 (1998).
B. Cossart and O. Piltant, em Resolution of singularities of threefolds in positive characteristic. I and II. Journal of Algebra, 320 (3) (2008) 1051–1082 and 321 (7) (2009) 1836–1976.
A. Craw, An introduction to motivic integration, In: Strings and Geometry: Clay Mathematics Proceedings (3). AMS, pp. 203–225.
T. De Fernex, and R. Docampo, Jacobian discrepancies and rational singularities, J. Eur. Math. Soc. 16 (2014) 165–199.
T. De Fernex, Three-dimensional counter-examples to the Nash problem, Compositio Math. 149 (2013), 1519–1534
T. De Fernex, and R. Docampo, Terminal valuations and the Nash problem, Invent. Math. 203 (2016), 303-331.
T. De Fernex, L. Ein and S. Ishii, Divisorial valuations via arcs, Publ. RIMS 44, (2008) 425-448.
T. De Fernex, L. Ein and S. Ishii, Jet closures and the local isomorphism problem, J. of Algebra, 501, (2018) 166–181.
J. Denef and F. Loeser, Motivic Igusa zeta-functions, J. Alg. Geom. 7 (1988) 505–537.
J. Denef and F. Loeser, Germs of arcs on singular varieties and motivic integration, Invent. Math. 135, (1999) 201–232.
J. Denef and F. Loeser, Motivic exponential integrals and a motivic Thom-Sebastiani Theorem, Duke Math. J. 99 (1999) 201–232.
J. Denef and F. Loeser, Motivic integration, quotient singularities and the McKay correspondence, Comositio Math. 131, (2002) 267-290.
J. Denef and F. Loeser, Motivic integration and the Grothendieck group of pseudo-finite fields, Proceeding of the International Congress of Mathematicians (Beijing, 2002) vol II, Higher Ed. Press, Beijing, (2002) 13–23.
V. Drinfeld, On the Grinberg-Kazhdan formal arc theorem, (2002) arXiv: math-AG/0203263.
L. Ein and S. Ishii, Singularities with respect to Mather-Jacobian discrepancies, MSRI Publications 67, (2015) 125–168.
L. Ein, M. Mustaţǎ and T. Yasuda, Jet schemes, log discrepancies and inversion of adjunction, Invent. Math. 153 (2003) 519-535.
L. Ein and M. Mustaţǎ. Inversion of Adjunction for local complete intersection varieties, Amer. J. Math. 126 (2004) 1355–1365.
L. Ein and M. Mustaţǎ, Jet schemes and singularities, Proc. Symp. Pure Math. 80. 2, (2009) 505–546.
L. Ein, R. Lazarsfeld and M. Mustaţǎ, Contact loci in arc spaces, Compositio Math. 140 (2004) 1229–1244.
R. Elkik, Rationalité des singularités canoniques, Inv. Math. 64 (1981) 1–6.
O. Fujino, Foundations of the minimal model program, MSJ Memoirs, 35 289 pages (2017)
W. Fulton, Introduction to Toric Varieties, Annals of Math. Studies 131, Princeton Univ. Press. (1993).
I. M. Gelfand, M. M. Kapranov and A. V. Zelevinsky, discriminants, Resultants and Multidimensional Determinants, Mathematics: Theory & Applications, Birkhäuser (1994)
P.D. González Pérez, Bijectiveness of the Nash Map for Quasi-Ordinary Hypersurface Singularities, Int. Math. Research Notices, 2007 (2007), rnm076, https://doi.org/10.1093/imrn/rnm076
G. Gonzalez-Sprinberg and M. Lejeune-Jalabert, Families of smooth curves on surface singularities and wedges, Annales Polonici Mathematici, LXVII.2, (1997) 179–190.
R.A. Goward, Jr. and K. Smith, The jet scheme of a monomial scheme, Com. Alg. 34 (2006), 1591–1598.
M. Greenberg, Rational points in henselian discrete valuation rings, Publ. Math. I.H.E.S. 31 (1966) 59–64.
M. Grinberg and D. Kazhdan, Versal deformations of formal arcs, Geom. Funct. Anal., 10 (3):543–555, 2000. URL: http://dx.doi.org/10.1007/PL00001628.
R. Hartshorne, Algebraic Geormetry, Graduate Texts in Math. 52 Springer-Verlag, (1977).
M. Hickel, Fonction de Artin et germes de courbes tracées sur un germe d’espace analytique, Amer. J. Math. 115, (1993) 1299–1334.
H. Hironaka, Resolution of singularities of an algebraic variety over a field of characteristic zero. I, Ann. of Math., 79 (1) (1964) 109–203, and part II, 79 (2) (1964) 205–326.
S. Ishii and J. Kollár, The Nash problem on arc families of singularities, Duke Math. J. 120 No.3 (2003) 601–620.
S. Ishii, Introduction of arc spaces and the Nash problem, RIMS Kokyu-Roku, 1374, (2004) 40–51.
S. Ishii, The arc space of a toric variety, J. Algebra, 278 (2004) 666–683
S. Ishii, Arcs, valuations and the Nash map, J. reine angew. Math, 588 (2005) 71–92.
S. Ishii, The local Nash problem on arc families of singularities, Ann. Inst. Fourier, Grenoble 56 (2006) 1207-1224.
S. Ishii, Jet schemes, arc spaces and the Nash problem, C.R.Math. Rep. Acad. Canada, 29 (2007) 1–21.
S. Ishii, Maximal divisorial sets in arc spaces, Adv. St. Pure Math. 50, (2008) 237–249.
S. Ishii and J. Winkelmann, Isomorphisms of jet schemes, C. R. Math. Rep. Acad. Sci. Canada. 32, (2010) 19–23.
S. Ishii, Nash problem for a toric pair and the minimal log-discrepancy, C. R. Math. Acad. Sci. Paris 348, (2010) 985–988.
S. Ishii, Smoothness and jet schemes, Adv. St. Pure Math. 56, Proceedings of “Singularities in Niigata\(\cdot \)Toyama 2007” (2009) 187–199.
S. Ishii, Geometric properties on jet schemes, Comm. Alg. 39, Number 5, (2011) 1872-1882.
S. Ishii, K-i. Watanabe and A. Sannai Jet schemes of homogeneous hypersurfaces, Singularities in Geometry and Topology, Strasbourg 2009, (2012) 39–49.
S. Ishii, Mather discrepancy and the arc spaces, Ann. de l’Institut Fourier, 63, (2013) 89–111.
S. Ishii and A. Reguera, Singularities with the highest Mather minimal log discrepancy, Math. Zeitschrift., 275, Issue 3-4, (2013) 1255–1274.
S. Ishii and A. Reguera, Singularities in arbitrary characteristic via jet schemes, Hodge theory and \(L^2\) analysis (2017) 419–449.
S. Ishii, Introduction to Singularities, 2nd ed. Springer Verlag, (2018) 236 pages.
Y. Kawamata, K. Matsuda and K. Matsuki, Introduction to the Minimal Model Problem, Adv. Studies in Pure Math. 10 (1987) 283–360.
J. M. Johnson and J. Kollár, Arc spaces of cA-type singularities, J. Singularities 7 (2013), 238–252.
E. R. Kolchin, Differential algebra and algebraic groups, Pure and Applied Mathematics, Vol. 54, Academic Press, New York-London, 1973.
J. Kollár and S. Mori, Birational Geometry of Algebraic Varieties. Cambridge Tracts in Mathematics, (1998).
J. Kollár, Lectures on Resolution of Singularities, Princeton: Princeton University Press, ISBN 978-0-691-12923-5, (2007).
M. Kontsevich, Lecture at Orsay (December 7, 1995).
M. Lejeune-Jalabert, Arcs analytiques et résolution minimale des surfaces quasihomogènes. in: Lecture Notes in Math. 777, (1980) 303–336.
M. Lejeune-Jalabert, Courbes tracées sur un germe d’hypersurface. Amer. J. Math. 112, (1990) 525–568.
M. Lejeune-Jalabert and A. J. Reguera-Lopez, Arcs and wedges on sandwiched surface singularities, Amer. J. Math. 121, (1999) 1191–1213.
M. Lejeune-Jalabert and A. J. Reguera-Lopez, Exceptional divisors which are not uniruled belong to the image of the Nash map, J. Inst. Math. Jussieu , 11, (2) ,(2012) 273–287.
F. Loeser, Seattle lectures on motivic integration. AMS. Proc. Symp. Pure Math. 80-(2) Algebraic Geometry, Part 2: Seattle 2005 (2009)
D. Mallory, Triviality of arc closures and the local isomorphism problem, Journal of Algebra, 544 (2020) 47–61.
M. Morales, Some numerical criteria for the Nash problem on arcs for surfaces Nagoya Math. J. 191 (2008) 1–19.
S. Mori, Flip Theorem and the Existence of Minimal Models for 3-Folds, Journal of the AMS 1(1) (1988) 117–253.
D. Mumford, J. Forgarty and F. Kirwan, Geometric Invariant Theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 2. Folge, 3 (1994) Springer-Verlag
M. Mustaţǎ, Jet schemes of locally complete intersection canonical singularities, with an appendix by David Eisenbud and Edward Frenkel, Invent. Math. 145 (2001) 397–424.
M. Mustaţǎ, Singularities of Pairs via Jet Schemes, J. Amer. Math. Soc. 15 (2002) 599–615.
M. Mustaţǎ and Y. Nakamura, A boundedness conjecture for minimal log discrepancies on a fixed germ, Contemporary Math. 712 (2018) 287–306.
S. Nasar, A Beautiful Mind: A Biography of John Forbes Nash, Jr., Winner of the Nobel Prize in Economics, 1994, Simon & Schuster (1998) 464 pages.
J. F. Nash, Arc structure of singularities, Duke Math. J. 81, (1995) 31–38.
A. Nobile, On Nash theory of arc structure of singularities, Ann. Mat. Pura Appl. 160 (1991) 129–146.
T. Oda, Convex Bodies and Algebraic Geometry, Ergeb. Math. Grenzgeb. 15, Springer-Verlag (1988).
M. P. Pereira, Nash problem for quotient surface singularities, J. London. Math. Soc. (2) 87 (2013), no. 1, 177–203.
P. Petrov, Nash problem for stable toric varieties, Math. Nach. 282 (2009) 1575–1583.
C. Plénat and P. Popescu Pampu, A class of non-rational surface singularities for which the Nash map is bijective Bull. Soc. math. France 134 (3) (2006) 383–394.
C. Plénat and P. Popescu-Pampu, Families of higher dimensional germs with bijective Nash map, Kodai Math. J. 31(2) (2008) 199–218.
C. Plénat, A solution to the Nash Problem for rational double points\(D_n\) (forngreater than 4), Annales de l’Institut Fourier, 58, no. 6 (2008) 2249–2278.
A. J. Reguera-Lopez, Families of arcs on rational surface singularities, Manuscr. Math. 88, (1995) 321–333.
A. J. Reguera-Lopez, Image of the Nash map in terms of wedge, C.R. Acad. Sci. Paris, Ser. I, 338 (2004) 385–390.
A. J. Reguera-Lopez, A curve selection lemma in spaces of arcs and the image of the Nash map, Compositio Math. 142 (2006) 119–130.
A. J. Reguera-Lopez, Arcs and wedges on rational surface singularities, J. Algebra, 366 (2012) 126–264.
W. Veys, Zeta functions and ‘Kontsevich invariants’ on singular varieties, Canadian J. Math. 53 (2001) 834–865.
W. Veys, Stringy invariants of normal surfaces, J. Alg. Geom. 13 (2004) 115–141.
W. Veys, Stringy zeta functions of\(\mathbf {Q}\)-Gorenstein varieties, Duke Math. J. 120 (2003) 469–514.
W. Veys and W. Zuniga-Galindo, Zeta functions and oscillatory integrals for meromorphic functions, Advances in Mathematics, 311 (2017) 295–337.
W. Veys, Arc spaces, motivic integration and stringy invariants, Advanced Studies in Pure Mathematics, (2006) 529–572.
P. Vojta, Jets via Hasse-Schmidt derivations, In: Diophantine geometry. Vol. 4 CRM Series. Ed. Norm., Pisa, 2007, pp. 335–361.
O. Zariski and P. Samuel, Commutative Algebra I, II, Van Nostrand (1958) (1970).
Z. Zhu, Log canonical thresholds in positive characteristic, Math. Zeitschrift DOI: https://doi.org/10.1007/s00209-017-1866-3 (2017).
Acknowledgements
This work is partially supported by Grant-In-Aid 19K03428, JSPS and by the Research Institute for Mathematical Sciences, an International Joint Usage/Research Center located in Kyoto University.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Ishii, S. (2023). Singularities, the Space of Arcs and Applications to Birational Geometry. In: Cisneros-Molina, J.L., Dũng Tráng, L., Seade, J. (eds) Handbook of Geometry and Topology of Singularities IV. Springer, Cham. https://doi.org/10.1007/978-3-031-31925-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-31925-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-31924-2
Online ISBN: 978-3-031-31925-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



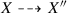 to get a new pair
to get a new pair