Study of the Convective-Radiative Moving Porous Fin with Temperature-Dependent Variables

Abstract

In this article, the temperature in a rectangular moving porous fin with a longitudinal profile has been studied, which involves internal heat generation, variable thermal conductivity, and heat transfer coefficient. In real life, we know that these parameters change with temperature, so in this study, we considered these parameters as temperature function. Darcy’s model has been used to form the equation. The heat transfer coefficient is taken as power-law form. A new contribution to this study is adding a porous medium to fin and taking thermal conductivity into four different cases: a constant, a linear, a quadratic, and an exponential form of temperature. The solution to the problem has been carried out by three methods, namely LWCM, LSM, and MM. A comparison of the results obtained by the above-mentioned methods and the exact results has been presented to demonstrate the novelty of the current study. The entire article has been carried out in a non-dimensional form.

Nomenclature

T :

: temperature distribution (K)

$T_a$ :

: ambient temperature (K)

$T_b$ :

: temperature at fin base (K)

h(T):

: heat transfer coefficient ($Wm^{-2}K^{-1}$)

K(T):

: thermal conductivity ($Wm^{-1}K^{-1}$)

L :

: fin length (m)

P :

: fin periphery (m)

$\dot{m}$ :

: mass flow rate of fluid $(kgs^{-1})$

$k_a$ :

: thermal conductivity at ambient temperature ($Wm^{-1}K^{-1}$)

$h_b$ :

: heat transfer coefficient at the fin base ($Wm^{-2}K^{-1}$)

g :

: gravitational acceleration $(ms^{-2})$

R :

: permeability $(m^{2})$

Y :

: thermal expansion coefficient $(K^{-1})$

$A_c$ :

: cross-section area $(m^{2})$

U :

: speed of moving fin ($ms^{-1}$)

$q*$ :

: heat generation ($Wm^{-3}$)

W :

: fin width (m)

x :

: spatial variable

n :

: constant

Greek symbols

$\beta$ :

: thermal conductivity gradient $(Wm^{-1}K^{-1})$

$\sigma$ :

: Stefan-Boltzmann constant $(Wm^{-2}K^{-4})$

v :

: kinematic viscosity $(m^{2}s^{-1})$

$\rho$ :

: density of material $(kgm^{-3})$

$\nu _{w}$ :

: velocity of fluid $(ms^{-1})$

c :

: specific heat $(JK^{-1}kg^{-1})$

Dimensionless parameters

$\theta$ :

: temperature

$\theta _a$ :

: ambient temperature

X :

: spatial variable

k :

: thermal conductivity

M :

: thermo-geometric

$N_r$ :

: radiation-conduction

$N_p$ :

: porosity parameter

$\varepsilon _{G}$ :

: heat generation gradient

$\varepsilon$ :

: emissivity

Pe :

: Peclet number

Abbreviation

ADM:

: Adomian decomposition method

DTM:

: Differential transformation method

FDM:

: Finite difference method

HAM:

: Homotopy analysis method

LSM:

: Least square method

LSSCM:

: Least square spectral collocation method

LWCM:

: Legendre wavelet collocation method

LVI:

: Laplace-variational iterative

MM:

: Moment method

R-K:

: Runge-Kutta

WCM:

: Wavelet collocation method

1 Introduction

Many engineering devices or machines generate heat during their processes, which results in heat being released into the environment. If this generated heat is not released quickly to its surrounding environment, it may cause a temperature rise in system devices, leading to their failure. To prevent this, fins or extended heat surfaces are used. Dongonchi and Ganji [1] evaluated heat transmission in a rectangular moving fin with a heat transfer coefficient, heat generation and thermal conductivity which depends on temperature using DTM. Kraus [2] provided a detailed review of extended surfaces or fins in his book. Gorla and Bakier [3]investigated the influence of convection and radiation in a rectangular porous fin. The performance is investigated in various fins, including the long fin with an insulated tip and the finite-length fin with an exposed tip. Kiwan et al. [4] investigated heat transfer in porous moving fins. A thermal performance study compares porous and solid fins. The effects of parameters and different profiles were studied in detail. Ndlovu and Moitsheki [5] performed the thermal analysis of rectangular and hyperbolic moving fins. DTM was applied to find the solution to the heat transmission equation. Khalaf et al. [6] gave a review on how fins, porous medium and nanofluid materials improve heat transmission in devices. They explained how the world has developed an interest in modern electronics and their applications in science and engineering, which also have a great impact on aspects of life such as optical devices, refrigeration devices, X-rays, etc. Gupta et al. [7] investigated the Cu and $Al_{2}O_{3}$ water-based nanofluid three-dimensional magnetohydrodynamic flow. In the presence of thermal radiation and convective mass and heat transmission boundary conditions, effects of nanoparticles as well as mass and heat transmission were carried out. Ndlovu et al. [8] found the fin efficiency and temperature in a rectangular moving fin with a porous medium using VIM. Unal et al. [9] investigated the temperature distribution in straight and rectangular fins in one dimension. Shateri and Salashour [10] found the heat performance and distribution of temperature in longitudinal fin with porous media using LSM. Fin efficiency and heat flux were also computed for the comparison of fins. Hatami et al. [11] used LSM, CM, and DTM to analyze the energy transfer and distribution of temperature in porous fin. Razzaghi and Yousefi [12] provided a Legendre wavelet-based operational integration P matrix. Singh et al. [13] studied heat transmission in moving fin with heat transfer coefficient, surface emissivity, and thermal conductivity, which is quadratic and linear function of temperature. Sobamowo et al. [14] discussed the performance of convective moving porous fin with different properties of the material and used the LVI method to find an analytical solution. Sobamowo [15] studied a porous moving fin with internal energy generation and thermal conductivity which are temperature function using the finite element method. Singh et al. [16] considered temperature variant parameters and several cases of thermal conductivity to solve heat problem. Fin efficiency was also calculated for the fin. Bhanja et al. [17] used ADM to find fin efficiency and temperature distribution in radiation-convection porous moving fins. LSSCM was used by Chen et al. [18] to predict efficiency and temperature in radiation-convection moving porous fins under combined convective-radiative and constant temperature boundary conditions. Singh et al. [19] solved a non-linear fin problem whose thermal conductivity is a variable function of temperature by using WCM. Moradi et al. [20] used HAM to find heat transmission in moving porous fin with two boundary conditions. Heat transfer and the impact of parameters on temperature are also discussed. Singh et al. [21] discussed non-Fourier and Fourier energy conduction applying boundary conditions which are periodic in nature. An analytical solution was found using the Laplace transform and its inversion. Wang et al. [22] tested DTM with the Pade approximant as one of the analytical approaches to resolve the ordinary system of heat transport, which is non-linear. For the radiation heat exchange, the Rosseland approximation was taken into consideration. Singh et al. [23] introduced the homotopy analysis transform method, a powerful hybrid computational methodology for analysing Jeffery-Hamel flow. Singh et al. [24] used a method called the homotopy perturbation Elzakie transform to find a solution to the boundary value problem of the non-linear type. With the help of Chebyshev polynomials, Singh et al. [25] solved the fractional version of Bratu’s equation, which plays a major role in the vibration-electrospinning and electrospinning processes.

In this present study, the impact of various parameters on temperature of fin is discussed. To find the better method for the study, a percentage error has been computed and a method with the minimum error has been applied for further computation. The formulation of the model is described in Sect. 2. The methodology of the applied methods is provided in Sect. 3. The exact solution is presented in Sect. 4. Section 5 contains a discussion of the findings. Lastly, the conclusion is provided in Sect. 6.

2 Problem Description

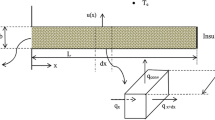
We consider a porous moving fin of longitudinal profile in one dimension along with its cross-section area $A_{c}$, length L and periphery P which horizontally moves with velocity U which is constant, presented in Fig. 1. The surface of the fin is exposed to a $T_a$ and $T_b$ radiative and convective environment. The radiation role can be more reasonable if the convection force is absent, occurs naturally, or is weak.

Fig. 1.

Schematic diagram of a moving porous fin.

For any material, thermal conductivity changes linearly with temperature. Some assumptions have been made about the problem, which are discussed as follows: Darcy’s model is used for the interplay in the fluid and porous medium; the porous part is considered to be homogeneous, saturated, and isotropic with single-phase liquids, and the physical properties of the fluid and solid walls depend on temperature. From these assumptions, the equation for moving fin in a porous medium is expressed as:

$$\begin{aligned}&\frac{d}{d x}\Big (K(T)\frac{d T}{d x}\Big )-\frac{P}{A_{c}}h(T)(T-T_{a})-\frac{\dot{m}c}{A_{c}dx}(T-T_{a})-\frac{\varepsilon \sigma P}{A_{c}}(T^4-T^4_{a})-\rho cU\frac{dT}{dx}+q^*=0\\&\,\,\; 0\le x\le L \nonumber \end{aligned}$$

(1)

where K(T) is the equivalent thermal conductivity of porous fin, which includes thermal conductivity of the solid part as well as the gas part present in the porous, h(T) is heat transfer coefficient, $(\dot{m})$ is mass flow of fluid and $q^{*}$ is energy generation which depends on temperature x is space variable, T is temperature distribution, $\sigma$ is Boltzmann constant, $\varepsilon$ is emissivity, c is specific heat and $\rho$ is density of material. In addition to conduction, convection, and radiative heat flux, Eq. 1 includes terms for internal heat generation and advection. One end of the fin is insulated with a base temperature, while the boundary conditions are specified by [2].

$$\begin{aligned} T(L)=T_{b}, \qquad \frac{dT}{dx}\Big \vert _{x=0}=0. \end{aligned}$$

(2)

If heat generation change with temperature [1], then we get

$$\begin{aligned} q^*=q^*_{a}(1+\varepsilon _{g}(T-T_{a})) \end{aligned}$$

(3)

where $q^*_{a}$ is internal heat generation at ambient temperature.

Mass flow rate of fluid which passes through porous media is [3]

$$\begin{aligned} \dot{m}=\rho \nu _{w}W\Delta X \end{aligned}$$

Darcy’s model gave the fluid velocity which passes through porous media [4],

$$\begin{aligned} \nu _{w}=\frac{gRY}{v}(T-T_{a}) \end{aligned}$$

Heat transfer coefficient is power law form of the temperature given by [5],

$$\begin{aligned} h(T)=h_{b}\left( \frac{T-T_{a}}{T_{b}-T_{a}}\right) ^{n} \end{aligned}$$

To simplify these equations, introduce non-dimensional parameters as follows [1, 8]:

$$\begin{aligned}&X=\frac{x}{L},\, \theta =\frac{T}{T_{b}},\,\theta _{a}=\frac{T_{a}}{T_{b}},\; k=\frac{K}{k_{a}},\; h=\frac{h(T)}{h_{b}},\,N_{r}=\frac{\varepsilon \sigma PL^2 T^3_{b}}{A_{c}k_{a}},\, M^2=\frac{Ph_{b}L^2}{A_{c}k_{a}}, \nonumber \\&\qquad \qquad N_{p}=\frac{\rho cgRYWL^{2}T_{b}}{vk_{a}A_{c}}, G=\frac{q^*_{a}A_{c}}{h_{b}PT_{b}}, Pe=\frac{UL\rho c}{k_{a}},\; \varepsilon _{G}=\varepsilon _{g}T_{b} \end{aligned}$$

(4)

On applying these parameters, Eq. (1) becomes

$$\begin{aligned} \begin{array}{cc} \frac{d}{d X}\Big (k(\theta )\frac{d \theta }{d X}\Big )-M^2 \frac{(\theta -\theta _{a})^{n+1}}{(1-\theta _{a})^{n}} -N_{r}(\theta ^4-\theta ^4_{a})-N_{p}(\theta -\theta _{a})^{2}-Pe\frac{d\theta }{dX} \\ +\,M^2G(1+\varepsilon _G(\theta -\theta _{a}))=0, \\ 0\le X\le 1. \end{array} \end{aligned}$$

(5)

and the boundary conditions becomes

$$\begin{aligned} \theta (1)=1, \qquad \frac{d \theta }{d X}\Big \vert _{X=0}=0 \end{aligned}$$

(6)

where X is dimensionless space variable, $\theta$ is dimensionless temperature, M is thermo-geometric, $N_r$ is radiation-conduction, and Pe is Peclet number (speed of fin), when $Pe=0$ means fin is stationary. In non-dimensional form, heat transfer coefficient is

$$\begin{aligned} h(T)=h_{b}\left( \frac{\theta -\theta _{a}}{1-\theta _{a}}\right) ^{n} \end{aligned}$$

The constant n can range between –6.6 and 5. However, in various practical cases, it lies in –3 and 3 [9]. The exponent n describes laminar film boiling at $n =\frac{1}{4}$, laminar natural convection at $n = 3$, and radiation at $n = 3$ [9].

2.1 Particular Cases

The following cases arise when dimensionless thermal conductivity is taken as a different function of temperature as shown below:

Case I  

If linear thermal conductivity, $k(\theta )=1+\beta \theta$

$$\begin{aligned} \begin{array}{cc} (1+\beta \theta )\frac{d^{2}\theta }{d X^{2}}+\beta \Big (\frac{d \theta }{d X}\Big )^{2}-M^2 \frac{(\theta -\theta _{a})^{n+1}}{(1-\theta _{a})^{n}} -N_{r}(\theta ^4-\theta ^4_{a})-N_{p}(\theta -\theta _{a})^{2}-Pe\frac{d\theta }{dX} \\ +\,M^2G(1+\varepsilon _G(\theta -\theta _{a}))=0, \end{array} \end{aligned}$$

(7)

Case II  

If constant thermal conductivity, $k(\theta )=1$

$$\begin{aligned} \frac{d^{2}\theta }{d X^{2}}-M^2 \frac{(\theta -\theta _{a})^{n+1}}{(1-\theta _{a})^{n}} -N_{r}(\theta ^4-\theta ^4_{a})-N_{p}(\theta -\theta _{a})^{2}-Pe\frac{d\theta }{dX}+M^2G(1+\varepsilon _G(\theta -\theta _{a}))=0, \end{aligned}$$

(8)

Case III  

If thermal conductivity is an exponential function of temperature, $k(\theta )=e^{\beta \theta }$

$$\begin{aligned} \begin{array}{cc} e^{\beta \theta }\frac{d^{2}\theta }{d X^{2}}+\beta e^{\beta \theta }\Big (\frac{d \theta }{d X}\Big )^{2}-M^2 \frac{(\theta -\theta _{a})^{n+1}}{(1-\theta _{a})^{n}} -N_{r}(\theta ^4-\theta ^4_{a})-N_{p}(\theta -\theta _{a})^{2}-Pe\frac{d\theta }{dX} \\ +\,M^2G(1+\varepsilon _G(\theta -\theta _{a}))=0, \end{array} \end{aligned}$$

(9)

Case IV  

If thermal conductivity is quadratic function of temperature, $k(\theta )=1+\beta \theta ^{2}$

$$\begin{aligned} \begin{array}{cc} (1+\beta \theta ^{2})\frac{d^{2}\theta }{d X^{2}}+2\beta \theta \Big (\frac{d \theta }{d X}\Big )^{2}-M^2 \frac{(\theta -\theta _{a})^{n+1}}{(1-\theta _{a})^{n}} -N_{r}(\theta ^4-\theta ^4_{a})-N_{p}(\theta -\theta _{a})^{2}-Pe\frac{d\theta }{dX}\\ +\, M^2G(1+\varepsilon _G(\theta -\theta _{a}))=0, \end{array} \end{aligned}$$

(10)

3 Computational Methods

3.1 Legendre Wavelet Collocation Method

Let

$$\begin{aligned} \theta ''(X)=c^{T} \psi (X) \end{aligned}$$

(11)

here

$$\begin{aligned} c^{T}\psi (X)=\sum _{m=1}^{2^{s-1}}\sum _{n=0}^{n-1} c_{m,n}\psi _{m,n}(X) \end{aligned}$$

and

$$\begin{aligned} c_{m,n}=\int _{0}^{1}f(X)\psi _{m,n}(X) \end{aligned}$$

The matrices c and $\psi (X)$ are $M\times 1$, expressed as

$$ c= \begin{bmatrix}c_{1,0}, c_{1,1}, ..., c_{1,M-1}, c_{2,0}, c_{2,1}, ..., c_{2,M-1},\\ c_{2^{s-1},0}, c_{2^{s-1},1}, ..., c_{2^{s-1},M-1} \end{bmatrix}^{T} $$

and

$$ \psi (X)= \begin{bmatrix}\psi _{1,0}(X), \psi _{1,1}(X), ..., \psi _{1,M-1}(X), \psi _{2,0}(X), \\ \psi _{2,1}(X), ..., \psi _{2,M-1}(X), \psi _{2^{s-1},0}(X), \\ \psi _{2^{s-1},1}(X), ..., \psi _{2^{s-1},M-1}(X) \end{bmatrix}^{T}$$

The Legendre wavelet is defined as $\psi _{m,n}(X)=\psi (s,\hat{m},n,X)$, where s is a positive integer, $m=1,2,...,2^{s-1}, \hat{m}=2m-1$, the order of the Legendre polynomial is n, and in the interval [0, 1], X is defined as:

$$\begin{aligned} \psi _{m,n}(X)={\left\{ \begin{array}{ll} \sqrt{(n+1/2)}2^{s/2}P_{n}(2^{s}X-\hat{n}), \quad \, \frac{\hat{m}-1}{2^{s}}\le X\le \frac{\hat{m}+1}{2^{s}}\\ 0, \qquad \; otherwise \end{array}\right. } \end{aligned}$$

(12)

where $m=1,2,...,2^{s-1}$ and $n=0,1,...,M-1$. $P_{n}(X)$ is Legendre polynomial of n order as given by [13].

$$\begin{aligned}&P_{0}(X)=1, P_{1}(X)=X, P_{n+1}(X)=\frac{2n+1}{n+1}(X) P_{n}(X) \nonumber \\&\qquad \;\; -\frac{n}{n+1}(X)P_{n-1}(X), n=1,2,3,...,M-1 \end{aligned}$$

(13)

Now, integrating with respect to X from 0 to X of Eq. (11), we get

$$\begin{aligned} \theta '(X)=\theta '(0)+c^{T}P\psi (X), \end{aligned}$$

(14)

where P is the integration operational matrix, which is $2^{s-1}M\times 2^{s-1}M, s=1,$ given by [12].

Substitute $X=1$ in Eq. (14), we get

$$\begin{aligned} \theta '(0)=\theta '(1)-c^{T}P\psi (1) \end{aligned}$$

$$\begin{aligned} \Rightarrow \theta '(0)=-c^{T}P\psi (1) \end{aligned}$$

From the Eq. (14), we have

$$\begin{aligned} \theta '(X)=-c^{T}P\psi (1)+c^{T}P\psi (X), \end{aligned}$$

(15)

Again, integrating with respect to X from 0 to X of the Eq. (15), we obtain

$$\begin{aligned} \theta (X)=1-c^{T}P\psi (1)d'P\psi (X)+c^{T}P^{2}\psi (X), \end{aligned}$$

(16)

Substituting the values of $\theta (X), \theta '(X)$ and $\theta '' (X)$ in Eq. 7 to 10. $\theta (X)$ is the approximate solution to these equations. Finding the residual $R(X,c_{1},c_{2},c_{3},...,c_{n})$ for n collocation points $X_{r}, r=1,2,3,...,n$. There must be equality between the coefficients and collocation points. As a result, the residuals will be obtained.

3.2 Least Square Method

This method is based on residual weighting and minimises the residual of the test function, which is used to solve a non linear differential equation given by [10]. The meaning of this method is to get the minimum continuous summation of squared residuals [11].

$$\begin{aligned} S=\int \limits _{x}R(x)R(x)dx=\int \limits _{x}R^2(x)dx \end{aligned}$$

(17)

The derivative of the above function with respect to all unfamiliar constants has to be zero in order to obtain the minimum scalar function [11], i.e.

$$\begin{aligned} \frac{\delta S}{\delta c_{i}}=2\int \limits _{x}R(x)\frac{\delta R}{\delta c_{i}}dx=0 \end{aligned}$$

(18)

here weight function is

$$\begin{aligned} W_{i}=2\frac{\delta R}{\delta c_{i}} \end{aligned}$$

(19)

the coefficient ‘2’ from this equation can be expelled. Then the weight function of this method will be just derivative of residual with respect to unfamiliar constants i.e.

$$\begin{aligned} W_{i}=\frac{\delta R}{\delta c_{i}} \end{aligned}$$

(20)

3.3 Moment Method

For this method, the weight function is selected from family of polynomials, expressed as

$$\begin{aligned} W_{i}(x)=x^{i}, \qquad i=0, 1, 2,...,n \end{aligned}$$

(21)

With the residual it is expressed as

$$\begin{aligned} \int \limits _{x}W_{i}(x)R(x)dx=0, \qquad i=0, 1, 2,...,n \end{aligned}$$

(22)

Using (21), Eq. (22) becomes

$$\begin{aligned} \int \limits _{x}x^{i}R(x)dx=0, \qquad \, i=0, 1, 2,...,n \end{aligned}$$

(23)

Now by using this, residual will be obtained.

4 Exact Solution

To calculate exact solution, we consider $\beta =0$, $n=0$, $N_{r}=0$ and porosity parameter $N_{p}=0$ in Eq. (4), then equation reduced in following form i.e.

$$\begin{aligned} \frac{d^{2}\theta }{d x^{2}}-M^2(\theta -\theta _{a})-Pe\frac{d\theta }{dx}+M^2G(1+\varepsilon _G(\theta -\theta _{a}))=0 \end{aligned}$$

(24)

The boundary conditions are

$$\begin{aligned} \theta (1)=1,\quad \; \frac{d \theta }{d x}\Big \vert _{x=0}=0 \end{aligned}$$

After applying boundary conditions to Eq. (24), we get

$$\begin{aligned} \theta =c_{1}e^{m_{1}x}+c_{2}e^{m_{2}x}+\frac{M^{2}G}{Q} \end{aligned}$$

(25)

where $c_{1}=-\frac{m_{2}(1-\frac{M^{2}G}{Q})}{m_{1}e^{m_{2}}-m_{2}e^{m_{1}}}, c_{2}=\frac{m_{1}(1-\frac{M^{2}G}{Q})}{m_{1}e^{m_{2}}-m_{2}e^{m_{1}}}$ and $Q=M^{2}-M^{2}G\varepsilon _{G}$.

5 Results and Discussion

We investigate heat transfer in a porous moving fin. Impact of different parameters namely thermal conductivity $(\beta )$, thermo-geometric (M), radiation-conduction $(N_{r})$, Peclet number (Pe), parameter G, heat generation $(\varepsilon _{G})$, dimensionless ambient temperature $(\theta _{a})$, porosity parameter $(N_p)$ on temperature distribution is investigated. Thermal conductivity is taken as a variable functions of temperature to study the distribution of temperature in fin. The four different cases for thermal conductivity are (i) linear function of temperature, (ii) constant, (iii) exponential function of temperature, and (iv) quadratic form of temperature, and heat transfer coefficient is taken as a power-law type. We find the analytic solution to the problem using LWCM, LSM, and MM. A comparison of the exact, LWCM, LSM, and MM is shown in Table 1 to validate the results obtained by these methods when compared to exact results. We can see from the table that the results of these methods are very close to the exact results, which shows the novelty of present work. To determine which method has the highest accuracy, we compute error analysis, as shown in Fig. 2. It has been observed that the error in LWCM is the lowest as compared to LSM and MM. So for further computation, we used LWCM. Reference values for parameters are taken as $\beta =1, M=1, Pe=1, G=0.1, \varepsilon _{G}=0.1, N_{r}=1, n=1, \theta _{a}=0.1, N_p=0.1$.

Figure 3 depicts the impact of thermal conductivity in four cases on temperature. In case III, where thermal conductivity is an exponential form of temperature, a maximum temperature has been observed, whereas in case II, a lower temperature has been observed. As a result, in cases of constant thermal conductivity, cooling is more effective.

Figure 4 describes the impact of thermal conductivity on temperature for cases I, III, and IV, while in case II, thermal conductivity is constant. From the figure, we have noted that by rising the thermal conductivity, fin temperature also rises. Case III has the maximum temperature distribution as compared to the other cases. So when fin has a lower thermal conductivity, cooling becomes more effective in the fin.

Table 1. Comparison between Exact result, LWCM, LSM and MM

Fig. 2.

Error analysis of LWCM, LSM and Moment method

Fig. 3.

Temperature distribution in fin for thermal conductivity in cases I, II, III and IV

Fig. 4.

Effect of $\beta$ on temperature distribution

Fig. 5.

Effect of M on temperature distribution

Fig. 6.

Effect of $N_{r}$ on temperature distribution

Fig. 7.

Effect of Pe on temperature distribution

Fig. 8.

Effect of G on temperature distribution

Fig. 9.

Effect of $\varepsilon _{G}$ on temperature distribution

Fig. 10.

Effect of $\theta _{a}$ on temperature distribution

Fig. 11.

Effect of $N_{p}$ on temperature distribution

Fig. 12.

Temperature distribution in porous and non-porous fin

Table 2. Effect of n on temperature distribution for case I and case II

Table 3. Effect of n on temperature distribution for case III and case IV

Figure 5 depicts the effect of thermo-geometric parameter. It has been noted that as M increases, the temperature in the fin decreases, implying that the enhancement of heat in the environment increases. At a constant value of the heat transfer coefficient, by increasing the fin length, the amount of heat moving through the fin also increases, resulting in a decrease in temperature. Among the cases, in case II temperature is minimum.

Figure 6 shows the impact of radiation-conduction. The radiative cooling happens to be more influential if radiative transport is stronger, resulting in lesser the fin temperature. This temperature drop causes the system to cool. We observed that by rising $N_{r}$ temperature in the fin drops. So case II has a lower temperature compared to other cases.

Figure 7 shows the impact of the Peclet number. We see that by increasing the parameter Pe, fin temperature drops. If Pe increases, then the fin will move faster, and consequently, the temperature in the fin will decrease rapidly because of the increased impact of the adjective on the fin surface. At $Pe=0$, the fin describes a stationary fin, the fin takes longer to cool down which has been represented by the maximum temperature than a moving fin. The temperature distribution in fin of Case II is lower means cooling process is more effective in this case. The impact of the G parameter is depicted in Fig. 8. It has been seen that by rising the value of G temperature also increases. So case III has a high temperature, whereas case II has a lower temperature. Heat transfer increases when a fin has constant thermal conductivity.

The impact of heat generation is shown in Fig. 9. It demonstrated that increasing the value of the $\varepsilon _{G}$ parameter raises the fin temperature. Among the cases, case III has a high temperature, and case II has a lower temperature. The physical implementation is that as the heat generation parameter increases, so does the heat transfer in fins.

Figure 10 depicts the impact of ambient temperature. It has been noted that by rising the value of $\theta _{a}$ temperature also rises in the fin. Heat transfer is reduced as the ambient temperature rises. Case III has a high temperature, but Case II has a lower temperature. So in this case, cooling will be effective when fin has constant thermal conductivity and a lower ambient temperature.

Figure 11 shows the effect of the porosity parameter. From the figure, it has been seen that as we increased the porosity parameter, the fin temperature decreases. For porosity, Case III has the maximum temperature distribution as compared to other cases. Therefore, in Case II, the heat transfer rate increases, which causes a drop in the fin temperature. Temperature distribution in the porous and non-porous fin is shown in Fig. 12. The figure explains that if there is no porous medium, i.e. $N_p=0$ then the temperature in fin is at its maximum, but if we add a porous medium to the fin, then temperature decreases. We observed that fin temperature is higher in non-porous compared to porous fin. So for higher porosity, heat transfer in the fin also increases, and cooling process in the fin becomes more effective.

Table 2 represents the impact of n on temperature in cases I and II, respectively, and for cases III and IV, it is represented in Table 3. According to the tables, as the value of n rises, so does the fin temperature. So when $n=-1/4$ = 1/4 (i.e., condensation or laminar film boiling), cooling is effective. Case III has a higher temperature as compared to other cases.

6 Conclusion

We have studied a porous moving fin in one-dimension with heat generation, temperature-dependent variable thermal conductivity, and a power-law heat transfer coefficient in this paper. The effect of parameters has been shown using LWCM because it achieves the minimum error among other applied methods. It has been determined that increasing thermal conductivity, heat generation, the parameter G, exponent n, and the ambient temperature raises the temperature in fins. On the other hand, as the temperature in fin decreases, the enhancement of heat increases by increasing the thermo-geometric, radiation-conduction, Peclet number, and porosity parameters. In case III, the fin temperature is high, while in case II, the fin temperature is low. A comparison of porous and non-porous fins revealed that the non-porous fin has a high temperature, whereas adding a porous medium to the fin results in a lower temperature. Because of the porous medium in the fin, heat transmission increases, making cooling more effective. Future studies may focus on the importance of enhancing heat transmission due to its usefulness in many applications directly affecting human life.