Introduction

Mechanical processes result in heat generation, and different cooling processes are required to release this heat. A fin is an extended surface that is primarily used to enhance heat dissipation from the equipment surface to the surrounding fluid [1,2,3]. Fins are generally used in automobile components, air conditioning and refrigeration systems, internal combustion engines, space vehicles, electric transformers, micro-electronic components, and photovoltaic panels [4, 5]. Sheikholeslami et al. [6] investigated the effects of fin length and shape as well as nanoparticle size on the performance of a nanoparticle-enhanced phase-change material (NEPCM)-based heat exchanger. Selimefendigil et al. [7] used a fuzzy-based model to predict heat transfer through a square cavity in the presence of an adiabatic thin fin. They further performed a numerical study to investigate the effects of an adiabatic thin fin mounted on an upper wall [8]. The fin was subjected to laminar forced convection over a backward-facing step in a channel. Selimefendigil et al. [9] employed a numerical model to study the fluid–structure interaction in a vertical lid-driven cavity field under a magnetic field. A fin was attached to the cavity to analyze the flow mixing and heat transfer behavior in the cavity. Fins are generally made of metals or alloys with high thermal conductivity, and porous fins have attracted considerable attention for effective energy utilization.

The concept of porous fins was first proposed by Kiwan and Al-Nimr [10] in 2001. Kahalerras and Targui [11] used porous fins to enhance heat transfer in a double-pipe heat exchanger, and the obtained numerical results based on the finite volume method revealed improved heat transfer due to a substantial alteration of the flow pattern in the presence of porous fins. Kiwan et al. [12, 13] employed Darcy’s model to analyze the fluid-flow pattern across a porous medium. Sheikholesmami [14] used a non-Darcy model to analyze the interaction between iron oxide–water nanofluid and a porous encloser. He studied the effects of an external magnetic field and temperature on the viscosity of ferrofluid by a control volume-based finite element method. Saedodin and Sadeghi [15] investigated the heat transfer through a cylindrical porous fin by the fourth-order Runge–Kutta method and observed that the heat loss rate in a porous fin was higher than that in a non-porous fin. Talukdar and Mishra [16] reported that the heat transfer rate was significantly improved in a flow channel between two isothermal plates with a solid porous matrix. Selimefendigil et al. [17] found that the use of porous fins greatly enhanced the performance of a solar photovoltaic (PV) module. Hatami and Ganji [18] assessed the performance of a convective–radiative circular porous fin with different geometric profiles and used the least-square method coupled with the fourth-order Runge–Kutta method to solve the governing equations of heat transfer through porous media. The exponential-shaped fin made of silicon nitride led to greater heat dissipation as compared to the triangular and rectangular fins made of the same material. Moreover, in comparison to the solid fin, a significant improvement in heat transfer through the porous fin was also reported in their analysis. Moradi et al. [19] used the differential transformation method (DTM) to obtain the temperature field in a triangular convective–radiative porous fin. In this study, the performance of the fin was discussed in terms of the porosity factor, and it was observed that the fin efficiency was improved with the increasing porosity. Ullmann and Kalman [20] performed a comprehensive study of convective–conductive annular fins with rectangular, triangular, parabolic, and hyperbolic profiles and estimated their optimal dimensions and efficiencies. Gorla and Bakier [21] analyzed the natural convection and radiation in a rectangular porous fin and found that the radiative energy directly influenced the transfer of more heat. Therefore, the incorporation of radiative parameters in the governing equations of heat transfer is essential to predict the actual heat transfer through a fin. Darvishi and Gorla [22] performed the unsteady thermal analysis of porous rectangular fins of infinite and finite lengths. Heat transfer equations based on Darcy’s model were formulated considering an insulated fin tip and a tip with a known convective heat transfer coefficient. It was noticed that the presence of pores altered the non-steady heat transfer rate and temperature distribution.

Ma et al. [23] predicted the performance of a longitudinal porous fin by the spectral collocation method and reported that the heat transfer coefficient, the surface emissivity, and heat generation parameters varied with the local temperature. A homogeneous isotropic porous medium with a single-phase fluid was considered in their analysis. Cuce and Cuce [24] developed the expressions of efficiency, effectiveness, and heat transfer rate for a longitudinal rectangular porous fin and compared the results with those of a solid fin. Kundu and Lee [25] developed an analytical model to predict the temperature distribution in a moving porous annular fin with a stepped profile. The optimization analysis revealed that for the same mass, the porous fin transferred more heat than its solid counterparts at optimum conditions. Das [26] inversely estimated the thermal parameters, porosity, solid thermal conductivity, emissivity, permeability, and thickness of a porous annular fin by the hybrid evolutionary algorithm. In this analysis, the heat transfer equation without considering heat generation and the convective heat transfer coefficient were solved numerically. Mosayebidorcheh et al. [27] employed the least-square method (LSM) to analyze the temperature fields in longitudinal fins of different cross-sections and performed an optimization study to select the best fin material in terms of heat transfer rate, effectiveness, and efficiency. Mesgarpour et al. [28] investigated the effect of a sintered porous fin on heat transfer and fluid flow through a channel. They employed CFD simulations to evaluate the effect of sintered balls on the porosity of a contact model. Turkyilmazoglu [29] studied the effects of temperature and humidity ratio on a wet porous fin. Hoshyar et al. [30] and Cuce et al. [24] employed the homotopy perturbation method (HPM) to predict the heat transfer through a longitudinal conductive–convective porous fin; however, the main drawback of their analysis was that radiation was not incorporated in the governing equation of heat transfer.

The best of our open literature search (Books, peered reviewed journal etc.) reveals that no experimental studies have yet been carried out for annular porous fins. Stark et al. [31] experimentally investigated the thermal characteristics of a porous fin with a square block structure. The thermal behavior obtained from the semi-analytical solution was compared with the results obtained from the experiment. In their paper, they only addressed numerical and analytical solutions for an axisymmetric annular porous fin.

The selection of proper conductive–convective parameters is crucial to achieving the best fin design. Considering variable parameters and all types of losses, it is generally found that the thermal properties of fins change significantly at high temperatures. No studies have been performed to obtain the closed-form solution of heat transfer through an annular porous fin with multiple variable thermal parameters, such as conduction, convection, radiation, and heat generation. In comparison to existing mathematical techniques for solving nonlinear heat transfer equations, HPM is relatively simple and does not require many terms to obtain the approximate closed-form solution. Cuce et al. [24] presented a complete overview of recent works on heat transfer through porous fins. Hoseinzadeh et al. [32] compared the numerical and analytical results for the thermal properties of a longitudinal porous fin.

The present paper aimed at disclosing the closed-form solutions of nonlinear heat transfer equations for an annular porous fin with multiple variable thermal parameters. The novelty lies in incorporating the temperature variation in the physical heat transfer parameters such as the surface emissivity, thermal conductivity of solid and fluid. The works also include the external convection from the solid matrix and the heat generation parameter as functions of temperature for a more realistic modeling of the phenomenon. The governing equations with multiple nonlinear parameters were solved by HPM. The thermal behavior of a rectangular fin was compared with that of a hyperbolic fin in terms of their temperature distributions, efficiencies, effectiveness, and heat transfer rates. The fluid velocity field across the porous matrix was simulated by Darcy’s model. The closed-form solution of the problem was compared with the numerical solution obtained by the finite difference method. The obtained temperature distribution was further validated by modeling the fin in Comsol-Multiphysics software.

Physical model and mathematical formulation

Physical model

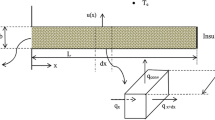
In the present analysis, rectangular and hyperbolic porous annular fins with an inner radius of rb and an outer radius of ro were considered (Fig. 1). In addition, the following assumptions and simplifications were made in the present analysis:

  • A steady-state heat transfer was considered.

  • The fin base was maintained at a constant temperature, and the contact resistance was neglected.

  • Darcy’s law governed the fluid flow across the porosity of the fins.

  • The porous medium was saturated with a homogenous single-phase isotropic fluid.

  • Temperature varied along the radial direction only.

  • The surface porosity of the fins was equal to the volumetric porosity.

  • All thermal parameters were a function of temperature.

Fig. 1
figure 1

Geometry of annular porous fin

Full size image

Thermal losses in the fins occurred by convection and radiation from the solid surface of the fins and the convection loss between the solid matrix and the fluid flowing through pores. Thus, a suitable multiplication factor was introduced to calculate the surface area of the solid matrix through which convection and radiation occurred.

Mathematical formulation

Considering heat flow along the radial direction of an annular porous fin, the steady-state energy balance equation for heat transfer can be expressed as

$$ q_{{\text{r}}} - q_{{{\text{r}} + {\text{dr}}}} = 2\varepsilon \sigma \pi (1 - \phi )\left( {T^{4} - T_{{\text{s}}}^{4} } \right)r{\text{d}}r + 2\pi hr(1 - \phi )(T - T_{{\text{a}}} ){\text{d}}r + \dot{m}C_{{\text{p}}} (T - T_{{\text{a}}} ) - 2\pi q^{*} tr{\text{d}}r $$
(1)

where q is heat flow at a radial distance r from the center, ε is the emissivity of the solid matrix, σ is the Stefan-Boltzmann constant, Ts is the radiation sink temperature, Ta is ambient temperature, h is the convective heat transfer coefficient from the solid matrix to the external atmosphere, ṁ is the mass flow rate, Cp is the specific heat capacity of the fluid, q* is the heat generation per unit volume, t is the thickness of the fin at a radial distance r, and ϕ is porosity.

In Eq. 1, the first term of the right-hand side signifies the loss due to radiation from the fin to the atmosphere, the second term implies the loss due to convective heat transfer between the solid matrix and the external fluid flow over it, the third term signifies the energy absorbed by the fluid flowing internally through pores of the fin, and the last term implies the heat generated in the given element. The mass flow rate of a homogenous single-phase isotropic fluid across the porous fin can be represented as

$$ \dot{m} = 2\pi \rho vr{\text{d}}r $$
(2)

The fluid velocity (v) was obtained based on Darcy’s model for fluid flow through a porous medium [33].

$$ v = \frac{g\kappa \beta }{\gamma }\left( {T - T_{{\text{a}}} } \right) $$
(3)

Now, substituting Eqs. 2 and 3 into Eq. 1,

$$ - \frac{{{\text{d}}q}}{{{\text{d}}r}} = 2\varepsilon \sigma \pi (1 - \phi )\left( {T^{4} - T_{{\text{s}}}^{4} } \right)r + 2\pi hr(1 - \phi )(T - T_{{\text{a}}} ) + \frac{{2\pi \rho \kappa \beta gC_{{\text{p}}} (T - T_{{\text{a}}} )^{2} r}}{\gamma } + 2\pi q^{*} tr $$
(4)

Fourier’s law of conductive heat flux can be expressed as

$$ q = - k_{{{\text{eff}}}} A_{{\text{c}}} \frac{{{\text{d}}T}}{{{\text{d}}r}} $$
(5)

Fins generally operate at high temperatures; thus, thermal parameters were considered as a linear function of temperature. The variations of different thermal parameters, such as convective heat transfer coefficient (h), emissivity (ε), conductivity of the solid matrix (ks), conductivity of the cooling fluid (kf), and heat generation coefficient (q), with temperature are presented below.

$$ h = h_{0} \left( {\frac{{T - T_{{\text{a}}} }}{{T_{{\text{b}}} - T_{{\text{a}}} }}} \right)^{n} ;\;\;\varepsilon = \varepsilon_{0} \left[ {1 + \lambda (T - T_{s} )} \right];\;\;q^{*} = q_{0} \left[ {1 + a(T - T_{{\text{a}}} )} \right];\;\;k_{{\text{f}}} = k_{{\text{f}}}^{0} \left[ {1 + \kappa_{1} (T - T_{{\text{a}}} )} \right]\;\;{\text{and}}\;\;k_{{\text{s}}} = k_{{\text{s}}}^{0} \left[ {1 + \kappa_{2} (T - T_{{\text{a}}} )} \right] $$
(6)

The relationship between the fin thickness and the radial distance was also considered in the present analysis.

$$ t(r) = t_{{\text{b}}} \left( {\frac{r}{{r_{{\text{b}}} }}} \right)^\text{m} $$
(7)

where t is the thickness of the fin and rb is the base radius of the fin. The parameters m = 0 and m = −1 correspond to uniform and hyperbolic fins, respectively. The cross-sectional area (Ac) and the effective thermal conductivity of the porous matrix of the fin can be expressed as

$$ A_{{\text{c}}} = 2\pi rt{\text{d}}r\;\;{\text{and}}\;\;k_{{{\text{eff}}}} = \phi k_{{\text{f}}} + (1 - \phi )k_{{\text{s}}} $$
(8)

Now, substituting Eqs. 5 and 8 into Eq. 4,

$$ \begin{aligned} \left( {\phi \kappa_{1} + k_{{\text{r}}} (1 - \phi )\kappa_{2} } \right)t\left( {\frac{{{\text{d}}T}}{{{\text{d}}r}}} \right)^{2} + (m + 1)\frac{t}{r}\frac{{k_{{{\text{eff}}}} }}{{k_{{\text{f}}}^{0} }}\frac{{{\text{d}}T}}{{{\text{d}}r}} + \frac{{k_{{{\text{eff}}}} }}{{k_{{\text{f}}}^{0} }}t\frac{{{\text{d}}^{2} T}}{{{\text{d}}r^{2} }} = & 2(1 - \phi )\sigma \frac{\varepsilon }{{k_{{\text{f}}}^{0} }}\left\{ {1 - \left( {T - T_{{\text{s}}} } \right)\lambda } \right\}\left( {T^{4} - T_{{\text{s}}}^{4} } \right) \\ & + 2\frac{{h_{0} }}{{k_{{\text{f}}}^{0} }}\left( {\frac{{T - T_{{\text{a}}} }}{{T_{{\text{b}}} - T_{{\text{a}}} }}} \right)^\text{n} (1 - \phi )\left( {T - T_{{\text{a}}} } \right) + \frac{{\rho \kappa \beta gC_{{\text{p}}} \left( {T - T_{{\text{a}}} } \right)^{2} r}}{{k_{{\text{f}}}^{0} \nu_{{\text{f}}} }} - q_{0} \frac{t}{{k_{{\text{f}}}^{0} }}\left\{ {1 + e\left( {T - T_{{\text{a}}} } \right)} \right\} \\ \end{aligned} $$
(9)

Further, in order to simplify the analysis, the following non-dimensional parameters were introduced.

$$ \begin{aligned} R = & \frac{r}{{r_{{\text{b}}} }},\;\;\theta = \frac{T}{{T_{{\text{b}}} }},\;\;\theta_{{\text{s}}} = \frac{{T_{{\text{s}}} }}{{T_{{\text{b}}} }},\;\;\theta_{{\text{a}}} = \frac{{T_{{\text{a}}} }}{{T_{{\text{b}}} }},\;\;\tau_{1} = \frac{{\phi \kappa_{1} T_{{\text{b}}} }}{{\phi + k_{r} (1 - \phi )}},\;\;\tau_{2} = \frac{{k_{{\text{r}}} (1 - \phi )\kappa_{2} T_{{\text{b}}} }}{{\phi + k_{{\text{r}}} (1 - \phi )}}, \\ Q^{*} = & \frac{{q_{0} r_{{\text{b}}}^{2} }}{{(\phi + k_{{\text{r}}} (1 - \phi ))k_{{\text{f}}}^{0} T_{{\text{b}}} }},\;\;\tau_{{\text{w}}} = \tau_{1} + \tau_{2} ,\;\;N_{{\text{r}}} = \frac{{2(1 - \phi )\sigma \varepsilon T_{{\text{b}}}^{3} r_{{\text{b}}} }}{{(\phi + k_{{\text{r}}} (1 - \phi ))k_{{\text{f}}}^{0} T_{{\text{b}}} t_{{\text{b}}} }}, \\ N_{{\text{c}}} = & \frac{{2h_{0} r_{{\text{b}}}^{2} (1 - \phi )}}{{(\phi + k_{{\text{r}}} (1 - \phi ))k_{{\text{f}}}^{0} t_{{\text{b}}} }},\;\;N_{{{\text{cc}}}} = \frac{{\rho \kappa \beta gC_{{\text{p}}} T_{{\text{b}}} r_{{\text{b}}}^{2} }}{{(\phi + k_{{\text{r}}} (1 - \phi ))k_{{\text{f}}}^{0} \nu_{{\text{f}}} t_{{\text{b}}} }},\;\;\lambda T_{{\text{b}}} = \lambda^{0} ,\;\;eT_{{\text{b}}} = e^{0} \\ \end{aligned} $$
(10)

The aforesaid non-dimensional parameters are described in the nomenclature. After carrying out non-dimensional transformations and substituting the previously stated variable parameters, the energy balance equation can be expressed in the following non-dimensional form.

$$ \begin{aligned} \tau_{{\text{w}}} R^\text{m} \left( {\frac{{{\text{d}}\theta }}{{{\text{d}}R}}} \right)^{2} + & (m + 1)R^{\text{m} - 1} \left[ {\phi + \tau_{{\text{w}}} (\theta - \theta_{{\text{a}}} ) + k_{{\text{r}}} (1 - \phi )} \right]\frac{{{\text{d}}\theta }}{{{\text{d}}R}} \\ + & \left[ {f + \tau_{{\text{w}}} (\theta - \theta_{{\text{a}}} ) + k_{{\text{r}}} (1 - f)} \right]R^\text{m} \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}R^{2} }} = N_{{\text{c}}} \left[ {\frac{{(\theta - \theta_{{\text{a}}} )^{\text{n} + 1} }}{{(1 - \theta_{{\text{a}}} )^\text{n} }}} \right] \\ + & N_{{{\text{cc}}}} (\theta - \theta_{{\text{a}}} )^{2} + N_{{\text{r}}} \left\{ {1 + \lambda^{0} (\theta - \theta_{{\text{s}}} )} \right\}\left( {\theta^{4} - \theta_{{\text{s}}}^{4} } \right) - Q^{*} \left\{ {1 + e^{0} (\theta - \theta_{{\text{a}}} )} \right\}R^\text{m} \\ \end{aligned} $$
(11)

where τw = τ1 + τ2 represents the variable thermal conductivity parameter for solid–fluid interactions.

Boundary conditions

For a finite-length fin with a constant base temperature and a well-insulated tip (no heat transfer from the fin tip), the following boundary conditions were considered.

$$ \left. {T_{{{\text{r}} = {\text{r}}_{{\text{b}}} }} = T_{{\text{b}}} \;\;{\text{and}}\;\;\frac{{{\text{d}}T}}{{{\text{d}}r}}} \right|_{{{\text{r}} = {\text{r}}_{0} }} = 0 $$
(12)

The non-dimensional forms of these boundary conditions can be expressed as

$$ \left. {\theta_{{{\text{R}} = 1}} = 1\;\;{\text{and}}\;\;\frac{{{\text{d}}\theta }}{{{\text{d}}R}}} \right|_{{{\text{R}} = \eta }} = 0 $$
(13)

Solution strategy

The nonlinear non-dimensional steady-state heat transfer equation with temperature-dependent thermal parameters was solved by the homotopy perturbation method (HPM), which has the advantages of both regular homotopy and the traditional perturbation method. In this method, the approximate analytical solution of linear and nonlinear partial differential equations can be obtained by introducing a small embedding parameter. This method is very powerful in solving nonlinear differential equations of multiple orders and does not require tedious calculations. In addition, the solutions converge after a few iterations. The core theory of HPM can be formulated as

$$ L(\theta ) + N(\theta ) - f(r) = 0\;\;{\text{for}}\;\;r \in \psi $$
(14)

with the specified boundary condition of

$$ B\left( {\theta ,\frac{\partial \theta }{{\partial n}}} \right) = 0\;\;{\text{for}}\;\;r \in \Omega $$
(15)

where L (θ) and N (θ) are linear and nonlinear differential operators, respectively, f (r) is an analytical function, B is a boundary operator, and ψ represents the boundary of the domain Ω. Now, an artificial parameter p is introduced to construct a homotopy.

$$ H(\theta ,p) = (1 - p)\left[ {L(\theta ) - L(\theta_{{\text{o}}} )} \right] + p\left[ {L(\theta ) + N(\theta ) - f(r)} \right] = 0 $$
(16)

where \(L = \frac{{{\text{d}}^{2} }}{{{\text{d}}\xi^{2} }}\) and θo are initial approximations that satisfy the boundary conditions. The embedding parameter p ∈ [0, 1] monotonically changes from 0 to 1; thus Eq. (16) becomes

$$ \begin{array}{*{20}l} {p = 0:\;\;L(\theta ) = L(\theta_{{\text{o}}} )} \hfill \\ {p = 1:\;\;L(\theta ) + N(\theta ) - f(r) = 0} \hfill \\ \end{array} $$
(17)

As p varies from 0 to unity, H(θ, p) simultaneously changes from θo to θ(r). With the help of the perturbation technique and considering smaller values of p, the solution of the above equation can be expressed as

$$ \theta = \theta_{0} + p\theta_{1} + p^{2} \theta_{2} + p^{3} \theta_{3} + p^{4} \theta_{4} + \cdots $$
(18)

As p approaches unity, an approximate solution is obtained.

$$ \theta = \theta_{0} + \theta_{1} + \theta_{2} + \theta_{3} + \theta_{4} + \cdots $$
(19)

Fin efficiency

The fin efficiency is defined as the ratio of the heat transferred from the fin material to the surrounding fluid in actual working conditions to the heat transferred in ideal operating conditions [34]. The actual heat transferred from a fin (considering conductive, convective, and radiative losses) is equal to the heat conducted from the base.

$$ Q_{{{\text{actual}}}} = \left. { - k_{{{\text{eff}}}} A_{{\text{c}}} \frac{{{\text{d}}T}}{{{\text{d}}r}}} \right|_{{{\text{r}} = {\text{r}}_{{\text{b}}} }} $$
(20)

where Ac is the cross-sectional area at the base of the fin. The heat transferred from a fin in ideal operating conditions can be expressed as

$$ Q_{{{\text{ideal}}}} = \int\limits_{{{\text{r}}_{{\text{b}}} }}^{{{\text{r}}_{{\text{t}}} }} {P\left[ {h_{0} \left( {T_{{\text{b}}} - T_{{\text{a}}} } \right) + \varepsilon \left( {T_{{\text{b}}} } \right)\sigma \left( {T_{{\text{b}}}^{4} - T_{{\text{s}}}^{4} } \right)} \right]} {\text{d}}r $$
(21)

where P is the perimeter of area Ac. Hence, the fin efficiency can be expressed as

$$ \eta = \frac{{\left. { - k_{{{\text{eff}}}} A_{{\text{c}}} \frac{{{\text{d}}T}}{{{\text{d}}r}}} \right|_{{{\text{r}} = {\text{r}}_{{\text{b}}} }} }}{{\int\limits_{{{\text{r}}_{{\text{b}}} }}^{{{\text{r}}_{{\text{t}}} }} {P\left[ {h_{0} \left( {T_{{\text{b}}} - T_{{\text{a}}} } \right) + \varepsilon \left( {T_{{\text{b}}} } \right)\sigma \left( {T_{{\text{b}}}^{4} - T_{{\text{s}}}^{4} } \right)} \right]} {\text{d}}r}} $$
(22)

The fin efficiencies for different values of the convection parameter (NC) were compared with the results given by Cuce et al. [24], and the comparison is presented in Fig. 3b.

Experimental study

It is evident that no experimental works for an annular porous fin have yet been conducted. Stark et al. [31] recently carried out an experimental analysis for a porous fin with a square block structure. In their study, aluminum metal foam with high porosity of about 0.941 was used as the fin material and was connected with a copper wick. The thermal characteristics measured from the semi-analytical solution were compared with the results obtained from experimental measurements. The experiment proposed by Stark et al. [31] can be modified and used for the experimental study of an axisymmetric annular fin in a porous media.

Results and discussion

The current section describes the results obtained from the approximate closed-form solution of heat transfer for an annular fin in a porous media, and the solution was obtained by solving the nonlinear governing equation of heat transfer by HPM. The effects of different temperature-dependent thermal parameters were presented. In order to examine the accuracy of the HPM-based solution, the obtained results were validated by numerical solutions and available experimental data.

Validation

Numerical solutions were presented to validate HPM-based closed-form solutions for rectangular and hyperbolic porous fins. The temperature fields of the fins in the dimensional form were verified by FEM in Comsol Multiphysics software (v5.2a), where the corresponding non-dimensional results were verified by the finite difference method (FDM). The fins were made of Al–204 alloy (solid), and the fluid flowing across the porous matrix was considered to be air (fluid). The thermophysical properties at ambient temperature are taken from online data [35] and the recent published work [26] (ho = 25 W m−2 K−1, εo = 0.702, ϕ = 0.4, \(k_{{\text{s}}}^{0}\) = 123.13 W m−1 K−1, \(k_{{\text{f}}}^{0}\) = 0.026 W m−1 K−1, g = 9.81 m s−2, ρ = 1.24 kg m−3, Cp = 1.005 J g−1 K−1, β = 3.5 × 10–3 K, κ = 5.1274 × 10–8 m2, and ν = 1.568 × 10–5 m2 s−1). The thickness and base temperature of the fins were t = 0.003 m and Tb = 600 K, respectively. The dimensionless parameters, NC, NCC, NR, and Q, were estimated using the same parameters mentioned above. In Table 1, HPM-based solutions for the temperature variation along the fin length are presented and compared with FEM results. The contours of temperature profiles for the rectangular and hyperbolic porous fins obtained from the FEM analysis are illustrated in Fig. 2, and the non-dimensional results for temperature fields are compared with FDM solutions in Table 2. In both dimensional and non-dimensional analyses, the maximum errors at the fin tip for the rectangular and hyperbolic profiles were less than 1% and 2%, respectively. The hyperbolic fin dissipated more heat to the surrounding, resulting in lower tip temperature as compared to the rectangular one. Furthermore, the temperature distribution for a set of different non-dimensional parameters is exhibited in Table 3. In both dimensional and non-dimensional analyses, the HPM analysis yielded a maximum error of 1.29% and 2.95% at the fin tip for the rectangular and hyperbolic profiles, respectively. It indicates that the percentage of error was dependent on parametric values. The error could be further reduced by considering higher-order terms in the assumed solution of Eq. 18. In Fig. 3a, the obtained temperature distribution is compared with the published work of Das [26]. The non-dimensional parameters that are common in the governing equation were used for comparison, and the remaining terms were set to zero. The fin efficiency obtained from Eq. (22) is compared with the result of Cuce and Cuce [24] in Fig. 3b. In order to maintain the equivalency of the results, the additional terms (radiation parameters) in the present formulation were neglected, and a good agreement was obtained. Therefore, it can be inferred that the proposed HPM-based closed-form solution yielded almost accurate results in both dimensional and non-dimensional forms.

Table 1 Dimensional analysis of HPM and FDM solutions for temperature distribution
Full size table
Fig. 2
figure 2

Temperature contour obtained using Comsol Multiphysics 5.2a, along the radius of a rectangular and b hyperbolic fins for the aforementioned thermo-physical (properties h = 25 Wm−2 K−1, ε = 0.702, ϕ = 0.4, ks = 123.13 Wm−1 K−1, kf = 0.026 Wm−1 K−1, and ρ = 1.24 kg/m3, Cp = 1.005 kJ/kgK)

Full size image
Table 2 Non-dimensional analysis of HPM and FDM solutions for temperature distribution considering dimensionless parameters Nr = 0.5, Nc = 0.7, Ncc = 1.5, Q* = 0.04, e = 0.3, λ = 0.2, Tw = 0.03
Full size table
Table 3 Non-dimensional analysis of HPM and FDM solutions for temperature distribution considering dimensionless parameters Nr = 1, Nc = 1, Ncc = 0.5, Q* = 0.04, e = 0.3, λ = 0.2, Tw = 0.03
Full size table
Fig. 3
figure 3

Comparison of the results obtained by the present formulation and those published in the literature for a temperature field (Das [26]) and b fin efficiency (Cuce and Cuce [24])

Full size image

Effect of the convection parameter (N c)

It was assumed that a certain portion of heat was dissipated from the solid matrix of the fin to the external far-field through convection. The temperature-dependent convective heat transfer coefficient was assumed to be a function of temperature. The power index of the heat transfer coefficient (n) denotes the heat transfer mode. The n values of  −0.25, 0.25, and 2 represent laminar film boiling, laminar natural convection, and nucleate boiling, respectively. In the present study, natural convection with the laminar fluid flow was considered as the mode of heat transfer from the fins to the surrounding. Natural convection occurred at two different solid–fluid interaction boundaries (a) solid surface of the porous matrix to the surrounding air flowing outside the fin along the surface and (b) solid porous matrix to the air flowing across pores. The natural convection phenomenon occurred due to the first interaction was denoted by the parameter NC, and the parameter NCC signifies the natural convection between the fluid inside pores and the solid porous matrix. The parameter NCC was a function of Darcy’s number and varied with the permeability of the porous media. Heat transfer from the solid porous matrix to the fluid inside pores was dependent on the orientation and shape of the pores. Figure 4 illustrates the effects of the parameter Nc on the non-dimensional temperature distributions of the porous rectangular and hyperbolic fins. It is evident that the gradients of the temperature curves became steeper with the increase of Nc. Hence, in both profiles, the tip temperature had a greater depression for a larger value of Nc, it indicates that the parameter Nc increased the convective heat transfer rate from the solid porous matrix to the surrounding. For the same values of NC, lower tip temperatures were detected for the hyperbolic profile as compared to the rectangular profile. The hyperbolic profile has a larger surface area than the rectangular profile and dissipated more heat from the fin surface to the surrounding. An interesting observation is that the reduction in the fin tip temperature is much more pronounced at higher values of NC in case of both the geometries. This highlights the prominence of external convection in the heat dissipation from the fin irrespective of the cross-section of the fin.

Fig. 4
figure 4

Influence of the convection parameter (NC) on the variation non-dimensional temperature distribution of a rectangular and b hyperbolic fin

Full size image

Effect of the conduction–convection parameter (N cc)

The parameter Ncc was a function of Darcy’s number and Rayleigh number. Figure 5 presents the effect of Ncc on the temperature distributions of the rectangular and hyperbolic fins. The increase of Darcy’s number reduced the hindrance to the fluid flow across pores and effectively enhanced the convective cooling of the fins. The Rayleigh number is a function of the Grashof number, which increased the conductive–convective parameter. The Grashof number is an approximate ratio of the buoyancy force and the viscous force acting on a fluid. Natural convection is a buoyancy-driven phenomenon; hence, a larger buoyancy force increased the convective cooling of the solid matrix by circulating fluid inside pores of the porous matrix. Consequently, the effect of the parameter Ncc increased with the increase of the buoyancy force acting on the fluid. Therefore, the temperature along the fin length dropped greatly for a larger value of Ncc for both cross-sectional profiles (Fig. 4). For the same values of Ncc, the hyperbolic profile had lower tip temperatures due to its larger surface area. However, the drop in the fin tip temperature is less prominent with greater values of NCC (NCC ~ 4). The reason for this behavior can be attributed to the fact that the natural convection inside the pores is affected by the flow of the fluid. The ease of flow of the fluid and hence its circulation has been plateaued by the maximum permeability the porous fin can achieve. When compared with the effect the increasing value of NC had on the temperature distribution it can be proposed that at optimal values of the parameters NC and NCC should be maintained for enhancing the heat dissipation from the fins.

Fig. 5
figure 5

Influence of conduction–convection parameter (NCC) on the non-dimensional temperature distribution along the fin length of a rectangular and b hyperbolic profile

Full size image

Effect of porosity

The effect of porosity was investigated for different values of ϕ, and the values of NC, NCC, NR, and other non-dimensional parameters were evaluated for a specific value of ϕ. It was observed that an increase in porosity of the porous medium caused a reduction of the fin tip temperature for both uniform and hyperbolic profiles (Fig. 6). The increase in porosity implies that a large amount of fluid was present per unit volume of the fins. Generally, the conductivity of the fluid was less than that of the solid matrix. The increase in porosity caused a decrease in the effective conductivity of the porous media; hence, less amount of heat dissipated along the fin length due to an increase of the thermal resistance. The domination of convective heat transfer over conductive heat transfer caused a decrease of the fin tip temperature. The presence of the term (1 − ϕ) in the numerator of term NC and its absence in case of the term NCC signifies the reduction in the external convection to the ambient and the increase in the internal natural convection inside the pores; with larger pore size the internal convection will be enhanced comparatively.

Fig. 6
figure 6

Influence of porosity value (ϕ) on the non-dimensional temperature distributions along the fin length of a rectangular and b hyperbolic profile

Full size image

Effect of the internal heat generation parameter

Internal heat generation generally occurs inside a fin due to chemical interactions between the fluid and the solid matrix or the presence of any heat source, such as electric current. In the present study, the temperature difference between the fin base and the tip was considerably large; therefore, the heat generation parameter was considered as a function of temperature. The effect of the heat generation parameter on the dimensionless temperature distributions of the rectangular and hyperbolic fins is displayed in Fig. 7. It can be observed that an increase in the heat generation parameter (Q*) caused an increase in the local temperature of the porous fins.

Fig. 7
figure 7

Temperature distribution of a rectangular and b hyperbolic fins as a function of non-dimensional radial distance for different values of heat generation parameter Q*

Full size image

Effect of the variable thermal conductivity parameter

It is already stated that the temperature difference between the fin base and the ambient generally remains high; hence, it will be a more realistic approach to consider the thermal conductivity of the fluid and the solid as a function of temperature. In the present analysis, the thermal conductivity parameter was dependent on the thermal conductivity coefficients of the solid and the fluid and varied linearly with the temperatures of the solid and the fluid. Generally, the thermal conductivity coefficient of fluid is very small as compared to that of a solid. The conductivity of pure metals decreases with temperature, whereas that of some materials increases with temperature. Therefore, the variable conductivity parameter for solid–fluid interactions (τw) can be positive or negative. The effect of τw on the dimensionless temperature distributions of the rectangular and hyperbolic fins is exhibited in Fig. 8. The dotted line shows the temperature distribution for the Al-204 alloy used in the dimensional study. Higher fin tip temperatures were detected for positive τw values, whereas an increase of the negative τw value caused a large decrease in the fin tip temperature. The thermal conductivity increased with the local temperature when τw was positive; hence, more heat dissipated from the fin base to the tip. The decrease in conductive resistance accelerated heat transfer through the solid matrix. The negative τw value restricted heat dissipation from the fin base and resulted in lower tip temperatures.

Fig. 8
figure 8

Effect of variable thermal parameter (τw) on non-dimensional temperature distribution along the fin length of a rectangular and b hyperbolic profiles

Full size image

Fin efficiency

The fin parameters, Nr = 0.5, Nc = 0.7, Ncc = 1.5, Q* = 0.04, e = 0.3, λ = 0.2, τw = 0.03, were considered to calculate the fin efficiency. Figure 9 compares the efficiencies of the rectangular and hyperbolic fins. It is clear that for all values of Nc, the hyperbolic fin exhibited a higher efficiency. The variation of the fin efficiency with the parameter Nc for different values of τw is illustrated in Fig. 10. The fin efficiency monotonically decreased with the increase of Nc for both rectangular and hyperbolic profiles, and a lower τw value resulted in a lower fin efficiency. It indicates that the conductive heat transfer through the solid matrix of the fin got restricted, resulting in lower efficiency. In comparison to the rectangular fin, the hyperbolic fin manifested higher efficiencies for positive τw values and lower efficiencies for negative τw values. The fin efficiency was affected by the effective conductivity of the porous matrix and the external convection from the solid part of the porous fin. The drop in the fin efficiency with an increase of the parameter Nc could be compensated with a higher value of τw.

Fig. 9
figure 9

Comparison of efficiencies of rectangular and hyperbolic profile fins as a function of convection parameter NC

Full size image
Fig. 10
figure 10

Fin efficiencies of a rectangular and b hyperbolic fins as a function of convection parameter NC for different values of variable thermal parameter τW

Full size image

The effect of emissivity on the fin efficiency for uniform and hyperbolic cross-sections is presented in Fig. 11. The surface to surface radiation inside the porous matrix was neglected in the present analysis. It was observed that the fin efficiency for a given value of Nc was reduced with the increasing surface emissivity of the fin material. Hence, for higher surface emissivity, the amount of heat radiated by the fin surface was larger. The increasing radiative heat transfer to the surrounding lowered the local fin temperature, and the large temperature variation along the fin length reduced the fin efficiency. The efficiency of the hyperbolic fin was not affected significantly by low Nc values, whereas the effect was prominent at higher values of the convection parameter. For a rectangular and hyperbolic profile, a distinct difference of the effect of emissivity on the variation of fin efficiencies as function of NC can be seen. From the analysis of Figs. 9–11, it can be concluded that the fin efficiency can attain optimal values by choosing materials having a high coefficient of thermal conductivity. However, the surface properties which affect the external convection and the emissivity the play a balancing role in the reducing the fin tip temperature and therefore the fin efficiency.

Fig. 11
figure 11

Fin efficiencies of a rectangular and b hyperbolic fins as a function of convection parameter NC for different values of emissivity

Full size image

Outlook and future perspectives

The work presented in this article has drawn an attention on the application of porous fin and its thermal analysis. A closed form solution targeting for temperature distribution in a hyperbolic and rectangular porous fin was established. This work further suggests us several research directions for the development of porous fins and their applications. A continuous effort is still required to choose the suitable materials with appropriate thermo-physical characteristics that can enhance the heat transfer from the hot body to the environment. The adequate knowledge of the various thermo-geometrical parameters for convective, conductive and radiative heat transfer through the fin in porous media may be the primary concern. For achieving the desired solution for heat transfer, an efficient approach for integrating various nonlinear parameters may be the prime importance. The non-dimensional thermo-geometrical parameters would be chosen in the correct form as they are flexible for alteration and refurbishment of the conventional fin. Further, the optimization of the thermo-geometrical parameters is essential for successful fin design for heat transfer. In this context, an inverse analysis [36] may be promising to select the right combination of thermo-geometrical parameters. The aspects of failure study due to thermal loading such as excessive thermal stresses, creep behavior and other mechanical demolition, need to be properly investigated [37] for the long-term and widely use of porous fin. The long-term thermal response, efficiency, effectiveness and stability of a porous fin need to be evaluated experimentally. Information on these aspects of the porous fin is currently limited in the literature. Furthermore, an inadequate heat transfer during energy recovery is another barrier that is hindering the development of thermal equipment. Efforts are still in demand at this point.

Conclusions

The afore-discussed research presented the heat transfer equations for porous annular fins with rectangular and hyperbolic cross-sections. The governing equations with different nonlinear thermal parameters were solved by HPM. The proposed closed-form solution was validated dimensionally and non-dimensionally by the results of FEM and FDM. The main inferences of the present study are depicted below.

  1. (1)

    A good agreement between the results obtained from the HPM-based semi-analytical approach and numerical simulations was noticed. The proposed HPM solution had distinct advantages over other closed-form solutions. HPM allowed the direct estimation of temperature fields to obtain accurate solutions of nonlinear heat transfer equations for porous fins.

  2. (2)

    In most cases, the annular fin with a hyperbolic cross-sectional profile was found to be more efficient than the fin with a uniform cross-section because the increased surface area of the hyperbolic fin resulted in a more substantial heat loss due to external convection.

  3. (3)

    The fin efficiency was greatly affected by the thermal conductivity coefficient of the fin material. The material with a positive thermal conductivity coefficient significantly improved the fin efficiency as compared to the material with a negative thermal conductivity coefficient.

  4. (4)

    Heat transfer from the base to the tip of the fin was greatly dependent on the pore volume fraction. Permeability also affected the heat transfer along the fin; however, the effects of porous parameters were reduced with the increase of permeability.