Keywords

1 Introduction

This chapter focuses on the optoelectronic properties of hybrid and all-inorganic lead halide perovskites. Such materials adopt the chemical stoichiometry ABX3 and are strong contenders for applications in solar photovoltaics. Among leading candidates are systems where the A cation is organic (e.g., methylammonium, CH3NH3+, MA; formamidinium, CH(NH2)2+, FA) or inorganic (e.g., Cs+), the B cation is Pb2+, and the X anion is I−, Br−, or Cl−. Important systems come from the methylammonium lead halide (CH3NH3PbX3, or MAPbX3), formamidinium lead halide [CH(NH2)2PbX3, or FAPbX3], and cesium lead halide (CsPbX3) families. Alloys are also possible and APbX3 materials can be produced as mixed cation, mixed anion, or even mixed cation/mixed anion alloys. Common mixed cation systems include A = FA/Cs or A = FA/MA alloys, e.g., FA1-yCsyPbI3 or FA1-yMAyPbI3. Mixed anion materials are often mixtures of iodine and bromine such as MAPb(I1-xBrx)3 and FAPb(I1-xBrx)3 while mixed cation/anion systems include FAxMAyCs1-x-yPb(I1-zBrz)3 (FAMACs).

Given prior discussion about the unique structural properties of ABX3 materials, we simply recall here that APbX3 perovskites adopt cubic/quasi-cubic structures at room temperature with corner sharing [PbI6]4− octahedra and with A+ cations (MA, FA, Cs) filling octahedral voids. Such structures satisfy the Goldschmidt tolerance factors required of ideal cubic structures (0.9 ≤ t ≤ 1.0) and for structures having tilted octahedra (0.7 < t < 0.9) [1]. The compositional diversity of mixed cation and mixed anion systems is limited by the existence of non-perovskite (δortho- and δhex- phases) phases that appear when A+ ionic radii are insufficient to stabilize interstitial voids in the structure [2, 3]. Although APbX3 perovskites can adopt other (e.g., orthorhombic) crystal structures at different temperatures [4], we focus on the photophysical properties of photovoltaically relevant cubic/pseudo-cubic structures in what follows.

The primary motivation for investigating and ultimately understanding the optical response of APbX3 perovskites stems from their successful implementation in high-efficiency photovoltaics. Today, perovskite solar cell power conversion efficiencies (PCEs) routinely exceed 20%. A maximum PCE of 25.7% has been reported in NREL’s benchmark efficiency chart [5] and will undoubtedly be supplanted shortly. These values collectively represent a remarkable rise of perovskite solar cell efficiencies given their modest starting value of 3.8% in 2009. In short, APbX3 perovskite solar cells are, from a PCE perspective, on par with crystalline silicon.

Responsible for this success are extraordinary and fortuitous perovskite properties. This entails facile solution processability, crystallinity despite low temperature processing, chemical and stoichiometric diversity, and large absorption efficiencies, all simultaneously coupled to low exciton binding energies, large carrier mobilities, and favorable energetics to engender defect tolerance. However, despite extensive research into improving perovskite solar cell PCEs, performance bottlenecks still remain. This prevents them from reaching their full Shockley-Queisser efficiency of ~31% for single-junction devices. A need therefore exists to fully understand the fundamental optical and electrical properties of APbX3 systems to realize their ultimate performance potentials.

2 Absorption

A key feature of lead halide perovskites is their favorable absorption properties. This includes sizable absorption coefficients (α), band edges close to the desired Shockley-Queisser value of 1.55 eV, and tunable absorption edges in mixed halide alloys. Figure 1a highlights these features by showing reported absorption spectra for common APbX3 systems.

Fig. 1
Two graphs of wavelength in nanometer and absorption spectrum versus energy in electron volts. The first graph depicts 7 lines including M A P b I 3, F A P b I 3, and C s P b I 3. The second graph depicts 5 lines of M A P b I 1 minus x B r x whole 3 for values from x equals 0 to x equals 1.

Summary of the absorption spectra of various APbX3 perovskites. Data extracted from References [6,7,8,9]. Spectral band edges highlighted using colored regions

Full size image

In the red, at approximately 1.6 eV lie MAPbI3, FAPbI3, and CsPbI3. Near 2.2 eV are MAPbBr3, FAPbBr3, and CsPbBr3. Further to the blue at ~3.1 eV is MAPbCl3. The figure makes apparent that perovskite band gaps are sensitive to the choice of halide anion, whether I−, Br−, or Cl−. This has previously suggested that the A-site cation plays a lesser role in determining the optical response of these materials. Instead, optical transitions are thought to be primarily established by perovskite’s inorganic [PbI6]4− framework [10,13,14,]. This is supported by electronic structure calculations, which suggest A-site cation-related states being energetically removed from corresponding band edges. Cation-influenced octahedral tilting and lattice contraction [11] do, however, influence band edge energies, as evidenced by measurements on mixed cation perovskites such as MA1-xFAxPbI3 or FA1-xCsxPbI3 where band gaps can be altered using cation stoichiometry [12,13,14,15].

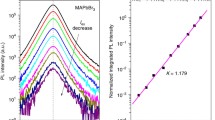
Figure 1b further illustrates the sensitivity of perovskite band gaps to halide stoichiometry by showing how increasing the Br fraction (x) in a MAPb(I1-xBrx)3 alloy causes its Eg to progressively shift towards the MAPbBr3 limit. Analogous trends are observed with MAPb(Cl1-xBrx)3 [16, 17] as well as with FAPb(I1-xBrx)3 [18]. The formation of continuous MAPb(I1-xClx)3 alloys is prevented by large differences in I− and Cl− ionic radii such that little if any Cl incorporation is achieved. Consequently, such systems are denoted MAPbI3(Cl) in what follows [19]. This ability to compositionally tune band gaps makes mixed halide alloys of potential use in tandem (perovskite/silicon) solar cells.

Figure 1 summarizes the absorption coefficients of these materials. Evident are sizable band edge values, which lie between 104 and 105 cm−1. These α-values correspond favorably to those of other photovoltaically relevant semiconductors. To illustrate, GaAs has an absorption coefficient of α ~ 104 cm−1 at its absorption edge. References [6, 20,21,22] highlight this favorable comparison by visually illustrating perovskite α-values relative to those of other semiconductors across a range of energies.

Table 1 summarizes compiled Eg and α-values for the various APbX3 perovskites being discussed. Apart from the general trends noted above, there is a sizable variability in reported values. MAPbI3 band gaps, for instance, range from 1.5 to 1.646 eV. This is also true of MAPbBr3 where Eg-values range from 2.24 to 2.392 eV. In either case, Eg spreads are of order 150 meV.

Table 1 Absorption parameters of various lead halide perovskites
Full size table

Associated absorption coefficients are also highly variable, as evident from tabulated α-values compiled at three different energies (2.0 eV, 2.3 eV, and 3.1 eV). In particular, Table 1 shows that MAPbI3 α-values at 2.0 eV range from 0.23 to 1.70 × 105 cm−1. At 2.3 eV, α-values range from 0.47 to 2.88 × 105 cm−1. Analogous variations exist with other perovskites. This variability and lack of accord are summarized visually in References [6, 36, 40, and 58].

Many reasons exist for apparent differences in reported optical parameters. Much has to do with variations in sample quality that stem from the numerous approaches used to prepare perovskite thin films. They include solution deposition (doctor blading, spray coating, slot-die coating, inkjet printing, etc.), solution deposition with solvent recrystallization (two-step spin-coating or antisolvent treatment), hot casting, chemical vapor deposition, and low-pressure vapor-assisted solution processing [73, 74]. Sample quality variability is especially highlighted when thin films are compared to APbX3 single crystals, which possess larger grains, reduced morphological disorder, and correspondingly reduced surface roughness [75].

Consequently, what results are thin film/single crystal specimens that possess varying degrees of crystallinity, thicknesses, apparent grain sizes, surface roughness, etc. All lead to measurement variations. Fujiwara [6], for example, attributes reported Eg and α-value variations to surface roughness that introduces significant light scattering to spectroscopic ellipsometry measurements. This degrades subsequent model extraction of perovskite optical constants (i.e., frequency-dependent refractive indices and permittivities) and leads to an underestimation of perovskite band gaps. When such surface roughness variations are explicitly accounted for, a closer agreement between researcher-reported α and Eg values is realized.

Beyond band gaps and absorption coefficients, Fig. 1 reveals other intriguing features of APbX3 materials. For MAPbI3, FAPbI3 and CsPbI3, band edges resemble those of bulk, direct gap semiconductors. No apparent excitonic features are seen. The absence of an excitonic response is corroborated by numerous estimates of their exciton binding energies (Eb), as summarized in Table 1. These estimates arise from magnetoabsorption and temperature-dependent emission and absorption measurements as well as from modeling experimental APbX3 band edge absorption spectra with Elliott’s model [76].

Table 1 shows a spread of reported Eb values. As with Eg and α, large variations can be seen where for MAPbI3 Eb ranges from 1.7 to 55 meV. Despite this, reported binding energies are of order kT and suggest that the optical response of MAPbI3 and FAPbI3 can be described in terms of free carriers. This conclusion is corroborated by time-resolved emission, transient differential absorption, and THz conductivity studies [76]. Note that this is not necessarily true of Br- and Cl-based APbX3 materials such as CsPbBr3 or MAPbCl3 where prominent band edge excitonic features are seen in the linear absorption. The suggestion is supported by their generally larger Eb-values in Table 1.

The specific origin of the optical transitions in lead halide perovskites has been the subject of numerous studies. Most entail density functional theory calculations to varying degrees of approximation [24, 36, 77]. Without delving into specifics, consensus exists that valence to conduction band transitions occurs at the R symmetry point and involves valence bands that originate from the antibonding combination of halide p and Pb(6s) orbitals. Corresponding conduction bands largely arise from Pb(6p) orbitals [77]. These bands are also responsible for above gap transitions and produce apparent structure at higher energies. For example, a feature in the absorption spectrum of MAPbI3 close to 2.5 eV (Fig. 1) is attributed to a valence/conduction band transition at the M symmetry point [24, 76, 77]. The antibonding nature of the APbX3 valence band is supported by apparent increases in perovskite band gap with increasing temperature. This contrasts itself to the response of traditional, tetrahedrally coordinated semiconductors where band gaps decrease (increase) with increasing (decreasing) temperature.

3 Carrier Dynamics

Having briefly summarized the general absorptive properties of APbX3 perovskites, we now provide insight into their carrier recombination processes, following photoexcitation. This is important since the fate of photogenerated carriers is fundamental to device operation and ultimately to their efficiencies. A kinetic model is therefore developed that qualitatively and quantitatively rationalizes the intrinsic photophysics of APbX3 systems [47, 78]. This includes experimental observations of photoluminescence, time-correlated emission decays, and transient differential absorption dynamics. In addition to numerical simulations, analytical approximations are provided to better visualize qualitative trends in both emission intensities and time-correlated decays. Although the model does not explicitly consider device operation, interested readers may refer to Reference [79] for an extension that includes charge extracting interfaces. Such a model has been used to establish the performance bottleneck(s) of a high-efficiency FAMACs solar cell.

In general, the primary recombination processes considered are (a) bimolecular (radiative) electron-hole recombination, (b) carrier trapping, and (c) nonradiative Auger recombination. The latter is nominally only important at high carrier densities, far beyond 1 sun conditions. These processes are summarized in Fig. 2 with the illustration showing photoexcitation creating transient electron and hole populations [n(t) and p(t)] in the perovskite conduction and valence bands. Carriers subsequently recombine via the three processes outlined above. Although the identity of APbX3 trap states remains debated, there appears to be some agreement that such states are electron traps. This is assumed in what follows. Note that other versions of this model exist, which account for exciton dissociation, unintentional doping, and carrier diffusion. The interested reader is therefore referred to References [80], [81], and [49] for details.

Fig. 2
A schematic of photophysical processes in lead halide perovskites. Two parallel horizontal lines n t and p t are given. G and k b are double-headed arrows between the two parallel lines. Two curved arrows that depict the excitation process, are labeled I e x c and I e m.

Schematic illustration of photophysical processes occurring in lead halide perovskites, following photoexcitation

Full size image

Kinetic expressions that summarize the model are

$$ {\displaystyle \begin{array}{c}\frac{dn}{dt}=G-{k}_t\left({N}_t-{n}_t\right)n-{k}_b np-\frac{1}{2}{k}_{\textrm{Auger}}\left[{n}^2p+n{p}^2\right]\\ {}\frac{dp}{dt}=G-{k}_h{n}_tp-{k}_b np-\frac{1}{2}{k}_{\textrm{Auger}}\left[{n}^2p+n{p}^2\right]\\ {}\frac{d{n}_t}{dt}={k}_t\left({N}_t-{n}_t\right)n-{k}_h{n}_tp\end{array}} $$
(1)

where G is the initial charge generation rate (cm−3 s−1), linked to the excitation intensity (Iexc, W cm−2), i.e., \( G=\frac{I_{\textrm{exc}}\alpha }{h\nu} \) with α the absorption coefficient (cm−1) and hν the photon energy (J), n (p) is the electron (hole) concentration (cm−3) in the perovskite conduction (valence) band, kt is an electron trapping rate constant (cm3 s−1), Nt is a corresponding trap density (cm−3), nt is the trap population (cm−3), kb is a bimolecular radiative recombination rate constant (cm3 s−1, referred to as k2 in the literature), and kAuger is the Auger, three-carrier rate constant (cm6 s−1, referred to as k3 in the literature).

Numerous studies now provided estimates for the various rate constants in Eq. (1) and Fig. 2. These literature estimates are summarized in Table 2 across various APbX3 systems. An inspection shows that most work has focused on MAPbI3 and MAPbI3(Cl) thin films with relatively less work carried out on corresponding FA-based materials.

Table 2 Literature rate constants for various lead halide perovskites
Full size table

Table 2 also makes apparent that while variations in rate constants exist across systems and even within a given material, there is general consistency in their values. Bimolecular radiative rate constants are of order 10−10 cm3 s−1, while Auger rate constants are of order 10−28 cm6 s−1 [85]. Measured pseudo-first-order rate constants for electron trapping are of order k1 ~ 107 s−1 from where corresponding kt values are of order kt ~ 10−10 cm3 s−1, provided estimated trap densities of order Nt ~ 10−16 cm−3.

The general photogenerated carrier dynamics, predicted by Eq. (1) at different excitation intensities, are now illustrated. Implicit to the discussion is continuous wave (CW) excitation. An identical analysis can be conducted assuming pulsed excitation. However, this is not pursued here since common applications of perovskite materials generally entail CW excitation conditions. Interested readers may refer to References [97] and [98] for details of a pulsed excitation analysis.

4 Low Excitation Intensities

At low excitation intensities, carrier trapping dominates radiative recombination. Low photogenerated carrier densities further mean that nonradiative Auger pathways can be ignored. Consequently, under the assumption that the material is intrinsic, Eq. (1) reduces to

$$ {\displaystyle \begin{array}{c}\frac{dn}{dt}\approx G-{k}_t{N}_tn\\ {}\frac{dp}{dt}\approx G-{k}_h{p}^2\end{array}} $$

The equations make apparent that at steady state \( n=\frac{G}{k_t{N}_t}\propto G \) and \( p=\sqrt{\frac{G}{k_h}}\propto \sqrt{G} \). Since the emission rate and corresponding intensity, Iem, are proportional to the product of n and p, Iem grows with increasing Iexc (G) in a power law fashion. Its growth exponent is ~3/2, i.e., \( {I}_{\textrm{em}}\propto {G}^{\frac{3}{2}} \).

Figure 3a illustrates this for the case where Nt = 1016 cm−3. Employed rate constants for the numerical simulation of Eq. (1) are kb = 10−10 cm3 s−1, kt = 10−9 cm3 s−1, kh = 10−11 cm3 s−1, and kAuger = 10−28 cm6 s−1. The model therefore reveals that Iem grows as G1.6 at low G where recombination is primarily trap-mediated (shaded red region). Figure 3b shows identical behavior for simulations where Nt has been varied between Nt = 1015 and 1018 cm−3. In all cases, fit-extracted growth exponents range from m = 1.5 to 1.6. Of note is the increasing range of G-values where m ~ 1.5. This is rationalized by delayed trap saturation due to larger Nt-values.

Fig. 3
Three graphs a, b, and c. Graph A plots I e m versus I e x c, and N equals 10 to the power 16 centimeter to the power minus 3. Graph B plots I e m versus G. Graph C is of M A P b I 3 and plots I e m in a u versus G. All the graphs follow an increase in trend.

(a) Iem versus G for Nt = 1016 cm−3. Dashed lines are linear fits to the data in a given growth regime (shaded regions). Fit-extracted growth exponents shown. G-values are linked to associated Iexc, assuming 405 nm excitation with α = 105 cm−1, for reference purposes. (b) Iem versus G for Nt varying between Nt = 1015–1018 cm−3. Dashed lines are linear fits in the trap-mediated recombination regime. Fit-extracted growth exponents shown. (c) Iem versus G data for a MAPbI3 single crystal and thin film. Data from Reference [78]. Dashed lines are fits to the data at smaller G with fit-extracted growth exponents shown

Full size image

Figure 3c shows experimental data for a MAPbI3 single crystal and thin film [78] that corroborate these model predictions. Acquired over ~3 orders of magnitude in G, the data reveal m ~ 1.5 power law growth exponents for either material, as established by fits to low G Iem-values (dashed lines with fit-extracted m-values shown). Differences in the range of Iem-values over which m ~ 1.5 qualitatively agree with Fig. 3b and suggest underlying Nt-value variations between MAPbI3 single crystals and thin films. Other data acquired on MAPbI3 and MAPbI3(Cl) over 8 orders of magnitude in G reveal identical m ~ 1.5 power law growth exponents at low G [47]. This further corroborates the analysis and conclusions drawn here. Note that under (low irradiance) pulsed excitation, analogous power law growth of the integrated emission intensity is predicted with an ideal model growth exponent of m = 2.0 [97, 98]. Such quadratic emission growth has previously been observed for MAPbI3 and MAPbI3(Cl) thin films [47].

Next, by assuming above-simplified kinetic expression for n and p, corresponding (normalized) photoluminescence decays take the form

$$ \textrm{PL}(t)=\frac{I_{\textrm{em}}(t)}{I_{\textrm{em},\max }}\approx \frac{e^{-{k}_t{N}_tt}}{1+{k}_h Gt}. $$
(2)

At small G or short times, the numerator in Eq. (2) dominates. Decays are therefore near exponential with an associated pseudo-first-order decay constant of ktNt~107 s−1 (Table 2). Figure 4a illustrates this for the model predicted decay when G = 1015 cm−3. An accompanying (superimposed) dotted line is Eq. (2). This qualitative prediction is supported by numerous studies, which report near exponential decays at low Iexc for various perovskite systems [80, 81, 84, 87, 99].

Fig. 4
Four graphs a, b, c, and d. Graph A plots P L in a u versus time in nanoseconds. Four lines of different G values are plotted. Graph B plots P L in a u versus time in nanoseconds. Five inclined lines of different G values are plotted. Graph C plots P L in a u versus time in nanoseconds. Four lines of different shapes of dots for different G values are plotted. Graph D plots 1 upon P L whole to the power 1 by 2 minus 1, versus time in nanoseconds. Two lines of different shapes dots are plotted

(a) Predicted PL decays from Eq. (1) for variable G between G = 1015 and 1023 cm−3. Superimposed over the data are analytical predictions from Eqs. (2)–(4) (dotted lines). (b) Predicted decays for G = 1015–7 × 1016 cm−3. (c) MAPbI3 PL decays from Reference [87]. (d) Large G MAPbI3 PL decays from Reference [87] replotted. Dashed lines are linear fits to the data

Full size image

5 Intermediate Excitation Intensities

As Iexc increases, progressive trap filling (nt → Nt) reduces the electron trapping rate such that n → p. This simplifies Eq. (1) and leads to the following effective rate expressions:

$$ {\displaystyle \begin{array}{c}\frac{dn}{dt}\approx G-{k}_b{n}^2\\ {}\frac{dp}{dt}\approx G-{k}_h{N}_tp-{k}_b{p}^2.\end{array}} $$

Invoking steady state conditions then means that \( n=\sqrt{\frac{G}{k_b}}\propto \sqrt{G} \) with \( p=\frac{-{k}_t{N}_t+\sqrt{{\left({k}_t{N}_t\right)}^2+4G}}{2}\propto \sqrt{G} \). The emission intensity therefore transitions to power law growth with a growth exponent of m ~ 1. Figure 3a illustrates this transition by showing a fit to the model data, highlighted in the shaded blue region. A fit-extracted power law growth exponent of m = 0.99 is found. Analogous behavior is observed in Fig. 3b when Nt is varied between 1015 and 1018 cm−3. In whole, the model data makes evident that increasing Nt extends the region of trap-mediated recombination (m ~ 1.5) to larger G-values before bimolecular (radiative) recombination (m ~ 1.0) dominates carrier dynamics following photoexcitation.

Using the above simplified rate expressions, associated (normalized) photoluminescence decays adopt the following bimolecular form:

$$ \textrm{PL}(t)=\frac{I_{\textrm{em}}(t)}{I_{\textrm{em},\max }}=\frac{1}{\left(1+{k}_b Gt\right)\left[1+\left({k}_t{N}_t+{k}_b Gt\right)\right]} $$
(3)

where Fig. 4a shows model-predicted decays for G = 1019 and G = 1022 cm−3 using the same parameters employed earlier at low Iexc. Analytical results from Eq. (3) are superimposed atop the model decays and are in excellent agreement. Model decays also highlight the transition in kinetic response in this Iexc regime. Figure 4b illustrates this for G-values between G = 1016 and 1017 cm−3 where for smaller G-values, near exponential behavior is seen. With increasing G, an apparent near exponential to bimolecular transition occurs. Such PL(t) transitions have previously been reported in the literature [80, 81, 87, 99] and an example from a MAPbI3 thin film is shown in Fig. 4c.

6 High Excitation Intensities

At sufficiently high excitation intensities, trap saturation causes bimolecular (radiative) recombination to dominate. In this limit, Eq. (1) effectively becomes

$$ {\displaystyle \begin{array}{c}\frac{dn}{dt}\approx G-{k}_b{n}^2\\ {}\frac{dp}{dt}\approx G-{k}_b{p}^2\end{array}} $$

so that \( n=p=\sqrt{\frac{G}{k_b}}\propto \sqrt{G} \). Iem thus continues to grow in a power law fashion with a growth exponent of m ~ 1. Figure 3 illustrates this for Nt = 1016 cm−3 (Fig. 3a) and across Nt-values between Nt = 1015 and 1018 cm−3 (Fig. 3b). It should be mentioned that a growth exponent of m ~ 1 is common to this intensity regime under pulsed excitation [47, 97, 98].

An associated (normalized) photoluminescence decay takes the bimolecular form

$$ \textrm{PL}(t)=\frac{I_{\textrm{em}}(t)}{I_{\textrm{em},\max }}\approx \frac{1}{{\left(1+{k}_b Gt\right)}^2}, $$
(4)

which is near identical to the expression derived earlier for intermediate excitation intensities (Eq. 3). Figure 4a plots a model-predicted decay for G = 1023 cm−3 with Eq. (4) superimposed. Again, there is excellent agreement with the analytical approximation.

Beyond bimolecular fits, predicted bimolecular decays can be confirmed visually by plotting \( \sqrt{\frac{I_{\textrm{em},\max }}{I_{\textrm{em}}(t)}}-1 \) versus time. In this case, linear behavior is expected [100]. Figure 4d illustrates this for the large G experimental data in Fig. 4c. Evident linear behavior is observed, as highlighted by dashed, linear fits.

Above this excitation regime, the onset of Auger-mediated nonradiative recombination causes emission efficiencies to decrease. This stems from competitive, nonradiative recombination of carriers. What results then is sublinear growth of Iem with an associated power law growth exponent m < 1. Figure 3a explicitly illustrates the onset of Auger recombination for Nt = 1016 cm−3 at high G where the simulated data shows m < 1. It can also be shown that in this regime, plotting \( \left[\frac{I_{\textrm{em},\max }}{I_{\textrm{em}}(t)}-1\right] \) versus time yields linear behavior [100].

7 Emission Quantum Yields

Equation (1) simultaneously allows internal emission quantum yields (QYs) to be estimated through the ratio of the bimolecular radiative recombination rate to the initial carrier generation rate, i.e.

$$ \textrm{QY}=\frac{k_b np}{G}. $$
(5)

The importance of this metric is that high emission efficiencies are requisite for optimizing APbX3 photovoltaic performance. More specifically, it is the associated external quantum efficiency (EQE, EQE = ηeQY where ηe is a photon extraction efficiency) that is fundamentally linked to the maximum open circuit voltage (and PCE) achievable in a solar cell [101]. The seemingly contradictory conclusion that arises then is that a good solar cell must also be a good light emitter [102].

Figure 5 shows model-predicted (internal) QYs plotted as functions of Nt when Nt is varied between 1015 cm−3 and 1018 cm−3. As with Figs. 3 and 4, employed rate constants have been kept constant at their nominal literature values of kb ~ 10−10 cm3 s−1, kt ~ 10−9 cm3 s−1, and kh ~ 10−11 cm3 s−1. Fig. 5 also provides model-predicted EQEs via \( \textrm{EQE}=\frac{\eta_e\left({k}_b np\right)}{G} \).

Fig. 5
Two graphs a and b. Graph A is of Q Y and I e x c versus G and B is of E Q E versus G. Graph A plots 4 different values of N t, and graph B plots 2 different values of N t.

(a) Predicted (internal) QYs for variable G between G = 1019–1027 cm−3 and Nt between 1015 and 1018 cm−3. For reference purposes, G-values are linked to associated Iexc assuming 405 nm excitation with α = 105 cm−1. (b) Experimental EQE estimates for a MAPbI3 single crystal and thin film. Data from Reference [78]. Fit extracted Nt-values shown

Full size image

The resulting figure illustrates several things. First, as discussed earlier, at low Iexc, trapping dominates carrier recombination. This leads to low QYs. Attesting to this are experimental perovskite, 1 sun EQEs in Table 3. Values for thin films, (surface) treated thin films, and devices are shown. Inspection of the data reveals that reported 1 sun EQEs are generally on the order of several percent with some notable exceptions. This is consistent with the lower QYs seen at low G in Fig. 5. Of note is that this bulk perovskite data contrasts itself to analogous results, summarized in Reference [115] for perovskite nanocrystals (NCs). In these materials, EQEs regularly approach or attain unity values.

Table 3 Literature APbX3 emission EQEs under effective 1 sun conditions. Additives shown in parenthesis: K = potassium, Rb = rubidium, TOPO = trioctylphosphine oxide, pyr = pyridine, TPPO = triphenylphosphine oxide, SPPO = 9,9-spirobifluoren-2-yl-diphenyl-phosphine oxide)
Full size table

Next, Table 3 shows that treating lead halide perovskite thin films with Lewis bases such as trioctylphosphine oxide (TOPO) or pyridine improves their EQEs. However, they only increase values to numbers of order 10%. This indicates that while defect passivation is possible, significant trap densities still remain. This is again unlike the case of perovskite NCs where effective surface passivation does appear possible and which leads to unity EQEs [116]. Finally, Table 3 shows that device EQEs are all suppressed from corresponding thin film or treated thin film values due to the inevitable competition for carriers by electron and hole extraction interfaces present in working devices.

Figure 5 shows that maximal QYs are achieved upon trap saturation at high excitation intensities. In the case where Nt = 1016 cm−3, near unity internal QYs are realized close to 1 sun conditions. The figure further shows that increasing Nt simply leads to progressively larger Iexc-values required to achieve peak QYs, which themselves become progressively smaller. In all cases, maximum QYs persist until a critical G beyond which the onset of Auger-mediated carrier recombination causes them to fall as discussed earlier.

This QY behavior has previously been modeled by reducing the kinetics in Eq. (1) to [85].

$$ \frac{dN}{dt}=G-\textrm{AN}-{\textrm{BN}}^2-{\textrm{CN}}^3. $$
(6)

In Eq. (6), N is an effective electron-hole density, A is a generic first-order rate constant that describes nonradiative, trap-mediated recombination of photogenerated carriers, B is a second-order (radiative) rate constant, and C is a third-order rate constant that accounts for nonradiative Auger recombination. The rate constants A, B, and C are effectively k1, kb, and kAuger in Table 2. A corresponding internal QY is then

$$ \textrm{QY}=\frac{{\textrm{BN}}^2}{\textrm{AN}+{\textrm{BN}}^2+{\textrm{CN}}^3}. $$
(7)

Equation (7) can be recast in terms of EQE via \( \textrm{EQE}=\frac{\eta_e{\textrm{BN}}^2}{\textrm{AN}+{\eta}_e{\textrm{BN}}^2+{\textrm{CN}}^3} \). In either case, a peak QY can be found by taking the derivative of QY (EQE) with respect to N to find a critical point (i.e., \( \frac{d\textrm{QY}}{dN}=\frac{d\textrm{EQE}}{dN}=0 \)) [85]. A resulting optimal carrier density (Nopt) is then

$$ {N}_{\textrm{opt}}=\sqrt{\frac{A}{C}}\sim \sqrt{\frac{k_1}{k_{\textrm{Auger}}}} $$
(8)

and is linked to a corresponding maximum internal QY of

$$ {\textrm{QY}}_{\textrm{max}}=\frac{1}{1+\frac{2\sqrt{AC}}{B}}\sim \frac{1}{1+\frac{2\sqrt{k_1{k}_{\textrm{Auger}}}}{k_2}} $$
(9)

with a corresponding maximum EQE of \( {\textrm{EQE}}_{\textrm{max}}=\frac{1}{1+\frac{2\sqrt{AC}}{\eta_eB}}\sim \frac{1}{1+\frac{2\sqrt{k_1{k}_{\textrm{Aug}}}}{\eta_e{k}_2}} \).

Equations (6) and (7) can be used to model experimental EQEs to extract relevant rate constants. They are, however, not predictive in that tabulated rate constants from Table 2 cannot be used to estimate QYs and EQE a priori. This is because Figs. 3–5 show that trap saturation occurs due to nt → Nt. Consequently, the pseudo-first-order trapping rate constant (here A) is Iexc-dependent. Immediate application of Eqs. (8) and (9) therefore leads to predicted Nopt and QYmax smaller than those revealed by full numerical simulations of Eq. (1) (Fig. 5).

Finally, beyond trap-mediated recombination, an important reason for small overall EQE values and for why EQEs are smaller than internal QYs is photon trapping within the perovskite. This originates from refractive index differences with the surrounding medium and is most prominent in APbX3 films and crystals where physical sizes approach the wavelength of light. This leads to estimated photon extraction efficiencies of ηe ~ 10% [104, 105]. Note that such trapping is not significant for NCs as they effectively behave as dipole emitters. This rationalizes why unity/near unity EQEs are readily seen with these materials [115].

8 Ion Migration

Finally, despite all of the notable properties of APbX3 materials, preventing their widespread commercialization is their well-known environmental sensitivities. Addressing this have been a number of studies [117, 118]. Less recognized but equally important are intrinsic instabilities linked to ion migration. Namely, both cations and anions in APbX3 materials are mobile with ion mobilities stemming from vacancy-mediated ion migration under bias or under illumination.

For cations, evidence for bias-induced A+ migration comes from observed device hysteresis thought to stem from cation accumulation at electrodes [119,120,121]. The phenomenon is better illustrated using more direct measurements such as time-of-flight secondary ion mass spectrometry and super-resolution infrared absorption measurements [122, 123], which explicitly reveal cation migration and accumulation near electrodes.

For anions, a well-known phenomenon is light-induced photosegregation whereby shining light on mixed I−/Br− systems [e.g., MAPb(I1-xBrx)3] induces halide segregation. This results in the formation of I-rich inclusions within parent, mixed halide perovskites. Such photoinduced halide segregation is experimentally observed as progressive photoluminescence redshifts due to photogenerated carriers being funneled to I-rich domains. Such domains act as emissive recombination centers because of favorable (valence) band offsets relative to those of parent mixed halide materials. Observed redshifts/photosegregation are reversible when specimens are no longer illuminated with remixing being entropically driven. References [4, 124, and 125] provide more details on the phenomenon.

At this point, an inevitable question that arises is the connection between the earlier photocarrier dynamics and the bias−/light-induced ion migration described here. Since ion migration, whether cation or anion, is thought to be vacancy-mediated and since point defects are likely responsible for carrier trapping, a connection between the two is suggested. Evidence for this can already be found in the literature where References [126, 127, and 128] already suggest that decreasing defect densities mitigates ion migration. Studies linking the two topics, however, are limited. Consequently, more work is required to establish a comprehensive picture of ion-inclusive carrier dynamics that follow photoexcitation of APbX3 systems. As such, linking the two sets the direction for future investigations of these unique materials.