Keywords

1 Introduction

The order penetration point defines the stage in the manufacturing value chain where a particular product is linked to a specific customer order through different product delivery strategies, such as make-to-stock, assemble-to-order, make-to-order and engineer-to-order [13]. In this paper, we study the case of an overproduction strategy for supplier to avoid shortage. During the order promising process, distributors normally make commitments with customers about the quantities and dates of orders. However, unexpected events may happen that could lead to a shortage supply. Researchers pointed out several causes of these unexpected events: (i) arrival of more priority customer orders that require already reserved products; (ii) delays in raw materials or components; (iii) machine breakdowns; (iv) workers absenteeism, among others [4]. These events might lead to the possibility of making partial or delayed deliveries, i.e., the shortage situation. In particular, cyclical industries face alternating periods of undersupply, when buyers know that a shortage is imminent and rationing will occur. Thus, suppliers can follow overproduction strategy to avoid partial, delayed and cancelled deliveries.

In practice, when supply delivery time increases, customers make multiple orders with the same supplier or with different suppliers. Such multiple orders may overload the capacity of a distribution network and increase lead-time. In the literature, there are studies of shortage gaming as a leading contributor to the bullwhip phenomenon [15]. Researchers considered shortage decision policies, investigated an integrated production and maintenance planning model with time windows and shortage costs [2, 11]. Machine learning techniques for reducing underproduction costs and overproduction costs were developed [6]. In this paper, we develop the distribution model that intends to minimize the costs of competing suppliers in case of an overproduction strategy. We show that the side effect of this strategy is the relocation of order deliveries in a distribution network. The basis of the model structure is a non-linear constrained optimization program.

Samuelson constructed the net social pay-off function and offered the first mathematical formulation of equilibrium commodity flow assignment problem in a network of finished goods in a form of constrained optimization program [16]. The supply-demand allocation pattern, which satisfies this program, is called equilibrium. Researchers generalized this model for the network of multi-commodity goods and, nowadays, this model is called spatial equilibrium model [18]. Worth mentioning that this model takes into account relationships between supply, demand and logistics costs. The study of general optimality conditions for this program is given in [5].

Today the problem of supply allocation in distribution networks is highly urgent. In particular, researchers discuss on implementation of this model when investigate actual transportation networks [19]. Some of them concentrate on spatial models under imperfect competition, others study integration of distribution networks under perfect competition [3, 9, 20]. On the one hand, the non-identity of equilibrium models for distribution networks and integrative models with non-zero commodity flow is pointed out [1, 12]. On the other hand, equilibrium spatial models demonstrate explainability and methodological potential for the analysis of commodity flows and pricing in logistic networks [7, 17].

Recently, the conditions on active flows in a network of homogeneous goods were obtained explicitly under linear mappings of elastic demand and supply [8]. However, when manufacturing faces such uncertainties as overproduction (shortage), supply (demand) can no longer consider elastic. In this paper, we study the reallocating supply problem that result from the order promising process under overproduction. We develop a competitive distribution model to facilitate decision-making for order managers and to provide an intelligent support tool. Section 2 contains the basis of the distribution model in a form of the non-linear constrained optimization program that intends to minimize the costs of competing actors suppliers and customers. In Sect. 3, we obtained explicit conditions for orders relocation under affine delivery costs. An explicit form of conditions on the current delivery pattern will allow one to develop intelligent tools for decision-making support in the field of order management. Section 4 discusses on strategies of suppliers under overproduction. Conclusions are given in the last section of the paper.

2 Equilibrium Flow Allocation in a Single-Commodity Network

Consider the set of suppliers M and the set of customers N, which are associated with commodity production, distribution, and consumption. We denote by \(s_i\) the supply of \(i \in M\), and by \(\lambda _i\) – the price of a unit of the ith supply, \(\lambda = (\lambda _1, \ldots , \lambda _m)^\textrm{T}\). By \(d_j\) we denote the demand of \(j \in N\), and by \(\mu _j\) – the price of a unit of the jth demand, \(\mu = (\mu _1, \ldots , \mu _n)^\textrm{T}\). Finally, let \(x_{ij} \ge 0\) be the commodity volume between a pair (i, j), while \(c_{ij} (x_{ij})\) is the delivery cost of a unit of \(x_{ij}\). Let us also introduce the indicator of delivery status:

$$\begin{aligned} \delta _{ij} = \left\{ \begin{array}{ll} 1 &{} \text{ for } x_{ij} > 0 ,\\ 0 &{} \text{ for } x_{ij} = 0 , \end{array} \right. \quad \forall (i,j) \in M \times N . \end{aligned}$$

Definition. The allocation pattern x is called equilibrium if

$$\begin{aligned} \begin{array}{ll} \lambda _i + c_{ij} (x_{ij}) = \mu _j &{} \text{ for } \quad x_{ij} > 0 , \\ \lambda _i + c_{ij} (x_{ij}) \ge \mu _j &{} \text{ for } \quad x_{ij} = 0 , \end{array} \quad \forall (i,j) \in M \times N . \end{aligned}$$

Thus, if the sum of the supplier’s price and the delivery costs for a customer exceeds his/her demand price, then the supplier will face with the cancelled delivery.

An equilibrium allocation pattern can be obtain as a solution of the following optimization problem [10, 14]:

$$\begin{aligned} \min _x \sum \limits _{i \in M} \sum \limits _{j \in N} \int \limits _0^{x_{ij}} c_{ij}(u)du \end{aligned}$$

subject to

$$\begin{aligned} \sum \limits _{j \in N} x_{ij} = s_i \quad \forall i \in M, \end{aligned}$$
$$\begin{aligned} \sum \limits _{i \in M} x_{ij} = d_j \quad \forall j \in N, \end{aligned}$$
$$\begin{aligned} x_{ij} \ge 0 \quad \forall i,j \in M \times N, \end{aligned}$$

under

$$\begin{aligned} \sum \limits _{i \in M} s_i = \sum \limits _{j \in N} d_j . \end{aligned}$$

In this paper, we develop a competitive distribution model based on the above non-linear constrained optimization program. We show that this model facilitates decision-making for order managers and provides an intelligent support tool. To this end, we obtain explicit conditions for orders relocation under affine delivery costs. Obtained supply relocation policy in a distribution network under overproduction is appeared to allow order manager relocate supply among customers in order to avoid cancelled deliveries. This relocation guarantees minimum costs for all customers caused by the unexpected shortage.

3 Competitive Supply Allocation in a Distribution Network Under Overproduction

Let us study a competitive supply allocation in a distribution network modelled by a single-commodity network with m suppliers and one customer (i.e., \(|M| = m\) and \(|N| = 1\)). We assume that available supply is more than the overall demand:

$$\begin{aligned} d < \sum \limits _{i \in M} s_i. \end{aligned}$$

In other words, a distributor faces competitive supply relocation in a distribution network under overproduction. Thus, we introduce \( \mathrm {\Delta } > 0\) as an overproduction value:

$$\begin{aligned} \sum \limits _{i \in M} s_i - d = \mathrm {\Delta }, \end{aligned}$$
(1)

while \(\epsilon _i \ge 0\) as the difference between i-th demand and its actual delivery volume, \(i, \; i \in M\), \( \epsilon = \left( \epsilon _1, \epsilon _2, \dots , \epsilon _m \right) \):

$$\begin{aligned} \sum \limits _{i \in M} \left( s_i - x_i \right) = \sum \limits _{i \in M} \epsilon _i = \mathrm {\Delta }. \end{aligned}$$
(2)

In terms of a single-commodity network, the allocation pattern \(x^*\), which satisfies the following optimization problem:

$$\begin{aligned} x^* = \textrm{arg} \min _x \sum \limits _{i \in M} \int \limits _0^{x_{i}} c_{i}(u) du , \end{aligned}$$
(3)

subject to

$$\begin{aligned} \begin{array}{c} \sum \limits _{i \in M} x_{i} = d,\\ x_i = s_i - \epsilon _i, \quad \forall i \in M, \\ x_{i} \ge 0, \quad \forall \; i \in M, \\ \epsilon _i \ge 0, \quad \forall i \in M, \\ \sum \limits _{i \in M} \epsilon _i = \mathrm {\Delta }. \\ \end{array} \end{aligned}$$
(4)

is the equilibrium deliveries allocation under overproduction.

Within the present paper, we examine equilibrium allocation in a case of affine delivery functions. In other words, we assume that

$$\begin{aligned} c_{i} (z) = c^0_{i} + k_{i} z, \quad c^0_{i} \ge 0, k_{i} > 0, \forall i \in M, \end{aligned}$$
(5)

i.e., delivery costs increase when the volume of the order increases.

Lemma 1

Equilibrium deliveries allocation of overproduction in problem (3)–(4) under affine delivery costs (5) is obtained be the following pattern:

$$\begin{aligned} x_{i} = \left\{ \begin{array}{ll} \frac{\mu - \lambda _i - c^0_{i}}{k_{i}}, &{} \text{ if } \mu - \lambda _i > c^0_{i},\\ 0, &{} \text{ if } \mu - \lambda _i \le c^0_{i}, \end{array} \right. \quad \forall i \in M, \end{aligned}$$
(6)

where \(\lambda \) and \(\mu \) satisfy

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum \limits _{i \in M} \frac{ \mu - \lambda _i - c^0_{i} }{ k_{i} } \delta _{i} = d, \\ \frac{ \mu - \lambda _i - c^0_{i} }{ k_{i} } \delta _{i} = s_i - \epsilon _i, \quad \forall i \in M \\ \sum \limits _{i \in M} \epsilon _i = \mathrm {\Delta } \\ \lambda _i = \eta , \quad \text {if } \epsilon _i > 0 \\ \lambda _i = \eta + \beta _i, \quad \text {if } \epsilon _i = 0 \\ \end{array}\right. } \end{aligned}$$
(7)

Proof

Since goal function (3) is convex as well as the restriction set (4), then Karush–Kuhn–Tucker (KKT) conditions are necessary and sufficient. Let us study the Lagrangian of problem (3)–(4):

$$\begin{aligned} L = \sum \limits _{i \in M} \int \limits _0^{x_{i}}( c^0_{i} + k_{i} u) du + \mu \left( d - \sum \limits _{i \in M} x_{i} \right) + \end{aligned}$$
$$\begin{aligned} + \sum \limits _{i \in M} \lambda _i \left( x_{i} - s_i + \epsilon _i \right) + \sum \limits _{i \in M} ( - \alpha _{i}x_{i}) + \end{aligned}$$
$$\begin{aligned} + \sum \limits _{i \in M} \left( - \beta _i \epsilon _i \right) + \eta \left( \mathrm {\Delta } - \sum \limits _{i \in M} \epsilon _i \right) . \end{aligned}$$

We differentiate this Lagrangian with respect to \(x_{i}\) and \(\epsilon _i\), \(i \in M\), and equate the results to zero:

$$\begin{aligned} \frac{\partial L}{\partial x_{i}} = c^0_{i} + k_{i} x_{i} - \mu + \lambda _i - \alpha _{i} = 0 \quad \forall i \in M, \end{aligned}$$
(8)
$$\begin{aligned} \frac{\partial L}{\partial \epsilon _i } = \lambda _i - \beta _{i} - \eta = 0 \quad \forall i \in M. \end{aligned}$$
(9)

According to complementary slackness,

$$\begin{aligned} -\alpha _{i} x_{i} = 0, \quad \forall i \in M, \end{aligned}$$
(10)
$$\begin{aligned} - \beta _i \epsilon _i = 0, \quad \forall i \in M. \end{aligned}$$
(11)

Using (10), due to (8) we obtain:

$$\begin{aligned} x_{i} = \left\{ \begin{array}{ll} \frac{ \mu - \lambda _i - c^0_{i} }{ k_{i} }, &{} \text { if } \mu - \lambda _i > c^0_{i}, \\ 0, &{} \text { if } \mu - \lambda _i \le c^0_{i}, \end{array} \right. \quad \forall i \in M, \end{aligned}$$

that leads to (6). Moreover, due to (9) and (11), we obtain:

$$\begin{aligned} \lambda _i = \left\{ \begin{array}{ll} \eta , &{} \text { if } \epsilon _i > 0, \\ \eta + \beta _i, &{} \text { if } \epsilon _i = 0, \end{array} \right. \quad \forall i \in M. \end{aligned}$$

However, since \( \sum \limits _{i \in M} x_{i} = d\) and \(x_{i} = s_i - \epsilon _i\), \(i \in M\), then:

$$\begin{aligned} \sum \limits _{i \in M} x_{i} \delta _{i} = d, \end{aligned}$$
(12)
$$\begin{aligned} x_{i} \delta _{i} = s_i - \epsilon _i \quad \forall i \in M. \end{aligned}$$
(13)

Therefore, taking into account \( \sum \limits _{i \in M} \epsilon _i = \mathrm {\Delta }\), when one substitutes the expression of \(x_{i}\), \(i \in M\), into (12)–(13), we obtain (7).    \(\square \)

Without loss of generality, we order suppliers as follows:

$$\begin{aligned} c^0_{1} + k_{1} s_1 \ge c^0_{2} + k_{2} s_2 \ge \dots \ge c^0_{m} + k_{m} s_m. \end{aligned}$$
(14)

Theorem 1

If there is \(\bar{m}\) such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum \limits _{i = 1}^{\bar{m}} \frac{ \left( c^0_{i} + k_{i} s_i \right) - \left( c^0_{\tau } + k_{\tau } s_{\tau } \right) }{k_{i}} < \mathrm {\Delta } , \quad \forall \tau = 1, \dots , \bar{m}, \\ \sum \limits _{i = 1}^{\bar{m}} \frac{ \left( c^0_{i} + k_{i} s_i \right) - \left( c^0_{\tau } + k_{\tau } s_{\tau } \right) }{k_{i}} \ge \mathrm {\Delta } , \quad \forall \tau = \bar{m}+1, \dots , m, \\ \end{array}\right. } \end{aligned}$$

then

$$\begin{aligned} x_{i} = \left\{ \begin{array}{cl} 0, &{} \text { if } c^0_{i} \ge \frac{\sum \limits _{l=1}^{\bar{m}} \frac{c^0_{l} + s_l k_{l}}{k_{l}} - \mathrm {\Delta }}{\sum \limits _{l=1}^{\bar{m}} \frac{1}{k_{l}}},\\ \\ \frac{ \sum \limits _{l=1}^{\bar{m}} s_l - \mathrm {\Delta } + \sum \limits _{l=1}^{\bar{m}} \frac{c^0_{l} - c^0_{i}}{k_{l}}}{k_{i} \sum \limits _{l=1}^{\bar{m}}\frac{1}{k_{l}}}, &{} \text { if } c^0_{i} < \frac{\sum \limits _{l=1}^{\bar{m}} \frac{c^0_{l} + s_l k_{l}}{k_{l}} - \mathrm {\Delta }}{\sum \limits _{l=1}^{\bar{m}} \frac{1}{k_{l}}} , \\ \end{array} \right. \quad \forall i = \overline{1, \bar{m}}, \end{aligned}$$

and \(x_{i} = s_i\) for all \(i = \overline{\bar{m}+1, m}\).

Proof

I. Let us introduce \(\bar{M} \subseteq M\) such that \(\epsilon _i > 0\) for all \(i \in \bar{M}\). We summarize equalities \(\frac{ \mu - \lambda _i - c^0_{i} }{ k_{i} } = s_i - \epsilon _i\), \(i \in M\), for all \(i \in \bar{M}\):

$$\begin{aligned} \sum \limits _{i \in \bar{M}} \frac{ \mu - \lambda _i - c^0_{i} }{ k_{i} } = \sum \limits _{i \in \bar{M}} s_i - \mathrm {\Delta }, \end{aligned}$$

due to \(\lambda _i = \eta \), for all \(i \in \bar{M}\), we obtain:

$$\begin{aligned} \sum \limits _{i \in \bar{M}} \frac{ \mu - \eta - c^0_{i} }{ k_{i} } = \sum \limits _{i \in \bar{M}} s_i - \mathrm {\Delta } \end{aligned}$$

or

$$\begin{aligned} \eta = \frac{ \sum \limits _{i \in \bar{M}} \frac{\mu - c^0_{i}}{k_{i}} - \sum \limits _{i \in \bar{M}} s_i + \mathrm {\Delta } }{\sum \limits _{i \in \bar{M}} \frac{1}{k_{i}}}. \end{aligned}$$
(15)

II. Since

$$\begin{aligned} \frac{ \mu - \lambda _i - c^0_{i} }{ k_{i} } = s_i, \quad \forall i \in M \backslash \bar{M}, \end{aligned}$$

or, in a matrix form,

$$\begin{aligned} \left( \begin{matrix} - \frac{1}{k_{i_1 }} &{} 0 &{} \dots &{} 0 \\ 0 &{} - \frac{1}{k_{ i_2 }} &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} - \frac{1}{k_{i_{\bar{m}} }} \\ \end{matrix} \right) \left( \begin{matrix} \lambda _{i_1} \\ \lambda _{i_2} \\ \vdots \\ \lambda _{i_{\bar{m}}} \end{matrix}\right) = \left( \begin{matrix} s_{i_1} - \frac{\mu - c^0_{i_1 }}{k_{i_1}} \\ s_{i_2} - \frac{\mu - c^0_{i_2 }}{k_{i_2}} \\ \vdots \\ s_{i_{\tilde{m}}} - \frac{\mu - c^0_{i_{\tilde{n}} }}{k_{i_{\bar{m}}}} \\ \end{matrix}\right) , \end{aligned}$$

then

$$\begin{aligned} \lambda _i = \mu - c^0_{i} - s_i k_{i}, \quad \forall i \in M \backslash \bar{M}. \end{aligned}$$
(16)

According to

$$\begin{aligned} \begin{array}{ll} \lambda _i = \eta , &{} \text { if } \epsilon _i > 0, \\ \lambda _i = \eta + \beta _i, &{} \text { if } \epsilon _i = 0, \\ \end{array} \quad \forall i \in M, \end{aligned}$$

that is

$$\begin{aligned} \begin{array}{ll} \lambda _i = \eta , &{} \quad \forall i \in \bar{M}, \\ \lambda _i = \eta + \beta _i, &{} \quad \forall i \in M \backslash \bar{M},\\ \end{array} \end{aligned}$$

one can see \(\lambda _i \ge \eta \), for all \(i \in M \backslash \bar{M}\). Thus, due to (15) and (16), we obtain:

$$\begin{aligned} \mu - c^0_{{\tau }} - s_{\tau } k_{{\tau }} \ge \frac{ \sum \limits _{i \in \bar{M}} \frac{\mu - c^0_{i}}{k_{i}} - \sum \limits _{i \in \bar{M}} s_i + \mathrm {\Delta } }{\sum \limits _{i \in \bar{M}} \frac{1}{k_{i}}} , \quad \forall \tau \in M \backslash \bar{M}, \end{aligned}$$

while, since \(\sum \limits _{i \in \bar{M}} \frac{1}{k_{i}} > 0\), then

$$\begin{aligned} \left( \mu - c^0_{{\tau }} - s_{\tau } k_{{\tau }} \right) \sum \limits _{i \in \bar{M}} \frac{1}{k_{i}} \ge \sum \limits _{i \in \bar{M}} \frac{\mu - c^0_{i}}{k_{i}} - \sum \limits _{i \in \bar{M}} s_i + \mathrm {\Delta } , \quad \forall \tau \in M \backslash \bar{M}, \end{aligned}$$

or

$$\begin{aligned} \sum \limits _{i \in \bar{M}} \frac{ \mu - c^0_{{\tau }} - s_{\tau } k_{{\tau }} }{k_{i}} \ge \sum \limits _{i \in \bar{M}} \frac{\mu - c^0_{i} - s_i k_i}{k_{i}} + \mathrm {\Delta } , \quad \forall \tau \in M \backslash \bar{M}, \end{aligned}$$

Eventually, we obtain:

$$\begin{aligned} \sum \limits _{i \in \bar{M}} \frac{ \left( c^0_{i} + k_{i} s_i \right) - \left( c^0_{\tau } + k_{ \tau } s_{\tau } \right) }{k_{i}} \ge \mathrm {\Delta } , \quad \forall \tau \in M \backslash \bar{M}. \end{aligned}$$
(17)

III. Since \(x_{\tau } < s_\tau \) for all \(\tau \in \bar{M}\), then for \(\tau \in \bar{M}\) either \( s_{\tau } > x_{\tau } = 0\) or \(s_{\tau }> x_{\tau }>0\). Thus, according to (6), we obtain

$$\begin{aligned} \begin{array}{ll} \lambda _{\tau } = \mu - c^0_{\tau } - k_{\tau } x_{\tau }, &{} \text { if } x_{\tau } > 0, \\ \lambda _{\tau } \ge \mu - c^0_{\tau }, &{} \text { if } x_{\tau } = 0, \end{array} \quad \forall \tau \in \bar{M}. \end{aligned}$$

Taking into account \(k_{\tau } s_{\tau } > 0\), for all \(\tau \in N\), we can re-write this system as follows:

$$\begin{aligned} \begin{array}{ll} \lambda _{\tau } = \mu - c^0_{\tau } - k_{\tau } x_{\tau }, &{} \text { if } x_{\tau }> 0, \\ \lambda _{\tau } > \mu - c^0_{\tau } - k_{\tau } s_{\tau }, &{} \text { if } x_{\tau } = 0, \end{array} \quad \forall \tau \in \bar{M}. \end{aligned}$$

Since \(\lambda _\tau = \eta \) and \(x_{\tau } < s_\tau \), for all \(\tau \in \bar{M}\), then

$$\begin{aligned} \eta > \mu - c^0_{\tau } - k_{\tau } s_{\tau } , \quad \forall \tau \in \bar{M}. \end{aligned}$$

Due to (15), we obtain:

$$\begin{aligned} \mu - c^0_{\tau } - k_{\tau } s_\tau < \frac{ \sum \limits _{i \in \bar{M}} \frac{\mu - c^0_{i}}{k_{i}} - \sum \limits _{i \in \bar{M}} s_i + \mathrm {\Delta } }{\sum \limits _{i \in \bar{M}} \frac{1}{k_{i}}} \quad \forall \tau \in \bar{M}, \end{aligned}$$

i.e.,

$$\begin{aligned} \sum \limits _{i \in \bar{M}} \frac{ \left( c^0_{i} + k_{i} s_i \right) - \left( c^0_{\tau } + k_{\tau } s_{\tau } \right) }{k_{i}} < \mathrm {\Delta } \quad \forall \tau \in \bar{M}. \end{aligned}$$
(18)

IV. If customers are ordered according to (14), then

$$\begin{aligned} \left( c^0_{i} + k_{i} s_i \right) - \left( c^0_{\tau } + k_{\tau } s_{\tau } \right) = t_{i}(s_i) - t_{\tau } (s_\tau ) {\left\{ \begin{array}{ll} \ge 0, \quad \text {if } i < \tau , \\ \le 0, \quad \text {if } i > \tau . \end{array}\right. } \end{aligned}$$

If \(\tau =1\), then

$$\begin{aligned} \frac{c_{i} (s_i) - c_{ 1} (s_{1})}{k_{i}} \le 0, \quad \forall i \in M. \end{aligned}$$

Since \(\mathrm {\Delta } > 0\), then \(\tau =1 \notin M \backslash \bar{M} \), i.e., \(\tau =1 \in \bar{M}\). If \(\tau =2\), then

$$\begin{aligned} {\left\{ \begin{array}{ll} c_{1} (s_1) - c_{2} (s_{2}) \ge 0 ,\\ c_{i} (s_i) - c_{2} (s_{2}) \le 0, \quad \forall j = 2, \dots , m. \end{array}\right. } \end{aligned}$$
(19)

Hence, either

$$\begin{aligned} \frac{c_{1} (s_1) - c_{2} (s_{2})}{k_{1}} \ge \mathrm {\Delta } \end{aligned}$$

or

$$\begin{aligned} \frac{c_{1} (s_1) - c_{2} (s_{2})}{k_{1}} < \mathrm {\Delta }. \end{aligned}$$

If \(\frac{c_{1} (s_1) - c_{2} (s_{2})}{k_{1}} \ge \mathrm {\Delta }\), then, due to (14),

$$\begin{aligned} \mathrm {\Delta } \le \frac{c_{1} (s_1) - c_{2} (s_{2})}{k_{1}} \le \frac{c_{1} (s_1) - c_{i} (s_{i})}{k_{1}}, \quad \forall j = 2, \dots , m. \end{aligned}$$

Thus, we obtain:

$$\begin{aligned} \bar{M} = \{ 1 \}, \quad M \backslash \bar{M} = \{2, \dots , n \}. \end{aligned}$$
(20)

However, if \(\frac{c_{1} (s_1) - c_{2} (s_{2})}{k_{1}} < \mathrm {\Delta }\), then, due to (19), \(\tau =2 \notin M \backslash \bar{M} \), i.e., \(\tau =2 \in \bar{M}\). Such a chain of reasoning leads to the existence of required \(\bar{m}, \; 1 \le \bar{m} \le n\).

V. Due to \(x_{i} = s_i - \epsilon _i\) and \(\epsilon _i = 0\) for all \(i = \overline{\bar{m}+1, m}\), then

$$\begin{aligned} x_{i} = s_i, \quad i = \overline{\bar{m}+1, m}. \end{aligned}$$

Moreover, due to (6) under \(\lambda _i = \eta \) for all \(i = \overline{1, \bar{m}}\), we have

$$\begin{aligned} x_{i} = \left\{ \begin{array}{cl} 0, &{} \text { if } c^0_{i} \ge \frac{\sum \limits _{l=1}^{\bar{m}} \frac{c^0_{i} + s_l k_{l}}{k_{l}} - \mathrm {\Delta }}{\sum \limits _{l=1}^{\bar{m}} \frac{1}{k_{l}}}\\ \\ \frac{\mu - \eta - c^0_{i}}{k_{i}}, &{} \text { if } c^0_{i} < \frac{\sum \limits _{l=1}^{\bar{m}} \frac{c^0_{l} + s_l k_{l}}{k_{l}} - \mathrm {\Delta }}{\sum \limits _{l=1}^{\bar{m}} \frac{1}{k_{l}}} \end{array} \right. \quad i = \overline{1, \bar{m}}, \end{aligned}$$

which is the required expression, due to (15).    \(\square \)

Theorem 1 gives the supply relocation policy in a distribution network under overproduction. In other words, the supply can be relocated among customers in such a way to avoid cancelled orders. This relocation guarantees minimum costs for all customers caused by the unexpected shortage.

4 Strategies of Suppliers Under Overproduction

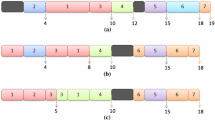
Let us consider the order management policy of suppliers in case of an overproduction strategy (Fig. 1).

Fig. 1.
figure 1

Order management: strategies of suppliers under overproduction

Full size image

Assume that the green supplier has four customers (Fig. 1a). We tend to study risks that can arise when the yellow supplier appears to offer its overproduction (Fig. 1b). One can see that customers 1, 2, and 3 are located quite close to the green supplier, while customers 2, 3, and 4 are located quite close to the yellow one. According to Theorem 1, if

$$\begin{aligned} c^0_{\tau } \ge \frac{\sum \limits _{l=1}^{\bar{m}} \frac{c^0_{l} + s_l k_{l}}{k_{l}} - \mathrm {\Delta }}{\sum \limits _{l=1}^{\bar{m}} \frac{1}{k_{l}}} , \end{aligned}$$
(21)

then the customer \(\tau \) can cancel order and change the supplier for the closer one. Moreover, according to Theorem 1, \(x_{i} = s_i\) for \(i = \overline{\bar{m}+1, m}\), while

$$\begin{aligned} c^0_{1} + k_{1} s_1 \ge c^0_{2} + k_{2} s_2 \ge \dots \ge c^0_{m} + k_{m} s_m, \end{aligned}$$
(22)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum \limits _{i = 1}^{\bar{m}} \frac{ \left( c^0_{i} + k_{i} s_i \right) - \left( c^0_{\tau } + k_{\tau } s_{\tau } \right) }{k_{i}} < \mathrm {\Delta } , \quad \forall \tau = 1, \dots , \bar{m}, \\ \sum \limits _{i = 1}^{\bar{m}} \frac{ \left( c^0_{i} + k_{i} s_i \right) - \left( c^0_{\tau } + k_{\tau } s_{\tau } \right) }{k_{i}} \ge \mathrm {\Delta } , \quad \forall \tau = \bar{m}+1, \dots , m. \\ \end{array}\right. } \end{aligned}$$
(23)
Table 1. Scenarios for decision-making support.
Full size table

In other words, a customer choose the closest suppliers with small orders rather than large order from distant supplier. Moreover, if

$$\begin{aligned} c^0_{i} < \frac{\sum \limits _{l=1}^{\bar{m}} \frac{c^0_{l} + s_l k_{l}}{k_{l}} - \mathrm {\Delta }}{\sum \limits _{l=1}^{\bar{m}} \frac{1}{k_{l}}} , \end{aligned}$$
(24)

then

$$\begin{aligned} x_{i} = \frac{ \sum \limits _{l=1}^{\bar{m}} s_l - \mathrm {\Delta } + \sum \limits _{l=1}^{\bar{m}} \frac{c^0_{l} - c^0_{i}}{k_{l}}}{k_{i} \sum \limits _{l=1}^{\bar{m}}\frac{1}{k_{l}}}, \end{aligned}$$
(25)

for all \(i = \overline{1, \bar{m}}\) from (23), where (25) is the value of a partially confirmed order. Hence, a supplier has the following set of risks (Table 1).

Therefore, if suppliers follow an overproduction strategy in order to avoid the shortage, they can face several risks raised as side effects of this strategy. The first risk is the cancelled order. In other words, if inequality (21) holds, the customer can cancel his/her order and choose another supplier. The second risk is partial order confirmation. Indeed, if inequality (24) holds, the customer can confirm the part of the order and choose another supplier for the rest.

5 Conclusion

The paper aimed to deal with the reallocating supply problem that result from the order promising process under overproduction. To this end, we developed a competitive distribution model to facilitate decision-making for order managers and to provide an intelligent support tool. The basis of the distribution model structure was a non-linear constrained optimization program that intends to minimize the costs of competing suppliers in case of an overproduction strategy. We obtained explicit conditions for orders relocation under affine delivery costs. An explicit form of conditions on the current delivery pattern will allow one to develop intelligent tools for decision-making support in the field of order management.