Robust Forecasting of Multiple Time Series with One-Sided Dynamic Principal Components

Abstract

Given a high-dimensional vector of time series, we define a class of robust forecasting procedures based on robust one-sided dynamic principal components. Peña et al. (J Am Stat Assoc 114(528):1683–1694, 2019) defined one-sided dynamic principal components as linear combinations of the present and past values of the series with optimal reconstruction properties. In order to make the estimation of these components robust to outliers, we propose here to compute the principal components by minimizing the sum of squares of the M-scales of the reconstruction errors of all the variables. The resulting robust components are called scale one-sided dynamic principal components (S-ODPC), and an alternating weighted least squares algorithm to compute them is presented. We prove that when both the number of series and the sample size tend to infinity, if the data follow a dynamic factor model, the mean of the squares of the M-scales of the reconstruction errors of the S-ODPC converges to the mean of the squares of the M-scales of the idiosyncratic terms, with rate $m^{1/2}$, where m is the number of dimensions. A Monte Carlo study shows that the S-ODPC introduced in this chapter can be successfully used for forecasting high-dimensional multiple time series, even in the presence of outlier observations.

1 Introduction

High-dimensional sets of correlated time series are nowadays automatically generated in many fields, from engineering to environmental science and economics. These large data sets are often collected by using wireless sensor networks that may fail to record the data correctly due to depletion of batteries or environmental influence. These failures will produce outliers in the time series recorded that can modify strongly the forecasting generated from these contaminated data. Thus, using robust forecasting procedures based on robust estimation methods, which can deal with large outliers, is very important in this high-dimensional data sets.

Robust estimation of multivariate data sets generated by vector autoregressive (VAR) models was studied by Muler and Yohai (2013). They generalized to the multivariate case the robust estimation procedure proposed by Muler et al. (2009) for ARMA univariate models. However, the multivariate approach requires the estimation of a VAR/VARMA model for the vector of time series, and for these models, the number of parameters grows at least with the square of the number of series, turning their estimation unfeasible for high-dimensional sets of time series. Therefore, other alternatives for robust estimation in these situations have been explored. Dynamic factor models have been shown useful to model high-dimensional sets of time series, and some procedures have been proposed for the robust estimation of these models, see Fan et al. (2019), Alonso et al. (2020), Fan et al. (2021), and Trucíos et al. (2021).

Peña and Yohai (2016), following Brillinger’s idea of dynamic principal components, see Brillinger (1964, 1981), proposed a new class of dynamic principal components that provide an optimal reconstruction of the observed set of series. These dynamic components are more general than those of Brillingers’s, as they are computed without the assumption of being linear combinations of the data. In Peña and Yohai (2016) was also developed a robust estimation procedure for these principal components. However, although they are useful for reconstruction of the set of time series, these components are not expected to work well in forecasting problems, as their last values will be computed with a smaller number of observations than the central ones.

In order to have dynamic components useful for forecasting, (Peña et al. 2019) proposed the one-sided dynamic principal components (ODPC) that are defined as linear combinations of the observations based on a one-sided filter of past and present observations, instead of the double filter of past and future values, as proposed by Brillinger (1964). See also Forni et al. (2015, 2017) for a related approach to build one-sided filters for dynamic factor models.

Since the estimation procedure applied in Peña et al. (2019) minimizes the mean square error of the series reconstruction, it can be very sensitive to outliers. To overcome this drawback, in this chapter, we introduce a robust ODPC procedure that is based on the minimization of the sum of squares of M-scales of the reconstruction error of all the variables. Thus, the resulting forecasting procedure can be applied to automatic forecasting of large high-dimensional data sets of time series. The M-scales introduced by Huber (1964) are robust estimators that measure how large in absolute value are the elements of a sample. These scales may have a 50 % breakdown point against outliers and inliers. Therefore, they protect for both types of anomalies. We call this procedure S-ODPC, and by means of a Monte Carlo procedure, we show that it produces accurate forecasts even with outlier contaminated data.

In Sect. 2 of this chapter, we review the one-sided dynamic principal components (ODPC) proposed by Peña et al. (2019). In Sect. 3, we introduce its robust version, the S-ODPC, and in Sect. 4, we describe an alternating weighted least squares to compute them. In Sect. 5, we discuss how to use the S-ODPC to forecast future values of a multiple time series. In Sect. 6, two possible robust strategies to determine the number of components and the number of lags to define each component and to reconstruct the time series are described. In Sect. 7, we show that asymptotically, when both the number of series and the sample size go to infinity, if the data follow a dynamic factor model, the reconstruction obtained with S-ODPC converges, in mean squared error, to the common part of a dynamic factor model. In Sects. 8 and 9, we illustrate with Monte Carlo simulations and with a real data example that in the presence of outliers the forecasting procedure based on S-ODPC performs much better than the one based on ODPC. Finally, Sect. 10 contains conclusions. An Appendix includes the mathematical proofs.

2 One-Sided Dynamic Principal Components

Consider a zero mean vector of stationary time series ${\mathbf {z}}_{1},\dots ,{\mathbf {z}}_{T}$, where ${\mathbf {z}}_{t}=(z_{t,1} ,\dots ,z_{t,m})^{\prime }$. Let $\mathbf {Z}$ be the data matrix of dimension $T\times m$ where each row is ${\mathbf {z}}_{t}^{\prime }$. We will use ${\mathbf E}$ for the expectation operator, for the Euclidean norm of vectors and the spectral norm of matrices and for the Frobenius norm of a matrix. Consider an integer number $k_{1}\geq 0$, and let $\mathbf {a}=({\mathbf {a}}_{0}^{\prime },\dots ,\mathbf {a} _{k_{1}}^{\prime })^{\prime }$, where ${\mathbf {a}}_{h}^{\prime }=(a_{h,1} ,\ldots ,a_{h,m})$ is a vector of dimension m. Following Peña et al. (2019), the scores of the first one-sided dynamic principal component are of the form

$$\displaystyle \begin{aligned} f_{t}(\mathbf{a)}=\sum_{h=0}^{k_{1}}{\mathbf{a}}_{h}^{\prime} {\mathbf{z}}_{t-h,}\quad t=k_{1}+1,\dots,T. {} \end{aligned} $$

(1)

This component, built with $k_{1}$ lags, is used to reconstruct each observation $z_{t,j}$ using $k_{2}\geq 0$ of its lags and the respective loading coefficients by

$$\displaystyle \begin{aligned} \widehat{z}_{t,j}(\mathbf{a},\mathbf{B)}=\varphi_{j}+\sum_{h=0}^{k_{2} }b_{j,h}f_{t-h}(\mathbf{a)}. {} \end{aligned} $$

(2)

Let $\mathbf {B}$ be the $m \times (k_{2}+2)$ loading matrix with row j equal to $(\varphi _{j},b_{j,0} ,\ldots ,b_{j,k_{2}})$. Then if

$$\displaystyle \begin{aligned} \widehat{\boldsymbol{z}}_{t}(\mathbf{a},\mathbf{B})=\widehat{z} _{t,1}(\mathbf{a},\mathbf{B),\ldots ,}\widehat{z}_{t,m}(\mathbf{a},\mathbf{B))} ^{\prime} \end{aligned}$$

and ${\mathbf {F}}_{t}(\mathbf {a}\boldsymbol {)}=(1,f_{t}(\mathbf {a),\ldots ,} f_{t-k_{2}}(\mathbf {a)),}$ (2) can be written as

$$\displaystyle \begin{aligned} \widehat{\mathbf{z}}_{t}(\mathbf{a},\mathbf{B)=BF}_{t}(\mathbf{a).} {}\end{aligned}$$

Note that we can consider the reconstruction (??) as the predictions of the common component in a dynamic factor model (DFM). This equation can be interpreted as the forecast of the common component of a DFM with one dynamic factor and $k_{2}$ lags. The loadings are given by the matrix $\mathbf {B}$. The dynamic factor is assumed to be a linear combination of the observations and their $k_{1}$ lags, defined by the $\mathbf {a}$ weights in (1).

We suppose here that $k_{1}$ and $k_{2}$ are given, and in Sect. 6, we will propose a method to choose them. We will call $T^{\ast }=T-(k_{1}+k_{2})$ to the number of observations that can be reconstructed. The population optimal values of $\mathbf {a}$ and $\mathbf {B}$ were defined by Peña et al. (2019) as those that minimize the mean squared error in the reconstruction of the data

Since if $(\mathbf {a},\mathbf {B)}$ is a solution of (2), then $(c\mathbf {a},\mathbf {B/}c\mathbf {),}$ for $c\neq 0$, will be one as well, we can normalize the vector $\mathbf {a}$, so that , although, as in standard principal components $\mathbf {-a}, \mathbf {-B}$ works as well as $\mathbf {a}, \mathbf {B}$. Given a sample, ${\mathbf {z}}_{1},\dots ,{\mathbf {z}}_{T}$, the estimators $\widehat {\mathbf {a}}$, and $\widehat {\mathbf {B}}$ of the optimal values $({\mathbf {a}}^{\ast },{\mathbf {B}}^{\ast }\mathbf {)}$ are defined as

(3)

and the estimated first dynamic principal component is given by

$$\displaystyle \begin{aligned} \widehat{f}_{t}=f_{t}(\widehat{\mathbf{a}}\mathbf{)=}\sum_{h=0}^{k_{1} }\widehat{\mathbf{a}}_{h}^{\prime}{\mathbf{z}}_{t-h},\ k_{1}+1\leq t\leq T, {} \end{aligned} $$

(4)

and $\widehat {\mathbf {z}}_{t}=\widehat {\mathbf {z}}_{t}(\widehat {\mathbf {a} },\widehat {\mathbf {B}})$ will provide an estimated optimal reconstruction of ${\mathbf {z}}_{t}$ using $k_{2}$ of its lags at periods t, $(k_{1} +k_{2})+1\leq t\leq T\$.

The second and higher orders of one-sided dynamic principal components are defined similarly. Let $k_{1} ^{(h)}$ and $k_{2}^{(h)}$ be the number of lags to define the h-th component, and suppose that we have already computed the first l principal components. Denote by ${\mathbf {r}}_{t}^{(l)},\max _{1\leq h\leq l}(k_{1} ^{(h)}+k_{2}^{(h)})+1\leq t\leq T$, the residual vector at time t using the first l components. Then, the $(l+1)$ one-sided dynamic estimated component is a vector with components of the form

$$\displaystyle \begin{aligned} f_{t}(\mathbf{a})=\ {\mathbf{a}}_{0}^{\prime}{\mathbf{z}}_{t}+\mathbf{a} _{1}^{\prime}{\mathbf{z}}_{t-1}+\ldots +{\mathbf{a}}_{k_{1}^{(l+1)}}^{\prime} {\mathbf{z}}_{t-k_{1}^{(l+1)}}, \max_{1\leq h\leq l+1}(k_{1}^{(h)} +k_{2}^{(h)})+1\leq t\leq T, {}\end{aligned} $$

(5)

where the vector $\mathbf {a}=({\mathbf {a}}_{0},{\mathbf {a}}_{1},\ldots ,\mathbf {a} _{k_{1}})$ is chosen so that it optimizes the reconstruction of ${\mathbf {r}}_{t}^{(l)},\max _{1\leq h\leq l+1}(k_{1}^{(h)}+k_{2}^{(h)})+1\leq t\leq T$. More precisely, consider reconstructions of ${\mathbf {r}}_{t}^{(l)}\$ of the form $\widehat {\mathbf {r}}_{t}^{(l)}(\mathbf {a},\mathbf {B)=BF} _{t}(\mathbf {a}),$ where $\mathbf {B}$ is a $m\times (k_{2}^{(l)}+2)\$ matrix, and then the $(l+1)$-th principal component has values $f_{t}(\widehat {\mathbf {a} }^{(l+1)}\mathbf {),}$ where $\widehat {\mathbf {a}}^{(l+1)}$ is defined so that there exists a ${ m}{ \times }$$(k_{2} ^{(l+1)}+2)\$ matrix $\widehat {\mathbf {B}}^{(l+1)}$ such that

More technical details can be found in Peña et al. (2019).

We will consider here only the estimating equations of the first component, and therefore, we will drop the superscript $(l)$. The estimating equations of higher order principal components can be found in Peña et al. (2019). Let ${\mathbf {Z}}_{h\ }$ be the $T^{\ast }\times m$ data matrix of $T^{\ast }$ consecutive observations

$$\displaystyle \begin{aligned} {\mathbf{Z}}_{h}= \begin{pmatrix} {\mathbf{z}}_{h+1}^{\prime}\\ {\mathbf{z}}_{h+2}^{\prime}\\ \vdots\\ {\mathbf{z}}_{h+T^{\ast}}^{\prime}, \end{pmatrix} \end{aligned} $$

(6)

and we will consider this matrix for $h\ =0,\dots ,(k_{1}+k_{2})$. Merging these matrices, we can write in a compact way the data used in the estimation. Note that the matrix ${\mathbf {Z}}_{k_{1}+k_{2}}$ includes all the values of the series to be reconstructed.

Second, we will consider the larger matrix ${\mathbf {Z}}_{l,k_{1} }=\left [ {\mathbf {Z}}_{h},{\mathbf {Z}}_{h-1},\ldots ,{\mathbf {Z}}_{h-k_{1}}\right ]$ of dimension $T^{\ast }\times m(k_{1}+1)$ that includes the observations and also their $k_{1}$ lags required for the computation of the first component. The matrix of values of the components used for the reconstruction is the $T^{\ast }\times (k_{2}+2)$ matrix ${\mathbf {F}}_{k_{1},k_{2}}(\mathbf {a)},$ which has as rows ${\mathbf {F}}_{t}(\widehat {\mathbf {a}}\mathbf {)},$$k_{1}+k_{2}+1\leq t\leq T$, and the reconstruction of the values ${\mathbf {Z}}_{k_{1}+k_{2}}$ is made with the $T^{\ast }\times m$ matrix $\widehat {\mathbf {Z}}_{k_{1}+k_{2}}$ computed as

$$\displaystyle \begin{aligned} \widehat{\mathbf{Z}}_{k_{1}+k_{2}}={\mathbf{F}}_{k_{1},k_{2}} (\widehat{\mathbf{a}}\mathbf{)}\widehat{\mathbf{B}}^{\prime}\mathbf{.} \end{aligned}$$

Third, let ${\mathbf {Z}}^{B}$ be the matrix with dimensions $T^{\ast } (k_{1}+1)\times m(k_{1}+1)$ given by

$$\displaystyle \begin{aligned} {\mathbf{Z}}^{B}=\left( \begin{array} [c]{c} {\mathbf{Z}}_{k_{1}+k_{2},k_{1}}\\ \vdots\\ {\mathbf{Z}}_{k_{1},k_{1}} \end{array} \right), {} \end{aligned} $$

(7)

${\mathbf {B}}_{1}$ the matrix $\mathbf {B}$ with its first column deleted and ${\mathbf {I}}_{d}$ the $d\times d$ identity matrix. Define the matrix of products of loadings and data values by

$$\displaystyle \begin{aligned} \mathbf{X(B)}=({\mathbf{B}}_{1}\otimes{\mathbf{I}}_{T^{\ast}}){\mathbf{Z}}^{B} {} \end{aligned} $$

(8)

as a $mT^{\ast }\times m(k_{1}+1)\$matrix with rank $m(k_{1}+1).$ Then, in Peña et al. (2019), it is shown that $(\widehat {\mathbf {a}},\widehat {\mathbf {B}})$ are values $(\mathbf {a,B)}$ satisfying

$$\displaystyle \begin{aligned} \mathbf{a}=\mathbf{(X(B)}^{\prime}\mathbf{X(B))}^{-1}\mathbf{X(B)}^{\prime }vec({\mathbf{Z}}_{k_{1}+k_{2}}), {} \end{aligned} $$

(9)

and this vector is standardized to unit norm. On the other hand, $\widehat {\mathbf {B}}$ can also be computed by least squares by

$$\displaystyle \begin{aligned} {\mathbf{B}}^{\prime}=({\mathbf{F}}_{k_{1},k_{2}}^{\prime}(\mathbf{a)F} _{k_{1},k_{2}}(\mathbf{a}))^{-1}{\mathbf{F}}_{k_{1},k_{2}}^{{}^{\prime} }(\mathbf{a}){\mathbf{Z}}_{k_{1}+k_{2}}. {} \end{aligned} $$

(10)

An alternating least squares algorithm to compute $(\widehat {\mathbf {a}},\widehat {\mathbf {B}})$ can be carried out as follows. Given an initial value of $\widehat {\mathbf {a}}$, the matrix of values of the component ${\mathbf {F}}_{k_{1},k_{2}}(\mathbf {a)}$ is computed by (9), and the matrix $\widehat {\mathbf {B}}$ is obtained by (10). Then, this matrix allows to compute a new value of $\widehat {\mathbf {a}}$, by first applying (8) and then using (9). This alternating process is continued until convergence. A similar algorithm can be applied to obtain the i-th component for $i>1.$

3 Robust One-Sided Dynamic Principal Components

Since the ODPC estimator described in Sect. 2 is based on the minimization of the reconstruction mean square error, this estimator is very sensitive to the presence of outliers in the sample. To address this problem, we are going to propose a class of robust one-sided principal components that will be called S-ODPC and that are based on a M-scale.

Given a random variable ${ x}$, the M-scale $S_{M}(x)$ is defined by

$$\displaystyle \begin{aligned} {\mathbf E}\left( \rho\left( \frac{x_{{}}}{S_{M}(x\mathbf{)}}\right) \right) =b, \end{aligned}$$

where $\rho$: $\mathbb {R}\rightarrow \mathbb {R}^{+}$ and $\rho$ and b satisfy: (a) $\rho (0)=0,$ (b) $\rho (-x)=\rho (x)$, (c) $\rho (x)$ is non-decreasing for $x\geq 0$, (d) $\lim _{x\rightarrow \infty }\rho (x)=1$, and (e) $0<b<1.$ The scale $S_{M}(\mathbf {x)}$ is a measure of how large are the values that x takes. Note that if $\rho (x)=x^{2}$ and $\ b=1,$ then $S_{M}(\mathbf {x)}$ is the $L_{2}$-scale given by $S_{M}^{2}(\mathbf {x)} ={\mathbf E}(x^{2}).$

Given a sample $\mathbf {x}=(x_{1},x_{2},\ldots x_{n})$ of ${ x, S_{M}(x)}$ may be estimated by $s_{M}(\mathbf {x)}$ satisfying

$$\displaystyle \begin{aligned} \frac{1}{n}\sum_{i=1}^{n}\rho\left( \frac{x_{i}}{s_{M}(\mathbf{x)}}\right) =b. \end{aligned} $$

(11)

Generally, it is required that $E_{\varPhi }(\rho (x))=b,$ where $\varPhi$ is the standard normal distribution. This condition implies that if ${\mathbf {x}}_{\mathbf {n}}$ is a sample of size n of a N(0,$\sigma ^2$) distribution, then $\lim _{n\rightarrow \infty }s_{M}({\mathbf {x}}_n)=\sigma ^2.$

A family of $\rho$ functions satisfying these properties is the Tukey biweight family defined by

$$\displaystyle \begin{aligned} \rho_{{c}}^{BS}(x)=\left[ 1-\left( 1-\left( \frac{x}{c}\right) ^{2}\right) ^{3}\right] I(|x|\leq c) . \end{aligned}$$

The breakdown point of a M-scale is $\varepsilon ^{\ast }=\min (b .1-b)$ and is maximized when $\delta =0.5$, and in this case, $\varepsilon ^{\ast }=0.5.$ The consistency condition $E_{\varPhi }(\rho _{{c}}^{BS}(x))=0.5$ is satisfied when $c=1.547.$ This is the function used in the simulations in Sect. 8 and in the example in Sect. 9.

The M-scales have been used to define robust estimators for many statistical problems. We will mention here two classes of estimators based on a M-scale: S-estimators for regression (see Rousseeuw and Yohai 1984) and S-estimators of the scatter matrix and multivariate location (see Davies 1987).

When the first component is used to reconstruct the series, the reconstruction error of the variable j at the period t is given by

$$\displaystyle \begin{aligned} r_{t,j}(\mathbf{a,B})=z_{t,j}-\widehat{z}_{t,j}^{{}}(\mathbf{a},\mathbf{B} ),\ k_{1}+k_{2}+1\leq t\leq T. {} \end{aligned} $$

(12)

The first population S-ODPC is defined by the values ${\mathbf {a}}_{S}^{\ast }$, ${\mathbf {B}}_{S}^{\ast }$ given by

where

$$\displaystyle \begin{aligned} \mathcal{K}_{M}(\mathbf{a,B})=\sum_{j=1}^{m}S_{M}^{2}(r_{t,j}(\mathbf{a,B})). \end{aligned}$$

Given a sample ${\mathbf {z}}_{t},1\leq t\leq T,$$\left ( {\mathbf {a}}_{S}^{\ast },{\mathbf {B}}_{S}^{\ast }\right )$ can be estimated by

where

$$\displaystyle \begin{aligned} k_{M}(\mathbf{a,B})=\sum_{j=1}^{m}s_{M}^{2}({\mathbf{r}}_{.j}(\mathbf{a,B})) \end{aligned}$$

and ${\mathbf {r}}_{.j}(\mathbf {a,B})=(r_{t,j}(\mathbf {a,}B))_{k_{1}+k_{2}+1\leq t\leq T}.$

Remark 1

Observe that if the performance of the principal components is measured by the sum of the squares of the M-scales of the empirical reconstruction residuals, then the S-ODPC defined above is still optimal when dealing with nonstationary series. Therefore, it may be used for forecasting even in this case.

In the Appendix, we prove that differentiating $S(\mathbf {a,B} ),$$\widehat {\mathbf {a}}$ and $\widehat {\mathbf {B}}$ satisfy expressions similar to (9) and (10), respectively. In fact, it can be shown that $\widehat {\mathbf {a}}_{S}$ and $\widehat {\mathbf {B}}_{S}$ are values $\mathbf {a}$ and $\mathbf {B}$ satisfying the following weighted least squares relationships:

$$\displaystyle \begin{aligned} \ {\mathbf{a}}^{*}=\mathbf{(X}(\mathbf{B)}^{\prime}\mathbf{W(a,B)X(B))} ^{-1}\mathbf{X(B)}^{\prime}\mathbf{W(a,B)}vec({\mathbf{Z}}_{k_{1}+k_{2} }), \end{aligned}$$

$$\displaystyle \begin{aligned} \widehat{\mathbf{a}}={\mathbf{a}}^{\ast}/\left\vert |{\mathbf{a}}^{\ast }\mathbf{|}\right\vert, {} \end{aligned} $$

(13)

where $\mathbf {W}$ is a $mT^{\ast }\times mT^{\ast }$ diagonal matrix of weights. On the other hand, fixing ${\mathbf {F}}_{k_{1},k_{2}}$$(\mathbf {a)}$, the optimal $\mathbf {B}$ also satisfies a weighted least squares expression. Then, ${\mathbf {B}}^{\prime }\mathbf {=(b}_{1},\ldots ,{\mathbf {b}}_{m}),\$where

$$\displaystyle \begin{aligned} {\mathbf{b}}_{j}=({\mathbf{F}}_{k_{1},k_{2}}^{{}}(\mathbf{a)}^{\prime} {\mathbf{W}}_{j}(\mathbf{a,B)F}_{k_{1},k_{2}}(\mathbf{a}))^{-1}\mathbf{F} _{k_{1},k_{2}}^{{}}(\mathbf{a)}^{\prime}{\mathbf{W}}_{j}(\mathbf{a,B)z} _{j\ }^{\ast}, {} \end{aligned} $$

(14)

where ${\mathbf {z}}_{j}^{\ast \ }$ is the j-th column of $\mathbf {Z} _{k_{1}+k_{2}}$ and ${\mathbf {W}}_{j}$ is a $T^{\ast }\times T^{\ast }$ matrix of weights. The matrices ${\mathbf {W}}_{j},\ 1\leq j\leq m$, are defined as follows: let $\psi (u)=\rho ^{\prime }(u)$ and $w(u)=\psi (u)/u$ if $u\neq 0$ and $w(0)=\lim _{u\rightarrow 0}w(u)$. Given $\mathbf {a}$ and $\mathbf {B}$, let $\sigma _{j}(\mathbf {a,B})=s_{M}^{{}}({\mathbf {r}}_{.j}(\mathbf {a},\mathbf {B}))$ and ${\mathbf {w}}_{j}(\mathbf {a,B)}=\ (w_{t,j}(\mathbf {a,B}))_{k_{1}+k_{2}+1\leq t\leq T}$, $1\leq j\leq$$m,$ where

$$\displaystyle \begin{aligned} w_{t,j}(\mathbf{a,B})=\frac{w(r_{t,j}(\mathbf{a,B})/\sigma_{j}(\mathbf{a,B} ))}{\frac{1}{T^{\ast}}\sum_{k=k_{1}+k_{2+1}}^{T}w(r_{k,j}(\mathbf{a,B} )/\sigma_{j}(\mathbf{a,B}))}. {} \end{aligned} $$

(15)

Then, ${\mathbf {W}}_{j}(\mathbf {a,B})$ and $\mathbf {W(a,b)}$ have as diagonals ${\mathbf {w}}_{j}(\mathbf {a,B})^{{ }^{\prime }}$ and $\mathbf {w}(\mathbf {a,B} )= ({\mathbf {w}}_{1}(\mathbf {a,B})_{{}}^{\prime },\ldots ,{\mathbf {w}}_{m}(\mathbf {a,B} )^{\prime })^{\prime }$, respectively. These weights penalize outliers reducing or removing their influence on the estimators.

Observe that ${\mathbf {w}}_{j}$, $\mathbf {W,F}_{k_{1},k_{2}}$, and $\mathbf {X}$ depend on $\mathbf {a}$ and $\mathbf {B}$, and therefore, Eqs. (13) and (14) cannot be used to directly compute them. In the next section, we propose an alternating weighted least squares algorithm that overcomes this problem.

The second and higher order S-ODPC can be defined in a similar way as that in the non-robust ODPC.

4 Computing Algorithm for the S-ODPC

We propose here an alternating weighted least squares algorithm for computing the first S-ODPC. Let ${\mathbf {a}}^{(i)}$, ${\mathbf {B}}^{(i)}$, and ${\mathbf {f}}^{(i)}$ be the values of $\mathbf {a}$, $\mathbf {B}$, and $\mathbf {f=(}f_{k_{1}+1,}\ldots ,f_{T})^{{ }^{\prime }}$ corresponding to the i-th iteration and $\delta \in (0,1)$, a tolerance parameter to stop the iterations. In order to define the algorithm, it is enough to give: (1) initial values ${\mathbf {a}}^{(0)}$ and ${\mathbf {B}}^{(0)},$ (2) a rule that given the values of the i-th iteration ${\mathbf {a}}^{(i)}$ and ${\mathbf {B}}^{(i)},$$1\leq j\leq m$, establishes how to compute ${\mathbf {a}}^{(i+1)}$ and ${\mathbf {B}}^{(i+1)},1\leq j\leq m$, and (3) a stopping rule. Then, the iterated algorithm is as follows:

• 1. To obtain the initial values, we first compute a standard (non- dynamic) robust principal component ${\mathbf {f}}^{(0)}=(f_{t}^{(0)})_{1\leq t\leq T}$, for example using the proposal of Maronna (2005). Then, we take ${\mathbf {B}}^{(0)}=({\mathbf {b}}_{1}^{(0)},\ldots , {\mathbf {b}}_{m}^{(0)})$, where ${\mathbf {b}}_{j}^{(0)},1\leq j\leq m$, is an S-regression estimator (see Rousseeuw and Yohai 1984) using as dependent variable ${\mathbf {z}}_{j,k_{1}+k_{2}}^{{}}=(z_{k_{1}+k_{2} +1,j},\ldots ,z_{T,j})$ and as matrix of independent variables $\mathbf {F} _{k_{1},k_{2}}^{(0)}$ with rows ${\mathbf {F}}_{t}^{(0)}=(1,f_{t}^{(0)} ,f_{t-1}^{(0)},\ldots ,f_{t-k_{2}}^{(0)}),$$k_{1}+k_{2}+1\leq t\leq T.$ Once obtained ${\mathbf {B}}^{(0)},$ we compute the matrix of residuals $\mathbf {R} ={\mathbf {Z}}_{k_{1}+k_{2}}-{\mathbf {F}}_{k_{1},k_{2}}^{(0)}{\mathbf {B}}^{(0)\prime }.$ This matrix is used to define the weights $w_{t,j}^{\ }$ as in (15) and the diagonal matrix ${\mathbf {W}}^{(0)}.$ We compute ${\mathbf {a}}^{(0)}$$={\mathbf {a}}^{\ast }/||{\mathbf {a}}^{\ast }||,$ where

  $$\displaystyle \begin{aligned} {\mathbf{a}}^{\ast}=\mathbf{(X(B}^{(0)})^{\prime}{\mathbf{W}}^{(0)}\mathbf{X(B} ^{(0)}\mathbf{)}^{-1}\mathbf{X(B}^{(0)})^{\prime}{\mathbf{W}}^{(0)} vec({\mathbf{Z}}_{k_{1}+k_{2}}) \end{aligned}$$

  and $\mathbf {X}(\mathbf {B})$ is defined as in (8).

• 2. Given ${\mathbf {a}}^{(i)}$ and ${\mathbf {B}}^{(i)}$, we compute the reconstruction residuals matrix $\mathbf {R}=\mathbf {Z} _{k_{1}+k_{2}}-{\mathbf {F}}_{k_{1},k_{2}}^{(i)}$${\mathbf {B}}^{(i)\prime }$ and the corresponding new M- scales $\sigma _{j}^{(i)},1\leq j\leq m$. Using these residuals and scales, we obtain new weights $w_{t,j}({\mathbf {a}}^{(i)}\mathbf {,B}^{(i)}),k_{1}+k_{2}+1\leq t\leq T,$ and the corresponding diagonal matrices ${\mathbf {W}}_{j}(\mathbf {a} ^{(i)}\mathbf {,B}^{(i)}),$$1\leq j\leq m$ and $\mathbf {W}(\mathbf {a} ^{(i)}\mathbf {,B}^{(i)})\mathbf {.}$ Then ${\mathbf {B}}^{(i+1)}=(\mathbf {b} _{1}^{(i+1)},\ldots ,{\mathbf {b}}_{m}^{(i+1)})$ is defined by (14) with $\mathbf {a=a}^{(i)}$. To compute ${\mathbf {a}}^{(i+1)}$, we use (13) with $\mathbf {B=B}^{(i+1)}.$

• 3. The stopping rule is as follows: stop when

  $$\displaystyle \begin{aligned} \frac{ S({\mathbf{a}}^{(i)},{\mathbf{B}}^{(i)})-S(\mathbf{a} ^{(i+1)},{\mathbf{B}}^{(i+1)}) }{S({\mathbf{a}}^{(i)},\mathbf{B} ^{(i)})}\leq\delta. \end{aligned}$$

As in Salibian-Barrera and Yohai (2006), it can be shown at each step the MSE decreases, and therefore, it converges to a local minimum. To obtain a global minimum, the initial value ${\mathbf {f}}^{(0)}$ should be close enough to the optimal one.

Note that, since the matrix $\mathbf {X(B)}=({\mathbf {B}}_{1} \otimes {\mathbf {I}}_{T^{\ast }}){\mathbf {Z}}^{B}$ has dimensions $mT^{\ast }\times m(k_{1}+1)$, solving the associated least squares problem can be time- consuming for high-dimensional (large m) problems. The iterative nature of the algorithm we propose implies that this least squares problem will have to be solved several times for different $\mathbf {B}$ matrices. However, as the matrix ${\mathbf {B}}^{\prime }\otimes {\mathbf {I}}_{T^{\ast }}$ is sparse, it can be stored efficiently, and multiplying it with a vector is relatively fast. We found that for problems with a moderately large m, the following modification of our algorithm works generally faster: instead of finding the optimal ${\mathbf {a}}^{(i+1)}$ corresponding to ${\mathbf {B}}^{(i+1)}$, just do one iteration of coordinate descent for ${\mathbf {a}}^{(i+1)}.$

5 Forecasting Using the S-ODPC

Suppose that we have computed estimators of $\ Q$ robust dynamic principal components and that the lags used for the q component were $(k_{1}^{(q)},k_{2}^{(q)})$. Let $\widehat {\mathbf {f}}^{(q)}=(\widehat {f}_{t}^{(q)})_{k_{1}^{(q)}+1\leq t\leq T},$$1\leq q\leq Q,$ be the estimated S-ODPC’s and $\widehat {\mathbf {B} }^{q}$ the estimated reconstruction matrices. We will show now how we can predict the values of ${\mathbf {z}}_{T+1},\ldots ,{\mathbf {z}}_{T+h}$ for some $h\geq 1.$ For that purpose, fit a time series model for each component $\widehat {\mathbf {f}}^{(q)},$$1\leq q\leq Q$ (e.g., an ARMA model), using a robust procedure, and with this model, obtain predictions $\ \widetilde {f} _{T+l}^{(q)}$ of $\ f_{T+l}^{(q)}$$,$$1\leq q\leq Q,$$1\leq l\leq h.$ We fit in the simulations AR models for each component, and these models were estimated using the filtered $\tau$-estimation procedure described in Chapter 8 of Maronna et al. (2019). This procedure selects automatically the order of the AR model, gives robust estimators of its coefficients, and provides a filtered series $\widetilde {\mathbf {f}}^{(q)}=(\widetilde {f}_{t} ^{(i)})_{k_{1}^{(q)}+1\leq t\leq T},1\leq q\leq Q$ cleaned of the detected outliers. With the help of these filtered series, we can obtain robust predictions as follows. Let $\widetilde {\mathbf {F}}_{T+l}^{(q)}=(1,$$\widetilde {f}_{T+l}^{(q)},$$\widetilde {f}_{T+l-1}^{(q)},\ldots ,$$\widetilde {f} _{T+l-k_{2}^{q}}^{(q)})^{\prime };$ then a robust prediction ${\mathbf {z}}_{T+l}$ given the first T observations is

$$\displaystyle \begin{aligned} \widehat{\mathbf{z}}_{T+l|T}=\sum_{q=1}^{Q}\widehat{\mathbf{B}}^{(q)} \widetilde{\mathbf{F}}_{t+l}^{(q)},1\leq l\leq h. \end{aligned}$$

The filtered $\tau$-estimation procedure is implemented in the function arima.rob of the R package robarima.

6 Selecting the Number of Lags and the Number of Components

An important problem is the selection of the number of dynamics components Q to use for prediction, and the number of lags $k_{1}^{(q)}$ and $k_{2}^{(q)} ,1\leq q\leq Q$, required to define each component. In order to simplify the presentation, we will assume that $k_{1}^{(q)}=k_{2}^{(q)} =k^{(q)}$. We can use two possible methods to select these values: (a) an information criterion and (b) cross-validation. Simulations performed for the ODPC in Peña et al. (2019) show that both procedures have similar efficiencies; However, (a) is much faster than (b). For that reason, we propose to use (a). In what follows, we describe implementations of both procedures.

6.1 Selection Using an Information Criterion

In Peña et al. (2019), an adaptation of the Bai and Ng (2002) criterion for factor model was used to choose $k^{(q)}$ and Q for ODPC. Here, we modify this procedure for its use in S-ODPC. We should start given a maximum value K for $k^{(q)}.$ We compute the first S-ODPC with $k^{(q)}=k$ for all values of k such that $0\leq k\leq K.$ For each of these values of k, we compute the residuals $(r_{t,j}^{(1,k)})_{2k+1\leq t\leq T,}1\leq j\leq m$ and compute the M-scale S$_{M}({\mathbf {r}}_{.j}^{(1,k)})$ of each vector ${\mathbf {r}}_{.j} ^{(1,k)}=(r_{2k+1,j}^{(1,k)},\ldots ,r_{T,j}^{(1,k)}),1\leq j\leq m.$ Let $\widehat {\sigma }_{1,k}=((1/m)\sum _{j=1}^{m}$S$_{M}({\mathbf {r}}_{.j} ^{(1,k)}))^{1/2}.$ Let $T_{1,k}^{\ast }=T-2k;$ then we choose as $k^{(1)}$ the value of k among $0,\ldots ,K$ that minimizes

$$\displaystyle \begin{aligned} \text{BNG}_{1,k}=\log(\widehat{\sigma}_{1,k)}^{2})+(k+1)\frac{\log (\min(T_{1,k}^{\ast},m))}{\min(T_{1,k}^{\ast},m)}. \end{aligned}$$

Suppose we have already computed $q-1$ dynamic principal components, where the component i uses $k^{(i)}$ lags. Then we compute the $\ q$ component with i lags for each $0\leq i\leq K$ and the corresponding residuals matrix $(r_{t,j}^{(q,k)})_{h_{q,k}+1\leq t\leq T,1\leq j\leq m}$, where $h_{q,k}=2\left ( k+\sum _{i=1}^{q-1}k^{(i)}\right ).$ Let $T_{q,k}^{\ast }=T-h_{q,k},$${\mathbf {r}}_{.j}^{(q,k)}=(r_{h_{q,k}+1,j} ^{(q,k)},\ldots ,r_{T,j}^{(q,k)})$ and $\widehat {\sigma }_{q,k}=((1/m)\sum _{j=1}^{m}$S$_{M}({\mathbf {r}}_{.j}^{(q,k)}))^{1/2}$; then the value of $k^{(q)}$ is the value of $k,0\leq k\leq K$, which minimize the following robustification of the Bai and Ng criterion

$$\displaystyle \begin{aligned} \text{BNG}_{q,k}=\log(\widehat{\sigma}_{q,k)}^{2})+(\sum_{i=1}^{q-1} ((k^{(i)}+1)+k+1)\frac{\log(\min(T_{q,k}^{\ast},m))}{\min(T_{q,k}^{\ast},m)} .\end{aligned}$$

The selected number of components is Q$=q-1$, where q is the minimum value q such that BNG$_{q,k^{(q)}}^{{}}\geq$ BNG$_{q,k^{(q-1)} }^{{}}.$

6.2 Selection Using Robust Cross-validation

Suppose that we are interested in using the S-ODPC to predict ${\mathbf {z}}_{T+1},\ldots ,{\mathbf {z}}_{T+h}$$.$ We can apply the following robust cross-validation procedure for selecting the number of components, Q, and $k^{(q)},1\leq q\leq Q$, the number of lags used for each component$.$ Suppose that the first ${ T}_{1}<T$ observations are chosen as the training set, and the last ${ T-T}_{{ 1}}$ observations as testing set. Then the training set will be used to compute all the loading vectors ${\mathbf {a}}^{(q,k)}$ for the q component with k lags and the testing set to evaluate the prediction power of any choice of the number of lags $k^{(q)}$ for each component q and the number of components $Q.$

The cross-validation procedure starts choosing $k_{1}$ as follows. For $0\leq d\leq T-T_{1}-i$, ${ 1} { \leq j\leq m,}$$1\leq i\leq h$ and $k\geq 0,$ let $\widehat {z}_{T_{1}+d+i,j|T_{1}+d}^{(1,k)}\$ be the prediction of $z_{T_{1}+d+i,j}$ using the first component with k lags and loading vector ${\mathbf {a}}^{(1,k)}$ corresponding to the periods $t\leq T_{1}+d$, and let $\widehat {r} _{T_{1}+d+i,j|T_{1}+d}^{(1,k)}=$$\widehat {z}_{T_{1}+d+i,j|T_{1}+d} ^{(1,k)}-z_{T_{1}+d+i,j}$ the corresponding prediction error. We evaluate the quality of the predictions up to h periods ahead using the first component with k lags by

$$\displaystyle \begin{aligned} SS_{k}^{(1)}=\sum_{j=1}^{m}\sum_{i=1}^{h}S_{\text{M}}(\widehat{\mathbf{r}} _{.j}^{(1,k,i)}), {} \end{aligned} $$

(16)

where $\widehat {\mathbf {r}}_{.j}^{(1,k,i)}=(\widehat {r} _{T_{1}+i,j|T_{1}}^{(1,k)},\ldots ,\widehat {r}_{T,j|T-i}^{(1,k)})$ is the vector of all the i periods ahead predictions$.$ We select as $k^{(1)}$ the first k, such that ${ SS}$$_{k} ^{(1)}\leq SS_{k+1}^{(1)}.$ Suppose now that we have already computed $q-1$ components with lags $k^{(1)},\ldots ,k^{(q-1)}$. To obtain $k^{(q)},$ we proceed as when computing $k^{(1)},$ that is, for each k, we compute

$$\displaystyle \begin{aligned} SS_{k}^{(q)}=\sum_{j=1}^{m}\sum_{i=1}^{h}S_{\text{M}}(\widehat{\mathbf{r}} _{.j}^{(q,k,i)}), {} \end{aligned} $$

(17)

where $\widehat {\mathbf {r}}_{.j}^{(q,k,i)}=$$({ \widehat {r}_{T_{1}+i,j|T_{1}}^{(q,k)}} ,\ldots ,{ \widehat {r}_{T-h+i,j|T-h}^{(q,k)}}),$$\widehat {r}_{T_{1}+d+i,j|T_{1}+d}^{(q,k)}=$$\widehat {z} _{T_{1}+d+i,j|T_{1}+d}^{(q,k)}-z_{T_{1}+d+i,j}$, and $\widehat {z} _{T_{1}+d+i,j|T_{1}+d}^{(q,k)}$ is the prediction of $z_{T_{1}+d+i,j}^{{}}$ assuming that ${\mathbf {z}}_{1},\ldots ,{\mathbf {z}}_{T_{1}+d}$ are known, using the first $q-1$ components with lags $k^{(1)},\ldots ,k^{(q-1)}$ and the q component with k lags. The number of lags $k^{(q)}$ for the q component is defined as the first value of $k,\$ such that ${ SS}_{k}\leq SS_{k+1}$. Similarly, the number of components Q is chosen as the first q such that $SS_{k^{(q)}}^{q}\leq SS_{k^{(q+1)}}^{q+1}.$ The robustness of this procedures follows from the fact that all the options selected by the procedure are evaluated using a robust scale, see (16) and (17). The procedure to make the forecasting is described in Sect. 5. The case where $k_{1}$ may be different of $k_{2}$ can be treated similarly but with more computational effort.

The forecasting of a particular time series can be improved if we add a specific or idiosyncratic component that explains the residuals of the series. For that purpose, we may fit for each variable an ARMA model for the respective S-ODPC reconstruction residuals.

7 Asymptotic Behavior of the S-ODPC in Factor Models

Let $z_{t,j}^{(m)},1\leq j\leq m,m>1$, be observations generated by a dynamic one-factor model with k lags, that is, they satisfy

$$\displaystyle \begin{aligned} z_{t,j}^{(m)}=\varphi_{j}^{(m)}+c_{j,0}^{(m)}f_{t}+\ldots +c_{j,k}^{(m)} f_{t-k}+u_{\substack{t,j} },1\leq j\leq m, {} \end{aligned} $$

(18)

where $f_{t}$ and $\ u_{t,j}$, $1\leq j\leq m$, are independent stationary process. We also have $\ {\mathbf E}(u_{t,j})={\mathbf E}(f_{t})=0$, var$(f_{t})=\tau ^{2}$, and var $(u_{t,j})=\sigma _{j}^{2}.\$

In this section, we study the behavior of the first population S-ODPC when $m$ tends to infinite. This is stated more precisely in Theorem 1, which is the analogous of Theorem 3 of Peña et al. (2019), but using S-ODPC instead of ODPC. Consider the following Assumptions:

• A1. There exist $\varepsilon >0$ and $A_{1}$ such that $\ 0<\varepsilon <\sigma _{j}^{2}<A_{1}<\infty$ for all $j.$

• A2. Let $\ s_{j}=S_{M}(u_{tj});$ then

  $$\displaystyle \begin{aligned} 0<s_{j}\leq A_{2}. \end{aligned} $$

  (19)

• A3. The function $\rho$ has a derivative $\psi$ that is continuous and bounded. Then $A_{3}=\sup \psi <\infty .$

• A4. $A_{4}=\inf _{j}{\mathbf E}(u_{t,j}\psi (u_{t,j}))>0$.

• A5. There exists C such that $\ \ \ \ \sup _{m}\sup _{1\leq j\leq m,0\leq i\leq k}|c_{j,i}^{(m)}|\leq C$ and $\sup _{m}\sup _{1\leq j\leq m}|\varphi _{j}^{(m)}|\leq C.$

• A6. Let ${\mathbf {c}}_{i}^{(m)}=(c_{1,i}^{(m)},....,c_{m,i}^{(m)}),0\leq i\leq k,$ and $E^{(m)}$ the subspace of $\mathbb {R}^{m}$ generated by $\ {\mathbf {c}}_{i}^{(m)},1\leq i\leq m.$ Then, we can write $\ \mathbf {c} _{0}^{(m)}={\mathbf {d}}^{(m)}+{\mathbf {e}}^{(m)},$where ${\mathbf {d}}^{(m)}$ is orthogonal to $E^{(m)}$ and ${\mathbf {e}}^{(m)}\in E^{(m)}.$ Then, there exists $\delta$ such that $||{\mathbf {d}}^{(m)}||{ }^{2}\geq m\delta$ for all $m.$ This condition implies that the common part of ${\mathbf {z}}_{t^{{}} }^{(m)}=(z_{t,1}^{(m)},\ldots ,z_{t,m}^{(m)})$ does not get close to the $k-1$- dimensional subspace $E^{(m)}$ when m increases.

Theorem 1

Assume A1–A6. Let${\mathbf {z}}_{t}^{(m)}=(z_{t,1}^{(m)} ,\ldots ,z_{t,m}^{(m)})$generated as the dynamic one-factor model given in (18) and${\mathbf {z}}_{t}^{(m){\ast }}=(z_{t,1}^{(m){\ast }},\ldots ,z_{t,m}^{(m){\ast }})$its population optimal reconstruction using the first S-ODPC with$k_{1}$equal to any nonnegative integer and$k_{2}$equal to$k,$the number of lags of the factor model. Then, there exists a constant K independent of m such that

$$\displaystyle \begin{aligned} \frac{1}{m^{1/2}}\left( \sum_{j=1}^{m}S_{M}^{2}(z_{t,j}^{(m)}-z_{t,j} ^{\ast(m)})^{2}-\sum_{j=1}^{m}S_{M}^{2}(u_{t,j})\right)\leq K. \end{aligned} $$

(20)

Remark 2

This theorem can be generalized to a model with k factors, if the first k S-ODPC are defined simultaneously instead of sequentially so that they minimize the sum of the squares of the population M-scales. The proof is similar to the case of one factor.

8 Simulation Results

We generate matrices $(z_{t,j})$ of $T=$102 observations and $m=50$ time series using the following dynamic factor model:

$$\displaystyle \begin{aligned} z_{t,j}=d_{j,1}f_{t}+d_{j},_{2}f_{t-1}+d_{j,3}f_{t-2}+0.2u_{t,j},1\leq t\leq 102,1\leq j\leq 50, \end{aligned}$$

where $u_{t,j}$ are i.i.d. $N(0,1)$ and $f_{t}$ follows the autoregressive model

$$\displaystyle \begin{aligned} f_{t}=0.85f_{t-1}+v_{t} \end{aligned}$$

and $v_{t}$ are i.i.d. $N(0,1)$. The coefficients $d_{j,i}$ are generated in each replication as i.i.d. with uniform distribution in $[0,1]$.

The first 100 observations are used to obtain the one-sided dynamic components (ODPC and S-ODPC), and the last two to evaluate the prediction performance of these methods.

These values $z_{t,j}$ are contaminated as follows: for $t=kT/H$, $k=1,2,\ldots ,H-1,$ the values of the observed series are

$$\displaystyle \begin{aligned} z_{t,j}^{\ast}=z_{t,j}+K. \end{aligned}$$

Three values of H are considered, 0, 5, and 10, that is, 0%, 4%, and 9% of outliers, respectively, and the values of K are $3, 5, 10$, and 15.

The number of replications is 500. For each case, we compute the first ODPC and the first S-ODPC with $k_{1}=1$ and $k_{2}=2$. The performance of both procedures for predicting the values of the series one and two periods ahead is evaluated by the sum of squares of the M-scales of the respective prediction error. Let $s_{M,j}$, $1\leq j\leq 50$, be the M-scale of the prediction errors of the j-th variable. Then the performance of each procedure is evaluated by

$$\displaystyle \begin{aligned} \sum_{j=1}^{50}s_{M,j}^{2}. \end{aligned}$$

The results are shown in Table 1.

Table 1 Sum of the squares of the M-scales of the prediction errors. Pr1 and Pr2 stand for one and two steps ahead, respectively

We observe that under outlier contamination the forecasting error using the S-ODPC is much smaller than that using ODPC.

9 Example with a Real Data Set

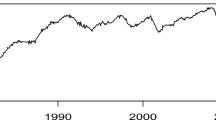
We consider a multiple time series $z_{t,j},1\leq t\leq 678,1\leq j\leq 24,$ the electricity price in the Connecticut region, New England, during the Thursdays of 676 weeks for each of the 24 hours of the day. Then we have 24 series of 676 observations. The data can be obtained at www.iso-ne.com and were previously considered for clustering time series by Alonso and Peña (2019).

Figure 1 shows plots of 12 of these 24 series. The series appear to be highly correlated, and therefore, dimension reduction is expected to be useful. We observe that at every hour of the day there are outliers especially between the weeks 500 and 600, and therefore, a robust procedure seems to be appropriate for these data.

Fig. 1

Electricity data

For each $d, 1\leq d\leq 177,$ we apply the ODPC and S-ODPC procedures to the set $z_{t,j}$, $1\leq t\leq 500+d$, and predict the values of $z_{500+d+1,j}$, $1\leq j\leq 24.$

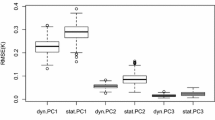
Figure 2 shows that in general the M-scales of the prediction errors of the S-ODPC are smaller than those of the ODPC specially between 10 am and 8 pm.

Fig. 2

M-scales of the one step ahead prediction errors

As indicated by one of the referees, the large values around weeks 500 and 600 may be due to some interesting facts that, if considered, can provide important insights in the data analysis. We have not investigated this important issue for a rigorous analysis of these data, as our objective here is to illustrate the performance of our robust procedure. Also, the plot of the series suggests that they are not stationary. However, as is mentioned in Remark 1, the S-ODPC may be a useful tool to predict future values of the series even in this case.

10 Conclusions

Given a vector series ${\mathbf {z}}_{t}$, $\leq t\leq T$, we have introduced the S one-sided dynamic principal components (S-ODPC) $f_{t},k_{1}+1\leq t\leq$$T,$ defined as a linear combination of ${\mathbf {z}}_{t},\mathbf {z} _{t-1}\ldots {\mathbf {z}}_{t-k_{1}}$ that have the following properties:

• It allows the reconstruction $\widehat {\mathbf {z}}_{t}\$ of the series ${\mathbf {z}}_{t}$ for $k_{1}+k_{2}-1\leq t\leq T$ as a linear combination of $f_{t},\ldots f_{t-k_{2}}.$

• It allows the forecasting of ${\mathbf {z}}_{T+h}.$

• The reconstruction of the series and the forecasting of future values of ${\mathbf {z}}_{t}$ can be improved taking higher order components.

• The values of $k_{1},k_{2}$ and the number of components q can be chosen by: (a) a robust version of the Bai and Ng (2002) criterion for factor models or (b) cross-validation.

• The procedure S-ODPC is robust, that is, it can be applied successfully even in the presence of outliers.

Appendix

1.1 Derivation of the Estimating Equations

Call $\boldsymbol {\theta }=(\mathbf {a},\mathbf {B});$ then the value of $\boldsymbol {\theta }$ for the S-ODPC estimator is obtained minimizing

$$\displaystyle \begin{aligned} k_{M}(\boldsymbol{\theta})=\sum_{j=1}^{m}s_{M}^{2}({\mathbf{r}}_{.j} (\boldsymbol{\theta} )), {} \end{aligned} $$

(21)

where ${\mathbf {r}}_{.j}(\boldsymbol {\theta })=(r_{k_{1}+k_{2}+1,j} (\boldsymbol {\theta } ),\ldots ,r_{T,j}(\boldsymbol {\theta })),$$r_{t,j} (\boldsymbol {\theta })=z_{t,j}-\widehat {z}_{t,j}(\boldsymbol {\theta })$ satisfies

$$\displaystyle \begin{aligned} \frac{1}{T^{\ast}}\sum_{t=k_{1}+k_{2}+1}^{T}\rho\left( \frac{r_{t,j} (\boldsymbol{\theta})}{s_{M}({\mathbf{r}}_{.j}(\boldsymbol{\theta}))}\right) =b, {}\end{aligned} $$

(22)

with $T^{\ast }=T-k_{1}-k_{2}.$ Differentiating (21), we get that the optimal $\boldsymbol {\theta }$ for the S-ODPC satisfies

$$\displaystyle \begin{aligned} \sum_{j=1}^{m}s_{M}({\mathbf{r}}_{.j}(\boldsymbol{\theta}))\frac{\partial s_{M}({\mathbf{r}}_{.j}(\boldsymbol{\theta}))}{\partial\boldsymbol{\theta}}=0. {} \end{aligned} $$

(23)

Let us differentiate (22). We have

$$\displaystyle \begin{aligned} \sum_{t=k_{1}+k_{2}+1}^{T}\psi\left( \frac{r_{t,j}(\boldsymbol{\theta} )}{s_{M}^{{}}({\mathbf{r}}_{.j}(\boldsymbol{\theta}))}\right) \frac{s_{M}^{{} }({\mathbf{r}}_{.j}(\boldsymbol{\theta}))\partial r_{t,j}(\boldsymbol{\theta} )/\partial\boldsymbol{\theta}-r_{tj}(\boldsymbol{\theta})\partial s_{M}({\mathbf{r}}_{.j}(\boldsymbol{\theta})/\partial\boldsymbol{\theta}\ } {s_{M}^{2}({\mathbf{r}}_{.j}(\boldsymbol{\theta}))}=0\end{aligned} $$

and

$$\displaystyle \begin{aligned} \frac{\partial s_{M}({\mathbf{r}}_{.j}(\boldsymbol{\theta}))}{\partial \boldsymbol{\theta}} \mathbf{=}\sum_{t=k_{1}+k_{2}+1}^{T}\psi\left( r_{t,j}(\boldsymbol{\theta} )/s_{M}^{{}}({\mathbf{r}}_{.j}(\boldsymbol{\theta }))\right) \frac{s_{M}^{{}}({\mathbf{r}}_{.j}(\boldsymbol{\theta}))\partial r_{t,j}(\boldsymbol{\theta} )/\partial\boldsymbol{\theta}}{\sum_{t=k_{1} +k_{2}+1}^{T}\psi\left( r_{t,j}(\boldsymbol{\theta})/s_{M}^{{}} ({\mathbf{r}}_{.j}(\boldsymbol{\theta}))\right) r_{t,j}(\boldsymbol{\theta})} .\end{aligned}$$

This can also be written as

where $w(u)=\psi (u)/u.$ Then the estimating Eq. (23) satisfies

$$\displaystyle \begin{aligned} \sum_{t=k_{1}+k_{2}+1}^{T}w_{tj}^{\ast}\left( \boldsymbol{\theta}\right) r_{t,j}(\boldsymbol{\theta})\frac{\partial r_{t,j}(\boldsymbol{\theta} )}{\partial\boldsymbol{\theta}}=0\ \ , {}\end{aligned} $$

(24)

where

$$\displaystyle \begin{aligned} w_{t,j}^{\ast}\left( \ \boldsymbol{\theta}\right) =\frac{s_{M} ^{2}({\mathbf{r}}_{.j}(\boldsymbol{\theta}))}{\frac{1}{T^{\ast}}\sum _{t=k_{1}+k_{2}+1}^{T}w\left( r_{t,j}(\boldsymbol{\theta})/s_{M}^{{} }({\mathbf{r}}_{.j}(\boldsymbol{\theta}))\right) r_{t,j}^{2}(\boldsymbol{\theta })}w(r_{t,j}(\boldsymbol{\theta})). \end{aligned}$$

Note that when $w_{t,j}^{\ast }\left ( \ \boldsymbol {\theta }\right ) =1$ for all $(t,j),$ (24) is the estimating equation of the ODPC. Therefore, the only difference between the estimating equation of the RODPC and the one of the ODPC is that the least squares solutions to obtain the optimal values of $\mathbf {a}$ and $\mathbf {B}$ for the RODPC give weight $w_{t,j}^{\ast }\left ( \ \boldsymbol {\theta }\right )$ to the observation $(t,j).$ Then we obtain (13) and (14).

1.2 Proof of Theorem 1

Lemma 1

Suppose that$z_{t,j}$satisfies A1, A4, A5, and A6 ; then there exist${\mathbf {a}}^{(m)}\in \mathbb {R}^{m}$and a$m\times (k+2)$matrix${\mathbf {B}}^{(m)}$such that if$g_{t}^{(m)}\mathbf {=a}^{\mathbf {(m)}\prime }{\mathbf {z}}_{t}$and${\mathbf {F}}_{t}^{(m)}=(1,g_{t}^{(m)},\ldots ,g_{t-k}^{(m)}),$the reconstruction$\widetilde {\mathbf {z}}_{t}^{(m)}={\mathbf {B}}^{(m)}{\mathbf {F}}_{t}^{(m)}$satisfies

$$\displaystyle \begin{aligned} {\mathbf E}(z_{tj}^{(m)}-\widetilde{z}_{t,j}^{(m)}-u_{t,j})^{2}\leq\frac{K_{1}} {m}{} \end{aligned} $$

(25)

for some constant $K_{1}.$

Proof

Let ${\mathbf {u}}_{t}^{(m)}=(u_{t,1},\ldots ,u_{t.m})$ and $\boldsymbol {\varphi }^{(m)}=(\varphi _{1}^{(m)},\ldots ,\varphi _{m}^{(m)});$ then

$$\displaystyle \begin{aligned} {\mathbf{z}}_{t}^{(m)}=\boldsymbol{\varphi}^{(m)}\mathbf{+}f_{t}(\mathbf{d} ^{(m)}+{\mathbf{e}}^{(m)})+f_{t-1}{\mathbf{c}}_{1}^{(m)}+\ldots +f_{t-k}\mathbf{c} _{k}^{(m)}+{\mathbf{u}}_{t}^{(m)}, \end{aligned}$$

where ${\mathbf {d}}^{(m)}$ and ${\mathbf {e}}^{(m)}$ are as in A6. Let $\ {\mathbf {a}}^{(m)}\mathbf {=d}^{(m)}/||{\mathbf {d}}^{(m)}||{ }^{2};$ then by A6,

$$\displaystyle \begin{aligned} ||{\mathbf{a}}^{(m)}||\leq1/(m^{1/2}\delta^{1/2}). {} \end{aligned} $$

(26)

Define $g_{t}^{(m)}={\mathbf {a}}^{(m)^{\prime }}{\mathbf {z}}_{t}^{(m)}$, and observe that

$$\displaystyle \begin{aligned} g_{t}^{(m)}=f_{t}+p^{(m)}+\boldsymbol{\eta}^{(m)}, \end{aligned}$$

where $\eta _{t}^{(m)}={\mathbf {a}}^{(m)\prime }{\mathbf {u}}_{t}^{(m)}$ and $p^{(m)}={\mathbf {a}}^{(m)\prime }\boldsymbol {\varphi }^{(m)}$. Then, by (26) and A1, we have

$$\displaystyle \begin{aligned} {\mathbf E}(\eta_{t}^{(m)2})\leq D/m {} \end{aligned} $$

(27)

with $D=A_{1}/\delta .$ Let us reconstruct ${\mathbf {z}}_{t}^{(m)}$ using $g_{t}^{(m)}$ as follows:

$$\displaystyle \begin{aligned} \widetilde{\mathbf{z}}_{t}^{(m)}=(\boldsymbol{\varphi}^{(m)}-p^{(m)} ({\mathbf{c}}_{0}+\ldots +{\mathbf{c}}_{k}))+g_{t}^{(m)}{\mathbf{c}}_{0}^{(m)} +g_{t-1}^{(m)}{\mathbf{c}}_{1}^{(m)}+\ldots +g_{t-k}^{(m)}{\mathbf{c}}_{k}^{(m)}. \end{aligned}$$

That is, if ${\mathbf {B}}^{(m)}$ is the $m\times (k+2)$ with columns $\boldsymbol {\varphi }^{(m)}-p^{(m)}({\mathbf {c}}_{0}+\ldots +{\mathbf {c}}_{k})$ and ${\mathbf {c}}_{i},0\leq i\leq k,$ we have

$$\displaystyle \begin{aligned} \widetilde{\mathbf{z}}_{t}^{(m)}={\mathbf{B}}^{(m)}{\mathbf{F}}_{t}^{(m)} \end{aligned}$$

and

$$\displaystyle \begin{aligned} z_{t,j}^{(m)}-\widetilde{z}_{t,j}^{(m)} & =-c_{j,0}\eta_{t}^{(m)}-c_{1} \eta_{t-1}^{(m)}-\ldots -c_{j,k}\eta_{t-k.}^{(m)}+u_{t,j}\\ & =v_{t,j}^{(m)}+u_{t,j}, \end{aligned} $$

where

$$\displaystyle \begin{aligned} v_{t,j}^{(m)}=-c_{j,0}\eta_{t}^{(m)}-c_{1}\eta_{t-1}^{(m)}-\ldots -c_{j,k} \eta_{t-k.}^{(m)}. {} \end{aligned} $$

(28)

Then by (27) and A5, there exists $K_{1}$ such that for all $1\leq j\leq m$

$$\displaystyle \begin{aligned} {\mathbf E}(v_{t,j}^{(m)2})\leq\frac{K_{1}}{m}, \end{aligned}$$

and this proves the Lemma.

Lemma 2

Suppose that$z_{t,j}$satisfies A1–A6, and let${\mathbf {a}}^{(m)}$, ${\mathbf {B}}^{(m)}$, and$\widetilde {\mathbf {z}}_{t}^{(m)}$as in Lemma1, and then there exists$K_{2}$independent of m such that

$$\displaystyle \begin{aligned} S_{M}(z_{tj}^{(m)}-\widetilde{z}_{t,j}^{(m)})\leq S_{M}(u_{t,j})+\frac{K_{2} }{m} {} \end{aligned} $$

(29)

for some constant $K_{2}.$

It is enough to show that there exists $m_{0}$ such that for $m\geq m_{0}$ (29) holds. Let for $k>0$ and v

$$\displaystyle \begin{aligned} L_{tj}(v,k)=\rho\left( \frac{v+u_{tj}}{s_{j}+k}\right), \end{aligned}$$

where $s_{j}=S_{M}(u_{t,j}).$

Using the mean value theorem at $(0,0)$, we get

$$\displaystyle \begin{aligned} L_{tj}(v,k)=L_{tj}(0,0)+v\frac{\psi\left( \frac{v^{\ast}+u_{tj}} {s_{j}+k^{\ast}}\right) \ }{s_{j}+k^{\ast}}-k\frac{\psi\left( \frac{v^{\ast }+u_{tj}}{s_{j}+k^{\ast}}\right) \frac{v^{\ast}+u_{tj}\ }{s_{j}+k^{\ast}} }{s_{j}+k^{\ast}}, {} \end{aligned} $$

(30)

where $|v^{\ast }|\leq |v|$ and $0\leq k^{\ast }\leq k.$ Put $k=K_{2}/m^{1/2}.$ Since $z_{t,j}^{(m)}-\widetilde {z}_{t,j}^{(m)}=v_{t,j}^{(m)}+u_{t,j},$ where $v_{t,j}^{(m)}$ is defined in Eq. (28) of Lemma 1, then using (30), we can write

$$\displaystyle \begin{aligned} {\mathbf E}\left( \rho\left( \frac{z_{t,j}^{(m)}-\widetilde{z}_{t,j}^{(m)}} {s_{j}+K_{2}/m^{1/2}}\right) \right) & ={\mathbf E}_{tj}(L(v_{t,j}^{(m)} ,K_{2}/m^{1/2}))\\ & =b+\frac{{\mathbf E}\left( v_{t,j}^{(m)}\psi\left( \frac{v^{\ast}+u_{t.j}} {s_{j}+K^{\ast}/m^{1/2}}\right) \right) \ }{s_{j}+K_{{}}^{\ast}/m^{1/2} } \\ &\quad -\frac{K_{2}}{m^{1/2}}\frac{{\mathbf E}\left( \psi\left( \frac{v^{\ast}+u_{t,j} }{s_{j}+K^{\ast}/m^{1/2}}\right) \frac{v^{\ast}+u_{tj}\ }{s_{j}+K^{\ast }/m^{1/2}\ }\right) \ }{s_{j}+K^{\ast}/m^{1/2}}, {} \end{aligned} $$

(31)

where $|v^{\ast }|\leq |v_{t,j}|$ and $K^{\ast }\leq K_{2}.$

Put

$$\displaystyle \begin{aligned} K_{2}=2A_{3}K_{1}^{!/2}/A_{4} {}. \end{aligned} $$

(32)

Since by Lemma 1${\mathbf E}(v_{t,j}^{(m)2})\leq K_{1}/m$ and by A3 $A_{3}=\max \psi (u),$ we have

$$\displaystyle \begin{aligned} \frac{\left\vert {\mathbf E}\left( v_{t,j}^{(m)}\psi\left( \frac{v^{\ast}+u_{t,j} }{s_{j}+K^{\ast}/m^{1/2}}\right) \right) \ \right\vert }{s_{j}+K_{{}}^{\ast }/m^{1/2}} & \leq\frac{{\mathbf E}(v_{t,j}^{(m)2})^{1/2}\max_{u}\psi(u)\ )} {s_{j}+K^{\ast}/m^{1/2}}\ {}\\ & \leq\frac{A_{3}K_{1}^{1/2}/m^{1/2}}{s_{j}+K^{\ast}/m^{1/2}}.\ \ \ \end{aligned} $$

(33)

Take

$$\displaystyle \begin{aligned} K_{2}>A_{3}K_{1}^{1/2}/A_{4}; {}, \end{aligned} $$

(34)

then since $K^{\ast }\leq K_{2}$ and $|v^{\ast }|\leq |v_{t,j}|$ by Lemma 1 and A4, there exists $m_{0}$ such that for $m\geq m_{0}$

$$\displaystyle \begin{aligned} & \frac{K_{2}}{m^{1/2}s_{j}+K^{\ast}/m^{1/2}}{\mathbf E}\left( \psi\left( \frac{v^{\ast}+u_{t,j}}{s_{j}+K^{\ast}/m^{1/2}}\right) \frac{v^{\ast} +u_{tj}\ }{s_{j}+K^{\ast}/m^{1/2}}\right) \ \\ & \geq\frac{K_{2}A_{4}/2}{m^{1/2}s_{j}+K^{\ast}/m^{1/2}}. {} \end{aligned} $$

(35)

Then by (31), (33), and (35), we have

$$\displaystyle \begin{aligned} \left( \rho\left( \frac{z_{t,j}^{(m)}-\widetilde{z}_{t,j}^{(m)}}{s_{j} +K_{2}/m^{1/2}}\right) \right) <b\ \ \ \ \ \ \ , \end{aligned}$$

and therefore, $S_{M}^{{}}(z_{t,j}^{(m)}-\widetilde {z}_{t,j}^{(m)})\leq s_{j}+K_{2}/m^{1/2}$. This proves the Lemma.

Proof of Theorem 1

From Lemma 2, it can be derived that if $z_{t,j}^{\ast (m)}$ is the reconstruction with the optimal first S-ODPC with any $k_{1}$ and $k_{2}=k,$ we should have

$$\displaystyle \begin{aligned} \frac{1}{m^{1/2}}\sum_{j=1}^{m}S_{M}^{2}(z_{t,j}^{(m)}-z_{t,j}^{\ast(m)}) & \leq\frac{1}{m^{1/2}}\sum_{j=1}^{m}S_{M}^{2}(z_{t,j}^{(m)}-\widetilde{z} _{t,j}^{(m)})\\ & \leq\sum_{j=1}^{m}\left( s_{j}^{2}+\frac{K_{2}^{2}}{m}+2\frac{K_{2} }{m^{1/2}}s_{j}\right) \\ & \leq\frac{1}{m^{1/2}}\sum_{j=1}^{m}\left( s_{j}^{2}+\frac{K}{m^{1/2} }\right) \\ & =\frac{1}{m^{1/2}}\sum_{j=1}^{m}s_{j}^{2}+K, \end{aligned} $$

where $\ K=\max (K_{2}^{2},K_{3}$) and $K_{3}=2K_{2}\max _{j}s_{j.}.$ This proves Theorem 1.