Abstract
Proving to someone else the knowledge of a secret without revealing any of its information is an interesting feature in cryptography. The best solution to solve this problem is a Zero-Knowledge Proof (ZKP) protocol.
Nurimisaki is a Nikoli puzzle. The goal of this game is to draw a kind of abstract painting (“Nuri”) that represents the sea with some capes (“Misaki”) of an island (represented by white cells). For this, the player has to fulfill cells of a grid in black (representing the sea) in order to draw some capes while respecting some simple rules. One of the specificity of the rules of this game is that the cells called “Misaki” can only have one white neighbour and all white cells need to be connected. In 2020, this puzzle has been proven to be NP-complete.
Using a deck of cards, we propose a physical ZKP protocol to prove that a player knows a solution of a Nurimisaki grid without revealing any information about the solution.
We thank the anonymous referees, whose comments have helped us to improve the presentation of the paper. This work was supported in part by JSPS KAKENHI Grant Numbers JP18H05289 and JP21K11881. This study was partially supported by the French ANR project ANR-18-CE39-0019 (MobiS5).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The democratization of computers and network systems has fuelled the virtualization of interactions and processes such as communication, payments, and elections. Proving the knowledge of some secret without revealing any bit of information from that secret is crucial in our today’s society. This issue can be applied to numerous contexts.
For instance, a client would like to connect to a server via a password without revealing the password. Another example is database management, where an entity could ask if a piece of information is in a database without asking for factual data. A third example can be given in the electronic voting system where the voters want to be sure that the ballots are correctly mixed (without revealing how the mix was done).
A cryptographic tool exists for all the previous examples, called a Zero-Knowledge Proof (ZKP) protocol. It enables a prover P to convince a verifier V that P knows a secret s without revealing anything other than it. A ZKP protocol must verify the following three properties:
-
Completeness: If P knows s then the protocol ends without aborting (meaning that V is convinced that P has s);
-
Soundness: If P does not have s then V will detect it;
-
Zero-Knowledge: V learns nothing about s.
In practice, ZKP protocols are typically executed by computers. However, their understanding is difficult for the uninitiated. We take a more direct approach to the notion of ZKP and construct a protocol using physical objects like playing cards and envelopes. It allows us to present the notion of ZKP protocols without deep mathematical backgrounds and also to extend the existing literature.
The first physical ZKP protocol [7] for a Sudoku grid was constructed using a deck of cards. Since this novel protocol was devised, several teams in the world have proposed physical ZKP protocols using a deck of cards for pencil puzzles, such as Sudoku [19, 25], Akari [1], Takuzu [1], Kakuro [1, 13], KenKen [1], Makaro [2], Norinori [5], Slitherlink [11], Suguru [16], Nurikabe [17], Ripple Effect [22], Numberlink [20], Bridges [21], Cryptarithmetic [8], Shikaku [23], and Nonogram [3, 18].
Why shall we propose a new card-based ZKP protocol for another Nikoli puzzle? For us, it is similar to the question: Why shall we prove that a puzzle is NP-complete? People want to know if a puzzle is NP-complete in order to know if the puzzle is difficult or not for a computer to solve it. Card-based ZKP protocols are quite similar; once a puzzle is shown to be NP-complete, a natural question is: Can we design a physical ZKP protocol? This is an intellectual challenge on the puzzle. Moreover, each puzzle has different rules and specificity, which force us to imagine new physical ZKP techniques. For instance, consider a Nikoli puzzle, Nurimisaki, which we will deal with in this paper; then, its rules combine for the first time some connectivity, neighbourhood restriction, and straight line with counting, as seen later. A previous work [24] (in Japanese, unpublished) proposed a card-based ZKP protocol for Nurimisaki. Yet, the protocol is not optimal since it prepares another grid to verify the rules (so the number of cards is large). Moreover, elaborate but complex techniques are used (e.g., using another grid to represent the in-spanning-tree of P’s solution). In contrast, our protocol has a more direct approach with closer interaction to the real game. Before giving our contributions, let us define the rules of the Nurimisaki puzzle.
Nurimisaki Rules. Figure 1 shows a puzzle instance of Nurimisaki. The goal for Nurimisaki puzzle is to color in black some cells on the grid, under the following rules:
-
1.
A cell with a circle is called a “Misaki”. A Misaki has only one cell of its neighbours (vertically or horizontally) remaining white and the rest black.
-
2.
The number written in a Misaki cell indicates the number of white cells in straight line from the Misaki. If there is no number, any number of white cells is allowed.
-
3.
White cells without a circle cannot be a Misaki.
-
4.
A \(2\times 2\) square cannot be composed of only black or white cells.
-
5.
White cells are connected.
Nurimisaki puzzle was recently proven NP-complete in [9]; hence, it is a natural question to construct a physical ZKP protocol for this fun puzzle. Although Goldwasser et al. [6] proved that any NP-complete problem has its corresponding interactive ZKP protocol, simple physical ZKP protocols are always sollicited as mentioned above.
Contributions. We propose a physical ZKP protocol that only uses cards and envelopes. We rely on some classical existing card-based sub-protocols in order to be able to construct our ZKP protocol. The main difficulty in this Nurimisaki game that seems to be simple, is that existing techniques proposed in the literature since few years cannot be applied directly. The main trick is to find an encoding that allows us to apply several sub-protocols in the right order to obtain a secure ZKP protocol. For this, we propose an original way to combine several techniques to design our ZKP protocol with a reasonable amount of cards and manipulations.
Outline. In Sect. 2, we introduce our encoding scheme using cards in order to represent a gird of the game and a solution. We also give some sub-protocols that are used in our construction. In Sect. 3, we give our ZKP protocol for Nurimisaki. Before concluding in the last section, we give the security proof of our ZKP protocol in Sect. 4.
2 Preliminaries
We explain the notations and sub-protocols used in our constructions.
Cards and Encoding. The cards we use in our protocols consist of clubs
 , hearts
, hearts
 , and numbered cards
, and numbered cards
 , whose backs are identical
, whose backs are identical
 . We encode three colors \(\{\text {black}, \text {white}, \text {red}\}\) with the order of two cards as follows:
. We encode three colors \(\{\text {black}, \text {white}, \text {red}\}\) with the order of two cards as follows:

We call a pair of face-down cards
 corresponding to a color according to the above encoding rule a commitment to the respective color. We also use the terms, a black commitment, a white commitment, and a red commitment. We sometimes regard black and white commitments as bit values, based on the following encoding scheme:
corresponding to a color according to the above encoding rule a commitment to the respective color. We also use the terms, a black commitment, a white commitment, and a red commitment. We sometimes regard black and white commitments as bit values, based on the following encoding scheme:

For a bit \(x\in \{0,1\}\), if a pair of face-down cards satisfies the encoding (2), we say that it is a commitment to x, denoted by
 .
.
We also define two other encoding [22, 26]:
-
 : for \(x\in \mathbb {Z}/{p}\mathbb {Z}\), there are p cards composed of \(p-1\) \(\heartsuit \)s and one \(\clubsuit \), where the \(\clubsuit \) is located at position \((x+1)\) from the left. For example, 2 in \(\mathbb {Z}/{4}\mathbb {Z}\) is represented as
: for \(x\in \mathbb {Z}/{p}\mathbb {Z}\), there are p cards composed of \(p-1\) \(\heartsuit \)s and one \(\clubsuit \), where the \(\clubsuit \) is located at position \((x+1)\) from the left. For example, 2 in \(\mathbb {Z}/{4}\mathbb {Z}\) is represented as
 .
. -
 : it is the same encoding as above but the \(\heartsuit \) and \(\clubsuit \) are reversed. For instance, 2 in \(\mathbb {Z}/{4}\mathbb {Z}\) is represented as
: it is the same encoding as above but the \(\heartsuit \) and \(\clubsuit \) are reversed. For instance, 2 in \(\mathbb {Z}/{4}\mathbb {Z}\) is represented as
 .
.
2.1 Pile-Shifting Shuffle [15, 26]
This shuffling action means to cyclically shuffle piles of cards. More formally, given m piles, each of which consists of the same number of face-down cards, denoted by \(({\textbf {p}}_1, {\textbf {p}}_2,\ldots , {\textbf {p}}_{m})\), applying a pile-shifting shuffle (denoted by \(\langle \cdot \Vert \cdots \Vert \cdot \rangle \)) results in \(({\textbf {p}}_{s\!+\!1},{\textbf {p}}_{s\!+\!2},\) \(\ldots ,{\textbf {p}}_{s\!+\!m})\):

where s is uniformly and randomly chosen from \(\mathbb {Z}/m\mathbb {Z}\). Implementing a pile-shifting shuffle is simple: we use physical cases that can store a pile of cards, such as boxes and envelopes; a player (or players) cyclically shuffles them manually until everyone (i.e., the prover P and the verifier V) loses track of the offset.
2.2 Input-Preserving Five-Card Trick [12]
Given two commitments to \(a,b\in \{0,1\}\) based on the encoding rule (2), this sub-protocol [4, 12] reveals only the value of \(a\vee b\) as well as restores commitments to a and b:

The original sub-protocol [4, 12] was designed for computing AND (\(a \wedge b\)), but we adjust it to compute OR \((a \vee b)\):
-
1.
Add helping cards and swap the two cards of the commitment to b so that we have the negation \(\overline{b}\), as follows:

-
2.
Rearrange the sequence of cards and turn over the face-up cards as:

-
3.
Regarding cards in the same column as a pile, apply a pile-shifting shuffle to the sequence:

-
4.
Reveal all the cards in the first row.
-
(a)
If it is
 (up to cyclic shifts), then \(a\vee b=0\).
(up to cyclic shifts), then \(a\vee b=0\). -
(b)
If it is
 (up to cyclic shifts), then \(a\vee b=1\).
(up to cyclic shifts), then \(a\vee b=1\).
-
(a)
-
5.
After turning over all the face-up cards, apply a pile-shifting shuffle.
-
6.
Reveal all the cards in the second row; then, the revealed cards should include exactly one
 .
. -
7.
Shift the sequence of piles so that the revealed
 is the leftmost card and swap the two cards of the commitment to \(\overline{b}\) to restore commitments to a and b.
is the leftmost card and swap the two cards of the commitment to \(\overline{b}\) to restore commitments to a and b.
2.3 Mizuki–Sone Copy Protocol [14]
Given a commitment to \(a\in \{0,1\}\) along with four cards
 , the Mizuki–Sone copy protocol [14] outputs two commitments to a:
, the Mizuki–Sone copy protocol [14] outputs two commitments to a:

-
1.
Turn all cards face-down and set the commitments as follows:

-
2.
Apply a pile-shifting shuffle as follows:

-
3.
Reveal the two above cards to obtain either a or \(\overline{a}\) as follows:

2.4 How to Form a White Polyomino [17]
We introduce the generic method of [17] to address the connectivity constraint (rule 5). Given a grid where all cells are black, it enables P to make white connected cells, i.e., white-polyomino, without revealing anything to V. We first describe two crucial sub-protocols: the chosen pile protocol and the 4-neighbor protocol.
Chosen Pile Protocol [5]. The chosen pile protocol allows P to choose a pile of cards without V knowing which one. This pile can be manipulated and all the commitments are replaced to their initial order afterward.
This protocol is an extended version of the “chosen pile cut” proposed in [10]. Given m piles \(({\textbf {p}}_1,{\textbf {p}}_2,\ldots ,{\textbf {p}}_m)\) with 2m additional cards, the chosen pile protocol enables a prover P to choose the i-th pile \({\textbf {p}}_i\) (without revealing the index i) and revert the sequence of m piles to their original order after applying other operations to \(p_i\).
-
1.
Using \(m-1\)
 s and one
s and one
 , P places m face-down cards encoding \(i-1\) in the
, P places m face-down cards encoding \(i-1\) in the
 (denoted by row 2) below the given piles, i.e., only the i-th card is
(denoted by row 2) below the given piles, i.e., only the i-th card is
 . We further put m cards encoding 0 in the
. We further put m cards encoding 0 in the
 (denoted by row 3):
(denoted by row 3): 
-
2.
Considering the cards in the same column as a pile, apply a pile-shifting shuffle to the sequence of piles.
-
3.
Reveal all the cards in row 2. Then, exactly one
 appears, and the pile above the revealed
appears, and the pile above the revealed
 is the i-th pile (and hence, P can obtain \({\textbf {p}}_i\)). After this step is invoked, other operations are applied to the chosen pile. Then, the chosen pile is placed back to the i-th position in the sequence.
is the i-th pile (and hence, P can obtain \({\textbf {p}}_i\)). After this step is invoked, other operations are applied to the chosen pile. Then, the chosen pile is placed back to the i-th position in the sequence. -
4.
Remove the revealed cards, i.e., the cards in row 2. (Note, therefore, that we do not use the card
 revealed in Step 3.) Then, apply a pile-shifting shuffle.
revealed in Step 3.) Then, apply a pile-shifting shuffle. -
5.
Reveal all the cards in row 3. Then, one
 appears, and the pile above the revealed
appears, and the pile above the revealed
 is \({\textbf {p}}_1\). Therefore, by shifting the sequence of piles (such that \({\textbf {p}}_1\) becomes the leftmost pile in the sequence), we can obtain a sequence of piles whose order is the same as the original one without revealing any information about the order of the input sequence.
is \({\textbf {p}}_1\). Therefore, by shifting the sequence of piles (such that \({\textbf {p}}_1\) becomes the leftmost pile in the sequence), we can obtain a sequence of piles whose order is the same as the original one without revealing any information about the order of the input sequence.
Sub-protocol: 4-Neighbor Protocol [17]. Given pq commitments placed on a \(p\times q\) grid, a prover P has a commitment in mind, which we call a target commitment. The prover P wants to reveal the target commitment and another one that lies next to the target commitment (without revealing their exact positions). Here, a verifier V should be convinced that the second commitment is a neighbor of the first one (without knowing which one) as well as V should be able to confirm the colors of both the commitments. To handle the case where the target commitment is at the edge of the grid, we place commitments to red (as “dummy” commitments) in the left of the first column and below the last row to prevent P from choosing a commitment that is not a neighbor. Thus, the size of the expanded grid is \((p+1)\times (q+1)\). This sub-protocol proceeds as follows.
-
1.
P and V pick the \((p+1)(q+1)\) commitments on the grid from left-to-right and top-to-bottom to make a sequence of commitments:

-
2.
P uses the chosen pile protocol to reveal the target commitment.
-
3.
P and V pick all the four neighbors of the target commitment. Since a pile-shifting shuffle is a cyclic reordering, the distance between commitments are kept (up to a given modulo). That is, for a target commitment (not at any the edge), the possible four neighbors are at distance one for the left or right one, and \(p+1\) for the bottom or top one so that P and V can determine the positions of all the four neighbors.
-
4.
Among these four neighbors, P chooses one commitment using the chosen pile protocol and reveals it.
-
5.
P and V end the second and first chosen pile protocols.
Forming White-Polyomino. Assume that there is a grid having \(p\times q\) cells. P wants to arrange white commitments on the grid such that they form a white-polyomino while V is convinced that the placement of commitments is surely a white-polyomino. The sub-protocol proceeds as follows.
-
1.
P and V place a commitment to black (i.e.,
 ) on every cell and commitments to red as mentioned above so that they have \((p+1)(q+1)\) commitments on the board.
) on every cell and commitments to red as mentioned above so that they have \((p+1)(q+1)\) commitments on the board. -
2.
P uses the chosen pile protocol to choose one black commitment that P wants to change.
-
(a)
V swaps the two cards constituting the chosen commitment so that it becomes a white commitment (recall the encoding (1)).
-
(b)
P and V end the chosen pile protocol to return the commitments to their original positions.
-
(a)
-
3.
P and V repeat the following steps exactly \(pq-1\) times.
-
(a)
P chooses one white commitment as a target and one black commitment among its neighbors using the 4-neighbor protocol; the neighbor is chosen such that P wants to make it white.
-
(b)
V reveals the target commitment. If it corresponds to white, then V continues; otherwise V aborts.
-
(c)
V reveals the neighbor commitment (chosen by P). If it corresponds to black, then P makes the neighbor white or keep it black (depending on P’s choice) by executing the following steps; otherwise V aborts.
-
i.
If P wants to change the commitment, P places face-down club-to-heart pair below it; otherwise, P places a heart-to-club pair:

-
ii.
Regarding cards in the same column as a pile, V applies a pile-shifting shuffle to the sequence of piles:
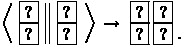
-
iii.
V reveals the two cards in the second row. If the revealed right card is
 , then V swaps the two cards in the first row; otherwise V does nothing.
, then V swaps the two cards in the first row; otherwise V does nothing.
-
i.
-
(d)
P and V end the 4-neighbor protocol.
-
(a)
V is now convinced that all the white commitments represent a white-polyomino. Therefore, this method allows a prover P to make a solution that only P has in mind, guaranteed to satisfy the connectivity constraint.
2.5 Sum in \(\mathbb {Z}\) [22]
We give a brief overview of the protocol described in [22] for the addition of elements in \(\mathbb {Z}/{2}\mathbb {Z}\) with a result in \(\mathbb {Z}\). This allows to compute \(S=\sum _{i=1}^n x_i\) with \(S\in \mathbb {Z}\) and \(x_i\in \mathbb {Z}/{2}\mathbb {Z}\) for \(i\in \{1,\dots ,n\}\). The idea is to compute the sum inductively; when starting by the two first elements \(x_1\) and \(x_2\), they are transformed into \(x_1-r\) and \(x_2+r\) for uniformly random \(r\in \mathbb {Z}/{2}\mathbb {Z}\). Then \(x_2+r\) is revealed (no information about \(x_2\) leaks since r is random), and the cards of \(x_1-r\) is shifted by \(x_2+r\) positions to encode value \((x_1-r)+(x_2+r)=x_1+x_2\). Note that this result is in \(\mathbb {Z}/{(p+1)}\mathbb {Z}\) (or simply \(\mathbb {Z}\) since the result is less than p) for elements \(x_1,x_2\) in \(\mathbb {Z}/{p}\mathbb {Z}\).
3 ZKP Protocol for Nurimisaki
We present our ZKP protocol for Nurimisaki. Hereinafter, we consider an instance of Nurimisaki as a rectangular grid of size \(p\times q\).
3.1 Setup Phase
The verifier V and the prover P place black commitments on all the cell of the \(p\times q\) grid and place red commitments (“dummy” commitments) around the grid so that we have \((p+1)(q+1)\) commitments.
3.2 Connectivity Phase
P and V apply the protocol given in Sect. 2.4: a white-polyomino is formed according to P’s solution. Now, V reveals all the commitments corresponding to Misaki to check that they are indeed white. After this phase, V is convinced that white commitments are connected (rule 5).
3.3 Verification Phase
The verifier V is now checking that the other rules are satisfied.
No \(2\times 2\) square (rule 4). We use an adapted verification phase of the one in [17] for checking that \(2\times 2\) square are not composed of only white (black) commitments. Note that for an initial grid \(p\times q\), there are \((p-1)(q-1)\) possible squares of size \(2\times 2\). Thus P and V consider each of those squares (in any order) and apply the following:
-
1.
P chooses a white commitment and a black one among the four commitments via the chosen-pile protocol (Sect. 2.4).
-
2.
V reveals both commitments marked by P in the previous step. If there are exactly a white commitment and a black one, V continues; otherwise, abort.
Misaki (rule 1 and 2). V wants to check that each Misaki cell (cell with a circle) has only one of its neighbours white and others black. Moreover, when a Misaki has a number in it, V wants to check that the straight line formed by white cells starting from the Misaki cell has the corresponding number of white cells.
P and V first consider Misaki cells with a number. For each Misaki cell (not at a border) with a number i in it, apply the following:
-
1.
P and V add black commitments (i.e., “dummy” commitments) at the border of the grid. This ensures that we delimit correctly the number of white commitments in a straight line.
-
2.
For each of the four neighbours, P and V form a pile composed of \(i+1\) commitments for each direction (top, bottom, left, right).

-
3.
P and V puts numbered cards under each pile as follows:

-
4.
P and V shuffle the piles and reveal the first commitment of each pile. If there is exactly one commitment corresponding to white then V continues. Otherwise, V aborts.
-
5.
V reveals the next i commitments of the pile with the first white commitment. If there are only white commitments for the first \(i-1\) commitments and a black commitment for the last one, then V continues; otherwise, aborts.
After this step, V is convinced that Misaki cells with a number are well-formed. In the case where there is no number, the first step consists of forming a pile with only one commitment. Hence, V is convinced that Misaki cells without a number satisfy only rule 1 but not rule 2 since any number of white cells could form the straight lineFootnote 1.
No circle, no Misaki (rule 3). V needs to check that white cells without a circle are not Misaki, meaning that any white cell of the grid has at least two of its neighbours white. This rule is somewhat challenging to verify without leaking information on the solution because the number and location of white cells are part of the solution (and must not be publicly revealed).
If the targeted cell is black then there is nothing to verify since any configurations could occur. Yet, if the targeted cell is white then there are at least (but it could be more) two neighbours that are white. The idea is to set the value of targeted cell being 5 if it is white and 0 if it is black. Then we add the neighbours to it (white is 0, and black is 1). If the cell is black then the sum is always less than or equal to 4 (which is permitted by the rules to have all black). But if the cell is white then the permitted value for the sum is less than or equal to 7 (a Misaki is equal to 8) for a targeted cell that is not at a border.
For a given cell, called targeted cell \(c_t\), we look at its neighbors (up to 4). The idea of verifying that a white cell is not a Misaki is to first sum the four neighbors (where a white cell is equal to 0 and a black cell is 1). Then by choosing another encoding, the targeted cell can be equal to 5 for white and 0 for black. Finally, adding the sum of the neighbors with \(c_t\) gives at most 4 for black \(c_t\) (which is permitted by the rules) and at most 7 for white \(c_t\) in a valid configuration and 8 or 9 for invalid configuration.
-
1.
Copy all the commitments using the copy protocol (Sect. 2.3). The number of copies for a \(p\times q\) grid is \(2(2pq-p-q)\);
-
2.
Sum the four neighbours by considering that a white commitment is equal to 0 and a black commitment is equal to 1. The result is given in the
 (i.e., there are four
(i.e., there are four
 s and one
s and one
 at position corresponding to the result of the sum).
at position corresponding to the result of the sum). -
3.
For the targeted cell, add 3
 s in the middle of the commitment as:
s in the middle of the commitment as: 
White is now 5 and black is 0 in the
 .
. -
4.
Sum the result of the two previous steps (the sum of the four neighbours and the inner cell). The result is encoded in the
 .
. -
5.
Reveal the last and penultimate cards. If a
 appears then abort; otherwise, continue.
appears then abort; otherwise, continue.
4 Security Proofs
Our protocol needs to verify three security properties given as theorems.
Theorem 1 (Completeness)
If P knows the solution of a Nurimisaki grid, then P can convince V.
Proof
First, notice that P convinces V in the sense that the protocol does not abort which mean that all the rules are satisfied. The protocol can be split in two: (1) the connectivity and (2) the verification phases.
-
(1)
Since P knows the solution, the white cells are connected and hence can always choose a black commitment at step 2 to swap it to white. Notice that there exists a proof for the connectivity in [17].
-
(2)
The verification of \(2\times 2\) square will not abort since if P has the solution then for any given \(2\times 2\) square there always exist a white commitment and a black commitment. For the Misaki rules, each Misaki cell has three of its neighbors black and one white; thus, the first commitment of piles \(p_1 , p_2,p_3,p_4\) will reveal exactly three black and one white commitments. Then, when looking at pile \(p_i\) of the first commitment corresponding to white, the number of white commitments corresponds to the number in the inner cell. Thus the protocol will continue. Finally, the non-Misaki rule is verified. Since P has the solution, any white cell (with no circle in it) has at least two white neighbors. Thus if the inner cell is white then the sum will start to 5 and the maximal value is 7 because a solution has at least two whites so at most two black commitments (of value 1 in this step). So the protocol will continue and hence V will be convinced that P has the solution. \(\square \)
Theorem 2 (Soundness)
If P does not provide a solution of the \(p\times q\) Nurimisaki grid, P is not able to convince V.
Proof
Suppose that P does not know the solution, hence at least one of the rules is not verified. If the white cells are not connected then P cannot choose a black commitment at step 2 hence V will detect it. Notice that there is also the proof of this phase in [17].
If P does not have the solution, then one of the verification phase will fail. We apply a case distinction for those verifications. Assume first that there is a block of \(2\times 2\) square composed of only white (black) commitments, then P cannot choose, during the chosen-pile protocol, two distinct commitments (i.e., a black and a white) thus the revealed commitments will attest to V that P does not have the solution. Second, assume that a Misaki cell is not well-formed in the sense that either (1) the number of white neighbour is not equal to 1 or that (2) the number of white cells in straight line does not correspond to the number of the Misaki cell. For (1) the neighbours are revealed (after a shuffle) so V will notice the number of white commitments; for (2) all the commitments next to the white neighbour are revealed thus V will also notice if there is a flaw. The last verification is for white cells which are not Misaki. It is equivalent of saying that any white cell (without a circle in it) has at least two white neighbours. If a white cell has only one white neighbour then during the sum process, then \(c_t=5\) (because the central cell is white) and the total for its neighbours is 3 (because there are 3 black commitments and 1 white). The final sum is then equal to 8, since V will look at the last and penultimate card of the sum (corresponding to a sum equal to 9 and 8) then V will detect that a white card is a Misaki. Notice that a sum equals to 9 means the white cell is surrounded by 4 black cells. It is not possible since white cells are connected. \(\square \)
Theorem 3 (Zero-knowledge)
V learns nothing about P’s solution of the given grid G.
Proof
We use the same proof technique as in [7], namely the description of an efficient simulator which simulates the interaction between an honest prover and a cheating verifier. The goal is to produce an indistinguishable interaction from the verifier’s view (with the prover). Notice that the simulator does not have the solution but it can swap cards during shuffles. Informally, the verifier cannot distinguish between two protocols, one that is run with the actual solution and one with random commitments. The simulator acts as follows: The simulator constructs a random connected white polyomino. During the \(2\times 2\) square verification, the simulator will swap cards to choose white and black commitments. For the Misaki verification, the simulator swaps three commitments to black for three piles and one to white for the last pile. The latter will also be modified by the simulator to contain the correct numbers of white commitments (and the last commitment to black). During the non-Misaki verification, when the sum is computed, the simulator swaps the cards to always put
 cards in position 8 and 9 (for the cell not at the edge, but the latter is done the same way).
cards in position 8 and 9 (for the cell not at the edge, but the latter is done the same way).
The simulated and real proofs are indistinguishable hence V learns nothing from the connectivity and verification phases. Finally, we conclude that the protocol is zero-knowledge. \(\square \)
5 Conclusion
We proposed a physical ZKP protocol for Nurimisaki that uses only cards and envelopes. The most difficult part was to prove that cells are not Misaki without leaking their color. Of course, we combined this part with the rest of the verifications that are stated by other rules. This new approach clearly demonstrates that showing that some cells do not have some properties is often more difficult than proving an explicit property without leaking any information.
Notes
- 1.
Note that we described the protocol for Misaki cell not at the border of the grid. If a Misaki cell is at a border (but not a corner) then the 4-neighbours becomes the 3-neighbours and the protocol is the same (there will be only three piles instead of four). For Misaki cells at a corner, P and V consider the 2-neighbours (thus only two piles).
References
Bultel, X., Dreier, J., Dumas, J.G., Lafourcade, P.: Physical zero-knowledge proofs for Akari, Takuzu, Kakuro and KenKen. In Demaine, E.D., Grandoni, F. (eds.) Fun with Algorithms, volume 49 of LIPIcs, pp. 8:1–8:20 (2016)
Bultel, X., et al.: Physical zero-knowledge proof for Makaro. In: Izumi, T., Kuznetsov, P. (eds.) SSS 2018. LNCS, vol. 11201, pp. 111–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03232-6_8
Chien, Y.-F., Hon, W.-K.: Cryptographic and physical zero-knowledge proof: from Sudoku to Nonogram. In: Boldi, P., Gargano, L. (eds.) FUN 2010. LNCS, vol. 6099, pp. 102–112. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13122-6_12
den Boer, B.: More efficient match-making and satisfiability: The five card trick. In: Quisquater, J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 208–217. Springer, Berlin, Heidelberg (1989). https://doi.org/10.1007/3-540-46885-4_23
Dumas, J.-G., Lafourcade, P., Miyahara, D., Mizuki, T., Sasaki, T., Sone, H.: Interactive physical zero-knowledge proof for Norinori. In: Du, D.-Z., Duan, Z., Tian, C. (eds.) COCOON 2019. LNCS, vol. 11653, pp. 166–177. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26176-4_14
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems. In: STOC 1985, pp. 291–304, New York. ACM (1985)
Gradwohl, R., Naor, M., Pinkas, B., Rothblum, G.N.: Cryptographic and physical zero-knowledge proof systems for solutions of Sudoku puzzles. Theory Comput. Syst. 44(2), 245–268 (2009)
Isuzugawa, R., Miyahara, D., Mizuki, T.: Zero-knowledge proof protocol for cryptarithmetic using dihedral cards. In: Kostitsyna, I., Orponen, P. (eds.) UCNC 2021. LNCS, vol. 12984, pp. 51–67. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-87993-8_4
Iwamoto, C., Ide, T.: Computational complexity of Nurimisaki and Sashigane. IEICE Trans. Fundam. 103(10), 1183–1192 (2020)
Koch, A., Walzer, S.: Foundations for actively secure card-based cryptography. In M. Farach-Colton, M., Prencipe, G., Uehara, R. (eds.) Fun with Algorithms, volume 157 of LIPIcs, pp. 17:1–17:23, Dagstuhl. Schloss Dagstuhl (2021)
Lafourcade, P., Miyahara, D., Mizuki, T., Robert, L., Sasaki, T., Sone, H.: How to construct physical zero-knowledge proofs for puzzles with a “single loop’’ condition. Theor. Comput. Sci. 888, 41–55 (2021)
D. Miyahara, et al.: Card-based ZKP protocols for Takuzu and Juosan. In Farach-Colton, M., Prencipe, G., Uehara, R. (eds.) Fun with Algorithms, volume 157 of LIPIcs, pp. 20:1–20:21, Dagstuhl. Schloss Dagstuhl (2021)
Miyahara, D., Sasaki, T., Mizuki, T., Sone, H.: Card-based physical zero-knowledge proof for Kakuro. IEICE Trans. Fundam. 102-A(9), 1072–1078 (2019)
Mizuki, T., Sone, H.: Six-card secure AND and four-card secure XOR. In: Deng, X., Hopcroft, J.E., Xue, J. (eds.) FAW 2009. LNCS, vol. 5598, pp. 358–369. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02270-8_36
Nishimura, A., Hayashi, Y.I., Mizuki, T., Sone, H.: Pile-shifting scramble for card-based protocols. IEICE Trans. Fundam. 101-A(9), 1494–1502 (2018)
Robert, L., Miyahara, D., Lafourcade, P., Libralesso, L., Mizuki, T.: Physical zero-knowledge proof and np-completeness proof of suguru puzzle. Inf. Comput. 285(Part), 104858 (2022)
Robert, L., Miyahara, D., Lafourcade, P., Mizuki, T.: Card-based ZKP for connectivity: applications to Nurikabe, Hitori, and Heyawake. New Gener. Comput. 40, 149–171 (2022)
Ruangwises, S.: An improved physical ZKP for Nonogram. In: Du, D.-Z., Du, D., Wu, C., Xu, D. (eds.) COCOA 2021. LNCS, vol. 13135, pp. 262–272. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92681-6_22
Ruangwises, S.: Two standard decks of playing cards are sufficient for a ZKP for Sudoku. New Gener. Comput. 40, 49–65 (2022)
Ruangwises, S., Itoh, T.: Physical zero-knowledge proof for Numberlink puzzle and k vertex-disjoint paths problem. New Gener. Comput. 39(1), 3–17 (2021)
Ruangwises, S., Itoh, T.: Physical ZKP for connected spanning subgraph: applications to bridges puzzle and other problems. In: Kostitsyna, I., Orponen, P. (eds.) UCNC 2021. LNCS, vol. 12984, pp. 149–163. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-87993-8_10
Ruangwises, S., Itoh, T.: Securely computing the N-variable equality function with 2N cards. Theor. Comput. Sci. 887, 99–110 (2021)
Ruangwises, S., Itoh, T.: How to physically verify a rectangle in a grid: a physical ZKP for Shikaku. In Fraigniaud, P., Uno, Y. (eds.), Fun with Algorithms, volume 226 of LIPIcs, pp. 24:1–24:12. Schloss Dagstuhl (2022)
Saito, K.: Physical zero-knowledge proof for the pencil puzzle Nurimisaki. Graduation Thesis, The University of Electro-Communications, Tokyo (2020)
Sasaki, T., Miyahara, D., Mizuki, T., Sone, H.: Efficient card-based zero-knowledge proof for Sudoku. Theor. Comput. Sci. 839, 135–142 (2020)
Shinagawa, K.: Card-based protocols using regular polygon cards. IEICE Trans. Fundam. 100-A(9), 1900–1909 (2017)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Robert, L., Miyahara, D., Lafourcade, P., Mizuki, T. (2022). Card-Based ZKP Protocol for Nurimisaki. In: Devismes, S., Petit, F., Altisen, K., Di Luna, G.A., Fernandez Anta, A. (eds) Stabilization, Safety, and Security of Distributed Systems. SSS 2022. Lecture Notes in Computer Science, vol 13751. Springer, Cham. https://doi.org/10.1007/978-3-031-21017-4_19
Download citation
DOI: https://doi.org/10.1007/978-3-031-21017-4_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-21016-7
Online ISBN: 978-3-031-21017-4
eBook Packages: Computer ScienceComputer Science (R0)






 : for
: for  .
. : it is the same encoding as above but the
: it is the same encoding as above but the  .
.


 (up to cyclic shifts), then
(up to cyclic shifts), then  (up to cyclic shifts), then
(up to cyclic shifts), then  .
. is the leftmost card and swap the two cards of the commitment to
is the leftmost card and swap the two cards of the commitment to 


 s and one
s and one
 , P places m face-down cards encoding
, P places m face-down cards encoding  (denoted by row 2) below the given piles, i.e., only the i-th card is
(denoted by row 2) below the given piles, i.e., only the i-th card is
 . We further put m cards encoding 0 in the
. We further put m cards encoding 0 in the
 (denoted by row 3):
(denoted by row 3): 
 appears, and the pile above the revealed
appears, and the pile above the revealed
 is the i-th pile (and hence, P can obtain
is the i-th pile (and hence, P can obtain  revealed in Step
revealed in Step  appears, and the pile above the revealed
appears, and the pile above the revealed
 is
is 
 ) on every cell and commitments to red as mentioned above so that they have
) on every cell and commitments to red as mentioned above so that they have 
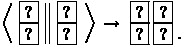
 , then V swaps the two cards in the first row; otherwise V does nothing.
, then V swaps the two cards in the first row; otherwise V does nothing.

 (i.e., there are four
(i.e., there are four
 s and one
s and one
 at position corresponding to the result of the sum).
at position corresponding to the result of the sum). s in the middle of the commitment as:
s in the middle of the commitment as: 
 .
. .
. appears then abort; otherwise, continue.
appears then abort; otherwise, continue.