Abstraction in Deductive Verification: Model Fields and Model Methods

Abstract

This Experience report compares using model fields and model methods for specifying abstractions in abstract implementations. Our experience is connected to past discussions of alternatives in modeling heap state changes and the axiomatic basis for deductive verification of programs with uninterpreted, underspecified or recursive methods.

1 Introduction

Deductive verification (DV) of software requires writing specifications in some specification language (SL) to complement an actual program implementation in some programming language (PL). Similarly to writing the implementation, specifications benefit from designs that abstract, clarify and simplify the intent of the program. Good abstractions can make the specification more obviously correct¹ and improve the performance of the underlying DV system in generating the proofs that verify that the specifications and implementation are consistent.

Tools that perform deductive verification of software translate a combination of program source code and specifications into a logical language that can then be submitted to a theorem prover to determine whether the source code and specifications are consistent with each other. The translation process incorporates the semantics of both the PL and the SL. It also must consider which formulation of logical language structure will provide the best proof success, both in proofs succeeding at all and in the time taken to do so.

In the Java Modeling Language (JML) [10, 15], as in some other SLs, one has a choice to use model fields or model methods (or a mixture) in writing specifications. In a recent (October 2021–March 2022) specification project for an industrial client, a target example was specified in each way.

The contribution of this Experience Report is to describe how model fields and model methods were used in OpenJML [6, 7] for this example, identify the advantages and disadvantages of each approach, and, in particular, how the logical encoding used by the deductive verification system was affected. To set the stage, early sections of this paper provide a summary of how DV systems encode PL and SL constructs, particularly the heap.

The context of this work is deductive verification for legacy software, in this case software written in Java. Thus we did not have the opportunity to use a system such as Dafny [18, 19] that is designed to verify software as it is written. Rather this project used a specification language (JML) and tool (OpenJML) appropriate to the target language (Java). In this case, OpenJML is translating to SMT-LIB [24], with Z3 [11] as its back-end, automated logical engine.

The examples given below use Java as the PL and JML as the SL; JML embeds specifications in Java code as Java comments beginning with . OpenJML was extended to handle reads clauses and recursive model fields and (which are then similar to dynamic frames), both of which were implicit in JML, but without carefully defined semantics. However these techniques and ideas are applicable to other imperative programming languages with heap data storage, such as object-oriented languages, and to other DV tools, particularly SMT-based tools like ACSL [1] and Frama-C [13].

The overall motivation for this project at the outset was to take the work of this report beyond what is reported here, namely to determine (a) which logical encodings of PL features are easier to write and understand (in tool implementations), (b) which encodings show better proof performance and success, and then (c) are the differences significant enough to warrant a substantial refactoring of a DV tool implementation.

2 Logical Encoding of Local Computations

Like other modular DV systems, JML and OpenJML verify a program method by method. Each method’s implementation is verified independently against its own specification, using just the specifications of methods on which its implementation and specification depend. The collection of verification proofs of all the methods in the program, together with proofs of termination, constitute a sound verification that the program and its specifications are consistent. A typical DV system translates PL+SL source into logic with a series of steps.

• 1. Using the semantics of the PL and SL, convert the source into an equivalent form that consists just of a DAG of basic blocks, where each basic block consists only of assignments, assert statements, assume statements and havoc statements. Into each back edge of a loop, where control returns to the loop’s beginning, an assertion of the loop’s inductive invariant is inserted. In Java, throwing exceptions, try-catch-finally statements, break and continue statements, and the interplay among these can lead to complex flows among many basic blocks. Havoc statements assign to listed variables an arbitrary value consistent with the variable’s type; these are used in the representation of loops and method calls.

• 2. Apply a single-static-assignment (SSA) transformation to all the assignments and variable uses so that each variable has a unique declaration/initialization statement.

• 3. Transform to a logical form by replacing program variables with logical variables, assignments with assumptions, basic blocks with chains of implications, and the whole DAG of basic blocks as a set of logical block equations. The logical encoding states the property that all the preconditions and other assumptions together imply that all the desired program properties (e.g., not throwing exceptions) and specification assertions hold. This is the property that if proved to always hold verifies that the program implementation and its specifications are consistent.

• 4. Those logical block equations are then transformed into the input language for a logical solver, such as into SMT-LIB for solvers such as CVC5 [3, 4] or Z3 [11].

• 5. The logical solver then pronounces that set of formulae to be unsatisfiable, satisfiable, or unknown. For SMT solvers, the property to be proved is negated, so that a response of satisfiable means that there is a particular, concrete assignment of values to logical variables that satisfies all the preconditions and other assumptions, but also satisfies the negated assertion (that is, falsifies the original assertion), thereby providing a counterexample to a desired proof of consistency. An unsatisfiable response means no such assignment exists, and thus the given assertions are entailed by the given assumptions (i.e., the implementation is consistent with the specification). A response of unknown means that the solver ran out of time or memory or otherwise could not eliminate all possible satisfying assignments.²

Our concern in this paper is principally with the SSA transformation and its interaction with the heap and with method calls. To set the stage for later complications, the following simple example code snippet shows the SSA and logical transformations when only stack variables are used. Stack variables are simple because in languages such as Java that do not permit arbitrary address and pointer calculations, there is no aliasing among stack variables.

Consider this source code snippet (using Java notation for assignments and operators). Here the assert statement can be considered the specification and the other statements the program implementation.

The construct says to evaluate its argument in the context at the beginning of the code snippet. This simple example just has one basic block.

The SSA transformation results in the following.

For the transformation to a logical form, we use logical variables that have the same name as the SSA variable, but using subscripts. We obtain the following:

$$\begin{aligned} (x_1 = x_0 + y_0) \rightarrow (y_1 = x_1 - y_0) \rightarrow (x_2 = x_1 - y_1) \rightarrow (x_2 = y_0 \wedge y_1 = x_0) \end{aligned}$$

(1)

In (1), $=$ is equality, $\rightarrow$ is right-associative boolean implication, and $\wedge$ is conjunction. Negating formula (1), converting to SMT-LIB, and passing the result to an SMT solver produces unsat, i.e., the assertion follows from the program code.

In this example, the + in the program source is addition in Java, the + in the assert statement is addition in the specification language, and the $+$ in the logical formula is addition in the logical language, which in SMT-LIB is addition over the unbounded mathematical integers. Here we mapped the first two into the latter, which is an interpretation of the semantics of the PL addition and SL addition as mathematical addition. However, for Java, addition must be interpreted as 2’s-complement addition; addition in JML specifications is by default mathematical addition.

3 Encoding Heap Access and Update—Previous and Related Work

3.1 Notation

The encoding process above becomes more complicated when the PL has references to objects in heap storage. This introduces the possibility of aliasing—different variables can refer to the same object—and objects have substructure in the form of named fields or as array elements. In Java, field names are constants and are not subject to any computation; in C/C++ by contrast, fields can overlap in memory as unions and pointer arithmetic can cause arbitrary aliasing. Java also has arrays, which are essentially objects with computable fields, but in Java array indexes can only refer to elements that are within the bounds of the array. The ensuing discussion will focus on fields, as arrays are handled similarly, with only minor modification.

A heap containing objects with fields is thus a mutable (updatable) structure, indexed by a reference value and a field name, that stores values that have PL types, such as integers of various bit-widths, boolean values and references. The discussion that follows uses the following notation:

• object references are denoted by symbols like and in programs with corresponding logical symbols as o and p

• references to arrays are denoted by variations on in PL and SL and a in logic

• variations on are PL and SL variables of various integer-like types; corresponding logical variables are i, j, and k

• field names use letters like and 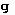; the logical equivalents are variations of f and g, as constants, or of F and G as maps

• letters like and v indicate values of various types stored in PL fields or in logical maps

• the heap is implicit in programs, but is represented as variations on h (as an index) or H (as a map) in logical equations

• brackets, as in f[o] or $\mathscr {L}[h,o,f]$, denote map lookup; the notation $f[o := v]$ and $\mathscr {L}[h,o,f := v]$ is map update: $f[o := v]$ denotes a new map $f'$ that is the same as f except that $f'[o] = v$. That is, these two operations satisfy the axioms $\forall f, o, v : f[o := v][o] = v$ and $\forall f, o, p, v : p \ne o \rightarrow f[o := v][p] = f[p]$ and similarly for maps with other types and numbers of indices.

3.2 Heaps as Maps

Most generally then, we can represent a heap access as a lookup $\mathscr {L}$ in a map h, where $\mathscr {L}[h,o,f]$ returns a value v corresponding to object o and field f in heap h, and $\mathscr {L}[h,o,f := v]$ returns a new heap value $h'$ in which the value v is now associated with o and f, but otherwise $h'$ is the same as h. One complication is that the type of v must match the type of f, for a typed PL like Java.

In 2011, Böhme and Moskal [5] published an assessment of a variety of heap encodings and measured their performance on a set of bespoke benchmarks when implemented for a number of logical engines. The encoding variations stem from treating the heap as an index in $\mathscr {L}$ or as a map itself; similarly, fields can be represented as either constant values that are indices into a map or as maps themselves. That gives a number of options, as presented and named in [5]:

synchronous heap:

the heap H is an updateable 2-dimensional map indexed on object and field, with lookup H[o, f]. (Standard SMT-LIB does not support explicitly two-dimensional arrays, though some SMT solvers, such as Z3, do.)

two-dimensional heap:

the heap H is a nested map of maps, where either the object or the field may be the first index, with lookup H[o][f] or H[f][o]. These nested maps make update more complicated: instead of $H[o, f := v]$, there is either $H[o := H[o][f := v]]$ or $H[f := H[f][o := v]]$.

field heap:

the heap is separated into a number of heaps by field, so each field f is represented by a map F[o]. This corresponds to currying the map H[f] into a map F (for each field) from references to values, which is possible because field names are pure constants.

The fact that the heap is implicit in the field heap encoding, whereas in all other encodings it is explicit, makes the field heap categorically different than the other encodings. In some ways the field heap encoding is simpler to use, particularly in the absence of method calls. However, it does lose the ability to quantify over fields, which can be useful in modeling features such as frame conditions. Thus axiomatization with non-field heaps can be more succinct, whereas with field heaps those axioms may need to be re-instantiated whenever the heap changes.

For C or C++ another option is needed to model pointer arithmetic:

linear heap:

lookup is H[dot(o, f)], which uses an operation, dot, that combines a pointer and a field.

Böhme and Moskal measured performance of these options, axiomatizing each encoding option for a variety of logical solvers. Variations of orders of magnitude in performance were measured. They reported several interesting observations:

• The field heap encoding was by far the most efficient in most cases; the two-dimensional heap of the form H[p][f] was comparable in time performance for Z3, but solved many fewer problems.

• Performance on other heap encodings varied considerably across solvers and across encodings.

• In the case of Z3, the performance varied significantly depending on the set of tool parameters used. It also varied significantly with the use of patterns to guide the instantiation of quantified formulas.

• SMT-based solvers (e.g., Z3, CVC3, Yices) performed overall better on this benchmark set than did ATP solvers (e.g., E, SPASS, Vampire).

• Breaking up a large verification formula can produce some performance improvement.

An overall observation is the importance of design choices (heap encoding, tool, tool parameters) to the performance of the DV system. However, the systems involved in this study were measured more than a decade ago; they have been significantly improved since then, as evidenced by the results of the annual SMTCOMP competition [8, 23, 25], but as the measurements have not been repeated, we are building, cautiously, on the original conclusions.

The reasons for differences in performance for different heap encodings are a matter of speculation. However, a reasonable hypothesis is that in the field heap the solver spends less time doing alias determination than in the two-dimensional heap mappings, since in H[f][p], some reasoning steps are needed to determine whether two field identifiers f and $f'$ are the same or different.

3.3 Arrays

Arrays are encoded like fields, but with an integer index. Like fields, there are a variety of ways to encode arrays. In Java, these must take account of the property that Java arrays are aliasable; that is, the assignment b = a; means that b now refers to the same array as a, not to a copy of it. Element i of array-typed field a of an object o, that is, o.a[i], might be encoded as $\mathscr {A}[\mathscr {L}[h,o,a], i]$ or $H_A[ H[o,a], i]$ or E[A[o]][i], where $\mathscr {A}$, $H_A$, E, and A are maps for the portion of the heap containing arrays. Type considerations add complexity because $\mathscr {L}[h,o,a]$ and A[o] are now an array type. There are now two layers of heap lookup, but otherwise the kinds of axioms and reasoning needed are similar to those for regular fields. It is also possible to consider integer indices (of arrays) to be just another kind of field identifier, further unifying the treatment of fields and arrays. We ignore arrays in the following discussion.

3.4 Embedding in SMT

If we use SMT-LIB [24] as the logical language, then we need to consider to what extent SMT-LIB supports these encoding models. (Even if a tool uses Boogie [17] as an intermediate language, the encoding will eventually be mapped into SMT-LIB.)

There is a design choice in how SMT-LIB is used to encode mappings with a single index: one can use either SMT-LIB’s uninterpreted functions or its maps with single-index but with arbitrary index and value types.

• The advantage of using SMT-LIB’s built-in maps is that then the solver can use the solver’s built-in, highly engineered decision procedures for read-over-write maps, which includes extensionality.³ However, SMT-LIB is also strictly typed, which means that different map types are needed for different field types.

• Objects can be treated more uniformly if the model uses generically axiomatized uninterpreted functions; e.g., heap values that are arrays can be treated the same as heap values that are other references. The types of different field values can be handled by defining injective functions that wrap values into a generic container and unwrap them into specified types.⁴ One disadvantage of this approach is that the solver then needs to reason its way through these wrapping and unwrapping functions.

Also, SMT-LIB does not support maps with more than one index (though Z3 does), so H[o, f] must necessarily be either axiomatized as uninterpreted functions or embedded in standard SMT-LIB as either H[o][f] or H[f][o].

In addition to Böhme and Moskal [5], other authors have discussed the use of these encodings in specific systems.

• Leino and Rümmer [20] present how these encodings are accommodated in the design of Boogie [17].

• Weiss [26] recaps Böhme and Moskal’s discussion of heap encodings in the context of the KeY tool [14] and its JavaDL logic.

• The KeY Book [2] also gives axioms for heap encoding in the KeY tool.

• Mostowski and Ulbrich [21] also discuss the semantics and implementation of JML model methods in the context of dynamic dispatch.

• Müller [22] discusses extensively the problems in verifying abstractions, though without detailed discussions of logical heap encodings.

OpenJML currently uses the field heap encoding, inheriting it from its predecessors ESC/Java2 [9] and ESC/Java [12]. Part of the goal of this project was to determine whether a change in heap encoding would be worth the refactoring effort.

4 Model Fields and Model Methods

As will be illustrated in the next section and discussed in more detail in Sect. 7, abstract properties of a class can be represented by either model fields or model methods.

A model field is a field that is only present in the specification. It may be completely uninterpreted, with its properties determined by axioms, invariants and pre- and post-conditions. Or it can be set equal to an expression using JML’s clause, in which case that equality results in an axiom or assumption about the value of the model field. In other respects, a model field is encoded just like other fields—as an array lookup as described in Sect. 3.2.

A model method is a pure (i.e. side-effect-free) method that is part of the specification but can be used with specification expressions. A model method typically has pre- and postconditions that stipulate when it is well-defined and what its value is. Generally speaking, method calls used in implementations or specifications are replaced by assertions of preconditions and assumptions of postconditions. But there are circumstances in which a matching logical function is defined that mirrors the definition of the model method. This helps with ensuring that underspecified model methods are deterministic and is also necessary for recursive methods.

5 Simple Example

Consider the simple example shown in Fig. 1. The interface has properties and , which are model fields. JML allows interfaces to have instance fields for this purpose. The Java methods and report these properties. In Java these are abstract methods with no implementation, but in JML we can give specifications telling their values in terms of the model fields. Another method doubles the linear dimensions of the . Consequently it is specified as assigning to (potentially modifying) , but not to .

The class is one implementation of . The notable item here is the use of the clauses to associate expressions with the interfaces’s model fields. One can easily imagine another class that also implements .

Figure 2 shows a test program. With the addition of features to avoid arithmetic overflow,⁵ this combination of program and specification verifies. Keep in mind that verification in JML is modular: the verification of test() refers only to the specifications of methods it calls, that is, only to methods in Shape and not to anything in Square. Similarly, Shape knows nothing about Square.

Fig. 1.

Simple example specified with model fields

Fig. 2.

A test program for Shape

The key question is this: the call of in modifies the heap, and only knows that it has a object, so how does the verifier know that the value of has changed but the value of has not? The answer combines information from two parts of ’s specification:

• (a) The frame condition (i.e., the assigns clause) of states that the method might change the value of the model field but not . (OpenJML enforces the rules that two model fields with different names have disjoint data groups. In derived classes, a field may not be added to two data groups unless one is explicitly a member of the other.)

• (b) The postcondition of uses the new value of but the call to only uses the not-changed value of .

That is, to verify the test program in Fig. 2, the verifier uses the frame condition () and the specifications of the model methods from . The specifications of the model methods are effectively inlined in the logical representation of the source and specifications for verification.

6 Using Model Methods

Now why are the model fields even needed? Could we not simply use the methods and to model the properties of the ? Note that in JML one can model the behavior of a system using mathematical types and operations, such as mathematical integers and reals, sequences, sets and maps. These mathematical functions do not interact with the heap; thus, one could declare model fields with such mathematical types and connect them to the implementation through represents clauses. However, doing so would require significant duplication of concepts and implementation: the actual implementation and a parallel structure, perhaps more abstract, in the specification. It is often more convenient and more concise, especially in simple situations, to use Java methods themselves (either ones in the actual Java implementation or ones added as model methods in the JML specification) as modeling elements. JML allows some Java methods (those that are declared pure, do not have side-effects, do not throw exceptions, and always terminate) to be used as such modeling functions.

For example we could write, in ,

(Here the clause captures a value computed in the pre-state as a local variable available in the post-conditions. It is used to simplify reading or to extract common subexpressions.) However, verification along these lines does not work without further modification. The first problem is that does not indicate what it might alter. We still need a frame condition, which can be specified using a datagroup that limits the changes that may perform.⁶ The second problem is that because there is no concrete field in which to ground the values of and , we need to implement in the encoded logic that the methods are deterministic. This determinism ensures that two successive calls of, say , with no intervening change in the heap produce the same result.

The standard encoding for method calls is that the preconditions are asserted, the frame conditions are translated into havoc statements, and the postconditions (giving the relationships of new values of the havoced variables to old ones) are assumed. In the absence of postconditions, the havoced variables are unconstrained. To encode that the method is deterministic, OpenJML adds an assumption of the form $result == f(args)$, where result is a logical variable representing the result of the method call and f is a logical function that represents the method being called. The encoding of such functions is discussed below; the effect of this assumption is that, within the same heap state, a given (pure) method always gives the same result, even if that result is underspecified.

A third problem, is that the postcondition of must include statements about how affects both and . Given this postcondition, the implementation of can be verified. But if there are 20 methods instead of two, all 20 would have to be listed. The reason? There is no specification of what these methods depend on. Even if we add the datagroup mentioned above, we have no indication about whether these methods depend on memory locations in that datagroup. Without knowing that does not depend on , the system cannot conclude that its value does not change when is called. The solution to this problem is to add reads (a.k.a. ) clauses to the specifications of functions that list the memory locations on which the functions depend.

The adjusted specification is shown in Fig. 3 (the code for is unchanged) and verifies without problem.

Fig. 3.

Specification using model methods

The important conclusions to draw from this example are these:

• In Shape, the model methods perimeter() and sides() are uninterpreted functions. They may have some properties that can be axiomatized, such as having non-negative values, but they are very underspecified.

• Reasoning about repeated invocations of such model methods within the same program state (i.e., with reference to the same heap) relies on these methods being deterministic—always producing the same values for the same arguments and evaluation context. Axioms relying on a definition of a corresponding logical function in the encoding must be added to the translation of a method call to ensure this determinism.

• Reasoning about invocations of a model method in different heaps relies on knowing that the memory locations that might have been changed in altering the heap are disjoint from the memory locations that are read by the model method.

The issues here concern underspecified functions—functions with insufficient specification to enable their results to be computed from their specification. It is worth noting that the same problems arise with recursive functions, even fully defined ones, because logical reasoning engines do not do induction on their own and do not unroll recursive definitions. Recursive functions are also essentially underspecified, axiomatized, uninterpreted functions.

Invariants pose one additional difficulty for model methods. With model fields one can easily state an invariant like in . With model fields one would write . But in JML, invariants must hold when methods are called; so in this case, must hold before is called. A circular invocation of results. The usual way to fix this is to declare as a method for which invariants are neither required nor guaranteed. But then in the call of the invariant cannot be assumed and an arithmetic overflow might occur. In such situations a model field might be needed in any case.

7 Encoding Model Methods

This section describes logical encodings for model methods, that is, methods that are used in specifications and so need a logical representation.

One can translate a method like into a corresponding logical function that has formal parameters for every entity on which the value of the method depends. In this case that is the reference itself and the heap; functions that represent Java methods with additional parameters will also need logical equivalents of those additional parameters.

There are variations on this theme that depend on the heap encoding. To explain these we use the logical type REF as the type of all Java objects and Heap as the logical type of heaps in the encoding.

• If heaps are encoded as synchronous or two-dimensional heaps, then a model method is encoded as a logical function that takes a heap parameter; e.g., is encoded as the logical function perimeter(h, p) where h has type Heap and p has type REF.

• If the field heaps encoding (see Sect. 3.2) is used, then the heap parameter is replaced by a list of the specific field heaps needed in the evaluation of the function’s specification. However, such a list might be long.

• The heap parameter can also be made implicit by currying perimeter(h, p) into $perimeter_h(p)$, where there is a different logical function for perimeter for each heap (i.e., for each program state). With this option neither the heap nor any field maps need be listed as parameters.

The last option works best with field heaps, for which the heap is already an implicit parameter. For other heap encodings the first option works best, because there is an explicit heap that can be passed as an argument; with some theorem provers, this is a rationale for preferring encodings other than field heaps. However, when working with underspecified methods, both alternatives suffer equally from the problem described next.

For underspecified methods, the reasoning problem is the lack of sufficient information about such methods. We can contrast this with completely specified methods, such as ’s method , which is specified to return a value of $4 \times \mathscr {L}[h,p,\#side]$, where $\#side$ is a constant corresponding to the field . By contrast, for an underspecified method, such as ’s model method , a call may have different results in different program states; because the heap h is a parameter to the encoding perimeter(h, p). For reasoning about such calls, the reads clause is crucial. Consider two heap states, h and $h'$, where $h'$ is derived from h by some sequence of heap-changing operations. Let $\Delta (h,h')$ be the set of memory locations which are changed between the two heaps; the prover knows that $\Delta (h,h')$ is at most the union of the frame location sets for each heap-changing operation in the sequence going from h to $h'$. In general, for a method m with receiver p, arguments args, and reads footprint $f_{reads}(h,p,args)$, if $f_{reads}(h,p,args)$ is disjoint from $\Delta (h,h')$, then $m(h,p,args) = m(h',p,args)$. (Note that in general a reads footprint depends on the function’s arguments and the current heap.)

There are a couple design options that encode such reasoning. On the one hand we can state the above relationship between heap-change footprints and function reads footprints as a general property of heaps, footprints, and functions. But this requires encoding heaps, frame footprints for heap changing methods, reads footprints of functions, and functions themselves as first-class elements in the logical encoding. Such an encoding adds to the reasoning load for the theorem prover.

On the other hand, we can introduce axioms stating under which conditions $m(h,p,args) = m(h',p,args)$ for each pair of heaps and each function as needed, but only as needed. This adds many more axioms, but they are tailored for specific situations in the program encoding; in addition the axioms can often be instantiated for the method arguments that are actually used, avoiding the need for the logic engine to figure out when to instantiate the quantified axiom.

Our experience in actual practice is that this latter approach works acceptably. It was implemented because it was the smaller step from the existing implementation, though an experiment contrasting this approach with the approach of using general axioms is still needed. We say “working acceptably” due to the smallish scale of our test examples and target system. The number of axioms and states was manageable because the size of methods was moderate and the numbers of methods used for modeling within a given method was not large.

8 Contrast and Conclusion

The goal of this work was to make a comparison between specifying using model fields vs. using model methods. To summarize the differences in practice of these two abstraction mechanisms,

a model field

• is a possibly-uninterpreted abstract specification-only field

• may be given an interpretation using a clause

• has an associated datagroup that, in combination with the frame conditions of heap-changing operations, implies when the model field (for a given object) is unchanged and when it might be changed by those heap-changing operations

a model method

• is a possibly uninterpreted abstract specification-only method

• may be given an interpretation using postconditions

• has an associated clause that, in combination with the frame conditions of heap-changing operations, implies when the value of the model method (for a given object and set of arguments) is unchanged and when it might be changed by those heap-changing operations

Summarized in this way, model fields and model methods are quite similar: model fields are like model methods that depend only on the heap and the receiver object; model methods can describe properties that have more parameters than just the receiver object.

Here are our experience-generated informal observations on using both mechanisms.

• Both means of modeling were overall successful in specifying the target example.

• Where both mechanisms were applicable, model fields were easier to use because:

  • They can precisely specify a method’s result for an otherwise underspecified abstract method.

  • They rely on a heap encoding that is already implemented in the tool.

• Model methods are necessary to specify properties that need arguments or that are not simple values characteristic of an object (e.g., a model method is needed to describe the value of a list element at some index, whereas the length of a list can be a model field).

• Reasoning about underspecified model methods in the presence of heap changes required implementing additional axioms that enabled reasoning about changes in those methods (or lack thereof) when the program’s state changed. This included implementing reads clauses and the infrastructure for comparing locations sets from assigns clauses and reads clauses.

• The interaction between invariants and model methods, particularly uninterpreted model methods in interfaces or abstract classes, typically makes it easier to write specifications using model fields (when invariants are involved).

• The simplest and most successful specifications were those that consisted of model fields that were values of some mathematical type. Those values and their operations are not part of the heap and so reasoning about them bypasses the issues noted in this paper; the model fields themselves are part of the program state and are part of assigns sets of memory locations.

These (informal) observations are from a single project’s experience and on a relatively small project. It will take future work on larger projects to determine how well they generalize.