Total Coloring of Planar Graphs Without Some Adjacent Cycles

Abstract

Let $G=(V,E)$ be a graph. If x, $y\in V\cup E$ are two adjacent or incident elements, then a k-total-coloring of graph G is a mapping $\varphi$ from $V\cup E$ to $\{1,2, \ldots , k\}$ on condition that $\varphi (x)\not =\varphi (y)$. In this paper, we define G to be a planar graph with maximum degree $\Delta \ge 8$. We prove that if for each vertex $v\in V(G)$, there exist two integers $i_v$, $j_v\in \{3,4,5,6,7,8\}$ on condition that v is not incident with adjacent $i_v$-cycles and $j_v$-cycles, then G has a $(\Delta +1)$-total-coloring.

1 Introduction

In this paper, all graphs mentioned are finite, simple and undirected. Undefined notions and terminologies can be referred to [1]. Suppose G is a graph, then V and d(v) are used to denote the vertex set and the degree of v. We use F, d(f) and E to denote the face set, the degree of f and the edge set respectively. Then $\Delta =\max \{d(v)|v\in V\}$ is the maximum degree of a graph and $\delta =\min \{d(v)|v\in V\}$ is the minimum degree. We use n-vertex, $n^+$-vertex, or $n^-$-vertex to denote the vertex v when $d(v)=n$, $d(v)\ge n$, or $d(v)\le n$ respectively. A n-face, $n^+$-face, or $n^-$-face are analogously defined. We use $(n_1,n_2,\ldots ,n_k)$ to denote a k-face and its boundary vertices are $n_i$-vertex $(i=1,2\ldots ,k)$. Similarly, we can define a $({n_1}^+,{n_2}^-,\ldots ,n_k)$-face. For instance, a $(l,m^+,n^-)$-face is a 3-face whose boundary vertices are l-vertex, $m^+$-vertex and $n^-$-vertex respectively. If two cycles or faces have at least one common edge, then we call they are adjacent. We use $n_k(f)$ to denote the number of k-vertices that is incident with f. The number of $k^+$-face incident with f is denoted as $n_{k^+}(f)$ and the number of $k^-$-face incident with f is denoted as $n_{k^-}(f)$. We use $n_k(v)$ to denote the number of k-vertices adjacent to v and use $f_k(v)$ to denote the number of k-faces incident with v. If G has a k-total-coloring, then we say that G can be totally colored by k colors. For the convenience of description, we say that G is total-k-colorable when G can be totally colored by k colors. If G can be totally colored by at least k colors, then k is the total chromatic number of G that is defined as $\chi ^{''}$. It is easy to know that $\chi ^{''}(G)\ge \Delta +1$. For the upper bound of $\chi ^{''}$, Behzad [2] and Vizing [3] put forth the Total Coloring Conjecture (for short, TCC):

Conjecture 1

For any graph, $\Delta +1\le \chi ^{''}(G)\le \Delta +2$.

TCC has attracted lots of researchers’ attention. However, this conjecture remains open even for planar graphs. In 1971, Rosenfeld [4] and Vijayaditya [5] confirmed TCC for all graphs with $\Delta \le 3$ independently. Kostochka [6] proved that $\chi ^{''}(G)\le \Delta +2$ when $\Delta \le 5$. For a planar graph, TCC is unsolved only when $\Delta =6$ (see [6, 18]). With the advances in research, some researchers found that $\chi ^{''}(G)$ of some specific graphs have an exact upper bound $\Delta +1$. In 1989, S$\acute{a}$nchez-Arroyo [7] demonstrated that it is a NP-complete problem to determine whether $\chi ^{''}(G)=\Delta +1$ for a specified graph G. Moreover, for every fixed $k\ge 3$, McDiarmid and S$\acute{a}$nchez-Arroyo [8] demonstrated that to determine whether a specific k-regular bipartite graph is total-$(\Delta +1)$-colorable or not is also a NP-complete problem. However, it is possible to prove that $\chi ^{''}(G)=\Delta +1$ when G is a planar graph having large maximum degree. It has been proved that $\chi ^{''}(G)=\Delta +1$ on condition that G is a planar graph when $\Delta (G)\ge 11$ [9], $\Delta (G)=10$ [10] and $\Delta (G)=9$ [11]. It is still open to determine whether a planar graph is total-$(\Delta +1)$-colorable when $\Delta =6$, 7 and 8. If G is a planar graph and $\Delta (G)=8$, then there are some relevant results obtained by adding some restrictions. For instance, for a planar graph with $\Delta (G)\ge 8$, it is proved that G is total-$(\Delta +1)$-colorable if G does not contain k-cycles $(k=5,6)$ [13], or adjacent 3-cycles [12], or adjacent 4-cycles [14]. Wang et al. [15] proved $\chi ^{''}(G)=\Delta +1$ if there exist two integers i, $j\in \{3,4,5\}$ such that G does not contain adjacent i-cycles and j-cycles. Recently, a result has been proved in [20] for a planar graph with $\Delta (G)=8$, that is, if for each vertex $v\in V$, there exist two integers $i_v$, $j_v\in \{3,4,5,6,7\}$ on condition that v is not incident with adjacent $i_v$-cycles and $j_v$-cycles, then G is total-$(\Delta +1)$-colorable. Now we improve some former results and get the following theorem.

Theorem 1

Suppose G is a planar graph with maximum degree $\Delta \ge 8$. If for each vertex $v\in V$, there exist two integers $i_v$, $j_v\in \{3,4,5,6,7,8\}$ on condition that v is not incident with adjacent $i_v$-cycles and $j_v$-cycles. Then G is total-$(\Delta +1)$-colorable.

2 Reducible Configurations

Theorem 1 has been proved for $\Delta \ge 9$ in [11]. So we presume that $\Delta =8$ in the rest of this paper. Suppose $G = (V, E)$ is a minimal counterexample to Theorem 1, that is, $|V|+| E|$ is as small as possible. In other words, G cannot be totally colored by $\Delta +1$ colors, but every proper subgraph of G can be totally colored with $\Delta +1$ colors. In this section, we give some information of configurations for our minimal counterexample G. A configuration is called to be reducible if it cannot occur in the minimal counterexample G. Firstly, we show some known properties of G.

Lemma 1

([9]). (a) G is 2-connected.

• (b) Suppose $v_1v_2$ is an edge of G. If $d(v_1)\le 4$, then $d(v_1)+d(v_2)\ge \Delta +2=10$.

• (c) Suppose $G_{28}$ is a subgraph of G that is induced by the edges joining 2-vertices to 8-vertices. Then $G_{28}$ is a forest.

Lemma 2

([16]). G has no subgraph isomorphic to the configurations depicted in Fig. 1, where $7-v$ is used to denote the vertex of degree of seven. If a vertex is marked by $\bullet$, then it has no more neighbors that are not depicted in G.

Fig. 1.

Reducible configurations of Lemma 2

Lemma 3

([19]). Suppose $v\in V$, $d(v)=d$ and $d\ge 6$. Let v be clockwise adjacent to $v_1,\ldots ,v_d$ and incident with $f_1,f_2,\ldots ,f_d$ such that $v_i$ is the common vertex of $f_{i-1}$ and $f_{i}$ $(i\in \{1,2,\ldots ,d\})$. Notice that $f_0$ and $f_d$ denote a same face. Let $d(v_1)=2$ and $N(v_1)=\{v,u_1\}$. Then G contains none of the following configurations.(see Fig. 2):

• (1) there exists an integer k $(2\le k\le d-1)$ such that $d(v_{k+1})=2$, $d(v_i)=3$ $(2\le i\le k)$ and $d(f_j)=4$ $(1\le j\le k)$.

• (2) there exist two integers k and t $(2\le k<t\le d-1)$ such that $d(v_k)=2$, $d(v_i)=3$ $(k + 1\le i\le t)$, $d(f_t)=3$ and $d(f_j)=4$ $(k\le j\le t-1)$.

• (3) there exist two integers k and t $(3\le k\le t\le d-1)$ such that $d(v_i)=3$ $(k\le i\le t)$, $d( f_{k-1})=d(f_t)=3$ and $d(f_j)=4$ $(k\le j\le t-1)$.

• (4) there exists an integer k $(2\le k\le d-2)$ such that $d(v_d)=d(v_i)=3$ $(2\le i\le k)$, $d(f_k)=3$ and $d(f_j)=4$ $(0\le j\le k-1)$.

Fig. 2.

Reducible configurations of Lemma 3

Lemma 4

([20]). Suppose u is a 6-vertex. If u is incident with one 3-cycle which is incident with a 4-vertex, then $n_{5^+}(u)=5$.

Lemma 5

([17]). G contains no $(6,6,4^+)$-cycles.

Lemma 6

Suppose $v\in G$. If $d(v)=8$ and $n_2(v)\ge 1$, then $n_{5^+}(v)\ge 1$.

Proof

Suppose $G^{'}$ is a subgraph of G. The mapping $\varphi$ is said to be a nice coloring of G if $G^{'}=G-\{v|v\in V,d(v)\le 4\}$ has a $(\Delta +1)$-total-coloring. It is clear that a nice coloring can be easily extended to a $(\Delta +1)$-total-coloring of G, because a $4^-$-vertex has at most 8 forbidden colors. Hence, in the following, we will always assume that every $4^-$-vertex is colored in the end.

Contrarily, we assume that G contains a configuration with $d(v)=8$, $n_2(v)\ge 1$, and $n_{5^+}(v)=0$. Suppose v is a 8-vertex. Let v be clockwise adjacent to $v_1,v_2,\ldots ,v_8$ and incident with $e_1,e_2,\ldots ,e_{8}$ such that $v_i$ is incident with $e_i$ ($i=1,2,\ldots ,8$). Since $d(v_i)\le 4$ ($i=1,2,\ldots ,8$), we uncolor the adjacent vertices of v and color them in the end. We may assume that $d(v_1)=2$. Then the one edge incident with $v_1$ is $e_1$, and the other edge incident with $v_1$ is denoted as $e_9$. Because of the minimality of G, $H=G-e_1$ has a nice coloring. Firstly, suppose $\varphi (e_9)=9$. Otherwise, we color $e_1$ with 9 to get a nice coloring of G, which is a contradiction, so $\varphi (e_9)=9$. We recolor v with 9, and color $e_1$ with 1 to get a nice coloring of G, which is a contradiction. $\square$

3 Discharging

In this section, we will accomplish the proof of Theorem 1 by using discharging method. The discharging method is a familiar and important way to solve coloring problems for a planar graph. By Euler’s formula $|V|-|E|+|F|=2$, we have

$$ \sum _{v\in V}(2d(v)-6)+\sum _{f\in F}(d(f)-6)=-6(|V|-|E|+|F|)=-12<0 $$

We define w(x) of $x\in V\cup F$ to be the original charge function. Let $w(v)=2d(v)-6$ for every $v \in V$ and $w(f)=d(f)-6$ for every$f \in F$. So $\sum _{v \in V\cup F}w(x)<0$. We use $\omega (x\rightarrow y)$ to denote the amount of total charge from x to y. We shall give proper discharging rules and transfer the original charge to get a new charge. We have two rounds of discharging rules. We use $w^{*}(x)$ to denote the charge of $x \in V\cup F$ after the first round of discharging and use $w^{'}(x)$ to denote the charge of $x \in V\cup F$ after the second round of discharging. If there is no discharging rule for $x\in V\cup F$, then the last charge of x is equal to the original charge of x. Notice that the total charge of G is unchangeable after redistributing the original charge, so $\sum _{x \in V\cup F}w^{'}(x)=\sum _{x \in V\cup F}w(x)=-6\chi (\Sigma )=-12<0$. We will get an obvious contradiction by proving that $\sum _{x \in V\cup F}w^{'}(x)\ge 0$.

These are the discharging rules:

• R1. Suppose v is a 2-vertex. If u is adjacent to v, then $\omega (u\rightarrow v)=1$.

• R2. Let f be a face which is incident with v. Suppose $d(v)=4$ or 5. If $d(f)=4$, then $\omega (v \rightarrow f)=\frac{1}{2}$. If $d(f)=5$, then $\omega (v \rightarrow f)=\frac{1}{3}$. Finally v sends the surplus charge to 3-faces incident with it evenly.

• R3. If a 3-face is incident with 6-vertices and $7^+$-vertices, then it receives $\frac{5}{4}$ from $7^+$-vertices.

• R4. Every $7^+$-face sends $\frac{d(f)-6}{d(f)}$ to its adjacent 3-faces.

If $w^{*}(f)<0$ of a $5^-$-face after the first round discharging, then we have the second round discharging:

• R5. If $w^{*}(f)<0$, then f receives $|{\frac{w^{*}(f)}{n_{6^+}(v)}|}$ from every $6^+$-vertices incident it which do not give any charge to f.

Lemma 7

Suppose f is a face which is incident with v.

• 1. If $d(v)=6$, then $\omega (v\rightarrow f)\le \left\{ \begin{array}{ll} \vspace{0.5em} \frac{5}{4}, &{} \text { if } d(f)=3\text { and } n_{4}(f)=1, \\ \vspace{0.5em} \frac{11}{10}, &{} \text { if } d(f)=3\text { and } n_{5}(f)\ge 1, \\ \vspace{0.5em} 1, &{} \text { if } d(f)=3\text { and } n_{6^+}(f)=3, \\ \vspace{0.5em} \frac{7}{8}, &{} \text { if } d(f)=3, n_{5^-}(f)=0\text { and } n_{7^+}(f)=1, \\ \vspace{0.5em} \frac{1}{2}, &{} \text { if } d(f)=3\text { and } n_{7^+}(f)=2, \\ \vspace{0.5em} \frac{2}{3}, &{} \text { if } d(f)=4\text { and } n_{3^-}(f)=1, \\ \vspace{0.5em} \frac{1}{2}, &{} \text { if } d(f)=4\text { and } n_{3^-}(f)=0, \\ \frac{1}{3}, &{} \text { if } d(f)=5. \\ \end{array}\right.$

• 2. If $d(v)\ge 7$, then $\omega (v\rightarrow f)\le \left\{ \begin{array}{ll} \vspace{0.5em} \frac{3}{2}, &{} \text { if } d(f)=3\text { and } n_{3^-}(f)=1, \\ \vspace{0.5em} \frac{5}{4}, &{} \text { if } d(f)=3 \text { and } n_{3^-}(f)=0, \\ \vspace{0.5em} 1, &{} \text { if } d(f)=4 \text { and } n_{3^-}(f)=2, \\ \vspace{0.5em} \frac{3}{4}, &{} \text { if } d(f)=4, n_{3^-}(f)=1 \text { and } n_{4}(f)=1, \\ \vspace{0.5em} \frac{2}{3}, &{} \text { if } d(f)=4, n_{3^-}(f)=1 \text { and } n_{5^+}(f)=3, \\ \vspace{0.5em} \frac{1}{2}, &{} \text { if } d(f)=4 \text { and } n_{3^-}(f)=0, \\ \frac{1}{3}, &{} \text { if } d(f)=5. \\ \end{array}\right.$

Proof

Suppose v is incident with a $4^+$-face f. Then it is clear that Lemma 7 is correct by R2 and R5. Now we think about that f is a 3-face that is incident with v. If $d(v)=6$, then there exist no $3^-$-vertices adjacent to v by Lemma 1(b). If there exists a 4-vertex incident with f, then f is incident with a $7^+$-vertex by Lemma 5. So $\omega (v\rightarrow f)\le 3- \frac{5}{4}-\frac{1}{4}=\frac{5}{4}$. If $n_5(f)=1$ and $n_{6^+}(v)=2$, then $\omega (v\rightarrow f)\le \frac{3-\frac{4}{5}}{2}=\frac{11}{10}$. Suppose $n_5(f)=2$. If there exists one 5-vertex incident with five 3-faces, then the other 5-vertex is incident with at least two $6^+$-faces. So $\omega (v\rightarrow f)\le 3-\frac{4}{5}-\frac{4}{3}\le \frac{11}{10}$. If there exists one 5-vertex incident with four 3-faces, then all of the two 5-vertices are incident with at least one $6^+$-face. So $\omega (v\rightarrow f)\le 3-1\times 2\le \frac{11}{10}$. Suppose $n_{6^+}(f)=3$. Then $\omega (v\rightarrow f)\le \frac{3}{3}=1$. If $n_{5^-}(f)=0$ and $n_{7^+}(f)=1$, then the $7^+$-vertex sends $\frac{5}{4}$ to f by R4, so $\omega (v\rightarrow f)\le \frac{3-\frac{5}{4}}{2}=\frac{7}{8}$. If $n_{7^+}(f)=2$, then $\omega (v\rightarrow f)\le 3-\frac{5}{4}\times {2}=\frac{1}{2}$. If $d(v)\ge 7$, then there exists at most one $3^-$-vertex adjacent to v, so $\omega (v\rightarrow f)\le \frac{3}{2}$. If $n_{3^-}(f)=0$, then $\omega (v\rightarrow f)\le \frac{3-\frac{1}{2}}{2}=\frac{5}{4}$. $\square$

Lemma 8

Suppose $d(v)=8$. Let v be clockwise adjacent to $v_1,v_2,\ldots ,v_n$ $(n\ge 3)$ and incident with $f_1,f_2,\ldots ,f_{n-1}$ such that $f_j$ is incident with $v_j$ and $v_{j+1}$. Clearly, $f_0$ and $f_d$ denote a same face. If $d(v_1)=d(v_n)=2$ and $d(v_i)\ge 3$ $(i=2,3,\ldots ,n-1)$, then $\sum _{i=1}^{n-1}\omega (v \rightarrow f_i)\le \frac{5}{4}n-\frac{9}{4}$.

Proof

By Lemma 2, we know that $d(f_1)\ge 4$ and $d(f_{n-1})\ge 4$. Firstly, suppose $d(f_1)=4$ and $d(f_{n-1})=4$. If $\min \{d(f_2),d(f_3),\ldots ,d(f_{n-2})\}\ge 5$, then $n\ge 4$, so $\sum _{i=1}^{n-1}\omega (v \rightarrow f_i)\le 1\times 2+\frac{1}{3}(n-3) \le \frac{5}{4}n-\frac{9}{4}$. If $\min \{d(f_2),d(f_3),\ldots ,d(f_{n-2})\}=4$ and $\max \{d(f_2),d(f_3),\ldots ,d(f_{n-2})\}=5$, then $\sum _{i=1}^{n-1}\omega (v \rightarrow f_i)\le n-2+\frac{1}{3} \le \frac{5}{4}n-\frac{9}{4}$. If $d(f_2)=d(f_3)=\ldots =d(f_{n-2})=4$, then $\sum _{i=1}^{n-1}\omega (v \rightarrow f_i)\le n-3+\frac{3}{4}\times 2 \le \frac{5}{4}n-\frac{9}{4}$ by Lemma 3. Suppose $\min \{d(f_2),d(f_3),\ldots ,d(f_{n-2})\}=3$ and $\max \{d(f_2),d(f_3),\ldots ,d(f_{n-2})\}=4$. If $d(f_2)=4$ or $d(f_{n-2})=4$, then $\omega (v \rightarrow f_1)+\omega (v \rightarrow f_2)\le \max \{1\times 2,\frac{3}{4}+\frac{5}{4}\}=2$ and $\omega (v \rightarrow f_{n-2})+\omega (v \rightarrow f_{n-1})\le \max \{1\times 2,\frac{3}{4}+\frac{5}{4}\}=2$. Moreover, v sends more charge to 3-faces than 4-faces, so we assume that v is incident with 3-faces as more as possible. Hence, $\sum _{i=1}^{n-1}\omega (v \rightarrow f_i)\le 2\times 2+\frac{5}{4}\times (n-5)\le \frac{5}{4}n-\frac{9}{4}$. Suppose $d(f_2)=d(f_3)=\ldots =d(f_{n-2})=3$, then $f_j$ $(2\le j\le n-2)$ receives at most $\frac{5}{4}$ from v by Lemma 3. Hence, $\sum _{i=1}^{n-1}\omega (v \rightarrow f_i)\le \frac{3}{4}\times 2+\frac{5}{4}\times (n-3) \le \frac{5}{4}n-\frac{9}{4}$. Secondly, suppose $\min \{d(f_1),d(f_{n-1})\}=4$ and $\max \{d(f_1),d(f_{n-1})\}\ge 5$. If $d(f_2)=d(f_3)=\ldots =d(f_{n-2})=3$, then $\sum _i^{n-1}\omega (v \rightarrow f_i)\le \frac{3}{4}+\frac{1}{3}+\frac{3}{2}+\frac{5}{4}\times (n-4)\le \frac{5}{4}n-\frac{9}{4}$. If $\max \{d(f_2),d(f_3),\ldots ,d(f_{n-2})\}=4$, then $\sum _{i=1}^{n-1}\omega (v \rightarrow f_i)\le 1\times 2+\frac{1}{3}+\frac{3}{2}+\frac{5}{4}\times (n-5)\le \frac{5}{4}n-\frac{9}{4}$. Finally, suppose $\min \{d(f_1),d(f_{n-1})\}\ge 5$. Then $\sum _{i=1}^{n-1}\omega (v \rightarrow f_i)\le \frac{1}{3}\times 2+\frac{3}{2}\times 2+\frac{5}{4}\times (n-5)\le \frac{5}{4}n-\frac{9}{4}$. $\square$

In the rest of this paper, we can check that $w^{'}(x)\ge 0$ for every $x\in V\cup F$ which is a contradiction to our assumption. Let $f\in F$. If $d(f)\ge 7$, then $w^{'}(f)\ge w(f)-\frac{d(f)-6}{d(f)}\times d(f)=0$ by R4. If f is a 6-face, then $w^{'}(f)=w(f)=0$. Suppose $d(f)\le 5$. If $n_{6^+}(f)\ge 1$, then $w^{'}(f)\ge 0$ by R5. If $n_{6^+}(f)=0$, then $n_{5}(f)=d(f)$. Suppose $d(f)=3$ and the boundary vertices of f are consecutively $v_1$, $v_2$ and $v_3$. Then $d(v_i)=5$ $(i=1,2,3)$. By R2, $4^+$-face receives at most $\frac{1}{2}$ from incident 4-vertices or 5-vertices. Suppose $f_3(v_i)\le 3$ $(i=1,2,3)$. Then $\omega (v_i \rightarrow f)\ge 1$, so $w^{'}(f)\ge 3-6+1\times 3=0$. Suppose there exists $f_3(v_i)\ge 4$. Without loss of generality, assume that $f_3(v_3)\ge 4$. Then we have $f_3(v_1)\le 4$ and $f_3(v_2)\le 4$. Otherwise, $f_3(v_1)=5$ or $f_3(v_2)=5$, then for any integers $j,k \in \{3,4,5,6,7,8\}$, there exists a vertex incident with adjacent j-cycles and k-cycles. So we get a contradiction to the condition of Theorem 1. If $f_3(v_1)=4$, then $v_1$ is incident with a $9^+$-face and $v_2$ is incident with at least two $6^+$-faces, so $\omega (v_1 \rightarrow f)\ge 1$ and $\omega (v_2 \rightarrow f)\ge 1$. Consequently, $w^{'}(f)\ge 3-6+\frac{4}{5}+1+\frac{4}{3}>0$. Similarly, we know that if $f_3(v_2)=4$, then $w^{'}(f)>0$. Suppose $f_3(v_1)=f_3(v_2)=3$. Then $v_1$ and $v_2$ is incident with at least one $6^+$-face, so $\omega (v_i \rightarrow f)\ge \frac{4-\frac{1}{2}}{3}=\frac{7}{6}$, $(i=1,2)$. Consequently, $w^{'}(f)\ge 3-6+\frac{4}{5}+\frac{7}{6}\times 2>0$. If $d(f)=4$, then $w^{'}(f)\ge 4-6+\frac{1}{2}\times 4=0$ by R2. If $d(f)=5$, then $w^{'}(f)\ge 5-6+\frac{1}{3}\times 5>0$ by R2. So for every $f\in F$, we prove that $w^{'}(f)\ge 0$. Next, we consider that $v\in V$. Suppose $d(v)=2$. Then it is clear that $w(v)=-2$, so $w^{'}(v)=-2+1\times 2=0$ by R1. If $d(v)=3$, then $w^{'}(v)=w(v)=0$. Suppose $d(v)=4$ or $d(v)=5$. Then $w^{'}(v)=0$ by R2.

If v is a $6^+$-vertex of G. Let v be clockwise adjacent to $v_1,\ldots ,v_d$ and incident with $f_1,f_2,\ldots ,f_d$ such that $v_i$ is the common vertex of $f_{i-1}$ and $f_{i}$ $(i\in \{1,2,\ldots ,d\})$. Notice that $f_0$ and $f_d$ denote the same face. Suppose $d(v)=6$. Then there exist no $3^-$-vertices incident with v by Lemma 1 (b). Clearly, $w(v)=2d(v)-6=6$. By Lemma 4, there exist at most two 3-faces incident with a 4-vertex. Hence, if $f_3(v)\le 3$, then $w^{'}(v)\ge 6-\frac{5}{4}\times 2-\frac{11}{10}\times 1-\frac{2}{3}\times 3>0$ by R4. Suppose $f_3(v)=4$. If $f_{5^+}(v)\ge 1$, then $w^{'}(v)\ge 6-\frac{5}{4}\times 2-\frac{11}{10}\times 2-\frac{2}{3}-\frac{1}{3}>0$. If $f_{4}(v)=2$, then there exist three boundary vertices of the two 4-faces adjacent v, that is, all of the two 4-faces are incident with four $4^+$-vertices. Hence, $w{'}(v)\ge 6- \frac{5}{4}\times 2-\frac{11}{10}\times 2-\frac{1}{2}\times 2>0$. Suppose $f_3(v)\ge 5$. If v is adjacent to a 5-vertex $v_0$ and f is a 3-face incident with v and $v_0$, then $f_3(v_0)\le 3$, so $\omega (v_0 \rightarrow f)\ge 1$ and $\omega (v \rightarrow f)\le 1$. Suppose $f_3(v)=5$. If $f_{5^+}(v)=1$, then $w^{'}(v)\ge 6- \frac{5}{4}\times 2-1\times 3-\frac{1}{3}>0$. If $f_{4}(v)=1$, then there exist three boundary vertices of the 4-faces adjacent to v, that is, the 4-face is incident with four $4^+$-vertices. Hence, $w^{'}(v)\ge 6- \frac{5}{4}\times 2-1\times 3-\frac{1}{2}=0$.

Suppose $f_3(v)=6$, that is, $d(f_i)=3$ $(i=1,2,\ldots ,6)$. By Lemma 4, v is incident with at most one 4-vertex. So we may assume that $d(v_6)=4$, then $d(v_1)\ge 7$ and $d(v_5)\ge 7$ by Lemma 5. Suppose $f_{6^+}(v_6)=2$. Then $\omega (v_6 \rightarrow f_5)\ge 1$ and $\omega (v_6 \rightarrow f_6)\ge 1$, so $\omega (v \rightarrow f_5)\le 1$ and $\omega (v \rightarrow f_6)\le 1$. Therefore, $w{'}(v)\ge 6-1\times 6=0$. Otherwise, $f_{5^-}(v)\ge 3$. Let $f_x$ be the $5^-$-face incident with $v_6$ except $f_5$ and $f_6$. Suppose $d(f_x)=5$. Then we get a contradiction to the condition of Theorem 1. Suppose $d(f_x)=4$. Then $v_6$ is adjacent to $v_4$ and $v_1$ is adjacent to $v_3$. So we know that $f_{6^+}(v_6)=1$ and $\omega (v_6 \rightarrow f_i)\ge \frac{2-\frac{1}{2}}{2}=\frac{3}{4}$ $(i=5,6)$. Therefore, $\omega (v \rightarrow f_i)\le 3-\frac{5}{4}-\frac{3}{4}\le 1$ $(i=5,6)$, and $w^{'}(v)\ge 6-1\,\times \,6=0$. Suppose $d(f_x)=3$. Then each of the boundary vertices of f is adjacent to v. If $v_6$ is adjacent to $v_4$ and $v_1$ is adjacent to $v_4$, then $d(v_4)\ge 7$ by Lemma 5. So $\omega (v_4 \rightarrow f_4)=\frac{5}{4}$ and $\omega (v_5 \rightarrow f_4)=\frac{5}{4}$, then $\omega (v \rightarrow f_4)\le \frac{1}{2}$ and $w^{'}(v)\ge 6- \frac{5}{4}\times 2-1\times 3-\frac{1}{2}=0$. If $v_6$ is adjacent to $v_3$ and $v_1$ is adjacent to $v_3$, then $d(v_3)\ge 7$ by Lemma 5. Suppose $d(v_2)\ge 6$ and $d(v_4)\ge 6$. Then $\omega (v \rightarrow f_i)\le \frac{3-\frac{5}{4}}{2}=\frac{7}{8}$ $(i=1,2,3,4)$. Hence, $w^{'}(v)\ge 6- \frac{5}{4}\times 2-\frac{7}{8}\times 4=0$. Suppose $d(v_2)=5$ or $d(v_4)=5$. Without of generality, assume that $d(v_4)=5$. Then $\omega (v_4 \rightarrow f_3)\ge 1$ and $\omega (v_4 \rightarrow f_4)\ge 1$. So $\omega (v \rightarrow f_3)\le 3-1-\frac{5}{4}=\frac{3}{4}$ and $\omega (v \rightarrow f_4)\le 3-1-\frac{5}{4}=\frac{3}{4}$. Therefore, $w^{'}(v)\ge 6-\frac{5}{4}\times 2-1\times 2-\frac{3}{4}\times 2=0$.

Suppose $d(v)=7$. Then it is easy to know that $f_3(v)\le 6$ and v is not adjacent to a $2^-$-vertices by Lemma 1 (b). Clearly, $w(v)=2d(v)-6=8$. Suppose there exist no 3-faces incident with a 3-vertex. If $f_3(v)=6$, then $f_{9^+}(v)=1$, so $w^{'}(v)\ge 8-\frac{5}{4}\times 6>0$ by Lemma 7. If $f_3(v)=5$, then there exist no 4-faces incident with two $3^-$-vertex. So $w^{'}(v)\ge 8-\frac{5}{4}\times 5-\frac{3}{4}\times 2>0$ by Lemma 7. If $f_3(v)\le 4$, then $w^{'}(v)\ge 8-\frac{5}{4}\times 4-1\times 3=0$. Now we presume that there exists at least one 3-face that is incident with a 3-vertex. Then all of the 4-faces are incident with at most one $3^-$-vertex. By Lemma 2, there exist at most two 3-faces incident with a 3-vertex. If $f_3(v)=6$, then $f_{9^+}(v)=1$, so $w^{'}(v)\ge 8-\frac{3}{2}\times 2-\frac{5}{4}\times 4=0$ by Lemma 7. Suppose $f_3(v)=5$. If v is incident with at least one $5^+$-face, then $w^{'}(v)\ge 8-\frac{3}{2}\times 2-\frac{5}{4}\times 3-\frac{2}{3}-\frac{1}{3}>0$ by Lemma 7. Otherwise, $f_4(v)=2$, then there exist three boundary vertices of the 4-face adjacent to v, so $w^{'}(v)\ge 8-\frac{3}{2}\times 2-\frac{5}{4}\times 3-\frac{3}{4}-\frac{1}{2}=0$. Suppose $f_3(v)\le 4$. Then $w^{'}(v)\ge 8-\frac{3}{2}\times 2-\frac{5}{4}\times 2-\frac{3}{4}\times 3>0$ by Lemma 7. If $d(v)=8$, then we know that $w(v)=2\times 8-6=10$, $f_3(v)\le 6$ and $n_2(v)\le 7$ by Lemma 6. By Lemma 7 and Lemma 8, we shall consider the following cases by discussing the number of $n_2(v)$.

Fig. 3.

$n_2(v)=0$ and $f_3(v)=6$

$\textbf{Case}$ $\textbf{1}.$ $n_2(v)=0$. Suppose $f_3(v)=6$. If $f_{6^+}(v)\ge 1$ or $f_{5^+}(v)\ge 2$, then $w^{'}(v)\ge 10-\frac{3}{2}\times 6-1=0$ by Lemma 7. Otherwise, $f_{6^+}(v)=0$ and $f_{5^+}(v)\le 1$. Suppose $f_4(v)=1$ and $f_5(v)=1$. According to the condition of Theorem 1, there is only one case in which the location of the faces satisfying the condition of 1. We depict this case in Fig. 3 (1). It is clear that there exist three boundary vertices of the 4-faces adjacent to v, and there is at least one 3-face which is not incident with a 3-vertex by Lemma 2. If the 4-face is incident with at most one 3-vertex, then $w^{'}(v)\ge 10-\frac{3}{2}\times 5-\frac{5}{4}-\frac{3}{4}-\frac{1}{3}>0$. Otherwise, there exist two 3-vertex incident with the 4-face, then there exist at least two 3-faces that are not incident with a 3-vertex by Lemma 2. Hence, $w^{'}(v)\ge 10-\frac{3}{2}\times 4-\frac{5}{4}\times 2-\frac{3}{4}-\frac{1}{3}>0$. Suppose $f_4(v)=2$. There are only two cases satisfying the condition of Theorem 1. We depict these cases in Fig. 3(2) and (3). In Fig. 3(2), there exist at least four 3-faces all of which are adjacent to a $8^+$-face. By R4, if there exists a $8^+$-face adjacent to a 3-face, then $8^+$-face sends $\frac{1}{4}$ to the 3-face, so each of the 3-face adjacent to a $8^+$-face receives at most $\frac{3-\frac{1}{4}}{2}=\frac{11}{8}$ from the boundary vertices. There exist at most one 4-face incident with two 3-vertices in Fig. 3(2). By Lemma 2, there exist at least one 3-face that is not incident with a 3-vertex, so $w^{'}(v)\ge 10-\frac{3}{2}-\frac{11}{8}\times 4-\frac{5}{4}-1-\frac{3}{4}=0$. In Fig. 3(3), there exist at least four 3-faces all of which are adjacent to a $8^+$-face. By Lemma 2, there is at most one 4-face incident with two 3-vertices. If all of the two 4-faces are incident with at most one 3-vertex, then $w^{'}(v)\ge 10-\frac{3}{2}\times 2-\frac{11}{8}\times 4-\frac{3}{4}\times 2=0$. Otherwise, there exists one 4-face that is incident with two 3-vertices, then there exist at least three 3-faces that are not incident with a 3-vertex by Lemma 2. Hence, $w^{'}(v)\ge 10-\frac{3}{2}\times 3-\frac{5}{4}\times 3-1-\frac{3}{4}=0$. Suppose $f_3(v)=5$. Then by the condition of Theorem 1, we know that $f_{5^+}(v)\ge 1$, so $w^{'}(v)\ge 10-\frac{3}{2}\times 5-1\times 2-\frac{1}{3}\times 2>0$.

$\textbf{Case}$ $\textbf{2}.$ $n_2(v)=1$. Then $2\times 8-6-1=9$.

$\textbf{Case}$ $\mathbf {2.1}.$ Let the 2-vertex be incident with a 3-cycle. It is clear that $f_3(v)\le 6$ and there exist no 3-faces incident with a 3-vertex by Lemma 2. So v is incident with at most one 3-face that receives $\frac{3}{2}$ from v. If $f_3(v)=6$, then by the condition of Theorem 1, we know that $f_{6^+}(v)\ge 1$ or $f_{5^+}(v)\ge 2$, so $w^{'}(v)\ge 9-\frac{3}{2}-\frac{5}{4}\times 5>0$ by Lemma 7. Suppose $f_3(v)=5$. If $f_4(v)=3$, then there are at least two $(8,4^+,4^+,2^+)$-faces between the three 4-faces by Lemma 2. Hence, $w^{'}\ge 9-\frac{3}{2}-\frac{5}{4}\times 4-1-\frac{3}{4}\times 2=0$. If $f_{4}(v)\le 2$, then we have $w^{'}(v)\ge 9-\frac{3}{2}-\frac{5}{4}\times 4-1\times 2-\frac{1}{3}>0$. Suppose $f_3(v)=4$. If $f_4(v)=4$, then there exist at least two $(8,4^+,4^+,2^+)$-faces between the four 4-faces by Lemma 2. Hence, $w^{'}\ge 9-\frac{3}{2}-\frac{5}{4}\times 3-1\times 2-\frac{3}{4}\times 2>0$. If $f_{4}(v)\le 3$, then $w^{'}(v)\ge 9-\frac{3}{2}-\frac{5}{4}\times 3-1\times 3-\frac{1}{3}>0$. If $f_3(v)\le 3$, then $w^{'}(v)\ge 9-\frac{3}{2}-\frac{5}{4}\times 2-1\times 5=0$.

$\textbf{Case}$ $\mathbf {2.2}.$ Let the 2-vertex not be incident with a 3-cycle. Then $f_3(v)\le 6$. Suppose $f_3(v)=6$. Then the six 3-faces are adjacent and $f_{9^+}(v)=1$, so there exist at least four $(8,4^+,4^+)$-faces between the six 3-faces by Lemma 3. Therefore, $w^{'}(v)\ge 9-\frac{3}{2}\times 2-\frac{5}{4}\times 4-1\times 1>0$ by Lemma 7. Suppose $f_3(v)=5$. It is easy to know that $f_{6^+}(v)\ge 1$ by the condition of Theorem 1. If $f_{4}(v)=2$, then there exist three the boundary vertices of the two 4-faces adjacent to v. So v is incident with at least two $(8,4^+,4^+)$-faces and one $(8,4^+,4^+,2^+)$-face by Lemma 3. Hence, $w^{'}(v)\ge 9-\frac{3}{2}\times 3-\frac{5}{4}\times 2-1\times 1-\frac{3}{4}\times 1>0$. If $f_{4}(v)=1$, then there exists at least one $(8,4^+,4^+)$-face between the five 3-faces. by Lemma 3. Hence, $w^{'}(v)\ge 9-\frac{3}{2}\times 4-\frac{5}{4}\times 1-1\times 1-\frac{1}{3}\times 2>0$. If $f_{4}(v)=0$, then $w^{'}(v)\ge 9-\frac{3}{2}\times 5-\frac{1}{3}\times 3>0$. Suppose $f_3(v)=4$. Then we have $f_{4}(v)\le 3$ by the condition of Theorem 1. If $f_{4}(v)=3$, then there exist at least two $(8,4^+,4^+)$-faces between four the 3-faces. Hence, $w^{'}(v)\ge 9-\frac{3}{2}\times 2-\frac{5}{4}\times 2-1\times 3-\frac{1}{3}\times 1>0$. If $f_{4}(v)\le 2$, then $w^{'}(v)\ge 9-\frac{3}{2}\times 4-1\times 2-\frac{1}{3}\times 2>0$. Suppose $f_3(v)=3$. If there exists a $5^+$-face incident with v, then $w^{'}(v)\ge 9-\frac{3}{2}\times 3-1\times 4-\frac{1}{3}>0$. Otherwise, $f_4(v)=5$, then there exist at least three $(8,4^+,4^+,2^+)$-faces between the five 4-faces. Hence, $w^{'}(v)\ge 9-\frac{3}{2}\times 3-1\times 2-\frac{3}{4}\times 3>0$. If $f_3(v)\le 2$, then $w^{'}(v)\ge 9-\frac{3}{2}\times 2-1\times 6=0$.

Fig. 4.

$n_2(v)=2$

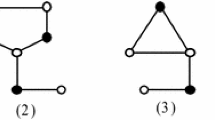
$\textbf{Case}$ $\textbf{3}.$ $n_2(v)=2$. Then $2\times 8-6-2=8$ and there are four cases in which 2-vertices are located. We depict these cases in Fig. 4. In Fig. 4 (1), $w^{'}(v)\ge 8-(\frac{5}{4}\times 8-\frac{9}{4})>0$ by Lemma 8. In Fig. 4 (2), $w^{'}(v)\ge 8-(\frac{5}{4}\times 7-\frac{9}{4})-(\frac{5}{4}\times 3-\frac{9}{4})=0$. In Fig. 4 (3), $w^{'}(v)\ge 8-(\frac{5}{4}\times 6-\frac{9}{4})-(\frac{5}{4}\times 4-\frac{9}{4})=0$. In Fig. 4 (4), $w^{'}(v)\ge 8-(\frac{5}{4}\times 5-\frac{9}{4})\times 2=0$ by Lemma 8.

Fig. 5.

$n_2(v)=3$

$\textbf{Case}$ $\textbf{4}.$ $n_2(v)=3$. Then $2\times 8-6-3=7$ and there are five cases in which 2-vertices are located. We depict these cases in Fig. 5. In Fig. 5(1), $w^{'}(v)\ge 7-(\frac{5}{4}\times 7-\frac{9}{4})>0$ by Lemma 8. In Fig. 5(2), $w^{'}(v)\ge 7-(\frac{5}{4}\times 6-\frac{9}{4})-(\frac{5}{4}\times 3-\frac{9}{4})>0$. In Fig. 5(3), $w^{'}(v)\ge 7-(\frac{5}{4}\times 5-\frac{9}{4})-(\frac{5}{4}\times 4-\frac{9}{4})>0$. In Fig. 5(4), $w^{'}(v)\ge 7-(\frac{5}{4}\times 5-\frac{9}{4})-(\frac{5}{4}\times 3-\frac{9}{4})\times 2=0$. In Fig. 5(5), $w^{'}(v)\ge 7-(\frac{5}{4}\times 3-\frac{9}{4})-(\frac{5}{4}\times 4-\frac{9}{4})\times 2=0$ by Lemma 8.

Fig. 6.

$n_2(v)=4$

$\textbf{Case}$ $\textbf{5}.$ $n_2(v)=4$. Then $2\times 8-6-4=6$ and there are eight cases in which 2-vertices are located. We depict these cases in Fig. 6. In Fig. 6(1), $w^{'}(v)\ge 6-(\frac{5}{4}\times 6-\frac{9}{4})>0$ by Lemma 8. In Fig. 5(2) and (4), $w^{'}(v)\ge 6-(\frac{5}{4}\times 5-\frac{9}{4})-(\frac{5}{4}\times 3-\frac{9}{4})>0$. In Fig. 6(3) and (7), $w^{'}(v)\ge 6-(\frac{5}{4}\times 4-\frac{9}{4})\times 2>0$. In Fig. 6(5) and (6), $w^{'}(v)\ge 6-(\frac{5}{4}\times 3-\frac{9}{4})\times 2-(\frac{5}{4}\times 4-\frac{9}{4})>0$. In Fig. 6(8), $w^{'}(v)\ge 6-(\frac{5}{4}\times 3-\frac{9}{4})\times 4=0$ by Lemma 8.

$\textbf{Case}$ $\textbf{6}.$ $n_2(v)\ge 5$. Suppose $n_2(v)=5$. Then $2\times 8-6-5=5$ and $f_3(v)\le 2$. Suppose $f_3(v)=2$. Then $f_{6^+}(v)\ge 4$ by Lemma 2. Consequently, $w^{'}(v)\ge 5-\frac{3}{2}\times 2-1\times 2=0$ by Lemma 7. If $f_3(v)=1$, then $f_{6^+}(v)\ge 3$ and $f_4(v)\le 4$. If $f_4(v)=4$. then all of the four 4-faces are $(8,4^+,4^+,2^+)$-faces. Hence, $w^{'}(v)\ge 5-\frac{3}{2}\times 1-\frac{3}{4}\times 4>0$. If $f_4(v)\le 3$, then $w^{'}(v)\ge 5-\frac{3}{2}\times 1-1\times 3-\frac{1}{3}>0$. Suppose $f_3(v)=0$. Then $f_{6^+}(v)\ge 2$. If $f_4(v)=6$, then all of the six 4-faces are $(8,4^+,4^+,2^+)$-faces. Hence, $w^{'}(v)\ge 5-\frac{3}{4}\times 6>0$. If $f_4(v)=5$, then there exist at least four $(8,4^+,4^+,2^+)$-faces between the five 4-faces. Hence, $w^{'}(v)\ge 5-1\times 1-\frac{3}{4}\times 4-\frac{1}{3}\times 1>0$. If $f_4(v)\le 4$, then $w^{'}(v)\ge 5-1\times 4-\frac{1}{3}\times 2>0$. Suppose $n_2(v)=6$. Then $2\times 8-6-6=4$ and $f_3(v)\le 1$. If $f_3(v)=1$, then $f_{6^+}(v)\ge 5$ and $f_4(v)\le 2$. So $w^{'}(v)\ge 4-\frac{3}{2}-1\times 2>0$. If $f_3(v)=0$, then $f_{6^+}(v)\ge 4$. Hence, $w^{'}(v)\ge 4-1\times 4=0$. Suppose $n_2(v)=7$. Then by Lemma 2 we know that $f_{6^+}(v)\ge 6$ by and $f_3(v)=0$, so $w^{'}(v)\ge 10-7-1\times 2>0$.

In summary, we know that $w^{'}(x)\ge 0$ for every $x\in V\cup F$, so $\sum _{x \in V\cup F}w^{'}(x)\ge 0$. Hence, we get the desired contradiction and finish the proof of Theorem 1.