Keywords

1 Introduction

In the last years, composite sandwich panels are used in a wide range of structural applications in order to realize lightweight structures designed to guarantee high stiffness and low weight ratio, high fatigue life, high damage tolerance and load capacity, both in compression and in bending. For specific applications, i.e. in automotive, aerospace, marine transportation etc., the technology used for the core realization is significant. In fact, composite sandwich panels with honeycomb, corrugated, tetrahedral, trapezoidal, 3D periodic, origami‐based fold‐cores and hybrid lattice cores have been broadly analyzed for their high mechanical properties in these specific industrial fields. In contrast to the commonly used polymeric foam core, structural cores provide optimal stiffness and strength characteristics, good stability under compressive loads as well as high energy-absorbing capacity and good and corrosion strength.

Between composite core, corrugated-cores offer significant potential for applications in composite construction [1, 2]. In more detail, a corrugated core is constituted by a corrugated composite sheet that keeps the skins apart allowing a high strength-to-weight ratio. In addition to guarantee an elevate bending stiffness and shear strength, an important feature of these structural cores it’s the ability to guarantee optimal ventilation characteristics, preventing moisture problems that are common in polymeric foam or honeycomb cores [1, 3].

However, despite of the remarkable mechanical characteristics of the corrugated core panel, the noticeable bending properties are strongly dependent on the core arrangement. The simplest solution that could be used to reduce this “not always desired” behavior is by placing corrugated core with both longitudinal and transverse directions (bi-directional corrugated core). In more detail, in this work, a corrugated composite sheet was cut into strips (ribbons) that where periodically cross-combined in two different directions and assembled into a novel three-dimensional lattice structure using epoxy resin.

An analysis of the influence of the different parameters involved in defining the core geometry is a complex task if, in the study, advanced numerical techniques are not used [4,5,6,7]. In fact, to reach the (near-) optimum solution is considerably complicated if, as in the current study, the number of independent variables involved in the analysis can be greater than or equal to ten. Recently, several metaheuristics algorithms are successfully employed for solving very complex problems [8]. Metaheuristic is a term that was coined by Glover in 1986 and it is a high-level problem-independent algorithm framework that provides a strategy that “guide” the search process. The goal is to efficiently explore the search space in order to find (near-) optimal solutions. Between them, nature-inspired optimization algorithms are metaheuristic techniques that are developed from the principles of biological evolution, swarm behavior, and physical and chemical processes [9]. Nature-inspired optimization techniques are computational methods that incorporate intelligence techniques within the code. They generate solutions that are close to the optimum (even if not exactly the global optimum) in a finite reasonable amount of time.

In the literature studies there are several metaheuristic techniques: Simulated annealing [10], neural networks [11], genetic algorithm [12], particle swarm [13], ant colony optimization [14], bacterial foraging [15], cuckoo search [16], bat algorithm [17], firefly algorithm [18,19,20], group search optimizer [21, 22], etc. Among them, the Group Search Optimizer (GSO) algorithm is an approximate method, conceptually simple and easy to implement, which is widely used in the literature study to analyze benchmark functions but, until now, it was never implemented in a finite element solver.

In this work, the GSO algorithm was implemented in ANSYS Academic Research Mechanical APDL (release 2022 R1) environment and extensively used to determine the influence of different design variables involved in the definition of the studied bi-directional corrugated core.

2 Novel Bi-directional Corrugated Core

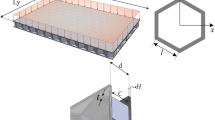
As shown in Fig. 1, the corrugated-core geometry is defined by a repeating a unit cell, characterized by a trapezoidal profile, in two orthogonal directions (x and y). A series of unit cells constitutes a ribbon.

Fig. 1.
figure 1

Schematic representation of the novel bi-directional corrugated core.

Full size image

In more detail, the bi-directional corrugated core is realized by bonding with epoxy resin four different series of ribbons in two different directions (x and y) and on four different layers (increasing z-value) in order to form a three-dimensional lattice structure. Due to the particular stacking sequence, the unit cells of layer 1 and 3 (odd layers) and the unit cells of layer 2 and 4 (even layers) have the same geometry. Specifically, with reference to Fig. 2, the unit cells 1 and 3 have the same size, as well as the unit cells 2 and 4. Figure 2 and Table 1 also shows the main geometric parameters of the unit cells.

Fig. 2.
figure 2

Main geometric parameters of the novel bi-directional corrugated core.

Full size image
Table 1. Main geometric parameters of the unit cells
Full size table

To realize the core structure, a carbon fiber/epoxy composite laminate (CFRP) made of unidirectional layers of Cycom 5320 carbon fiber prepreg was considered [23]. The stacking sequence of the composite laminate is shown in Fig. 3(b), with reference to the local coordinate system situated at the vertex of each area of the unit cell (Fig. 3a).

Fig. 3.
figure 3

(a) Local coordinate system; (b) stacking sequence of the composite laminate for the unit cell 1 and 3

Full size image

In more detail, as shown in the Fig. 3(b), the ribbon is constituted of a symmetric laminate according to the lay-up sequences shown in Table 1.

Two CFRP composite laminates (skins) constituted by 6 layers of unidirectional carbon/epoxy prepreg with stacking sequence [0, 90, 0]s are bonded to the corrugated core by means of epoxy resin. The thickness of the single composite layer is equal to 0.25 mm. Therefore, the total thickness of the skin is equal to 1.5 mm.

Table 2 shows the main mechanical properties of the carbon fiber prepreg. The numerical subscript (1) denotes the direction of the fiber, (2) in-plane transverse to the fibers and (3) through the thickness of each lamina. The letter subscript denotes tensile (t) and compressive (c) while the capital letter F denotes the ultimate stress values.

Table 2. Mechanical properties of Cycom 5320 carbon fiber prepreg
Full size table

The corrugated ribbons can be obtained cutting into strips a corrugated laminate obtained through a mold properly machined (see Fig. 4a). The mold can be also obtained by means of additive manufacturing process [24]. The Fig. 4(b) shows the three-dimensional lattice structure of the core.

Fig. 4.
figure 4

(a) corrugated mold; (b) three-dimensional corrugated core.

Full size image

The mechanical properties of the composite sandwich panel realized with the novel bi-directional corrugated core have been numerically obtained by three-point bending loading configuration. As shown in Fig. 5, the main dimensions are W = 40 mm, L = 200 mm, H = 12 mm, Ls = 180 mm. The applied load is equal to P = 1000 N.

Fig. 5.
figure 5

schematic representation of the three-point bending test configuration.

Full size image

3 Group Search Optimizer (GSO)

In order to study the influence of the main parameters that define the geometry of the novel bi-directional corrugated core, a metaheuristic optimization algorithm called Group Search Optimizer (GSO) was implemented in ANSYS APDL environment. The GSO algorithm was proposed by He et al. in 2006 [21] and it is based on animal searching behavior. This algorithm, as evidenced by several literature studies, shows over time good search performance for complex structural optimization problems. As defined in the original version of the algorithm, there are three kinds of member in the available research space (n-dimensional):

  1. a)

    Producers, that search for opportunities (i.e. food);

  2. b)

    Scroungers, that perform strategies to join the resources found by the others members (in particular by producers).

  3. c)

    Rangers, that perform random searches to avoid entrapment in local minima.

At the kth searching iteration, the member located at the most promising resource is the producer, a specified number of members are classified as scroungers, and the remaining members are selected as rangers.

3.1 Scanning Mechanism of the Producers

General animal scanning mechanism are employed for producers. In more detail, the scanning field in 3D space is a series wedges or cones [22], which were characterized by maximum pursuit angle θmax and maximum pursuit distance lmax (Fig. 6).

Fig. 6.
figure 6

General scanning field in 3D space

Full size image

In particular, in an n-dimensional search space, θmax = π/a2, \(a = round\left( {\sqrt {n + 1} } \right)\), \(l_{\max } = \sqrt {\mathop{\sum}\nolimits_{i = 1}^n {\left( {u_i - l_i } \right)^2 } }\) where ui and li are, respectively, upper and lower bounds for the n-th dimension. In this work, considering that the variables will vary from 0 to 1, \(l_{\max } = \sqrt n\) is the largest diagonal of a unitary n-dimensional hypercube.

At each iteration, the producer searches the space for optimal resources. At the k-th iteration, the member with the best fitness is named \({\varvec{x}}_p^k = (x_1^k ,x_2^k , \ldots ,x_n^k )\), where each value in the vector is ranging from 0 to 1.

The scanning mechanism of the producer consists in the search at zero degrees (forward direction or z direction), one point on the right side (r direction) and on point on the left side (l direction) of the hypercube. In more detail, at the new iteration, the routine determines the three following vectors:

$$ {\varvec{x}}_z^k = {\varvec{x}}_p^k + r_1 l_{\max } {\varvec{D}}^k \left( {{\varvec{\varphi }}^k } \right) $$
(1)
$$ {\varvec{x}}_r^k = {\varvec{x}}_p^k + r_1 l_{\max } {\varvec{D}}^k \left( {{\varvec{\varphi }}^k + r_2 \theta_{\max } /2} \right) $$
(2)
$$ {\varvec{x}}_l^k = {\varvec{x}}_p^k + r_1 l_{\max } {\varvec{D}}^k \left( {{\varvec{\varphi }}^k - r_2 \theta_{\max } /2} \right) $$
(3)

where r1 is a normally distributed random number (with mean 0 and standard deviation 1), \(r_2 \in [0,1]\), D is a unit vector responsible for the search direction (see Eq. 4), φ is the head angle vector (see Eq. 5).

$$ {\varvec{D}}^k \left( {{\varvec{\varphi }}^k } \right) = \left( {d_1^k ,d_2^k ,d_3^k , \ldots ,d_n^k } \right) \in R^n $$
(4)
$$ {\varvec{\varphi }}^k = \left( {\varphi_1^k ,\varphi_2^k ,\varphi_3^k , \ldots ,\varphi_{n - 1}^k } \right) \in R^{n - 1} $$
(5)

The values of the \({\varvec{D}}^k \left( {{\varvec{\varphi }}^k } \right)\) vector can be obtained by the following equations:

$$ d_1^k = \prod_{i = 1}^{n - 1} {\cos \left( {\varphi_i^k } \right)} $$
$$ d_j^k = \sin \left( {\varphi_{j - 1}^k } \right)\prod_{i = j}^{n - 1} {\cos \left( {\varphi_i^k } \right)} \quad \left( {j = 2,3, \ldots ,n - 1} \right) $$
(6)
$$ d_n^k = \sin \left( {\varphi_{n - 1}^k } \right) $$

At the first iteration, the initial head angle vector φ1 is set to \(\left( {\frac{\pi }{4},\frac{\pi }{4},\,...\,,\frac{\pi }{4}} \right)\,\). The following values are obtained by the Eq. 7.

$$ {\varvec{\varphi }}^{k + 1} = {\varvec{\varphi }}^k + r_2 \,\alpha_{\max } $$
(7)

where \(\alpha_{\max } = \frac{{\theta_{\max } }}{2}\) is the maximum turning angle. If the producer cannot find a better result after “a” iterations, the head angle vector is set to the initial one.

3.2 Scrounging Mechanism

In this work, the commonest scrounging behavior explained in [22] is adopted. In more detail, at each iteration, all the selected scroungers perform a movement toward the producer (see Eq. 8).

$$ {\varvec{x}}_S^{k + 1} = {\varvec{x}}_S^k + r_3 \circ \left( {{\varvec{x}}_P^k - {\varvec{x}}_S^k } \right) $$
(8)

where \(r_3 \in [0,1]\), while the operator “∘” is the Hadamard product to compute the product of the two vectors. During iterations, if the algorithm computes a better solution for the scrounger, the software automatically updates the position of producer and scrounger.

3.3 Ranger Simulations

In GSO algorithm, dispersed members are called rangers. In particular, at each producer it possible to associate several rangers. Each ranger performs a random walk in the available research space. In the APDL routine, in the contrary of the common procedures, three different possibility of ranger simulations are available:

  1. a)

    by randomly selecting the design variables in the whole search space;

  2. b)

    by randomly selecting the design variables in a producer-centric search space;

  3. c)

    with a combination of a) and b).

During iterations, if the algorithm computes a better solution for the ranger, the software automatically updates the position of producer and ranger.

4 Finite Element Analysis

The GSO algorithm was implemented in several macros realized in ANSYS APDL language [25,26,27,28,29]. The geometry of the composite sandwich panel was modeled by means of the parametric definition of keypoints and areas. Shell181 elements, suitable for analyzing thin to moderately-thick shell structures, were used to discretize the ribbon areas of the corrugated core and the skin surfaces. An average element size equal to 0.5 mm was used to discretize the model. Orthotropic material properties were defined using the same laminate coordinate system shown in Fig. 3. As shown in Table 3, ten Design Variables (DV) were defined for the optimization problem (see also Table 1). In particular, the design variables DV_i (i = 1, 2, …, 10) are decimal numbers in the range [0, 1]; a specific ANSYS macro converts the decimal number into a variable allowing to define the geometry of the corrugated core.

Table 3. Design variables of the optimization problem
Full size table

As example, the following figures show, respectively, the geometry of the composite sandwich panel for δ1 = δ2 = 10°, l1 = l2 = 2 mm (Fig. 7a) and δ1 = δ2 = 60°, l1 = l2 = 2 mm (Fig. 7b).

Fig. 7.
figure 7

ANSYS model for different geometric characteristics: (a) δ1 = δ2 = 10°, l1 = l2 = 2 mm; (b) δ1 = δ2 = 60°, l1 = l2 = 2 mm

Full size image

At the end of each analysis, in order to determine if the composite sandwich panel reaches the failure condition, an appropriate macro calculates the failure index IF. As already made in a previous work [21], the failure index IF was determined by using the Tsai-Wu criterion. In more detail, the failure is predicted when IF ≥ 1 in at least one node of the numerical model.

4.1 Optimization Study

As input parameters, 3 producers, 3 scroungers and 3 rangers were defined as members of the structural optimization problem. The first analysis involves the execution of random simulations in order to initialize the first feasible members. In more detail, an APDL routine generates random design variables (see Table 3) that allow the definition of the numerical model of the composite sandwich panel. The 10 design variables are stored in a row of a specific array. Each row is defined as a “member” of the analysis. The ANSYS macros automatically apply load and constraints on the model (with the same load configuration shown in the Fig. 5) determining the Tsai-Wu failure index IF, the stiffness and the total weight of the composite. The achievement of a Tsai-Wu failure index IF ≤ 1was selected as State Variable SV, while the achievement of the minimum weight was selected as Objective Function Value (OFV) of the optimization problem. At the end of the random analysis, the routine sorts the feasible members according to the increasing OFV defining the first optimal geometry of the composite sandwich panel (first best member).

In subsequent iteration cycles, the operations carried out during the execution of the GSO Algorithm are described below.

  1. 1)

    For each producer member, the routine scans at zero degree and then scan laterally by using Eqs. 1 to 3. If the weight of the new geometry is less than the optimal one, the macro generates the sandwich composite model and then calculates the stiffness and the Tsai-Wu failure index IF. This member will be considered as “feasible” only when IF ≤ 1. In this case, this current member has a better resource than the optimal one and, therefore, the new best member was found. Otherwise it will stay in its current position and turn its head to a new angle using Eq. 7. If the producer cannot find a better area after “a” iterations, it will turn its head back to zero degree initializing the head angle vector.

  2. 2)

    As already mentioned, for each producer member, the analysis considers three scroungers. Each scrounger member performs a movement toward the producer using Eq. 8. If the algorithm computes a better weight of the composite than the optimal one, the software automatically generates the model verifying the compliance with the condition IF ≤ 1. In this case, the algorithm updates the position of producer and scrounger redefining the new best member.

  3. 3)

    For each producer member, three rangers perform random searches as already shown in the Sect. 3.3 (methodology c).

As shown in the Fig. 8, the GSO algorithm needs less than 80 iterations to converge to the optimal solution. In particular, Fig. 8 shows the convergence analysis for 10 independent run of the algorithm. The analysis time is approximately 1.45 h on a Windows-based workstation equipped with Xeon E5-2630 2.4 GHz CPU and 32 GB of RAM.

The minimum weight of the composite sandwich panel is equal to W* = 32.67 g with Tsai-Wu failure index IF = 0.998. The optimal design variables are shown in Table 4. Table 5 shows, instead, the optimal values of the main geometric parameters of the novel bi-directional corrugated core.

Fig. 8.
figure 8

Convergence analysis

Full size image
Table 4. Best design variables of the composite sandwich panel
Full size table
Table 5. Best geometric parameters of the composite sandwich panel
Full size table

The Fig. 9(a) shows the optimal geometry of the core. The Fig. 9(b) shows a detail of the discretization realized on the model.

Fig. 9.
figure 9

Optimal geometry of the corrugated core; (b) detail of the mesh realized on the model.

Full size image

The maximum deflection of the composite sandwich panel is equal to zmax = 1.21 mm (see Fig. 10) while the corresponding stiffness is equal to K = 826.5 N/mm.

Fig. 10.
figure 10

Maximum deflection of the optimal geometry of the composite sandwich panel

Full size image

A specific study was also conducted to verify the influence of the random analyses in the determination of the optimal result. In particular, 5000 independent random analyses were started recording, in a specific array, only the unique results obtained (see Fig. 11).

Fig. 11.
figure 11

Totality of random analyses

Full size image

In particular, out of 5000 random iterations, 1103 unique results were recorded. The best random result is equal to 37.61 g that is greater than about 13% of the best result obtained by using the GSO algorithm. Moreover, the random analyses were concluded after 82.6 h, which are about 57 times greater than the time needed to complete the numerical simulations using the GSO algorithm.

5 Conclusions

The Group Search Optimizer (GSO) is an optimization algorithm inspired by animal behavior used to solve highly constrained problems. In the literature study, the algorithm is used to analyze systems in dominant subject areas, i.e. engineering, computer science, robotic, etc. confirming to be one of the most promising methods providing, in some cases, higher performance than other important heuristic methods. However, until now, the algorithm was never implemented in a finite element solver. In this work, the GSO algorithm is implemented in ANSYS APDL environment in order to determine the optimal geometric parameters of a novel bi-directional corrugated core used to realize a CFRP composite sandwich panel. In particular, the optimization study involves the determination of the minimum weight of the analyzed model subject to three-point bending loading. The study shows that using the methodology of analysis presented here it is possible to optimize the structure of the core with high accuracy (up to 13% if we compare the achieved optimal result with that obtained from only random analyses), with significantly reduced analysis time (about 57 times lower) and satisfactory repeatability of results.

In conclusion, GSO algorithm can be considered an interesting alternative method for solving complex optimization problems. The implementation in an ANSYS environment of the presented code has a perspective of extending to optimization of large scale models, to analyze structures with complicated geometries (considering linear or nonlinear effects) and to determine material properties where analytical solutions cannot be easily obtained.