Keywords

Mathematics Subject Classification (2010)

1 Introduction

Viscoelastic materials, as their name suggests, combine two different properties: viscosity and elasticity. They are used for isolating vibration, dampening noise, and absorbing shock. They are intended to dissipate mechanical energy from vibrations or noises, to limit their propagation in structures, they have a decisive impact on the fatigue of these structures and on our comfort.

Viscoelastic materials have applications in all fields of engineering and mechanical systems, from the automotive to civil engineering, from space to home appliances (engine and machine mounts and supports, transmission seals and belts, glazing edges and fixing of subsystems, damping of metal plates and shells, parts of seats and interior of cabs, tire and wheels, tuned damping systems) [7, 15, 24, 40].

Since the 1980s, the development of modern technologies has required the use of innovative materials with high mechanical properties, suitable for their use, and having low densities. A composite material meets most of these requirements; it is a kind of mixture of different materials whose properties are superior to each of its components taken separately. These materials were first developed and used in the 1940s in the aeronautical field (essentially for military airplanes and helicopters) and are today in automobile construction, in shipbuilding, and in buildings. But these materials are excellent transmitters of mechanical and acoustic vibrations, which can affect the integrity of the entire system. Also, thanks to these composite materials it is possible to reduce the number of parts of a structure, there would then be less frictions at connections between elements. It is, therefore, imperative to associate with these materials effective damping techniques. One solution is to add full or partial layers of viscoelastic materials, glued on (or incarnated between) the parts. A viscoelastic product can be integrated into the composite material [28, 36].

In this context we have chosen to study a network of elastic and viscoelastic materials; More precisely, we investigate the asymptotic stability of a graph of elastic strings with local Kelvin–Voigt damping.

Models of the transient behavior of some or all of the state variables describing the motion of flexible structures have been of great interest in recent years, for more details about physical motivation for the models, see also [23, 29], and the references therein. Mathematical analysis of transmission partial differential equations is detailed in [29]. For the feedback stabilization problem for the wave or Schrödinger equations (in networks, in particular), we refer the readers to references [3,4,5,6, 8,9,10,11,12,13, 29].

A wave equation on a (single) string of length ℓ, with (local) Kelvin–Voigt damping is modeled by the following equation

$$\displaystyle \begin{aligned} \frac{\partial^2 u}{\partial t^2} - \, \frac{\partial }{\partial x} \left( \frac{\partial u}{\partial x} + a(x) \, \frac{\partial^2 u}{\partial x \partial t} \right) = 0\;\;\;\text{in}\;\;\;(0,\ell)\times (0,\infty), {} \end{aligned} $$
(1)

where a(x), x ∈ [0, ℓ] is a nonnegative function.

As boundary conditions, we often associate the Dirichlet conditions:

$$\displaystyle \begin{aligned} u(0,t)=u(\ell,t)=0. \end{aligned}$$

From a mathematical point of view, the Kelvin–Voigt damping model (1) has been studied by several authors. let us recall some results in the literature,

  • Huang proved in 1988 [27] that when the damping is global (i.e., distributed over the entire domain), the corresponding semigroup is not only exponentially stable but also analytic. Thus, the Kelvin–Voigt damping is much stronger than the viscous damping (i.e., the damping term is replaced by \(-a(x)\, \frac {\partial u}{\partial t}\)), where the corresponding semigroup is only exponentially stable and not analytic (see, e.g., [21] and [18]).

    Such a comparison is not valid anymore if the damping is localized:

  • Chen et al. [21] proved in 1991 that in the case of localized viscous damping, the associated semigroup is exponentially stable no matter the size or the location of the subinterval where the damping is effective, and even if the damping coefficient function has a jump discontinuity at the interface.

However, the local Kelvin-Voigt damping does not follow the same analogue.

  • It was first proved in 1998 by S. Chen et al. [30] that, when the viscoelastic damping is locally distributed ( precisely, they took a(x) = a 0 χ (α,β), with a 0 > 0), the associated semigroup is not exponentially stable.

  • In 2002, K. Liu and Z. Liu [31] proved that if \(a \in \mathcal {C}^{2}[0,\ell ]\), and \(\int _0^\ell a(x)dx>0\), then the system is exponentially stable: the asymptotic behavior depends on the regularity of the damping coefficient.

The works cited below consider the domain [−1, 1] instead of [0, ℓ] and suppose that a(x) = 0 on [−1, 0) and a(x) = b(x) on (0, 1].

  • In 2004, Renardy [41] supposed that a(x) = 0 on [−1, 0] and a(x) > 0 on (0, 1] and he assumed that

    $$\displaystyle \begin{aligned} \lim\limits_{x\rightarrow 0^+}\frac{a^\prime(x)}{x^\alpha}=k>0\;\;\text{ for some}\;\;\alpha>0, {} \end{aligned} $$
    (2)

    then the eigenvalues of the system (1) are such that the decay rate tends to infinity with frequency.

  • Z. liu and B. Rao [32], 2005, and M. Alves et al. [2], 2014, proved that if b(x) ≥ c > 0 on (0, 1) and \(b \in \mathcal {C}(0,1).\) The associated semigroup is polynomially stable of order 2.

  • In 2010, Q. Zhang [43] improved the result in [32]: the author took \(a \in \mathcal {C}^{1}[-1,1],\) b(0) = b ′(0) = 0 and supposed the existence of a positive constant c such that \(\int _0^x\frac {\vert b^\prime (s)\vert ^2}{b(s)}ds \leq c \vert b^\prime (x)\vert \) for all x ∈ [0, 1], (for example, b(x) = x α, α > 1).

  • In 2016 Z. Liu and Q. Liu [35] took over the condition (2) of Renardy. Precisely they took a ∈ L ∞(−1, 1), b(x) > 0 on (0, 1] and b(0) = 0; b ′, b ′′∈ L ∞(0, 1), and supposed that \(\lim \limits _{x\rightarrow 0^+}\frac {a(x)}{x^\alpha }=k>0.\) Then the system (1) is exponentially stable for α = 1 and polynomially, nonexponentially stable for 0 ≤ α < 1.

  • It is proved [33] in 2017 that if \(a \in \mathcal {C}^1[-1,1]\) and satisfies conditions in the last point, then the system (1) remains exponentially stable for α > 1.

In this work we study a more general case, it is about a network of strings with local Kelvin–Voigt damping.

We first introduce some notations needed to formulate the problem under consideration (as introduced in [1, 37] or [7]. Let \({\mathcal G}\) be a planar connected graph embedded in \(\mathbb {R}^3,\) with N edges e 1, …, e N, N ≥ 1 and p vertices s 1, …, s p, p ≥ 2. By degree of a vertex of \(\mathcal {G}\) we mean the number of edges incident at the vertex. If the degree is equal to one, the vertex is called exterior; otherwise, it is said to be interior. We denote by I int and I ext, respectively, the sets of indices of interior and exterior vertices, then I := I int ∪ I ext is the set of indices of all vertices. Finally, we define J := {1, ⋯ , N} and for k ∈ I, we will denote by J k the set of indices of edges adjacent to the vertex s k. If k ∈ I ext, then the unique element of J k will be denoted by j k.

The length of the edge e j is denoted by ℓ j. Then, e j may be parametrized by its arc length by means of the functions π j : [0, ℓ j]→e j, x↦π j(x). But sometimes, we identify e j with the interval (0, ℓ j).

For a function \( \underline {u}:\mathcal {G}\longrightarrow \mathbb {C}\) we set \(u_j= \underline {u}\circ \pi _j\) its restriction to the edge e j. For simplicity, we will write \( \underline {u}=(u_1,\ldots ,u_N)\) and we will denote u j(x) = u j(π j(x)) for any x ∈ (0, ℓ j).

The incidence matrix D = (d kj)p×N is defined by,

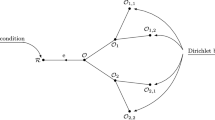
$$\displaystyle \begin{aligned} d_{kj}=\left\{ \begin{array}{l} 1\mbox{ if }\pi _{j}(\ell _{j})=s_{k}, \\ -1\mbox{ if }\pi _{j}(0)=s_{k}, \\ 0\mbox{ otherwise.} \end{array} \right. \end{aligned}$$

Suppose that the equilibrium position of our network of elastic strings coincides with the graph \(\mathcal {G}.\) Then, we consider the following initial and boundary value problem (Fig. 1):

$$\displaystyle \begin{aligned} \frac{\partial^2 u_{j}}{\partial t^2}(x,t) - \, \frac{\partial }{\partial x} \left( \frac{\partial u_{j}}{\partial x} + a_{j}(x) \, \frac{\partial^2 u_{j}}{\partial x \partial t} \right) (x,t) = 0, \quad 0<x<\ell_{j},\ t>0, \, j \in J, \end{aligned} $$
(3)
$$\displaystyle \begin{aligned} u_{j_{k}}(s_{k},t)=0, \, k \in I_{ext}, \, t >0, \end{aligned} $$
(4)
$$\displaystyle \begin{aligned} u_{j}(s_{k},t)= u_{l}(s_{k},t), \quad t>0, \, j,l\in J_{k},\;\;k\in I_{int}, \end{aligned} $$
(5)
$$\displaystyle \begin{aligned} \displaystyle \sum_{j\in J_{k}}d_{kj} \left( \frac{\partial u_{j}}{\partial x}(s_{k},t)+a_{j}(s_{k}) \frac{\partial^2 u_{j}}{\partial x \partial t}(s_{k},t) \right) = 0, \quad t>0, \, k \in I_{int}, \end{aligned} $$
(6)
$$\displaystyle \begin{aligned} u_{j}(x, 0) = u^0_{j}(x), \, \frac{\partial u_{j}}{\partial t} (x, 0) = u^1_{j}(x), \quad 0<x<\ell_{j}, \, j \in J, \end{aligned} $$
(7)

where u j : [0, ℓ j] × (0, +∞) →ℝ, j ∈ J, be the transverse displacement in e j, a j ∈ L ∞(0, ℓ j) and, either a j is zero, that is, e j is a purely elastic edge, or there exists a subinterval w j of (0, ℓ j), nonreduced to a singleton, such that a j(x) > 0, a.e. on w j. Such edge will be called a K-V edge.

Fig. 1
figure 1

A Graph

Full size image

We assume that \(\mathcal {G}\) contains at least one K-V edge and contain at least one external node (i.e., \(I_{ext} \neq \varnothing \)). Furthermore, we suppose that every maximal subgraph of purely elastic edges is a tree, whose leaves are attached to K-V edges.

Our aim is to prove, under some assumptions on damping coefficients a j, j ∈ J, exponential and polynomial stability results for the system (3)–(7).

We define the natural energy E(t) of a solution \( \underline {u} = (u_{j})_{j \in J}\) of (3)–(7) by

$$\displaystyle \begin{aligned} E(t)=\frac{1}{2} \displaystyle \sum_{j \in J} \int_0^{\ell_{j}} \left( \left|\frac{\partial u_{j}}{\partial t}(x,t)\right|{}^2 + \left|\frac{\partial u_{j}}{\partial x}(x,t)\right|{}^2 \right) \, dx. \end{aligned} $$
(8)

It is straightforward to check that every sufficiently smooth solution of (3)–(7) satisfies the following dissipation law

$$\displaystyle \begin{aligned} \frac{d}{dt} E(t) = - \displaystyle \sum_{j \in J} \int_0^{\ell_{j}} a_{j}(x) \, \left|\frac{\partial^2 u_{j}}{\partial x \partial t}(x,t)\right|{}^2 \, dx \leq 0, \end{aligned} $$
(9)

and; therefore, the energy is a nonincreasing function of the time variable t.

The main results of this paper then concern the precise asymptotic behavior of the solutions of (3)–(7). Our technique is a special frequency domain analysis of the corresponding operator.

This work is organized as follows: In Sect. 2, we give the proper functional setting for system (3)–(7)and prove that the system is well-posed. In Sect. 3, we analyze the resolvent of the wave operator associated with the dissipative system (3)–(7) and prove the asymptotic behavior of the corresponding semigroup. For more details in the proofs, see [14].

2 Well-Posedness of the System

In order to study system (3)–(7) we need a proper functional setting. We define the following space

$$\displaystyle \begin{aligned}{\mathcal H} = V \times H, \end{aligned}$$

where H =∏ j ∈ JL 2(0, ℓ j) and

$$\displaystyle \begin{aligned} u_{j}(s_k)= u_{l}(s_k):=\underline{u}(s_k), \,\,k\in I_{int},\;\; j,l \in J_{k}, \end{aligned} $$
(10)

and equipped with the inner products

$$\displaystyle \begin{aligned} <(\underline{u},\underline{v}, (\underline{\tilde{u}},\underline{\tilde{v}})>_{{\mathcal H}}= \displaystyle \sum_{j \in J} \int_0^{\ell_{j}} \left( v_{j}(x) \, \bar{\tilde{v}}_{j}(x) + u^\prime_{j}(x) \, \bar{ \tilde{u}}^\prime_{j}(x)\right)\, dx. \end{aligned} $$
(11)

System (3)–(7) can be rewritten as the first order evolution equation

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\partial }{\partial t} \left( \begin{array}{c} \underline{u} \\ \frac{\partial \underline{u}}{\partial t} \end{array} \right) =\mathcal{A} \left( \begin{array}{c} \underline{u} \\ \frac{\partial \underline{u}}{\partial t} \end{array} \right),\\ \underline{u}(0)= \underline{u}^{0}, \, \displaystyle \frac{\partial \underline{u}}{\partial t} = \underline{u}^{1}\end{array}\right.{} \end{aligned} $$
(12)

where the operator \(\mathcal {A} : {\mathcal D}(\mathcal {A}) \subset {\mathcal H} \rightarrow {\mathcal H}\) is defined by

$$\displaystyle \begin{aligned}\mathcal{A} \left( \begin{array}{c} \underline{u} \\ \underline{v} \end{array} \right):= \left( \begin{array}{c} \underline{v} \\ ( \underline{u^{\prime}} + \underline{a} * \underline{v^{\prime}} )^\prime \end{array} \right), \end{aligned}$$

with

$$\displaystyle \begin{aligned}\underline{a} := (a_{j})_{j \in J} \; \;\text{and}\; \; \underline{a} * \underline{v^{\prime}} := (a_{j} v^{\prime}_{j})_{j \in J}, \end{aligned}$$

and

$$\displaystyle \begin{aligned}{\mathcal D}(\mathcal{A}):= \left\{(\underline{u}, \underline{v}) \in \mathcal{H}, \, \underline{v} \in V, ( \underline{u^{\prime}} + \underline{a} * \underline{v^{\prime}} ) \in \displaystyle \prod_{j \in J} H^1(0,\ell_{j})\,: (\underline{u}, \underline{v}) \, \mbox{satisfies} \, (\mbox{13}) \right\}, \end{aligned}$$
$$\displaystyle \begin{aligned} \displaystyle \sum_{j \in J_k} d_{kj}\left( u^\prime_{j}(s_k)+ a_{j}(s_k) v^{\prime}_{j}(s_k)\right), \quad \,t>0,\; k \in I_{int}. \end{aligned} $$
(13)

Lemma 2.1

The operator \(\mathcal {A}\) is dissipative, \(0 \in \rho (\mathcal {A}):\) the resolvent set of \(\mathcal {A}.\)

Proof

For \(( \underline {u}, \underline {v})\in \mathcal {D}(\mathcal {A}),\) we have

$$\displaystyle \begin{aligned} Re(\left\langle \mathcal{A}(\underline{u},\underline{v}),(\underline{u}, \underline{v})\right\rangle _{\mathcal{H}})=Re\sum_{j\in J}\left( \int_{0}^{\ell _{j}}v^{\prime}_{\bar{ \alpha }}\overline{u^{\prime}_{j}}dx+\int_{0}^{\ell _{j}}(u^{\prime}_{j}+a_{ j}v^{\prime}_{j})^{\prime}\overline{v_{ j}}dx\right).\end{aligned} $$

Performing integration by parts and using transmission and boundary conditions, a straightforward calculations leads to

$$\displaystyle \begin{aligned} Re(\left\langle \mathcal{A}(\underline{u},\underline{v}),(\underline{u}, \underline{v})\right\rangle _{\mathcal{H}})=-\sum_{j\in J}\int_{0}^{\ell _{j}}a_{j}(x)\left| v^{\prime}_{j}(x)\right|{}^{2}dx\leq 0\end{aligned} $$

which proves the dissipativeness of the operator \(\mathcal {A}\) in \( \mathcal {H}.\)

Next, using Lax–Milgram’s lemma, we prove that \(0 \in \rho (\mathcal {A}).\) For this, let \((f,g)\in \mathcal {H}\) and we look for \(( \underline {u}, \underline {v})\in \mathcal {D}(\mathcal {A})\) such that

$$\displaystyle \begin{aligned} \mathcal{A}(\underline{u},\underline{v})=(\underline{f}, \underline{g})\end{aligned} $$

which can be written as

$$\displaystyle \begin{aligned} \begin{array}{rcl} v_{j} & =&\displaystyle f_{j},\; j\in J, {} \end{array} \end{aligned} $$
(14)
$$\displaystyle \begin{aligned} \begin{array}{rcl} (u^{\prime}_{j}+a_{ j}v^{\prime}_{j})^{\prime} & =&\displaystyle g_{j},\;j\in J. {} \end{array} \end{aligned} $$
(15)

\( \underline {v}\) is completely determined by (14). Let \( \underline {w} \in V\); multiplying (15) by w j, then summing over j ∈ J, we obtain, using transmission and boundary conditions,

$$\displaystyle \begin{aligned} \sum_{j\in J}\int_{0}^{\ell _{j}}\left( u^{\prime}_{j}+a_{j}v^{\prime}_{j}\right) \overline{w^{\prime}_{j}}dx =-\sum_{j\in J}\int_{0}^{\ell _{j}}g_{j}\overline{w_{j}} dx. {} \end{aligned} $$
(16)

Replacing v j in the last equality by (14), we get

$$\displaystyle \begin{aligned} \varphi (\underline{u},\underline{w})=\psi (\underline{w}), {} \end{aligned} $$
(17)

where

$$\displaystyle \begin{aligned} \varphi (\underline{u},\underline{w})=\sum_{j\in J} \int_{0}^{\ell _{j}}u^{\prime}_{j}\overline{w^{\prime}_{ j}} \end{aligned}$$

and

$$\displaystyle \begin{aligned} \psi (\underline{w})=-\sum_{j\in J}\left( \int_{0}^{\ell _{ j}} g_{j} \, \overline{ w_{j}}dx+\int_{0}^{\ell _{j}}a_{j}f^{\prime}_{j}\overline{w^{\prime}_{ j}}dx\right). \end{aligned}$$

The function φ is a continuous sesquilinear form on V × V and ψ is a continuous anti-linear form on V ; here V is equipped with the inner product

$$\displaystyle \begin{aligned} \left\langle \underline{f},\underline{g}\right\rangle =\sum_{j\in I}\int_{0}^{\ell _{j}}u^{\prime}_{j}\overline{w^{\prime}_{ j}}. \end{aligned}$$

Since φ is coercive on V, by the Lax–Milgram lemma, equation (17) has a unique solution \( \underline {u} \in V.\) Then taking \( \underline {w} \in \displaystyle \prod _{j \in J} \mathcal {D}(0,\ell _{j})\) in (17) and integrating by parts, we deduce that \(( \underline {u^{\prime }} + \underline {a} * \underline {v^{\prime }} ) \in \displaystyle \prod _{j \in J} H^1(0,\ell _{j})\) and \(( \underline {u}, \underline {v})\) satisfies (15). Moreover \(( \underline {u}, \underline {v})\) satisfies (13).

Return back to the Lax–Milgram lemma, \(( \underline {u}, \underline {v})\) verifies

$$\displaystyle \begin{aligned}\left\| (\underline{u},\underline{v})\right\|{}_{\mathcal{H}} \leq \left\| (\underline{f},\underline{g})\right\|{}_{\mathcal{H}}.\end{aligned}$$

In conclusion \(( \underline {u}, \underline {v}) \in \mathcal {A}\) and \(\mathcal {A}^{-1} \in \mathcal {L}(\mathcal {H}),\) which assert that \(0 \in \rho (\mathcal {A}).\) □

By the Lumer–Phillip’s theorem (see [38, 42]), we have the following proposition.

Proposition 2.2

The operator \(\mathcal {A}\) generates a \(\mathcal {C} _{0}\) -semigroup of contraction (S d(t))t≥0 on the Hilbert space \(\mathcal {H}\).

Hence, for an initial datum \(( \underline {u}^{0}, \underline {u}^{1}) \in {\mathcal H}\) , there exists a unique solution \(\left ( \underline {u}, \frac {\partial \underline {u}}{\partial t} \right )\in C([0,\,+\infty ),\, {\mathcal H})\) to problem (12). Moreover, if \(( \underline {u}^{0}, \underline {u}^{1}) \in \mathcal {D}(\mathcal {A})\) , then

$$\displaystyle \begin{aligned}\left(\underline{u},\frac{\partial \underline{u}}{\partial t} \right) \in C([0,\,+\infty),\, \mathcal{D}(\mathcal{A})).\end{aligned}$$

Furthermore, the solution \(( \underline {u},\frac {\partial \underline {u}}{\partial t})\) of (3)–(7)with initial datum in \(\mathcal {D}(\mathcal {A})\) satisfies (9). Therefore, the energy is decreasing.

3 Asymptotic Behavior

In order to analyze the asymptotic behavior of system (3)–(7), we shall use the following characterizations for exponential and polynomial stability of a \(\mathcal {C}_{0}\)-semigroup of contraction:

Lemma 3.1 ([26, 39])

A \(\mathcal {C}_{0}\) -semigroup of contraction \((e^{t\mathcal {B}})_{t \geq 0}\) defined on the Hilbert space \(\mathcal {H}\) and such that

$$\displaystyle \begin{aligned} \mathbf{i}\mathbb{R}\subset \rho (\mathcal{B}) {} \end{aligned} $$
(18)

is exponentially stable if and only if

$$\displaystyle \begin{aligned} \limsup_{\beta \in \mathbb{R}, \left| \beta \right| \rightarrow +\infty} \left\| (\mathbf{i} \beta \mathcal{I}-\mathcal{B})^{-1}\right\|{}_{\mathcal{L}(\mathcal{H} )}<\infty. {} \end{aligned} $$
(19)

Lemma 3.2 ([19])

A \(\mathcal {C}_{0}\) -semigroup of contraction \((e^{t\mathcal {B}})_{t \geq 0}\) on the Hilbert space \(\mathcal {H}\) such that \(i \mathbb {R} \subset \rho (\mathcal {B})\) satisfies

$$\displaystyle \begin{aligned} \left\| e^{t\mathcal{B}}\right\|{}_{\mathcal{L}(\mathcal{D}(\mathcal{B}),\mathcal{H})} \leq \frac{C}{t^{\frac{1}{\alpha }}} \end{aligned}$$

for some constant C > 0 and for α > 0 if and only if

$$\displaystyle \begin{aligned} \limsup_{\beta \in \mathbb{R}, \left| \beta \right| \rightarrow +\infty} \frac{1}{ |\beta|{}^{\alpha }}\left\| (\mathbf{i}\beta \mathcal{I}-\mathcal{B} )^{-1}\right\|{}_{\mathcal{L}(\mathcal{H})}<\infty . {} \end{aligned} $$
(20)

Lemma 3.3 (Asymptotic Stability)

The operator \(\mathcal {A}\) verifies (18) and then the associated semigroup (S(t))t≥0 is asymptotically stable on \(\mathcal {H}\).

Proof

Since \(0\in \rho (\mathcal {A})\) we only need here to prove that \((i\beta \mathcal {I}-\mathcal {A})\) is a one-to-one correspondence in the energy space \(\mathcal {H}\) for all \(\beta \in \mathbb {R}^{*}\). The proof will be done in two steps: in the first step we will prove the injective property of \((i\beta \mathcal {I}-\mathcal {A})\) and in the second step we will prove the surjective property of the same operator.

  • Suppose that there exists \(\beta \in \mathbb {R}^*\) such that \(Ker (\mathbf {i} \beta \mathcal {I} - \mathcal {A}) \neq \left \{0 \right \}\). So λ = i β is an eigenvalue of \(\mathcal {A},\) then let \(( \underline {u}, \underline {v})\) an eigenvector of \(\mathcal {D}(\mathcal {A})\) associated with λ. For every j in J we have

    $$\displaystyle \begin{aligned} \begin{array}{rcl} v_{j} & =&\displaystyle \mathbf{i}\beta u_{j}, {} \end{array} \end{aligned} $$
    (21)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} (u^{\prime}_{j}+a_{j }v^{\prime}_{j})^{\prime} & =&\displaystyle \mathbf{i}\beta v_{j}. {} \end{array} \end{aligned} $$
    (22)

    We have

    $$\displaystyle \begin{aligned} \left\langle \mathcal{A}(\underline{u},\underline{v}),(\underline{u}, \underline{v})\right\rangle _{\mathcal{H}}=\sum_{j\in J}\int_{0}^{\ell _{j}}a_{j}\left| v^{\prime}_{j}\right|{}^{2}dx=0. \end{aligned}$$

    Then \(a_{j}v^{\prime }_{j}=0\) a.e. on (0, ℓ j).

    Let e j a K-V edge. According to (21) and the fact that \(a_{j}v^{\prime }_{j}=0\) a.e. on (0, ℓ j), we have \(u^{\prime }_{j}=0\) a.e. on ω j. Using (22), we deduce that v j = 0 on ω j. Return back to (21), we conclude that u j = 0 on ω j.

    Putting \(y=u^{\prime }_{j}+a_{j }v^{\prime }_{j}=(1+\mathbf {i}\beta a_{j })u^{\prime }_{j},\) we have y ∈ H 2(0, ℓ j) and y ′ = −β 2 u j. Hence y satisfies the Cauchy problem

    $$\displaystyle \begin{aligned} y^{\prime \prime}+\frac{\beta ^{2}}{1+\mathbf{i}\beta a_{j}}y=0,\;\;y(z_{0})=0, \;\;y^{\prime}(z_{0})=0 \end{aligned}$$

    for some z 0 in ω j. Then y is zero on (0, ℓ j) and hence \(u^{\prime }_{j }\) and u j are zero on (0, ℓ j). Moreover u j and \(u^{\prime }_{j}+a_{j}v^{\prime }_{j}\) vanish at 0 and at ℓ j.

    If e j is a purely elastic edge attached to a K-V edge at one of its ends, denoted by x j, then \(u_{ j}(x_{j})=0,\;u^{\prime }_{\bar { \alpha }}(x_{j})=0.\) Again, by the same way we can deduce that \( u^{\prime }_{j}\) and u j are zero in L 2(0, ℓ j) and at both ends of e j. We iterate such procedure on every maximal subgraph of purely elastic edges of \(\mathcal {G}\) (from leaves to the root), to obtain finally that \(( \underline {u}, \underline {v})=0\) in \(\mathcal {D}(\mathcal {A}),\) which is in contradiction with the choice of \(( \underline {u}, \underline {v}).\)

  • Now given \(( \underline {f}, \underline {g})\in \mathcal {H}\), we solve the equation

    $$\displaystyle \begin{aligned}(\mathbf{i} \beta \mathcal{I}-\mathcal{A})(\underline{u},\underline{v})=(\underline{f},\underline{g}) \end{aligned}$$

    or equivalently,

    $$\displaystyle \begin{aligned} \left\{\begin{array}{l} \underline{v} = \mathbf{i}\beta \underline{u} - \underline{f}\\ \beta^{2} \underline{u} + \underline{u}^{\prime \prime} + \mathbf{i}\beta\,(\underline{a} \ast \underline{u}^\prime)^\prime =(\underline{a} \ast \underline{f}^\prime)^\prime - \mathbf{i} \beta \underline{f}- \underline{g}. \end{array}\right. \end{aligned} $$
    (23)

    Let us define the operator

    $$\displaystyle \begin{aligned}A \underline{u} = - \underline{u}^{\prime \prime} - \mathbf{i} \beta \,(\underline{a} \ast \underline{u}^\prime)^\prime,\quad \forall\, \underline{u}\in V. \end{aligned}$$

    It is easy to show that A is an isomorphism from V onto V ′ (where V ′ is the dual space of V obtained by means of the inner product in H). Then the second line of (23) can be written as follows

    $$\displaystyle \begin{aligned} \underline{u}-\beta^{2}A^{-1} \underline{u}=A^{-1}\left(\underline{g}+ \mathbf{i} \beta \underline{f}-(\underline{a} \ast \underline{f}^\prime)^\prime\right). \end{aligned} $$
    (24)

    If \( \underline {u}\in \mathrm {Ker}(\mathcal {I}-\beta ^{2}A^{-1})\), then \(\beta ^{2} \underline {u}-A \underline {u}=0\). It follows that

    $$\displaystyle \begin{aligned} \beta^{2}\underline{u}+\underline{u}^{\prime \prime}+\mathbf{i}\beta (\underline{a}\ast \underline{u}^\prime)^\prime=0. \end{aligned} $$
    (25)

    Multiplying (25) by \(\overline { \underline {u}}\) and integrating over \(\mathcal {T}\), then by Green’s formula we obtain

    $$\displaystyle \begin{aligned}\beta^{2} \sum_{{j} \in J} \int_0^{\ell_{j}}|u_{j}(x)|{}^{2}\,\mathrm{d} x- \sum_{{j} \in J} \int_0^{\ell_{j}}| u^\prime_{j}(x)|{}^{2}\,\mathrm{d} x-\mathbf{i}\beta \sum_{{j} \in J} \int_0^{\ell_{j}} a_{j}(x) \, |u^\prime_{j}(x)|{}^{2}\,\mathrm{d} x=0. \end{aligned}$$

    This shows that

    $$\displaystyle \begin{aligned}\sum_{{j} \in J} \int_0^{\ell_{j}} a_{j} (x) \, |u_{j}^\prime(x)|{}^{2}\,\mathrm{d} x=0, \end{aligned}$$

    which imply that \( \underline {a} \ast \underline {u}^\prime =0\) in \(\mathcal {G}\).

    Inserting this last equation into (25) we get

    $$\displaystyle \begin{aligned}\beta^{2}\underline{u} +\underline{u}^{\prime \prime} =0,\qquad \text{in }\mathcal{G}. \end{aligned}$$

    According to the first step, we have that \(\mathrm {Ker}(\mathcal {I}-\beta ^{2}A^{-1})=\{0\}\). On the other hand, thanks to the compact embeddings V ↪H and H↪V ′ we see that A −1 is a compact operator in V . Now thanks to Fredholm’s alternative, the operator \((\mathcal {I}-\beta ^{2}A^{-1})\) is bijective in V , hence the Eq. (24) have a unique solution in V , which yields that the operator \((\mathbf {i}\beta \mathcal {I}-\mathcal {A})\) is surjective in the energy space \(\mathcal {H}\). The proof is thus complete.

□

Before stating the main result, we define a property (P) on \( \underline {a}\) as follows

$$\displaystyle \begin{aligned} (P)\;\;\;\forall j\in J,\;\;a_{j }^{\prime },a_{j}^{\prime \prime }\in L^{\infty }(0,\ell _{ j})\;\; \text{and}\;\; \;\;\forall k\in I_{\mathcal{M} },\;\;\displaystyle \sum_{j\in J_k}d_{kj}a_{j}^{\prime }(s_k)\leq 0. \end{aligned}$$

Theorem 3.4

Suppose that the function \( \underline {a}\) satisfies property (P), then

  1. (i)

    If \( \underline {a}\) is continuous at every inner node of \(\mathcal {T}\) , then (S d(t))t≥0 is exponentially stable on \(\mathcal {H}\).

  2. (ii)

    If \( \underline {a}\) is not continuous at least at an inner node of \(\mathcal {T}\) , then (S d(t))t≥0 is polynomially stable on \(\mathcal {H}\) , in particular, there exists C > 0 such that for all t > 0 we have

    $$\displaystyle \begin{aligned} \left\| e^{\mathcal{A}t}(\underline{u}^{0},\underline{u}^{1})\right\|{}_{ \mathcal{H}}\leq \frac{C}{t^{2}}\left\| (\underline{u}^{0},\underline{u} ^{1})\right\|{}_{\mathcal{D}(\mathcal{A})}, \, \forall \, (\underline{u}^{0},\underline{u}^{1})\in \mathcal{D}(\mathcal{A}). \end{aligned}$$

Proof

According to Lemmas 3.1, 3.2, and 3.3, it suffices to prove that for γ = 0, when \( \underline {a}\) is continuous at every inner node, or γ = 1∕2, when \( \underline {a}\) is not continuous at an inner node, there exists r > 0 such that

$$\displaystyle \begin{aligned} \inf_{\left\| (\underline{u},\underline{v})\right\|{}_{\mathcal{H}}, \beta \in \mathbb{R}}\beta ^{\gamma}\left\| (\mathbf{i}\beta \mathcal{I}-\mathcal{A})(\underline{u}, \underline{v})\right\|{}_{\mathcal{H}} \geq r. {} \end{aligned} $$
(26)

Suppose that (26) fails. Then there exists a sequence of real numbers β n, with β n →∞ (without loss of generality, we suppose that β n > 0 ), and a sequence of vectors \(( \underline {u}_{n}, \underline {v}_{n})\) in \(\mathcal {D}(\mathcal {A})\) with \( \left \| ( \underline {u}_{n}, \underline {v}_{n})\right \|{ }_{\mathcal {H}}=1\) such that

$$\displaystyle \begin{aligned} \beta _{n}^{\gamma}\left\| (\mathbf{i}\beta _{n}\mathcal{I}-\mathcal{A})(\underline{u}_{n}, \underline{v}_{n})\right\|{}_{\mathcal{H}}\rightarrow 0. {} \end{aligned} $$
(27)

We shall prove that \(\left \| ( \underline {u}_{n}, \underline {v}_{n})\right \|{ }_{ \mathcal {H}}=o(1),\) which contradict the hypotheses on \(( \underline {u}_{n}, \underline {v}_{n}).\)

Writing (27) in terms of its components, we get for every j ∈ J,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta _{n}^{\gamma}(\mathbf{i}\beta _{n}u_{j,n}-v_{j,n}) & =:&\displaystyle f_{ j,n}=o(1)\;\;\;\text{in }H^{1}(0,\ell _{j }), {} \end{array} \end{aligned} $$
(28)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta _{n}^{\gamma}(\mathbf{i}\beta _{n}v_{j,n}-(u^{\prime}_{ j,n}+a_{j}v^{\prime}_{j,n})^{\prime}) & =:&\displaystyle g_{j,n}=o(1)\;\;\;\text{in }L^{2}(0,\ell _{ j}). {} \end{array} \end{aligned} $$
(29)

Note that

$$\displaystyle \begin{aligned} \beta _{n}^{\gamma}\sum_{j\in J}\int_{0}^{\ell _{j}}a_{ j}(x)\left| v^{\prime}_{j}(x)\right| ^{2}dx=Re\left( \left\langle \beta _{n}^{\gamma} (\mathbf{i}\beta _{n}\mathcal{I}-\mathcal{A} _{d})(\underline{u}_{n},\underline{v}_{n}),(\underline{u}_{n},\underline{v} _{n})\right\rangle _{\mathcal{H}}\right) =o(1). \end{aligned}$$

Hence, for every j ∈ J

$$\displaystyle \begin{aligned} \beta _{n}^{\frac{\gamma}{2}}\left\| a_{j}^{\frac{1}{2}}v^{\prime}_{j,n}\right\|{}_{L^{2}(0,\ell _{j})}=o(1). {} \end{aligned} $$
(30)

Then from (28), we get that

$$\displaystyle \begin{aligned} \beta _{n}^{\frac{\gamma}{2}} \left\| a_{j}^{\frac{1}{2}}\beta _{n}u^{\prime}_{ j,n}\right\|{}_{L^{2}(0,\ell _{j})}=o(1). {} \end{aligned} $$
(31)

Define \(T_{j,n}=(u^{\prime }_{j,n}+a_{ j}v^{\prime }_{j,n})\) and multiplying ( 29) by \(\beta _{n}^{-\gamma }qT_{j,n}\) where q is any real function in H 2(0, ℓ j), we get, using (28) and some integrations by parts,

$$\displaystyle \begin{gathered} \frac{1}{2}\int_{0}^{\ell _{j}}q^{\prime}\left| v_{ j,n}\right|{}^{2}dx+\frac{1}{2}\int_{0}^{\ell _{j}}q^{\prime}\left| T_{j,n}\right| ^{2}dx-Im\int_{0}^{\ell _{j}}qa_{j}\beta _{n}v_{j,n}\overline{v^{\prime}_{j,n}} dx \\ -\frac{1}{2}\left( \left[ q(x)\left| v_{j,n}(x)\right|{}^{2} \right] _{0}^{\ell _{j}}+\left[ q(x)\left| T_{j,n}(x)\right|{}^{2}\right] _{0}^{\ell _{j}}\right) =o(1). {} \end{gathered} $$
(32)

□

Lemma 3.5

The following property holds

$$\displaystyle \begin{aligned} Im\int_{0}^{\ell _{j}}qa_{j}\beta _{n}v_{ j,n}\overline{v^{\prime}_{j,n}}dx=o(1). {} \end{aligned} $$
(33)

Proof

Since \( \beta _{n}^{\frac {\gamma }{2}}a_{j}^{\frac {1}{2}}v^{\prime }_{j,n }\rightarrow 0\) in L 2(0, ℓ j) and q ∈ L ∞(0, ℓ j), it suffices to prove that

$$\displaystyle \begin{aligned} \beta _{n}^{1-\frac{\gamma}{2}}\left\| a_{j}^{\frac{1}{2}}v_{j ,n}\right\|{}_{L^{2}(0,\ell _{j})}=O(1). {} \end{aligned} $$
(34)

For this, taking the inner product of (29) by \(\mathbf {i} \beta _{n}^{1-2 \gamma }a_{j}v_{j,n}\) leads to

$$\displaystyle \begin{aligned} \beta _{n}^{2-\gamma}\left\| a_{j}^{\frac{1}{2}}v_{j ,n}\right\|{}_{L^{2}(0,\ell _{j})}^{2}=-\mathbf{i} \beta _{n}^{1-\gamma}\int_{0}^{\ell _{j}}T^{\prime}_{j ,n}a_{j}\overline{v_{j,n}}dx-\mathbf{i} \beta _{n}^{1-2\gamma}\int_{0}^{\ell _{j}}g_{j,n}a_{ j}\overline{v_{j,n}}dx. {} \end{aligned} $$
(35)

Since a j ∈ L ∞(0, ℓ j) and \(g_{\bar { \alpha },n}\rightarrow 0\) in L 2(0, ℓ j) we can deduce the inequality

$$\displaystyle \begin{aligned} -Re(\mathbf{i}\beta _{n}^{1-2\gamma}\int_{0}^{\ell _{j}}g_{\bar{ \alpha },n}a_{j}\overline{v_{j,n}}dx)\leq \frac{1}{4}\beta _{n}^{2-\gamma}\left\| a_{j}^{\frac{1}{2}}v_{ j,n}\right\|{}_{L^{2}(\omega _{j })}^{2}+o(1). {} \end{aligned} $$
(36)

On the other hand, we have [14]

$$\displaystyle \begin{aligned} \begin{array}{rcl} -Re(\mathbf{i}\beta _{n}^{1-\gamma}\int_{0}^{\ell _{j}}T^{\prime}_{ j,n}a\overline{v_{j,n}}dx) \leq -Re\left[ \mathbf{i}\beta _{n}^{1-\gamma}T_{j,n}(x)a_{j}(x) \overline{v_{j,n}}(x)\right] _{0}^{\ell _{j }} \\ +\frac{1}{2}\left[\beta _{n}^{-\gamma} a^{\prime}_{j}(x)\left| v_{j ,n}(x)\right|{}^{2}\right] _{0}^{\ell _{j}}+\frac{1}{4}\beta _{n}^{2-\gamma}\left\| a_{j}^{\frac{1}{2}}v_{j,n}\right\|{}_{L^{2}(0,\ell _{j})}^{2} + O(1). {} \end{array} \end{aligned} $$
(37)

Note that in the proof of (37) we have used that \(a_j^\prime \) and \(a_j^{\prime \prime }\) belong to L ∞(0, ℓ j).

Thus, substituting (36) and (37) into (35) leads to

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{1}{2}\beta _{n}^{2-\gamma}\left\| a_{j}^{\frac{1}{2}}v_{j,n}\right\|{}_{L^{2}(0,\ell _{j})}^{2} & \leq &\displaystyle -Re\left[ \mathbf{i}\beta _{n}^{1-\gamma}T_{j,n}(x)a_{j}(x) \overline{v_{j,n}}(x)\right] _{0}^{\ell _{j }} \\ & &\displaystyle +\frac{1}{2}\left[\beta _{n}^{-\gamma} a^{\prime}_{j}(x)\left| v_{j ,n}(x)\right|{}^{2}\right] _{0}^{\ell _{j}} +O(1). {} \end{array} \end{aligned} $$
(38)

Summing over j ∈ J,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{j\in J}\beta _{n}^{2}\left\| a_{j}^{\frac{1}{2} }v_{j,n}\right\|{}_{L^{2}(0,\ell _{j})}^{2}& \leq &\displaystyle -2 \sum_{k\in I_{int}}Re \left( \mathbf{i}\beta _{n}^{1-\gamma}\overline{\underline{v}}_{n}(s_k)\sum_{j\in J_k}d_{kj} a_{j_k}(s_k)T_{j_k,n}(s_k)\right) \\ & &\displaystyle +\beta_n^{-\gamma}\sum_{k\in I_{int}}\left| \overline{\underline{v}}_{n}(s_k)\right|{}^{2}\sum_{j\in J_k}d_{kj} a^{\prime}_{j_k}(s_k) +O(1). {} \end{array} \end{aligned} $$
(39)

We have used the continuity condition of \( \underline {v}_n\) and the compatibility condition (7) at inner nodes and the Dirichlet condition of \( \underline {u}\) and \( \underline {v}\) at external nodes.

Notes that from property (P) we have

$$\displaystyle \begin{aligned} \sum_{k\in I_{\mathcal{M}}}\left| \overline{\underline{v}}_{n}(s_k)\right|{}^{2}\sum_{j\in J_k}d_{kj} a^{\prime}_{j}(s_k) \leq 0,{} \end{aligned} $$
(40)

then to conclude, it suffices to estimate

$$\displaystyle \begin{aligned} \sum_{k\in I_{int}}Re \left( \mathbf{i}\beta _{n}^{1-\gamma}\overline{\underline{v}}_{n}(s_k)\sum_{j\in J_k}d_{kj} a_{j_k}(s_k)T_{j_k,n}(s_k)\right). \end{aligned}$$

Case (i), corresponding to γ = 0: Here \( \underline {a}\) is continuous in all nodes. It follows that

\(\sum _{k\in I_{int}}Re \left ( \mathbf {i}\beta _{n}^{1-\gamma }\overline { \underline {v}}_{n}(s_k)\sum _{j\in J_k}d_{kj} a_{j_k}(s_k)T_{j_k,n}(s_k)\right )=0\).

Then, (39) and (40), yield

$$\displaystyle \begin{aligned} \beta _{n}^{2}\left\| a_{j}^{\frac{1}{2}}v_{j ,n}\right\|{}_{L^{2}(0,\ell _{j})}^{2}=O(1) \end{aligned}$$

for every j ∈ J, and the proof of Lemma 3.5 is complete for case (i).

Case (ii), corresponding to \(\gamma =\frac {1}{2}\): Recall that here the function \( \underline {a}\) is not continuous at some internal nodes. We want estimate the first term in the right hand side of (38). To do this it suffices to estimate \(Re (\mathbf {i}\beta _{n}^{1-\gamma }T_{j,n}(x)a_{j}(x_{j})\overline {v_{j,n}}(x))\) at an inner node x = x j when a j(x j) ≠ 0. By means of some Gagliardo–Nirenberg inequality [34] we proved in [14] the following estimate

$$\displaystyle \begin{aligned} -Re (\mathbf{i}\beta _{n}^{\frac{1}{ 2}} T_{j,n}(x_j)\overline{v_{j,n}}(x_j)) =o(1). \end{aligned}$$

We then conclude that the first term on the right hand side of (39) converges to zero.

Then, again, using (40), we obtain that

$$\displaystyle \begin{aligned} \sum_{j\in I}\beta _{n}^{\frac{1}{2}}\left\| a_{j}^{\frac{1}{2} }\beta _{n}v_{j,n}\right\|{}_{L^{2}(0,\ell _{j})}^{2}=O(1), \end{aligned}$$

then

$$\displaystyle \begin{aligned} \beta _{n}^{\frac{3}{2}}\left\| a_{j}^{\frac{1}{2}}v_{j ,n}\right\|{}_{L^{2}(0,\ell _{j})}^{2}=O(1) \end{aligned}$$

for every j ∈ I, and the proof of Lemma 3.5 is complete for case (ii). □

Return back to the proof of Theorem 3.4. Substituting (33) in (32) leads to

$$\displaystyle \begin{aligned} \frac{1}{2}\int_{0}^{\ell _{j}} q^{\prime} \, \left| v_{ j,n}\right|{}^{2}dx+\frac{1}{2}\int_{0}^{\ell _{j}} q^{\prime}\left| T_{j,n}\right|{}^{2}dx-\frac{1}{2 }\left[ q(x)\left( \left| v_{j,n}(x)\right|{}^{2}+\left| T_{ j,n}(x)\right|{}^{2}\right) \right] _{0}^{\ell _{j}}=o(1) {} \end{aligned} $$
(41)

for every j ∈ J.

Let j ∈ J such that e j is a K-V string. First, note that from (34), we deduce that

$$\displaystyle \begin{aligned} \left\| a_{j}^{\frac{1}{2}}v_{j,n}\right\| _{L^{2}(0,\ell _{j})}^{2}=o(1). \end{aligned}$$

Then, we take \(q(x)=\int _{0}^{x}a_{j}(s)ds\) in (41 ) to obtain

$$\displaystyle \begin{aligned} \frac{1}{2}\int_{0}^{\ell _{j}}a_{j}\left| T_{j,n}\right|{}^{2}dx-\frac{1}{2}\left( \int_{0}^{\ell _{ j}}a_{j}(s)ds\right) \left( \left| v_{ j,n}(\ell _{j})\right|{}^{2}+\left| T_{ j,n}(\ell _{j})\right|{}^{2}\right) =o(1). {} \end{aligned} $$
(42)

Since \( \frac {1}{2}\int _{0}^{\ell _{j}}a_{j}\left | T_{j,n}\right |{ }^{2}dx=o(1) \) and \(\int _{0}^{\ell _{j}}a_{ j}(s)ds>0\), then (42) implies

$$\displaystyle \begin{aligned} \left| T_{j,n}(\ell _{j})\right| ^{2}+\left| v_{j,n}(\ell _{j})\right| ^{2}=o(1). {} \end{aligned} $$
(43)

Therefore, (41) can be rewritten as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{1}{2}\int_{0}^{\ell _{j}} q^{\prime} \, \left| v_{ j,n}\right|{}^{2}dx+\frac{1}{2}\int_{0}^{\ell _{\bar{ \alpha }}} q^{\prime} \, \left| T_{j,n}\right|{}^{2}dx \\ +\frac{1}{2}\left( q(0)\left| v_{j,n}(0)\right| ^{2}+q(0)\left| T_{j,n}(0)\right|{}^{2}\right) & =&\displaystyle o(1). {} \end{array} \end{aligned} $$
(44)

By taking q = x + 1 in (44) we deduce that

$$\displaystyle \begin{aligned} \left\| v_{j,n}\right\|{}_{L^{2}(0,\ell _{j })}=o(1)\text{ and }\left\| u^{\prime}_{j,n}\right\| _{L^{2}(0,\ell _{j})}=o(1) {} \end{aligned} $$
(45)

and moreover

$$\displaystyle \begin{aligned} v_{j,n}(\ell _{j})=o(1)\text{ and }T_{ j,n}(\ell _{j})= o(1) {} \end{aligned} $$
(46)

implies that \(\left \| v_{j ,n}\right \|{ }_{L^{2}(0,\ell _{j})}=o(1)\) and \(\left \| T_{ j,n}\right \|{ }_{L^{2}(0,\ell _{j})}=o(1).\)

Moreover, \(\left \| u^{\prime }_{j,n}\right \| _{L^{2}(0,\ell _{j})}=\left \| T_{j,n}-a_{ j}v_{j,n}\right \|{ }_{L^{2}(0,\ell _{ j})}=o(1).\) Also we have

$$\displaystyle \begin{aligned} v_{j,n}(0)=o(1)\text{ and }T_{j,n}(0)= o(1). {} \end{aligned} $$
(47)

Finally, notice that (43) signifies that

$$\displaystyle \begin{aligned} v_{j,n}(\ell _{j})=o(1)\text{ and }T_{ j,n}(\ell _{j})= o(1). {} \end{aligned} $$
(48)

To conclude, it suffices to prove that (45) holds. For every j ∈ I such that e j is purely elastic. As in the proof of Lemma 3.3, we start by proving (45) for a string e j attached at one end to only K-V strings. Then we iterate such procedure on each maximally connected subgraph of purely elastic strings (from leaves to the root).

Thus \(\left \| ( \underline {u}_{n}, \underline {v}_{n})\right \|{ }_{\mathcal {H} }=o(1),\) which contradicts the hypothesis \(\left \| ( \underline {u}_{n}, \underline {v}_{n})\right \|{ }_{\mathcal {H}}=1.\)

Remark 6

  1. 1.

    If for every j ∈ J, a j is continuous on [0, ℓ j] and not vanish in such interval, then we do not need the property (P) in the Theorem 3.4.

    Indeed (P) is used only to estimate

    $$\displaystyle \begin{aligned}-Re\left(\mathbf{i}\beta _{n}^{1-\gamma}\int_{0}^{\ell _{j}}T^{\prime}_{j,n}a_{j}\overline{v_{j,n}}dx\right)\end{aligned}$$

    in (35), according to \(\beta _{n}^{1-\frac {\gamma }{2}}\left \| a_{j}^{\frac {1}{2}}v_{j ,n}\right \|{ }_{L^{2}(0,\ell _{j})}\).

    This is equivalent to estimate

    $$\displaystyle \begin{aligned}-Re\left(\mathbf{i}\beta _{n}^{1-\gamma}\int_{0}^{\ell _{j}}T^{\prime}_{j,n}\overline{v_{j,n}}dx\right)\end{aligned}$$

    according to \(\beta _{n}^{1-\frac {\gamma }{2}}\left \|v_{j ,n}\right \|{ }_{L^{2}(0,\ell _{j})}\):

    $$\displaystyle \begin{aligned} \begin{array}{rcl}& &\displaystyle - \, Re \left( \mathbf{i} \beta_n^{1-\gamma} \, \int_0^{\ell_{j}} T^{\prime}_{j,n}\overline{v_{j,n}}dx\right) \\ & &\displaystyle \quad =- Re \left[\mathbf{i} \beta_n^{1-\gamma} \, T_{j,n} \, \overline{v_{j,n}}\right]_0^{\ell_{j}} + Re\left(\mathbf{i}\beta _{n}^{1-\gamma}\int_{0}^{\ell _{j}}T_{j,n} \overline{v^{\prime}_{j,n}}dx\right) \\ & &\displaystyle \quad =- Re \left[\mathbf{i} \beta_n^{1-\gamma} \, T_{j,n}(x) \, \overline{v_{j,n}}(x)\right]_0^{\ell_{j}} + o(1) \end{array} \end{aligned} $$

    as in case (ii) (proof of Theorem 3.4) we prove without using (P) that

    $$\displaystyle \begin{aligned}- Re \left[\mathbf{i} \beta_n^{1-\gamma} \, T_{j,n}(x) \, \overline{v_{j,n}}(x)\right]_0^{\ell_{j}} \leq \frac{\beta _{n}^{2-\gamma}}{4} \, \left\|v_{j ,n}\right\|{}^2_{L^{2}(0,\ell _{j})} + o(1). \end{aligned}$$
  2. 2.

    We find here the particular cases studied in [2, 25, 30, 31, 33]. Note that concerning the result of polynomial stability in [2, 25] the authors proved that the \(\frac {1}{t^2}\) decay rate of solution is optimal when the damping coefficient is a characteristic function.