Stabilization for the Wave Equation with Singular Kelvin–Voigt Damping

Abstract

We consider the wave equation with Kelvin–Voigt damping in a bounded domain. The exponential stability result proposed by Liu and Rao (Z Angew Math Phys (ZAMP) 57:419–432, 2006) or Tebou (C R Acad Sci Paris Ser I 350: 603–608, 2012) for that system assumes that the damping is localized in a neighborhood of the whole or a part of the boundary under some consideration. In this paper we propose to deal with this geometrical condition by considering a singular Kelvin–Voigt damping which is localized far away from the boundary. In this particular case Liu and Liu (SIAM J Control Optim 36:1086–1098, 1998) proved the lack of the uniform decay of the energy. However, we show that the energy of the wave equation decreases logarithmically to zero as time goes to infinity. Our method is based on the frequency domain method. The main feature of our contribution is to write the resolvent problem as a transmission system to which we apply a specific Carleman estimate.

1 Introduction and main results

There are several mathematical models representing physical damping. The most often encountered type of damping in vibration studies are linear viscous damping [1, 3, 14, 15] and Kelvin–Voigt damping [10, 12, 16,17,18], which are special cases of proportional damping. Viscous damping usually models external friction forces such as air resistance acting on the vibrating structures and is thus called "external damping", while Kelvin–Voigt damping originates from the internal friction of the material of the vibrating structures and in thus called "internal damping" or "material damping". This type of material is encountered in real life when one uses patches to suppress vibrations, the modeling aspect of which may be found in [2]. This type of question was examined in the one-dimensional setting in [16] where it was shown that the longitudinal motion of an Euler-Bernoulli beam modeled by a locally damped wave equation with Kelvin–Voigt damping is not exponentially stable when the junction between the elastic part and the viscoelastic part of the beam is not smooth enough. Later on, the wave equation with Kelvin–Voigt damping in the multidimensional setting was examined in [18]; in particular, those authors showed the exponential decay of the energy by assuming that the damping region is a neighborhood of the whole boundary. Later on, it was shown that the exponential decay of the energy could be obtained with just imposing that the damping is a neighborhood of part of the boundary [21].

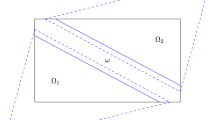
Let $\Omega \subset {\mathbb {R}}^{n}$, $n \geqq 2$ be a connected bounded domain with a sufficiently smooth boundary $\Gamma =\partial \Omega$. Let $\omega$ be a nonempty and open subset of $\Omega$ with smooth boundary ${\mathcal {I}}=\partial \omega$ (see Fig. 1).

Consider the damping wave system

$$\begin{aligned}&\partial _t^2 u - \Delta u - \, \mathrm {div}(a(x) \, \nabla \partial _t u) = 0, \, \Omega \times (0,+\infty ), \end{aligned}$$

(1.1)

$$\begin{aligned}&u = 0, \, \partial \Omega \times (0,+\infty ), \end{aligned}$$

(1.2)

$$\begin{aligned}&u(x,0) = u^0, \, \partial _t u(x,0) = u^1 (x), \, \Omega , \end{aligned}$$

(1.3)

where $a(x)=d\,\mathbb {1}_{\omega }(x)$ and $d>0$ is a constant.

Fig. 1

The domain $\Omega$

System (1.1)–(1.3), involving a constructive viscoelastic damping $\mathrm {div}(a(x)\nabla u_{t})$, models the vibrations of an elastic body which has one part made of viscoelastic material. In the case of global viscoelastic damping $(a>0$), the wave equation (1.1)–(1.3) generates an analytic semigroup, the spectrum of which is contained in a sector of the left half complex plan (see [8]). While the situation of local viscoelastic damping is more delicate due to the unboundedness of the viscoelastic damping and the discontinuity of the materials.

In [16], it was proved that the energy of a one-dimensional wave equation with local viscoelastic damping does not decay uniformly if the damping coefficient a is discontinuous across the interface of the materials. Because of the discontinuity of the materials across the interface, the dissipation is badly transmitted from the viscoelastic region to the elastic region, where the energy decays slowly. Nevertheless, this does not contradict the well-known “geometric optics” condition in [3], since the viscoelastic damping is unbounded in the energy space. The loss of uniform stability is caused by the discontinuity of material properties across the interface and the unboundedness of the viscoelastic damping. In this paper, we prove a logarithmical decay of energy. Our idea is to transform the resolvent problem of system (1.1)–(1.2) to a transmission system to be able to quantify the discontinuity of the material properties across the interface through the so-called Carleman estimate. Note that recently the same problem was treated in [10], where it was proved that the energy is polynomially decreasing over the time but only in the one-dimensional case (even for a transmission system).

We define the natural energy of u solution of (1.1)–(1.3) at instant t by

$$\begin{aligned} E(u,t)= \frac{1}{2} \left\| (u(t),\partial _t u(t))\right\| _{H^1_0 (\Omega ) \times L^2(\Omega )}^2, \, \forall \, t \geqq 0. \end{aligned}$$

Simple formal calculations give

$$\begin{aligned} E(u,t)-E(u,0)= - \, d \,\int \nolimits _{0}^{t} \int \nolimits _{\omega }\left| \nabla \partial _{t} u(x,s)\right| ^2 \,{\mathrm {d}}x\,{\mathrm {d}}s,\forall t\geqq 0, \end{aligned}$$

and therefore the energy is a non-increasing function of the time variable t.

Theorem 1.1

For any $k\in {\mathbb {N}}^*$ there exists $C>0$ such that for any initial data $(u^{0},u^{1})\in {\mathcal {D}}({\mathcal {A}}^{k})$ the solution u(x, t) of (1.1) starting from $(u^{0},u^{1})$ satisfying

$$\begin{aligned} E(u,t)\leqq \frac{C}{(\ln (2+t))^{2k}}\Vert (u^{0},u^{1})\Vert _{{\mathcal {D}}({\mathcal {A}}^{k})}^{2},\quad \forall \,t>0, \end{aligned}$$

where $({\mathcal {A}}, {\mathcal {D}}({\mathcal {A}}))$ is defined in Section 2.

This paper is organized as follows: in Section 2, we give the proper functional setting for systems (1.1)–(1.3), and prove that this system is well-posed. In Section 3, we establish some Carleman estimate which corresponds to the system (1.1)–(1.3). Finally, in Section 4, we study the stabilization for (1.1)–(1.3) by the resolvent method and give the explicit decay rate of the energy of the solutions of (1.1)–(1.3).

2 Well-posedness and strong stability

We define the energy space by ${\mathcal {H}}=H_{0}^{1}(\Omega )\times L^{2}(\Omega )$ which is endowed with the usual inner product

$$\begin{aligned} \left\langle (u_{1},v_{1});(u_{2},v_{2})\right\rangle =\int \nolimits _{\Omega }\nabla u_{1}(x).\nabla {\overline{u}}_{2}(x)\,{\mathrm{d}}x+\int \nolimits _{\Omega }v_{1}(x){\overline{v}}_{2}(x)\,{\mathrm{d}}x. \end{aligned}$$

We next define the linear unbounded operator ${\mathcal {A}}:{\mathcal {D}}({\mathcal {A}})\subset {\mathcal {H}}\longrightarrow {\mathcal {H}}$ by

$$\begin{aligned} {\mathcal {D}}({\mathcal {A}})=\{(u,v)\in {\mathcal {H}}: v\in H_{0}^{1}(\Omega ),\; \Delta u+\mathrm {div}(a\nabla v)\in L^{2}(\Omega )\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {A}}(u,v)^{t}=(v,\Delta u+\mathrm {div}(a\nabla v))^{t}. \end{aligned}$$

Then, putting ${\dot{m}}v=\partial _{t} u$, we can write (1.1)–(1.3) as the following Cauchy problem:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}(u(t),v(t))^{t}={\mathcal {A}}(u(t),v(t))^{t},\;(u(0),v(0))=(u^{0}(x),u^{1}(x)). \end{aligned}$$

Theorem 2.1

The operator ${\mathcal {A}}$ generates a $C_{0}$-semigroup of contractions on the energy space ${\mathcal {H}}$.

Proof

Firstly, it is easy to see that for all $(u,v)\in {\mathcal {D}}({\mathcal {A}})$, we have

$$\begin{aligned} \mathrm {Re}\left\langle {\mathcal {A}}(u,v);(u,v)\right\rangle =-\int \nolimits _{\Omega }a|\nabla v(x)|^{2}\,{\mathrm{d}}x, \end{aligned}$$

which shows that the operator ${\mathcal {A}}$ is dissipative.

Next, for any given $(f,g)\in {\mathcal {H}}$, we solve the equation ${\mathcal {A}}(u,v)=(f,g)$, which is recast m the following way:

$$\begin{aligned} \left\{ \begin{array}{l} v=f, \\ \Delta u+\mathrm {div}(a\nabla f)=g. \end{array}\right. \end{aligned}$$

(2.1)

It is well known that by Lax–Milgram’s theorem the system (2.1) admits a unique solution $u\in H_{0}^{1}(\Omega )$. Moreover, by multiplying the second line of (2.1) by ${\overline{u}}$ and integrating over $\Omega$ and using Poincaré inequality and Cauchy–Schwarz inequality we find that there exists a constant $C>0$ such that

$$\begin{aligned} \int \nolimits _{\Omega }|\nabla u(x)|^{2}\,{\mathrm{d}}x\leqq C\left( \int \nolimits _{\Omega }|\nabla f(x)|^{2}\,{\mathrm{d}}x+\int \nolimits _{\Omega }|g(x)|^{2}\,{\mathrm{d}}x\right) . \end{aligned}$$

It follows that for all $(u,v)\in {\mathcal {D}}({\mathcal {A}}),$ we have

$$\begin{aligned} \Vert (u,v)\Vert _{{\mathcal {H}}}\leqq C\Vert (f,g)\Vert _{{\mathcal {H}}}. \end{aligned}$$

This implies that $0\in \rho ({\mathcal {A}})$ and by the contraction principle, we easily get $R(\lambda \mathrm {I}-{\mathcal {A}})={\mathcal {H}}$ for sufficiently small $\lambda >0$. The density of the domain of ${\mathcal {A}}$ follows from [19, Theorem 1.4.6]. Then, thanks to the Lumer-Phillips Theorem (see [19, Theorem 1.4.3]), the operator ${\mathcal {A}}$ generates a $C_{0}$-semigroup of contractions on the Hilbert ${\mathcal {H}}$. $\quad \square$

Theorem 2.2

The semigroup $e^{t{\mathcal {A}}}$ is strongly stable in the energy space ${\mathcal {H}}$, that is,

$$\begin{aligned} \lim _{t\rightarrow +\infty }\Vert e^{t{\mathcal {A}}}(u_{0},v_{0})^{t}\Vert _{{\mathcal {H}}}=0,\;\forall \,(u_{0},v_{0})\in {\mathcal {H}}. \end{aligned}$$

Proof

To show that the semigroup $(e^{t{\mathcal {A}}})_{t\geqq 0}$ is strongly stable we only have to prove that the intersection of $\sigma ({\mathcal {A}})$ with $i{\mathbb {R}}$ is an empty set. Since the resolvent of the operator ${\mathcal {A}}$ is not compact (see [16, 18]) but $0\in \rho ({\mathcal {A}})$ we only need to prove that $(i\mu I-{\mathcal {A}})$ is a one-to-one correspondence in the energy space ${\mathcal {H}}$ for all $\mu \in {\mathbb {R}}^{*}$. The proof will be done in two steps: in the first step we will prove the injective property of $(i\mu I-{\mathcal {A}})$ and in the second step we will prove the surjective property of the same operator.

i) Let $(u,v)\in {\mathcal {D}}({\mathcal {A}})$ such that

$$\begin{aligned} {\mathcal {A}}(u,v)^{t}=i\mu (u,v)^{t}. \end{aligned}$$

(2.2)

Then taking the real part of the scalar product of (2.2) with (u, v), we get

$$\begin{aligned} \mathrm {Re}(i\mu \Vert (u,v)\Vert _{{\mathcal {H}}}^{2})=\mathrm {Re}\left\langle {\mathcal {A}}(u,v),(u,v)\right\rangle =-d\int \nolimits _{\omega }|\nabla v|^{2}{\mathrm{d}}x=0, \end{aligned}$$

which implies that

$$\begin{aligned} \nabla v=0 \quad \text { in }\,\omega . \end{aligned}$$

(2.3)

Inserting (2.3) into (2.2), we obtain

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \mu ^{2}u+\Delta u=0&{}\text {in }\Omega \backslash \omega , \\ \nabla u=0&{}\text {in }\omega \\ u=0&{}\text {on }\Gamma . \end{array}\right. \end{aligned}$$

(2.4)

We denote by $w_{j}=\partial _{x_{j}}u$ and we derive the first and the second equations of (2.4), one gets

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \mu ^{2}w_{j}+\Delta w_{j}=0&{}\text {in }\Omega , \\ w_{j}=0&{}\text {in }\omega . \end{array}\right. \end{aligned}$$

Hence, from the unique continuation theorem we deduce that $w_{j}=0$ in $\Omega$ and therefore u is constant in $\Omega$ and since $u_{|\Gamma }=0$ we follow that $u\equiv 0$. We have thus proved that $\mathrm {Ker}(i\mu I-{\mathcal {A}})=0$.

ii) Now, given $(f,g)\in {\mathcal {H}}$, we solve the equation

$$\begin{aligned} (i\mu I-{\mathcal {A}})(u,v)=(f,g); \end{aligned}$$

or, equivalently,

$$\begin{aligned} \left\{ \begin{array}{l} v=i\mu u-f \\ \mu ^{2}u+\Delta u+i\mu \,\mathrm {div}(a\nabla u)=\mathrm {div}(a\nabla f)-i\mu f-g. \end{array}\right. \end{aligned}$$

(2.5)

Let us define the operator

$$\begin{aligned} Au=-(\Delta u+i\mu \,\mathrm {div}(a\nabla u)),\quad \forall \, u\in H_{0}^{1}(\Omega ). \end{aligned}$$

It is easy to show that A is an isomorphism from $H_{0}^{1}(\Omega )$ onto $H^{-1}(\Omega )$. Then the second line of (2.5) can be written as follows:

$$\begin{aligned} u-\mu ^{2}A^{-1}u=A^{-1}\left[ g+i\mu f-\mathrm {div}(a\nabla f)\right] . \end{aligned}$$

(2.6)

If $u\in \mathrm {Ker}(I-\mu ^{2}A^{-1})$, then $\mu ^{2}u-Au=0$. It follows that

$$\begin{aligned} \mu ^{2}u+\Delta u+i\mu \mathrm {div}(a\nabla u)=0. \end{aligned}$$

(2.7)

Multiplying (2.7) by ${\overline{u}}$ and integrating over $\Omega$, by Green’s formula we obtain

$$\begin{aligned} \mu ^{2}\int \nolimits _{\Omega }|u(x)|^{2}\,{\mathrm{d}}x-\int \nolimits _{\Omega }|\nabla u(x)|^{2}\,{\mathrm{d}}x-id\mu \int \nolimits _{\omega }|\nabla u(x)|^{2}\,{\mathrm{d}}x=0. \end{aligned}$$

This shows that

$$\begin{aligned} d\int \nolimits _{\omega }|\nabla u(x)|^{2}\,{\mathrm{d}}x=0, \end{aligned}$$

which implies that $\nabla u=0$ in $\omega$.

Inserting this last equation into (2.7) we get

$$\begin{aligned} \mu ^{2}u+\Delta u=0,\quad \text {in }\Omega . \end{aligned}$$

Once again, using the unique continuation theorem as in the first step, where we recall that $u_{|\Gamma }=0$, we get $u=0$ in $\Omega$. This implies that $\mathrm {Ker}(I-\mu ^{2}A^{-1})=\{0\}$. On the other hand, thanks to the compact embeddings $H_{0}^{1}(\Omega )\hookrightarrow L^{2}(\Omega )$ and $L^{2}(\Omega )\hookrightarrow H^{-1}(\Omega ),$ we see that $A^{-1}$ is a compact operator in $H_{0}^{1}(\Omega )$. Now, thanks to Fredholm’s alternative, the operator $(I-\mu ^{2}A^{-1})$ is bijective in $H_{0}^{1}(\Omega )$, hence the equation (2.6) has a unique solution in $H_{0}^{1}(\Omega )$, which yields that the operator $(i\mu I-{\mathcal {A}})$ is surjective in the energy space ${\mathcal {H}}$. The proof is thus complete. $\quad \square$

3 Carleman estimate

For any $s\in {\mathbb {R}}$ we define the Sobolev space with a parameter $\tau$, $H_{\tau }^{s}({\mathbb {R}}^{n})$ by

$$\begin{aligned} u(x,\tau )\in H^{s}_{\tau }({\mathbb {R}}^{n})\,\Longleftrightarrow \,\left\langle \xi ,\tau \right\rangle ^{s}{\hat{u}}(\xi ,\tau )\in L^{2}({\mathbb {R}}^{n});\quad \langle \xi ,\tau \rangle ^{2}=|\xi |^{2}+\tau ^{2}, \end{aligned}$$

where $\tau$ is a large enough parameter and ${\hat{u}}$ denote the partial Fourier transform with respect to x. The class of symbols of order m defined by

$$\begin{aligned} {\mathcal {S}}_{\tau }^{m}=\left\{ a(x,\xi ,\tau )\in {\mathcal {C}}^{\infty }({\mathcal {U}}\times {\mathbb {R}}^{n}); \;|\partial _{x}^{\alpha }\partial _{\xi }^{\beta }a(x,\xi ,\tau )|\leqq C_{\alpha ,\beta }\langle \xi ,\tau \rangle ^{m-|\beta |} \right\} \end{aligned}$$

and the class of tangential symbols of order m by

$$\begin{aligned} \mathcal {TS}_{\tau }^{m}=\left\{ a(x,\xi ',\tau )\in {\mathcal {C}}^{\infty }({\mathcal {U}}\times {\mathbb {R}}^{n-1}) ;\;|\partial _{x}^{\alpha }\partial _{\xi '}^{\beta }a(x,\xi ',\tau )|\leqq C_{\alpha ,\beta }\langle \xi ',\tau \rangle ^{m-|\beta |} \right\} , \end{aligned}$$

where ${\mathcal {U}}$ is an open set of ${\mathbb {R}}^{n}$ and $\tau$ is a large parameter. We denote by ${\mathcal {O}}^{m}$ (resp. $\mathcal {TO}^{m}$) the set of pseudo-differential operators $A={\mathrm {op}}(a)$, $a\in {\mathcal {S}}_\tau ^{m}$ (resp. $a\in \mathcal {TS}^{m}_\tau$). We shall use the symbol $\Lambda =\langle \xi ',\tau \rangle =(|\xi '|^{2}+\tau ^{2})^{\frac{1}{2}}$.

Consider a bounded smooth open set ${\mathcal {U}}$ of ${\mathbb {R}}^{n}$ with boundary $\partial {\mathcal {U}}=\gamma$. We set ${\mathcal {U}}_{1}$ and ${\mathcal {U}}_{2}$ two smooth open subsets of ${\mathcal {U}}$ with boundaries $\partial {\mathcal {U}}_{1}=\gamma _{0}$ and $\partial {\mathcal {U}}_{2}=\gamma \cup \gamma _{0}$ such that ${\overline{\gamma }}\cap {\overline{\gamma }}_{0}=\emptyset$. We denote by $\nu (x)$ the unit outer normal to ${\mathcal {U}}_{2}$ if $x\in \gamma _{0}\cup \gamma$.

For $\tau$ a large parameter and $\varphi _{1}$ and $\varphi _{2}$ two weight functions of class ${\mathcal {C}}^{\infty }$ in $\overline{{\mathcal {U}}}_{1}$ and $\overline{{\mathcal {U}}}_{2}$ respectively such that $\varphi _{1|\gamma _{0}}=\varphi _{2|\gamma _{0}}$ we denote by $\varphi (x)=\mathrm {diag}(\varphi _{1}(x),\varphi _{2}(x))$ and let $\alpha$ be a non-null complex number.

We set the differential operator

$$\begin{aligned} {\mathcal {P}}=\mathrm {diag}({\mathcal {P}}_{1},{\mathcal {P}}_{2})=\mathrm {diag}\left( -\Delta +\frac{\tau ^{2}}{1+\alpha \tau },-\Delta -\tau ^{2}\right) , \end{aligned}$$

and its conjugate operator

$$\begin{aligned} P(x,D,\tau )={\mathrm {e}}^{\tau \varphi }{\mathcal {P}}{\mathrm {e}}^{-\tau \varphi }=\mathrm {diag}(P_{1}(x,D,\tau ),P_{2}(x,D,\tau )), \end{aligned}$$

with

$$\begin{aligned} P_{1}(x,D,\tau )={\mathrm {e}}^{\tau \varphi _{1}}{\mathcal {P}}_{1}{\mathrm {e}}^{-\tau \varphi _{1}}\quad \text { and }\quad P_{2}(x,D,\tau )={\mathrm {e}}^{\tau \varphi _{2}}{\mathcal {P}}_{2}{\mathrm {e}}^{-\tau \varphi _{2}}. \end{aligned}$$

The principal symbols of the operators $P(x,D,\tau )$, $P_{1}(x,D,\tau )$ and $P_{2}(x,D,\tau )$ are, respectively, $p(x,\xi ,\tau )$, $p_{1}(x,\xi ,\tau )$ and $p_{2}(x,\xi ,\tau ),$ and are given as follows:

$$\begin{aligned}&p(x,\xi ,\tau )\\&\quad =\mathrm {diag}(p_{1}(x,\xi ,\tau ),p_{2}(x,\xi ,\tau )) \\&\quad =\mathrm {diag}(|\xi |^{2} +2i\tau \xi \nabla \varphi _{1}-\tau ^{2}|\nabla \varphi _{1}|^{2},|\xi |^{2}+2i\tau \xi \nabla \varphi _{2}-\tau ^{2}|\nabla \varphi _{2}|^{2}-\tau ^{2}). \end{aligned}$$

In a small neighborhood W of a point $x_{0}$ of $\gamma _{0}$, we place ourselves in normal geodesic coordinates and we denote by $x_{n}$ the variable that is normal to the interface $\gamma _{0}$ and by $x'$ the reminding spacial variables, that is, $x=(x',x_{n})$. The interface $\gamma _{0}$ is now given by $\gamma _{0}=\{x\,;\;x_{n}=0\}$ and we denote this by

$$\begin{aligned} W_{1}=\{x\in {\mathbb {R}}^{n},\;x_{n}>0\}\cap W,\quad \text {and}\quad W_{2}=\{x\in {\mathbb {R}}^{n},\;x_{n}<0\}\cap W. \end{aligned}$$

The operators ${\mathcal {P}}_{1}$ and ${\mathcal {P}}_{2}$ can be identified locally as operators of the following form:

$$\begin{aligned} {\mathcal {P}}_{1}(x,D)=D_{x_{n}}^{2}+{\mathcal {R}}_{1}(x_{n},x',D_{x'})+\frac{\tau ^{2}}{1+\alpha \tau } \end{aligned}$$

and

$$\begin{aligned} {\mathcal {P}}_{2}(x,D)=D_{x_{n}}^{2}+{\mathcal {R}}_{2}(x_{n},x',D_{x'})-\tau ^{2}, \end{aligned}$$

where $R_{1}$ and $R_{2}$ are two tangential operators, with the ${\mathcal {C}}^{\infty }$ coefficients and with principal symbol ${\mathbf {r}}_{1}(x,\xi ')$ and ${\mathbf {r}}_{2}(x,\xi '),$ respectively, where the quadratic form $r_{k}(x,\xi ')$, $k=1,2$ satisfies

$$\begin{aligned} \exists \,C>0,\quad \forall \,(x,\xi ')\in W_{k}\times {\mathbb {R}}^{n-1},\quad {\mathbf {r}}_{k}(x,\xi ')\geqq C|\xi '|^{2},\quad k=1,2. \end{aligned}$$

We can assume that $x_{0}=(0,0)$ and that W is symmetric with respect to $x_{n}\mapsto -x_{n}$ so, according to Bellassoued [5], we can reduce the problem of transmission in only one side of the interface $\gamma _{0}$ (here we choose reduce the problem in $W_{1}$). Then the operator ${\mathcal {P}}_{1}$ and ${\mathcal {P}}_{2}$ defined in $W_{1}$ are given as follows:

$$\begin{aligned} {\mathcal {P}}_{1}(x,D)=D_{x_{n}}^{2}+{\mathcal {R}}(+x_{n},x',D_{x'})+\frac{\tau ^{2}}{1+\alpha \tau } \end{aligned}$$

and

$$\begin{aligned} {\mathcal {P}}_{2}(x,D)=D_{x_{n}}^{2}+{\mathcal {R}}(-x_{n},x',D_{x'})-\tau ^{2}, \end{aligned}$$

where ${\mathcal {R}}(\pm x_{n},x',D_{x'})$ denote a tangential operators. We denote also the tangential operator, with the ${\mathcal {C}}^{\infty }$ coefficients defined in $W_{1}$ by

$$\begin{aligned} R(x,D_{x'})=\mathrm {diag}({\mathcal {R}}(+x_{n},x',D_{x'}),{\mathcal {R}}(-x_{n},x',D_{x'})), \end{aligned}$$

with the principal symbol $r(x,\xi ')=\mathrm {diag}({\mathbf {r}}(+x_{n},x',\xi '),{\mathbf {r}}(-x_{n},x',\xi ')),$ where ${\mathbf {r}}(\pm x_{n},x',\xi ')$ are quadratic forms which satisfy

$$\begin{aligned} \exists \,C>0,\quad \forall \,(x,\xi ')\in W_{1}\times {\mathbb {R}}^{n-1},\quad {\mathbf {r}}(\pm x_{n},x',\xi ')\geqq C|\xi '|^{2}. \end{aligned}$$

We assume that $\varphi$ satisfies

$$\begin{aligned}&|\nabla \varphi _{k}(x)|> 0,\;\forall \,x\in {\overline{W}}_{1},\quad k=1,2, \end{aligned}$$

(3.1)

$$\begin{aligned}&\partial _{x_{n}}\varphi _{1}(x',0)<0\quad \text {and}\quad \partial _{x_{n}}\varphi _{2}(x',0)>0 \end{aligned}$$

(3.2)

$$\begin{aligned}&\left( \partial _{x_{n}}\varphi _{1}(x',0)\right) ^{2}-\left( \partial _{x_{n}}\varphi _{2}(x',0)\right) ^{2}>1. \end{aligned}$$

(3.3)

The principal symbol $p(x,\xi ,\tau )$ of $P(x,D,\tau )$ is now given by

$$\begin{aligned} p(x,\xi ,\tau )= & {} \mathrm {diag}(p_{1}(x,\xi ,\tau ),p_{2}(x,\xi ,\tau ))\\= & {} \left( \xi +i\tau (\partial _{x_{n}}\varphi )\right) ^{2} +r(x,\xi '+i\tau (\partial _{x'}\varphi ))-\mathrm {diag}(0,\tau ^{2})\,\in {\mathcal {S}}_{\tau }^{2}, \end{aligned}$$

where we assume that it satisfies the following sub-ellipticity condition:

$$\begin{aligned}&\exists \,c>0,\;\forall \,(x,\xi )\in {\overline{W}}_{1}\times {\mathbb {R}}^{n},\;p_{k}(x,\xi ,\tau )=0\,\Longrightarrow \,\left\{ \mathrm {Re}(p_{k}),\mathrm {Im}(p_{k})\right\} (x,\xi ,\tau )\nonumber \\&\quad \geqq c\langle \xi ,\tau \rangle ^3. \end{aligned}$$

(3.4)

We defined on the boundary $\{x_{n}=0\}\cap W$ the operators

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} {\mathrm {op}}(b_{1})w=w_{1}-w_{2}&{}\text {on }\{x_{n}=0\}\cap W \\ {\mathrm {op}}(b_{2})w=\left( D_{x_{n}}+i\tau \partial _{x_{n}}\varphi _{1}\right) w_{1}+\left( D_{x_{n}}+i\tau \partial _{x_{n}}\varphi _{2}\right) w_{2}&{}\text {on }\{x_{n}=0\}\cap W. \end{array}\right. \end{aligned}$$

We denote by $\Vert v\Vert =\Vert v\Vert _{L^{2}(W_{1})}$ the correspondent scalar product denoted by $(v_{1},v_{2})$. For $s\in {\mathbb {R}}$ we use $\Vert v\Vert _{s}^{2}=\Vert {\mathrm {op}}(\Lambda ^{s})v\Vert ^{2}$ and $|v|_{s}^{2}=\Vert v_{|x_{n}=0}\Vert _{s}^{2}$ such that when $s=0$, the norm $|v|_{0}$ with the scalar product $(v_{1},v_{2})_{0}=(v_{1|x_{n}=0},v_{2|x_{n}=0})$ will be denoted simply |v|. Finally, we denote $|v|_{1,0,\tau }^{2}=|v|_{1}^{2}+|D_{x_{n}}v|^{2}$.

Before proving the Carleman estimate we recall the following theorem given by [15, Proposition 1] and [20, Theorem 2.1]:

Proposition 3.1

Let $\varphi$ satisfies (3.13.23.3)–(3.4). Then there exist $C>0$ and $\tau _{0}>0$ such that for any $\tau \geqq \tau _{0}$ we have the following estimate:

$$\begin{aligned} \tau ^{3}\Vert w\Vert ^{2}+\tau \Vert \nabla w\Vert ^{2}\leqq C\left( \Vert P(x,D,\tau )w\Vert ^{2}+\tau |w|_{1,0,\tau }^{2}\right) \end{aligned}$$

(3.5)

and

$$\begin{aligned}&\tau ^{3}\Vert w\Vert ^{2}+\tau \Vert \nabla w\Vert ^{2}+\tau |w|_{1,0,\tau }^{2}\nonumber \\&\quad \leqq C\left( \Vert P(x,D,\tau )w\Vert ^{2}+\tau |{\mathrm {op}}(b_{1})w|_{1}^{2}+\tau |{\mathrm {op}}(b_{2})w|^{2}\right) , \end{aligned}$$

(3.6)

for any $w\in {\mathcal {C}}_{0}^{\infty }(K)$ where $K\subset {\overline{W}}_{1}$ is a compact subset.

Noting that the Carleman estimate (3.5) is precisely given in proof of Proposition 1 page 482 of [15] and the estimate (3.6) is precisely given in the end of the proof of Theorem 2.1 page 984 of [20].

Now we are ready to state our local Carleman estimate whose main ingredients are estimates (3.5) and (3.6). In fact, the Carleman estimate established here is an estimate analogous to the previous one but with another scale of Sobolev spaces.

Theorem 3.1

Let $\varphi$ satisfies (3.13.23.3)–(3.4). There exist $C>0$ and $\tau _{0}>0$ such that for any $\tau \geqq \tau _{0}$ we have the following estimate:

$$\begin{aligned}&\tau ^{3}\Vert w\Vert ^{2}+\tau \Vert \nabla w\Vert ^{2}+\tau ^{2}|w|_{\frac{1}{2}}^{2}+\tau ^{2}|D_{x_{n}}w|_{-\frac{1}{2}}^{2}\nonumber \\&\quad \leqq C\left( \Vert P(x,D,\tau )w\Vert ^{2} +\tau ^2 |{\mathrm {op}}(b_{1})w|_{\frac{1}{2}}^{2}+\tau |{\mathrm {op}}(b_{2})w|^{2}\right) , \end{aligned}$$

(3.7)

for any $w\in {\mathcal {C}}_{0}^{\infty }(K)$ where $K\subset {\overline{W}}_{1}$ is a compact subset.

Proof

We can write the operator $P(x,D,\tau )$ as follows:

$$\begin{aligned} P(x,D,\tau )=D_{x_{n}}^{2}+R+\tau c_{0}(x)D_{x_{n}}+\tau C_{1}(x)+\tau ^{2} c_{0}'(x), \end{aligned}$$

where $c_{0},\,c_{0}'\in \mathcal {TO}^{0}$, $C_{1}\in \mathcal {TO}^{1}$ and $R\in \mathcal {TO}^{2}$ with $R=\sum _{j,k=1}^{n-1}a_{j,k}D_{x_{j}}D_{x_{k}}$. Let $v\in {\mathcal {C}}_{0}^{\infty }({W}_{1})$. Then we have

$$\begin{aligned} \begin{aligned} \Vert (D_{x_{n}}^{2}+R){\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}&\leqq C\Big (\Vert P{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\tau ^{2}\Vert {\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\Vert ^{2} \\&\quad +\tau ^{2}\Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\tau ^{4}\Vert {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\Big ). \end{aligned} \end{aligned}$$

(3.8)

We can estimate the three last terms of the right hand side of (3.8) as follows:

$$\begin{aligned} \tau ^{2}\Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\tau ^{4}\Vert {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\leqq C(\tau \Vert D_{x_{n}}v\Vert ^{2}+\tau ^{3}\Vert v\Vert ^{2}), \end{aligned}$$

and

$$\begin{aligned} \tau ^{2}\Vert {\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\Vert ^{2}= & {} \tau ^{2}\left( \frac{1}{\sqrt{\tau }}{\mathrm {op}}(\Lambda )v,\sqrt{\tau }v\right) \leqq C\left( \tau \Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}+\tau ^{3}\Vert v\Vert ^{2}\right) \nonumber \\\leqq & {} C\tau \Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}. \end{aligned}$$

(3.9)

Then, following (3.8), we obtain

$$\begin{aligned}&\Vert (D_{x_{n}}^{2}+R){\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\nonumber \\&\quad \leqq C\left( \Vert P{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\tau \Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}+\tau ^{3}\Vert v\Vert ^{2} +\tau \Vert D_{x_{n}} v\Vert ^{2} \right) . \end{aligned}$$

(3.10)

Combining (3.5) and (3.10) and using the fact that $\tau (\Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}+\Vert D_{x_{n}}v\Vert ^{2})\sim \tau ^{3}\Vert v\Vert ^{2}+\tau \Vert \nabla v\Vert ^{2}$, we obtain

$$\begin{aligned} \Vert (D_{x_{n}}^{2}+R){\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\leqq C\left( \Vert P{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\Vert Pv\Vert ^{2}+\tau |v|_{1,0,\tau }^{2}\right) .\nonumber \\ \end{aligned}$$

(3.11)

We can write

$$\begin{aligned}&P{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\nonumber \\&\quad ={\mathrm {op}}(\Lambda ^{-\frac{1}{2}})Pv+[P,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v={\mathrm {op}}(\Lambda ^{-\frac{1}{2}})Pv+[R,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v \nonumber \\&\qquad +\tau [c_{0}(x)D_{x_{n}},{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v+\tau [C_{1}(x),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v+\tau ^{2}[c_{0}'(x),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v.\nonumber \\ \end{aligned}$$

(3.12)

Since $[R,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{\frac{1}{2}}$, then, following (3.5), we have

$$\begin{aligned} \left\| [R,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v\right\| ^{2}\leqq & {} C\Vert {\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\Vert ^{2}\leqq C\Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}\nonumber \\\leqq & {} C\left( \Vert Pv\Vert ^{2}+\tau |v|_{1,0,\tau }^{2}\right) . \end{aligned}$$

(3.13)

Since $[c_{0}(x)D_{x_{n}},{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{1}{2}}D_{x_{n}}$, then following (3.5), we have

$$\begin{aligned} \tau ^{2}\left\| [c_{0}(x)D_{x_{n}},{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v\right\| ^{2}\leqq & {} C\tau ^{2}\Vert {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})D_{x_{n}}v\Vert ^{2}\nonumber \\\leqq & {} C\tau \Vert D_{x_{n}}v\Vert ^{2}\leqq C\left( \Vert Pv\Vert ^{2}+\tau |v|_{1,0,\tau }^{2}\right) .\nonumber \\ \end{aligned}$$

(3.14)

Since $[C_{1}(x),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{1}{2}},$ then following (3.5), we have

$$\begin{aligned} \tau ^{2}\left\| [C_{1}(x),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v\right\| ^{2}\leqq & {} C\tau ^{2}\Vert {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\leqq C\tau \Vert v\Vert ^{2}\nonumber \\\leqq & {} C\left( \Vert Pv\Vert ^{2}+\tau |v|_{1,0,\tau }^{2}\right) . \end{aligned}$$

(3.15)

Since $[c_{0}'(x),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{3}{2}}$, then following (3.5), we have

$$\begin{aligned} \tau ^{4}\left\| [c_{0}'(x),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]v\right\|\leqq & {} C\tau ^{4}\Vert {\mathrm {op}}(\Lambda ^{-\frac{3}{2}})v\Vert ^{2}\nonumber \\\leqq & {} C\tau ^{3}\Vert v\Vert ^{2}\leqq C\left( \Vert Pv\Vert ^{2}+\tau |v|_{1,0,\tau }^{2}\right) . \end{aligned}$$

(3.16)

From (3.12)–(3.16), one gets

$$\begin{aligned} \Vert P{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\leqq C\left( \Vert Pv\Vert ^{2}+\tau |v|_{1,0,\tau }^{2}\right) . \end{aligned}$$

(3.17)

Then the combination of (3.11) and (3.17) gives

$$\begin{aligned} \Vert (D_{x_{n}}^{2}+R){\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\leqq C\left( \Vert Pv\Vert ^{2}+\tau |v|_{1,0,\tau }^{2}\right) . \end{aligned}$$

(3.18)

On the other hand, by integration by parts we find that

$$\begin{aligned}&\Vert (D_{x_{n}}^{2}+R){\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\nonumber \\&\quad =\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2} \nonumber \\&\qquad +\Vert R{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2} \nonumber +2{\mathrm {Re}}(D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v,R{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v) \nonumber \\&\quad =\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\Vert R{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2} \\&\qquad +2{\mathrm {Re}}\Big (i\big (D_{x_{n}}v,R{\mathrm {op}}(\Lambda ^{-1})v\big )_{0} +i\big (D_{x_{n}}v,[{\mathrm {op}}(\Lambda ^{-\frac{1}{2}}),R]{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\big )_{0}\Big ) \nonumber \\&\qquad +2{\mathrm {Re}}\big (RD_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v,D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\big ) \nonumber \\&\qquad +2{\mathrm {Re}} \big (D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v,[D_{x_{n}},R]{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\big ). \nonumber \end{aligned}$$

(3.19)

Let $\chi _{0}\in {\mathcal {C}}_{0}^{\infty }(\overline{{\mathbb {R}}_{+}^{n}})$ be a positive function such that $\chi _{0}\equiv 1$ in support of v. Then by integration by parts and using the fact that $(1-\chi _{0})v\equiv 0,$ we obtain

$$\begin{aligned}&\left\| {\mathrm {op}}(\Lambda ^{\frac{3}{2}})v\right\| ^{2}\nonumber \\&\quad =({\mathrm {op}}(\Lambda ^{2}){\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v) =\tau ^{2}\left\| {\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right\| ^{2}\nonumber \\&\qquad +\sum _{j=1}^{n-1}\left( D_{x_{j}}^{2}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \nonumber \\&\quad =\tau ^{2}\left\| {\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right\| ^{2} +\sum _{j=1}^{n-1}\left( D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \nonumber \\&\quad =\tau ^{2}\left\| {\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right\| ^{2} +\sum _{j=1}^{n-1}\left( \chi _{0} D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \\&\qquad +\sum _{j=1}^{n-1}\left( [(1-\chi _{0}),D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})]v,D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \nonumber \end{aligned}$$

(3.20)

Since $[(1-\chi _{0}),D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})]\in \mathcal {TO}^{\frac{1}{2}}$ and $D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})\in \mathcal {TO}^{\frac{3}{2}}$ for $j=1,\ldots ,n-1$, we show that

$$\begin{aligned} \left| \sum _{j=1}^{n-1}\left( [(1-\chi _{0}),D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})]v,D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \right| \leqq C\Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}. \end{aligned}$$

(3.21)

We recall that $\sum _{j,k=1}^{n-1}\chi _{0} a_{j,k}D_{x_{j}}v\overline{D_{x_{k}}v}\geqq c\chi _{0}\sum _{j=1}^{n-1}|D_{x_{j}}v|^{2}$ for some constant $c>0,$ and using the fact that $[\chi _{0},a_{j,k}D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})]\in \mathcal {TO}^{\frac{1}{2}}$ and $D_{x_{k}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})\in \mathcal {TO}^{\frac{3}{2}}$, we obtain

$$\begin{aligned}&\sum _{j=1}^{n-1}\left( \chi _{0} D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \nonumber \\&\quad \leqq C\sum _{j,k=1}^{n-1}\left( \chi _{0} a_{j,k}D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,D_{x_{k}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \\&\quad \leqq C\sum _{j,k=1}^{n-1}\left( [\chi _{0},a_{j,k}D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})]v,D_{x_{k}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \nonumber \\&\qquad +C\sum _{j,k=1}^{n-1}\left( a_{j,k}D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,D_{x_{k}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \nonumber \\&\quad \leqq C\sum _{j,k=1}^{n-1}\left( a_{j,k}D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,D_{x_{k}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) +C\Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}.\nonumber \end{aligned}$$

(3.22)

Integrating by parts the first term of the right hand side of (3.22) with $R=\sum \nolimits _{j,k=1}^{n-1}a_{j,k}D_{x_{j}}D_{x_{k}}$, one gets

$$\begin{aligned}&\sum _{j,k=1}^{n-1}\left( a_{j,k}D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,D_{x_{k}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \nonumber \\&\quad =(R{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v) \\&\qquad +\sum _{j,k=1}^{n-1}\left( [D_{x_{k}},a_{j,k}]D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) . \nonumber \end{aligned}$$

(3.23)

Since $[D_{x_{k}},a_{j,k}]D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})\in \mathcal {TO}^{\frac{3}{2}}$,

$$\begin{aligned} \left| \sum _{j,k=1}^{n-1}\left( [D_{x_{k}},a_{j,k}]D_{x_{j}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\right) \right| \leqq C\Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}. \end{aligned}$$

(3.24)

Since,

$$\begin{aligned}&(R{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v)\nonumber \\&\quad =(R{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{3}{2}})v)+([{\mathrm {op}}(\Lambda ),R]{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v),\nonumber \\ \end{aligned}$$

(3.25)

and using the fact that $[{\mathrm {op}}(\Lambda ),R]{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})\in \mathcal {TO}^{\frac{3}{2}},$ plus the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned}&\left| (R{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v,{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v)\right| \nonumber \\&\quad \leqq C\left( \varepsilon \Vert {\mathrm {op}}(\Lambda ^{\frac{3}{2}})v\Vert ^{2}+\frac{1}{\varepsilon }\Vert R{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}\right) . \end{aligned}$$

(3.26)

Combining (3.20)–(3.26), we obtain, for $\varepsilon$ small enough that

$$\begin{aligned} \Vert R{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}\geqq C\left( \Vert {\mathrm {op}}(\Lambda ^{\frac{3}{2}})v\Vert ^{2}-\tau \Vert {\mathrm {op}}(\Lambda )v\Vert ^{2}\right) , \end{aligned}$$

(3.27)

where we have used (3.9) again. The same computation shows that

$$\begin{aligned}&{\mathrm {Re}}\left( RD_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v,D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\right) \nonumber \\&\quad \geqq C\left( \Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\Vert ^{2}-\tau \Vert D_{x_{n}}v\Vert ^{2}\right) . \end{aligned}$$

(3.28)

Since $[{\mathrm {op}}(\Lambda ^{-\frac{1}{2}}),R]{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})\in \mathcal {TO}^{0}$ and $R{\mathrm {op}}(\Lambda ^{-1})\in \mathcal {TO}^{1}$, we have

$$\begin{aligned}&\left| \left( D_{x_{n}}v,R{\mathrm {op}}(\Lambda ^{-1})v\right) _{0}\right| +\left| \left( D_{x_{n}}v,[{\mathrm {op}}(\Lambda ^{-\frac{1}{2}}),R]{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\right) _{0}\right| \nonumber \\&\quad \leqq C\left( |D_{x_{n}}v|^{2}+|v|_1^{2}\right) \leqq C|v|_{1,0,\tau }^{2}, \end{aligned}$$

(3.29)

and

$$\begin{aligned} \left| \left( D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v,[D_{x_{n}},R]{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\right) \right| \leqq C\left( \Vert v\Vert ^{2}+\Vert \nabla v\Vert ^{2}\right) . \end{aligned}$$

(3.30)

Putting (3.18) and (3.27)–(3.30) into (3.19), we find

$$\begin{aligned}&\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\Vert ^{2}+\Vert {\mathrm {op}}(\Lambda ^{\frac{3}{2}})v\Vert ^{2} \nonumber \\&\quad \leqq C\left( \Vert Pv\Vert ^{2}+\tau ^{3}\Vert v\Vert ^{2}+\tau \Vert \nabla v\Vert ^{2}+\tau |v|_{1,0,\tau }^{2}\right) . \end{aligned}$$

(3.31)

Following (3.6) and (3.31), we deduce that

$$\begin{aligned}&\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}+\Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\Vert ^{2}+\Vert {\mathrm {op}}(\Lambda ^{\frac{3}{2}})v\Vert ^{2}+\tau |v|_{1,0,\tau }^{2} \nonumber \\&\quad \leqq C\left( \Vert Pv\Vert ^{2}+\tau |{\mathrm {op}}(b_{1})v|_{1}^{2}+\tau |{\mathrm {op}}(b_{2})v|^{2}\right) . \end{aligned}$$

(3.32)

Let $\chi \in {\mathcal {C}}_{0}^{\infty }({\mathbb {R}}^{n})$ be such that $\chi \equiv 1$ in the support of w. We set $v=\chi {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w$ and we write

$$\begin{aligned} \begin{aligned} Pv&={\mathrm {op}}(\Lambda ^{-\frac{1}{2}})Pw+[P,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w+P[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w \\&={\mathrm {op}}(\Lambda ^{-\frac{1}{2}})Pw+[P,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w+D_{x_{n}}^{2}[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\\&\quad +R[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w \\&\quad +\tau c_{0}(x)D_{x_{n}}[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w+\tau C_{1}(x)[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\\&\qquad +\tau ^{2}c_{0}'(x)[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w. \end{aligned} \end{aligned}$$

(3.33)

We have $[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{3}{2}}$, so

$$\begin{aligned}&\left\| D_{x_{n}}^{2}[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\right\| ^{2}\nonumber \\&\quad \leqq C\left( \left\| D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-\frac{3}{2}})w\right\| ^{2}+\left\| D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{3}{2}})w\right\| ^{2}+\left\| {\mathrm {op}}(\Lambda ^{-\frac{3}{2}})w\right\| ^{2}\right) ,\nonumber \\ \end{aligned}$$

(3.34)

and

$$\begin{aligned}&\tau ^{2}\left\| c_{0}(x)D_{x_{n}}[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\right\| ^{2}\nonumber \\&\quad \leqq C\tau ^{2}\left( \left\| D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{3}{2}})w\right\| ^{2}+\left\| {\mathrm {op}}(\Lambda ^{-\frac{3}{2}})w\right\| ^{2}\right) . \end{aligned}$$

(3.35)

Since $R[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{\frac{1}{2}}$, $C_{1}(x)[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{1}{2}}$ and $c_{0}'(x)[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{3}{2}}$, we obtain

$$\begin{aligned}&\left\| R[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\right\| ^{2}+\tau ^{2}\left\| C_{1}(x)[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\right\| ^{2}\nonumber \\&\quad +\tau ^{4}\left\| c_{0}'(x)[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\right\| ^{2}\leqq C\left\| {\mathrm {op}}(\Lambda ^{\frac{1}{2}})w\right\| ^{2}. \end{aligned}$$

(3.36)

Since we can write

$$\begin{aligned}&{[}P,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\\&\quad =[R,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]+\tau [c_{0}(x)D_{x_{n}},{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]+\tau [C_{1}(x),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\\&\qquad +\tau ^{2}[c_{0}'(x),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})], \end{aligned}$$

by using (3.13)–(3.16), we obtain

$$\begin{aligned} \left\| [P,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\right\| ^{2}\leqq C\left( \left\| {\mathrm {op}}(\Lambda ^{\frac{1}{2}})w\right\| ^{2}+\tau ^{-1}\left\| D_{x_{n}}w\right\| ^{2}\right) . \end{aligned}$$

(3.37)

Inserting (3.34)–(3.37) into (3.33), we find that

$$\begin{aligned}&\Vert Pv\Vert ^{2}\nonumber \\&\quad \leqq C\left( \tau ^{-1}\Vert Pw\Vert ^{2}+\tau ^{-1}\Vert {\mathrm {op}}(\Lambda )w\Vert ^{2}\right. .\nonumber \\&\qquad \left. +\tau ^{-1}\Vert D_{x_{n}}w\Vert ^{2}+\tau ^{-1}\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-1})w\Vert ^{2}\right) . \end{aligned}$$

(3.38)

We have

$$\begin{aligned} {\mathrm {op}}(b_{1})v= & {} {\mathrm {op}}(b_{1})\chi {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w={\mathrm {op}}(\Lambda ^{-\frac{1}{2}}){\mathrm {op}}(b_{1})w+{\mathrm {op}}(b_{1})[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\\&+[{\mathrm {op}}(b_{1}),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w. \end{aligned}$$

Since ${\mathrm {op}}(b_{1})\in \mathcal {TO}^{0},$ then ${\mathrm {op}}(b_{1})[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{3}{2}}$ and $[{\mathrm {op}}(b_{1}),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{3}{2}},$ which gives

$$\begin{aligned} \begin{aligned} \tau |{\mathrm {op}}(b_{1})v|_{1}^{2}&=\tau |{\mathrm {op}}(\Lambda ){\mathrm {op}}(b_{1})v|^{2}\\&\leqq C\left( \tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}}){\mathrm {op}}(b_{1})w|^{2}+|{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2}\right) \\&\leqq C\left( \tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}}){\mathrm {op}}(b_{1})w|^{2}+\tau ^{-2}|{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}\right) . \end{aligned} \end{aligned}$$

(3.39)

We have

$$\begin{aligned} {\mathrm {op}}(b_{2})v= & {} {\mathrm {op}}(b_{2})\chi {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w={\mathrm {op}}(\Lambda ^{-\frac{1}{2}}){\mathrm {op}}(b_{2})w+{\mathrm {op}}(b_{2})[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w\\&+[{\mathrm {op}}(b_{2}),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w. \end{aligned}$$

Since ${\mathrm {op}}(b_{2})\in D_{x_{n}}+\mathcal {TO}^{1},$ it is clear that ${\mathrm {op}}(b_{2})[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{3}{2}}D_{x_{n}}+\mathcal {TO}^{-\frac{1}{2}}$ and $[{\mathrm {op}}(b_{2}),{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{3}{2}}D_{x_{n}}+\mathcal {TO}^{-\frac{1}{2}},$ hence

$$\begin{aligned}&\tau |{\mathrm {op}}(b_{2})v|^{2}\nonumber \\&\quad \leqq C\tau \left( |{\mathrm {op}}(\Lambda ^{-\frac{1}{2}}){\mathrm {op}}(b_{2})w|^{2}+|{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2}+|D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{3}{2}})w|^{2}\right) \nonumber \\&\quad \leqq C\left( \tau |{\mathrm {op}}(\Lambda ^{-\frac{1}{2}}){\mathrm {op}}(b_{2})w|^{2}+\tau ^{-1}|{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}+\tau ^{-1}|D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2}\right) .\nonumber \\ \end{aligned}$$

(3.40)

Moreover, we can write

$$\begin{aligned} {\mathrm {op}}(\Lambda )v={\mathrm {op}}(\Lambda )\chi {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w={\mathrm {op}}(\Lambda ^{\frac{1}{2}})w+{\mathrm {op}}(\Lambda )[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w, \end{aligned}$$

since ${\mathrm {op}}(\Lambda )[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{-\frac{1}{2}}.$ Then we get

$$\begin{aligned} \tau |{\mathrm {op}}(\Lambda )v|^{2}\geqq & {} \tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}-C\tau |{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2}\geqq \tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}\\&-C\tau ^{-1}|{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}, \end{aligned}$$

and for $\tau$ large enough, we obtain

$$\begin{aligned} \tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}\leqq C\tau |{\mathrm {op}}(\Lambda )v|^{2}. \end{aligned}$$

(3.41)

By using (3.41) similarly, we can prove that for $\tau$ large enough, we have

$$\begin{aligned} \tau |D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2}\leqq C\tau |D_{x_{n}}v|^{2}+ C\tau |v |_1^{2}. \end{aligned}$$

(3.42)

Recalling that

$$\begin{aligned} \tau |v|_{1,0,\tau }^{2}=\tau |v|_{1}^{2}+\tau |D_{n}v|^{2}=\tau |{\mathrm {op}}(\Lambda )v|^{2}+\tau |D_{n}v|^{2}, \end{aligned}$$

and combining (3.41) and (3.42), we obtain

$$\begin{aligned} \tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}+\tau |D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2}\leqq C\tau |v|_{1,0,\tau }^{2}. \end{aligned}$$

(3.43)

Since we have

$$\begin{aligned} {\mathrm {op}}(\Lambda ^{\frac{3}{2}})v={\mathrm {op}}(\Lambda ^{\frac{3}{2}})\chi {\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w={\mathrm {op}}(\Lambda )w+{\mathrm {op}}(\Lambda ^{\frac{3}{2}})[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]w, \end{aligned}$$

where ${\mathrm {op}}(\Lambda ^{\frac{3}{2}})[\chi ,{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})]\in \mathcal {TO}^{0},$ we obtain

$$\begin{aligned} \Vert {\mathrm {op}}(\Lambda )w\Vert ^{2}-C\Vert w\Vert ^{2}\leqq \Vert {\mathrm {op}}(\Lambda ^{\frac{3}{2}})v\Vert ^{2}. \end{aligned}$$

(3.44)

Similarly, we can also prove that

$$\begin{aligned} \Vert D_{x_{n}}w\Vert ^{2}-C\left( \Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{-1})w\Vert ^{2}+\Vert {\mathrm {op}}(\Lambda ^{-1})w\Vert ^{2}\right) \leqq \Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\Vert ^{2},\nonumber \\ \end{aligned}$$

(3.45)

and

$$\begin{aligned}&\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-1})w\Vert ^{2}-C\big (\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-2})w\Vert ^{2}\nonumber \\&\qquad +\Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{-2})w\Vert ^{2} +\Vert {\mathrm {op}}(\Lambda ^{-2})w\Vert ^{2}\big )\nonumber \\&\quad \leqq \Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2}. \end{aligned}$$

(3.46)

Combining (3.44)–(3.46), we find that

$$\begin{aligned}&\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-1})w\Vert ^{2}+\Vert D_{x_{n}}w\Vert ^{2}+\Vert {\mathrm {op}}(\Lambda )w\Vert ^{2} \nonumber \\&\quad \leqq \Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})v\Vert ^{2} +\Vert D_{x_{n}}{\mathrm {op}}(\Lambda ^{\frac{1}{2}})v\Vert ^{2}+\Vert {\mathrm {op}}(\Lambda ^{\frac{3}{2}})v\Vert ^{2}. \end{aligned}$$

(3.47)

Inserting (3.38)–(3.40), (3.43) and (3.47) into (3.32), we obtain

$$\begin{aligned}&\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-1})w\Vert ^{2}+\Vert D_{x_{n}}w\Vert ^{2}+\Vert {\mathrm {op}}(\Lambda )w\Vert ^{2} +\tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}\\&\qquad +\tau |D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2} \\&\quad \leqq C\Big (\tau ^{-1}\Vert Pw\Vert ^{2}+\tau ^{-1}\Vert {\mathrm {op}}(\Lambda )w\Vert ^{2}+\tau ^{-1}\Vert D_{x_{n}}w\Vert ^{2}+\tau ^{-1}\Vert D_{x_{n}}^{2}{\mathrm {op}}(\Lambda ^{-1})w\Vert ^{2}\\&\qquad +\tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}}){\mathrm {op}}(b_{1})w|^{2} +\tau ^{-2}|{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}+\tau |{\mathrm {op}}(\Lambda ^{-\frac{1}{2}}){\mathrm {op}}(b_{2})w|^{2}+\tau ^{-1}|{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}\\&\qquad +\tau ^{-1}|D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2}\Big ). \end{aligned}$$

For $\tau$ large enough, we get

$$\begin{aligned}&\Vert D_{x_{n}}w\Vert ^{2}+\Vert {\mathrm {op}}(\Lambda )w\Vert ^{2}+\tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}})w|^{2}+\tau |D_{x_{n}}{\mathrm {op}}(\Lambda ^{-\frac{1}{2}})w|^{2} \\&\quad \leqq C\left( \tau ^{-1}\Vert Pw\Vert ^{2}+\tau |{\mathrm {op}}(\Lambda ^{\frac{1}{2}}){\mathrm {op}}(b_{1})w|^{2}+\tau |{\mathrm {op}}(\Lambda ^{-\frac{1}{2}}){\mathrm {op}}(b_{2})w|^{2}\right) , \end{aligned}$$

which obviously leads to the Carleman estimate. This ends the proof. $\quad \square$

For $u=(u_{1},u_{2})\in H^{1}({\mathcal {U}}_{1})\times H^{1}({\mathcal {U}}_{2}),$ we define the tangential operators ${\mathrm {op}}(B_{1})$ and ${\mathrm {op}}(B_{2})$ by

$$\begin{aligned} {\mathrm {op}}(B_{1})u=u_{1|\gamma _{0}}-u_{2|\gamma _{0}}\quad \text {and}\quad {\mathrm {op}}(B_{2})u=\partial _{\nu }u_{1|\gamma _{0}}-\partial _{\nu }u_{2|\gamma _{0}}. \end{aligned}$$

(3.48)

We note that ${\mathrm {op}}(B_{1})$ measures the continuity of the displacement of u through the interface $\gamma _{0},$ where ${\mathrm {op}}(B_{2})$ describes the difference of the flux through $\gamma _{0}$ of the two sides of the interface.

Corollary 3.1

Let $\varphi$ satisfy (3.13.23.3)–(3.4). There exist $C>0$ and $\tau _{0}>0$ such that for any $\tau \geqq \tau _{0}$ we have the following estimate:

$$\begin{aligned}&\tau ^{3}\Vert {\mathrm {e}}^{\tau \varphi }u\Vert ^{2}+\tau \Vert {\mathrm {e}}^{\tau \varphi }\nabla u\Vert ^{2}\leqq C\left( \Vert {\mathrm {e}}^{\tau \varphi }{\mathcal {P}}(x,D)u\Vert ^{2}\right. \nonumber \\&\quad \left. +\tau ^2 |{\mathrm {e}}^{\tau \varphi }{\mathrm {op}}(B_{1})u|_{\frac{1}{2}}^{2}+\tau |{\mathrm {e}}^{\tau \varphi }{\mathrm {op}}(B_{2})u|^{2}\right) , \end{aligned}$$

(3.49)

for any $u\in {\mathcal {C}}_{0}^{\infty }(K)$ where $K\subset {\overline{W}}_{1}$ is a compact subset.

Proof

Letting $w={\mathrm {e}}^{\tau \varphi }u$ and recalling that $P(x,D,\tau )w={\mathrm {e}}^{\tau \varphi }{\mathcal {P}}(x,D)u$, ${\mathrm {op}}(b_{1})w={\mathrm {e}}^{\tau \varphi _{1}}.{\mathrm {op}}(B_{1})u$ and ${\mathrm {op}}(b_{2})w={\mathrm {e}}^{\tau \varphi _{1}}.{\mathrm {op}}(B_{2})u,$ then using the fact that $\varphi _{1}$ and $\varphi _{2}$ have the same trace on $\gamma _{0}$ and the estimate (3.7), we obtain (3.49). $\quad \square$

Now we can state the global Carleman estimate in ${\mathcal {U}}_{1}$ and ${\mathcal {U}}_{2}$ (defined at the beginning of this section on page 5), which is given by the following theorem:

Theorem 3.2

Assume that $\varphi$ satisfies

$$\begin{aligned}&|\nabla \varphi _{k}(x)|> 0,\,\forall \,x\in \overline{{\mathcal {U}}}_{k},\, k=1,2,\nonumber \\&\quad \text { except in a set }{\mathcal {W}}_{k}\text { of finite number of points of } {\mathcal {U}}_{k} \end{aligned}$$

(3.50)

$$\begin{aligned}&\partial _{\nu }\varphi _{2|\gamma }(x)< 0, \end{aligned}$$

(3.51)

$$\begin{aligned}&\partial _{\nu }\varphi _{k|\gamma _{0}}(x)>0,\quad k=1,2, \end{aligned}$$

(3.52)

$$\begin{aligned}&\left( \partial _{\nu }\varphi _{1|\gamma _{0}}(x)\right) ^{2}-\left( \partial _{\nu }\varphi _{2|\gamma _{0}}(x)\right) ^{2}>1, \end{aligned}$$

(3.53)

and the sub-ellipticity condition

$$\begin{aligned}&\exists \,c>0,\;\forall \,(x,\xi )\in \overline{{\mathcal {U}}}_{k}\times {\mathbb {R}}^{n},\;p_{k}(x,\xi )=0\,\nonumber \\&\quad \Longrightarrow \,\left\{ \mathrm {Re}(p_{k}),\mathrm {Im}(p_{k})\right\} (x,\xi ,\tau )\geqq c\langle \xi ,\tau \rangle ^{3}. \end{aligned}$$

(3.54)

Then there exist $C>0$ and $\tau _{0}>0$ such that we have the following estimate:

$$\begin{aligned}&\tau ^{3}\Vert {\mathrm {e}}^{\tau \varphi }u\Vert _{L^{2}({\mathcal {U}})}^{2}+\tau \Vert {\mathrm {e}}^{\tau \varphi }\nabla u\Vert _{L^{2}({\mathcal {U}})}^{2} \\&\quad \leqq C\Big (\Vert {\mathrm {e}}^{\tau \varphi }{\mathcal {P}}u\Vert _{L^{2}({\mathcal {U}})}^{2}+\tau ^{2}\Vert {\mathrm {e}}^{\tau \varphi }{\mathrm {op}}(B_{1})u\Vert _{H^{\frac{1}{2}}(\gamma _{0})}^{2} +\tau \Vert {\mathrm {e}}^{\tau \varphi }{\mathrm {op}}(B_{2})u\Vert _{L^{2}(\gamma _{0})}^{2}\Big ), \nonumber \end{aligned}$$

(3.55)

for all $\tau \geqq \tau _{0}$ and $u=(u_{1},u_{2})\in H^{2}({\mathcal {U}}_{1})\times H^{2}({\mathcal {U}}_{2})$ such that $u_{2|\gamma }=0$ and $u_{k}=0$ at the neighborhood of ${\mathcal {W}}_{k}$, $k=1,2$.

In Theorem 3.2, the fact that u is vanishing around the critical points of the weight function $\varphi$ means that a part of the data is lost, as we can see in the next section. To deal with this our idea here is composed of three steps: in the first step, we apply Theorem 3.2 with a state vanishing around the critical point (using a cutoff function) of the weight function. In a second step, we do the same thing as in the first step, but this time with a second (well-made) weight function with new and different critical points. For the last step, we just add the two estimates in order to recover the missing information around the critical points (this is possible thanks to the properties of the weight function that we have made).

4 Stabilization result

In this section, we will prove the logarithmic stability of the system (1.1). To this end, we establish a particular resolvent estimate. More precisely, we will show that for some constant $C>0,$ we have

$$\begin{aligned} \Vert ({\mathcal {A}}-i\mu \,I)^{-1}\Vert _{{\mathcal {L}}({\mathcal {H}})}\leqq C{\mathrm {e}}^{C|\mu |},\quad \forall \,|\mu |\gg 1, \end{aligned}$$

(4.1)

and then by Burq’s result [7] and the remark of Duyckaerts [9, section 7] (see also [4, 6]), we obtain the expected decay rate of the energy.

Let $\mu$ be a real number such that $|\mu |$ is large, and assume that

$$\begin{aligned} ({\mathcal {A}}-i\mu \,I)(u,v)^{t}=(f,g)^{t},\quad (u,v)\in {\mathcal {D}}({\mathcal {A}}),\quad (f,g)\in {\mathcal {H}}, \end{aligned}$$

(4.2)

which can be written as follows:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} v-i\mu u=f&{}\text {in }\Omega \\ \Delta u+\mathrm {div}(a(x)\nabla v)-i\mu v=g&{}\text {in }\Omega , \end{array}\right. \end{aligned}$$

or, equivalently, as

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} v=f+i\mu u&{}\text {in }\Omega \\ \Delta u+i\mu \mathrm {div}(a(x)\nabla u)+\mu ^{2}u=g+i\mu f-\mathrm {div}(a(x)\nabla f)&{}\text {in }\Omega . \end{array}\right. \end{aligned}$$

(4.3)

Multiplying the second line of (4.3) by ${\overline{u}}$ and integrating over $\Omega ,$ then, by Green’s formula, we obtain

$$\begin{aligned}&\int \nolimits _{\Omega }(g-i\mu f){\overline{u}}\,{\mathrm {d}}x+d\int \nolimits _{\omega }\nabla f.\nabla {\overline{u}}\,{\mathrm {d}}x\nonumber \\&\quad =\mu ^{2}\int \nolimits _{\Omega }|u|^{2}\,{\mathrm {d}}x-\int \nolimits _{\Omega }|\nabla u|^{2}\,{\mathrm {d}}x-id\mu \int \nolimits _{\omega }|\nabla u|^{2}\,{\mathrm {d}}x. \end{aligned}$$

(4.4)

Taking the imaginary part of (4.4) and using the Cauchy–Schwarz inequality and Poincaré inequality, we find that

$$\begin{aligned} d|\mu |\int \nolimits _{\omega }|\nabla u|^{2}\,{\mathrm{d}}x\leqq C\left( \mu ^{2}\int \nolimits _{\Omega }|\nabla f|^{2}\,{\mathrm {d}}x+\int \nolimits _{\Omega }|g|^{2}\,{\mathrm {d}}x\right) . \end{aligned}$$

(4.5)

By setting $u=u_{1}\,\mathbb {1}_{\omega }+ u_{2}\, \mathbb {1}_{\Omega \setminus {\bar{\omega }}}$, $v=v_{1}\,\mathbb {1}_{\omega }+v_{2}\,\mathbb {1}_{\Omega \setminus {\bar{\omega }}}$, $f=f_{1}\,\mathbb {1}_{\omega }+f_{2}\, \mathbb {1}_{\Omega \setminus {\bar{\omega }}}$ and $g=g_{1}\,\mathbb {1}_{\omega }+g_{2}\,\mathbb {1}_{\Omega \setminus {\bar{\omega }}},$ system (4.3) is transformed into the following transmission equation:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} v_{1}=i\mu u_{1}+f_{1}&{}\text {in }\omega \\ v_{2}=i\mu u_{2}+f_{2}&{}\text {in }\Omega \backslash {\overline{\omega }} \\ \Delta ((1+id\mu ) u_{1}+df_{1})+\mu ^{2} u_{1}=g_{1}+i\mu f_{1}&{}\text {in }\omega \\ \Delta u_{2}+\mu ^{2}u_{2}=g_{2}+i\mu f_{2}&{}\text {in }\Omega \backslash {\overline{\omega }}, \end{array}\right. \end{aligned}$$

(4.6)

with the transmission conditions

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} u_{1}=u_{2}&{}\text {on }{\mathcal {I}} \\ \partial _{\nu }((1+id\mu )u_{1}+df_{1})=\partial _{\nu }u_{2}&{}\text {on }{\mathcal {I}}, \end{array}\right. \end{aligned}$$

(4.7)

and the boundary condition

$$\begin{aligned} u_{2}=0\quad \text {on }\Gamma , \end{aligned}$$

(4.8)

where $\nu (x)$ denote the outer unit normal to $\Omega \setminus \omega$ on $\Gamma$ and on ${\mathcal {I}}$ (see Fig. 1).

To prove Theorem 1.1 we need the following technical lemma:

Lemma 4.1

Let ${\mathcal {O}}$ be a bounded open set of ${\mathbb {R}}^{n}$. Then there exist $C>0$ and $\mu _{0}>0$, such that, for any w and F satisfying

$$\begin{aligned} \Delta w+\frac{\mu ^{2}}{1+id\mu }w=F\quad \text {in }{\mathcal {O}}, \end{aligned}$$

and for all $|\mu |>\mu _{0},$ we have the following estimate:

$$\begin{aligned} \Vert w\Vert _{H^{1}}^{2}\leqq C\left( \Vert \nabla w\Vert _{L^{2}({\mathcal {O}})}^{2}+\Vert F\Vert _{L^{2}({\mathcal {O}})}^{2}\right) . \end{aligned}$$

(4.9)

Proof

We need to distinguish two cases:

$\underline{\hbox {Inside }{\mathcal {O}}}$: Letting $\chi \in {\mathcal {C}}_{0}^{\infty }({\mathcal {O}})$, we have, by integration by parts,

$$\begin{aligned} \int \nolimits _{{\mathcal {O}}}\left( \Delta w+\frac{\mu ^{2}}{1+id\mu }w\right) .\chi ^{2}{\overline{w}}\,{\mathrm {d}}x= & {} \frac{\mu ^{2}}{1+id\mu }\Vert \chi w\Vert _{L^{2}({\mathcal {O}})}^{2}-\int \nolimits _{{\mathcal {O}}}|\chi \nabla w|^{2}\,{\mathrm {d}}x\\&-2\int \nolimits _{{\mathcal {O}}}\nabla \chi .\nabla w\chi {\overline{w}}\,{\mathrm {d}}x. \end{aligned}$$

Then we obtain

$$\begin{aligned}&\frac{\mu ^{2}}{\sqrt{1+d^{2}\mu ^{2}}}\Vert \chi w\Vert _{L^{2}({\mathcal {O}})}^{2}\\&\quad \leqq C\left( \Vert F\Vert _{L^{2}({\mathcal {O}})}.\Vert \chi ^{2}w\Vert _{L^{2}({\mathcal {O}})}+\Vert \nabla w\Vert _{L^{2}({\mathcal {O}})}^{2}+\Vert \nabla w\Vert _{L^{2}({\mathcal {O}})}.\Vert \chi w\Vert _{L^{2}({\mathcal {O}})}\right) . \end{aligned}$$

Using Cauchy–Schwarz inequality, and for $|\mu |$ large enough, one gets that

$$\begin{aligned} \Vert \chi w\Vert _{L^{2}({\mathcal {O}})}^{2}\leqq C\left( \Vert \nabla w\Vert _{L^{2}({\mathcal {O}})}^{2}+\Vert F\Vert _{L^{2}({\mathcal {O}})}^{2}\right) , \end{aligned}$$

(4.10)

hence the result inside ${\mathcal {O}}$.

In the neighborhood of the boundary: Let $x=(x',x_{n})\in {\mathbb {R}}^{n-1}\times {\mathbb {R}}$. Then

$$\begin{aligned} \partial {\mathcal {O}}=\{x\in {\mathbb {R}}^{n},\; x_{n}=0\}. \end{aligned}$$

Let $\varepsilon >0$ such that $0<x_{n}<\varepsilon$. Then we have

$$\begin{aligned} w(x,\varepsilon )-w(x',x_{n})=\int \nolimits _{x_{n}}^{\varepsilon }\partial _{x_{n}}w(x',t)\,{\mathrm {d}}t. \end{aligned}$$

It follows that

$$\begin{aligned} |w(x',x_{n})|^{2}\leqq 2|w(x',\varepsilon )|^{2}+2\left( \int \nolimits _{x_{n}}^{\varepsilon }|\partial _{x_{n}}w(x',t)|\,{\mathrm {d}}t\right) ^{2}. \end{aligned}$$

Using the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} |w(x',x_{n})|^{2}\leqq 2|w(x',\varepsilon )|^{2}+2\varepsilon \int \nolimits _{x_{n}}^{\varepsilon }|\partial _{x_{n}}w(x',t)|^{2}\,{\mathrm {d}}t. \end{aligned}$$

Integrating with respect to $x'$, we obtain

$$\begin{aligned} \int \nolimits _{|x'|<\varepsilon }|w(x',x_{n})|^{2}\,{\mathrm {d}}x'\leqq & {} 2\int \nolimits _{|x'|<\varepsilon }|w(x',\varepsilon )|^{2}\,{\mathrm {d}}x'\nonumber \\&+2\varepsilon \int \nolimits _{|x'|<\varepsilon }\int \nolimits _{|x_{n}|<\varepsilon }|\partial _{x_{n}}w(x',t)|^{2}\,{\mathrm {d}}t\,{\mathrm {d}}x'.\nonumber \\ \end{aligned}$$

(4.11)

Using the trace theorem, we have

$$\begin{aligned} \int \nolimits _{|x'|<\varepsilon }|w(x',\varepsilon )|^{2}\,{\mathrm {d}}x'\leqq C\int \nolimits _{|x'|<2\varepsilon ,|x_{n}-\varepsilon |<\frac{\varepsilon }{2}}\left( |w(x)|^{2}+|\nabla w(x)|^{2}\right) \,{\mathrm {d}}x.\nonumber \\ \end{aligned}$$

(4.12)

We introduce the following cut-off functions:

$$\begin{aligned} \chi _{1}(x)=\left\{ \begin{array}{l@{\quad }l@{\quad }l} 1&{}\text {if}&{}\displaystyle 0<x_{n}<\frac{\varepsilon }{2} \\ 0&{}\text {if}&{}\displaystyle x_{n}>\varepsilon , \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \chi _{2}(x)=\left\{ \begin{array}{l@{\quad }l@{\quad }l} 1&{}\text {if}&{}\displaystyle \frac{\varepsilon }{2}<x_{n}<\frac{3\varepsilon }{2} \\ 0&{}\text {if}&{}\displaystyle x_{n}<\frac{\varepsilon }{4},\quad x_{n}>2\varepsilon . \end{array}\right. \end{aligned}$$

Combining (4.11) and (4.12), we obtain, for $\varepsilon$ small enough, that

$$\begin{aligned} \Vert \chi _{1} w\Vert ^{2}\leqq C\left( \Vert \chi _{2}w\Vert ^{2}+\Vert \nabla w\Vert ^{2}\right) . \end{aligned}$$

(4.13)

From (4.10), we have

$$\begin{aligned} \Vert \chi _{2} w\Vert ^{2}\leqq C\left( \Vert \nabla w\Vert ^{2}+\Vert F\Vert ^{2}\right) . \end{aligned}$$

(4.14)

Inserting (4.14) into (4.13), we find that

$$\begin{aligned} \Vert \chi _{1} w\Vert ^{2}\leqq C\left( \Vert \nabla w\Vert ^{2}+\Vert F\Vert ^{2}\right) , \end{aligned}$$

(4.15)

hence the result in the neighborhood of the boundary.

Following (4.10), we can write

$$\begin{aligned} \Vert (1-\chi _{1})w\Vert ^{2}\leqq C\left( \Vert \nabla w\Vert ^{2}+\Vert F\Vert ^{2}\right) . \end{aligned}$$

(4.16)

Adding (4.15) and (4.16), we obtain (4.9). $\quad \square$

Now we can prove Theorem 1.1. We set $w_{1}=(1+id\mu )u_{1}+df_{1}$ and $w_{2}=u_{2}$, then the system (4.6)–(4.8) can be recast as follows:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \Delta w_{1}+\frac{\mu ^{2}}{1+id\mu }w_{1}=\Phi _{1}&{}\text {in }\omega \\ \displaystyle \Delta w_{2}+\mu ^{2}w_{2}=\Phi _{2}&{}\text {in }\Omega \setminus \omega , \end{array}\right. \end{aligned}$$

(4.17)

with the transmission conditions

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} w_{1}=w_{2}+\phi &{}\text {on }{\mathcal {I}} \\ \partial _{\nu }w_{1}=\partial _{\nu }w_{2}&{}\text {on }{\mathcal {I}}, \end{array}\right. \end{aligned}$$

(4.18)

and the boundary condition

$$\begin{aligned} \begin{array}{l@{\quad }l} w_{2}=0&\text {on }\Gamma , \end{array} \end{aligned}$$

(4.19)

where we have denoted that $\Phi _{1}=g_{1}+\frac{i\mu }{1+id\mu }f_{1}$, $\Phi _{2}=g_{2}+i\mu f_{2}$ and $\phi =df_{1}+id\mu u_{1}$.

We denote by $B_{r}$ a ball of radius $r>0$ in $\omega$ and $B_{r}^{c}$ its complement such that $B_{4r}\subset \omega$. Let’s introduce the cut-off function $\chi \in {\mathcal {C}}^{\infty }(\omega )$ by

$$\begin{aligned} \chi (x)=\left\{ \begin{array}{l@{\quad }l} 1&{}\text {in } B_{3r}^{c} \\ 0&{}\text {in } B_{2r}. \end{array}\right. \end{aligned}$$

Next, we denote ${\widetilde{w}}_{1}=\chi w_{1}$, then, from the first line of (4.17), one sees that

$$\begin{aligned} \begin{array}{l@{\quad }l} \displaystyle \Delta {\widetilde{w}}_{1}+\frac{\mu ^{2}}{1+id\mu }{\widetilde{w}}_{1}={\widetilde{\Phi }}_{1}&\text {in }\omega , \end{array} \end{aligned}$$

(4.20)

where ${\widetilde{\Phi }}_{1}=\chi \Phi _{1}-[\Delta ,\chi ]w_{1}$. We denote $\Omega _{1}=\omega \setminus {\overline{B}}_{r}$ and $\Omega _{2}=\Omega \setminus {\overline{\omega }}$.

According to [7, 11] or [13], we can find four weight functions $\varphi _{1,1}$, $\varphi _{1,2}$, $\varphi _{2,1}$ and $\varphi _{2,2}$, a finite number of points $x_{j,k}^{i}$ where $\overline{B(x_{j,k}^{i},2\varepsilon )}\subset \Omega _{j}$ for all $j,k=1,2$ and $i=1,\ldots ,N_{i,k}$ such that, by denoting $U_{j,k}=\displaystyle \Omega _{k}\bigcap \left( \bigcup \nolimits _{i=1}^{N_{j,k}}\overline{B(x_{j,k}^{i},\varepsilon )}\right) ^{c}$, the weight function $\varphi _{k}=\mathrm {diag}(\varphi _{1,k},\varphi _{2,k})$ verifies the assumption (3.50)–(3.54) in $U_{1,k}\cup U_{2,k}$ with $\gamma =\Gamma$ and $\gamma _{0}={\mathcal {I}}$. Moreover, $\varphi _{j,k}<\varphi _{j,k+1}$ in $\bigcup _{i=1}^{N_{j,k}}B(x_{j,k}^{i},2\varepsilon )$ for all $j,k=1,2,$ where we have denoted $\varphi _{j,3}=\varphi _{j,1}$.

Let $\chi _{j,k}$ (for $j,k=1,2$) four cut-off functions equal to 1 in $\left( \bigcup _{i=1}^{N_{j,k}}B(x_{j,k}^{i},2\varepsilon )\right) ^{c}$ and supported in $\left( \bigcup _{i=1}^{N_{j,k}}B(x_{j,k}^{i},\varepsilon )\right) ^{c}$ (in order to eliminate the critical points of the weight functions $\varphi _{j,k}$). We set $w_{1,1}=\chi _{1,1}{\widetilde{w}}_{1}$, $w_{1,2}=\chi _{1,2}{\widetilde{w}}_{1}$, $w_{2,1}=\chi _{2,1}w_{2}$ and $w_{2,2}=\chi _{2,2}w_{2}$. Then from system (4.18) and equations (4.8) and (4.20), for $k=1,2,$ we obtain

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \Delta w_{1,k}+\frac{\mu ^{2}}{1+id\mu }w_{1,k}=\Psi _{1,k}&{}\text {in }\omega \\ \Delta w_{2,k}+\mu ^{2}w_{2,k}=\Psi _{2,k}&{}\text {in }\Omega \setminus \omega \\ w_{1,k}=w_{2,k}+\phi &{}\text {on }{\mathcal {I}} \\ \partial _{\nu }w_{1,k}= \partial _{\nu } w_{2,k}&{}\text {on }{\mathcal {I}} \\ w_{2,k}=0&{}\text {on }\Gamma , \end{array}\right. \end{aligned}$$

(4.21)

where

$$\begin{aligned} \left\{ \begin{array}{l} \Psi _{1,k}=\chi _{1,k}{\widetilde{\Phi }}_{1}-[\Delta ,\chi _{1,k}]{\widetilde{w}}_{1} \\ \Psi _{2,k}=\chi _{2,k}\Phi _{2}-[\Delta ,\chi _{2,k}]w_{2}. \end{array}\right. \end{aligned}$$

(4.22)

Applying the Carleman estimate (3.55) to the system (4.21) with $\tau =|\mu |,$ for $k=1,2$ we have

$$\begin{aligned}&\tau ^{3 }\sum _{j=1,2}\Vert {\mathrm {e}}^{\tau \varphi _{j,k}}w_{j,k}\Vert _{L^{2}(U_{j,k})}^{2} +\tau \sum _{j=1,2}\Vert {\mathrm {e}}^{\tau \varphi _{j,k}}\nabla w_{j,k}\Vert _{L^{2}(U_{j,k})}^{2} \\&\quad \leqq C\Big (\Vert {\mathrm {e}}^{\tau \varphi _{1,k}}\Psi _{1,k}\Vert _{L^{2}(U_{1,k})}^{2} +\Vert {\mathrm {e}}^{\tau \varphi _{2,k}}\Psi _{2,k}\Vert _{L^{2}(U_{2,k})}^{2} +\tau ^{2}\Vert {\mathrm {e}}^{\tau \varphi _{1,k}}\phi \Vert _{H^{\frac{1}{2}}({\mathcal {I}})}^{2}\Big ). \end{aligned}$$

Recalling the expression of $\Psi _{1,k}$ and $\Psi _{2,k}$ in (4.22), we can write

$$\begin{aligned}&\tau ^{3 }\sum _{j=1,2}\Vert {\mathrm {e}}^{\tau \varphi _{j,k}}w_{j,k}\Vert _{L^{2}(U_{j,k})}^{2} +\tau \sum _{j=1,2}\Vert {\mathrm {e}}^{\tau \varphi _{j,k}}\nabla w_{j,k}\Vert _{L^{2}(U_{j,k})}^{2} \\&\quad \leqq C\Big (\Vert {\mathrm {e}}^{\tau \varphi _{1,k}}\Phi _{1}\Vert _{L^{2}(U_{1,k})}^{2}+\Vert {\mathrm {e}}^{\tau \varphi _{2,k}}\Phi _{2}\Vert _{L^{2}(U_{2,k})}^{2} +\Vert {\mathrm {e}}^{\tau \varphi _{1,k}}[\Delta ,\chi _{1,k}]{\widetilde{w}}_{1}\Vert _{L^{2}(U_{1,k})}^{2} \\&\qquad +\Vert {\mathrm {e}}^{\tau \varphi _{1,k}}[\Delta ,\chi ]w_{1}\Vert _{L^{2}(U_{1,k})}^{2} +\Vert {\mathrm {e}}^{\tau \varphi _{2,k}}[\Delta ,\chi _{2,k}]w_{2,k}\Vert _{L^{2}(U_{2,k})}^{2}\\&\qquad +\tau ^{2}\Vert {\mathrm {e}}^{\tau \varphi _{1,k}}\phi \Vert _{H^{\frac{1}{2}}({\mathcal {I}})}^{2}\Big ). \end{aligned}$$

Adding the two last estimates and using the property of the weight functions $\varphi _{j,1}<\varphi _{1,2}$ in $\bigcup _{i=1}^{N_{j,1}}B(x_{j,1}^{i},2\varepsilon )$ and $\varphi _{j,2}<\varphi _{j,1}$ in $\bigcup _{i=1}^{N_{j,2}}B(x_{j,2}^{i},2\varepsilon )$ for all $j=1,2$, we can absorb first order the terms $[\Delta ,\chi _{1,k}]{\widetilde{w}}_{1}$ and $[\Delta ,\chi _{2,k}]w_{2}$ at the right hand side into the left hand side for $\tau >0$ sufficiently large, so mainly we obtain

$$\begin{aligned}&\tau \int \nolimits _{\Omega _{1}}\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |\nabla w_{1}|^{2}\,{\mathrm {d}}x+\tau \int \nolimits _{\Omega _{2}}\left( {\mathrm {e}}^{2\tau \varphi _{2,1}}+{\mathrm {e}}^{2\tau \varphi _{2,2}}\right) |\nabla w_{2}|^{2}\,{\mathrm {d}}x \\&\quad \leqq C\bigg (\int \nolimits _{\Omega _{1}}\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |\Phi _{1}|^{2}\,{\mathrm {d}}x+\tau \int \nolimits _{\Omega _{2}}\left( {\mathrm {e}}^{2\tau \varphi _{2,1}}+{\mathrm {e}}^{2\tau \varphi _{2,2}}\right) |\Phi _{2}|^{2}\,{\mathrm {d}}x \\&\qquad +\int \nolimits _{\Omega _{1}}\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |[\Delta ,\chi ]w_{1}|^{2}\,{\mathrm {d}}x\\&\qquad +\tau ^{2}\left( \Vert {\mathrm {e}}^{\tau \varphi _{1,1}}\phi \Vert _{H^{\frac{1}{2}}({\mathcal {I}})}^{2}+\Vert {\mathrm {e}}^{\tau \varphi _{1,2}}\phi \Vert _{H^{\frac{1}{2}}({\mathcal {I}})}^{2}\right) \bigg ). \end{aligned}$$

Since we can write $\phi =\frac{id\mu }{1+id\mu }w_{1}+\frac{d}{1+id\mu }f_{1},$ using the trace theorem, Green’s formula and the fact that the operator $[\Delta ,\chi ]$ is of the first order with support in $\omega ,$ we find that

$$\begin{aligned}&\tau \int \nolimits _{\omega }\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |\nabla w_{1}|^{2}\,{\mathrm {d}}x+\tau \int \nolimits _{\Omega \setminus \omega }\left( {\mathrm {e}}^{2\tau \varphi _{2,1}}+{\mathrm {e}}^{2\tau \varphi _{2,2}}\right) |\nabla w_{2}|^{2}\,{\mathrm {d}}x \nonumber \\&\quad \leqq C\bigg (\int \nolimits _{\omega }\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |\Phi _{1}|^{2}\,{\mathrm {d}}x+\tau \int \nolimits _{\Omega \setminus \omega }\left( {\mathrm {e}}^{2\tau \varphi _{2,1}}+{\mathrm {e}}^{2\tau \varphi _{2,2}}\right) |\Phi _{2}|^{2}\,{\mathrm {d}}x \nonumber \\&\qquad +\tau ^{4}\int \nolimits _{\omega }\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |w_{1}|^{2}\,{\mathrm {d}}x+\tau ^{2}\int \nolimits _{\omega }\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |\nabla w_{1}|^{2}\,{\mathrm {d}}x \nonumber \\&\qquad +\tau ^{4}\int \nolimits _{\omega }\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |f_{1}|^{2}\,{\mathrm {d}}x+\tau ^{2}\int \nolimits _{\omega }\left( {\mathrm {e}}^{2\tau \varphi _{1,1}}+{\mathrm {e}}^{2\tau \varphi _{1,2}}\right) |\nabla f_{1}|^{2}\,{\mathrm {d}}x\bigg ).\nonumber \\ \end{aligned}$$

(4.23)

Using the expressions of $\Phi _{1}$ and $\Phi _{2}$, taking the maximum of $\varphi _{1,1}$, $\varphi _{1,2}$, $\varphi _{2,1}$ and $\varphi _{2,2}$ in the right hand side of (4.23) and their minimum in the left hand side, and Lemma 4.1 we have

$$\begin{aligned} \begin{aligned} \Vert \nabla w_{1}\Vert _{L^{2}(\omega )}^{2}+\Vert \nabla w_{2}\Vert _{L^{2}(\Omega \setminus \omega )}^{2}\leqq&C{\mathrm {e}}^{C\tau }\Big (\Vert f_{1}\Vert _{L^{2}(\omega )}^{2}+\Vert \nabla f_{1}\Vert _{L^{2}(\omega )}^{2}+\Vert f_{2}\Vert _{L^{2}(\Omega \setminus \omega )}^{2} \\&+\Vert g_{1}\Vert _{L^{2}(\omega )}^{2}+\Vert g_{2}\Vert _{L^{2}(\Omega \setminus \omega )}^{2}+\Vert \nabla w_{1}\Vert _{L^{2}(\omega )}^{2}\Big ). \end{aligned} \end{aligned}$$

We evoke $u_{1}$ and $u_{2}$ through the expression of $w_{1}$ and $w_{2}$ to get

$$\begin{aligned} \begin{aligned} \Vert \nabla u_{1}\Vert _{L^{2}(\omega )}^{2}+\Vert \nabla u_{2}\Vert _{L^{2}(\Omega \setminus \omega )}^{2}\leqq&C{\mathrm {e}}^{C\tau }\Big (\Vert f_{1}\Vert _{L^{2}(\omega )}^{2}+\Vert \nabla f_{1}\Vert _{L^{2}(\omega )}^{2}+\Vert f_{2}\Vert _{L^{2}(\Omega \setminus \omega )}^{2} \\&+\Vert g_{1}\Vert _{L^{2}(\omega )}^{2}+\Vert g_{2}\Vert _{L^{2}(\Omega \setminus \omega )}^{2}+\Vert \nabla u_{1}\Vert _{L^{2}(\omega )}^{2}\Big ). \end{aligned} \end{aligned}$$

Using the Poincaré inequality, we have

$$\begin{aligned} \Vert \nabla u\Vert _{L^{2}(\Omega )}^{2}\leqq C{\mathrm {e}}^{c|\mu |}\left( \Vert \nabla f\Vert _{L^{2}(\Omega )}^{2}+\Vert g\Vert _{L^{2}(\Omega )}^{2}+\Vert \nabla u\Vert _{L^{2}(\omega )}^{2}\right) . \end{aligned}$$

(4.24)

The combination of the two estimates (4.5) and (4.24) leads to

$$\begin{aligned} \Vert \nabla u\Vert _{L^{2}(\Omega )}^{2}\leqq C{\mathrm {e}}^{c|\mu |}\left( \Vert \nabla f\Vert _{L^{2}(\Omega )}^{2}+\Vert g\Vert _{L^{2}(\Omega )}^{2}\right) . \end{aligned}$$

(4.25)

We can obtain the same estimate as (4.25) with the v variable with the $L^{2}$ norm instead of u by again using the Poincaré inequality and recalling the expression of v in the first line of (4.3); namely, we have

$$\begin{aligned} \Vert v\Vert _{L^{2}(\Omega )}^{2}\leqq C{\mathrm {e}}^{c|\mu |}\left( \Vert \nabla f\Vert _{L^{2}(\Omega )}^{2}+\Vert g\Vert _{L^{2}(\Omega )}^{2}\right) . \end{aligned}$$

(4.26)

Thus, the estimate (4.1) is obtained by the combination of the two estimates (4.25) and (4.26).