Keywords

1 Introduction

Global health as well as the science of epidemiology are currently experiencing the greatest challenge in history. The pandemic caused by COVID-19, severe acute respiratory syndrome-related coronavirus SARS-COV-2, this disease which appeared in Wuhan, China, in December 2019, belongs to a large family of viruses that can cause various diseases in humans, ranging from the common cold to respiratory syndrome (MERS) and severe acute respiratory syndrome (SARS). All nations have entered a fierce race to find an effective cure or vaccine to curb the death rate among the populations which is growing day by day, as well as to bring a glimmer of optimism after the state of horror and panic that humanity has experienced and also save States from an unprecedented economic crisis after the total shutdown and confinement of the people that this mysterious COVID-19 has pushed the authorities to establish in the world whole.

Expected as the savior of humanity, many specialists consider the vaccine as our only means of regaining the “life before”, but many questions arise about its effectiveness and its duration of protection whether in humans or population. All the epidemics that mankind has known have been eradicated by effective vaccines, it reveals the truth that a good vaccination strategy saves millions of lives around the world. The work of a vaccine is to excite and then prepare the immune system to recognize viruses, then, if the body is exposed to these same pathogens, it is immediately ready to destroy them, which helps prevent against the disease.

To fight COVID-19, it has been reported that more than 409.6 million doses of the vaccine have been administered worldwide. There is already a large gap between the vaccination programs of different countries, because of this and due to insufficient vaccine doses around the world, most countries have focused their early immunization efforts on priority groups such as people. Clinically vulnerable people in their sixties, sixties and over, with a few exceptions such as doctors, nurses, police and gendarmes as well as teachers and professors. There are ten different vaccines so far. The Pfizer-BioNTech vaccine, which has been shown to be 95 percent effective in reducing coronavirus infections, is currently in use in 77 countries. Most of the vaccines currently in use require two doses for a patient to be fully immunized, as recently the United States authorized a single dose vaccine called Johnson and Johnson—this data is compiled from government sources by the University of Oxford.

Mathematical modeling contributes enormously to the development of epidemiological research allowing a better understanding the evolution of pandemics. To illustrate this, Many mathematical models have been successfully developed in order to describe the evolution of infectious diseases [1,2,3,4,5,6,7,8]. The first mathematical models developed to study the evolution of the COVID-19 pandemic were inspired by SIR models [9,10,11]. Then, mathematics researchers proposed a SIQR models with quarantine strategy [12,13,14,15,16]. Kucharski et al. [17] have studied a mathematical model considering all the positive COVID-19 infected cases of Wuhan. An autonomous system of mathematical model to study the spread of COVID-19 in the Wuhan city have presented by Ndairou et al. [18] . The controlling status of COVID-19 of Wuhan city have analyzed by Prem et al. [19]. Also, the effective procedure of COVID-19 disease using isolation have described by Hellewell et al. [20].

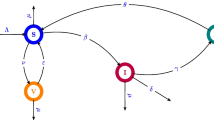
In the same epic, we proposed a mathematical model describing all the scenarios of evolution of the COVID-19 pandemic with a vaccination strategy, we estimate that the infected individuals, after their recovery, can become susceptible after. We define our model consisting of four ordinary differential equations illustrating the interaction between the susceptible S, the real infected I, the hospitalized infected H and the vaccinated-treated individuals V  (Fig. 1).

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} \frac{dS}{dt} &= \; \Lambda- \beta (1-\rho)SI+ \eta I+ \theta H + \varepsilon V -(d+\gamma)S, \\ \frac{dI}{dt} &= \; \beta (1-\rho)SI - (d+\delta_{1}+\eta+\alpha) I \;, \\ \frac{dH}{dt} &= \alpha I - (d+\delta_{2}+\theta) H \;, \\ \frac{dV}{dt} &= \; \gamma S - (d+\varepsilon) V\;, \\ \end{aligned} \right. \end{aligned} $$
(1)
Fig. 1
figure 1

The flowchart of SIHV  epidemic modeling of COVID-19

Full size image

With

$$\displaystyle \begin{aligned} S(0)\geq0 ,\ I(0)\geq0 ,\ H(0)\geq0 ,\ V(0)\geq0. \end{aligned}$$

Where Λ is the recruitment rate, β is the disease transmission rate, ρ is the portion of susceptible human would maintain proper precaution measure for disease transmission (0 < ρ < 1), ε is the rate of vaccinated individuals who became susceptible, η and θ are the recovery rates of real infected individuals and the confirmed infected, respectively, δ 1 is the COVID-19 induced death rate of real infected individuals, α is the rate of transmission from the class of real infected to the class of confirmed infected, δ 2 is the COVID-19 induced death rate of confirmed infected individuals, γ is the vaccinated susceptible individuals rate and d is the natural death rate of the population.

Our paper is organized as follows. In Sect. 2, we will study the local stability of our model. In the next section, we will prove the positivity and the boundedness results. After, we give the two equilibrium points and calculate the basic reproduction number of our COVID-19 epidemic model. Section 4 is devoted to illustrate our theoretical findings by numerical simulations, we will give also a comparison between the model results and COVID-19 clinical data. The last section concludes our work.

2 Positivity and Boundedness of Solutions

Since our problem is related to the population dynamics, we will prove that all model variables are positive and bounded. First, we will assume that all the parameters in our model are positive.

Proposition 2.1

For any positive initial conditions S(0), I(0), H(0) and V (0), the variables of the model (1) S(t), I(t), H(t) and V (t) will remain positive for all t > 0.

Proof

We have the following results :

$$\displaystyle \begin{aligned}\dot{S}|{}_{S=0} = \; \lambda + \eta I+ \theta H + \varepsilon V \; \geq \; 0, \end{aligned}$$
$$\displaystyle \begin{aligned}\dot{I}|{}_{I=0} = \; 0 \; \geq \; 0, \end{aligned}$$
$$\displaystyle \begin{aligned}\dot{H}|{}_{H=0} = \; \alpha I \; \geq \; 0, \end{aligned}$$

et

$$\displaystyle \begin{aligned}\dot{V}|{}_{V=0} = \; \gamma S \; \geq \; 0, \end{aligned}$$

this shows the positivity of solutions for all t ≥ 0.

For the boundedness of the solutions, Let

$$\displaystyle \begin{aligned}N(t)=S(t)+I(t)+C(t)+V(t),\end{aligned}$$

according to system (1), we have

$$\displaystyle \begin{aligned} \frac{dN(t)}{dt}=\Lambda - d N(t)-\delta_1I(t)-\delta_{2}C(t)) \leq d\left( \dfrac{\Lambda}{d} - N(t))\right), \end{aligned}$$

then we have

$$\displaystyle \begin{aligned} \dfrac{d\left( \frac{\Lambda}{d}-N(t)\right) }{dt}+d\left( \dfrac{\Lambda}{d} -N(t) \right)dt\geq 0. \end{aligned}$$

Therefore

$$\displaystyle \begin{aligned} \dfrac{\Lambda}{d}-N(t)\geq \left(\dfrac{\Lambda}{d}-N(0)\right)e^{-d t } \end{aligned}$$

if \(\dfrac {\Lambda }{d}-N(0)\geq 0 \), i.e., \(S(0)+I(0)+C(0)+V(0)\leq \dfrac {\Lambda }{d}\), then

$$\displaystyle \begin{aligned} S(t)+I(t)+C(t)+V(t)\leq \dfrac{\Lambda}{d}. \end{aligned}$$

Thus the region

$$\displaystyle \begin{aligned} \Delta=\left\lbrace(S,I,C,V)\in \mathbb{R}_+^4: S + I + C + V \leq \dfrac{\Lambda}{d} \right\rbrace \end{aligned}$$

is a positively invariant set of system (1).

3 Steady States and Local Stability

3.1 Basic Reproduction Number

The basic reproduction number denoted by R 0, is the average number of new infected cases generated by one infected individual when all the population are susceptible individuals [21]. In order to calculate the basic reproduction number, we will use the next generation matrix FV −1, where F is the nonnegative matrix of new infection cases, and V  is the matrix of the transition of infections associated to the model (1)

So,

with \(S_{0}= \dfrac {\Lambda (d+\epsilon )}{d(d+\epsilon +\gamma )}\). The basic reproduction number is the spectral radius of the matrix FV −1. This fact implies that

$$\displaystyle \begin{aligned}R_{0}= \dfrac{ \Lambda \beta (1- \rho) (d+\epsilon)}{d(d+\epsilon+\gamma)(\delta_{1} + d + \alpha + \eta)}. \end{aligned}$$

3.2 Steady States

The steady states of our studied problem (1)are illustrated by the following theorem

Theorem 3.1

The model (1) has a disease-free equilibrium E f and an endemic equilibrium E 1.

Proof

To find the steady states of the system 1, we solve the following system

$$\displaystyle \begin{aligned} \Lambda- \beta (1-\rho)\;SI + \varepsilon V + \theta H + \eta I- (d+\gamma)S \;&=0, \\ \beta (1-\rho)\;SI - \delta_{1} I - (d+\alpha+\eta) I \;&=0, \\ \alpha I - \delta_{2} H - (d+\theta) H \;&=0, \\ \gamma S - (d+\varepsilon) V \;&=0. \\ \end{aligned} $$

After a simple resolution, we obtain

  • When I = 0 we find the disease-free equilibrium

    $$\displaystyle \begin{aligned}E_f=\left(\displaystyle{\dfrac{\Lambda (d+\epsilon)}{d(d+\epsilon+\gamma)}}, 0, 0, \displaystyle{\dfrac{\Lambda \gamma }{d (d+\epsilon+\gamma)}} \right).\end{aligned}$$

  • When I ≠ 0 we find the endemic equilibrium defined as follows \(\displaystyle {E_1=\left ( S^{*}, I^{*}, C^{*}, V^{*} \right )},\)

    where

    $$\displaystyle \begin{aligned}S^{*}= \dfrac{S_{0}}{R_0},\end{aligned}$$
    $$\displaystyle \begin{aligned}I^{*} = \dfrac{(R_0 - 1)}{\Gamma R_0 }\; \;,\end{aligned}$$
    $$\displaystyle \begin{aligned}H^{*} = \dfrac{\alpha (R_0 - 1)}{(\delta_{2} + d + \theta) \Gamma R_0} ,\end{aligned}$$
    $$\displaystyle \begin{aligned}V^{*}= \dfrac{\gamma S_{0}}{ (d +\epsilon) R_0} .\end{aligned}$$

    Where \( \Gamma = \dfrac {(d +\epsilon )(\delta _{2} + d + \theta ) + \alpha (\delta _{2} + d )}{\Lambda (\delta _{2} + d + \theta )}\) and \(S_{0}= \dfrac {\Lambda (d+\epsilon )}{d(d+\epsilon +\gamma )}\).

    It’s clear that E 1 is well defined when R 0 > 1.

3.3 Local Stability

3.3.1 Local Stability of the Disease-Free Equilibrium

The local stability of the disease-free equilibrium point \(E_f =\left (\displaystyle {\frac {\Lambda (d+\epsilon )}{d(d+\epsilon +\gamma )}},\right .\) \(\left . 0,\ 0, \displaystyle {\frac {\Lambda \gamma }{d (d+\epsilon +\gamma )}} \right ),\) is given by the following result:

Prop 3.1

When R 0 < 1, then the disease-free equilibrium point, E 0 , is locally asymptotically stable.

Proof

The Jacobian matrix of the system (1) at E 0 is given by:

$$\displaystyle \begin{aligned} J_{E_{f}}=\left( \begin{array}{cccc} -(d+ \gamma) & -\beta (1- \rho) S_{0} + \eta & \theta & \epsilon \\ 0 & \beta (1- \rho) S_{0} - (\delta_{1} + d + \alpha + \eta) & 0 & 0 \\ 0 & \alpha & -(\delta_{2} + d + \theta) & 0 \\ \gamma & 0 & 0 & -(d+ \epsilon) \end{array} \right ). \end{aligned} $$
(2)

The characteristic polynomial of \(J_{E_{0}}\) is

$$\displaystyle \begin{aligned} P_{E_0}(\lambda)= [\lambda+d][\lambda+(d+ \gamma + \epsilon)]\;[\lambda+ (\delta_{2} + d + \theta)] \; [\lambda + (\delta_{1} + d + \alpha + \eta) ( 1 - R_0) ]. \end{aligned} $$

Therefore, the eigenvalues of J(E 0) are given as follow,

$$\displaystyle \begin{aligned} &\lambda_1 = -d < 0, \\ & \lambda_2 = -(d+ \gamma + \epsilon) < 0, \\ &\lambda_3 = - (\delta_{2} + d + \theta) < 0, \\ &\lambda_4 = - (\delta_{1} + d + \alpha + \eta) ( 1 - R_0) . \end{aligned} $$

clearly, λ 1, λ 2 and λ 3 are negative. However, λ 4 is negative when R 0 < 1.

Consequently E f is locally asymptotically stable when R 0 < 1.

3.3.2 Local Stability of the Endemic Equilibrium

The local stability of the endemic equilibrium point \(\displaystyle {E_1=\left ( S^{*}, I^{*}, C^{*}, V^{*} \right )},\) is given by the following result:

Prop 3.2

When R 0 > 1 then the endemic equilibrium point E 1 is locally asymptotically stable.

Proof

The Jacobian matrix of the system (1) at E 1 is given by:

$$\displaystyle \begin{aligned} J_{E_{1}}=\left( \begin{array}{cccc} -\beta (1- \rho) I - (d+ \gamma) & -\beta (1- \rho) S + \eta & \theta & \epsilon \\ -\beta (1- \rho) I & \beta (1- \rho) S - (\delta_{1} + d + \alpha + \eta) & 0 & 0 \\ 0 & \alpha & -(\delta_{2} + d + \theta) & 0 \\ \gamma & 0 & 0 & -(d+ \epsilon) \end{array} \right ). \end{aligned} $$
(3)

The characteristic polynomial of \(J_{E_{1}}\) is

$$\displaystyle \begin{aligned} P_{E_1}(\lambda)= (d + \epsilon + \lambda)\left( \lambda^{3} + A_{1} \lambda^{2} + A_{2} \lambda + A_{3} \right) \end{aligned} $$

such that:

$$\displaystyle \begin{aligned}A_{1} = d + \delta_{2} + \theta + \dfrac{ \Lambda (d + \epsilon)}{S_{0}} \; ,\end{aligned}$$
$$\displaystyle \begin{aligned}A_{2} = \dfrac{ \Lambda (d + \epsilon)}{S_{0}} (d + \delta_{2} + \theta) + \dfrac{\beta (1-\rho) (d + \delta_{1} + \alpha) (d + \epsilon) I^{*} S_{0} }{ R_0 S^{*}} \; ,\end{aligned}$$
$$\displaystyle \begin{aligned}A_{3} = \dfrac{\beta (1-\rho) I^{*} S_{0}}{R_0 S^{*}} \left( d + \delta_{1} + \alpha + (d + \epsilon)(d + \delta_{2} + \theta) - \alpha \theta (d +\epsilon) \right) .\end{aligned}$$

The first eigenvalue of (3) is λ 1 = −(d + 𝜖) < 0, also it is easy to verify that A 1 > 0, A 1 A 2 − A 3 > 0 and A 3 > 0 if R 0 > 1 then by using the Routh-Hurwitz Theorem, the other eigenvalues of (3) have negative real parts.

Consequently, E 1 is locally asymptotically stable when R 0 > 1.

4 Numerical Simulations

In this section, we will perform some numerical simulations in order to confirm our theoretical results and to check the impact of vaccination strategy in fighting against the spread of COVID-19 pandemic. Indeed, Fig. 2 shows the evolution of infection for Λ = 1, ρ = 0.1, η = 0.1, θ = 0.6, d = 0.1,γ = 1.2, 𝜖 = 0.03, β = 1.3, δ 1 = 0.7, δ 2 = 0.6 and α = 0.4.

Fig. 2
figure 2

The dynamical behavior of compartments S, I, H and V  revealing the extinction of COVID-19 disease with R 0 = 0.8797 < 1

Full size image

Figure 2 depicts the dynamics of all SIHV variables. In this figure, we observe that all curves drop to zero, except the curves representing the susceptible and vaccinated individuals. With the used parameters, the basic reproduction number is less than one (R 0 = 0.8797 < 1). Figure 3 shows the time evolution of our SICV four compartments model. With the used parameters, the basic reproduction number is more than one (R 0 = 1.19721 > 1). We observe that the trajectories representing real and confirmed infected individuals remain at a strictly positive level which means that the disease persists. Which is in good agreement with the theoretical result concerning the stability of equilibria, the disease free and the endemic equilibrium points.

Fig. 3
figure 3

The dynamical behavior of compartments S, I, H and V  revealing the persistence of COVID-19 disease with R 0 = 1.19721 > 1

Full size image

Figure 3 shows the evolution of infection for Λ = 1, ρ = 0.1, η = 0.1, θ = 0.6, d = 0.1,γ = 0.75, 𝜖 = 0.01, β = 1.3, δ 1 = 0.7, δ 2 = 0.6 and α = 0.35.

4.1 Application to Morocco COVID-19 Clinical Data

We have chosen to make our comparison, the Moroccan clinical data during the period between September 12 and March 28 [22]. for the following parameter values: Λ = 1; ρ = 0.1; a = 0.001; η = 0.1; θ = 0.6; d = 0.1; γ = 0.6; 𝜖 = 0.01; β = 1; δ 1 = 0.7; δ 2 = 0.6; α = 0.2. Figure 4 shows the time evolution of infected cases, we observe a significant good approach between the curves representing the model numerical results and the clinical data. Therefore, our model have shown its efficiency in approaching and predicting the second wave of COVID-19 pandemic.

Fig. 4
figure 4

The time evolution of infected cases trajectory (blue color). The clinical infected cases are illustrated by magenta circles

Full size image

4.2 The Effect of the Vaccination Strategy on COVID-19 Pandemic Spread

In this subsection, we will study the role of the vaccination strategy in reducing the infection severity of COVID-19 pandemic. Figure 5 shows the time evolution of the real infected cases for the parameters Λ = 0.95, ρ = 0, η = 0.1, θ = 0.6, d = 0.1, γ = 0.1, 𝜖 = 0.01, β = 2.6, δ 1 = 0.2, dδ 2 = 0.1 and α = 0.3. We observe the effect of vaccination strategy on reducing the spread of the COVID-19 infection. Indeed, by increasing the vaccination rate a significant reduce of the real infected individuals is observed which clearly reveals the impact of vaccination strategy in fighting against the spread of COVID-19 pandemic.

Fig. 5
figure 5

The dynamical behavior of real infected cases for our model revealing the effect of vaccination rate on COVID-19 pandemic model

Full size image

5 Discussion and Conclusion

Mathematical modeling contributes enormously in epidemiological research via both theoretical and numerical methods allowing a better understanding of the evolution of the pandemic within populations and to unearth the interactions between the various factors responsible for the spread of infections between individuals, but also to provide conditions for the stability of the variables that cause the disease. Due to the rapid spread of COVID-19, scientific researchers are working day and night to find an ideal vaccine that eradicates this pandemic. Those efforts can bring the world back to a normal pre-COVID-19 normal life. The main objective is to find an adequate vaccination strategy to curb the rapid spread of the virus as well as to obtain collective immunity to prevent the appearance of new variants of COVID-19.

In this paper, we have studied a mathematical model describing the spread of the COVID-19 pandemic with a vaccination strategy. The model consisted of four compartments, namely, the susceptible S, the real infected I, the confirmed infected H and the vaccinated individuals V , this type of model takes the abbreviation SIHV . We have first studied the local stability of our model two state states by calculating the basic reproduction number of our COVID-19 epidemic model. Finally, we have confirmed our theoretical results by adequate numerical simulations. An interesting comparison was also made between the model theoretical results and the COVID-19 clinical data from Morocco between September 2020 and April 2021. It was also shown that vaccination strategy plays an essential role in controlling COVID-19 spread. We can conclude from our study that a good vaccination strategy leads to controlling COVID-19 in target populations.