Abstract
Oblivious Linear Evaluation (OLE) is the arithmetic analogue of the well-know oblivious transfer primitive. It allows a sender, holding an affine function \(f(x)=a+bx\) over a finite field or ring, to let a receiver learn f(w) for a w of the receiver’s choice. In terms of security, the sender remains oblivious of the receiver’s input w, whereas the receiver learns nothing beyond f(w) about f. In recent years, OLE has emerged as an essential building block to construct efficient, reusable and maliciously-secure two-party computation.
In this work, we present efficient two-round protocols for OLE over large fields based on the Learning with Errors (LWE) assumption, providing a full arithmetic generalization of the oblivious transfer protocol of Peikert, Vaikuntanathan and Waters (CRYPTO 2008). At the technical core of our work is a novel extraction technique which allows to determine if a non-trivial multiple of some vector is close to a q-ary lattice.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Oblivious Linear Evaluation (OLE) is a cryptographic primitive between a sender and a receiver, where the sender inputs an affine function \(f(x)=a+bx\) over a finite field \(\mathbb {F}\), the receiver inputs an element \(w\in \mathbb {F}\), and in the end the receiver learns f(w). The sender remains oblivious of the receiver’s input w and the receiver learns nothing beyond f(w) about f. OLE can be seen as a generalization of the well-known Oblivious Transfer (OT) primitive.Footnote 1 In fact, just as secure computation of Boolean circuits can be based on OT, secure computation of arithmetic circuits can be based on OLE [2, 20, 22].
In recent years, OLE has emerged as one of the most promising avenues to realize efficient two-party secure computation in different settings [1, 2, 6, 11, 13, 21, 22]. Interestingly, OLE has found applications, not just in the secure computation of generic functions, but also in specific tasks such as Private Set Intersection [18, 19] or Machine Learning related tasks [23, 28].
Other aspects that set OLE apart from OT are reusability, meaning that the first message of a protocol is reusable across multiple executions,Footnote 2 and the fact that even a semi-honest secure OLE can be used to realize maliciously secure two-party computation [21].
Although OLE secure against semi-honest adversaries is complete for maliciously-secure two-party computation [21], this comes at the cost of efficiency and, thus, is it always preferable to start with a maliciously-secure one. Moreover, some applications of OLE even ask specifically for a maliciously-secure one [18]. Given this state of affairs and the importance of OLE in constructing two-party secure computation protocols, we ask the following question:
Can we build efficient and maliciously-secure two-round OLE protocols from (presumed) post-quantum hardness assumptions?
1.1 Our Results
In this work, we give an affirmative answer to the question above. Specifically, we present two simple, efficient and round-optimal protocols for OLE based on the hardness of the Learning with Errors (LWE) assumption [31], which is conjectured to be post-quantum secure.
Before we start, we clarify what type of OLE we obtain. OLE comes in many flavors, one of the most useful being vector OLE where the sender inputs two vectors \(a=\mathbf {a},b=\mathbf {b}\in \mathbb {F}^\ell \) and the receiver obtains a linear combination of them \(\mathbf {z}=\mathbf {a}+w\mathbf {b}\in \mathbb {F}^\ell \) [6]. For simplicity, we just refer to this variant as OLE.
Both of our protocols implement the functionality in just two-rounds and have the following properties:
-
Our first protocol (Sect. 5) for OLE achieves statistical security against a corrupted receiver and computational semi-honest security against a corrupted sender based on LWE. Additionally, we show how we can extend this protocol to implement batch OLE, a functionality similar to OLE where the receiver can input a batch of values \(\{x_i\}_{i\in [k']}\), instead of just one value.
-
Our main technical innovation is a new extraction technique which allows to determine if a vector \(\mathbf {z} \in \mathbb {Z}_q^n\) is of the form \(\mathbf {z} = \mathbf {s}\mathbf {A} + \alpha \boldsymbol{e}\), where the matrix \(\mathbf {A} \in \mathbb {Z}_q^{k \times n}\) is given, and the unknown \(\mathbf {s} \in \mathbb {Z}_q^k\), \(\alpha \in \mathbb {Z}_q\) and short vector \(\mathbf {e}\) are to be determined. We provide an algorithm which solves this problem efficiently given a trapdoor for the lattice \(\varLambda _q^\perp (\mathbf {A})\). We believe that this contribution is of independent interest. In particular, our extractor immediately leads to an efficient simulation strategy for the PVW protocol [29] even for super-polynomial moduli q.
-
We then show how to extend our OLE protocol to provide malicious security for both parties (Sect. 6). The protocol makes \(\lambda \) invocations of a two-round Oblivious Transfer protocol (which exists under LWE [29, 30]), where \(\lambda \) is the security parameter. By instantiating the OT with the LWE-based protocols of [29, 30], we preserve statistical security against a malicious receiver.
1.2 Related Work and Comparison
In the following, we briefly review some proposals from prior work and compare them with our proposal. We only consider schemes that are provable UC-secure as our protocols. OLE can be trivially implemented using Fully/Somewhat Homomorphic Encryption (e.g., [23]) but these solutions are usually just proven secure against semi-honest adversaries and it is unclear how to extend security against malicious adversaries without relying on generic approaches such as Non-Interactive Zero-Knowledge (NIZK) proofs.Footnote 3 OLE can also be trivially implemented using generic solutions for two-party secure computation (via OT) such as [32]. However, these solutions fall short in achieving an acceptable level of efficiency.
The work of Döttling et al. [14, 15] proposed an OLE protocol with unconditional security, in the stateful tamper-proof hardware model. The protocol takes only two rounds, however further interaction with the token is needed by the parties.
In [22], a semi-honest protocol for oblivious multiplication was proposed, which can be easily extended to a OLE protocol. The protocol is based on noisy encodings. Based on the same assumption, [17] proposed a maliciously-secure OLE protocol, which extends the techniques of [22]. However, their protocol takes eight rounds of interaction.
Chase et al. [11] presented a round-optimal reusable OLE protocol based on the Decisional Composite Residuosity (DCR) and the Quadratic Residuosity (QR) assumptions. The protocol is maliciously-secure and, to the best of our knowledge, it is the most efficient protocol for OLE proposed so far. However, it is well-known that both the DCR and the QR problems are quantumly insecure.
Recently, two new protocols for OLE based on the Ring LWE assumption were presented in [5, 10]. Both protocols run in two rounds but the protocol of [5] either requires a PKI or a setup phase, and the protocol of [10] is secure only against semi-honest adversaries.
We also remark that our protocols implement vector OLE where the sender’s input are vectors over a field, as in [17].
In Table 1, a brief comparison between several UC-secure OLE protocols is presented.
1.3 Open Problems
Our first protocol is secure against semi-honest senders and, thus, it is trivially reusable. However, our fully maliciously-secure protocol (in Sect. 6) does not have reusability of the first message. Hence, the main open problem left in our work is the following: Can we construct a reusable maliciously-secure two-round OLE protocol based on the LWE assumption?
2 Technical Outline
We will now give a brief overview of our protocol. In abuse of notation, we drop the transposition operator for transposed vectors and always assume that vectors multiplied from the right side are transposed.
2.1 The PVW Protocol
Our starting point is the LWE-based oblivious transfer protocol of Peikert, Vaikuntanathan and Waters [29], which is based on Regev’s encryption scheme [31]. Since our goal is to construct an OLE protocol, we will describe the PVW scheme as a \(\mathbb {F}_2\) OLE rather than the standard OT functionality. Assume for simplicity that the LWE modulus q is even.
The PVW scheme uses a common reference string which consists of a random matrix \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) and a vector \(\mathbf {a} \in \mathbb {Z}_q^m\), which together syntactically form a Regev public key. Given the CRS \((\mathbf {A},\mathbf {a})\), the receiver, whose input is a choice bit \(b \in \{0,1\}\) chooses a uniformly random \(\mathbf {s} \in \mathbb {Z}_q^n\) and a \(\mathbf {e} \in \mathbb {Z}_q^m\) from a (short) LWE error distribution, e.g. a discrete gaussian. The receiver now sets \(\mathbf {z} = \mathbf {s} \mathbf {A} + \mathbf {e} - b \cdot \mathbf {a}\). In other words, if \(b = 0\) then \((\mathbf {A},\mathbf {z})\) is a well-formed Regev public key, whereas if \(b = 1\) then \((\mathbf {A},\mathbf {z} + \mathbf {a})\) is a well-formed Regev public key.
The receiver now sends \(\mathbf {z}\) to the sender who proceeds as follows. Say the sender’s input are \(v_0,v_1 \in \{0,1\}\). The sender now encrypts \(v_0\) under the public key \((\mathbf {A},\mathbf {z})\) and \(v_1\) under \((\mathbf {A},\mathbf {a})\) using the same randomness \(\mathbf {r}\). Specifically, the sender chooses \(\mathbf {r} \in \mathbb {Z}^m\) from a wide enough discrete gaussian, sets \(\mathbf {c} = \mathbf {A} \mathbf {r}\), \(c_0 = \mathbf {z} \mathbf {r} + \frac{q}{2} v_0\) and \(c_1 = \mathbf {a} \mathbf {r} + \frac{q}{2} v_1\). Now the sender sends \((\mathbf {c},c_0,c_1)\) back to the receiver. The receiver then computes and outputs \(y = \lceil b \cdot c_1 + c_0 - \mathbf {s} \mathbf {c} \rfloor _2\). Here \(\lceil \cdot \rfloor _2\) denotes the rounding operation with respect to q/2.
To see that this scheme is correct, note that
Since both \(\mathbf {e}\) and \(\mathbf {r}\) are short, \(\mathbf {e} \mathbf {r}\) is also short and we can conclude that \(y = \lceil b \cdot c_1 + c_0 - \mathbf {s} \mathbf {c} \rfloor _2 = b v_1 + v_0\).
Security. Security against semi-honest senders follows routinely from the hardness of LWE. We will omit the discussion on security against malicious senders for now and focus on security against malicious receivers.
The basic issue here is that a malicious receiver may choose \(\mathbf {z}\) not of the form \(\mathbf {z} = \mathbf {s} \mathbf {A} + \mathbf {e} - b \mathbf {a}\) but rather arbitrarily.
It can now be argued that except with negligible probability over the choice of \(\mathbf {a}\), one of the matrices  or
or  does not have a short vector in its row-span. We can then invoke the Smoothing Lemma [27] to argue that given \(\mathbf {c} = \mathbf {A} \mathbf {r}\) either \(\mathbf {z} \mathbf {r}\) or \((\mathbf {z} +\mathbf {a})\mathbf {r}\) is statistically close to uniform. In the first case we get that \((\mathbf {c},c_0,c_1)\) statistically hides \(v_0 = v_0 + 0 \cdot v_1\), in the second case \(v_0 + v_1 = v_0 + 1 \cdot v_1\) is statistically hidden. In order to simulate, we must determine which one of the two cases holds.
does not have a short vector in its row-span. We can then invoke the Smoothing Lemma [27] to argue that given \(\mathbf {c} = \mathbf {A} \mathbf {r}\) either \(\mathbf {z} \mathbf {r}\) or \((\mathbf {z} +\mathbf {a})\mathbf {r}\) is statistically close to uniform. In the first case we get that \((\mathbf {c},c_0,c_1)\) statistically hides \(v_0 = v_0 + 0 \cdot v_1\), in the second case \(v_0 + v_1 = v_0 + 1 \cdot v_1\) is statistically hidden. In order to simulate, we must determine which one of the two cases holds.
In [29] this is achieved as follows. First, the matrix \(\mathbf {A}\) is chosen together with a lattice trapdoor [16, 26] which allows to efficiently decode a point \(\mathbf {x} \in \mathbb {Z}_q^m\) to the point in the row-span of \(\mathbf {A}\) closest to \(\mathbf {x}\) (given that \(\mathbf {x}\) is sufficiently close to the row-span of \(\mathbf {A}\)). The PVW extractor now tries to determine whether there is a short vector in the row-span of \(\mathbf {A}_0\) by going through all multiples \(\alpha \mathbf {z}\) of \(\mathbf {z}\) (for \(\alpha \in \mathbb {Z}_q\)) and testing whether \(\alpha \mathbf {z}\) is close to the row-span of \(\mathbf {A}\). If such an \(\alpha \) is found, we know by the above argument that given \(\mathbf {A} \mathbf {r}\) and \(\mathbf {z}\mathbf {r}\) it must hold that \((\mathbf {z} + \mathbf {a})\mathbf {r}\) is statistically close to uniform, and the simulator can set the extracted choice bit b to 0. On the other hand, if no such \(\alpha \) is found, it sets the extracted choice bit to 1 since we know that in this case \(\mathbf {z}\mathbf {r}\) is statistically close to uniform given \(\mathbf {A}\mathbf {r}\) and \((\mathbf {z}+\mathbf {a})\mathbf {r}\).
A severe drawback of this method is that the extractor must iterate over all \(\alpha \in \mathbb {Z}_q\). Consequently, for the extractor to be efficient q must be of polynomial size. A recent work of Quach [30] devised an extraction method for superpolynomial modulus q by using Hash Proof Systems (HPS)Footnote 4. To make this approach work the underlying Regev encryption scheme must be modified in a way that unfortunately deteriorates correctness and prohibits linear homomorphism.
2.2 An Oblivious Linear Evaluation Protocol Based on PVW
We will now discuss our OLE modification of the PVW scheme. The basic idea is very simple: We will modify the underlying Regev encryption scheme to support a larger plaintext space, namely \(\mathbb {Z}_{q_1}\) for a modulus \(q_1\) and exploit linear homomorphism over \(\mathbb {Z}_{q_1}\), which will lead to an OLE over \(\mathbb {Z}_{q_1}\).
Concretely, let \(q = q_1 \cdot q_2\) for a sufficiently large \(q_2\). We have the same CRS as in the PVW scheme, i.e. a random matrix \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) and a random vector \(\mathbf {a} \in \mathbb {Z}_q^m\). Now the receiver’s input is a \(x \in \mathbb {Z}_{q_1}\), and he computes \(\mathbf {z}\) by \(\mathbf {z} = \mathbf {s} \mathbf {A} + \mathbf {e} - x \cdot \mathbf {a}\) (where \(\mathbf {s}\) and \(\mathbf {e}\) are as above). The sender’s input is now a pair \(v_0,v_1 \in \mathbb {Z}_{q_1}\), and the sender computes \(\mathbf {c} = \mathbf {A}\mathbf {r}\), \(c_0 = \mathbf {z} \mathbf {r} + q_2 v_0\) and \(c_0 = \mathbf {a} \mathbf {r} + q_2 v_1\) (again \(\mathbf {r}\) as above). Given \((\mathbf {c},c_0,c_1)\) the receiver can recover y by computing \(y = \lceil x \cdot c_1 + c_0 - \mathbf {s} \mathbf {c} \rfloor _{q_1}\). Here \(\lceil \cdot \rfloor _{q_1}\) is as usual defined by \(\lceil u \rfloor _{q_1} = \cdot \lceil u / q_2 \rfloor \). We can establish correctness as above:
Now, given that \(\mathbf {e}\) and \(\mathbf {r}\) are sufficiently short, specifically such that \(\mathbf {e} \mathbf {r}\) is shorter than \(q_2 / 2\) it holds that \(y = \lceil x \cdot c_1 + c_0 - \mathbf {s} \mathbf {c} \rfloor _{q_1} = x v_1 + v_0\) and correctness follows.
A detailed description of the protocol is presented in Sect. 5.Footnote 5 The protocol described there directly implements vector OLE, instead of just OLE as presented above.
Security. Security against semi-honest senders follows, just as above, routinely from the LWE assumption. But for superpolynomial moduli \(q_1\) (which, in the OLE setting, is the case we are mostly interested in) we are seemingly at an impasse when it comes to proving security against malicious receivers: In this case, the PVW extractor is not efficient and Quach’s technique [30] is incompatible with our reliance on linear homomorphism of the Regev encryption scheme.
Consequently, we need to devise an alternative method of extracting the receiver’s input x. The core idea of our extractor is surprisingly simple: While PVW choose the matrix \(\mathbf {A}\) together with a lattice trapdoor, we will instead choose the matrix  together with a lattice trapdoor \(\mathbf {T} \in \mathbb {Z}^{m \times m}\) (i.e. a short square matrix \(\mathbf {T}\) such that \(\mathbf {A}' \mathbf {T} = 0\)). This is possible as the vector \(\mathbf {a}\) is also provided in the CRS.
together with a lattice trapdoor \(\mathbf {T} \in \mathbb {Z}^{m \times m}\) (i.e. a short square matrix \(\mathbf {T}\) such that \(\mathbf {A}' \mathbf {T} = 0\)). This is possible as the vector \(\mathbf {a}\) is also provided in the CRS.
How does this help us to extract a \(\tilde{x} \in \mathbb {Z}_q\) from the malicious receiver’s message \(\mathbf {z}\)? Let \(\mathbf {z} \in \mathbb {Z}_q^m\) be arbitrary, write \(\mathbf {z}\) as \(\mathbf {z} = \mathbf {s} \mathbf {A} - x \cdot \mathbf {a} + \alpha \mathbf {d}\) for some \(\mathbf {s} \in \mathbb {Z}_q^n\), \(x \in \mathbb {Z}_q\), \(\alpha \in \mathbb {Z}_q\) and a \(\mathbf {d} \in \mathbb {Z}^m\) of minimal length. In other words, there exists no \(\mathbf {d}^*\) with \(\Vert \mathbf {d}^*\Vert < \Vert \mathbf {d} \Vert \) such that \(\mathbf {z}\) can be written as \(\mathbf {z} = \mathbf {s}^*\mathbf {A} + \alpha ^*\mathbf {d}^*- x^*\mathbf {a}\) for some \(\mathbf {s}^*\), \(x^*\) and \(\alpha ^*\).
Then it holds that
In other words, we can simulate \((\mathbf {c},c_0,c_1)\) given only \(x v_1 + v_0\). In the above derivation, (4) holds as by the partial smoothing lemma [7] as \((\mathbf {A}\mathbf {r},\mathbf {a}\mathbf {r},\mathbf {d}\mathbf {r}) = (\mathbf {A}'\mathbf {r},\mathbf {d}\mathbf {r})\approx _s (\mathbf {u}',\mathbf {d}\mathbf {r}) = (\mathbf {u},u,\mathbf {d}\mathbf {r})\) where \(\mathbf {u} \in \mathbb {Z}_q^m\) and \(u \in \mathbb {Z}_q\) are uniformly random. Equation (5) follows by a simple substitution \(u \rightarrow u' - q_2 v_1\), where \(u' \in \mathbb {Z}_q\) is also uniformly random. Equation (7) follows analogously to (4) via the smoothing lemma.
Efficient Extraction. It remains to be discussed how we can efficiently recover x from \(\mathbf {z}\) given the lattice trapdoor \(\mathbf {T}\) for \(\varLambda _q^\bot (\mathbf {A}')\). We will recover the representation \(\mathbf {z} = \mathbf {s}^*\mathbf {A} + \alpha ^*\mathbf {d}^*- x^*\mathbf {a}\). Note that we can write \(\mathbf {z} = \mathbf {s}'\mathbf {A}' + \alpha \mathbf {d}\), where \(\mathbf {s}' = ( \mathbf {s}, -x )\). Setting \(\mathbf {f} = \mathbf {z}\mathbf {T}\) we get
Assuming that \(\mathbf {d}\) is sufficiently short, it holds that \(\mathbf {d}' = \mathbf {d} \mathbf {T}\) is also short. We will now solve the equation system \(\alpha \mathbf {d}' = \mathbf {f}\), in which \(\mathbf {f}\) is known, for \(\alpha \) and \(\mathbf {d}'\). Write \(\mathbf {f} = (f_1,\dots ,f_m)\) and \(\mathbf {d}' = (d'_1,\dots ,d'_m)\). Then we get the equation system
We can eliminate \(\alpha \) using the first equation and obtain the equations
Now assume for simplicity \(f_1\) is invertible, i.e. \(f_1 \in \mathbb {Z}_q^{\times }\). Then we can express the above equations as
Consequently, it is sufficient to find the first coordinate \(d'_1\) to find all other \(d'_j = (f_j / f_1) \cdot d'_1\).
To find the first coordinate \(d'_1\), we rely on the fact that solving the Shortest Vector Problem (SVP) in a two-dimensional lattice can actually be done in polynomial time (and essentially independently of the modulus q) [24]. Consider the lattice \(\varLambda _j\) defined by \(\varLambda _j = \varLambda _q^\perp (\mathbf {b}_j)\), where \(\mathbf {b}_j=(-f_j/f_1,1)\). First note that \(\mathbf {d}'_j = (d'_1,d'_j)\) is a short vector in \(\varLambda _i\). Furthermore, notice that \(\det (\varLambda _j) = q\) as the second component of \(\mathbf {b}_j\) is 1 (\(\mathbf {b}_j\) is primitive). Letting \(B = \Vert \mathbf {d}'_j \Vert \), we can then argue via Hadamard’s inequality that any vector \(\mathbf {v} \in \varLambda _i\) shorter than q/B must be linearly dependent with \(\mathbf {d}'_j\).
By applying a SVP solver, we are able to find the shortest vector \(\mathbf {g}_j=(g_j^{(1)},g_j^{(2)})\) in \(\varLambda _i\). Observe that \(d'_1\) must be a multiple of \(g_j^{(1)}\) for all \(j=2,\dots , n\) (otherwise, \(\mathbf {g}_j\) would not be the shortest solution of the SVP instance). Hence, \(d'_1\) can be computed by taking the least common multiple of \(g_1^{(1)}, \dots , g_n^{(1)}\).
Having recovered \(\mathbf {d}' \in \mathbb {Z}^m\), we can recover \(\mathbf {d}\) by solving the linear equation system \(\mathbf {d} \mathbf {T} = \mathbf {d}'\) over \(\mathbb {Z}\) to recover \(\mathbf {d}\). Finally, given \(\mathbf {d}\) we can efficiently find \(\mathbf {s}' \in \mathbb {Z}_q^{n+1}\) and \(\alpha \in \mathbb {Z}_q\) using basic linear algebra by solving the equation system \(\mathbf {s}' \mathbf {A}' = \mathbf {z} - \alpha \mathbf {d}\). Given \(\mathbf {s}'\) we can set x to \(s'_{n + 1}\). If no solution is found in this process we set \(x = 0\) by default. Now notice that we can write
where \(\mathbf {s} = (s'_1,\dots ,s'_n)\). We remark that for a prime modulus q the above analysis readily applies, whereas for composite moduli we need to take into account several fringe cases.
Using a variant of the Smoothing Lemma [7] we can finally argue that \((\mathbf {A}\mathbf {r},\mathbf {z}\mathbf {r} + q_2 v_0,\mathbf {a}\mathbf {r} + q_2 v_1)\) only contains information about \(x v_1 + v_0\), but leaks otherwise no information about \(v_0,v_1\).
2.3 Applications to PVW OT
Note that by setting \(q_1 = 2\) our OLE protocol realizes exactly the PVW protocol [29]. Thus, our new extraction mechanism immediately improves the PVW protocol by allowing the modulus q to be superpolynomial. Furthermore, we can combine our extractor with the smoothing technique of Quach [30] to obtain a UC-secure variant of the PVW protocol with reusable CRS without the correctness and efficiency penalties incurred by Quach’s protocol.
2.4 Extending to Malicious Adversaries
It might seem that Quach’s smoothing technique [30] immediately allows us to prove security against malicious senders as well. And indeed, by choosing \(\mathbf {a}\) as a well-formed LWE sample \(\mathbf {a} = \mathbf {s}^*\mathbf {A} + \mathbf {e}^*\) we can extract the sender’s input \(v_0,v_1\) from \(\mathbf {c},c_0,c_1\). However, the issue presents itself slightly different: In the real protocol the receiver computes and outputs \(y = \lceil x \cdot (c_1 - \mathbf {s}^*\mathbf {c}) + c_0 - \mathbf {s}\mathbf {c} \rfloor _{q_1}\). If \(\mathbf {c},c_0,c_1\) are well-formed this is indeed a linear function in x. However, if \(c_1 - \mathbf {s}^*\mathbf {c}\) or \(c_0 - \mathbf {s}\mathbf {c}\) is not close to a multiple of \(q_2\), then this is a non-linear function! But by the functionality of OLE in the ideal model we have to compute a linear function. Observe that this is not an issue in the case of OT (i.e. \(q_1 = 2\)), as in this case any 1-bit input function is a linear function. To overcome this issue for OLE, we need to deploy a technique which ensures that \(\mathbf {c},c_0,c_1\) are well-formed.
In a nutshell, the idea to make the protocol secure against malicious senders is to use a cut-and-choose-style approach using a two-round OT protocolFootnote 6, which exists under various assumptions [12, 29, 30]. Using the OT, the receiver is able to check if the vectors \(\mathbf {c}_j=\mathbf {A}\mathbf {r}_j\) provided by the sender are well-formed. More precisely, our augmented protocol works as follows:Footnote 7
-
1.
The receiver computes \(\mathbf {z}=\mathbf {s}\mathbf {A} + \mathbf {e} - x \mathbf {a}\) for a uniform input x (in Sect. 6 we show how to remove the condition of x being uniform). Additionally, it runs \(\lambda \) instances of the OT in parallel (playing the role of the receiver), with input bits
 chosen uniformly at random; and sends the first messages of each instance.
chosen uniformly at random; and sends the first messages of each instance. -
2.
For \(j\in [\lambda ]\), the sender (with input \((v_0,v_1)\)) computes \(\mathbf {c}_j=\mathbf {A}\mathbf {r}_j\), \(c_{0,j}=\mathbf {z}\mathbf {r}_j + q_2 u_{0,j}\) and \(c_{1,j}=\mathbf {a}\mathbf {r}_j + q_2 u_{1,j}\) for a gaussian \(\mathbf {r}_j\) and uniform \((u_{0,j},u_{1,j}\). It sets \(M_{0,j}=(\mathbf {r}_j,u_{0,j},u_{1,j})\) and \(M_{1,j}=(\bar{v}_{0,j}=v_0+u_{0,j},\bar{v}_{1,j}=v_1+u_{1,j})\) and inputs \((M_{0,j},M_{1,j})\) into the OT. Moreover, \(\mathbf {c}_j,c_{0,j},c_{1,j}\) are sent to the receiver in the plain.
-
3.
If \(b_j=0\), the receiver can check that the values \(\mathbf {c}_j,c_{0,j},c_{1,j}\) are indeed well-formed, i.e. it holds \(\mathbf {c}_j = \mathbf {A} \mathbf {r}_j\), \(c_{0,j}=\mathbf {z}\mathbf {r}_j + q_2 u_{0,j}\), \(c_{1,j}=\mathbf {a}\mathbf {r}_j + q_2 u_{1,j}\) and \(\mathbf {r}_j\) is short. If \(b_j=1\), the receiver obtains a random OLE \(u_{0,j}+xu_{1,j}\) (which can be obtained by computing \(y = \lceil x \cdot c_{1,j} + c_{0,j} - \mathbf {s} \mathbf {c}_j \rfloor _{q_1}\)). This random OLE instance can be derandomized by computing \(y_j=\bar{v}_{0,j}+x\bar{v}_{0,j}-(u_{0,j}+xu_{1,j})\). If \(y_j\) coincides at all the positions where \(b_j=1\), then it outputs this value. Else, it aborts.
Security against an unbounded receiver in the OT-hybrid model essentially follows the same reasoning as in the previous protocol.
We now argue how we can build the simulator \(\mathsf {Sim}\) against a corrupted sender. \(\mathsf {Sim}\) checks for which of the positions j, the message \(M_{0,j}\) is well-formed. If all but a small number of them are well-formed, \(\mathsf {Sim}\) proceeds; else, it aborts. Then, having recovered the randomness \((\mathbf {r}_j,u_{0,j},u_{1,j})\), \(\mathsf {Sim}\) can extract a pair \((v_{0,j},v_{0,1})\) from \((\mathbf {c}_j,c_{0,j},c_{1,j})\). If \((v_{0,j},v_{0,1})\) coincides in at least half of the positions, then \(\mathsf {Sim}\) outputs this pair; else, if no such pair exists, \(\mathsf {Sim}\) aborts.
3 Preliminaries
Throughout this work, \(\lambda \) denotes the security parameter and PPT stands for “probabilistic polynomial-time”.
Let \(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) and \(\mathbf {x}\in \mathbb {Z}_q^n\). Then \(\left\| \mathbf {x}\right\| \) denotes the usual \(\ell _2\) norm of a vector \(\mathbf {x}\). Moreover, \(\left\| \mathbf {A}\right\| =\max _{i\in [m]}\{\left\| \mathbf {a}^{(i)}\right\| \}\) where \(\mathbf {a}^{(i)}\) is the i-th column of \(\mathbf {A}\). For a vector \(\mathbf {b}\in \{0,1\}^k\), we denote its weight, that is the number of non-null coordinates, by \( wt (\mathbf {b})\).
If S is a (finite) set, we denote by  an element \(x\in S\) sampled according to a uniform distribution. Moreover, we denote by U(S) the uniform distribution over S. If D is a distribution over S,
an element \(x\in S\) sampled according to a uniform distribution. Moreover, we denote by U(S) the uniform distribution over S. If D is a distribution over S,  denotes an element \(x\in S\) sampled according to D. If \(\mathcal {A}\) is an algorithm, \(y\leftarrow \mathcal {A}(x)\) denotes the output y after running \(\mathcal {A}\) on input x.
denotes an element \(x\in S\) sampled according to D. If \(\mathcal {A}\) is an algorithm, \(y\leftarrow \mathcal {A}(x)\) denotes the output y after running \(\mathcal {A}\) on input x.
A negligible function \(\mathsf {negl}(n)\) in n is a function that vanishes faster than the inverse of any polynomial in n.
Given two distributions \(D_1\) and \(D_2\), we say that they are \(\varepsilon \)-statistically indistinguishable, denoted by \(D_1\approx _\varepsilon D_2\), if the statistical distance is at most \(\varepsilon \).
The function \(\mathsf {lcm}(i_1,\dots , i_j)\) between j integers \(i_1,\dots , i_j\) is the smallest integer \(a\in \mathbb {Z}\) such that a is divisible by all \(i_1,\dots , i_j\).
Error-Correcting Codes. We define Error-Correcting Codes (ECC). An ECC over \(\mathbb {Z}_q\) is composed by the following algorithms \(\mathsf {ECC}_{q',q,\ell ,k,\delta }=(\mathsf {Encode},\mathsf {Decode})\) such that: i) \(\mathbf {c}\leftarrow \mathsf {Encode}(\mathbf {m})\) takes as input a message \(\mathbf {m}\in \mathbb {Z}_{q'}^\ell \) and outputs a codeword \(\mathbf {c}\in \mathbb {Z}_q^k\); ii) \(\mathbf {m}\leftarrow \mathsf {Decode}(\tilde{\mathbf {c}})\) takes as input corrupted codeword \(\tilde{\mathbf {c}}\in \mathbb {Z}_q^k\) and outputs a message \(\mathbf {m}\in \mathbb {Z}_{q'}^\ell \) if \(\left\| \tilde{\mathbf {c}}-\mathbf {c}\right\| \le \delta \) where \(\mathbf {c}\leftarrow \mathsf {Encode}(\mathbf {m})\). In this case, we say that \(\mathsf {ECC}\) corrects up to \(\delta \) errors. We say that \(\mathsf {ECC}\) is linear if any linear combination of codewords of \(\mathsf {ECC}\) is also a codeword of \(\mathsf {ECC}\).
An example of such code is the primitive lattice of [26] which allows for efficient decoding and fulfills all the properties that we need. In this code, \(q=q'\) and \(\ell <k\).
Alternatively, if \(\mathbf {m}\in \mathbb {Z}_{q'}^\ell \) for \(q't=q\) for some \(t\in \mathbb {N}\), we can use the encoding \(\mathbf {c}= t\cdot \mathbf {m}\) which is usually used in lattice-based cryptography (e.g., [4]). Decoding a corrupted codeword \(\tilde{\mathbf {c}}\) works by rounding \(\left\lceil \tilde{\mathbf {c}} \right\rfloor _{q'}= \left\lceil (1/t)\cdot \tilde{\mathbf {c}} \right\rfloor \mod q'\).
3.1 Universal Composability
UC-framework [9] allows to prove security of protocols even under arbitrary composition with other protocols. Let \(\mathcal {F}\) be a functionality, \(\pi \) a protocol that implements \(\mathcal {F}\) and \(\mathcal {Z}\) be a environment, an entity that oversees the execution of the protocol in both the real and the ideal worlds. Let \(\mathsf {IDEAL}_{\mathcal {F},\mathsf {Sim},\mathcal {Z}}\) be a random variable that represents the output of \(\mathcal {Z}\) after the execution of \(\mathcal {F}\) with adversary \(\mathsf {Sim}\). Similarly, let \(\mathsf {REAL}_{\pi ,\mathcal {A},\mathcal {Z}}^{\mathcal {G}}\) be a random variable that represents the output of \(\mathcal {Z}\) after the execution of \(\pi \) with adversary \(\mathcal {A}\) and with access to the functionality \(\mathcal {G}\).
A protocol \(\pi \) UC-realizes \(\mathcal {F}\) in the \(\mathcal {G}\)-hybrid model if for every PPT adversary \(\mathcal {A}\) there is a PPT simulator \(\mathsf {Sim}\) such that for all PPT environments \(\mathcal {E}\), the distributions \(\mathsf {IDEAL}_{\mathcal {F},\mathsf {Sim},\mathcal {Z}}\) and \( \mathsf {REAL}_{\pi ,\mathcal {A},\mathcal {Z}}^{\mathcal {G}}\) are computationally indistinguishable.
In this work, we only consider static adversaries. That is, parties involved in the protocol are corrupted at the beginning of the execution.
We now present the ideal functionalities that we will use in this work.
CRS functionality. This functionality generates a \(\mathsf {crs}\) and distributes it between all the parties involved in the protocol. Here, we present the ideal functionality as in [29].

OT functionality. Oblivious Transfer (OT) can be seen as a particular case of OLE. We show the ideal OT functionality below.

OLE functionality. We now present the OLE functionality. This functionality involves two parties: the sender \(\mathsf {S}\) and the receiver \(\mathsf {R}\).

Batch OLE functionality. Here we define a batch version of the functionality defined above. In this functionality, the receiver inputs several OLE inputs at the same time. The sender can then input an affine function together with an index corresponding to which input the receiver should receive the linear combination. The formal description of the functionality is presented in the full version of the paper [8].
3.2 Lattices and Hardness Assumptions
Notation. Let \(\mathbf {B}\in \mathbb {R}^{k\times n}\) be a matrix. We denote the lattice generated by \(\mathbf {B}\) by \(\varLambda =\varLambda (\mathbf {B})=\{\mathbf {x}\mathbf {B}: \mathbf {x}\in \mathbb {Z}^k\}\).Footnote 8 The dual lattice \(\varLambda ^*\) of a lattice \(\varLambda \) is defined by \(\varLambda ^*=\{\mathbf {x}\in \mathbb {R}^n:\forall y\in \varLambda , \mathbf {x}\cdot \mathbf {y}\in \mathbb {Z}\}\). It holds that \((\varLambda ^*)^*=\varLambda \).
We denote by \(\gamma \mathcal {B}\) the ball of radius \(\gamma \) centered on zero. That is
A lattice \(\varLambda \) is said to be q-ary if \((q\mathbb {Z})^n\subseteq \varLambda \subseteq \mathbb {Z}^n\). For every q-ary lattice \(\varLambda \), there is a matrix \(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) such that
The orthogonal lattice \(\varLambda _q^\perp \) is defined by \(\{\mathbf {y}\in \mathbb {Z}^n:\mathbf {A}\mathbf {y}^T=0\mod q\}\). It holds that \(\frac{1}{q}\varLambda ^\perp _q=\varLambda _q^*\).
Let \(\rho _s(\mathbf {x})\) be probability distribution of the Gaussian distribution over \(\mathbb {R}^n\) with parameter s and centered in 0. We define the discrete Gaussian distribution \(D_{S,s}\) over S and with parameter s by the probability distribution \(\rho _s(\mathbf {x})/\rho (S)\) for all \(\mathbf {x}\in S\) (where \(\rho _s(S)=\sum _{\mathbf {x}\in S}\rho _s(\mathbf {x})\)).
For \(\varepsilon >0\), the smoothing parameter \(\eta _\varepsilon (\varLambda )\) of a lattice \(\varLambda \) is the least real number \(\sigma >0\) such that \(\rho _{1/\sigma }(\varLambda ^*\setminus \{0\})\le \varepsilon \) [27].
Useful Lemmata. The following lemmas are well-known results on discrete Gaussians over lattices.
Lemma 1
([3]). Let \(\sigma >0\) and  . Then we have that
. Then we have that
The next lemma is a consequence of the smoothing lemma [27] and it tells us that \(\mathbf {A}\mathbf {e}^T\) is uniform, when \(\mathbf {e}\) is sampled from a discrete Gaussian for a proper choice of parameters.
Lemma 2
([16]). Let \(q\in \mathbb {N}\) and \(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) be a matrix such that \(n=\mathsf {poly}(k\log q)\). Moreover, let \(\varepsilon \in (0,1/2)\) and \(\sigma \ge \eta _\varepsilon (\varLambda ^\perp _q(\mathbf {A}))\). Then, for  ,
,
where  .
.
The partial smoothing lemma tells us that the famous smoothing lemma [27] still holds even given a small leak.
Lemma 3
(Partial Smoothing [7]). Let \(q\in \mathbb {N}\), \(\gamma >0\) be a real number, \(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) and \(\sigma ,\varepsilon >0\) be such that \(\rho _{q/\sigma }(\varLambda _q(\mathbf {A})\setminus \gamma \mathcal {B})\le \varepsilon \). Moreover, let \(\mathbf {D}\in \mathbb {Z}_q^{m\times k}\) be a full-rank matrix with \(\varLambda ^\perp _q(\mathbf {D})=\{\mathbf {x}\in \mathbb {Z}^n:\mathbf {x}\cdot \mathbf {y}^T=0, \forall \mathbf {y}\in \varLambda _q(\mathbf {A})\cap \gamma \mathcal {B}\}\). Then we have that
where  and
and  .
.
Recall Hadamard’s inequality.
Theorem 1
(Hadamard’s inequality). Let \(\varLambda \subseteq \mathbb {R}^n\) be a lattice and let \(\mathbf {e}_1,\dots ,\mathbf {e}_n\) be a basis of \(\varLambda \). Then it holds that
The following two lemmas give us an upper-bound on and the value of the determinant of a two-dimensional lattice \(\varLambda ^\perp _q(\mathbf {a})\) for \(\mathbf {a}\in \mathbb {Z}^2_q\).
Lemma 4
Let \(q\in \mathbb {N}\), \(B\in \mathbb {R}\) and \(\mathbf {a}\in \mathbb {Z}_q^2\) such that \(\mathbf {a}\ne 0\). Let \(\mathbf {e},\mathbf {e}'\in \mathbb {Z}^2\) such that \(\mathbf {e},\mathbf {e}'\in \varLambda _q^\perp (\mathbf {a})\), \(\left\| \mathbf {e}\right\| ,\left\| \mathbf {e}'\right\| <B\) and \(\mathbf {e},\mathbf {e}'\) are linearly independent over \(\mathbb {Z}\). Then \(\det \left( \varLambda _q^\perp (\mathbf {a})\right) \le B^2\).
The proof is presented in the full version of the paper [8].
We will need the following simple Definition and Lemma.
Definition 1
Let q be a modulus. We say that a vector \(\mathbf {a} \in \mathbb {Z}_q^n\) is primitive, if the row-span of of \(\mathbf {a}^\top \) is \(\mathbb {Z}_q\). In other words it holds that every \(z \in \mathbb {Z}_q\) can be expressed as \(z = \langle \mathbf {a},\mathbf {x} \rangle \) for some \(\mathbf {x} \in \mathbb {Z}_q^n\).
Lemma 5
Let q be a modulus an let \(\mathbf {a} \in \mathbb {Z}_q^n\) be primitive. Then it holds that \( \det (\varLambda ^\perp (\mathbf {a})) = q\).
The proof is presented in the full version of the paper [8].
The following lemma states that, for two-dimensional lattices, we can efficiently find the shortest vector of the lattice.
Lemma 6
([24]). Let \(q\in \mathbb {N}\), and let \(\varLambda \subseteq \mathbb {Z}^2\) be a q-ary lattice. There exists an algorithm \(\mathsf {SolveSVP}\) that takes as input (a basis of) \(\varLambda \) and outputs the shortest vector \(\mathbf {e}\in \varLambda \). This algorithm runs it time \(\mathcal {O}(\log q)\).
We will also need the following lemma which states that any sufficiently short vector of the lattice \(\varLambda ^\perp _q(\mathbf {a})\) must be a multiple of the shortest vector \(\mathbf {e}'\leftarrow \mathsf {SolveSVP}(\mathbf {a})\).
Lemma 7
Let \(q\in \mathbb {N}\), \(B<\sqrt{q}\), \(\mathbf {a}\in \mathbb {Z}^2_q\) be a primitive 2-dimensional vector such that \(\mathbf {a}\ne 0\), and \(\mathbf {e}\in \mathbb {Z}^2\) be the shortest vector of the lattice \(\varLambda ^\perp _q(\mathbf {a})\). If \(\left\| \mathbf {e}\right\| <B\) then for any \(\mathbf {e}'\in \mathbb {Z}^2\) such that \(\mathbf {e}'\in \varLambda _q^\perp (\mathbf {a})\) and \(\left\| \mathbf {e}'\right\| <B\) we have that \(\mathbf {e}'=t\mathbf {e}\) for some \(t\in \mathbb {Z}\), i.e., \(\mathbf {e}'\) is a multiple of \(\mathbf {e}\) over \(\mathbb {Z}\).
Proof
We have that \(\mathbf {e},\mathbf {e}'\in \varLambda _q^\perp (\mathbf {a})\) and \(\left\| \mathbf {e}\right\| ,\left\| \mathbf {e}'\right\| <B\). Assume towards contradiction that \(\mathbf {e},\mathbf {e}'\) are linearly dependent over \(\mathbb {Z}\). Then by Lemma 4 \(\det \left( \varLambda _q^\perp (\mathbf {a}_i)\right) \le B^2\).
On the other hand, we have that \(\det \left( \varLambda _q^\perp (\mathbf {a})\right) =q\) by Lemma 5. Then \(q\le B^2\) and thus \(\sqrt{q}\le B\), which contradicts the assumption that \(B<\sqrt{q}\). We conclude that \(\mathbf {e}\) must be a multiple of \(\mathbf {e}'\) over the integers.
The LWE Assumption. The Learning with Errors assumption was first presented in [31]. The assumption roughly states that it should be hard to solve a set linear equations by just adding a little noise to it.
Definition 2
(Learning with Errors). Let \(q,k\in \mathbb {N}\) where \(k\in \mathsf {poly}(\lambda )\), \(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) and \(\beta \in \mathbb {R}\). For any \( n=\mathsf {poly}(k\log q)\), the \(\mathsf {LWE}_{k,\beta ,q}\) assumption holds if for every PPT algorithm \(\mathcal {A}\) we have
for  ,
,  and
and  .
.
Regev proved in [31] that there is a (quantum) worst-case to average-case reduction from some problems on lattices which are believed to be hard even in the presence of a quantum computer.
Trapdoors for Lattices. Recent works [16, 26] have presented trapdoors functions based on the hardness of LWE.
Lemma 8
([16, 26]). Let \(\tau (k)\in \omega \left( \sqrt{\log k}\right) \) be a function. There is a pair of algorithms \((\mathsf {TdGen},\mathsf {Invert} )\) such that if \((\mathbf {A},\mathsf {td})\leftarrow \mathsf {TdGen}(1^\lambda ,n,k,q)\) then:
-
\(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) where \(n\in \mathcal {O}(k\log q)\) is a matrix whose distribution is \(2^{-k} \) close to the uniform distribution over \( \mathbb {Z}_q^{k\times n}\).
-
For any \(\mathbf {s}\in Z_q^k\) and \(\mathbf {e}\in \mathbb {Z}_q^n\) such that \(\left\| \mathbf {e}\right\| < q/(\sqrt{n}\tau (k))\), we have that
$$\mathbf {s}\leftarrow \mathsf {Invert} (\mathsf {td},\mathbf {s}\mathbf {A}+\mathbf {e}).$$
In the lemma above, \(\mathsf {td}\) corresponds to a short matrix \(\mathbf {T}\in \mathbb {Z}^{n\times n}\) (that is, \(\left\| \mathbf {T}\right\| <B\), for some \(B\in \mathbb {R}\) and B determines the trapdoor quality [16, 26]) such that \(\mathbf {A}\mathbf {T}=0\) and \(\mathbf {T}^{-1}\) can be easily computed. To invert a sample of the form \(\mathbf {y}=\mathbf {s}\mathbf {A}+\mathbf {e}\), we simply compute \(\mathbf {y}\mathbf {T}=\mathbf {s}\mathbf {A}\mathbf {T}+\mathbf {e}\mathbf {T}=\mathbf {e}\mathbf {T}\). The error vector \(\mathbf {e}\) can be easily recovered by multiplying by \(\mathbf {T}^{-1}\).
Observe that, if \((\mathbf {A},\mathsf {td}_\mathbf {A})\leftarrow \mathsf {TdGen}(1^\lambda ,n,k,q)\), then \(\varLambda (\mathbf {A})\) has no short vectors. That is, for all \(\mathbf {y}\in \varLambda (\mathbf {A})\), then \(\left\| \mathbf {y}\right\| >B=q/(\sqrt{n}\tau (k))\) [26]. If this does not happen, then the algorithm \(\mathsf {Invert}\) would not output the right \(\mathbf {s}\) for a non-negligible number of cases.
4 Finding Short Vectors in a Lattice with a Trapdoor
In this section, we provide an algorithm that, given a matrix \(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) together with the corresponding lattice trapdoor \(\mathsf {td}_\mathbf {A}\) (in the sense of Lemma 8), we can decide if a vector \(\mathbf {a}\in \mathbb {Z}_q^n\) is close to the row-span of \(\mathbf {A}\), i.e. if \(\mathbf {a}\) is close to the lattice \(\varLambda _q(\mathbf {A})\), and even find the closest vector in \(\varLambda _q(\mathbf {A})\).
To keep things simple, we will only consider the case where q is either a prime or the product of a “small” prime \(q_1\) and a “large” prime \(q_2\).
Before providing the algorithm, we will first prove the following structural result about equation systems of the form \(\mathbf {y} = r \mathbf {e} (\mod q)\), where \(\mathbf {y} \in \mathbb {Z}_q^n\) is given and \(r \in \mathbb {Z}_q\) and a short \(\mathbf {e} \in \mathbb {Z}^n\) are to be determined.
Lemma 9
Let q be a modulus and let \(B^2 \le q\). Let \(\mathbf {y} \in \mathbb {Z}_q^n\) be a vector such that there is an index i for which \(y_i \in \mathbb {Z}_q^*\). Assume wlog that \(y_1 \in \mathbb {Z}_q^*\). Define the q-ary lattice \(\varLambda \) as the set of all \(\mathbf {x} = (x_1,\dots ,x_n) \in \mathbb {Z}^n\) for which it holds that \(-y_i / y_1 \cdot x_1 + x_i = 0 (\mod q)\) for \(i = 2,\dots ,n\). Now let \(r \in \mathbb {Z}_q\) and \(\mathbf {e} \in \mathbb {Z}^n\) be such that \(\mathbf {y} = r \cdot \mathbf {e}\). Then \(\mathbf {e} \in \varLambda \). Furthermore, all \(\mathbf {x} \in \varLambda \) with \(\Vert \mathbf {x} \Vert \le B\) are linearly dependent. In other words, if there exists a \(\mathbf {x} \in \varLambda \backslash \{ 0 \}\) with \(\Vert \mathbf {x} \Vert \le B\), then there exists a \(\mathbf {x}^*\in \varLambda \) such that every \(\mathbf {x} \in \varLambda \) with \(\Vert \mathbf {x} \Vert \le B\) can be written as \(\mathbf {x} = t \cdot \mathbf {x}^*\) for a \(t \in \mathbb {Z}\).
Proof
First not that if \(\mathbf {y} = r \cdot \mathbf {e}\) for an \(r \in \mathbb {Z}_q\) and an \(\mathbf {e} \in \mathbb {Z}^n\), then it holds routinely that \(-y_i / y_1 \cdot e_1 + e_i = 0\) for all \(i = 2,\dots ,n\). We will now show the second part of the lemma, namely that if there exists an \(\mathbf {x} \in \varLambda \backslash \{ 0 \}\) with \(\Vert \mathbf {x} \Vert \le B\), then any such \(\mathbf {x}\) can be written as \(\mathbf {x} = t \cdot \mathbf {x}^*\) for a \(\mathbf {x}' \in \varLambda \), which is the shortest non-zero vector in \(\varLambda \). Let \(\mathbf {x} = (x_1,\dots ,x_n) \in \mathbb {Z}^n\) and define the shortened vectors \(\mathbf {x}_i = (x_1,x_i) \in \mathbb {Z}^2\). Note that since \(\Vert \mathbf {x} \Vert \le B\), it also holds that \(\Vert \mathbf {x}_i \Vert \le B\). Further define the lattices \(\varLambda _i \subseteq \mathbb {Z}^2\) (for \(i = 2,\dots ,n\)) via the equation \(- y_i/y_1 x_1 + x_i = 0\), and observe that \(\mathbf {x}_i \in \varLambda _i\). Further let \(\mathbf {x}_i^*= (x_{1,i}^*,x_i^*)\) be the shortest non-zero vector in \(\varLambda _i\). Set \(x_1^\dagger = \mathsf {lcm}(x_{1,2}^*,\dots ,x_{1,n}^*)\) and \(x_i^\dagger = x_i^*\cdot x_1^\dagger / x_{1,i}^*\), and set set \(\mathbf {x}^\dagger = (x_1^\dagger ,\dots ,x_n^\dagger )\). Note that \(\mathbf {x}^\dagger \in \varLambda \). We claim that \(\mathbf {x}\) can be written as \(\mathbf {x} = t \cdot \mathbf {x}^\dagger \), hence \(\mathbf {x}^\dagger \) is the shortest vector in \(\varLambda \).
Since \(\Vert \mathbf {x}_i \Vert \le B\) it follows by Lemma 7 that we can write \(\mathbf {x}_i\) as \(\mathbf {x}_i = t_i \cdot \mathbf {x}_i^*\) for a \(t_i \in \mathbb {Z}\). That is \(x_1 = t_i \cdot x_{1,i}^*\) and \(x_i = t_i \cdot x_i^*\). Now, since \(x_{1,i}^*\) divides \(x_1\) for \(i = 2,\dots ,n\), it also holds that \(x_1^\dagger = \mathsf {lcm}(x_{1,2}^*,\dots ,x_{1,n}^*)\) divides \(x_1\). Thus write \(x_1 = t^\dagger \cdot x_1^\dagger \) for some \(t^\dagger \), and it follows that
for \(i = 2,\dots ,n\). We conclude that \(\mathbf {x} = t^\dagger \cdot \mathbf {x}^\dagger \).
The proof of Lemma 9 suggest an approach to recover \(\mathbf {e}\) for \(\mathbf {y}\): Compute the shortest vectors of the two-dimensional lattices \(\varLambda _i\) and use them to find the shortest vector \(\mathbf {e}^\dagger \) in \(\varLambda \). Since \(\mathbf {e}\) is a multiple of \(\mathbf {e}^\dagger \), \(\mathbf {e}^\dagger \) also must be a short solution to \(\mathbf {y} = r^\dagger \mathbf {e}^\dagger \).
The following algorithm receives as input a vector \(\mathbf {y}\) and allows us to find \((r,\mathbf {e})\) such that \(r\mathbf {e}=\mathbf {y}\mod q\) and \(\mathbf {e}\) is a short vector (if such a vector exists).
Construction 1
Let q be a modulus and let \(n=\mathsf {poly}(\lambda )\). Let \(\mathbf {y} \in \mathbb {Z}_q^n\) be such that at least one component \(y_i\) is invertible, i.e. \(y_i \in \mathbb {Z}_q^*\). Without loss of generality, we assume that this component is \(y_1\).
\(\mathsf {RecoverError}_{q,n}(\mathbf {y},B)\) :
-
Parse \(\mathbf {y}\in \mathbb {Z}_q^n\) as \((y_1,\dots , y_n)\) and \(B>0\). If \(\left\| \mathbf {y}\right\| \le B\) output \(\mathbf {y}\).
-
Since \(y_i \in \mathbb {Z}_q^*\), compute for all \(i=2,\dots ,n\) \(v_i=y_i \cdot (y_1)^{-1}\) over \(\mathbb {Z}_q\), and set \(\mathbf {a}_i = (v_i \ -1)\).
-
For \(i = 2,\dots ,n\) consider the lattice \(\varLambda _i = \varLambda ^\perp _q(\mathbf {a}_i) \subseteq \mathbb {Z}^2\) and run \(\mathsf {SolveSVP}(\varLambda _i)\) to obtain \(\mathbf {e}_i^*\in \varLambda _i\). Parse \(\mathbf {e}_i = (e_{1,i}^*,e_i^*)\).
-
Compute \(e_1^\dagger =\mathsf { lcm}\left( e_{1,2},\dots , e_{1,n} \right) \).
-
For all \(i=2,\dots , n\), set \(\alpha _i = e_1^\dagger / e_{1,i} \in \mathbb {Z}\)
-
Set \(e_i^\dagger = \alpha _i \cdot e_i^*\).
-
Set \(\mathbf {e}^\dagger = (e_1^\dagger ,\dots ,e_n^\dagger )\) and \(r^\dagger = y_1 \cdot (e_1^\dagger )^{-1} \in \mathbb {Z}_q\)
-
If \(\left\| \mathbf {e}^\dagger \right\| _\infty < B\), output \((r^\dagger ,\mathbf {e}^\dagger )\). Else, output \(\perp \).
Lemma 10
Given that \(B^2 \le q\) and the vector \(\mathbf {y}\) is of the form \(\mathbf {y}=r\mathbf {e}\) for some \(r\in \mathbb {Z}_q\) and \(\mathbf {e}\in \mathbb {Z}^n\) with \(\left\| \mathbf {e}\right\| _\infty \le B\), and further there exists an \(y_i \in \mathbb {Z}_q^*\), then \(\mathsf {RecoverError}_{q,n}(\mathbf {y},B)\) outputs a pair \((r^\dagger ,\mathbf {e}^\dagger )\) with \(\mathbf {y} = r^\dagger \cdot \mathbf {e}^\dagger \) for an \(r^\dagger \in Z_q\) and \(\mathbf {e}^\dagger \in \mathbb {Z}^n\) with \(\left\| \mathbf {e}^\dagger \right\| \le B\). Furthermore, \(\mathbf {e}\) is a short \(\mathbb {Z}\)-multiple of \(\mathbf {e}^\dagger \), i.e. \(\mathbf {e}\) and \(\mathbf {e}^\dagger \) are linearly dependent. The algorithm runs in time \(\mathsf {poly}(\log q,n)\).
Proof
We first analyze the runtime of the algorithm. Note that, since \(\varLambda _i\) has dimension 2, then \(\mathsf {SolveSVP}\) runs in time \(\mathcal {O}(\log q)\) by Lemma 6. All other procedures run in time \(\mathsf {poly}(\log q,n)\).
We will now show that algorithm \(\mathsf {RecoverError}\) is correct. Let
for an \(r \in \mathbb {Z}_q\) and a \(\mathbf {e} \in \mathbb {Z}^n\) with \(\left\| \mathbf {e}\right\| _\infty \le B\). We claim that algorithm \(\mathsf {RecoverError}\), on input \(\mathbf {y}\) outputs an \(r^*\in \mathbb {Z}_q\) and a \(\mathbf {e}^*\in \mathbb {Z}^n\) with \(\left\| \mathbf {e}^*\right\| _\infty \le \left\| \mathbf {e}\right\| _\infty \).
We can expand (9) as the following non-linear equation system:
Eliminating r via the first equation, using that \(y_1 \in \mathbb {Z}_q^*\) we obtain the equation system
i.e. we conclude that any solution to the above problem must also satisfy this linear equation system. Now write \(v_i=y_i/y_1\) and set \(\mathbf {a}_i=(-v_i,1)\) and \(\mathbf {e}_i = (e_1,e_i)\). The above equation system can be restated as for all \(i = 2,\dots ,n\) that \(\mathbf {e}_i \in \varLambda _i = \varLambda ^\perp (\mathbf {a}_i)\).
Since \(\Vert \mathbf {e} \Vert _\infty \le B\), it immediately follows that \(\left\| \mathbf {e}_i\right\| _\infty \le B\). Note further that all vectors \(\mathbf {a}_i \in \mathbb {Z}_q^2\) are primitive (as their second component is 1). Now, let \(\mathbf {e}_i^*\) be the shortest (non-zero) vector in \(\varLambda _i\). As by the above argument \(\mathbf {e}_i \in \varLambda _i\) and \(\left\| \mathbf {e}_i\right\| _\infty < B\), it follows by Lemma 7 that \(\mathbf {e}_i\) must be of the form \(\mathbf {e}_i = r_i \cdot \mathbf {e}_i^*\) for an \(r_i \in \mathbb {Z}\).
Parsing \(\mathbf {e}_i^*\) as \(\mathbf {e}_i^*= (e_{i,1}^*,e_i^*)\), the above implies for all i that \(e_1 = r_i \cdot e_{i,1}^*\), in other words \(e_{i,1}^*\) divides \(e_1\). But this means that also the least common multiple \(e_1^\dagger \) of the \(e_{i,1}^*\) divides \(e_1\), i.e. \(e_1 = t_i e_1^\dagger \). Consequently, it holds that \(|e_1^\dagger | \le |e_1|\). Now set \(\alpha _i = e_1^\dagger / e_{1,i}^*\) and \(\mathbf {e}_i^\dagger = \alpha _i \cdot \mathbf {e}_i^*\). Since \(|e_1^\dagger | \le |e_1|\), it must hold that \(\alpha _i \le r_i\) (as the linear combination \(\mathbf {e}_i = r_i \cdot \mathbf {e}_i^*\) is unique) and therefore \(\left\| \mathbf {e}_i^\dagger \right\| _\infty \le \left\| \mathbf {e}_i\right\| _\infty \). Now parse \(\mathbf {e}_i^\dagger = (e_1^\dagger ,e_i^\dagger )\) and set \(\mathbf {e}^\dagger = (\mathbf {e}_1^\dagger ,\dots ,\mathbf {e}_n^\dagger )\). It follows that \(\left\| \mathbf {e}^\dagger \right\| _\infty \le B\). By the above it follows that \(\mathbf {e}^\dagger \) is a B-short solution to the linear equation system. It follows that \(r^\dagger = y_1 \cdot (e_1^\dagger )^{-1} \in \mathbb {Z}_q\) provides us a solution to the non-linear system.
Algorithm \(\mathsf {RecoverError}\) requires that the vector \(\mathbf {y}\) has a component in \(\mathbb {Z}_q^*\). If the modulus q is prime, then the existence of such a component follows from \(\mathbf {y} \ne 0\). However, this is generally not the case for composite moduli q. We will now present an algorithm \(\mathsf {RecoverError}^+\) which also covers composite moduli of the form q is of the form \(q = q_1 \cdot q_2\), where \(q_2\) is a “large” prime and \(q_1\) is either 1 or a small prime.
Construction 2
Let q be a modulus of the form \(q = q_1 \cdot q_2\) (where the factors \(q_1\) and \(q_2\) are explicitly known) and let \(n=\mathsf {poly}(\lambda )\). Let \(\mathbf {y} \in \mathbb {Z}_q^n\).
\(\mathsf {RecoverError}^+_{q,q_1,q_2,n}(\mathbf {y},B)\) :
-
If it holds for all i that \(q_1 | y_i\), proceed as follows:
-
Compute \(\bar{\mathbf {y}} = \mathbf {y} \mod q_2\) (i.e. \(\bar{\mathbf {y}} \in \mathbb {Z}_{q_2}^n\))
-
Compute \((r_0,\mathbf {e}) = \mathsf {RecoverError}_{q_2,n}(\bar{\mathbf {y}})\)
-
Set \(r_1 = (q_1)^{-1} r_0\)
-
Let \(r_1'\) be the lifting of \(r_1\) to \(\mathbb {Z}_q\) and set \(r = q_1 \cdot r'_1 \in \mathbb {Z}_q\).
-
Output \((r,\mathbf {e})\)
-
-
Otherwise, if it holds for all i that \(q_2 | y_i\) proceed as follows:
-
Compute \(\bar{\mathbf {y}} = \mathbf {y} \mod q_1\) (i.e. \(\bar{\mathbf {y}} \in \mathbb {Z}_{q_1}^n\))
-
Set \(\bar{\mathbf {e}} = (q_2)^{-1} \cdot \bar{\mathbf {y}} \in \mathbb {Z}_{q_2}^n\) (Note that \(q_2\) has an inverse modulo \(q_1\) as \(q_1\) and \(q_2\) are co-prime).
-
Lift \(\bar{\mathbf {e}}\) to an \(\mathbf {e} \in [-q_1/2,q_2/2]^n \subseteq \mathbb {Z}^n\) for which \(\mathbf {e} \mod q_1 = \bar{\mathbf {e}}\).
-
Set \(r = q_2\).
-
Output \((r,\mathbf {e})\).
-
-
In the final case, there must exist components \(y_i\) and \(y_j\) such that \(q_1 \not \mid y_i\) and \(q_2 \not \mid y_j\). Proceed as follows:
-
If \(q_2 \not \mid y_i\) it holds that \(y_i \in \mathbb {Z}_q^*\). Likewise, if \(q_1 \not \mid y_j\) it holds that \(y_j \in \mathbb {Z}_q^*\). If one of these two trivial cases happen compute and output \((r,e) = \mathsf {RecoverError}_{q,n}(\mathbf {y})\).
-
Otherwise, set \(y_{n+1} = y_i + y_j\) and \(\mathbf {y}' = (\mathbf {y}, y_{n+1}) \in \mathbb {Z}_q^{n + 1}\). Compute \((r,\mathbf {e}') = \mathsf {RecoverError}_{q,n+1}(\mathbf {y}')\). Set \(\mathbf {e} = \mathbf {e}'_{1,\dots , n} \in \mathbb {Z}^n\). If \(\Vert \mathbf {e} \Vert \le B\) Output \((r,\mathbf {e})\), otherwise try this step again for \(y_{n+1} = y_i - y_j\) and output \((r,\mathbf {e})\).
-
Lemma 11
Let \(q = q_1 \cdot q_2\), where \(q_1 \le 2B\) is either 1 or a prime and \(q_2 > B^2\) is a prime. If \(\mathbf {y}\) is of the form \(\mathbf {y}=r' \mathbf {e}'\) for some \(r' \in \mathbb {Z}_q\) and \(\mathbf {e}'\in \mathbb {Z}^n\) with \(\left\| \mathbf {e}'\right\| _\infty \le B\), then \(\mathsf {RecoverError}^+_{q,q_1,q_2,n}(\mathbf {y},B)\) outputs a pair \((r,\mathbf {e})\) with \(\left\| \mathbf {e}\right\| _\infty \le B\) such that \(\mathbf {y} = r \cdot \mathbf {e}\). The algorithm runs in time \(\mathsf {poly}(\log q,n)\).
Proof
It follows routinely that \(\mathsf {RecoverError}^+_{q,q_1,q_2,n}(\mathbf {y},B)\) runs in polynomial time. We will proceed to the correctness analysis and distinguish the same cases as \(\mathsf {RecoverError}^+\).
-
In the first case, given that \(\mathbf {y} = r' \cdot \mathbf {e}'\) (for a \(\mathbf {e}' \in \mathbb {Z}^n\) with \(\left\| \mathbf {e}'\right\| _\infty \le B\)) it holds that \(\bar{\mathbf {y}} = \bar{r}' \cdot \mathbf {e}'\), where \(\bar{r}' = r \mod q_2\). Consequently, as \(q_2 > B^2\) it holds that \(\mathsf {RecoverError}_{q_2,n}(\bar{\mathbf {y}})\) will output a pair \((r_0,\mathbf {e})\) with \(\left\| \mathbf {e}\right\| _\infty \le B\) such that \(r_0 \cdot \mathbf {e} \mod q_2 = \bar{\mathbf {y}}\). Now it holds that
$$ (r \cdot \mathbf {e}) \mod q_2 = q_1 \cdot (q_1)^{-1} \cdot r_0 \cdot \mathbf {e} = r_0 \cdot \mathbf {e} = \bar{\mathbf {y}} = \mathbf {y} \mod q_2. $$Furthermore, it holds that \((r \cdot \mathbf {e}) \mod q_1 = q_1 \cdot r_1' \cdot \mathbf {e} = 0 = \mathbf {y} \mod q_1\). Thus, by the Chinese remainder theorem it holds that \(r \cdot \mathbf {e} = \mathbf {y}\).
-
In the second case, if for all i that \(q_2 | y_i\), then it holds that \(\left\| \mathbf {e}\right\| _\infty \le q_1/2 \le B\). Furthermore, it holds that \((r \cdot \mathbf {e}) \mod q_1 = (q_2 \cdot (q_2)^{-1} \bar{\mathbf {e}}) \mod q_1 = \bar{\mathbf {e}} = \mathbf {y} \mod q_1\) and \((r \cdot \mathbf {e}) \mod q_2 = (q_2 \cdot \mathbf {e}) \mod q_2 = 0 = \mathbf {y} \mod q_2\). Consequently, by the Chinese remainder theorem it holds that \(r \cdot \mathbf {e} = \mathbf {y}\).
-
In the third case, if \(q_2 \not \mid y_i\) or \(q_1 \not \mid y_j\) correctness follows immediately from the correctness of \(\mathsf {RecoverError}\), as in this case either \(y_i\) or \(y_j\) is the required invertible component. Thus, assume that \(q_1 | y_i\) but \(q_2 \not \mid y_i\) and \(q_2 | y_j\) but \(q_1 \not \mid y_j\). It holds that \((y_i \pm y_j) \mod q_2 = y_i \mod q_2 \ne 0\) and \((y_i \pm y_j) \mod q_1 = \pm y_j \mod q_1 \ne 0\). Consequently, \(y_i \pm y_j \in \mathbb {Z}_q^*\). Finally given that \(y_i = r \cdot e_i\) and \(y_j = r \cdot e_j\) with \(|e_i|,|e_j| \le B\), it holds that \(y_i \pm y_j = r \cdot (e_i \pm e_j)\) and either \(|e_i + e_j| \le B\) or \(|e_i - e_j| \le B\). Consequently, for one of these two cases correctness follows from the correctness of \(\mathsf {RecoverError}\), as in this case \(\mathbf {y}'\) is of the form \(\mathbf {y}' = r \cdot \mathbf {e}'\) for an \(\mathbf {e}' \in \mathbb {Z}^n\) with \(\left\| \mathbf {e}'\right\| _\infty \le B\).
We now present the main result of this section. The algorithm presented in Construction 3 allows us decide if a given vector \(\mathbf {a}\) is close to the row-span of \(\mathbf {A}\), if \(\mathbf {A}\) is generated together with a lattice trapdoor.
Construction 3
Let \(q = q_1 \cdot q_2\) be a product of primes, \((\mathbf {A},\mathsf {td}_\mathbf {A})\leftarrow \mathsf {TdGen}(1^\lambda ,n,k,q)\) and let \(\mathsf {RecoverError}^+\) be the algorithm from Construction 2.
\(\mathsf {InvertCloseVector}(\mathsf {td}_\mathbf {A},\mathbf {a},B){:}\)
-
Parse \(\mathsf {td}_\mathbf {A}=\mathbf {T}\in \mathbb {Z}^{n\times n}\), \(\mathbf {a}\in \mathbb {Z}_q^n\) and \(B>0\). Let \(C\in \mathbb {R}\) be such that \(\left\| \mathbf {T}\right\| <C\).
-
Compute \(\mathbf {z}=\mathbf {a}\mathbf {T}\).
-
Run \(\varGamma \leftarrow \mathsf {RecoverError}^+_{q,q_1,q_2,n}(\mathbf {z},B')\) where \(B'=BC\sqrt{n}\). If \(\varGamma =\perp \), abort the protocol. Else, parse \(\varGamma =(r^\dagger ,\mathbf {e}^\dagger )\).
-
Let \(t \in \mathbb {Z}\) be the smallest integer for which \(\tilde{\mathbf {e}} =t \cdot \mathbf {e}^\dagger \mathbf {T}^{-1} \in \mathbb {Z}^n\) (t is the least common multiple of the denominators of \(\mathbf {e}^\dagger \mathbf {T}^{-1}\)).
-
Check if \(\left\| \tilde{\mathbf {e}}\right\| <B\) and recover \(\mathbf {x}',r\) such that \(\mathbf {x}'\mathbf {A}+r\cdot \tilde{\mathbf {e}}=\mathbf {a}\) (using gaussian elimination).
-
If \(\left\| \mathbf {e}\right\| >B\) output \(\perp \). Else, output \((\mathbf {x}',r,\tilde{\mathbf {e}})\).
Theorem 2
Let \(C = C(\lambda ) > 0\) be a parameter, let \(q = q_1 \cdot q_2\), where \(q_1 \le 2B C \sqrt{n}\) is either 1 or a prime and \(q_2 > B^2 C^2 n\) is a prime. Let \(\mathsf {TdGen}\) be the algorithm from Lemma 8 and \(\mathsf {RecoverError}_{q,n}\) be the algorithm of Construction 1. Let \((\mathbf {A},\mathsf {td}_\mathbf {A})\leftarrow \mathsf {TdGen}(q,k)\) where \(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) and \(\mathsf {td}_\mathbf {A}=\mathbf {T}\in \mathbb {Z}^{n\times n}\) with \(\left\| \mathbf {T}\right\| <C\). If there are \(\mathbf {x}\in \mathbb {Z}_q^k\) and \(r\in \mathbb {Z}_q\) such that \(\mathbf {a}=\mathbf {x}\mathbf {A}+ r\mathbf {e}\) for some \(\mathbf {e}\in \mathbb {Z}^n\) such that \(\left\| \mathbf {e}\right\| \le B\) (where \(\mathbf {e}\) is the shortest vector with this property), then the algorithm \(\mathsf {InvertCloseVector}\) outputs \((\mathbf {x},r,\mathbf {e})\).
Proof
Assume now that \(\mathbf {e}\) is the shortest vector for which we can write \(\mathbf {a}=\mathbf {x}\mathbf {A}+r\mathbf {e}\) for some \(\mathbf {x}\) and r. Then it holds that
where \(\mathbf {e}'=\mathbf {e}\mathbf {T}\) and where the last equality holds because \(\mathbf {A}\mathbf {T}=0\mod q\). Note that \(\left\| \mathbf {e}'\right\| <\left\| \mathbf {e}\right\| \left\| \mathbf {T}\right\| \sqrt{n}\le BC\sqrt{n} = B'\).
By Lemma 10, \(\mathsf {RecoverError}(\mathbf {y},B')\) will recover a pair \((r^\dagger ,\mathbf {e}^\dagger )\) satisfying \(\mathbf {y} = r^\dagger \cdot \mathbf {e}^\dagger \), and \(\mathbf {e}^\dagger \) is the shortest vector with this property. By Lemma 9 it holds that \(\mathbf {e}'\) and \(\mathbf {e}^\dagger \) are linearly dependent, i.e. it holds that \(\mathbf {e}' = t^\dagger \cdot \mathbf {e}^\dagger \). Thus, it holds that \(\mathbf {e} = \mathbf {e}' \mathbf {T}^{-1} = t^\dagger \cdot \boldsymbol{e}^\dagger \mathbf {T}^{-1}\). Since the t computed by \(\mathsf {RecoverError}(\mathbf {y},B')\) is the shortest integer for which \(t \cdot \boldsymbol{e}^\dagger \mathbf {T}^{-1} \in \mathbb {Z}^n\), it must hold that \(t = t^\dagger \). Thus it holds that \(\tilde{\boldsymbol{e}} = \boldsymbol{e}\). This concludes the proof.
5 Oblivious Linear Evaluation Secure Against a Corrupted Receiver
In this section, we present a semi-honest protocol for OLE based on the hardness of the LWE assumption. The protocol implements functionality \(\mathcal {F}_\mathsf {OLE}\) defined in Sect. 3.
5.1 Protocol
We begin by presenting the protocol.
Construction 4
The protocol is composed by the algorithms \((\mathsf {GenCRS}, \mathsf {\mathsf {R}_1}, \mathsf {\mathsf {S}},\mathsf {\mathsf {R}_2})\). Let \(k,n,\ell ,\ell ',q \in \mathbb {Z}\) such that q is as in Theorem 2, \(n=\mathsf {poly}(k\log q)\) and \(\ell '\le \ell \), and let \(\beta ,\delta ,\xi \in \mathbb {R}\) such that \(q/C>\beta \sqrt{n}\) (where \(C\in \mathbb {R}\) is as in Theorem 2), \(\delta>\beta >1\) and \(\beta >q/\delta \). Additionally, let \(\mathsf {ECC}_{\ell ',\ell ,\xi }=(\mathsf {ECC.Encode},\mathsf {ECC.Decode})\) be an ECC over \(\mathbb {Z}_{q}\). We present the protocol in full detail.
\(\mathsf {GenCRS}(1^\lambda )\) :
-
Sample
 and
and 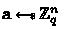 .
. -
Output \(\mathsf {crs}=(\mathbf {A}, \mathbf {a})\).
\(\mathsf {\mathsf {R}_1}\left( \mathsf {crs}, x\in \mathbb {Z}_{q}\right) \) :
-
Parse \(\mathsf {crs}\) as \((\mathbf {A},\mathbf {a})\).
-
Sample
 and an error vector
and an error vector  .
. -
Compute \(\mathbf {a}'=\mathbf {s}\mathbf {A}+\mathbf {e}- x\mathbf {a}\).
-
Output \({\mathsf {ole}_1}=\mathbf {a}'\) and \(\mathsf {st}=(\mathbf {s},x)\).
\(\mathsf {\mathsf {S}}\left( \mathsf {crs},\left( \mathbf {z}_0,\mathbf {z}_1\right) \in \left( \mathbb {Z}_{q}^{\ell '}\right) ^2,\mathsf {ole}_1\right) \) :
-
Parse \(\mathsf {crs}\) as \((\mathbf {A},\mathbf {a})\) and \({\mathsf {ole}_1}\) as \(\mathbf {a}'\).
-
Sample
 .
. -
Compute \(\mathbf {C}=\mathbf {A}\mathbf {R}\in \mathbb {Z}_q^{k\times \ell }\), \(\mathbf {t}_0=\mathbf {a}'\mathbf {R}+\mathsf {ECC.Encode}(\mathbf {z}_0)\) and \(\mathbf {t}_1=\mathbf {a}\mathbf {R}+\mathsf {ECC.Encode}(\mathbf {z}_1)\).
-
Output \({\mathsf {ole}_2}=(\mathbf {C},\mathbf {t}_0,\mathbf {t}_1)\).
\(\mathsf {R_2}\left( \mathsf {crs},\mathsf {st},\mathsf {ole}_2\right) \) :
-
Parse \({\mathsf {ole}_2}\) as \((\mathbf {C},\mathbf {t}_0,\mathbf {t}_1)\) and \(\mathsf {st}\) as \((\mathbf {s},x)\in \mathbb {Z}_q^k\times \mathbb {Z}_{q}\).
-
Compute \(\mathbf {y}\leftarrow \mathsf {ECC.Decode}(x\mathbf {t}_1+\mathbf {t}_0-\mathbf {s}\mathbf {C})\). If \(\mathbf {y}= \perp \), abort the protocol.
-
Output \(\mathbf {y}\in \mathbb {Z}_{q}^{\ell '}\).
5.2 Analysis
Theorem 3
(Correctness). Let \(\mathsf {ECC}_{\ell ',\ell ,\xi }\) be a linear ECC where \(\xi \ge \sqrt{\ell }\beta \delta n\). Then the protocol presented in Construction 4 is correct.
Proof
To prove correctness, we have to prove that \(\mathsf {R}_2\) outputs \(\mathbf {z}_0+x\mathbf {z}_1\), where \((\mathbf {z}_0,\mathbf {z}_1)\) is the input of \(\mathsf {S}\).
We have that
where \(\mathbf {e}'=\mathbf {e}\mathbf {R}\), \(\hat{\mathbf {z}}_1\leftarrow \mathsf {ECC.Encode(\mathbf {z}_1)}\) and \(\hat{\mathbf {z}}_0\leftarrow \mathsf {ECC.Encode}(\mathbf {z}_0)\). Now since \(\mathsf {ECC}\) is a linear code over \(\mathbb {Z}_{q'}\), then
Finally, by Lemma 1, we have that \(\left\| \mathbf {e}\right\| \le \beta \sqrt{n}\). Moreover, if \(\mathbf {r}^{(i)}\) is a column of \(\mathbf {R}\), then \(\left\| \mathbf {r}^{(i)}\right\| \le \delta \sqrt{n}\). Therefore, each coordinate of \( \mathbf {e}'\) has norm at most \(\left\| \mathbf {e}\right\| \cdot \left\| \mathbf {r}^{(i)}\right\| \le \beta \delta n\). We conclude that \(\left\| \mathbf {e}'\right\| \le \sqrt{\ell }\beta \delta n\). Since \(\mathsf {ECC}\) corrects errors with norm up to \(\xi \ge \sqrt{\ell }\beta \delta n\), the output of \(\mathsf {ECC.Decode}(\tilde{\mathbf {y}})\) is exactly \(\mathbf {z}_0+x_1\mathbf {z}_1\).
Theorem 4
(Security). Assume that the \(\mathsf {LWE}_{k,\beta ,q}\) assumption holds, q is as in Theorem 2, \(q/C >\beta \sqrt{n}\) (where \(C\in \mathbb {R}\) is as in Theorem 2), \(\delta>\beta >1\), \(\beta >q/\delta \) and \(n=\mathsf {poly}(k\log q)\). The protocol presented in Construction 4 securely realizes the functionality \(\mathcal {F}_\mathsf {OLE}\) in the \(\mathcal {G}_\mathsf {CRS}\)-hybrid model against:
-
a semi-honest sender given that the \(\mathsf {LWE}_{k,\beta ,q}\) assumption holds;
-
a malicious receiver where security holds statistically.
Proof
We begin by proving security against a computationally unbounded corrupted receiver.
Simulator for corrupted receiver: We describe the simulator \(\mathsf {Sim}\). Let \((\mathsf {TdGen},\mathsf {Invert})\) be the algorithms described in Lemma 8 and \(\mathsf {InvertCloseVector}\) be the algorithm of Theorem 2.
-
CRS generation: \(\mathsf {Sim}\) generates \((\mathbf {A}',\mathsf {td}_{\mathbf {A}'})\leftarrow \mathsf {TdGen}(1^\lambda ,k+1,n,q)\) and parse \(\mathbf {A}'=\begin{pmatrix}\mathbf {A}\\ \mathbf {a}\end{pmatrix}\) where \(\mathbf {A}\in \mathbb {Z}_q^{k\times n}\) and \(\mathbf {a}\in \mathbb {Z}_q^n\). Additionally, parse \(\mathsf {td}_{\mathbf {A}'}\) as \(\mathbf {T}\in \mathbb {Z}^{n\times n}\) and let \(C\in \mathbb {R}\) be such that \(\left\| \mathbf {T}\right\| <C\). It publishes \(\mathsf {crs}=(\mathbf {A},\mathbf {a})\) and keeps \(\mathsf {td}_{\mathbf {A}'}\) to itself.
-
Upon receiving a message \(\mathbf {a}'\) from \(\mathsf {R}\), \(\mathsf {Sim}\) runs \((\tilde{\mathbf {s}},\alpha ,\mathbf {e})\leftarrow \mathsf {InvertCloseVector}(\mathsf {td}_{\mathbf {A}'},\mathbf {a}',B)\) where \(B=\beta \sqrt{n}\). There are two cases to consider:
-
If \(\tilde{\mathbf {s}}=\perp \), then \(\mathsf {Sim}\) samples
 and
and  . It sends \(\mathsf {ole}_2=(\mathbf {C},\mathbf {t}_0,\mathbf {t}_1)\).
. It sends \(\mathsf {ole}_2=(\mathbf {C},\mathbf {t}_0,\mathbf {t}_1)\). -
Else if \(\tilde{\mathbf {s}}\ne \perp \), then \(\mathsf {Sim}\) sets \(x=\tilde{s}_{k+1}\) where \(\tilde{s}_{k+1}\) is the \((k+1)\)-th coordinate of \(\tilde{\mathbf {s}}\). It sends x to \(\mathcal {F}_\mathsf {OLE}\). When it receives a \(\mathbf {y}\in \mathbb {Z}_q^{\ell '}\) from \(\mathcal {F}_\mathsf {OLE}\), \(\mathsf {Sim}\) samples a uniform matrix
 , which is parsed as \(\mathbf {U}'=\begin{pmatrix}\mathbf {U}\\ \mathbf {u}\end{pmatrix}\), and a matrix
, which is parsed as \(\mathbf {U}'=\begin{pmatrix}\mathbf {U}\\ \mathbf {u}\end{pmatrix}\), and a matrix  . It sets $$\begin{aligned} \mathbf {C}&=\mathbf {U}\\ \mathbf {t}_0&= \tilde{\mathbf {s}}\mathbf {U}'+ \alpha \mathbf {e}\mathbf {R}+ \mathsf {ECC.Encode}(\mathbf {y}) \\ \mathbf {t}_1&=\mathbf {u}. \end{aligned}$$
. It sets $$\begin{aligned} \mathbf {C}&=\mathbf {U}\\ \mathbf {t}_0&= \tilde{\mathbf {s}}\mathbf {U}'+ \alpha \mathbf {e}\mathbf {R}+ \mathsf {ECC.Encode}(\mathbf {y}) \\ \mathbf {t}_1&=\mathbf {u}. \end{aligned}$$It sends \(\mathsf {ole}_2=(\mathbf {C},\mathbf {t}_0,\mathbf {t}_1)\).
-
We now proceed to show that the real-world and the ideal-world executions are indistinguishable. The following lemma shows that the CRS generated in the simulation is indistinguishable from one generated in the real-world execution. Then, the next two lemmas deal with the two possible cases in the simulation.
Lemma 12
The CRS generated above is statistically indistinguishable from a CRS generated according to \(\mathsf {GenCRS}\).
Proof
The only thing that differs in both CRS’s is that the matrix \(\mathbf {A}'=\begin{pmatrix}\mathbf {A}\\ \mathbf {a}\end{pmatrix}\) is generated via \(\mathsf {TdGen}\) in the simulation (instead of being chosen uniformly). By Lemma 8, it follows that the CRS is statistically indistinguishable from one generated using \(\mathsf {GenCRS}\).
Lemma 13
Assume that \(\tilde{\mathbf {s}}=\perp \). Then, the simulated execution is indistinguishable from the real-world execution.
Proof
We prove that no (computationally unbounded) adversary can distinguish both executions, except with negligible probability. First, note that, if \(\tilde{\mathbf {s}}=\perp \) where \((\tilde{\mathbf {s}},\alpha ,\mathbf {e})\leftarrow \mathsf {InvertCloseVector}(\mathsf {td}_{\mathbf {A}'},\mathbf {a}',B)\), then for any \((\alpha ,\mathbf {s},x)\in \mathbb {Z}_q \times \mathbb {Z}_q^k\times \mathbb {Z}_q\) we have that \(\mathbf {a}' = \mathbf {s}\mathbf {A}+x\mathbf {a}+ \alpha \mathbf {e}\) for an \(\mathbf {e}\) with \(\left\| \mathbf {e}\right\| >\beta \sqrt{n}\) since, by Theorem 2, only in this case algorithm \(\mathsf {InvertCloseVector}\) fails to invert \(\mathbf {a}'\). In other words, consider the matrix \(\hat{\mathbf {A}}=\begin{pmatrix}\mathbf {A}' \\ \mathbf {a}'\end{pmatrix}\). If \(\mathbf {a}'\) is of the form described above, then the matrix \(\hat{\mathbf {A}}\) has no short vectors in its row-span. That is, there is no vector \(\mathbf {v}\ne 0\) in \(\varLambda _q(\hat{\mathbf {A}})\) such that \(\left\| \mathbf {v}\right\| \le \beta \sqrt{n}\). This is a direct consequence of the definition of algorithm \(\mathsf {InvertCloseVector}\) of Theorem 2.
Hence \( \rho _{\beta }(\varLambda _q(\hat{\mathbf {A}})\setminus \{0\})\le \mathsf {negl}(\lambda )\). Moreover, we have that
where the first and the second inequalities hold because \(\delta>\beta >1\) by hypothesis and the last equality holds because \(\frac{1}{q}\varLambda ^\perp _q(\hat{\mathbf {A}})=\varLambda _q(\hat{\mathbf {A}})^*\). Since
then \(\delta \ge \eta _\varepsilon (\varLambda ^\perp (\hat{\mathbf {A}}))\), for \(\varepsilon =\mathsf {negl}(\lambda )\). Moreover \(n=\mathsf {poly}(k\log q)\) by assumption. Thus the conditions of Lemma 2 are met.
Therefore, we can switch to a hybrid experiment where \(\hat{\mathbf {A}}\mathbf {R}\mod q\) is replaced by  incurring only negligible statistical distance. That is,
incurring only negligible statistical distance. That is,
where \(\hat{\mathbf {z}}_j\) is the encoding \(\mathsf {ECC.Encode}(\mathbf {z}_j)\) for \(j\in \{0,1\}\).
We conclude that, in this case, the real-world and the ideal-world execution (where \(\mathsf {Sim}\) just sends a uniformly chosen triple \((\mathbf {C},\mathbf {t}_0,\mathbf {t}_1)\)) are statistically indistinguishable.
Lemma 14
Assume that \(\tilde{\mathbf {s}}\ne \perp \). Then, the simulated execution is indistinguishable from the real-world execution.
Proof
In this case, \(\mathbf {a}'=\tilde{\mathbf {s}}\mathbf {A}+\alpha \mathbf {e}\) for some \(\tilde{\mathbf {s}}\in \mathbb {Z}_1^k\) and \(\mathbf {e}\in \mathbb {Z}^n\) such that \(\left\| \mathbf {e}\right\| <\beta \sqrt{n}\). The proof follows the following sequence of hybrids:
Hybrid \(\mathcal {H}_0\). This is the real-world protocol. In particular, in this hybrid, the simulator behaves as the honest sender and computes
for some \(\alpha \in \mathbb {Z}_q\setminus \{0\}\) and where \(\mathbf {A}'=\begin{pmatrix}\mathbf {A}\\ \mathbf {a}\end{pmatrix}\).
Hybrid \(\mathcal {H}_1\). This hybrid is similar to the previous one, except that \(\mathsf {Sim}\) computes \(\mathbf {t}_0=\tilde{\mathbf {s}}\mathbf {U}'+\alpha \mathbf {e}\mathbf {R}+\mathsf {ECC.Encode}(\mathbf {z}_0)\), \(\mathbf {C}=\mathbf {U}\) and \(\mathbf {t}_1=\mathbf {u}+\mathsf {ECC.Encode}(\mathbf {z}_1)\), where  .
.
Claim 1
\(\left| \Pr \left[ 1\leftarrow \mathcal {A}:\mathcal {A}\text { plays } \mathcal {H}_0\right] -\Pr \left[ 1\leftarrow \mathcal {A}:\mathcal {A}\text { plays } \mathcal {H}_1\right] \right| \le \mathsf {negl}(\lambda )\).
To prove this claim, we will resort to the partial smoothing lemma (Lemma 3). Using the same notation as in Lemma 3, consider \(\gamma =\beta \sqrt{n}\). Then, we have that
since, by assumption, \(\beta > q/\delta \) and where \(\mathbf {A}'=\begin{pmatrix}\mathbf {A}\\ \mathbf {a}\\ \mathbf {a}' \end{pmatrix}\).
Hence, by applying Lemma 3, we obtain
for  (here, in the notation of Lemma 3, we consider \(\mathbf {D}=\mathbf {e}\)).
(here, in the notation of Lemma 3, we consider \(\mathbf {D}=\mathbf {e}\)).
We now argue that \(\mathbf {A}'\mathbf {X}\mod q\approx _{\mathsf {negl}(\lambda )} \mathbf {U}'\) for  . Let \(\mathbf {B}\in \mathbb {Z}_q^{n\times k'}\) be a basis of \(\varLambda ^\perp (\mathbf {e})\), that is, \(\mathbf {e}\mathbf {B}=0\). Let us assume for the sake of contradiction that \(\mathbf {A}'\mathbf {B}\) does not have full rank (hence, \(\mathbf {A}'\mathbf {X}\mod q\) is not uniform over \(\mathbb {Z}_q^{(k+1)\times \ell }\)). Then, there is a vector \(\mathbf {v}\in \mathbb {Z}_q^{k+1}\) such that \(\mathbf {v}\mathbf {A}'\mathbf {B}=0\).
. Let \(\mathbf {B}\in \mathbb {Z}_q^{n\times k'}\) be a basis of \(\varLambda ^\perp (\mathbf {e})\), that is, \(\mathbf {e}\mathbf {B}=0\). Let us assume for the sake of contradiction that \(\mathbf {A}'\mathbf {B}\) does not have full rank (hence, \(\mathbf {A}'\mathbf {X}\mod q\) is not uniform over \(\mathbb {Z}_q^{(k+1)\times \ell }\)). Then, there is a vector \(\mathbf {v}\in \mathbb {Z}_q^{k+1}\) such that \(\mathbf {v}\mathbf {A}'\mathbf {B}=0\).
Since \(\mathbf {B}\) is a basis of \(\varLambda ^\perp (\mathbf {e})\), this means that \(\mathbf {v}\mathbf {B}\in (\varLambda ^\perp (\mathbf {e}))^\perp =\varLambda (\mathbf {e})\). In other words, \(\mathbf {v}\mathbf {A}'=t\cdot \mathbf {e}\) for some \(t\in \mathbb {Z}_q\). Consequently, we have \(\mathbf {e}=t^{-1}\mathbf {v}\mathbf {A}'\) and thus \(\mathbf {e}\) is in the row-span of \(\mathbf {A}'\), that is, \(\varLambda (\mathbf {A}')\) has a vector of norm shorter than \(\beta \sqrt{n}\). However, this happens only with negligible probability over the uniform choice of \(\mathbf {A}\) and, thus, we reach a contradiction. We conclude that \(\mathbf {A}'\mathbf {B}\) needs to have full rank. Now, since \(\mathbf {X}\) is sampled uniformly from \(\varLambda ^\perp (\mathbf {e})\), we have that \(\mathbf {A}'\mathbf {X}\) is uniform over \(\mathbb {Z}_q^{(k+1)\times \ell }\). Thus, \(\mathbf {A}'\mathbf {X}\mod q \approx _{\mathsf {negl}(\lambda )} \mathbf {U}'\) where  .
.
Hybrid \(\mathcal {H}_2\). This hybrid is similar to the previous one, except that \(\mathsf {Sim}\) computes \(\mathbf {t}_0=\tilde{\mathbf {s}}\mathbf {U}'+\alpha \mathbf {e}\mathbf {R}+\mathsf {ECC.Encode}(\mathbf {y})\), \(\mathbf {C}=\mathbf {U}\) and \(\mathbf {t}_1=\mathbf {u}\), where  .
.
This hybrid corresponds to the simulator for the corrupted receiver.
Claim 2
\(\left| \Pr \left[ 1\leftarrow \mathcal {A}:\mathcal {A}\text { plays } \mathcal {H}_1\right] -\Pr \left[ 1\leftarrow \mathcal {A}:\mathcal {A}\text { plays } \mathcal {H}_2\right] \right| \le \mathsf {negl}(\lambda )\).
Since \(\mathbf {u}\) is uniformly at random, then it is statistically indistinguishable from \(\mathbf {u}'-\mathsf {ECC.Encode}(\mathbf {z}_1)\) where  is a uniformly random vector. Thus, replacing the occurrences of \(\mathbf {u}\) by \(\mathbf {u}'-\mathsf {ECC.Encode}(\mathbf {z}_1)\), we obtain
is a uniformly random vector. Thus, replacing the occurrences of \(\mathbf {u}\) by \(\mathbf {u}'-\mathsf {ECC.Encode}(\mathbf {z}_1)\), we obtain
where \(\overline{\mathbf {U}}'\) is the matrix whose rows are equal to \(\mathbf {U}'\), except for the \((k+1)\)-th which is equal to \(\mathbf {u}'-\mathsf {ECC.Encode}(\mathbf {z}_1)\), \(x=\tilde{s}_{k+1}\) is the \((k+1)\)-th coordinate of \(\tilde{\mathbf {s}}\) and \(\tilde{\mathbf {s}}_{-(k+1)}\in \mathbb {Z}_q^k\) is the vector \(\tilde{\mathbf {s}}\) with the \((k+1)\)-th coordinate removed.
This concludes the description of the simulator for the corrupted receiver. We now resume the proof of Theorem 4 by presenting the simulator for the semi-honest sender.
Simulator for corrupted sender. We describe how the simulator \(\mathsf {Sim}\) proceeds: It takes \(\mathsf {S}\)’s inputs \((\mathbf {z}_0,\mathbf {z}_1)\) and sends them to the ideal functionality \(\mathcal {F}_\mathsf {OLE}\), which returns nothing. It simulates the dummy \(\mathsf {R}\) by sampling  and sending it to the corrupted sender.
and sending it to the corrupted sender.
It is trivial to see that both the ideal and the real-world executions are indistinguishable given that the \(\mathsf {LWE}_{k,q,\beta }\) assumption holds.
5.3 Batch OLE
We now show how we can extend the protocol described above in order to implement a batch reusable OLE protocol, that is, in order to implement the functionality \(\mathcal {F}_\mathsf {bOLE}\) described in Sect. 3.
This variant improves the efficiency of the protocol since the receiver \(\mathsf {R}\) can commit to a batch of inputs \(\{x_i\}_{i\in [k']}\), and not just one input, using the same first message of the two-round OLE. Hence, the size of the first message can be amortized over the number of \(\mathsf {R}\)’s inputs, to achieve a better communication complexity.
Construction 5
The protocol is composed by the algorithms \((\mathsf {GenCRS}, \mathsf {\mathsf {R}_1}, \mathsf {\mathsf {S}},\mathsf {\mathsf {R}_2})\). Let \(k,n,\ell ,\ell ',q ,k'\in \mathbb {Z}\) such that q is as in Theorem 2 and \(n=\mathsf {poly}((k+k')\log q)\), and let \(\beta ,\delta ,\xi \in \mathbb {R}\) such that \(\frac{q}{\sqrt{n}\tau (k)}>\beta \) (where \(\tau (k)=\omega (\sqrt{\log k})\) as in Lemma 8), \(\delta>\beta >1\), \(\beta >q/\delta \) and \(n=\mathsf {poly}((k+k')\log q)\). Additionally, let \(\mathsf {ECC}_{\ell ',\ell ,\xi }=(\mathsf {ECC.Encode},\mathsf {ECC.Decode})\) be an ECC over \(\mathbb {Z}_{q}\).
\(\mathsf {GenCRS}(1^\lambda )\): This algorithm is similar to the one described in Construction 4 except that \(\mathsf {crs}=(\mathbf {A},\mathbf {a}_1,\dots , \mathbf {a}_{k'})\) where  for \(i\in [k']\)
for \(i\in [k']\)
\(\mathsf {\mathsf {R}_1}\left( \mathsf {crs}, \{x_j\}_{j\in [k']}\in \mathbb {Z}_q\right) \): The algorithm is similar to the one described in Construction 4, except that it outputs \({\mathsf {ole}_1}=\mathbf {a}'\) and \(\mathsf {st}=(\mathbf {s},\{x_i\}_{i\in [k']})\), where \(\mathbf {a}'=\mathbf {s}\mathbf {A}+\mathbf {e}- \left( \sum _{i=1}^{k'} x_i\mathbf {a}_i\right) \).
\(\mathsf {\mathsf {S}}\left( \mathsf {crs},\left( \mathbf {z}_0,\mathbf {z}_1\right) \in \left( \mathbb {Z}_q^{\ell '}\right) ^2,\mathsf {ole}_1,j\in [k']\right) \): This algorithm is similar to the one described in Construction 4, except that; i) it computes \(\mathbf {t}_1=-\mathbf {a}_j\mathbf {R}\); ii) It computes \(\mathbf {w}_i=\mathbf {a}_i\mathbf {R}\) for all \(i\in [k']\) such that \(i\ne j\); and iii) it outputs \(\mathsf {ole}_2=(\mathbf {C},\mathbf {t}_0,\mathbf {t}_1,\{\mathbf {w}_i\}_{i\ne j},j)\) (where j corresponds to which \(x_j\) the receiver \(\mathsf {R}\) is supposed to use in that particular execution of the protocol) and \(\{\}\).
\(\mathsf {R_2}(\mathsf {crs},\mathsf {st},\mathsf {ole}_2)\): This algorithm is similar to the one described in Construction 4, except that it outputs
It is easy to see that correctness holds following a similar analysis as the one of Theorem 3. We now state the theorem that guarantees security of the scheme.
Theorem 5
(Security). Assume that the \(\mathsf {LWE}_{k,\beta ,q}\) assumption holds, \(q\in \mathbb {N}\) is as in Theorem 2, \(q/C>\beta \sqrt{n}\) (where \(C\in \mathbb {R}\) is as in Lemma 8), \(\delta>\beta >1\), \(\beta >q/\delta \) and \(n=\mathsf {poly}((k+k')\log q)\). The protocol presented in Construction 5 securely realizes the functionality \(\mathcal {F}_\mathsf {bOLE}\) in the \(\mathcal {G}_\mathsf {CRS}\)-hybrid model against:
-
a semi-honest sender given that the \(\mathsf {LWE}_{k,\beta ,q}\) assumption holds;
-
a malicious receiver where security holds statistically.
The proof of the theorem stated above essentially follows the same blueprint as the proof of Theorem 4, except that the simulator for the corrupted receiver extracts the first \(k'\) coordinates \(\{x_j\}_{j\in [k']}\) of \(\mathbf {x}\) and sends these values to \(\mathcal {F}_{bOLE}\). From now on, it behaves exactly as the simulator in the proof of Theorem 4. Indistinguishability of executions follows exactly the same reasoning.
Communication Efficiency Comparison. Comparing with the protocol presented in Construction 4, this scheme achieves the same communication complexity for the receiver (that is, the receiver message is of the same size in both constructions). On the other hand, the sender’s message now depends on \(k'\).
6 OLE from LWE Secure Against Malicious Adversaries
In this section, we extend the construction of the previous section to support malicious sender. The idea is to use a cut-and-choose approach via the use of an OT scheme in two rounds and extract the sender’s input via the OT simulator.
6.1 Protocol
Construction 6
The protocol is composed by the algorithms \((\mathsf {GenCRS}, \mathsf {\mathsf {R}_1}, \mathsf {\mathsf {S}},\mathsf {\mathsf {R}_2})\). Let \(\mathsf {OLE}=(\mathsf {GenCRS},\mathsf {R}_1,\mathsf {S},\mathsf {R})\) be a two-round OLE protocol which is secure against malicious receivers and semi-honest senders and \(\mathsf {OT}=(\mathsf {GenCRS},\mathsf {R}_1,\mathsf {S},\mathsf {R}_2)\) be a two-round OT protocol. We now present the protocol in full detail.
\(\mathsf {GenCRS}(1^\lambda )\) :
-
Run \(\mathsf {crs}_\mathsf {OLE}\leftarrow \mathsf {OLE.GenCRS}(1^\lambda )\) and \(\mathsf {crs}_\mathsf {OT}\leftarrow \mathsf {OT.GenCRS}(1^\lambda )\).
-
Output \(\mathsf {crs}=(\mathsf {crs}_\mathsf {OLE},\mathsf {crs}_\mathsf {OT})\).
\(\mathsf {R}_1\left( \mathsf {crs}, x\in \mathbb {Z}_q\right) \) :
-
Parse \(\mathsf {crs}\) as \((\mathsf {crs}_\mathsf {OLE},\mathsf {crs}_\mathsf {OT})\).
-
Sample
 such that \(x_1+x_2=x\).
such that \(x_1+x_2=x\). -
Compute \((\mathsf {ole}_{1,1},\mathsf {st}_{1,1})\leftarrow \mathsf {OLE}.\mathsf {R}_1(\mathsf {crs}_\mathsf {OLE},x_1)\) and \((\mathsf {ole}_{1,2},\mathsf {st}_{1,2})\leftarrow \mathsf {OLE}.\mathsf {R}_1(\mathsf {crs}_\mathsf {OLE},x_2)\).
-
Additionally, choose uniformly at random
 and compute \((\mathsf {ot}_{1,i},\tilde{\mathsf {st}}_{i})\leftarrow \mathsf {OT}.\mathsf {R}_1(\mathsf {crs}_\mathsf {OT},b_i)\) for all \(i\in [\lambda ]\).
and compute \((\mathsf {ot}_{1,i},\tilde{\mathsf {st}}_{i})\leftarrow \mathsf {OT}.\mathsf {R}_1(\mathsf {crs}_\mathsf {OT},b_i)\) for all \(i\in [\lambda ]\). -
Output \(\mathsf {ole}_1=(\mathsf {ole}_{1,1},\mathsf {ole}_{1,2},\{\mathsf {ot}_{1,i}\}_{i\in [\lambda ]})\) and \(\mathsf {st}=\left( \mathsf {st}_{1,1},\mathsf {st}_{1,2},\{\tilde{\mathsf {st}}_{i}\}_{j\in [\lambda ]}\right) \).
\(\mathsf {S}\left( \mathsf {crs},(\mathbf {z}_0,\mathbf {z}_1)\in \mathbb {Z}_q^{\ell },\mathsf {ole}_1\right) \) :
-
Parse \(\mathsf {crs}\) as \((\mathsf {crs}_\mathsf {OLE},\mathsf {crs}_\mathsf {OT})\) and \(\mathsf {ole}_1\) as \((\mathsf {ole}_{1,1},\mathsf {ole}_{1,2},\{\mathsf {ot}_{1,i}\}_{i\in [\lambda ]})\).
-
Sample
 such that \(\mathbf {z}_{1,1}+\mathbf {z}_{1,1}=\mathbf {z}_1\).
such that \(\mathbf {z}_{1,1}+\mathbf {z}_{1,1}=\mathbf {z}_1\). -
For all \(j\in [\lambda ]\), do the following:
-
Sample random coins
 .
. -
Compute \(\mathsf {ole}_{2,j,1}\leftarrow \mathsf {OLE}.\mathsf {S}(\mathsf {crs}_\mathsf {OLE},\mathsf {ole}_{1,1},(\mathbf {u}_{0,j,1},\mathbf {u}_{1,j,1});r_{j,1})\) for uniformly chosen
 . Additionally, compute \(\mathsf {ole}_{2,j,2}\leftarrow \mathsf {OLE}.\mathsf {S}(\mathsf {crs}_\mathsf {OLE}, \mathsf {ole}_{1,2},(\mathbf {u}_{0,j,2},\mathbf {u}_{1,j,2});r_{j,2})\) for uniformly chosen
. Additionally, compute \(\mathsf {ole}_{2,j,2}\leftarrow \mathsf {OLE}.\mathsf {S}(\mathsf {crs}_\mathsf {OLE}, \mathsf {ole}_{1,2},(\mathbf {u}_{0,j,2},\mathbf {u}_{1,j,2});r_{j,2})\) for uniformly chosen  .
. -
Set \(M_{0,j}=(r_{j,1},r_{j,2},\mathbf {u}_{0,j,1},\mathbf {u}_{1,j,1},\mathbf {u}_{0,j,2},\mathbf {u}_{1,j,2})\) and \(M_{1,j}=(\mathbf {u}_{0,j,1}+ \mathbf {z}_0,\mathbf {u}_{1,j,1}+\mathbf {z}_{1,1},\mathbf {u}_{0,j,2}+\mathbf {z}_0,\mathbf {u}_{1,j,2}+\mathbf {z}_{1,2})\). Compute \(\mathsf {ot}_{2,j}\leftarrow \mathsf {OT}.\mathsf {S}(\mathsf {crs}_\mathsf {OT},\mathsf {ot}_{1,j}, (M_{0,j},M_{1,j}))\).
-
-
Output \(\mathsf {ole}_2=\{\mathsf {ole}_{2,j,1},\mathsf {ole}_{2,j,2},\mathsf {ot}_{2,j}\}_{j\in [\lambda ]}\).
\(\mathsf {R}_2(\mathsf {crs},\mathsf {st},\mathsf {ole}_2)\) :
-
Parse \(\mathsf {ole}_2\) as \(\{\mathsf {ole}_{2,j,1},\mathsf {ole}_{2,j,2},\mathsf {ot}_{2,j}\}_{j\in [\lambda ]}\) and \(\mathsf {st}\) as \(\left( \mathsf {st}_{1,1},\mathsf {st}_{1,2},\{\tilde{\mathsf {st}}_{i}\}_{j\in [\lambda ]}\right) \).
-
For all \(j\in [\lambda ]\), do the following:
-
Recover \(M_{b_j,j}\leftarrow \mathsf {OT}.\mathsf {R}_2(\mathsf {crs}_\mathsf {OT},\tilde{\mathsf {st}}_i)\).
-
If \(b_j=0\), parse \(M_{0,j}=(r_{j,1},r_{j,2},\mathbf {u}_{0,j,1},\mathbf {u}_{1,j,1},\mathbf {u}_{0,j,2},\mathbf {u}_{1,j,2})\). Compute
$$\mathsf {ole}_{2,j,1}'\leftarrow \mathsf {OLE}.\mathsf {S}(\mathsf {crs}_\mathsf {OLE},\mathsf {ole}_{1,1},(\mathbf {u}_{0,j,1},\mathbf {u}_{1,j,1});r_{j,1})$$and
$$\mathsf {ole}_{2,j,2}'\leftarrow \mathsf {OLE}.\mathsf {S}(\mathsf {crs}_\mathsf {OLE},\mathsf {ole}_{1,2},(\mathbf {u}_{0,j,2},\mathbf {u}_{1,j,2});r_{j,2}).$$If \(\mathsf {ole}_{2,j,1}'\ne \mathsf {ole}_{2,j,1}\) or if \(\mathsf {ole}_{2,j,1}'\ne \mathsf {ole}_{2,j,1}\), abort the protocol.
-
If \(b_j=1\), parse \(M_{1,j}\) as \((\mathbf {v}_{0,j,1},\mathbf {v}_{1,j,1},\mathbf {v}_{0,j,2},\mathbf {v}_{1,j,2})\). Compute \(\mathbf {y}_{j,1}\leftarrow \mathsf {OLE}.\mathsf {R}_2(\mathsf {crs}_\mathsf {OLE},\mathsf {ole}_{2,j,1},\mathsf {st}_{j,1})\) and \(\mathbf {y}_{j,2}\leftarrow \mathsf {OLE}.\mathsf {R}_2(\mathsf {crs}_\mathsf {OLE},\mathsf {ole}_{2,j,2},\mathsf {st}_{j,2})\). Compute \(\mathbf {w}_{j,1}=\mathbf {v}_{0,j,1}+x_1\tilde{\mathbf {v}}_{1,j,1}-\mathbf {y}_{j,1}\) and \(\mathbf {w}_{j,2}=\mathbf {v}_{0,j,2}+x_2\tilde{\mathbf {v}}_{1,j,2}-\mathbf {y}_{j,2}\).
-
-
Let \(I_1\subseteq [\lambda ]\) be the set of indices j such that \(b_j=1\) and let \(\{\mathbf {w}_{j,1},\mathbf {w}_{j,2}\}_{j\in I_1}\). If \(\mathbf {w}_1=\mathbf {w}_{j,1}=\mathbf {w}_{j',1}\), \(\mathbf {w}_2=\mathbf {w}_{j,2}=\mathbf {w}_{j',2}\) and \(\mathbf {w}=\mathbf {w}_{j,1}+w_{j,2}=\mathbf {w}_{j',1}+\mathbf {w}_{j',2}\) for all pairs \((j,j')\in I_1^2\) then output \(\mathbf {w}\). Else abort the protocol.
6.2 Analysis
We now proceed to the analysis of the protocol described above.
Theorem 6
(Correctness). Assume \(\mathsf {OLE}\) and \(\mathsf {OT}\) implement the functionalities \(\mathcal {F}_{\mathsf {OLE}}\) and \(\mathcal {F}_\mathsf {OT}\). Then the protocol presented in Construction 6 is correct.
Theorem 7
(Security). Let \(q=2^\omega (\log \lambda )\). Assume that \(\mathsf {OLE}\) implements \(\mathcal {F}_{\mathsf {OLE}}\) against malicious receivers and semi-honest sender and that \(\mathsf {OT}\) implements the functionality \(\mathcal {F}_\mathsf {OT}\). The protocol presented in Construction 6 securely realizes the functionality \(\mathcal {F}_\mathsf {OLE}\) in the \(\mathcal {G}_\mathsf {CRS}\)-hybrid model against static malicious adversaries.
The proof of the theorem is presented in the full version of the paper available at [8].
On the choice of the modulus q. The scheme presented above is only secure if q is chosen to be superpolynomial in \(\lambda \). The scheme can be adapted to support fields of polynomial size by running \(\lambda \) instances of the underlying OLE, instead of running only two instances.
6.3 Instantiating the Functionalities
We now discuss how we can instantiate the underlying functionalities \(\mathcal {F}_\mathsf {OT}\) and \(\mathcal {F}_\mathsf {OLE}\) (secure against semi-honest receivers) used in the protocol described above.
When we instantiate \(\mathcal {F}_\mathsf {OT}\) with the OT schemes from [29, 30] and \(\mathcal {F}_\mathsf {OLE}\) (secure against semi-honest receivers) with the scheme from Sect. 5, we obtain a maliciously secure OLE protocol with the following properties:
-
1.
It has two rounds;
-
2.
It is statistically secure against a malicious receiver since the the OT of [29, 30] and the scheme from Sect. 5 are statistically secure against a malicious receiver.
-
3.
Security against a malicious sender holds under the LWE assumption since both the schemes of [29, 30] are secure against malicious senders and the scheme from Sect. 5 is secure against semi honest senders under the LWE assumption.
Notes
- 1.
It is easy to see that, if we consider the affine function \(f:\{0,1\}\rightarrow \{0,1\}\) such that \(f(b)=m_0+b(m_1-m_0)\), OLE trivially implements OT.
- 2.
While two-party reusable non-interactive secure computation (NISC) is impossible in the OT-hybrid model [11], reusable NISC for general Boolean circuits is known to be possible in the (reusable) OLE-hybrid model assuming one-way functions [11]. The result stated above is meaningful only if we have access to a reusable two-round OLE protocol. The only efficient realizations of this primitive are based on the Decisional Composite Residuosity (DCR) and the Quadratic Residuosity assumptions [11].
- 3.
As an example consider the work of [11], where the Paillier cryptosystem is extended into an OLE protocol with malicious security and the construction is highly non-trivial.
- 4.
Despite numerous efforts, HPS in the lattice setting fall short in efficiency when comparing to their group-based counterpart.
- 5.
The protocol presented in Sect. 5 is presented in a slightly, but equivalent, form.
- 6.
The approach is similar in spirit as previous works, e.g. [25].
- 7.
The construction actually works for any OLE scheme that is secure against semi-honest senders and malicious receivers. In the technical sections we present the generic construction.
- 8.
The matrix \(\mathbf {B}\) is called a basis of \(\varLambda (\mathbf {B})\).
References
Applebaum, B., Damgård, I., Ishai, Y., Nielsen, M., Zichron, L.: Secure arithmetic computation with constant computational overhead. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 223–254. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_8
Applebaum, B., Ishai, Y., Kushilevitz, E.: How to garble arithmetic circuits. In: 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, pp. 120–129 (2011)
Banaszczyk, W.: New bounds in some transference theorems in the geometry of numbers. Math. Ann. 296(4), 625–636 (1993). http://eudml.org/doc/165105
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_42
Baum, C., Escudero, D., Pedrouzo-Ulloa, A., Scholl, P., Troncoso-Pastoriza, J.R.: Efficient protocols for oblivious linear function evaluation from ring-LWE. In: Galdi, C., Kolesnikov, V. (eds.) SCN 2020. LNCS, vol. 12238, pp. 130–149. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-57990-6_7
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y.: Compressing vector OLE. In: Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS 2018, pp. 896–912. Association for Computing Machinery, New York (2018). https://doi.org/10.1145/3243734.3243868
Brakerski, Z., Döttling, N.: Two-message statistically sender-private OT from LWE. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11240, pp. 370–390. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_14
Branco, P., Döttling, N., Mateus, P.: Two-round oblivious linear evaluation from learning with errors. Cryptology ePrint Archive, Report 2020/635 (2020). https://ia.cr/2020/635
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: Proceedings 42nd IEEE Symposium on Foundations of Computer Science, pp. 136–145 (2001)
de Castro, L., Juvekar, C., Vaikuntanathan, V.: Fast vector oblivious linear evaluation from ring learning with errors. Cryptology ePrint Archive, Report 2020/685 (2020). https://eprint.iacr.org/2020/685
Chase, M., et al.: Reusable non-interactive secure computation. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 462–488. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_15
Döttling, N., Garg, S., Hajiabadi, M., Masny, D., Wichs, D.: Two-round oblivious transfer from CDH or LPN. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12106, pp. 768–797. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_26
Döttling, N., Ghosh, S., Nielsen, J.B., Nilges, T., Trifiletti, R.: TinyOLE: efficient actively secure two-party computation from oblivious linear function evaluation. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS 2017, pp. 2263–2276. Association for Computing Machinery, New York (2017). https://doi.org/10.1145/3133956.3134024
Döttling, N., Kraschewski, D., Müller-Quade, J.: Statistically secure linear-rate dimension extension for oblivious affine function evaluation. In: Smith, A. (ed.) ICITS 2012. LNCS, vol. 7412, pp. 111–128. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32284-6_7
Döttling, N., Kraschewski, D., Müller-Quade, J.: David & Goliath oblivious affine function evaluation - asymptotically optimal building blocks for universally composable two-party computation from a single untrusted stateful tamper-proof hardware token. Cryptology ePrint Archive, Report 2012/135 (2012). https://eprint.iacr.org/2012/135
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing, STOC 2008, pp. 197–206. ACM, New York (2008). https://doi.org/10.1145/1374376.1374407
Ghosh, S., Nielsen, J.B., Nilges, T.: Maliciously secure oblivious linear function evaluation with constant overhead. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 629–659. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_22
Ghosh, S., Nilges, T.: An algebraic approach to maliciously secure private set intersection. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 154–185. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_6
Ghosh, S., Simkin, M.: The communication complexity of threshold private set intersection. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 3–29. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_1
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game, or a completeness theorem for protocols with honest majority. In: Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali, pp. 307–328 (2019)
Hazay, C., Ishai, Y., Marcedone, A., Venkitasubramaniam, M.: LevioSA: lightweight secure arithmetic computation. In: Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, CCS 2019, pp. 327–344. Association for Computing Machinery, New York (2019). https://doi.org/10.1145/3319535.3354258
Ishai, Y., Prabhakaran, M., Sahai, A.: Secure arithmetic computation with no honest majority. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 294–314. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_18
Juvekar, C., Vaikuntanathan, V., Chandrakasan, A.: GAZELLE: a low latency framework for secure neural network inference. In: Proceedings of the 27th USENIX Conference on Security Symposium, SEC 2018, pp. 1651–1668. USENIX Association, USA (2018)
Lempel, M., Paz, A.: An algorithm for finding a shortest vector in a two-dimensional modular lattice. Theor. Comput. Sci. 125(2), 229–241 (1994). http://www.sciencedirect.com/science/article/pii/030439759200021I
Lindell, Y., Pinkas, B.: An efficient protocol for secure two-party computation in the presence of malicious adversaries. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 52–78. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_4
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on gaussian measures. SIAM J. Comput. 37(1), 267–302 (2007). https://doi.org/10.1137/S0097539705447360
Mohassel, P., Zhang, Y.: SecureML: a system for scalable privacy-preserving machine learning. In: 2017 IEEE Symposium on Security and Privacy (SP), pp. 19–38 (2017)
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Quach, W.: UC-secure OT from LWE, revisited. In: Galdi, C., Kolesnikov, V. (eds.) SCN 2020. LNCS, vol. 12238, pp. 192–211. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-57990-6_10
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing, STOC 2005, pp. 84–93. ACM, New York (2005). https://doi.org/10.1145/1060590.1060603
Yao, A.C.: Protocols for secure computations. In: 23rd Annual Symposium on Foundations of Computer Science (SFCS 1982), pp. 160–164 (1982)
Acknowledgment
Pedro Branco thanks the support from DP-PMI and FCT (Portugal) through the grant PD/BD/135181/2017. Part of the work was done while the author was at CISPA.
Pedro Branco and Paulo Mateus are partially supported by national funds through Fundação para a Ciência e a Tecnologia (FCT) with reference UIDB/50008/2020 (Instituto de Telecomunicações via actions QuRUNNER, QUESTS) and Projects QuantumMining POCI-01-0145-FEDER-031826, PREDICT PTDC/CCI-CIF/29877/2017 and QuantumPrime PTDC/EEI-TEL/8017/2020.
Nico Döttling was supported by the Helmholtz Association within the project “Trustworthy Federated Data Analytics” (TFDA) (funding number ZT-I- OO1 4).
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 International Association for Cryptologic Research
About this paper
Cite this paper
Branco, P., Döttling, N., Mateus, P. (2022). Two-Round Oblivious Linear Evaluation from Learning with Errors. In: Hanaoka, G., Shikata, J., Watanabe, Y. (eds) Public-Key Cryptography – PKC 2022. PKC 2022. Lecture Notes in Computer Science(), vol 13177. Springer, Cham. https://doi.org/10.1007/978-3-030-97121-2_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-97121-2_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-97120-5
Online ISBN: 978-3-030-97121-2
eBook Packages: Computer ScienceComputer Science (R0)





 chosen uniformly at random; and sends the first messages of each instance.
chosen uniformly at random; and sends the first messages of each instance. and
and 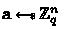 .
. and an error vector
and an error vector  .
. .
. and
and  . It sends
. It sends  , which is parsed as
, which is parsed as  . It sets
. It sets  such that
such that  and compute
and compute  such that
such that  .
. . Additionally, compute
. Additionally, compute  .
.