Abstract
Private set intersection (PSI) is an important area of research and has been the focus of many works over the past decades. It describes the problem of finding an intersection between the input sets of at least two parties without revealing anything about the input sets apart from their intersection.
In this paper, we present a new approach to compute the intersection between sets based on a primitive called Oblivious Linear Function Evaluation (OLE). On an abstract level, we use this primitive to efficiently add two polynomials in a randomized way while preserving the roots of the added polynomials. Setting the roots of the input polynomials to be the elements of the input sets, this directly yields an intersection protocol with optimal asymptotic communication complexity \(O(m\kappa )\). We highlight that the protocol is information-theoretically secure against a malicious adversary assuming OLE.
We also present a natural generalization of the 2-party protocol for the fully malicious multi-party case. Our protocol does away with expensive (homomorphic) threshold encryption and zero-knowledge proofs. Instead, we use simple combinatorial techniques to ensure the security. As a result we get a UC-secure protocol with asymptotically optimal communication complexity \(O((n^2+nm)\kappa )\), where n is the number of parties, m is the set size and \(\kappa \) is the security parameter. Apart from yielding an asymptotic improvement over previous works, our protocols are also conceptually simple and require only simple field arithmetic. Along the way we develop techniques that might be of independent interest.
S. Ghosh—Supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement #669255 (MPCPRO), the European Union’s Horizon 2020 research and innovation programme under grant agreement #731583 (SODA) and the Independent Research Fund Denmark project BETHE.
T. Nilges—Part of the research leading to these results was done while the author was at Aarhus University. Supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement #669255 (MPCPRO).
Access provided by Autonomous University of Puebla. Download conference paper PDF
1 Introduction
Private set intersection (PSI) has been the focus of research for decades and describes the following basic problem. Two parties, Alice and Bob, each have a set \(S_\mathsf {A}\) and \(S_\mathsf {B}\), respectively, and want to find the intersection \(S_\cap =S_\mathsf {A}\cap S_\mathsf {B}\) of their sets. This problem is non-trivial if both parties must not learn anything but the intersection. There are numerous applications for PSI from auctions [29] over advertising [32] to proximity testing [30].
Over the years several techniques for two-party PSI have been proposed, which can be roughly placed in four categories: constructions built from specific number-theoretic assumptions [8, 9, 21, 23, 28, 38], using garbled circuits [20, 32], based on oblivious transfer (OT) [10, 26, 31, 33,34,35,36] and based on oblivious polynomial evaluation (OPE) [7, 12, 13, 17, 18]. There also exists efficient PSI protocols in server-aided model [24].
Some of these techniques translate to the multi-party setting. The first (passively secure) multi-party PSI (MPSI) protocol was proposed by Freedman et al. [13] based on OPE and later improved in a series of works [5, 25, 37] to achieve full malicious security. Recently, Hazay and Venkitasubramaniam [19] proposed new protocols secure against semi-honest and fully malicious adversaries. They improve upon the communication efficiency of previous works by designating a central party that runs a version of the protocol of [13] with all other parties and aggregates the results.
Given the state of the art, it remains an open problem to construct a protocol with asymptotically optimal communication complexity in the fully malicious multi-party setting. The main reason for this is the use of zero-knowledge proofs and expensive checks in previous works, which incur an asymptotic overhead over passively secure solutions.
In a concurrent and independent work, Kolesnikov et al. [27] presented a new paradigm for solving the problem of MPSI from oblivious programmable pseudorandom functions (OPPRF). Their approach yields very efficient protocols for multi-party PSI, but the construction achieves only passive security against \(n-1\) corruptions. However, their approach to aggregate the intermediate results uses ideas similar to our masking scheme in the multi-party case.
1.1 Our Contribution
We propose a new approach to (multi-party) private set intersection based on oblivious linear function evaluation (OLE). OLE allows two mutually distrusting parties to evaluate a linear function \(ax+b\), where the sender knows a and b, and the receiver knows x. Nothing apart from the result \(ax+b\) is learned by the receiver, and the sender learns nothing about x. OLE can be instantiated in the OT-hybrid model from a wide range of assumptions with varying communication efficiency, like LPN [1], Quadratic/Composite Residuosity [22] and Noisy Encodings [14, 22], or even unconditionally [22].
Our techniques differ significantly from previous works and follow a new paradigm which leads to conceptually simple and very efficient protocols. Our approach is particularly efficient if all input sets are of similar size. To showcase the benefits of our overall approach, we also describe how our MPSI protocol can be modified into a threshold MPSI protocol.
Concretely, we achieve the following:
-
Two-party PSI with communication complexity \(O(m\kappa )\) and computational cost of \(O(m\log m)\) multiplications. The protocol is information theoretically secure against a malicious adversary in the OLE-hybrid model.
-
UC-secure Multi-party PSI in fully malicious setting with communication complexity \(O((n^2+nm)\kappa )\) and computational complexity dominated by \(O(nm\log m)\) multiplications for the central party and \(O(m\log m)\) multiplications for other parties.
-
A simple extension of the multi-party PSI protocol to threshold PSI, with the same complexity. To the best of our knowledge, this is the first actively secure threshold multi-party PSI protocol.Footnote 1
In comparison to previous works which rely heavily on exponentiations in fields or groups, our protocols require only field addition and multiplication (and OWF in the case of MPSI).
If we compare our result with the asymptotically optimal 2-party PSI protocols by [8, 23], which have linear communication and computation, our first observation is that although they only have a linear number of modular exponentiations, the number of field operations is not linear but rather in the order of \(O(m \kappa )\), and further they need a ZK proof in the ROM for each exponentiation, which is also expensive. Additionally, their result is achieved with specific number-theoretic assumptions, so the parameter sizes are probably not favourable compared to our protocol, and the construction is not black-box. We provide a detailed comparison of the concrete efficiency of our result with the recent protocol by Rindal and Rosulek [36], which has very good concrete efficiency.
In the setting of MPSI, our techniques result in asymptotic efficiency improvements over previous works in both communication and computational complexity (cf. Table 1).
We want to emphasize that our efficiency claims hold including the communication and computation cost for the OLE, if the recent instantiation by Ghosh et al. [14] is used, which is based on noisy Reed-Solomon codes. This OLE protocol has a constant communication overhead per OLE if instantiated with an efficient OT-extension protocol like [31] and therefore does not influence the asymptotic efficiency of our result.
Our results may seem surprising in light of the information-theoretic lower bound of \(O(n^2m\kappa )\) in the communication complexity for multi-party PSI in the fully malicious UC setting. We circumvent this lower bound by considering a slightly modified ideal functionality, resulting in a UC-secure solution for multi-party PSI with asymptotically optimal communication overhead. By asymptotically optimal, we mean that our construction matches the optimal bounds in the plain model for \(m>n\), even for passive security, where n is the number of parties, m is the size of the sets and \(\kappa \) is the security parameter. All of our protocols work over fields \(\mathbb {F}^{}_{}\) that are exponential in the size of the security parameter \(\kappa \).
We believe that our approach provides an interesting alternative to existing solutions and that the techniques which we developed can find application in other settings as well.
1.2 Technical Overview
Abstractly, we let both parties encode their input set as a polynomial, such that the roots of the polynomials correspond to the inputs. This is a standard technique, but usually the parties then use OPE to obliviously evaluate the polynomials or some form of homomorphic encryption. Instead, we devise an OLE-based construction to add the two polynomials in an oblivious way, which results in an intersection polynomial. Kissner and Song [25] also create an intersection polynomial similar to ours, but encrypted under a layer of homomorphic encryption, whereas our technique results in a plain intersection polynomial. Since the intersection polynomial already hides everything but the intersection, one could argue that the layer of encryption in [25] incurs additional overhead in terms of expensive computations and complex checks.
In our case, both parties simply evaluate the intersection polynomial on their input sets and check if it evaluates to 0. This construction is information-theoretically secure in the OLE-hybrid model and requires only simple field operations. Conceptually, we compute the complete intersection in one step. In comparison to the naive OPE-based approachFootnote 2, our solution directly yields an asymptotic communication improvement in the input size. Another advantage is that our approach generalizes to the multi-party setting.
We start with a detailed overview of our constructions and technical challenges.
Oblivious polynomial addition from OLE. Intuitively, OLE is the generalization of OT to larger fields, i.e. it allows a sender and a receiver to compute a linear function \(c(x)=ax+b\), where the sender holds a, b and the receiver inputs x and obtains c. OLE guarantees that the receiver learns nothing about a, b except for the result c, while the sender learns nothing about x.
Based on this primitive, we define and realize a functionality OPA that allows to add two polynomials in such a way that the receiver cannot learn the sender’s input polynomial, while the sender learns nothing about the receiver’s polynomial or the output. We first describe a passively secure protocol. Concretely, assume that the sender has an input polynomial \(\mathbf {a}\) of degree 2d, and the receiver has a polynomial \(\mathbf {b}\) of degree d. The sender additionally draws a uniformly random polynomial \(\mathbf {r}\) of degree d. Both parties point-wise add and multiply their polynomials, i.e. they evaluate their polynomials over a set of \(2d+1\) distinct points \(\alpha _1,\ldots ,\alpha _{2d+1}\), resulting in \(a_i=\mathbf {a}(\alpha _i), b_i=\mathbf {b}(\alpha _i)\) and \(r_i=\mathbf {r}(\alpha _i)\) for \(i\in [2d+1]\). Then, for each of \(2d+1\) OLEs, the sender inputs \(r_i, a_i\), while the receiver inputs \(b_i\) and thereby obtains \(c_i=r_ib_i+a_i\). The receiver interpolates the polynomial \(\mathbf {c}\) from the \(2d+1\) \((\alpha _i, c_i)\) and outputs it. Since we assume semi-honest behaviour, the functionality is realized by this protocol.
The biggest hurdle in achieving active security for the above protocol lies in ensuring a non-zero \(\mathbf {b}\) and \(\mathbf {r}\) as input. Otherwise, e.g. if \(\mathbf {b}=0\), the receiver could learn \(\mathbf {a}\). One might think that it is sufficient to perform a coin-toss and verify that the output satisfies the supposed relation, i.e. pick a random x, compute \(\mathbf {a}(x),\mathbf {b}(x),\mathbf {r}(x)\) and \(\mathbf {c}(x)\) and everyone checks if \(\mathbf {b}(x)\mathbf {r}(x)+\mathbf {a}(x)=\mathbf {c}(x)\) and if \(\mathbf {b}(x),\mathbf {r}(x)\) are non-zeroFootnote 3. For \(\mathbf {r}(x)\ne 0\), the check is actually sufficient, because \(\mathbf {r}\) must have degree at most d, otherwise the reconstruction fails, and only d points of \(\mathbf {r}\) can be zero (\(\mathbf {r}=0\) would require \(2d+1\) zero inputs). For \(\mathbf {b}\ne 0\), however, just checking for \(\mathbf {b}(x)\ne 0\) is not sufficient, because at this point, even if the input \(\mathbf {b}\ne 0\), the receiver can input d zeroes in the OLE, which in combination with the check is sufficient to learn \(\mathbf {a}\) completely. We resolve this issue by constructing an enhanced OLE functionality which ensures that the receiver input is non-zero. We believe that this primitive is of independent interest and describe it in more detail later in this section.
Two-party PSI from OLE. Let us first describe a straightforward two-party PSI protocol with one-sided output from the above primitive. Let \(S_\mathsf {A}\) and \(S_\mathsf {B}\) denote the inputs for Alice and Bob, respectively, where \(|S_\mathsf {P}|=m\). Assuming that Bob is supposed to get the intersection, they pick random \(\mathbf {p}_\mathsf {A}\) and \(\mathbf {p}_\mathsf {B}\) with the restriction that \(\mathbf {p}_\mathsf {P}(\gamma )=0\) for \(\gamma \in S_\mathsf {P}\). As they will use OPA, \(\deg {\mathbf {p}_\mathsf {A}}=2m\), while \(\deg {\mathbf {p}_\mathsf {B}}=m\). Further, Alice picks a uniformly random polynomial \(\mathbf {r}_\mathsf {A}\) of degree m and inputs \(\mathbf {p}_\mathsf {A},\mathbf {r}_\mathsf {A}\) into OPA. Bob inputs \(\mathbf {p}_\mathsf {B}\), obtains \(\mathbf {p}_\cap =\mathbf {p}_\mathsf {A}+\mathbf {p}_\mathsf {B}\mathbf {r}_\mathsf {A}\) and outputs all \(\gamma _j\in S_\mathsf {B}\) for which \(\mathbf {p}_\cap (\gamma _j)=0\). Obviously, \(\mathbf {r}_\mathsf {A}\) does not remove any of the roots of \(\mathbf {p}_\mathsf {B}\), and therefore all points \(\gamma \) where \(\mathbf {p}_\mathsf {B}(\gamma )=0=\mathbf {p}_\mathsf {A}(\gamma )\) remain in \(\mathbf {p}_\cap \).
However, as a stepping stone for multi-party PSI, we are more interested in protocols that provide output to both parties. If we were to use the above protocol and simply announce \(\mathbf {p}_\cap \) to Alice, then Alice could learn Bob’s input. Therefore we have to take a slightly different approach. Let \(\mathbf {u}_\mathsf {A}\) be an additional random polynomial chosen by Alice. Instead of using her own input in the OPA, Alice uses \(\mathbf {r}_\mathsf {A},\mathbf {u}_\mathsf {A}\), which gives \(\mathbf {s}_\mathsf {B}=\mathbf {u}_\mathsf {A}+\mathbf {p}_\mathsf {B}\mathbf {r}_\mathsf {A}\) to Bob. Then they run another OPA in the other direction, i.e. Bob inputs \(\mathbf {r}_\mathsf {B},\mathbf {u}_\mathsf {B}\) and Alice \(\mathbf {p}_\mathsf {A}\). Now, both Alice and Bob have a randomized “share” of the intersection, namely \(\mathbf {s}_\mathsf {A}\) and \(\mathbf {s}_\mathsf {B}\), respectively. Adding \(\mathbf {s}_\mathsf {A}\) and \(\mathbf {s}_\mathsf {B}\) yields a masked but correct intersection. We still run into the problem that sending either \(\mathbf {s}_\mathsf {B}\) to Alice or \(\mathbf {s}_\mathsf {A}\) to Bob allows the respective party to learn the other party’s input. We also have to use additional randomization polynomials \(\mathbf {r}'_\mathsf {A},\mathbf {r}'_\mathsf {B}\) to ensure privacy of the final result.
Our solution is to simply use the masks \(\mathbf {u}\) to enforce the addition of the two shares. Let us fix Alice as the party that combines the result. Bob computes \(\mathbf {s}'_\mathsf {B}=\mathbf {s}_\mathsf {B}-\mathbf {u}_\mathsf {B}+\mathbf {p}_\mathsf {B}\mathbf {r}'_\mathsf {B}\) and sends it to Alice. Alice computes \(\mathbf {p}_\cap =\mathbf {s}'_\mathsf {B}+\mathbf {s}_\mathsf {A}-\mathbf {u}_\mathsf {A}+\mathbf {p}_\mathsf {A}\mathbf {r}'_\mathsf {A}\). This way, the only chance to get rid of the blinding polynomial \(\mathbf {u}_\mathsf {B}\) is to add both values. But since each input is additionally randomized via the \(\mathbf {r}\) polynomials, Alice cannot subtract her own input from the sum. Since the same also holds for Bob, Alice simply sends the result to Bob.
The last step is to check if the values that are sent and the intersection polynomial are consistent. We do this via a simple coin-toss for a random x, and the parties evaluate their inputs on x and can abort if the relation \(\mathbf {p}_\cap =\mathbf {p}_\mathsf {B}(\mathbf {r}_\mathsf {A}+\mathbf {r}'_\mathsf {B})+\mathbf {p}_\mathsf {A}(\mathbf {r}'_\mathsf {A}+\mathbf {r}_\mathsf {B})\) does not hold, i.e. \(\mathbf {p}_\cap \) is computed incorrectly. This type of check enforces semi-honest behaviour, and was used previously e.g. in [2].
A note on the MPSI functionality. We show that by slightly modifying the ideal functionality for multi-party PSI we get better communication efficiency, without compromising the security at all. A formal definition is given in Sect. 6.1. Typically, it is necessary for the simulator to extract all inputs from the malicious parties, input them into the ideal functionality, and then continue the simulation with the obtained ideal intersection. In a fully malicious setting, however, this requires every party to communicate in \(O(m\kappa )\) with every other party—otherwise the input is information-theoretically undetermined and cannot be extracted—which results in \(O(n^2m\kappa )\) communication complexity.
The crucial observation here is that in the setting of multi-party PSI, an intermediate intersection between a single malicious party and all honest parties is sufficient for simulation. This is due to the fact that inputs by additional malicious parties can only reduce the size of the intersection, and as long as we observe the additional inputs at some point, we can correctly reduce the intersection in the ideal setting before outputting it. On a technical level, we no longer need to extract all malicious inputs right away to provide a correct simulation of the intersection. Therefore, it is not necessary for every party to communicate in \(O(m\kappa )\) with every other party. Intuitively, the intermediate intersection corresponds to the case where all malicious parties have the same input. We therefore argue that the security of this modified setting is identical to standard MPSI up to input substitution of the adversary.Footnote 4
Multi-party PSI. The multi-party protocol is a direct generalization of the two-party protocol, with some small adjustments. We consider a network with a star topology, similar to the recent result of [19]. One party is set to be the central party, and all other parties (mainly) interact with this central party to compute the result. The main idea here is to delegate most of the work to the central party, which in turn allows to reduce the communication complexity. Since no party is supposed to get any intermediate intersections, we let each party create an additive sharing of their intersection with the central party.
First, consider the following (incorrect) toy example. Let each party \(P_i\) execute the two-party PSI as described above with \(P_0\), up to the point where both parties have shares \(\mathbf {s}_{P_0}^i,\mathbf {s}'_{P_i}\). All parties \(P_i\) send their shares \(\mathbf {s}'_{P_i}\) to \(P_0\), who adds all polynomials and broadcasts the output. By design of the protocols and the inputs, this yields the intersection of all parties. Further, the communication complexity is in \(O(nm\kappa )\), which is optimal. However, this protocol also allows \(P_0\) to learn all intermediate intersections with the other parties, which is not allowed. Previously, all maliciously secure multi-party PSI protocols used threshold encryption to solve this problem, and indeed it might be possible to use a similar approach to ensure active security for the above protocol. For example, a homomorphic threshold encryption would allow to add all these shares homomorphically, without leaking the intermediate intersections. But threshold encryption incurs a significant computational overhead (and increases the complexity of the protocol and its analysis) which we are unwilling to pay.
Instead, we propose a new solution which is conceptually very simple. We add another layer of masking on the shares \(\mathbf {s}_{P_i}\), which forces \(P_0\) to add all intermediate shares—at least those of the honest parties. For this we have to ensure that the communication complexity does not increase, so all parties exchange seeds (instead of sending random polynomials directly), which are used in a PRG to mask the intermediate intersections. This technique is somewhat reminiscent of the pseudorandom secret-sharing technique by Cramer et al. [6]. We emphasize that we do not need any public key operations.
Concretely, all parties exchange a random seed and use it to compute a random polynomial in such a way that every pair of parties \(P_i, P_j\) holds two polynomials \(\mathbf {v}_{ij},\mathbf {v}_{ji}\) with \(\mathbf {v}_{ij}+\mathbf {v}_{ji}=0\). Then, instead of sending \(\mathbf {s}'_{P_i}\), each party \(P_i\) computes \(\mathbf {s}''_{P_i}=\mathbf {s}'_{P_i}+\sum {\mathbf {v}_{ij}}\) and sends this value. If \(P_0\) obtains this value, it has to add the values \(\mathbf {s}''_{P_i}\) of all parties to remove the masks, otherwise \(\mathbf {s}''_{P_i}\) will be uniformly random.
Finally, to ensure that the central party actually computed the aggregation, we add a check similar to two-party PSI, where the relation, i.e. computing the sum, is verified by evaluating the inputs on a random value x which is obtained by a multi-party coin-toss.
Threshold (M)PSI. We defer the threshold extensions to the full version of this paper [15] and only give a very brief technical overview.
First of all, we clarify the term threshold PSI. We consider the setting where all parties have m elements as their input, and the output is only revealed if the intersection of the inputs among all parties is bigger than a certain threshold \(\ell \). In [16] Hallgren et al. defined this notion for two party setting, and finds application whenever two entities are supposed to be matched once a certain threshold is reached, e.g. for dating websites or ride sharing.
We naturally extend the idea of threshold PSI from [16] to the multi-party setting and propose the first actively secure threshold multi-party PSI protocol. On a high level, our solution uses a similar idea to [16], but we use completely different techniques and achieve stronger security and better efficiency. The main idea is to use a robust secret sharing scheme, and the execution of the protocol basically transfers a subset of these shares to the other parties, one share for each element in the intersection. If the intersection is large enough, the parties can reconstruct the shared value.
Specifically, the trick is to modify the input polynomials of each party \(\mathsf {P}_i\) for the MPSI protocol and add an additional check. Instead of simply setting \(\mathbf {p}_i\) such that \(\mathbf {p}_i(\gamma _j)=0\) for all \(\gamma _j\in S_i\), we set \(\tilde{\mathbf {p}}_i(\gamma _j)=1\). Further, for each of the random polynomials \(\tilde{\mathbf {r}}_i,\tilde{\mathbf {r}}'_i\) we set \(\tilde{\mathbf {r}}_i(\gamma _j)=\rho _j\) and \(\tilde{\mathbf {r}}'_i(\gamma _j)=\rho _j'\), where \(\rho _1,\ldots ,\rho _n\), \(\rho _1',\ldots ,\rho _n'\) are the shares of two robust \((\ell ,n)\)-secret sharings of random values \(s^0_i\) and \(s^1_i\), respectively. Now, by computing the modified intersection polynomial \(\tilde{\mathbf {p}}_\cap \) as before, each party obtains exactly \(m_\cap =|S_\cap |\) shares, one for each \(\gamma _j\in S_i\).
Now if \(m_\cap \ge \ell \) then each party can reconstruct \(r_\cap =\sum _{i=1}^n{(s^0_i+s^1_i)}\). Otherwise the intersection remains hidden completely. We omitted some of the details due to the space constraints and refer to the full version [15].
A New Flavour of OLE. One of the main technical challenges in constructing our protocols is to ensure a non-zero input into the OLE functionality by the receiver. Recall that an OLE computes a linear function \(ax+b\). We define an enhanced OLE functionality (cf. Sect. 3) which ensures that \(x\ne 0\), otherwise the output is uniformly random. Our protocol which realises this functionality makes two black-box calls to a normal OLE and is otherwise purely algebraic.
Before we describe the solution, let us start with a simple observation. If the receiver inputs \(x=0\), an OLE returns the value b. Therefore, it is critical that the receiver cannot force the protocol to output b. One way to achieve this is by forcing the receiver to multiply b with some correlated value via an OLE, let’s call it \(\hat{x}\). Concretely, we can use an OLE where the receiver inputs \(\hat{x}\) and a random s, while the sender inputs b and obtains \(\hat{x}b+s\). Now if the sender uses \(a+b\hat{x}+s,0\) as input for another OLE, where the receiver inputs x, the receiver obtains \(ax+b\hat{x}x + sx\). Which means that if \(\hat{x}=x^{-1}\) then the receiver can extract the correct output. This looks like a step in the right direction, since for \(x=0\) or \(\hat{x}=0\), the output would not be b. On the other hand, the receiver can now force the OLE to output a by choosing \(\hat{x}=0\) and \(x=1\), so maybe we only shifted the problem.
The final trick lies in masking the output such that it is uniform for inconsistent inputs \(x,\hat{x}\). We do this by splitting b into two shares that only add to b if \(x\cdot \hat{x}=1\). The complete protocol looks like this: the receiver plays the sender for one OLE with input \(x^{-1},s\), and the sender inputs a random u to obtain \(t=x^{-1}u+s\). Then the sender plays the sender for the second OLE and inputs \(t+a, b-u\), while the receiver inputs x and obtains \(c'=(t+a)x+b-u=ux^{-1}x+sx+ax+b-u=ax+b+sx\), from which the receiver can subtract sx to get the result. A cheating receiver with inconsistent input \(x^*,\hat{x}^*\) will get \(ax+b+u(x^*\hat{x}^*-1)\) as an output, which is uniform over the choice of u.
2 Preliminaries
We assume \(|\mathbb {F}^{}_{}|\in \theta (2^\kappa )\), where \(\kappa \) is a statistical security parameter. Typically, \(x\in \mathbb {F}^{}_{}\) denotes a field element, while \(\mathbf {p}\in \mathbb {F}^{}_{}[X]\) denotes a polynomial. Let \(\mathcal {M}_0(\mathbf {p})\) denote the zero-set for \(\mathbf {p}\in \mathbb {F}^{}_{}[X]\), i.e. \(\forall x\in \mathcal {M}_0(\mathbf {p}),\mathbf {p}(x)=0\).
In the proofs, \(\hat{x}\) denotes an element either extracted or simulated by the simulator, while \(x^*\) denotes an element sent by the adversary.
We slightly abuse notation and denote by \(\mathbf {v}=\mathsf {PRG}_d(s)\) the deterministic pseudorandom polynomial of degree d derived from evaluating \(\mathsf {PRG}\) on seed s.
2.1 Security Model
We prove our protocol in the Universal Composability (UC) framework [4]. In the framework, security of a protocol is shown by comparing a real protocol \(\pi \) in the real world with an ideal functionality \(\mathcal {F}\) in the ideal world. \(\mathcal {F}\) is supposed to accurately describe the security requirements of the protocol and is secure per definition. An environment \(\mathcal {Z}\) is plugged either to the real protocol or the ideal protocol and has to distinguish the two cases. For this, the environment can corrupt parties. To ensure security, there has to exist a simulator in the ideal world that produces a protocol transcript indistinguishable from the real protocol, even if the environment corrupts a party. We say \(\pi \) UC-realises \(\mathcal {F}\) if for all adversaries \(\mathcal {A}\) in the real world there exists a simulator \(\mathcal {S}\) in the ideal world such that all environments \(\mathcal {Z}\) cannot distinguish the transcripts of the parties’ outputs.
Oblivious Linear Function Evaluation. Oblivious Linear Function Evaluation (OLE) is the generalized version of OT over larger fields. The sender has as input two values \(a,b\in \mathbb {F}^{}_{}\) that determine a linear function \(f(x) = a\cdot x+ b\) over \(\mathbb {F}^{}_{}\), and the receiver gets to obliviously evaluate the linear function on input \(x \in \mathbb {F}^{}_{}\). The receiver will learn only f(x), and the sender learns nothing at all. The ideal functionality is shown in Fig. 1.
2.2 Technical Lemmas
We state several lemmas which are used to show the correctness of our PSI protocols later on.
Lemma 2.1
Let \(\mathbf {p},\mathbf {q}\in \mathbb {F}^{}_{}[X]\) be non-trivial polynomials. Then,
This lemma shows that the sum of two polynomials contains the intersection with respect to the zero-sets of both polynomials.
Proof
Let \(\mathcal {M}_\cap =\mathcal {M}_0(\mathbf {p})\cap \mathcal {M}_0(\mathbf {q})\).
\(``\supseteq "\): \(\forall x\in \mathcal {M}_\cap \): \(\mathbf {p}(x)=\mathbf {q}(x)=0\). But \(\mathbf {p}(x)+\mathbf {q}(x)=0\), so \(x\in \mathcal {M}_0(\mathbf {p}+\mathbf {q})\).
\(``\subseteq "\): It remains to show that there is no x such that \(x\in \mathcal {M}_0(\mathbf {p})\cap \mathcal {M}_0(\mathbf {p}+\mathbf {q})\) but \(x\notin \mathcal {M}_\cap \), i.e. \(\mathcal {M}_0(\mathbf {p})\cap (\mathcal {M}_0(\mathbf {p}+\mathbf {q})\setminus \mathcal {M}_\cap )=\emptyset \). Similarly, \(\mathcal {M}_0(\mathbf {q})\cap (\mathcal {M}_0(\mathbf {p}+\mathbf {q})\setminus \mathcal {M}_\cap )=\emptyset \).
Assume for the sake of contradiction that \(\mathcal {M}_0(\mathbf {p})\cap (\mathcal {M}_0(\mathbf {p}+\mathbf {q})\setminus \mathcal {M}_\cap )\ne \emptyset \). Let \(x\in \mathcal {M}_0(\mathbf {p})\cap (\mathcal {M}_0(\mathbf {p}+\mathbf {q})\setminus \mathcal {M}_\cap )\). Then, \(\mathbf {p}(x)=0\), but \(\mathbf {q}(x)\ne 0\), otherwise \(x\in \mathcal {M}_\cap \). But this means that \(\mathbf {p}(x)+\mathbf {q}(x)\ne 0\), i.e. \(x\notin \mathcal {M}_0(\mathbf {p}+\mathbf {q})\). This contradicts our assumption, and we get that \(\mathcal {M}_0(\mathbf {p})\cap (\mathcal {M}_0(\mathbf {p}+\mathbf {q})\setminus \mathcal {M}_\cap )=\emptyset \).
Symmetrically, we get that \(\mathcal {M}_0(\mathbf {q})\cap (\mathcal {M}_0(\mathbf {p}+\mathbf {q})\setminus \mathcal {M}_\cap )=\emptyset \). The claim follows. \(\square \)
Lemma 2.2
Let \(d\in \mathsf {poly}(\log |\mathbb {F}^{}_{}|)\). Let \(\mathbf {p}\in \mathbb {F}^{}_{}[X]\), \(\deg (\mathbf {p})=d\) be a non-trivial random polynomial with \(\Pr [x\in \mathcal {M}_0(\mathbf {p})]\le \mathsf {negl}(|\mathbb {F}^{}_{}|)\) for all x. Then, for all \(\mathbf {q}_1,\ldots ,\mathbf {q}_l\in \mathbb {F}^{}_{}[X]\) with \(\deg (\mathbf {q}_i)\le d\),
This lemma is basically an extension of Lemma 2.1 and shows that the sum of several polynomials does not create new elements in the intersection unless the supposedly unknown zero-set of \(\mathbf {p}\) can be guessed with non-negligible probability.
Proof
“\(\subseteq \)”: We first observe that \(\bigcap _{i=1}^l\mathcal {M}_0(\mathbf {q}_i)\subseteq \mathcal {M}_0(\sum _{i=1}^l{\mathbf {q}_i})\): it holds that for all \(x\in \bigcap _{i=1}^l\mathcal {M}_0(\mathbf {q}_i)\), \(\mathbf {q}_i(x)=0\) for \(i\in [l]\). It follows that \(\sum _{i=1}^l{\mathbf {q}_i(x)}=0\), i.e. \(x\in \mathcal {M}_0(\sum _{i=1}^l{\mathbf {q}_i})\).
“\(\supseteq \)”: Assume for the sake of contradiction that
with non-negligible probability \(\epsilon \). Let \(\mathcal {M}=\mathcal {M}_0(\sum _{i=1}^l{\mathbf {q}_i}+\mathbf {p})\setminus \bigcap _{i=1}^l\mathcal {M}_0(\mathbf {q}_i)\).
Then with probability at least \(\epsilon \), the set \(\mathcal {M}\) is not empty. Further, we can bound \(|\mathcal {M}|\le d\). Pick a random \(x\in \mathcal {M}\). It now holds that \(\Pr [x\in \mathcal {M}_0(\mathbf {p})]\ge \epsilon /d\), which directly contradicts our assumption that for an unknown \(\mathbf {p}\) the probability of guessing \(x\in \mathcal {M}_0(\mathbf {p})\) is negligible over choice of \(\mathbf {p}\). The claim follows. \(\square \)
Lemma 2.3
Let \(d,d'\in \mathsf {poly}(\log |\mathbb {F}^{}_{}|)\). Let \(\mathbf {r}\in \mathbb {F}^{}_{}[X]\), \(\deg (\mathbf {r})=d\) be a uniformly random polynomial. For all non-trivial \(\mathbf {p}\in \mathbb {F}^{}_{}[X]\), \(\deg (\mathbf {p})=d'\),
This lemma establishes that the intersection of a random polynomial with another polynomial is empty except with negligible probability.
Proof
This follows from the fundamental theorem of algebra, which states that a polynomial of degree d evaluates to 0 in a random point only with probability \(d/|\mathbb {F}^{}_{}|\).
Since \(\mathbf {r}\) (and therefore all \(x\in \mathcal {M}_0(\mathbf {r})\)) is uniformly random and \(|\mathcal {M}_0(\mathbf {r})|=d\), while \(|\mathcal {M}_0(\mathbf {p})|=d'\), we get that
\(\square \)
Lemma 2.4
Let \(d\in \mathsf {poly}(\log |\mathbb {F}^{}_{}|)\). Let \(\mathbf {p}\in \mathbb {F}^{}_{}[X]\), \(\deg (\mathbf {p})=d\) be a fixed but unknown non-trivial polynomial. Further let \(\mathbf {r}\in \mathbb {F}^{}_{}[X]\), \(\deg (\mathbf {r})=d\) be a uniformly random polynomial. For all non-trivial \(\mathbf {q},\mathbf {s}\in \mathbb {F}^{}_{}[X]\) with \(\deg (\mathbf {q})\le d\) and \(\deg (\mathbf {s})\le d\),
This lemma shows that the multiplication of (possibly maliciously chosen) polynomials does not affect the intersection except with negligible probability, if one random polynomial is used.
Proof

From Lemma 2.3 it follows that \(\Pr [\mathcal {T}_1\ne \emptyset ]\le d^2/|\mathbb {F}^{}_{}|\), and also \(\Pr [\mathcal {T}_2\ne \emptyset ]\le d^2/|\mathbb {F}^{}_{}|\). Since
we get
\(\square \)
3 Enhanced Oblivious Linear Function Evaluation 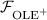
In this section we present an enhanced version of the OLE functionality. The standard OLE functionality allows the sender to input a, b, while the receiver inputs x and obtains \(ax+b\). For our applications, we do not want the receiver to be able to learn b, i.e. it has to hold that \(x\ne 0\). Our approach is therefore to modify the OLE functionality in such a way that it outputs a random field element upon receiving an input \(x=0\) (cf. Fig. 2). A different approach might be to output a special abort symbol or 0, but crucially the output must not satisfy the relation \(ax+b\). This is a particularly useful feature, as we will show in the next section.
While it might be possible to modify existing OLE protocols in such a way that a non-zero input is guaranteed, we instead opt to build a protocol black-box from the standard OLE functionality  .
.
We refer to the introduction for an abstract overview and a description of the ideas of our construction. The formal description of the protocol is given in Fig. 3.
Lemma 3.1
 unconditionally UC-realizes
unconditionally UC-realizes  in the
in the  -hybrid model.
-hybrid model.
Proof
The simulator against a corrupted sender simulates both instances of  . Let \(\alpha _1\) be the sender’s input in the first OLE, and \((\alpha _2,\alpha _3)\) be the inputs into the second OLE. The simulator sets \(\hat{b}=\alpha _1+\alpha _3\) and \(\hat{a}=\alpha _2-\hat{t}\), where \(\hat{t}\) is chosen as the uniformly random output to \(\mathcal {A}_\mathsf {S}\) of the first OLE. The simulator simply inputs \((\mathtt {inputS},(\hat{a},\hat{b}))\) into
. Let \(\alpha _1\) be the sender’s input in the first OLE, and \((\alpha _2,\alpha _3)\) be the inputs into the second OLE. The simulator sets \(\hat{b}=\alpha _1+\alpha _3\) and \(\hat{a}=\alpha _2-\hat{t}\), where \(\hat{t}\) is chosen as the uniformly random output to \(\mathcal {A}_\mathsf {S}\) of the first OLE. The simulator simply inputs \((\mathtt {inputS},(\hat{a},\hat{b}))\) into  . Let us briefly argue that this simulation is indistinguishable from a real protocol run. The value \(\hat{t}\) is indistinguishable from a valid t, since the receiver basically uses a one-time-pad s to mask the multiplication. Therefore, the sender can only change his inputs into the OLEs. Since his inputs uniquely determine both \(\hat{a}\) and \(\hat{b}\), the extraction by the simulator is correct and the simulation is indistinguishable from a real protocol run.
. Let us briefly argue that this simulation is indistinguishable from a real protocol run. The value \(\hat{t}\) is indistinguishable from a valid t, since the receiver basically uses a one-time-pad s to mask the multiplication. Therefore, the sender can only change his inputs into the OLEs. Since his inputs uniquely determine both \(\hat{a}\) and \(\hat{b}\), the extraction by the simulator is correct and the simulation is indistinguishable from a real protocol run.
Against a corrupted receiver, the simulator simulates the two instance of  and obtains the receiver’s inputs \((\xi _1,\xi _3)\) and \(\xi _2\). If \(\xi _1\cdot \xi _2=1\), the simulator sets \(\hat{x}=\xi _2\), sends \((\mathtt {inputR},\hat{x})\) to
and obtains the receiver’s inputs \((\xi _1,\xi _3)\) and \(\xi _2\). If \(\xi _1\cdot \xi _2=1\), the simulator sets \(\hat{x}=\xi _2\), sends \((\mathtt {inputR},\hat{x})\) to  and receives \((\mathtt {output},c)\). It forwards \(c'=c+\xi _2\xi _3\) to \(\mathcal {A}_\mathsf {R}\). If \(\xi _1\cdot \xi _2\ne 1\), the simulator sends \((\mathtt {inputR},0)\) to
and receives \((\mathtt {output},c)\). It forwards \(c'=c+\xi _2\xi _3\) to \(\mathcal {A}_\mathsf {R}\). If \(\xi _1\cdot \xi _2\ne 1\), the simulator sends \((\mathtt {inputR},0)\) to  and forwards the output c to the receiver. It remains to argue that this simulation is indistinguishable from the real protocol. From \(\mathcal {A} \)’s view, the output c is determined as
and forwards the output c to the receiver. It remains to argue that this simulation is indistinguishable from the real protocol. From \(\mathcal {A} \)’s view, the output c is determined as
We can ignore the last term, since it is known to \(\mathcal {A} \). If \(\xi _1\xi _2\ne 1\), then \(u(\xi _1\xi _2-1)\) does not vanish and the result will be uniform over the choice of u. Thus, by using \(\xi _2\) as the correct input otherwise, we extract the correct value and the simulation is indistinguishable from the real protocol. \(\square \)
4 Randomized Polynomial Addition from OLE
Concretely, we have two parties, the sender with a polynomial of degree 2d as input and the receiver with a polynomial of degree d as input. The goal is that the receiver obtains the sum of these two polynomials such that it cannot learn the sender’s polynomial fully. We want to achieve this privacy property by using a randomization polynomial that prevents the receiving party from simply subtracting its input from the result. This functionality is defined in Fig. 4.
Notice that we have some additional requirements regarding the inputs of the parties. First, the degree of the inputs has to be checked, but the functionality also makes sure that the receiver does not input a 0 polynomial, because otherwise he might learn the input of the sender. Also note that the functionality leaks some information about the sender’s polynomial. Looking ahead in the PSI protocol, where the input of the sender is always a uniformly random 2d degree polynomial, this leakage of the ideal functionality will not leak any non-trivial information in the PSI protocol.
It is instructive to first consider a passively secure protocol. In the semi-honest case, both sender and receiver evaluate their input polynomials on a set of distinct points \(\mathcal {P}=\{\alpha _1,\ldots ,\alpha _{2d+1}\}\), where d is the degree of the input polynomials. The sender additionally picks a random polynomial \(\mathbf {r}\in \mathbb {F}^{}_{}[X]\) of degree d and also evaluates it on \(\mathcal {P}\).
Instead of using OLE in the “traditional” sense, i.e. instead of computing \(\mathbf {a}\mathbf {b}\,+\,\mathbf {r}\) where \(\mathbf {r}\) blinds the multiplication of the polynomials, we basically compute \(\mathbf {r}\mathbf {b}\,+\,\mathbf {a}\). This means that the sender randomizes the polynomial of the receiver, and then adds his own polynomial. This prevents the receiver from simply subtracting his input polynomial and learning \(\mathbf {a}\). In a little more detail, sender and receiver use \(2d\,+\,1\) OLEs to add the polynomials as follows: for each \(i\in [2d\,+\,1]\), the sender inputs \((r_i,a_i)\) in OLE i, while the receiver inputs \(b_i\) and obtains \(s_i=r_ib_i+a_i\). He then interpolates the resulting polynomial \(\mathbf {s}\) of degree 2d using the \(2d+1\) values \(s_i\).
In going from passive to active security, we have to ensure that the inputs of the parties are correct. Here, the main difficulty obviously lies in checking for \(\mathbf {b}=0\). In fact, since  does not even leak a single point \(a_i\) we have to make sure that all \(b_i\ne 0\). However, this can easily be achieved by using
does not even leak a single point \(a_i\) we have to make sure that all \(b_i\ne 0\). However, this can easily be achieved by using  instead of
instead of  . We also have to verify that the inputs are well-formed via a simple polynomial check. For a more detailed overview we refer the reader to the introduction.
. We also have to verify that the inputs are well-formed via a simple polynomial check. For a more detailed overview we refer the reader to the introduction.
The complete actively secure protocol is shown in Fig. 5. Here, we use two instances of  that implement a commitment and a check. We named the first OLE that is used for a commitment to a blinding value u
that implement a commitment and a check. We named the first OLE that is used for a commitment to a blinding value u
 . The check is performed by comparing the blinded reconstructed polynomial \(\mathbf {s}\) evaluated in \(x_\mathsf {S}\) with the inputs in this location using the second OLE denoted by
. The check is performed by comparing the blinded reconstructed polynomial \(\mathbf {s}\) evaluated in \(x_\mathsf {S}\) with the inputs in this location using the second OLE denoted by
 .Footnote 5
.Footnote 5
Lemma 4.1
 unconditionally UC-realizes
unconditionally UC-realizes  in the
in the  -hybrid model.
-hybrid model.
Proof
(Sketch). Corrupted Sender. The simulator \(\mathcal {S}_\mathsf {S}\) against a corrupted sender proceeds as follows. It simulates  and thereby obtains \((r^*_i,a^*_i)\) for all \(i\in [2d+1]\). From these values, the simulator reconstructs \(\hat{\mathbf {r}}\) and \(\hat{\mathbf {a}}\). It aborts in Step 3 if \(\deg (\hat{\mathbf {r}})>d\) or \(\deg (\hat{\mathbf {a}})>2d\). It also aborts if \(\hat{\mathbf {a}}\) or \(\hat{\mathbf {r}}\) are zero, and otherwise sends \((\mathtt {inputS},(\hat{\mathbf {a}},\hat{\mathbf {r}}))\) to
and thereby obtains \((r^*_i,a^*_i)\) for all \(i\in [2d+1]\). From these values, the simulator reconstructs \(\hat{\mathbf {r}}\) and \(\hat{\mathbf {a}}\). It aborts in Step 3 if \(\deg (\hat{\mathbf {r}})>d\) or \(\deg (\hat{\mathbf {a}})>2d\). It also aborts if \(\hat{\mathbf {a}}\) or \(\hat{\mathbf {r}}\) are zero, and otherwise sends \((\mathtt {inputS},(\hat{\mathbf {a}},\hat{\mathbf {r}}))\) to  .
.
The extraction of the corrupted sender’s inputs is correct if his inputs \(\mathbf {r}^*\) corresponds to a polynomial of degree d and \(\mathbf {a}^*\) corresponds to a polynomial of degree 2d. Thus, the only possibility for an environment to distinguish between the simulation and the real protocol is by succeeding in answering the check while using a malformed input, i.e. a polynomial of incorrect degree or 0-polynomials. If the polynomials have degree greater than d and 2d, respectively, the resulting polynomial \(\mathbf {s}\) has degree \(2d+1\) instead of 2d, i.e. the receiver cannot reconstruct the result from \(2d+1\) points. Since the sender learns nothing about the receiver’s inputs, the thus incorrectly reconstructed polynomial will be uniformly random from his point of view and the probability that his response to the challenge is correct is \(1/|\mathbb {F}^{}_{}|\). Also, both \(\hat{\mathbf {a}}\) and \(\hat{\mathbf {r}}\) have to be non-zero, because in each case the polynomials are evaluated in \(2d+1\) points, and it requires \(2d+1\) zeros as \(a_i,r_i\) to get a 0 polynomial. But since both \(\mathbf {a},\mathbf {r}\) have degree at most 2d, there are at most 2d roots of these polynomials. Therefore, in order to pass the check, \(\mathbf {a}(x)\) and \(\mathbf {b}(x)\) would need to be 0, which is also checked for.
Corrupted Receiver. The simulator \(\mathcal {S}_\mathsf {R}\) against a corrupted receiver simulates  and obtains \(\mathbf {b}^*_i\) for all \(i\in [2d+1]\). It reconstructs \(\hat{\mathbf {b}}\) and aborts the check in Step 3 if \(\deg (\hat{\mathbf {b}})>d\). The simulator sends \((\mathtt {inputR},\hat{\mathbf {b}})\) to
and obtains \(\mathbf {b}^*_i\) for all \(i\in [2d+1]\). It reconstructs \(\hat{\mathbf {b}}\) and aborts the check in Step 3 if \(\deg (\hat{\mathbf {b}})>d\). The simulator sends \((\mathtt {inputR},\hat{\mathbf {b}})\) to  and receives \((\mathtt {res},\hat{\mathbf {s}})\). It evaluates \(\hat{\mathbf {s}}\) on \(\mathcal {P}\) and returns \(s_i\) for the corresponding OLEs. \(\mathcal {S}_\mathsf {R}\) simulates the rest according to the protocol.
and receives \((\mathtt {res},\hat{\mathbf {s}})\). It evaluates \(\hat{\mathbf {s}}\) on \(\mathcal {P}\) and returns \(s_i\) for the corresponding OLEs. \(\mathcal {S}_\mathsf {R}\) simulates the rest according to the protocol.
Clearly, if the corrupted receiver \(\mathcal {A}_\mathsf {R}\) inputs a degree d polynomial, the simulator will extract the correct polynomial. In order to distinguish the simulation from the real protocol, the adversary can either input 0 in an OLE or has to input a polynomial of higher degree, while still passing the check. In the first case, assume w.l.o.g. that \(\mathcal {A}_\mathsf {R}\) cheats in  for some j. This means \(\mathcal {A}_\mathsf {R}\) receives a value \(\hat{s}_i\), which is uniformly random. This means that only with probability \(1/|\mathbb {F}^{}_{}|\) will \(\hat{s}_i\) satisfy the relation \(\mathbf {r}\mathbf {b}+\mathbf {a}\) and the check will fail, i.e. he can lie about u, but the commitment to u cannot be opened without knowing t. In the second case, the resulting polynomial would be of degree \(2d+1\), while the receiver only gets \(2d+1\) points of the polynomial. Therefore the real polynomial is underdetermined and \(\mathcal {A} \) can only guess the correct value \(\hat{\mathbf {s}}(x)\), i.e. the check will fail with overwhelming probability. \(\square \)
for some j. This means \(\mathcal {A}_\mathsf {R}\) receives a value \(\hat{s}_i\), which is uniformly random. This means that only with probability \(1/|\mathbb {F}^{}_{}|\) will \(\hat{s}_i\) satisfy the relation \(\mathbf {r}\mathbf {b}+\mathbf {a}\) and the check will fail, i.e. he can lie about u, but the commitment to u cannot be opened without knowing t. In the second case, the resulting polynomial would be of degree \(2d+1\), while the receiver only gets \(2d+1\) points of the polynomial. Therefore the real polynomial is underdetermined and \(\mathcal {A} \) can only guess the correct value \(\hat{\mathbf {s}}(x)\), i.e. the check will fail with overwhelming probability. \(\square \)
5 Maliciously Secure Two-Party PSI
In this section we provide a maliciously secure two-party PSI protocol with output for both parties, i.e. we realize \(\mathcal {F}^{\text {}}_{\text {PSI}}\) as described in Fig. 6.
We briefly sketch the protocol in the following; a more detailed overview can be found in the introduction. First, Alice and Bob simply transform their input sets into polynomials. Then, both compute a randomized share of the intersection via our previously defined OPA in such a way that Alice can send her share to Bob without him being able to learn her input. This can be achieved by adding a simple mask to the intermediate share. Bob adds both shares and sends the output to Alice. The protocol only requires two OPA and a simple check which ensures semi-honest behaviour, and no computational primitives. A formal description is given in Fig. 7.
Theorem 5.1
The protocol  UC-realises
UC-realises  in the
in the  -hybrid model with communication complexity \(O(m\kappa )\).
-hybrid model with communication complexity \(O(m\kappa )\).
Proof
Let us argue that \(\mathbf {p}_\cap =\mathbf {p}_\mathsf {A}(\mathbf {r}'_\mathsf {A}+\mathbf {r}_\mathsf {B})+\mathbf {p}_\mathsf {B}(\mathbf {r}_\mathsf {A}+\mathbf {r}'_\mathsf {B})\) actually hides the inputs. The main observation here is that \(\mathbf {r}'_\mathsf {P}+\mathbf {r}_\mathsf {\bar{P}}\) is uniformly random as long as one party is honest. Since \(\mathbf {p}_\mathsf {A}+\mathbf {p}_\mathsf {B}\) validly encodes the intersection (see Lemma 2.1), \(\mathbf {p}_\cap \) is uniformly random over the choice of the randomization polynomials \(\mathbf {r}_\mathsf {A},\mathbf {r}'_\mathsf {A},\mathbf {r}_\mathsf {B}\) and \(\mathbf {r}'_\mathsf {B}\), except for the roots denoting the intersection.
Corrupted Alice. We show the indistinguishability of the simulation of \(\mathcal {S}_\mathsf {A}\) (cf. Fig. 8). The simulator extracts Alice’s inputs and then checks for any deviating behaviour. If such behaviour is detected, it aborts, even if the protocol would succeed. Proving indistinguishability of the simulation shows that the check in the protocol basically enforces semi-honest behaviour by Alice, up to input substitution.
Consider the following series of hybrid games.
-
Hybrid 0: \(\mathsf {Real}^{\mathcal {A} _\mathsf {A}}_{\varPi ^{\text {}}_{\text {2PSI}}}\).
-
Hybrid 1: Identical to Hybrid 0, except that \(\mathcal {S}_1\) simulates
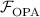 , learns all inputs and aborts if \(\alpha _\mathsf {A}^*\ne \hat{\mathbf {p}}_\mathsf {A}(x)\) or \(\beta _\mathsf {A}^*\ne \hat{\mathbf {r}}_\mathsf {A}(x)\), but the check is passed. Let \(\alpha _\mathsf {A}^*=\alpha _\mathsf {A}+e\) be \(\mathcal {A} _\mathsf {A}\)’s check value. Then the check in Step 6 will fail with overwhelming probability. Let \(\sigma \) denote the outcome of the check. If \(\mathcal {A} _\mathsf {A}\) behaves honestly, then $$\begin{aligned} \sigma =\alpha _\mathsf {A}^*(\mathbf {r}_\mathsf {B}(x)+\delta _\mathsf {A}^*)+\mathbf {p}_\mathsf {B}(x)(\beta _\mathsf {A}^*+\mathbf {r}'_\mathsf {B}(x))-\mathbf {p}_\cap (x)=0. \end{aligned}$$
, learns all inputs and aborts if \(\alpha _\mathsf {A}^*\ne \hat{\mathbf {p}}_\mathsf {A}(x)\) or \(\beta _\mathsf {A}^*\ne \hat{\mathbf {r}}_\mathsf {A}(x)\), but the check is passed. Let \(\alpha _\mathsf {A}^*=\alpha _\mathsf {A}+e\) be \(\mathcal {A} _\mathsf {A}\)’s check value. Then the check in Step 6 will fail with overwhelming probability. Let \(\sigma \) denote the outcome of the check. If \(\mathcal {A} _\mathsf {A}\) behaves honestly, then $$\begin{aligned} \sigma =\alpha _\mathsf {A}^*(\mathbf {r}_\mathsf {B}(x)+\delta _\mathsf {A}^*)+\mathbf {p}_\mathsf {B}(x)(\beta _\mathsf {A}^*+\mathbf {r}'_\mathsf {B}(x))-\mathbf {p}_\cap (x)=0. \end{aligned}$$Using \(\alpha _\mathsf {A}^*=\alpha _\mathsf {A}+e\), however, we get
$$\begin{aligned} \sigma '=(\alpha _\mathsf {A}+e)(\mathbf {r}_\mathsf {B}(x)+\delta _\mathsf {A}^*)+\mathbf {p}_\mathsf {B}(x)(\beta _\mathsf {A}^*+\mathbf {r}'_\mathsf {B}(x))-\mathbf {p}_\cap (x) = e\cdot (\mathbf {r}_\mathsf {B}(x)+\delta _\mathsf {A}^*)\ne \mathsf {const}. \end{aligned}$$This means that the outcome of the check is uniformly random from \(\mathcal {A} _\mathsf {A}\)’s view over the choice of \(\mathbf {r}_\mathsf {B}\) (or \(\mathbf {p}_\mathsf {B}\) for \(\beta _\mathsf {A}^*\ne \mathbf {r}_\mathsf {A}(x)\)). Therefore, the check will fail except with probability \(2/|\mathbb {F}^{}_{}|\) and Hybrids 0 and 1 are statistically close.
-
Hybrid 2: Identical to Hybrid 1, except that \(\mathcal {S}_2\) aborts according to Step 6 in Fig. 8.
An environment distinguishing Hybrids 1 and 2 must manage to send \(\mathbf {s}_\mathsf {A}^{\prime *}\) such that
$$\begin{aligned} \mathbf {s}_\mathsf {A}^{\prime *}+\hat{\mathbf {u}}_\mathsf {A}-\hat{\mathbf {u}}_\mathsf {B}\ne \hat{\mathbf {p}}_\mathsf {A}\cdot (\hat{\mathbf {r}}_\mathsf {B}+\hat{\mathbf {r}}'_\mathsf {A}) \end{aligned}$$while passing the check in Step 6 with non-negligible probability.
Let \(\mathbf {f}=\mathbf {s}_\mathsf {A}^{\prime *}+\hat{\mathbf {u}}_\mathsf {A}-\hat{\mathbf {u}}_\mathsf {B}-\hat{\mathbf {p}}_\mathsf {A}\cdot (\hat{\mathbf {r}}_\mathsf {B}+\hat{\mathbf {r}}'_\mathsf {A})\). We already know that \(\mathbf {f}(x)=0\), otherwise we have \(\alpha _\mathsf {A}^*=\alpha _\mathsf {A}+\mathbf {f}(x)\ne \alpha _\mathsf {A}\) (or an invalid \(\beta _\mathsf {A}^*\)), and the check fails. But since x is uniformly random, the case that \(\mathbf {f}(x)=0\) happens only with probability \(m/|\mathbb {F}^{}_{}|\), which is negligible. Therefore, Hybrid 1 and Hybrid 2 are statistically close.
-
Hybrid 3: Identical to Hybrid 2, except that \(\mathcal {S}_3\) generates the inputs \(\hat{\mathbf {s}}_\mathsf {A},\hat{\mathbf {s}}_\mathsf {B}\) according to Step 5 in Fig. 8 and adjusts the output. This corresponds to \(\mathsf {Ideal}^{\mathcal {S}_\mathsf {A}}_{\mathcal {F}^{\text {}}_{\text {PSI}}}\).
The previous hybrids established that the inputs \(\hat{\mathbf {p}}_\mathsf {A},\hat{\mathbf {r}}_\mathsf {A}\) are extracted correctly. Therefore, by definition, \(\hat{S}_\mathsf {A}=\mathcal {M}_0(\hat{\mathbf {p}}_\mathsf {A})\). It remains to argue that the simulated outputs are indistinguishable. First, note that the received intersection \(\hat{S}_\cap =\mathcal {M}_0(\hat{\mathbf {p}}_\mathsf {B})\) defines \(\hat{\mathbf {p}}_\mathsf {B}\). From Lemma 2.4 it follows that \(\mathcal {M}_0(\mathbf {p}_\cap )=\mathcal {M}_0(\hat{\mathbf {p}}_\mathsf {A})\cap \mathcal {M}_0(\hat{\mathbf {p}}_\mathsf {B})=\hat{S}_\cap \) w.r.t. \(\mathcal {M}_0(\hat{\mathbf {p}}_\mathsf {B})\), even for a maliciously chosen \(\hat{\mathbf {r}}_\mathsf {A}\), i.e. the \(\mathcal {A} _\mathsf {A}\) cannot increase the intersection even by a single element except with negligible probability.
Further, note that \(\hat{\mathbf {s}}_\mathsf {A}=\hat{\mathbf {p}}_\mathsf {A}\cdot \hat{\mathbf {r}}_\mathsf {B}+\hat{\mathbf {u}}_\mathsf {B}\) is uniformly distributed over the choice of \(\hat{\mathbf {u}}_\mathsf {B}\), and \(\hat{\mathbf {p}}_\cap \) is uniform over the choice of \(\hat{\mathbf {r}}_\mathsf {B},\hat{\mathbf {r}}'_\mathsf {B}\).
Finally, since \(\hat{\mathbf {r}}_\mathsf {B},\hat{\mathbf {r}}'_\mathsf {B}\) are uniformly random and the degree of \(\hat{\mathbf {p}}_\mathsf {B}\) is \(m\), i.e. \(\max _i{|\mathcal {S}_i|}+1\), the values \(\hat{\alpha }_\mathsf {B}\), \(\hat{\beta }_\mathsf {B}\) and \(\hat{\delta }_\mathsf {B}\) are uniformly distributed as well. In conclusion, the Hybrids 2 and 3 are statistically close.
As a result we get that for all environments \(\mathcal {Z}\),
Corrupted Bob. The simulator against a corrupted Bob is essentially the same as the one against a corrupted Alice, except for a different way to check his inputs.For the full proof we refer the reader to the full version [15] of the paper.
Efficiency. The protocol makes two calls to OPA, which in turn is based on OLE. Overall, 2m calls to OLE are necessary in OPA. Given the recent constant overhead OLE of Ghosh et al. [14], the communication complexity of \(\varPi ^{\text {}}_{\text {2PSI}}\) lies in \(O(m\kappa )\).
The computational cost of the protocol is dominated by multi-point evaluation of polynomials of degree m, which requires \(O(m\log m)\) multiplications using fast modular transform [3]. Note that this cost includes computational cost of the OLE instantiation from [14]. This concludes the proof. \(\square \)
6 Maliciously Secure Multi-party PSI
6.1 Ideal Functionality
The ideal functionality for multi-party private set intersection \(\mathcal {F}^{\text {*}}_{\text {MPSI}}\) simply takes the inputs from all parties and computes the intersection of these inputs. Our functionality \(\mathcal {F}^{\text {*}}_{\text {MPSI}}\) in Fig. 9 additionally allows an adversary to learn the intersection and then possibly update the result to be only a subset of the original result.
Let us briefly elaborate on why we chose to use this modified functionality. In the UC setting, in order to extract the inputs of all malicious parties, any honest party has to communicate with all malicious parties. In particular, since the simulator has to extract the complete input, this requires at least O(nm) communication per party for the classical MPSI functionality. In turn, for the complete protocol, this means that the communication complexity lies in \(O(n^2m)\).
Instead, we want to take an approach similar to the recent work of Hazay et al. [19], i.e. we have one central party, and some of the work is delegated to this party. This removes the need for the other parties to extensively communicate with each other and potentially allows communication complexity O(mn), which is asymptotically optimal in any setting. However, if we assume that the central party and at least one additional party are corrupted, the honest party does not (extensively) interact with this additional party and does not learn its inputs; it can only learn the input of the central party. If the input set of the other malicious party is the same as the one of the central party, the output remains the same. If this input is different, however, the actual intersection might be smaller. One might argue that this case simply corresponds to input substitution by the malicious party, but for any type of UC simulation this poses a problem, since the output of the honest party in the protocol might be different from the intersection in the ideal world. Thus, \(\mathcal {F}^{\text {*}}_{\text {MPSI}}\) allows a malicious party to modify the output. Crucially, the updated intersection can only be smaller and may not changed arbitrarily by the adversary. We believe that this weaker multiparty PSI functionality is sufficient for most scenarios.
6.2 Multi-party PSI from OLE
Our multi-party PSI protocol uses the same techniques that we previously employed to achieve two-party PSI. This is similar in spirit to the approach taken in [19], who employ techniques from the two-party PSI of [13] and apply them in the multi-party setting. We also adopt the idea of a designated central party that performs a two-party PSI with the remaining parties, because this allows to delegate most of the computation to this party and saves communication. Apart from that, our techniques differ completely from [19]. Abstractly, they run the two-party PSI with each party and then use threshold encryption and zero-knowledge proofs to ensure the correctness of the computation. These tools inflict a significant communication and computation penalty.
In our protocol (cf. Fig. 10) we run our two-party PSI between the central party and every other party, but we ensure privacy of the aggregation not via threshold encryption and zero-knowledge proofs, but instead by a simple masking of the intermediate values and a polynomial check. This masking is created in a setup phase, where every pair of parties exchanges a random seed that is used to create two random blinding polynomials which cancel out when added.
Once the central party receives all shares of the computation, it simply add these shares, thereby removing the random masks. The central party broadcasts the result to all parties. Then, all parties engage in a multi-party coin-toss and obtain a random value x. Since all operations in the protocol are linear operations on polynomials, the parties evaluate their input polynomials on x and broadcast the result. This allows every party to locally verify the relation and as a consequence also the result. Here we have to ensure that a rushing adversary cannot cheat by waiting for all answers before providing its own answer. We solve this issue by simply committing to the values first, and the unveiling them in the next step. This leads to malleability problems, i.e. we have to use non-malleable commitmentsFootnote 6.
Theorem 6.1
The protocol  computationally UC-realises \({\mathcal {F}^{*}_{{\mathrm{MPSI}}}}\) in the
computationally UC-realises \({\mathcal {F}^{*}_{{\mathrm{MPSI}}}}\) in the  -hybrid model with communication complexity in \(O((n^2+nm)\kappa )\).
-hybrid model with communication complexity in \(O((n^2+nm)\kappa )\).
Proof
We have to distinguish between the case where the central party is malicious and the case where it is honest. We show UC-security of \(\varPi ^{\text {}}_{\text {MPSI}}\) by defining a simulator \(\mathcal {S}\) for each case which produces an indistinguishable simulation of the protocol to any environment \(\mathcal {Z}\) trying to distinguish the ideal world from the real world. The approach of the simulation is straightforward: the simulator extracts the input polynomials into  and thus obtains an intersection of the adversary’s inputs.
and thus obtains an intersection of the adversary’s inputs.
In the case of an honest central party, all parties communicate with this party, i.e. the simulator can extract all inputs of all malicious parties. In the case where \(P_0\) is malicious, however, the simulator can at most learn the central party’s input at the beginning. He inputs this result into the ideal functionality and uses the intermediate result for the simulation. The malicious central party can later “simulate” the other malicious parties and thereby possibly change the intersection for the honest parties. We show that \(\mathcal {A} \) can only reduce the intersection unless it already knows \(x\in S_j\) for at least one \(j\in \mathsf {H}\), i.e. we assume that \(\mathcal {A} \) cannot predict a single element of the set of an honest party except with negligible probability. This reduced intersection can be passed by the simulator to the ideal functionality.
- \(P_0\) is malicious::
-
Consider the simulator in Fig. 11.
We show the indistinguishability of the simulation and the real protocol through the following hybrid games. In the following, let \(\mathcal {A} \) denote the dummy adversary controlled by \(\mathcal {Z}\).
-
Hybrid 0: \(\mathsf {Real}^{\mathcal {A}}_{\varPi ^{\text {}}_{\text {MPSI}}}\).
-
Hybrid 1: Identical to Hybrid 0, except that \(\mathcal {S}_1\) simulates
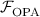 and learns all inputs.
and learns all inputs. -
Hybrid 2: Identical to Hybrid 1, except that \(\mathcal {S}_2\) aborts according to Step 7 in Fig. 11.
-
Hybrid 3: Identical to Hybrid 2, except that \(\mathcal {S}_3\) aborts if the extracted \(\hat{\mathbf {p}}_0\) are not identical, but the check is passed.
-
Hybrid 4: Identical to Hybrid 3, except that \(\mathcal {S}_4\) replaces the \(\mathbf {v}_{jl}\) between honest parties j, l by uniformly random polynomials.
-
Hybrid 5: Identical to Hybrid 4, except that \(\mathcal {S}_5\) generates the inputs \(\hat{\mathbf {s}}_0^j,\hat{\mathbf {s}}_j\) according to Step 6 in Fig. 11 and adjusts the output. This corresponds to \(\mathsf {Ideal}^{\mathcal {S}_{P_0}}_{\mathcal {F}^{\text {*}}_{\text {MPSI}}}\).
Hybrids 0 and 1 are trivially indistinguishable. We show that Hybrid 1 and Hybrid 2 are computationally indistinguishable in Lemma 6.1.1. This step ensures that the correct \(\hat{p}_0\) was extracted, and that all the intermediate values of the honest parties are added up. Hybrids 2 and 3 are indistinguishable due to the security of the coin-toss. This is formalized in Lemma 6.1.2. As an intermediate step to complete the full simulation, we replace all pseudorandom polynomials \(\mathbf {v}_{jl}\) between honest parties j, l by uniformly random ones. Computational indistinguishability of Hybrid 3 and Hybrid 4 follows from a straightforward reduction to the pseudorandomness of \(\mathsf {PRG}\). We establish the statistical indistinguishability of Hybrids 4 and 5 in Lemma 6.1.3. As a result we get that for all PPT environments \(\mathcal {Z}\),
Lemma 6.1.1
Assume that \(\mathsf {NMCOM}\) is a bounded-concurrent non-malleable commitment scheme against synchronizing adversaries. Then Hybrid 1 and Hybrid 2 are computationally indistinguishable.
Proof
The only difference between Hybrid 1 and Hybrid 2 lies in the fact that \(\mathcal {S}_2\) aborts if the extracted \(\hat{\mathbf {p}}_\mathsf {A}\) evaluated on x does not match the check value \(\alpha _0\), but the check is still passed. Therefore, in order for \(\mathcal {Z}\) to distinguish both hybrids, it has to be able to produce a value \(\alpha _0^*\ne \hat{\mathbf {p}}_\mathsf {A}(x)\) and pass the check with non-negligible probability \(\epsilon \). W.l.o.g. it is sufficient that \(\alpha _0^*\) is incorrect for only one \(\hat{\mathbf {p}}_0\). We show that such a \(\mathcal {Z}\) breaks the non-malleability property of \(\mathsf {NMCOM}\).
Let \(\sigma \) denote the outcome of the check. If \(\mathcal {A} \) is honest, i.e. \(\alpha _0=\hat{\mathbf {p}}_0(x)\) and \(\beta _0^i=\hat{\mathbf {r}}_0^i(x)\), then
where
We first observe that \(\sum _{j\in \mathsf {H}}{(\mathbf {s}_j+\mathbf {s}_0^j)}=\sum _{j\in \mathsf {H}}{\hat{\mathbf {p}}_j(\hat{\mathbf {r}}_0^j+\hat{\mathbf {r}'_j})+\hat{\mathbf {p}}_0(\hat{\mathbf {r}'_0}+\hat{\mathbf {r}}_j})\) is uniform over the choice of the \(\hat{\mathbf {r}}_j,\hat{\mathbf {r}}'_j\). Therefore, if \(\mathcal {A} \) uses \(\mathbf {p}^*_\cap \) without adding \(\sum _{j\in \mathsf {H}}{(\mathbf {s}_j+\mathbf {s}_0^j)}\), the check will fail with overwhelming probability.
Since \(\mathcal {A} \) controls the inputs of the malicious parties \(i\in \mathsf {A}\), in order to pass the check it is sufficient for \(\mathcal {A} \) to satisfy the following simplification of Eq. (1).
Here \(\mathsf {const}\) is a fixed constant known to \(\mathcal {A} \) (0 if \(\mathcal {A} \) is honest) determined by setting the inputs \(\alpha _i,\beta _i\) for \(i\in \mathsf {A}\) accordingly. But if \(\alpha _0^*\ne \hat{\mathbf {p}}_0(x)\), i.e. \(\alpha _0^*=\alpha _0+e\), then we get that
Similarly for \(\beta _0^j\ne \hat{\mathbf {r}}_0^j(x)\) for any \(j\in \mathsf {H}\). Thus, except for the case of \(\alpha _0^*=\alpha _0+e/\sum _{j\in \mathsf {H}}{\beta _j}\), the check will fail for \(\alpha _0^*\ne \hat{\mathbf {p}}_0(x)\). But since we assumed that \(\mathcal {A} \) passes the check with non-negligible probability, and \(\mathsf {NMCOM}\) is statistically binding, \(\mathcal {A} \) has to produce a valid commitment to \(\tilde{\alpha }_0=\alpha _0+e/\sum _{j\in \mathsf {H}}{(\beta _j+\delta _0)}\) with the same probability.
Note, that \(\mathcal {A} \) interacts in both the left and right session of \(\mathsf {NMCOM}\) with the same party (actually all parties simultaneously, since everything is broadcast). But this means that \(\mathcal {A} \) cannot let the left session finish before starting the right session, i.e. \(\mathcal {A} \) is a synchronizing adversary against \(\mathsf {NMCOM}\). Concretely, in the left session, \(\mathcal {S}_2\) commits to \((\hat{\mathbf {p}}_j(x),\hat{\mathbf {r}}_j(x),\hat{\mathbf {r}}'_j(x))=(\alpha _j,\beta _j,\delta _j)\) for \(j\in \mathsf {H}\), while \(\mathcal {A} \) commits in the right session to \((\alpha _0,\{\beta _0^{i}\}_{i\in [n]},\delta _0)\) and \((\alpha _i,\beta _i,\delta _i)\) for \(i\in \mathsf {A}\) to \(\mathcal {S}_2\). Further, the number of sessions that \(\mathcal {A} \) can start is bounded in advance at \(n-1\), i.e. it is sufficient to consider bounded-concurrency.
Consider the two views
where \(\mathsf {com}_j\leftarrow \mathsf {NMCOM}.\mathsf {Commit}(\alpha _j,\beta _j)\) and \(\widehat{\mathsf {com}}_j\leftarrow \mathsf {NMCOM}.\mathsf {Commit}(0)\). \(\mathsf {Real}\) corresponds to a real protocol view of \(\mathcal {A} \) before committing itselfFootnote 7.
Obviously, \(\mathsf {Real}\approx _c\mathsf {Rand}\) if \(\mathsf {NMCOM}\) is non-malleable. However, we will argue that \(\mathcal {A} \) cannot output a valid commitment on \(\tilde{\alpha }_0\) except with negligible probability, i.e.
where \(\mathsf {valid}\) is the event that \(\mathsf {NMCOM}.\mathsf {Open}(\mathsf {com}^*_0,\mathsf {unv}^*_0,(\tilde{\alpha }_0,\{\tilde{\beta }_0^i\}_{i\in [n]},\delta _0)=1\). We first observe that \(\hat{\mathbf {p}}_j\) and \(\hat{\mathbf {r}}_j\) for \(j\in \mathsf {H}\) cannot be obtained by \(\mathcal {A} \) via \(\hat{\mathbf {s}}_j=\hat{\mathbf {p}}_j\cdot \hat{\mathbf {r}}_0^j-\hat{\mathbf {u}}_j\). The polynomial \(\hat{\mathbf {s}}_j\) itself is uniformly random over the choice of \(\hat{\mathbf {u}}_j\), and the only equation that \(\mathcal {A} \) has is \(\hat{\mathbf {p}}_\cap =\sum _{i\in \mathsf {A}}{(\mathbf {s}_i+\mathbf {s}_0^i)}+\sum _{j\in \mathsf {H}}{(\mathbf {s}_j+\mathbf {s}_0^j)}=\sum _{i\in \mathsf {A}}{(\hat{\mathbf {p}}_0\cdot (\hat{\mathbf {r}}_i+\hat{\mathbf {r}}'_0)+\hat{\mathbf {p}}_i\cdot (\hat{\mathbf {r}}_0^i+\hat{\mathbf {r}}'_i))}+\sum _{j\in \mathsf {H}}{(\hat{\mathbf {p}}_0\cdot (\hat{\mathbf {r}}_j+\hat{\mathbf {r}}'_0)+\hat{\mathbf {p}}_j\cdot (\hat{\mathbf {r}}_0^j+\hat{\mathbf {r}}'_j))}\). Note, that the honest \(\hat{\mathbf {r}}_j,\hat{\mathbf {r}}'_j\) have degree d and therefore hide \(\hat{\mathbf {p}}_j\). Further, the commitments \(\mathsf {com}_j\) contain the value 0 and are therefore independent of \(\hat{\mathbf {p}}_j\) and \(\hat{\mathbf {r}}_j\). Thus, the probability that \(\mathcal {A} \) obtains a commitment on \(\tilde{\alpha }_0\) is negligible.
But since \(\mathsf {Real}\approx _c\mathsf {Rand}\), we also get that
which contradicts our assumption that \(\mathcal {A} \) produces the commitment with non-negligible probability \(\epsilon \).
In conclusion, Hybrid 1 and Hybrid 2 are computationally indistinguishable. \(\square \)
Lemma 6.1.2
Assume that  provides a uniformly random x with computational security. Then Hybrid 2 and Hybrid 3 are computationally indistinguishable.
provides a uniformly random x with computational security. Then Hybrid 2 and Hybrid 3 are computationally indistinguishable.
Proof
Assume that there exists an environment \(\mathcal {Z}\) that distinguishes Hybrids 2 and 3 with non-negligible probability \(\epsilon \). In order to distinguish Hybrid 2 and Hybrid 3 \(\mathcal {Z}\) has to provide two distinct polynomials for a malicious \(P_0\) and still pass the check in the protocol. Then we can construct from \(\mathcal {Z}\) an adversary \(\mathcal {B}\) that predicts the outcome of \(\varPi ^{\text {}}_{\text {CT}}\) with non-negligible probability.
Let \(\mathcal {A} \) input w.l.o.g. two polynomials \(\hat{\mathbf {p}}_0^1\ne \hat{\mathbf {p}}_0^2\). The check with the random challenge x allows \(\mathcal {A} \) to send only one value \(\alpha _0^*\), but from Lemma 6.1.1 we know that it has to hold that \(\alpha _0^*=\hat{\mathbf {p}}_0^1(x)=\hat{\mathbf {p}}_0^2(x)\), or the check will fail. First note that two polynomials of degree \(m\) agree in a random point x over \(\mathbb {F}^{}_{}\) only with probability \(m/|\mathbb {F}^{}_{}|\), which is negligible in our case.
Our adversary \(\mathcal {B}\) proceeds as follows. It simulates the protocol for \(\mathcal {Z}\) according to \(\mathcal {S}_1\) up to the point where \(\mathcal {S}_1\) learns the polynomials \(\hat{\mathbf {p}}_0^1\ne \hat{\mathbf {p}}_0^2\). \(\mathcal {B}\) sets \(\mathbf {f}=\hat{\mathbf {p}}_0^1-\hat{\mathbf {p}}_0^2\) and computes the roots \(\gamma _1,\ldots ,\gamma _{m}\) of \(\mathbf {f}\). One of these roots has to be the random point x, otherwise \(\hat{\mathbf {p}}_0^1(x)-\hat{\mathbf {p}}_0^2(x)\ne 0\) and the check in \(\varPi ^{\text {}}_{\text {MPSI}}\) fails (since there is only one \(\alpha _0^*\)). \(\mathcal {B}\) picks a random index \(l\in [m]\) and predicts the output of the coin-flip as \(\gamma _l\). Thus, \(\mathcal {B}\) predicts the outcome of the coin-toss correctly with probability \(\epsilon /m\), which is non-negligible. This contradicts the security of \(\varPi ^{\text {}}_{\text {CT}}\).
This establishes the indistinguishability of Hybrid 2 and Hybrid 3. \(\square \)
Lemma 6.1.3
Hybrid 4 and Hybrid 5 are statistically close.
Proof
A malicious environment \(\mathcal {Z}\) can distinguish Hybrid 4 and Hybrid 5 if (a) the extracted inputs are incorrect or if (b) the simulated messages can be distinguished from real ones.
Concerning (a), if the inputs were not correctly extracted, \(\mathcal {Z}\) would receive different outputs in the two hybrids. We already established that the extracted polynomial \(\hat{\mathbf {p}}_0\) is correct. Similarly, the extracted \(\hat{\mathbf {r}}_0^j\) are also correct. By implication this also ensures that the intermediate intersection is computed correctly.
We argue that the correction of the intersection is also correct, i.e. the set \(\hat{S}^\prime _\cap \) is computed correctly and in particular it holds that \((\mathcal {M}_0(\mathbf {p}^*_\cap )\cap \mathcal {M}_0(\hat{\mathbf {p}}_j))\subseteq \hat{S}_\cap \). First of all, we have to show that the intermediate intersection polynomial \(\hat{\mathbf {p}}_\mathsf {int}\) actually provides the intersection for all parties. For all \(P_j\) it holds with overwhelming probability:

Once the intermediate intersection is computed, the adversary can only add an update polynomial \(\hat{\mathbf {p}}_\mathsf {upt}\) to get the final intersection polynomial \(\mathbf {p}^*_\cap \). It remains to show that this final intersection does not include any points that were not already in the intermediate intersection for any of the parties’ polynomials \(\hat{\mathbf {p}}_j\).
For this, we consider the intersection of every honest party’s (unknown) input \(\mathbf {p}_j\) with the intersection. It has to hold that \(\hat{S}^\prime _\cap \subseteq \hat{S}_\cap \) for all \(P_j\) except with negligible probability. Here we require that \(\Pr [x\in \mathcal {M}_0(\mathbf {p}_j)]\le \mathsf {negl}(|\mathbb {F}^{}_{}|)\) for all x, i.e. the adversary can only guess an element of \(P_j\)’s input set.

Therefore, \(\hat{S}^\prime _\cap \subseteq \hat{S}_\cap \), and the output in both hybrids is identical.
Regarding (b), we make the following observations. Since \(\mathcal {S}_4\) sends \(\hat{\mathbf {s}}_j^\prime =\hat{\mathbf {s}}_j-\mathbf {u}_j+\sum _{i\ne j}{\mathbf {v}_{ij}}\), the value \(\hat{\mathbf {s}}_j^\prime \) is uniformly random over the choice of \(\mathbf {u}_j\) (and over \(\sum {\mathbf {v}_{ij}}\), if \(t\le n-2\)). Therefore, the simulation of \(\hat{\mathbf {s}}_j^\prime \) is identically distributed to Hybrid 4.
Similarly, we have:
We can ignore the \(\mathbf {v}_{ij}\) values, since these are known to \(\mathcal {A} \). The sum is uniform over the choice of the \(\hat{\mathbf {r}}_j,\hat{\mathbf {r}}'_j\) apart from the points \(\gamma \in \hat{S}_\cap \) (since  guarantees that \(\hat{p}_0\ne 0\)) and therefore identically distributed to Hybrid 5, since the extraction in correct.
guarantees that \(\hat{p}_0\ne 0\)) and therefore identically distributed to Hybrid 5, since the extraction in correct.
\(\square \)
-
\(P_0\) is honest: The proof itself is very similar to the proof of a corrupted \(P_0\). It is actually easier to simulate in the sense that \(\mathcal {S}_{\bar{P}_0}\) observes the inputs of all malicious parties. In this sense, \(\varPi ^{\text {}}_{\text {MPSI}}\) actually realises \(\mathcal {F}^{\text {}}_{\text {MPSI}}\) if \(P_0\) is honest, since no adjustment of the output is necessary. We refer to the full version [15] of the paper for the proof.
Efficiency. The setup, i.e. the distribution of seeds, has communication complexity \(O(n^2\kappa )\). The oblivious addition of the polynomials has communication overhead of \(O(nm\kappa )\). The check phase first requires a multi-party coin-toss.
In the full version of this paper [15], we sketch a coin-tossing protocol in combination with an OLE-based commitment scheme (replacing the non-malleable commitment for better efficiency) that results in an asymptotic communication overhead of \(O(n^2\kappa )\) for the check and the coin-toss phase. Combining this with the above observations, \(\varPi ^{\text {}}_{\text {MPSI}}\) has communication complexity \(O((n^2+nm)\kappa )\) in the  -hybrid model.
-hybrid model.
For concrete instantiations of  , the OLE protocol of Ghosh et al. [14] has a constant communication overhead per OLE. In summary, the complete protocol has communication complexity \(O((n^2+nm)\kappa )\), which is asymptotically optimal for \(m\ge n\).
, the OLE protocol of Ghosh et al. [14] has a constant communication overhead per OLE. In summary, the complete protocol has communication complexity \(O((n^2+nm)\kappa )\), which is asymptotically optimal for \(m\ge n\).
Similar to the two-party case, the computational cost is dominated by the cost of polynomial interpolation. In particular, the central party has to run the two-party protocol n times, which leads to a computational overhead of \(O(n m\log m)\) multiplications. The other parties basically have the same computational overhead as in the two-party case. \(\square \)
7 Performance Analysis
In this section, we give an estimation of the communication efficiency with concrete parameters and provide a comparison with existing results. For this, we simply count the number of field elements that have to be sent for the protocols. We first look at the communication overhead of the OLE primitive. Instantiated with the result by Ghosh et al. [14], each OLE has an overhead of 64 field elements including OT extension (32 without), which translates to 256 field elements per item per OPA. The factor 4 stems from the fact that OPA needs 2d OLE to compute a degree d output, and OLE+ requires two OLE per instance.
2-party PSI. To get a feeling for the concrete communication efficiency of our two-party protocol, we compare it with the recent maliciously UC-secure protocols from [36]. These protocols give only one-sided output, whereas our protocol gives two-sided output. However, OPA is sufficient for one-sided PSI, consequently a one-sided PSI would cost 256 field elements per item in our case.
Table 2 clearly shows that the communication overhead of our protocol is significantly less than the standard model (SM) protocol from [36]. Note that our instantiation is also secure in SM, given \(O(\kappa )\) base OTs. Like [36] we use the OT-extension protocol from [31] for the instantiation. Even if we compare our result to the ROM approach of [36], we achieve fairly competitive communication efficiency.
One should consider that in the ROM there exist other PSI protocols with linear communication complexity [8, 23]. The concrete bandwidth of those protocols are much less than our specific instantiation, for example for sets of \(2^{20}\) elements the total communication cost of [8] is about 213 MBFootnote 8. Further [23] has lower bandwidth than [8]. However, in both the cases communication efficiency comes at the cost of huge computational expenses due to lots of public key operations. We believe that the simple field arithmetic of our protocols (including the cost of the OLE of [14]) does not incur such a drawback in practice.
Multi-party PSI. To the best of our knowledge, there are currently no maliciously secure MPSI implementations with which we could compare our result. A direct comparison with the passively secure MPSI from [27], however, directly shows the difference in asymptotic behaviour to our result. Their communication costs per party increase with the number of parties, whereas it remains constant in our case (except for the central party). If we average over all parties, the central party’s overhead can be distributed over all parties, which at most doubles the average communication cost per party (cf. Table 3). We can upper bound the communication cost per party by 2.5 GB for \(2^{20}\) elements (excluding the cost for OT extension in order to get comparable results to [27]). From the table we can deduce that with only 6 parties, our actively secure protocol is more efficient than their passive one. Replacing the actively secure OPA in our MPSI protocol with the passively secure one yields a passively secure MPSI protocol. We gain another factor of 2 in communication efficiency and our construction is more efficient than [27] starting from 4 parties.
Notes
- 1.
Please see the full version of the paper [15].
- 2.
- 3.
Since this check leaks some information about the inputs, we have to perform the check in a secure manner.
- 4.
Our multi-party PSI functionality uses similar idea as augmented semi-honest multi-party PSI as in previous works [27].
- 5.
The commitment we implicitly use has been used previously in [11], as has the check sub-protocol.
- 6.
In order to achieve our claimed efficiency we actually use UC commitments, but non-malleable commitments are sufficient for the security of the protocol.
- 7.
For ease of notation, here we assume that the commitments are completely sent before \(\mathcal {A} \) commits himself. The very same argument also holds if \(\mathcal {A} \) only received synchronized messages of \(\mathsf {com}_j\) and has to start committing concurrently.
- 8.
For reference see Figure 8 of [36].
References
Applebaum, B., Damgård, I., Ishai, Y., Nielsen, M., Zichron, L.: Secure arithmetic computation with constant computational overhead. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 223–254. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_8
Ben-Sasson, E., Fehr, S., Ostrovsky, R.: Near-linear unconditionally-secure multiparty computation with a dishonest minority. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 663–680. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_39
Borodin, A., Moenck, R.: Fast modular transforms. J. Comput. Syst. Sci. 8(3), 366–386 (1974). http://dx.doi.org/10.1016/S0022-0000(74)80029-2
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145. IEEE Computer Society Press, October 2001
Cheon, J.H., Jarecki, S., Seo, J.H.: Multi-party privacy-preserving set intersection with quasi-linear complexity. IEICE Trans. 95–A(8), 1366–1378 (2012)
Cramer, R., Damgård, I., Ishai, Y.: Share conversion, pseudorandom secret-sharing and applications to secure computation. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 342–362. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_19
Dachman-Soled, D., Malkin, T., Raykova, M., Yung, M.: Efficient robust private set intersection. In: Abdalla, M., Pointcheval, D., Fouque, P.-A., Vergnaud, D. (eds.) ACNS 2009. LNCS, vol. 5536, pp. 125–142. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01957-9_8
De Cristofaro, E., Kim, J., Tsudik, G.: Linear-complexity private set intersection protocols secure in malicious model. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 213–231. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_13
De Cristofaro, E., Tsudik, G.: Practical private set intersection protocols with linear complexity. In: Sion, R. (ed.) FC 2010. LNCS, vol. 6052, pp. 143–159. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14577-3_13
Dong, C., Chen, L., Wen, Z.: When private set intersection meets big data: an efficient and scalable protocol. In: Sadeghi, A.R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, pp. 789–800. ACM Press, November 2013
Döttling, N., Ghosh, S., Nielsen, J.B., Nilges, T., Trifiletti, R.: TinyOLE: efficient actively secure two-party computation from oblivious linear function evaluation. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 2017, pp. 2263–2276. ACM Press, October/November 2017
Freedman, M.J., Hazay, C., Nissim, K., Pinkas, B.: Efficient set intersection with simulation-based security. J. Cryptol. 29(1), 115–155 (2016)
Freedman, M.J., Nissim, K., Pinkas, B.: Efficient private matching and set intersection. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 1–19. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_1
Ghosh, S., Nielsen, J.B., Nilges, T.: Maliciously secure oblivious linear function evaluation with constant overhead. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 629–659. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_22
Ghosh, S., Nilges, T.: An algebraic approach to maliciously secure private set intersection. Cryptology ePrint Archive, Report 2017/1064 (2017). https://eprint.iacr.org/2017/1064
Hallgren, P.A., Orlandi, C., Sabelfeld, A.: Privatepool: privacy-preserving ridesharing. In: 30th IEEE Computer Security Foundations Symposium, CSF 2017, 21–25 August 2017, Santa Barbara, CA, USA, pp. 276–291 (2017)
Hazay, C.: Oblivious polynomial evaluation and secure set-intersection from algebraic PRFs. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 90–120. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_4
Hazay, C., Nissim, K.: Efficient set operations in the presence of malicious adversaries. J. Cryptol. 25(3), 383–433 (2012)
Hazay, C., Venkitasubramaniam, M.: Scalable multi-party private set-intersection. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10174, pp. 175–203. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54365-8_8
Huang, Y., Evans, D., Katz, J.: Private set intersection: are garbled circuits better than custom protocols? In: NDSS 2012. The Internet Society, February 2012
Huberman, B.A., Franklin, M., Hogg, T.: Enhancing privacy and trust in electronic communities. In: Proceedings of the 1st ACM Conference on Electronic Commerce, EC 1999, pp. 78–86 (1999)
Ishai, Y., Prabhakaran, M., Sahai, A.: Secure arithmetic computation with no honest majority. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 294–314. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_18
Jarecki, S., Liu, X.: Fast secure computation of set intersection. In: Garay, J.A., De Prisco, R. (eds.) SCN 2010. LNCS, vol. 6280, pp. 418–435. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15317-4_26
Kamara, S., Mohassel, P., Raykova, M., Sadeghian, S.: Scaling private set intersection to billion-element sets. In: Christin, N., Safavi-Naini, R. (eds.) FC 2014. LNCS, vol. 8437, pp. 195–215. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45472-5_13
Kissner, L., Song, D.: Privacy-preserving set operations. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 241–257. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_15
Kolesnikov, V., Kumaresan, R., Rosulek, M., Trieu, N.: Efficient batched oblivious PRF with applications to private set intersection. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 818–829. ACM Press, October 2016
Kolesnikov, V., Matania, N., Pinkas, B., Rosulek, M., Trieu, N.: Practical multi-party private set intersection from symmetric-key techniques. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 2017, pp. 1257–1272. ACM Press, October/November 2017
Meadows, C., Mutchler, D.: Matching secrets in the absence of a continuously available trusted authority. IEEE Trans. Softw. Eng. SE-13(2), 289–292 (1987)
Naor, M., Pinkas, B., Sumner, R.: Privacy preserving auctions and mechanism design. In: EC, pp. 129–139 (1999)
Narayanan, A., Thiagarajan, N., Lakhani, M., Hamburg, M., Boneh, D.: Location privacy via private proximity testing. In: NDSS 2011. The Internet Society, February 2011
Orrù, M., Orsini, E., Scholl, P.: Actively secure 1-out-of-N OT extension with application to private set intersection. In: Handschuh, H. (ed.) CT-RSA 2017. LNCS, vol. 10159, pp. 381–396. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-52153-4_22
Pinkas, B., Schneider, T., Segev, G., Zohner, M.: Phasing: private set intersection using permutation-based hashing. In: 24th USENIX Security Symposium, USENIX Security 2015, 12–14 August 2015, Washington, D.C., USA, pp. 515–530 (2015)
Pinkas, B., Schneider, T., Zohner, M.: Faster private set intersection based on OT extension. In: Proceedings of the 23rd USENIX Security Symposium, 20–22 August 2014, San Diego, CA, USA, pp. 797–812 (2014)
Pinkas, B., Schneider, T., Zohner, M.: Scalable private set intersection based on OT extension. ACM Trans. Priv. Secur. 21(2), 7:1–7:35 (2018)
Rindal, P., Rosulek, M.: Improved private set intersection against malicious adversaries. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 235–259. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_9
Rindal, P., Rosulek, M.: Malicious-secure private set intersection via dual execution. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 2017, pp. 1229–1242. ACM Press, October/November 2017
Sang, Y., Shen, H.: Privacy preserving set intersection based on bilinear groups. In: Proceedings of the Thirty-First Australasian Conference on Computer Science, ACSC 2008, vol. 74. pp. 47–54 (2008)
Shamir, A.: On the power of commutativity in cryptography. In: de Bakker, J., van Leeuwen, J. (eds.) ICALP 1980. LNCS, vol. 85, pp. 582–595. Springer, Heidelberg (1980). https://doi.org/10.1007/3-540-10003-2_100
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Ghosh, S., Nilges, T. (2019). An Algebraic Approach to Maliciously Secure Private Set Intersection. In: Ishai, Y., Rijmen, V. (eds) Advances in Cryptology – EUROCRYPT 2019. EUROCRYPT 2019. Lecture Notes in Computer Science(), vol 11478. Springer, Cham. https://doi.org/10.1007/978-3-030-17659-4_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-17659-4_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17658-7
Online ISBN: 978-3-030-17659-4
eBook Packages: Computer ScienceComputer Science (R0)



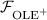


 in the
in the  -hybrid model.
-hybrid model.

 in the (
in the ( ,
,  )-hybrid model.
)-hybrid model.

 -hybrid model.
-hybrid model.
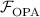 , learns all inputs and aborts if
, learns all inputs and aborts if 

 -hybrid model.
-hybrid model.
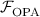 and learns all inputs.
and learns all inputs.