Fractional Chaotic System Solutions and Their Impact on Chaotic Behaviour

Abstract

This paper is devoted to the analysis of calculation methods for solving fractional chaotic systems and the impact of these different approaches on the behavior of the fractional chaotic system. Two widely used time domain fractional differential equations solving approaches are discussed, the fractional ABM corrector-predictor method based on Caputo fractional derivative definition, and the long memory calculation approach based on Grunwald fractional derivative. These numerical solutions calculation methods are employed to depict the phase portrait of a class of commensurate fractional chaotic systems. The Lyapunov exponent and bifurcation diagrams of the systems over various fractional orders and parameters are illustrated to detect the impact on the dynamics of the chaotic system applying different calculation approaches.

1 Introduction

Chaos is a random-like behavior exhibited by many nonlinear dynamic systems. The very first proponent of this topic can be dated back to 1880 while the three body problem was studied [1]. Eighty years later, when Edward Lorenz worked on weather prediction, the so-called ’Lorenz attractor’ was found [2]. By giving it a description and a poetic name of ’butterfly effect’, the gate of the mathematical and scientific world in Chaos was opened. Since then, many researchers have tried to uncover the deterministic laws behind the apparently random states of disorder of different chaotic systems.

One of the characteristics of the chaotic system is that it is very sensitive to the initial conditions as described by the butterfly effect. This sensitivity can be measured by Lyapunov Exponent(LE) which calculates the rate of exponential divergence of trajectories starting from two close initial conditions. This characteristic also contributes to the application of chaotic systems in many domains of science and engineering, such as biology [3], economics [4], finance [5], cryptography [6, 7] and etc.

In the meantime, fractional calculus is considered as the generalization of classical integer-order integration and differentiation operators to real, or complex orders [8]. Many mathematicians have discussed the fractional calculus since 1695 by introducing different mathematical characterisations (definitions) for fractional derivative and integration. In many cases, these characterisations are equivalent if the initial conditions are ad hoc [9], and the most well known three are Rienmann-Liouville(RL), Grunwald-Letnikov(GL), and Caputo characterisations.

The analysis and discussion of fractional calculus remained purely in the domain of mathematics for centuries. It was not until the 1980s that the application of fractional calculus in the domain of science and engineering has started to be studied and explored. Due to the memory effect possessed by fractional calculus, it is considered to be suitable to model many real-life systems. After years of research, the fractional differential equations have now been used in diverse disciplines like physics, biology, economics, etc. [10, 11].

The fractional chaotic system also attracts a lot of attention. The difficulties for this research owes to the intricate geometric interpretation of fractional derivatives [12] and the fact that there exist, as mentioned above, different definitions for fractional derivatives. One basically considers continuous systems, and uses numerical methods to approximate the solution. In the case of a fractional system, the discrete approximating system may inherit the chaotic behaviour of the initial continuous system, but this relationship is somehow complex. What adds to the intricacy is that the chaotic behavior of the approximating can be different for different numerical methods employed to solve the fractional differential equations [13]. Therefore, the understanding of the impact on the chaoticity of the system applying one or another numerical calculation approaches is of great importance, in order to choose the most appropriate one for a given application.

In the following, two numerical calculation methods under GL and Caputo characterisation for fractional differential equations are recalled. Then, we employ both methods to obtain the states of two fractional chaotic systems extended from classical integer order chaotic system. The impact on the chaoticity of the systems applying the two approaches has been analyzed in terms of LE and from the aspect of bifurcation diagram and time responses.

2 Preliminaries on Fractional Calculus and Fractional Systems

In this section, some preliminaries on fractional calculus and fractional systems are introduced to give a rough idea on the topic. The widely-accepted stability criteria for a commensurate fractional system is also illustrated.

2.1 Fractional Calculus

As mentioned before, the fractional calculus studies the fractional derivative and integral which can be considered as the extension of classical integer order differentiation and integration to real or complex orders. In the long history of the study of fractional calculus, many mathematicians have contributed and introduced different characterisations(referred as ‘definitions’ in many papers) towards the topic. Here after, we give two well-known definitions Grünwald-Letnikov (GL) and Caputo definitions [14, 15].

The fractional derivatives under GL characterisation can be writen as

$$\begin{aligned} _aD_t^\alpha f(t) = \lim _{h\rightarrow 0}\frac{1}{h^\alpha }\sum _{j=0}^{[\frac{t-a}{h}]} (-1)^j \genfrac(){0.0pt}0{\alpha }{j} f(t-jh) \end{aligned}$$

(1)

The term $[\frac{t-a}{h}]$ in (1) stands for the integer part of $\frac{t-a}{h}$; a and t are the bounds of the derivative operation $_aD_t^\alpha$ for f(t); $\alpha$ represents the fractional derivative order. The term $\genfrac(){0.0pt}1{\alpha }{j}$ in (1) is defined in (2), where $\varGamma (.)$ is the Euler Gamma function in the form of (3).

$$\begin{aligned} \left( \begin{array}{c} \alpha \\ j \end{array} \right) = \frac{{\varGamma (\alpha + 1)}}{{\varGamma (j + 1)\varGamma (\alpha - j + 1)}} \end{aligned}$$

(2)

$$\begin{aligned} \varGamma \left( \alpha \right) = \int \limits _0^\infty {\frac{{{t^{\alpha - 1}}}}{{{e^t}}}dt} \end{aligned}$$

(3)

The Caputo type fractional derivative holds the form as following,

$$\begin{aligned} _a^cD_t^\alpha f(t) = \frac{1}{\varGamma (n-\alpha )}\int \limits _a^t \frac{f^{(n)}(\tau )}{(t-\tau )^{\alpha -n+1}} d\tau , \text{ for } n-1<\alpha <n \end{aligned}$$

(4)

where $\alpha$ denotes the fractional derivative order; a and t are the bounds for the operation; n is the smallest integer greater than $\alpha$; $\varGamma (.)$ is the Euler Gamma function in (3); and $f^{(n)}(t)$ is the n-th derivative of f(t).

The Caputo type fractional derivative is often used for engineering application since the fractional differential equations with this type of derivative can provide the applied problem with an interpretable initial condition.

2.2 Fractional System

A fractional system is a dynamic system which can be modeled by fractional differential equations [16]. A general form of fractional system is as follows,

$$\begin{aligned} \begin{array}{*{20}{l}} _0D_{^t}^{{\alpha _i}}{x_i}\left( t \right) = {f_i}\left( {{x_1}\left( t \right) ,{x_2}\left( t \right) ,...,{x_n}\left( t \right) ,t} \right) \\ \mathrm{{ }}{x_i}\left( 0 \right) = {c_i},i = 1,2,...,n. \end{array} \end{aligned}$$

(5)

In (5), $x_i(0)(i=1,2,...n)$ denotes the initial conditions for each component constituting the state vectors; $\alpha _i(i = 1,2,...n)$ is the fractional derivative order for i-th differential equations consisting the system, and $f_i$ is a linear or non-linear function.

The equilibrium points of system (5) can be obtained by solving the equation $f_i(x)=0(i=1,2,...,n)$. If a commensurate system with $\alpha _i=\alpha ,i=1,2,...,n$ is considered, then, according to the stability theorem defined in [17], the equilibrium points are locally asymptotically stable if the eigenvalue of the Jacobian matrix of system (5) satisfies the following equation evaluated at equilibria.

$$\begin{aligned} \left| {\mathrm{{arg}}\left( {\mathrm{{eig}}\left( {{\mathrm{{J}}}} \right) } \right) } \right| = \left| {\mathrm{{arg}}\left( {{\lambda _i}} \right) } \right| > {\alpha }\frac{\pi }{2}, i = 1,2,...,n \end{aligned}$$

(6)

where $\mathrm{{J}}$ denotes the Jacobian matrix of (5), $\lambda _i(i=1,2,...n)$ are its eigenvalues.

3 Numerical Calculation Methods for Fractional Differential Equations

In this section, two numerical solutions calculation methods for fractional differential equations are introduced. The methods are based on Gr${\ddot{u}}$nwald-Letnikov and Caputo fractional derivative characterisations.

3.1 Gr$\ddot{u}$nwald-Letnikov Calculation Method

The explicit numerical approximation of q-th derivative under GL characterisation at the points $kh,(h = 1,2,...)$ is expressed as follows [14]

$$\begin{aligned} _{(k - {L_m})/h}D_{{t_k}}^\alpha f(t) \approx {h^{ - \alpha }}\sum \limits _{j = 0}^k {{{( - 1)}^j}} \left( \begin{array}{c} \alpha \\ j \end{array} \right) f({t_{k - j}}). \end{aligned}$$

(7)

In expression (7), $L_m$ is the memory length; $t_k = kh$, where h is the calculation time step; the binomial coefficient $(-1)^{j} \genfrac(){0.0pt}1{\alpha }{j}$ can be denoted as $c_j^{(\alpha )}(j=0,1,...)$ which is expressed using the following expression [18],

$$\begin{aligned} c_{0}^{(\alpha )}=1, c_{j}^{(\alpha )} =\left( 1-\frac{1+\alpha }{j}\right) c_{j-1}^{(\alpha )}. \end{aligned}$$

(8)

Thus, the general numerical solution of the fractional differential equation described by (9) can be expressed as given in (10).

$$\begin{aligned} _{a}D_{t}^{\alpha }y(t)=f(y(t),t) \end{aligned}$$

(9)

$$\begin{aligned} y(t_{k}) = f(y(t_{k}),t_{k})h^{\alpha }-\sum _{j=\nu }^{k}c_{j}^{(\alpha )}y(t_{k-j})) \end{aligned}$$

(10)

The sum in (10) stands for the memory term. If a ’long memory effect’ is considered, then the lower index $\nu = 1$ for all k, otherwise $\nu =1$ for $k<(L_{m}/h)$ and $\nu = k-L_{m}$ for $k>(L_{m}/h)$.

3.2 Fractional ABM Corrector-Predictor Method

The fractional ABM corrector-predictor method is another widely used time domain numerical calculation method in the domain of engineering. It is a generalization of the classical Adams-Bashforth-Moulton integrator which is used for the numerical calculation of classical first order problem.

From the analytical point of view, the fractional differential equations under Caputo characterization with initial conditions $y^{k}(0) = y^k_0, k = 0,1,2...m-1$ where $m:=\lceil \alpha \rceil$, is equivalent to Volterra integral equation expressed as follows,

$$\begin{aligned} y(x) = \sum _{k=0}^{\lceil \alpha \rceil -1}y_0^{(k)} \frac{x^k}{k!}+\frac{1}{\varGamma (\alpha )}\int \limits _0^x(x-t)^{\alpha -1}f(t,y(t))dt \end{aligned}$$

(11)

The algorithm is developed on a uniform grid $\{t_n=nh:n=0,1,...N\}$. The basic idea of the algorithm is to obtain the approximation of the latter point on the grid from the former point. Detailed formula derivation for the algorithm can be found in [19]. Here, we only give out the derived equations for the next states values in (12)–(15).

$$\begin{aligned} {\begin{matrix} y_h(t_{n+1})=&{}\sum _{k=0}^{\lceil \alpha \rceil -1}\frac{t_{n+1}^k}{k!}y_0^{(k)}+\frac{h^\alpha }{\varGamma (\alpha +2)}f(t_{n+1},y_h^P(t_{n+1}))\\ &{}+\frac{h^\alpha }{\varGamma (\alpha +2)}\sum _{j=0}^n a_{j,n+1}f(t_j,y_h(t_j)), \end{matrix}} \end{aligned}$$

(12)

$$\begin{aligned} y_h^P(t_{n+1})=\sum _{k=0}^{\lceil \alpha \rceil -1}\frac{t_{n+1}^k}{k!}y_0^{(k)} + \frac{1}{\varGamma (\alpha )}\sum _{j=0}^nb_{j,n+1}f(t_j,y_h(t_j)). \end{aligned}$$

(13)

$$\begin{aligned} a_{j,{n+1}} = {\left\{ \begin{array}{ll} n^{\alpha +1}-(n-\alpha )(n+1)^\alpha ,&{}\text{ if } j = 0, \\ (n-j+2)^{\alpha +1}+(n-j)^{\alpha +1}-2(n-j+1)^{\alpha +1},&{}\text{ if } 1\le j\le n,\\ 1, &{}\text{ if } j=n+1. \end{array}\right. } \end{aligned}$$

(14)

$$\begin{aligned} b_{j,n+1} =\frac{h^\alpha }{\alpha }((n+1-j)^\alpha -(n-j)^\alpha ) \end{aligned}$$

(15)

In the above equations, $y_h(t_{n+1})$ stands for the next state, $y_h^P(t_{n+1})$ denotes the predictor value for the next state, a and b are coefficients.

4 Fractional Chaotic Chen and Lu Systems

4.1 Fractional Chaotic Chen Systems

The system equation for fractional Chen system can be expressed as following[20],

$$\begin{aligned} {f_c}\left( x \right) = \left\{ \begin{array}{l} {D^{{\alpha _c}}}{x_1}\left( t \right) = {a_c}\left( {{x_2}\left( t \right) - {x_1}\left( t \right) } \right) \\ {D^{{\alpha _c}}}{x_2}\left( t \right) = \left( {{c_c} - {a_c}} \right) {x_1}\left( t \right) - {x_1}\left( t \right) {x_3}\left( t \right) + {c_c}{x_2}\left( t \right) \\ {D^{{\alpha _c}}}{x_3}\left( t \right) = {x_1}\left( t \right) {x_2}\left( t \right) - {b_c}{x_3}\left( t \right) \end{array} \right. \end{aligned}$$

(16)

In the equation, $D^{\alpha _c}$ denotes the fractional derivative with order $\alpha _c$, $(a_c$, $b_c$, $c_c)$ are the parameters of the system. The system is an extension from integer order chaotic Chen system studied in [21].

The equilibria of the system can be obtained through the same way as its original integer order system, by setting the right-hand side system equation equal to zero ${f_c}\left( {{x^*}} \right) = 0$ as given below,

$$\begin{aligned} \left\{ \begin{array}{l} {a_c}\left( {{x_2}\left( t \right) - {x_1}\left( t \right) } \right) =0\\ \left( {{c_c} - {a_c}} \right) {x_1}\left( t \right) - {x_1}\left( t \right) {x_3}\left( t \right) + {c_c}{x_2}\left( t \right) =0\\ {x_1}\left( t \right) {x_2}\left( t \right) - {b_c}{x_3}\left( t \right) =0 \end{array} \right. \end{aligned}$$

(17)

The singularity of the equilibrium points can also be acquired through the classical method as given below, by evaluating the eigenvalue of the jacobian matrix of the system at equilibrium points.

$$\begin{aligned} \mathrm{{det}}\left( {{\lambda _c}\mathrm{{I - }}{\mathrm{{J}}_c}} \right) = \left[ {\begin{array}{*{20}{c}} {{\lambda _c} + {a_c}}&{}{ - {a_c}}&{}0\\ { - {c_l} + {a_l} + x_3^*}&{}{{\lambda _c} - {c_c}}&{}{x_1^*}\\ { - x_2^*}&{}{ - x_1^*}&{}{{\lambda _c} + {b_c}} \end{array}} \right] = 0 \end{aligned}$$

(18)

$\mathrm {J}_c$ in (18) represents the Jacobian matrix of the system equation, $\mathrm {I}$ is the identity matrix, $\lambda _c$ denotes the eigenvalue, and $(x_1^*,x_2^*,x_3^*)$ stands for the equilibrium point.

The singularity of the three equilibrium points of fractional Chen system for system parameters $(a_c, b_c, c_c)=(35, 3, 28)$ can be obtained through above analytical expressions and are given in Table 1.

4.2 Fractional Chaotic Lu System

The system equation for fractional chaotic Lu system extended from integer order Lu system can be described as follows [22],

$$\begin{aligned} {f_l}\left( x \right) = \left\{ \begin{array}{l} {D^{{\alpha _l}}}{x_1}\left( t \right) = a_l\left( {{x_2}\left( t \right) - {x_1}\left( t \right) } \right) \\ {D^{{\alpha _l}}}{x_2}\left( t \right) = - {x_1}\left( t \right) {x_3}\left( t \right) + c_l{x_2}\left( t \right) \\ {D^{{\alpha _l}}}{x_3}\left( t \right) = {x_1}\left( t \right) {x_2}\left( t \right) - b_l{x_3}\left( t \right) \end{array} \right. \end{aligned}$$

(19)

where $D^{\alpha _l}$ denotes the fractional derivative with order $\alpha _l$, $a_l$, $b_l$, and $c_l$ are the parameters of the system. The equilibrium points of the system can be acquired calculating the solutions of the following system of equations,

$$\begin{aligned} \left\{ \begin{array}{l} {a_l}\left( {{x_2}\left( t \right) - {x_1}\left( t \right) } \right) =0\\ -{x_1}\left( t \right) {x_3}\left( t \right) {x_1}\left( t \right) + {c_l}{x_2}\left( t \right) =0\\ {x_1}\left( t \right) {x_2}\left( t \right) - {b_l}{x_3}\left( t \right) =0 \end{array} \right. \end{aligned}$$

(20)

The singularity of the equilibria can be obtained the same way as discussed previously for the fractional Chen system through the following identities,

$$\begin{aligned} \mathrm{{det}}\left( {{\lambda _l}\mathrm{{I - }}{\mathrm{{J}}_l}} \right) \mathrm{{ }} = \left[ {\begin{array}{*{20}{c}} {{\lambda _l} + {a_l}}&{}{ - {a_l}}&{}0\\ {x_3^*}&{}{{\lambda _l} - {c_c}}&{}{x_1^*}\\ { - x_2^*}&{}{ - x_1^*}&{}{{\lambda _l} + {b_l}} \end{array}} \right] = 0 \end{aligned}$$

(21)

where $\mathrm {J}_l$ in (21) represents the Jacobian matrix of the fractional Lu system, $\lambda _l$ denotes the eigenvalue, and $(x_1^*,x_2^*,x_3^*)$ stands for the equilibrium point. When the parameters of the system is set to $(a_c, b_c, c_c)=(36, 3, 20)$, three equilibrium points $E_1^* = (0,0,0)$, $E_2^* = (7.460,7.460,20)$ and $E_3^*=(-7.460,-7.460,20)$ can be obtained applying (20). The singularity of the equilibria is also given in Table 1.

Table 1 Fractional Chen and Lu systems’ equilibria and their singularity

5 Solutions for the Chaotic Systems Applying Different Approaches

In this section, the solutions for fractional Chen and Lu solutions are obtained applying both GL method and fractional ABM corrector-predictor method discussed in Sect. 3. The impact of the two approaches on the chaotic behavior of the systems are also discussed.

5.1 Chaotic System Applying GL Method

With the numerical solution of fractional differential equation calculated under GL method derived as in (10), the calculation for the states of fractional Chen system and fractional Lu system (expression (16) and (19)) can be expressed by the following identities (22) and (23), respectively.

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{x_1}(n) = (a_c({x_2}(n) - {x_1}(n - 1))){h^{{\alpha _c}}} - \sum \limits _{j = \nu }^n {c_j^{({\alpha _c})}} {x_1}(n - j)}\\ {{x_2}(n) = ((c_c - a_c){x_1}(n) - {x_1}(n){x_3}(n - 1) + c_c{x_3}(n - 1)){h^{{\alpha _c}}} - \sum \limits _{j = \nu }^n {c_j^{({\alpha _c})}} {x_2}(n - j)}\\ {{x_3}(n) = ({x_1}(n){x_2}(n) - b_c{x_3}(n - 1)){h^{{\alpha _c}}} - \sum \limits _{j = \nu }^n {c_j^{({\alpha _c})}} {x_3}(n - j)} \end{array}}\right. \end{aligned}$$

(22)

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{x_1}(n) = (a_l({x_2}(n - 1) - {x_1}(n - 1))){h^{{\alpha _l}}} - \sum \limits _{j = \nu }^n {c_j^{({\alpha _l})}} {x_1}(n - j)}\\ {{x_2}(n) = ( - {x_1}(n){x_3}(n - 1) + c_l{x_2}(n - 1)){h^{{\alpha _l}}} - \sum \limits _{j = \nu }^n {c_j^{({\alpha _l})}} {x_2}(n - j)}\\ {{x_3}(n) = ({x_1}(n){x_2}(n) - b_l{x_3}(n - 1)){h^{{\alpha _l}}} - \sum \limits _{j =\nu }^n {c_j^{({\alpha _l})}} {x_3}(n - j)} \end{array}} \right. \end{aligned}$$

(23)

To be mentioned is that in our work, the ’long memory effect’ is adopted applying GL method which means that the number $\nu$ in (22) and (23) is equal to 1. The time step h in the above equations is set to a fixed value 0.001.

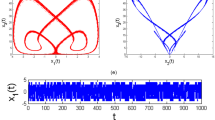
We plotted the phase portraits of the two systems with fractional orders $\alpha _c=0.9$ and $\alpha _l=0.95$ in Fig. 1a and b, respectively. The parameters and initial conditions for Chen system are (35, 3, 28) and $(-9,-5,14)$. Those of Lu system are chosen to be (36, 3, 20) and (0.2, 0.5, 0.3).

Fig. 1

Phase portrait of fractional Chen and Lu systems characterized by GL and ABM method

5.2 Chaotic Systems Applying ABM Corrector-Predictor Approach

Based on the fractional ABM corrector-predictor numerical calculation approach for the solution of fractional differential equations given in (12)–(15), the states of fractional Chen system applying ABM predictor corrector approach can be expressed as follows,

$$\begin{aligned} \begin{array}{ll} {{\mathrm {X}}_c}(n + 1) &{}= {{\mathrm {X}}_c}(0) + \frac{h^{\alpha _c}}{\varGamma (\alpha _c + 2)}f_c( {\mathop {\mathrm{X}}\nolimits }_{c}^{P}(n + 1))\\ &{} \quad + \frac{{{h^{{\alpha _c}}}}}{{\varGamma \left( {{\alpha _c} + 2} \right) }}\sum \limits _{j = 0}^n {{a_{j,n + 1}}f_c\left( {{{\mathrm {X}}_c}\left( j \right) } \right) } \end{array} \end{aligned}$$

(24)

$$\begin{aligned} \mathrm{{X}}_c^P\left( {n + 1} \right) = {\mathrm{{X}}_c}\left( 0 \right) + \frac{1}{{\varGamma \left( {{\alpha _c}} \right) }}\sum \limits _{j = 0}^n {b_{j,n+1}^1} f_c\left( {{\mathrm{{X}}_c}\left( j \right) } \right) \end{aligned}$$

$$\begin{aligned} \begin{aligned}&{a_{j,n + 1}} = \left\{ {\begin{array}{*{20}{l}} {{n^{{\alpha _c} + 1}} - (n - {\alpha _c}){{(n + 1)}^{{\alpha _c}}},}&{}{\mathrm{{if }}\;j = 0,}\\ {{{(n - j + 2)}^{{\alpha _c} + 1}} + {{(n - j)}^{{\alpha _c} + 1}} - 2{{(n - j + 1)}^{{\alpha _c} + 1}},}&{}{\mathrm{{if }}\;1 \le j \le n,}\\ {1,}&{}{\mathrm{{if }}\;j = n + 1.} \end{array}} \right. \\&{b_{j,l + 1}} = \frac{{{h^{{\alpha _c}}}}}{{{\alpha _c}}}({(n + 1 - j)^{{\alpha _c}}} - {(n - j)^{{\alpha _c}}}) \end{aligned} \end{aligned}$$

(25)

In the above expressions, $\mathrm{{X}}_c(n+1)$, $\mathrm{{X}}_c(n)$ and $\mathrm{{X}}_c^{P}(n+1)$ are state vectors composed of all the state components $x_1$, $x_2$, and $x_3$; $\alpha _c$ is the fractional order between (0, 1); $f_c$ stands for the Chen system equations.

The formula for the calculation of the states of fractional Lu system can be obtained by substituting the state vectors, fractional order and system equations in (24)–(25) with $\mathrm{{X}}_l$, $\alpha _l$ and $f_l$ where $0<\alpha _l<1$. The phase portraits of the two systems acquired employing the corrector-predictor approach are given in Fig. 1c and d, respectively. The fractional orders, parameters and initial conditions are the same as those for the GL method.

5.3 Impact on System Chaoticity with Chosen Methods

For the work in this section, we used the same parameters and initial conditions for the two systems as adopted in the previous section, which are $(a_c,b_c,c_c) = (35,3,28)$, $\mathrm{X}_c(0) = (-9,-5,14)$; $(a_l,b_l,c_l) = (36,3,20)$, $\mathrm{X}_l(0) = (0.2,0.5,0.3)$, respectively. The time step h is set to 0.005. The MATLAB code [23] for ABM corrector-predictor method and [24] is employed for the following simulation and the calculation of LE.

According to the stability criteria introduced by the inequality (6) , the reference [17] states that for a fractional system $D^\alpha x=f(x)$ to remain chaotic, a necessary condition is keeping the eigenvalues $\lambda$ in the unstable region, which gives the following equation for the fractional derivative order $\alpha$.

$$\begin{aligned} \alpha >\frac{2}{\pi }\tan ^{-1}\left( \frac{|Im(\lambda )|}{Re(\lambda )}\right) \end{aligned}$$

(26)

where $\lambda$ denotes the eigenvalues of the Jacobian matrix of the system, $\alpha$ is the commensurate fractional order. Therefore, for the given parameter values, the fractional chaotic Chen system should have a fractional order $\alpha _c$ greater than or equal to 0.8244.

Fig. 2

Phase portrait and time response of Chen system at boundary fractional order values

In Fig. 2, we plot the phase portrait of fractional Chen system at boundary fractional values 0.82 and 0.83 applying both GL and ABM corrector-predictor methods. The time response of the last 2000 states obtained through both methods are also given. The states calculated by GL method is in red and ABM corrector-predictor in blue. It is not difficult to observe from Fig. 2a and c that with order 0.82 there are only one red point in the figure, which indicates that the states stay at the same fixed point applying GL method. Whereas for the applied ABM method(blue dots), they appear to have the shape of the attractors. When the system order is equal to 0.83, both methods display the shapes with attractors. This indicates that when applying GL calculation method with long memory effect, the system’s dynamic behavior is in accordance with the stability criteria given by equation (26). While the ABM calculation method applied in this paper provides the system with a smaller derivative order for the system to be

The time response figures given by Fig. 2b and d confirm the founding. The blue curve stands for the states obtain through ABM method and red for GL. It is clear that for derivative order 0.82, the red attractors stays at the same value for the three state vector components $x_1,x_2$ and $x_3$, while the blue curves appear to be oscillating.

Fig. 3

LE and bifurcation results for Chen and Lu systems over different fractional derivatives employing different methods $(a_c,b_c,c_c) = (35,3,28)$, $(a_l,b_l,c_l) = (36,3,20)$

Fig. 4

LE and bifurcation results for Chen and Lu systems over different fractional parameters employing different methods

We also give the Lyapunov exponent and bifurcation diagrams over different fractional orders of fractional Chen and Lu systems in Fig. 3. For each fractional derivative orders, $10^4$ states were generated and the LEs were calculated throughout the iterations. The LE spectrum curves in 3a and 3b are obtained by combining LE values of the last iteration for every evaluated order. The plots show that only $x_1$ component possesses LE value greater than 0 applying both methods. It can be observed that applying ABM corrector-predictor approach, for the fractional Chen system, the LE of $x_1$ greater than 0 appears before order 0.53, whereas for GL method, the LE exceeds 0 after fractional order of 0.8. The LEs for fractional Lu system calculated using both methods show the similar results, with ABM method having a smaller chaotic fractional derivative value. This is in accordance with our previous findings concerning the phase portrait and time response which draws to the conclusion that GL method give a more accurate approximation of original fractional system. Apart from this, from the y-coordinates of the bifurcation diagram where the system is non-chaotic, it can be observed that the solution obtained using ABM method stays at the equilibrium point as obtained through analytical analysis.

The LEs results and bifurcation diagram over different parameters of the fractional Lu system are also given in Fig. 4 to illustrate the dynamics possessed by the system. We set the system fractional order fixed to 0.9. It can be observed that applying different numerical calculation methods, the system dynamics is quite different. It is worth mentioning that the results for different parameters are conducted by changing one parameter at a time and fixing the other two unchanged.

6 Conclusion

In this paper, we recalled two numerical solutions calculation methods for fractional differential equations adopting Gr$\ddot{u}$nward-Leinikov and Caputo characterization of fractional derivative, respectively. Two fractional chaotic systems, fractional Chen system and fractional Lu system are discussed and their discretized states were calculated employing both methods. The results show that compared to the adopted ABM corrector-predictor method, the GL approach with long memory effect provide the original fractional system with a better approximation in coherence with the analytical studies. On the contrary, employing ABM method, the approximation accuracy appears to be deteriorated. However, in terms of chaoticity, it has a greater chaotic range for fractional derivatives.