Keywords

1 Introduction

The problems of elastic kinematic chains may be divided into two categories: problems concerning the mechanism in which one or more components are elastic ones, or problems dealing with platforms hanged by elastic kinematic chains. In the first situation, researchers study the case of two flexible elements linked one to another by different kinematic linkages, develop some numerical algorithms, and then apply the theory to a four-bar mechanism [1]. In the case of a simple mechanism, like the crank-shaft one, they [2] start from the second-order Lagrange equations and use a multibody approach. The analysis of the rigidity of kinematic chains in a particular case of manipulator for a platform is made in [3], while the case of a platform with elastic elements in kinematic chains is discussed in [4]. For a Stewart platform, one may consider that linkages are flexible, and use the Kane equations and principle of virtual work in order to perform the kinematic analysis and, by linearization of the moving equations, one may deduce the small oscillations of a satellite [5]. For the case of a double platform with flexible kinematic linkages, in Ref. [6] the authors performed the static analysis and proved that the rigidity of the manipulator depends on its position. The study of the mobile platforms may be realized using different algorithms [7], or writing special programs [8]. Pandrea [9] underlay the study of the mechanism and kinematic chains in plückerian coordinates and developed the corresponding linear elastic calculation in the screw coordinates.

2 Mechanical System

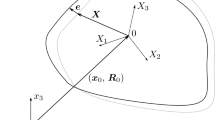
One considers the rigid \(AB\) (Fig. 1) hanged by the kinematic chains \(AC_{1} D_{1}\) and \(AC_{2} D_{2}\), each kinematic chain consisting of two elastic bars \(AC_{1}\), \(C_{1} D_{1}\), and \(BC_{2}\), \(C_{2} D_{2}\), respectively. The kinematic linkages at the points \(C_{1}\) and \(C_{2}\) are cylindrical ones. We attach the reference system \(Cxyz\) to the rigid \(AB\) and the reference frames \(C_{1} x_{1} y_{1} z_{1}\) and \(C_{2} x_{2} y_{2} z_{2}\) as in Fig. 1. One knows the dimensions \(l\) and \(a\), and the mechanical and geometric properties of each bar. The rigid \(AB\) is acted by the forces \({\mathbf{P}}\), which are parallel to the \(Cx\)-axis. The requirements are the study of the free and forced vibrations of the rigid \(AB\) in two cases: each kinematic chain is elastic, and the \(BC_{2} D_{2}\) kinematic chain is rigid.

Fig. 1.
figure 1

Mechanical model.

Full size image

3 Rigidity Matrix

We calculate:

  • rotational matrices of the systems \(C_{i} x_{i} y_{i} z_{i}\) with respect to the reference system \(Cxyz\) \(\left[ {{\mathbf{R}}_{1} } \right] = \left[ {{\mathbf{R}}_{2} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ 0 & 1 & 0 \\ { - 1} & 0 & 0 \\ \end{array} } \right]\);

  • the matrices \(\left[ {{\mathbf{G}}_{Ci} } \right] = \left[ {\begin{array}{*{20}c} 0 & { - Z_{{C_{i} }} } & {Y_{{C_{i} }} } \\ {Z_{{C_{i} }} } & 0 & { - X_{{C_{i} }} } \\ { - Y_{{C_{i} }} } & {X_{{C_{i} }} } & 0 \\ \end{array} } \right]\), where \(X_{{C_{i} }}\), \(Y_{{C_{i} }}\), \(Z_{{C_{i} }}\) are the coordinates of the point \(C_{i}\), \(i = \overline{{1,{ 2}}}\), with respect to the reference frame \(Cxyz\);

  • the matrices \(\left[ {{\mathbf{T}}_{Ci} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {{\mathbf{R}}_{i} } \right]} & {\left[ {\mathbf{0}} \right]} \\ {\left[ {{\mathbf{G}}_{Ci} } \right]} & {\left[ {{\mathbf{R}}_{i} } \right]} \\ \end{array} } \right]\), \(\left[ {{\mathbf{T}}_{Ci} } \right]^{ - 1} = \left[ {\begin{array}{*{20}c} {\left[ {{\mathbf{R}}_{i} } \right]^{{\text{T}}} } & {\left[ {\mathbf{0}} \right]} \\ {\left[ {{\mathbf{R}}_{i} } \right]^{{\text{T}}} \left[ {{\mathbf{G}}_{Ci} } \right]^{{\text{T}}} } & {\left[ {{\mathbf{R}}_{i} } \right]^{{\text{T}}} } \\ \end{array} } \right]\), \(i = \overline{{1,{ 2}}}\);

  • the column matrices of the linkages at \(C_{1}\) and \(C_{2}\) relative to the \(C_{1} x_{1} y_{1} z_{1}\) and \(C_{2} x_{2} y_{2} z_{2}\) systems, \(\left\{ {{\mathbf{u}}_{{C_{1} }} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} } \right]^{{\text{T}}}\), and \(\left\{ {{\mathbf{u}}_{{C_{2} }} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{{\text{T}}}\), respectively;

  • the column matrices of the plückerian coordinates of the linkages at points \(C_{i}\), \(i = \overline{{1,{ 2}}}\), relative to the \(Cxyz\) reference system \(\left\{ {{\mathbf{U}}_{{C_{i} }} } \right\} = \left[ {{\mathbf{T}}_{{C_{i} }} } \right]\left\{ {{\mathbf{u}}_{{C_{i} }} } \right\}\), \(i = \overline{{1,{ 2}}}\);

  • the rigidity matrices of each kinematic chain (\(i = \overline{{1,{ 2}}}\)), relative to the \(C_{i} x_{i} y_{i} z_{i}\) reference system

    $$\left[ {{\mathbf{k}}_{i} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {\frac{{E_{i} A_{i} }}{l}} & 0 & 0 \\ 0 & 0 & {\frac{{6E_{i} I_{{z_{i} }} }}{{l^{2} }}} & 0 & {\frac{{12E_{i} I_{{z_{i} }} }}{{l^{3} }}} & 0 \\ 0 & {\frac{{6E_{i} I_{{y_{i} }} }}{{l^{2} }}} & 0 & 0 & 0 & {\frac{{12E_{i} I_{{y_{i} }} }}{{l^{3} }}} \\ {\frac{{G_{i} I_{{x_{i} }} }}{l}} & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{{4E_{i} I_{{y_{i} }} }}{l}} & 0 & 0 & 0 & { - \frac{{6E_{i} I_{{y_{i} }} }}{{l^{2} }}} \\ 0 & 0 & {\frac{{4E_{i} I_{{z_{i} }} }}{l}} & 0 & {\frac{{6E_{i} I_{{z_{i} }} }}{{l^{2} }}} & 0 \\ \end{array} } \right];$$
    (1)

  • the rigidity matrices of each kinematic chain, \(i = \overline{{1,{ 2}}}\), relative to the \(Cxyz\) reference system \(\left\{ {{\mathbf{K}}_{i} } \right\} = \left[ {{\mathbf{T}}_{{C_{i} }} } \right]\left[ {{\mathbf{k}}_{i} } \right]\left[ {{\mathbf{T}}_{{C_{i} }} } \right]^{ - 1}\).

4 Case of Elastic Kinematic Chains

In this situation, the rigidity matrix of the system reads

$$\left[ {\mathbf{K}} \right] = \left[ {{\mathbf{K}}_{1} } \right] + \left[ {{\mathbf{K}}_{2} } \right].$$
(2)

Denoting the inertial matrix of the rigid \(AB\) by \(\left[ {\mathbf{M}} \right]\),

$$\left[ {\mathbf{M}} \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & m & 0 & 0 \\ 0 & 0 & 0 & 0 & m & 0 \\ 0 & 0 & 0 & 0 & 0 & m \\ {J_{x} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {J_{y} } & 0 & 0 & 0 & 0 \\ 0 & 0 & {J_{z} } & 0 & 0 & 0 \\ \end{array} } \right],$$
(3)

the column matrix of the displacements of the point \(C\) by \(\left\{ {{\varvec{\Delta}}} \right\}\),

$$\left\{ {{\varvec{\Delta}}} \right\} = \left[ {\begin{array}{*{20}c} {\theta_{X} } & {\theta_{Y} } & {\theta_{Z} } & {\delta_{X} } & {\delta_{Y} } & {\delta_{Z} } \\ \end{array} } \right]^{{\text{T}}} ,$$
(4)

one obtains the matrix equation of the free vibration as

$$\left[ {\mathbf{M}} \right]\left\{ {{\mathbf{{\Delta }}}} \right\} + \left[ {\mathbf{K}} \right]\left\{ {{\varvec{\Delta}}} \right\} = \left\{ {\mathbf{0}} \right\}.$$
(5)

If the expression of force \({\mathbf{P}}\) is \({\mathbf{P}} = {\mathbf{P}}_{0} \cos \left( {\omega t + \varphi } \right){\mathbf{i}}\), where \({\mathbf{i}}\) is the unit vector of the \(Cx\) direction, then the column matrix of the forces reads

$$\left\{ {\mathbf{F}} \right\} = \left[ {\begin{array}{*{20}c} {P_{0} \cos \left( {\omega t + \varphi } \right)} & 0 & 0 & 0 & 0 & {aP_{0} \cos \left( {\omega t + \varphi } \right)} \\ \end{array} } \right]^{{\text{T}}} ,$$

while the matrix equation of the forced vibrations is

$$\left[ {\mathbf{M}} \right]\left\{ {{\mathbf{{\Delta }}}} \right\} + \left[ {\mathbf{K}} \right]\left\{ {{\varvec{\Delta}}} \right\} = \left\{ {\mathbf{F}} \right\}.$$
(6)

5 Case of a Rigid Kinematic Chain

In this situation, we denote by \(\left\{ {{{\varvec{\upxi}}}_{{C_{2} }} } \right\}\) the matrix of possible displacement in the linkage at the point \(C_{2}\).

The equation of the free vibrations takes the from

$$\left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}^{{\text{T}}} \left[ {{\varvec{\upeta}}} \right]\left[ {\mathbf{M}} \right]\left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}\left\{ {{\mathbf{{\xi }}}_{{C_{2} }} } \right\} + \left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}^{{\text{T}}} \left[ {{\varvec{\upeta}}} \right]\left[ {{\mathbf{K}}_{1} } \right]\left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}\left\{ {{{\varvec{\upxi}}}_{{C_{2} }} } \right\} = \left\{ {\mathbf{0}} \right\}.$$
(7)

Taking into account that \(\left\{ {{{\varvec{\upxi}}}_{{C_{2} }} } \right\} = \left[ {\begin{array}{*{20}c} 0 & {\tau_{Y} } & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{{\text{T}}}\) and performing the calculations required by Eq. (7), one gets

$$\left( {ml^{2} + J_{Y} } \right)\ddot{\tau }_{Y} + \frac{{4E_{1} I_{{y_{1} }} }}{l}\tau_{Y} = 0,$$
(8)

that is, a periodical motion in the form \(\tau_{Y} = \tau_{{Y_{0} }} \cos \left( {\omega_{0} t + \varphi_{0} } \right)\), where

$$\omega_{0} = \sqrt {\frac{{4E_{1} I_{{y_{1} }} }}{{\left( {ml^{2} + J_{Y} } \right)l}}} ,$$
(9)

while \(\tau_{{Y_{0} }}\) and \(\varphi_{0}\) are constants obtained from the initial conditions.

In the case of the forced vibrations, we have the equation

$$\left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}^{{\text{T}}} \left[ {{\varvec{\upeta}}} \right]\left[ {\mathbf{M}} \right]\left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}\left\{ {{\mathbf{{\xi }}}_{{C_{2} }} } \right\} + \left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}^{{\text{T}}} \left[ {{\varvec{\upeta}}} \right]\left[ {{\mathbf{K}}_{1} } \right]\left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}\left\{ {{{\varvec{\upxi}}}_{{C_{2} }} } \right\} = \left\{ {{\mathbf{U}}_{{C_{2} }} } \right\}^{{\text{T}}} \left[ {{\varvec{\upeta}}} \right]\left\{ {\mathbf{F}} \right\},$$
(10)

where

$$\left\{ {\mathbf{F}} \right\} = \left[ {\begin{array}{*{20}c} {P_{0} \cos \left( {\omega t + \varphi } \right)} & 0 & 0 & 0 & 0 & {2aP_{0} \cos \left( {\omega t + \varphi } \right)} \\ \end{array} } \right]^{{\text{T}}} .$$
(11)

It results in the equation

$$\left( {ml^{2} + J_{Y} } \right)\ddot{\tau }_{Y} + \frac{{4E_{1} I_{{y_{1} }} }}{l}\tau_{Y} = P_{0} l\cos \left( {\omega t + \varphi } \right).$$
(12)

The square matrix \(\left[ {{\varvec{\upeta}}} \right]\) is given by

$$\left[ {{\varvec{\upeta}}} \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} } \right].$$
(13)

6 Numerical Example

In this section, we will consider six cases. The following values are common for all cases: \(E_{1} = E_{2} = 2.1 \times 10^{11} \, {{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{m}}^{{2}} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{{2}} }}\), \(G_{1} = G_{2} = 8.1 \times 10^{10} \, {{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{m}}^{{2}} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{{2}} }}\), \(l = 0.2{\text{ m}}\), \(a = 0.2{\text{ m}}\), \(m = 50{\text{ kg}}\), \(r = 0.1{\text{ m}}\) (the radius of the rigid \(AB\) considered as a homogeneous bar), \(\omega = 20 \, {{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\), \(\varphi = 0{\text{ rad}}\), \(t_{\max } = 3{\text{ s}}\) (the interval of simulations), the bars of the kinematic chains are homogeneous. For the first, the third, and the fifth case, one has \(P = 0{\text{ N}}\) (free vibration), while for the second, the fourth, and the sixth case \(P = 1000{\text{ N}}\) (force vibrations). The first and the second case are characterized by \(d_{1} = 0.005{\text{ m}}\) (the diameter of the bars of the first kinematic chain), \(d_{2} = 0.005{\text{ m}}\) (the diameter of the bars of the second kinematic chain), the force \(P = 0{\text{ N}}\), while the initial conditions are: \(\theta_{X} = 0.002{\text{ rad}}\), \(\theta_{Y} = - 0.001{\text{ rad}}\), \(\theta_{Z} = 0.001{\text{ rad}}\), \(\delta_{X} = 0.001{\text{ m}}\), \(\delta_{Y} = 0.002{\text{ m}}\), \(\delta_{Z} = -0.001{\text{ m}}\), \(\dot{\theta }_{X} = \dot{\theta }_{Y} = \dot{\theta }_{Z} = 0 \, {{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\), \(\dot{\delta }_{X} = \dot{\delta }_{Y} = \dot{\delta }_{Z} = 0 \, {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\). For the third and the fourth case, we consider \(d_{1} = 0.010{\text{ m}}\), and \(d_{2} = 0.005{\text{ m}}\), while for the fifth and the second case \(d_{1} = 0.005{\text{ m}}\), \(d_{2} = 0.005{\text{ m}}\). The initial conditions for the second, the third, and the fourth case are the same as in the first case, while for the fifth and the sixth case, the initial conditions are: \(\tau_{Y} = 0.002{\text{ rad}}\), \(\dot{\tau }_{Y} = 0 \, {{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\). The results are captured in the next figures (Figs. 2, 3, 4, 5, 6, and 7). In all figures \(\theta_{X}\) and \(\delta_{X}\) were drawn in blue, \(\theta_{Y}\) and \(\delta_{Y}\) were drawn in green, while \(\theta_{Z}\) and \(\delta_{Z}\) were drawn in red. The reader may easily observe the periodicity of the free and forced vibrations in all cases. In the first four cases, the variable \(\delta_{Z}\) presents a transitory period in which the amplitude decreases, after this period, the oscillations being periodical.

Fig. 2.
figure 2

Time histories in the first case.

Full size image
Fig. 3.
figure 3

Time histories in the second case.

Full size image
Fig. 4.
figure 4

Time histories in the third case.

Full size image
Fig. 5.
figure 5

Time histories in the fourth case.

Full size image
Fig. 6.
figure 6

Time histories in the fifth case.

Full size image
Fig. 7.
figure 7

Time histories in the sixth case.

Full size image

In the fifth and the sixth case, the amplitudes of the parameters \(\theta_{X}\), \(\theta_{Z}\), \(\delta_{Y}\), and \(\delta_{Z}\) are equal to zero.

It results that when the two kinematic chains are elastic, then the vibration of the rigid \(AB\) is a complex one, the motion having non-zero components. In the case when a kinematic chain is a rigid one, the dynamics of the rigid simplifies and consists only in a rotational motion about the \(Y\)-axis, and a translational one along the \(X\) axis. The same observation concerning the diminishing of the amplitude of vibrations may be also stated in the third and fourth case when the bars which compound the first kinematic chain have greater rigidities.

7 Conclusions

This paper deals with the study of the dynamics of the rigid hanged by two elastic kinematic chains or hanged by an elastic kinematic chain and a rigid kinematic chain. In both situations, we determined the rigidity matrix of the system and the equations of the free and forced vibration.

The numerical results prove that in the case when both kinematic chains are elastic, the dynamics of the rigid simplifies, remaining periodic

In many cases, the platforms are acted by asymmetric loads resulting in different reactions in the legs; consequently, the legs may have different rigidities. In this way, it is possible that one leg has a rigidity much greater than the other ones. It results that the flexibility matrix that corresponds to the kinematic chain assigned to that leg may be neglected compared to the flexibility matrices of the rest of the kinematic chain and, consequently, the flexibility matrix of the system may be calculated only as a function of the flexibility matrices of the rest of the kinematic chains. The results obtained using this approach are different from those obtained using the approach proposed in this paper. Our model considers that the hanged rigid solid with one rigid kinematic chain has a constrained motion; hence the model may be generalized to systems with more general constraints and kinematic chains.

In our future studies, we will consider more complicated cases of the mechanical system with one rigid kinematic chain and several elastic kinematic chains with different acting forces, and we will discuss their dynamics. Greater attention will be paid to the platforms, especially the Stewart ones.