1 Introduction

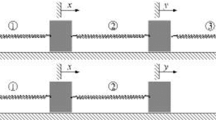
Although conservative chain structured multibody oscillators seem to be quite simple, they are valuable for describing a wide variety of mechanical systems. For example, layered soil above a bedrock exposed to dynamic loads resulting from e. g. earthquakes is modelled by means of such linear vibration chains, see e. g. [3, 11] and Fig. 1.

Besides these apparent applications, the determination of both eigenfrequencies and eigenvectors is of general interest in both civil engineering and mechanical engineering, as these characterise the dynamical behaviour of the respective structure. As the eigenfrequencies and eigenvectors (that is, eigenmodes/mode shapes and eigenforces) are calculated numerically in most cases, the respective computer programs should have a known performance, i. e. accuracy, in determining the eigenfrequencies and eigenvectors. Thus, there is a need for structures having known eigenfrequencies and eigenvectors, which may serve as reference solutions to computer programs.

Fig. 1
figure 1

Idealisation of a soil column by means of an undamped vibration chain

Full size image

In general, a linear undamped vibration system with n degrees of freedom (dof) can be described by [1]

$$\begin{aligned} \mathbf {M} \ddot{\mathbf{x}} (t) + \mathbf {K} \mathbf {x} (t) = \mathbf {0}. \end{aligned}$$

Herein \(\mathbf {M}\) and \(\mathbf {K}\) denote the mass and stiffness matrix, \(\mathbf {x} (t)\) denotes the vector of the time-dependent displacements. For the linear vibration chain depicted in Fig. 1, these matrices take the form

$$\begin{aligned} \mathbf {M}&= \text {diag} \left( m_i \right) , \nonumber \\ \mathbf {K}&= \text {diag} \left\{ \left( k_1 + k_2, \, -k_2 \right) , \, \ldots \, , \, \left( -k_{i}, \, k_i + k_{i+1}, \, -k_{i+1} \right) , \, \ldots \, , \, \left( -k_n, \, k_n \right) \right\} . \end{aligned}$$
(1)

In this contribution, a special distribution of the single masses and stiffnesses is used, which was originally suggested by Mikota [7]. There, the masses and stiffness coefficients are chosen as

$$\begin{aligned} {m_{i}} = \frac{1}{i} m \quad \text {and} \quad {k_{i}} = \left( n - i + 1 \right) k \quad \text {where} \quad i = 1, \, 2, \, \ldots \, , \, n; \quad n \in \mathbb {N}. \end{aligned}$$
(2)

Herein k denotes the stiffness of the last spring, whereas m is the mass assigned to the first dof. If the number of dof of the vibration chain is increased from n to \(n+1\), then the mass \(m_{n+1} = m/\left( n+1\right) \) is added at the \(\left( n+1\right) \)-th dof, whereas the other masses remain unchanged. As can readily be seen from Eq. (2), for increasing dof the stiffnesses \(k_{i}\) of the system with n dof possess the same value as the stiffnesses \(k_{i+1}\) of Mikota’s oscillator with \(n+1\) dof. Thus, for the enlarged vibration chain, a new stiffness \(k_1 = \left( n +1 \right) k\) is attached to the first dof, while the stiffnesses of the former vibration chain having n dof simply change their positions from the i-th dof to the \(\left( i+1\right) \)-th dof, see [12]. Due to this counter pattern in assembling the mass matrix \(\mathbf {M}\) and the stiffness matrix \(\mathbf {K}\), established analytical methods to analyse eigenvalue problems for arbitrary n dof as given in e. g. [1] are not suitable here for obtaining closed form solutions. The vibration chains investigated in [5] do possess other structures than Mikota’s oscillator. Consequently, the analytical procedures given in [5] cannot be applied either. Of course, numerical procedures allow for calculating the eigenvalues and eigenvectors of the dynamical system investigated here. However, they give neither major insights for arbitrary n dof nor closed form solutions. Thus, an analytical approach is desired and will be conducted in this contribution.

The specific undamped vibration chain at hand was firstly introduced by Mikota [7]. Mikota conjectured that this vibration chain has the eigenfrequencies

$$\begin{aligned} \Omega _l = l \Omega \quad \text {with} \quad l = 1, \, 2, \, \ldots \, n; \quad n \in \mathbb {N}, \end{aligned}$$
(3)

where \(\Omega = \sqrt{k/m}\) is the first eigenfrequency. Two proofs of Mikota’s conjecture concerning the eigenfrequencies are given in [8, 12] and a sketch of the second proof is given in [14]. In [12], it could be shown that by increasing the dof from n to \(n+1\), the known n-tuple of the eigenvalues \(\left( \lambda _1, \, \lambda _2, \, \ldots \, , \, \lambda _n \right) \) is enlarged only by one new eigenvalue \(\lambda _{n+1}\), that is

$$\begin{aligned} \left( \lambda _1, \, \lambda _2, \, \ldots \, , \, \lambda _n \right) \longrightarrow \left( \lambda _1, \, \lambda _2, \, \ldots \, , \, \lambda _n, \, \lambda _{n+1} \right) , \end{aligned}$$

whereas all other eigenvalues remain the same.

Some results concerning the eigenvectors were presented in [8, 13]. In [8], both left- and right-eigenvectors are calculated by means of a recursion. In [13], the calculation is done by means of polynomials. However, both contributions focus on the numerical calculation rather than the evolution of the eigenvectors with increasing n dof. Thus, the investigation of the structure of the eigenvectors of this special vibration chain is still open and the task of this paper.

The outline of this contribution is as follows: in Sect. 2, explicit formulae are found for calculating the coordinates of the first two mode shapes of Mikota’s oscillator. Based on these insights, a proof of the formulae describing the remaining \(n-2\) mode shapes is provided. Often, the first l modes shapes and eigenforces (with \(l \le n\)) are of particular interest in engineering practice. This is taken into account by providing formulae allowing for the successive calculation of these eigenvectors. Thus, the calculations can be completed, once l is reached. The relation between the mode shapes (the right-eigenvectors) and eigenforces (associated to the left-eigenvectors) is shown in Sect. 3. It is revealed that the mode shapes of Mikota’s oscillator are (partly) orthogonal to each other with respect to the standard scalar product. The applicability of the suggested approach for determining the sought mode shapes is shown exemplarily in Sect. 4. A summary and conclusions are given in Sect. 5.

2 Structure of the mode shapes

2.1 Involved matrices

By means of the ansatz \(\mathbf {x} (t) = \bar{\mathbf {x}}_l \exp \{\imath \Omega _l t\}\), where \(\imath \) is the imaginary unit and \(\Omega _l\) denotes the circular frequency, the eigenvalue problem of the undamped vibration chain emerges to

$$\begin{aligned} \left( \mathbf {M}^{-1} \mathbf {K} - \Omega _l^2 \mathbf {I} \right) \bar{\mathbf {x}}_l = \left( \mathbf {M}^{-1} \mathbf {K} - \lambda _l \Omega ^2 \mathbf {I} \right) \bar{\mathbf {x}}_l = \mathbf {0}, \quad \lambda _l \Omega ^2 := \Omega _l^2 \end{aligned}$$
(4)

with the identity matrix \(\mathbf {I}\) and the eigenvalues \(\lambda _l := \Omega _l^2/\Omega ^2\) of to the (dimensionless) matrix \(\mathbf {A}:=\mathbf {M}^{-1} \mathbf {K}/\Omega ^2\). Typically, the eigenfrequencies \(\Omega _l\) would be determined numerically [4, 10]. However, in [8, 12], Mikota’s conjecture is proved and thus the eigenfrequencies can be identified analytically as given with Eq. (3). Hence, the eigenvalues are known as well and thus, in this contribution, focus is set on the eigenvectors. Within the next steps, the matrix

$$\begin{aligned} \mathbf {A}\!:=\!\frac{1}{\Omega ^2} \mathbf {M}^{-1}\mathbf {K} \! = \! \begin{bmatrix} 1 \left( 2n - 1 \right)&\quad 1 \left( -n + 1 \right)&&\\ 2 \left( -n + 1 \right)&\quad 2 \left( 2n - 3 \right)&\quad 2 \left( -n + 2 \right)&&\\ \qquad \ddots&&\quad \ddots&\\&\!\!\! \ddots&\quad \left( i - 1 \right) \left( -n + i - 1 \right)&\\&\!\!\! i \left( -n + i - 1 \right)&\quad i \left( 2n - 2i + 1 \right) \phantom {\ddots }&\quad i \left( -n + i \right)&\\&&\quad \! \left( i + 1 \right) \left( -n + i \right)&\quad \ddots&\\&&\quad \ddots&\\&&\quad \ddots&\quad \ddots \\&&\quad \!\!\! n \left( -1\right)&\quad n \cdot 1 \end{bmatrix} \end{aligned}$$
(5)

arising from the eigenvalue problem in Eq. (4) is looked at. Again, \(\Omega =\sqrt{k/m}\) holds. Within each matrix element in Eq. (5), the first factor of each product corresponds to the inverse mass matrix \(\mathbf {M}^{-1}\), whereas the second factor belongs to the stiffness matrix \(\mathbf {K}\). As can readily be seen, the number n of dof occurs in each non-vanishing matrix element of \(\mathbf {A}\). As \(\mathbf {M}\) is real, symmetric, and positive definite and \(\mathbf {K}\) is real and symmetric, there exist n left- and n right-eigenvectors, which are real, too. In engineering practice, the right-eigenvectors are more common, as they give the so-called eigenmodes or mode shapes and thus the characteristic displacements of the vibrating structure. In what follows, the right-eigenvector is given the notation \(\mathbf {u}_l\), where the subscript l equals the number of the eigenvalue \(\lambda _l = l^2\) this right-eigenvector corresponds to. In detail, it is

$$\begin{aligned} \left( \mathbf {K} - \lambda _l \Omega ^2 \mathbf {M}\right) \mathbf {u}_l = \mathbf {0} \Longleftrightarrow \mathbf {A} \mathbf {u}_l = \lambda _l \mathbf {u}_l. \end{aligned}$$
(6)

The left-eigenvectors give useful insights into the forces associated with the respective displacements. Consequently, the left-eigenvectors are denoted as \(\mathbf {f}_l\) throughout this contribution. They can be determined using

$$\begin{aligned} \mathbf {f}_l^{{\text{ T }}} \mathbf {M}^{-1} \left( \mathbf {K} - {\lambda }_l {\Omega }^2 \mathbf {M}\right) = 0 \Longleftrightarrow \mathbf {f}_{l}^{{\text{ T }}} \mathbf {A} = {\lambda }_l \mathbf {f}_l^{{\text{ T }}}. \end{aligned}$$
(7)

For the eigenforces \(\hat{\mathbf {f}}_l\)

$$\begin{aligned} \hat{\mathbf {f}}_l = \Omega _l^2 \mathbf {f}_l \end{aligned}$$
(8)

holds, cf. [2].

2.2 Mode shape to the first eigenvalue \(\lambda _1 = 1\)

In this section, the mode shape \(\mathbf {u}_{l=1} = \left( u_{1,1}, \, u_{2,1}, \, \ldots \, , u_{i,1}, \, \ldots \, , u_{n,1} \right) ^{{\text{ T }}}\) to the first eigenvalue \(\lambda _1\) is determined. Herein, the first subscript of \(u_{i,l}\) denotes the coordinate index of the vector, whereas the second subscript indicates the number of the eigenvalue that the vector corresponds to. According to [6], the coordinates of the (right-)eigenvectors can be calculated by means of polynomials. For the present case, the coordinates of \(\mathbf {u}_1\) are assumed to be given by means of the polynomial \(p_1 (i)\) of order 1 in the coordinate index i

$$\begin{aligned} u_{i,1} = p_1 (i) = i \quad \text {with} \quad i = 1, \, 2, \, \ldots \, , \, n ; \quad n \in \mathbb {N} \end{aligned}$$
(9)

and multiples of it. In detail, evaluating row \(r=i\) of Eq. (6) with respect to Eq. (5) results in

$$\begin{aligned} i \left( -n + i-1 \right) u_{i-1,1} + i \left( 2n - 2i + 1 \right) u_{i,1} + i \left( -n+i\right) u_{i+1,1}&= 1 u_{i,1}. \end{aligned}$$

Inserting Eq. (9) for the coordinates yields

$$\begin{aligned} \underset{=i}{\underbrace{ i \left( -n + i-1 \right) \left( i-1\right) + i \left( 2n - 2i + 1 \right) i + i \left( -n+i\right) \left( i+1\right) }}&= 1 i \end{aligned}$$

and confirms the assumption.

2.3 Mode shape to the second eigenvalue \(\lambda _2 = 4\)

Concerning the polynomial \(p_2 (i)\) in the coordinate index i giving the coordinates of the right-eigenvector \(\mathbf {u}_2\) to the eigenvalue \(\lambda _2\), the ansatz

$$\begin{aligned} u_{i,2} = p_2 (i) = d_2 i^2 + d_1 i + d_0 \quad \text {with} \quad i = 1, \, 2, \, \ldots \, , \, n ; \quad n \in \mathbb {N} \end{aligned}$$

is made. Inserting this ansatz into Eq. (6) and evaluating its first row by means of Eq. (5) give

$$\begin{aligned} \left[ d_2 1^2 + d_1 1 + d_0\right] 1 \left( 2n-1\right) +\left[ d_2 4 + d_1 2 + d_0\right] 1 \left( -n+1\right) = 4 \left[ d_2 1^2 + d_1 1 + d_0\right] , \end{aligned}$$

where terms relating to the right-eigenvector are written in square brackets for the sake of clarity. Simplifying yields

$$\begin{aligned} d_2 \left( -2n - 1\right) = 3 d_1 + d_0 \left( 4-n\right) . \end{aligned}$$
(10)

The i-th row of Eq. (6) gives

$$\begin{aligned} \left[ d_2 \left( i-1\right) ^2 + d_1 \left( i-1\right) + d_0\right] i \left( -n+i-1\right) + \left[ d_2 i^2 + d_1 i + d_0\right]&i \left( 2n - 2i + 1 \right) \nonumber \\ + \ldots + \left[ d_2 \left( i+1\right) ^2 + d_1 \left( i+1\right) + d_0\right] i \left( -n+i\right)&= 4 \left[ d_2 i^2 + d_1 i + d_0\right] \nonumber \\ d_2 \left( -2n - 1\right)&= 3 d_1 + 4 d_0. \end{aligned}$$
(11)

Both conditions (10), (11) can only be true for \(d_0 = 0\). Consequently, \(d_1 = \left[ \left( -2n - 1\right) /3\right] d_2\). As a multiple of a (right-)eigenvector fulfils Eq. (6), too,

$$\begin{aligned} d_2 = 1, \quad d_1 = \frac{\left( -2n - 1\right) }{3}\quad d_2 = -\frac{\left( 2n + 1\right) }{3} \end{aligned}$$

is set. Then, the coordinates of a right-eigenvector \(\mathbf {u}_2\) to the eigenvalue \(\lambda _2\) can be calculated by means of the polynomial \(p_2 (i)\) of order 2 in the coordinate index i

$$\begin{aligned} u_{i,2} = p_2 (i) = i^2 -\frac{\left( 2n + 1\right) }{3} i, \quad n \ge 2. \end{aligned}$$
(12)

2.4 Structure of the remaining \(n-2\) mode shapes

According to [6], the coordinates of the eigenvectors can be described by polynomials in the coordinate i. With respect to Sects. 2.2 and 2.3, it is assumed that the respective polynomial for the mode shape \(\mathbf {u}_l\) corresponding to the l-th eigenvalue \(\lambda _l = l^2\) is of order l. Herein, \(1 \le l \le n\) holds. Then, each mode shape \(\mathbf {u}_l\) may be expressed as a linear combination of vectors containing the powers of the coordinate indices of the eigenvector

$$\begin{aligned} \mathbf {u}_l&= \left( \begin{array}{c} u_{1,l}\\ u_{2,l}\\ u_{3,l}\\ \vdots \\ u_{n,l} \end{array}\right) = \underset{\mathbf {Y}_l}{\underbrace{\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1^1 &{} 1^2 &{} 1^3 &{} \ldots &{} 1^l \\ 2^1 &{} 2^2 &{} 2^3 &{} \ldots &{} 2^l \\ 3^1 &{} 3^2 &{} 3^3 &{} \ldots &{} 3^l \\ \vdots &{} \vdots &{} \vdots &{} \ldots &{} \vdots \\ n^1 &{} n^2 &{} n^3 &{} \ldots &{} n^l \end{array}\right] }} \underset{\mathbf {c}_l}{\underbrace{\left( \begin{array}{c} c_{1,l-1}\\ c_{2,l-1}\\ c_{3,l-1}\\ \vdots \\ c_{l,l-1} \end{array}\right) }} = \left[ \begin{array}{ccccc} \mathbf {y}_1&\mathbf {y}_2&\mathbf {y}_3&\ldots&\mathbf {y}_l \end{array}\right] \left( \begin{array}{c} c_{1,l-1}\\ c_{2,l-1}\\ c_{3,l-1}\\ \vdots \\ c_{l,l-1} \end{array}\right) . \end{aligned}$$
(13)

Note that \(\mathbf {Y}_l\) is of dimension \(\left( n, l\right) \) and \(\mathbf {c}_l\) has dimension l. In the following, \(m=k=1\) is set for the sake of clarity. Due to the special structure of the mass matrix \(\mathbf {M}\), according to Eqs. (1) and (2)

$$\begin{aligned} \mathbf {y}_{j-1} = \mathbf {M} \mathbf {y}_j \end{aligned}$$
(14)

holds. The mode shapes \(\mathbf {u}_l\) are orthogonal with respect to the mass- and stiffness matrix [1, 9]

$$\begin{aligned} \mathbf {u}_l^{\text{ T }} \mathbf {M} \mathbf {u}_k = 0, \quad \mathbf {u}_l^{\text{ T }} \mathbf {K} \mathbf {u}_k = 0, \quad l \ne k. \end{aligned}$$
(15)

In what follows, use of a shortened modal matrix

$$\begin{aligned} \mathbf {U}_j = \left[ \begin{array}{cccc} \mathbf {u}_1&\mathbf {u}_2&\ldots&\mathbf {u}_j \end{array}\right] , \quad j = 1, \, 2, \, \ldots \, , \, n \end{aligned}$$

is made. It contains the first j mode shapes of the vibration chain. Consequently, the orthogonality of the mode shapes with respect to the mass matrix \(\mathbf {M}\) and the stiffness matrix \(\mathbf {K}\) can be rewritten

$$\begin{aligned} \mathbf {U}_j^{\text{ T }} \mathbf {M} \mathbf {U}_j = \varvec{\mu }_j = \text {diag} \left( \mu _1, \, \mu _2, \, \ldots \, \mu _j \right) \quad , \quad \mathbf {U}_j^{\text{ T }} \mathbf {K} \mathbf {U}_j = \varvec{\kappa }_j = \text {diag} \left( \kappa _1, \, \kappa _2, \, \ldots \, \kappa _j \right) \end{aligned}$$
(16)

and

$$\begin{aligned} \varvec{\mu }_j^{-1} \varvec{\kappa }_j = {\varvec{\Lambda }}_j = \text {diag} \left( 1, \, 4, \, \ldots \, , \, j^2 \right) \end{aligned}$$
(17)

gives the shortened spectral matrix \({\varvec{\Lambda }}_j\).

Induction basis:

According to Eq. (9), the first mode shape is

$$\begin{aligned} \mathbf {u}_1 = \mathbf {y}_1 = \left( 1, \, 2, \, \ldots \, , \, n \right) ^{\text{ T }}. \end{aligned}$$
(18)

Herein with respect to Eq. (13), \(c_{1,0} = 1\) holds. In what follows, in general \(c_{j,j-1} := 1\) is set in order to perform normalisation. Then, for \(j=2\), Eq. (13) gives

$$\begin{aligned} \mathbf {u}_2 = \mathbf {y}_2 + c_{2,1} \mathbf {y}_1. \end{aligned}$$

Inserting this into the eigenvalue problem given with Eq. (6), making use of \(\lambda _{2} = 4\) and applying Eq. (18) results in

$$\begin{aligned} \left( \mathbf {K} - 4 \mathbf {M}\right) \left( \mathbf {y}_2 + c_{2,1} \mathbf {u}_1\right) = \mathbf {0} \quad \Longleftrightarrow \quad c_{2,1} \left( \mathbf {K} - 4 \mathbf {M}\right) \mathbf {u}_1 = - \left( \mathbf {K} - 4 \mathbf {M}\right) \mathbf {y}_2. \end{aligned}$$
(19)

For \(\lambda _1 = 1\), Eq. (6) gives

$$\begin{aligned} \mathbf {K} \mathbf {u}_1 = \mathbf {M} \mathbf {u}_1, \end{aligned}$$
(20)

so that Eq. (19) reads

$$\begin{aligned} c_{2,1} \left( \mathbf {M} - 4 \mathbf {M}\right) \mathbf {u}_1 = - \left( \mathbf {K} - 4 \mathbf {M}\right) \mathbf {y}_2. \end{aligned}$$

Multiplying with \(\mathbf {u}_1^{\text{ T }}\) from the left and using \(\mathbf {u}_1^{\text{ T }} \mathbf {M} \mathbf {u}_1 = \mu _1\) according to Eq. (16) yields

$$\begin{aligned} 3 c_{2,1} \mu _1 = \mathbf {u}_1^{\text{ T }} \left( \mathbf {K} - 4 \mathbf {M}\right) \mathbf {y}_2 = -3 \mathbf {u}_1^{\text{ T }} \mathbf {M} \mathbf {y}_2, \end{aligned}$$

where the Eq. (20) is used. Thus, the sought coefficient is

$$\begin{aligned} c_{2,1} = -\frac{\mathbf {u}_1^{\text{ T }} \mathbf {M} \mathbf {y}_2}{\mu _1}. \end{aligned}$$
(21)

The numerator of \(c_{2,1}\) can be evaluated using Eqs. (1), (2) and (9) and \(\mathbf {y}_2 = \left( 1^2, \, 2^2, \, 3^2, \, \ldots \, , \, n^2 \right) ^{\text{ T }}\) according to Eq. (13)

$$\begin{aligned} \mathbf {u}_1^{\text{ T }} \mathbf {M} \mathbf {y}_2 = \sum \limits _{k=1}^{n} k^2 = \frac{n \left( n+1\right) \left( 2n+1\right) }{6}, \end{aligned}$$

and the denominator is

$$\begin{aligned} \varvec{\mu }_1 = \sum \limits _{k=1}^{n} k = \frac{n \left( n+1\right) }{2}. \end{aligned}$$
(22)

Therefore, the mode shape \(\mathbf {u}_2\) reads as

$$\begin{aligned} \mathbf {u}_2 = \mathbf {y}_2 -\frac{\mathbf {u}_1^{\text{ T }} \mathbf {M} \mathbf {y}_2}{\mu _1} \mathbf {y}_1 = \mathbf {y}_2 -\frac{2n+1}{3} \mathbf {y}_1 , \end{aligned}$$
(23)

which has been obtained with Eq. (12) in Sect. 2.3, too.

Induction hypothesis:

It is assumed that the j-th mode shape \(\mathbf {u}_{j}\) with \(j \le n\) can be calculated by

$$\begin{aligned} \mathbf {u}_j = \left( \mathbf {I}_n - \mathbf {U}_{j-1} \varvec{\mu }_{j-1}^{-1} \mathbf {U}_{j-1}^{\text{ T }} \mathbf {M} \right) \mathbf {y}_{j}, \end{aligned}$$

which is true for \(j=1, \, 2\) according to Sects. 2.2 and 2.3.

Induction step:

An ansatz

$$\begin{aligned} \mathbf {u}_{j+1} = \mathbf {y}_{j+1} + \mathbf {U}_j \mathbf {s}_j \end{aligned}$$
(24)

for the yet unknown mode shape is made. Equation (6) then reads as

$$\begin{aligned} \left[ \mathbf {K} -\left( j+1\right) ^2 \mathbf {M} \right] \left( \mathbf {y}_{j+1} + \mathbf {U}_j \mathbf {s}_j \right) = \mathbf {0}. \end{aligned}$$

Multiplying with \(\mathbf {U}_j^{\text{ T }}\) from the left gives

$$\begin{aligned} \left[ \mathbf {U}_j^{\text{ T }} \mathbf {K} -\left( j+1\right) ^2 \mathbf {U}_j^{\text{ T }} \mathbf {M} \right] \left( \mathbf {y}_{j+1} + \mathbf {U}_j \mathbf {s}_j \right) = \mathbf {0}. \end{aligned}$$

Making use of \(\mathbf {U}_j^{\text{ T }} \mathbf {K} = \mathbf {\Lambda }_j \mathbf {U}_j^{\text{ T }} \mathbf {M}\), factoring out \(\mathbf {U}_j^{\text{ T }} \mathbf {M}\), and applying Eq. (16) results in

$$\begin{aligned} \left[ \mathbf {\Lambda }_j -\left( j+1\right) ^2 \mathbf {I}_j \right] \mathbf {U}_j^{\text{ T }} \mathbf {M} \left( \mathbf {y}_{j+1} + \mathbf {U}_j \mathbf {s}_j \right) = \underset{\text {regular}}{\underbrace{\left[ \mathbf {\Lambda }_j -\left( j+1\right) ^2 \mathbf {I}_j \right] }} \left( \mathbf {U}_j^{\text{ T }} \mathbf {M} \mathbf {y}_{j+1} + \varvec{\mu }_j \mathbf {s}_j \right) = \mathbf {0}. \end{aligned}$$
(25)

According to Eq. (17), the largest matrix element in \(\mathbf {\Lambda }_j\) is \(j^2\). Thus, the matrix term within the square brackets is regular and a solution of Eq. (25) exists only, if

$$\begin{aligned} \mathbf {s}_j = -\varvec{\mu }_j^{-1} \mathbf {U}_j^{\text{ T }} \mathbf {M} \mathbf {y}_{j+1}. \end{aligned}$$

Inserting this into Eq. (24) gives

$$\begin{aligned} \mathbf {u}_{j+1}&= \mathbf {y}_{j+1} - \mathbf {U}_j \varvec{\mu }_j^{-1} \mathbf {U}_j^{\text{ T }} \mathbf {M} \mathbf {y}_{j+1} = \left[ \mathbf {I}_{n} - \mathbf {U}_j \varvec{\mu }_j^{-1} \mathbf {U}_j^{\text{ T }} \mathbf {M} \right] \mathbf {y}_{j+1}, \end{aligned}$$
(26)

which concludes the proof. \(\blacksquare \)

3 Orthogonality of the mode shapes

3.1 Relating the mode shapes and eigenforces

In the following, the relation between the mode shapes and the eigenforces is given. Although the general result is well-known, it leads to a neat result for the present special vibration chain. This result will be of interest in the next Sect. 3.2, too.

Comparing Eqs. (6) and (7) yields the well-known relation

$$\begin{aligned} \mathbf {M} \mathbf {u}_l = \mathbf {f}_l, \end{aligned}$$

which is true for every conservative vibration system [9]. For the sake of clarity \(m=k=1\) is set. Then, Eqs. (1) and (2) give the following relations between the coordinates of the mode shape \(\mathbf {u}_l\), the left-eigenvector \(\mathbf {f}_l\), and the eigenforce \(\hat{\mathbf {f}}_l\) to the l-th eigenvalue \(\lambda _l\)

$$\begin{aligned} u_{i,l} = i \, f_{i,l}, \qquad f_{i,l} = \frac{1}{i} u_{i,l}, \qquad \text {and} \qquad \hat{f}_{i,l} = l^2 \frac{1}{i} u_{i,l}; \quad i, \, l = 1, \, 2, \, \ldots \, , \, n; \quad n \in \mathbb {N}, \end{aligned}$$
(27)

see also Eq. (8). That is, once the mode shape \(\mathbf {u}_l\) has been determined by Eq. (26), the eigenforces \(\hat{\mathbf {f}}_l\) are known, too.

3.2 Investigating the orthogonality of the mode shapes

Although some authors claim that the single mode shapes are orthogonal with respect to the standard scalar product, this does not hold generally. However, for Mikota’s oscillator, some mode shapes are indeed orthogonal with respect to the standard scalar product, as shall be seen next.

Referring back to Eq. (24) and making use of Eq. (14) yields

$$\begin{aligned} \mathbf {y}_{l-1}&= \mathbf {u}_{l-1} - \mathbf {U}_{l-2}\mathbf {s}_{l-2} = \mathbf {M} \mathbf {y}_l = \mathbf {M} \left( \mathbf {u}_l - \mathbf {U}_{l-1} \mathbf {s}_{l-1}\right) \quad . \end{aligned}$$
(28)

Left-multiplication with the k-th mode shape \(\mathbf {u}_k\) gives

$$\begin{aligned} \mathbf {u}_k^{\text{ T }}\mathbf {y}_{l-1}&= \mathbf {u}_k^{\text{ T }} \mathbf {M} \left( \mathbf {u}_l - \mathbf {U}_{l-1} \mathbf {s}_{l-1}\right) = \underset{= 0 \text { for } k \ne l}{\underbrace{\mathbf {u}_k^{\text{ T }} \mathbf {M} \mathbf {u}_l}} - \underset{= 0 \text { for } k > l-1}{\underbrace{\mathbf {u}_k^{\text{ T }} \mathbf {M} \mathbf {U}_{l-1}}} \mathbf {s}_{l-1} . \end{aligned}$$

The first term on the right-hand side is zero for \(k \ne l\), which is due to the orthogonality of the right-eigenvectors with respect to the mass matrix \(\mathbf {M}\). For the same reason and as the shortened modal matrix \(\mathbf {U}_{l-1}\) contains the first \(l-1\) right-eigenvectors, the matrix product in the second term on the right-hand side is zero at least for \(k > l-1\). Consequently,

$$\begin{aligned} \mathbf {u}_k^{\text{ T }}\mathbf {y}_{l-1}&= 0 \quad \text {for } k > l. \end{aligned}$$
(29)

Applying successively Eq. (28) to Eq. (29) yields

$$\begin{aligned} \mathbf {u}_{k}^{\text{ T }}\mathbf {u}_{l-1}&= 0 \quad \text {for } k > l. \end{aligned}$$
(30)

As \(\mathbf {U}^{\text{ T }} \mathbf {U}\) is symmetric, also the standard scalar product

$$\begin{aligned} \mathbf {u}_{l-1}^{\text{ T }}\mathbf {u}_{k}&= 0 \quad \text {vanishes for} \quad l = 1, \, \ldots \, , \, k-1, \end{aligned}$$
(31)

and hence, \(\mathbf {U}^{\text{ T }} \mathbf {U}\) is tri-diagonal.

4 Example

As an example, the third right-eigenvector \(\mathbf {u}_3\) is calculated for arbitrary n dof. According to Eq. (26) with \(j=3\)

$$\begin{aligned} \mathbf {u}_3 = \left( \mathbf {I}_n - \mathbf {U}_{2} \varvec{\mu }_{2}^{-1} \mathbf {U}_{2}^{\text{ T }} \mathbf {M} \right) \mathbf {y}_{3} = \mathbf {y}_{3} - \mathbf {U}_{2} \varvec{\mu }_{2}^{-1} \mathbf {U}_{2}^{\text{ T }} \mathbf {y}_{2} \end{aligned}$$

has to be evaluated, where Eq. (14) has been applied. With Eqs. (18), (23), \(\mathbf {U}_{2}\) reads as

$$\begin{aligned} \mathbf {U}_{2} = \left[ \begin{array}{cc} \mathbf {y}_1&\mathbf {y}_2 - \frac{2n+1}{3} \mathbf {y}_1 \end{array}\right] \end{aligned}$$

and thus, two sums resulting from the scalar products occurring in \(\mathbf {U}_{2}^{\text{ T }} \mathbf {y}_{2}\) (e. g. \(\mathbf {y}_1 \cdot \mathbf {y}_2\)) have to be determined

$$\begin{aligned} \mathbf {U}_{2}^{\text{ T }} \mathbf {y}_{2} = \left[ \begin{matrix} \sum \limits _{i=1}^{n} i^3\\ \sum \limits _{i=1}^{n} \left( i^4 - \frac{2n+1}{3} i^3 \right) \end{matrix}\right] = \frac{n\left( n+1\right) }{4} \left[ \begin{matrix} n \left( n+1\right) \\ \frac{2n +1}{15} \left( n^2 + n - 2\right) \end{matrix}\right] . \end{aligned}$$

With \(\mu _1 = n \left( n + 1 \right) /2\) according to Eq. (22) and

$$\begin{aligned} \mu _2&= \mathbf {u}_2^{\text{ T }} \mathbf {M} \mathbf {u}_2 = \sum \limits _{i=1}^{n} \left( i^2 - \frac{2n+1}{3} i \right) \frac{1}{i} \left( i^2 - \frac{2n+1}{3} i \right) = \frac{n\left( n+1\right) }{36} \left( n^2 + n - 2 \right) \end{aligned}$$

it is

$$\begin{aligned} \varvec{\mu }_2^{-1} = \frac{2}{n\left( n+1\right) }\left[ \begin{matrix} 1 &{} \\ &{} \frac{18}{n^2 + n - 2} \end{matrix}\right] \quad \text {and} \quad \varvec{\mu }_2^{-1} \mathbf {U}_{2}^{\text{ T }} \mathbf {y}_{2} = \frac{1}{2}\left[ \begin{matrix} n\left( n+1\right) \\ \frac{6}{5} \left( 2n + 1 \right) \end{matrix}\right] . \end{aligned}$$

Finally,

$$\begin{aligned} \mathbf {U}_{2} \varvec{\mu }_{2}^{-1} \mathbf {U}_{2}^{\text{ T }} \mathbf {y}_{2} = \left[ \begin{array}{cc} \mathbf {y}_1&\mathbf {y}_2 - \frac{2n+1}{3} \mathbf {y}_1 \end{array}\right] \frac{1}{2}\left[ \begin{array}{c} n\left( n+1\right) \\ \frac{6}{5} \left( 2n + 1 \right) \end{array}\right] = \frac{3}{5} \left( 2n+1\right) \mathbf {y}_2 - \frac{1}{5} \left[ \frac{3}{2} n \left( n+1\right) + 1 \right] \mathbf {y}_1, \end{aligned}$$

and thus

$$\begin{aligned} \mathbf {u}_3 = \left( \mathbf {I}_n - \mathbf {U}_{2} \varvec{\mu }_{2}^{-1} \mathbf {U}_{2}^{\text{ T }} \mathbf {M} \right) \mathbf {y}_{3} = \mathbf {y}_{3} - \frac{3}{5} \left( 2n+1\right) \mathbf {y}_2 + \frac{1}{5} \left[ \frac{3}{2} n \left( n+1\right) + 1 \right] \mathbf {y}_1. \end{aligned}$$
(32)

By means of Eqs. (32) and (27), the eigenforces to the third eigenvalue can be calculated for arbitrary n dof, too. Evaluating Eq. (32) exemplarily for \(n=4\) gives

$$\begin{aligned} \mathbf {u}_3&= \left( \begin{matrix} 1^3\\ 2^3\\ 3^3\\ 4^3 \end{matrix}\right) -\frac{27}{5} \left( \begin{matrix} 1^2\\ 2^2\\ 3^2\\ 4^2 \end{matrix}\right) +\frac{31}{5} \left( \begin{matrix} 1^1\\ 2^1\\ 3^1\\ 4^1 \end{matrix}\right) = \frac{1}{5} \left( \begin{matrix} 9\\ -6\\ -15\\ 12 \end{matrix}\right) \hat{=} \left( \begin{matrix} 9\\ -6\\ -15\\ 12 \end{matrix}\right) . \end{aligned}$$

In Sect. 3.2, the product \(\mathbf {U}^{\text{ T }} \mathbf {U}\) is proved to be tri-diagonal. For the example at hand, this means that \(\mathbf {u}_1 \perp \mathbf {u}_3\). In detail,

$$\begin{aligned} \mathbf {u}_1^{\text{ T }} \mathbf {u}_3&= \left( \begin{matrix} 1, &{} 2, &{} 3, &{} 4 \\ \end{matrix}\right) ^{\text{ T }} \left( \begin{matrix} 9\\ -6\\ -15\\ 12 \end{matrix}\right) = 9 - 12 - 45 + 48 = 0. \end{aligned}$$

It is emphasised again that this is a remarkable property, as in general the right-eigenvectors are orthogonal (only) with respect to the mass and stiffness matrix, but not with respect to the standard scalar product.

5 Summary and conclusions

In the preceding sections, some investigations concerning the mode shapes and eigenforces of Mikota’s oscillator with arbitrary n dof are performed. The foundations of these investigations were laid by the proofs [8, 12] of Mikota’s conjecture [7]. As a result of the present work, explicit formulae are given, which allow for the calculation of each coordinate of the mode shapes and eigenforces for the first two eigenvalues of Mikota’s oscillator in a closed form. Based on the structure of these first eigenvectors, an analytical expression is found providing a possibility to calculate all remaining eigenvectors in a successive manner. Thus, the calculations of the left- and/or the right-eigenvectors can be restricted up to the highest eigenvalue of interest. Additionally, an example of calculation is given, which provides an explicit formula for the mode shape and eigenforce to the third eigenvalue for arbitrary n dof. These analytically known eigenvectors may also be used as reference solutions for numerical investigations.