Keywords

1 Introduction

For many systems, disregarding the influence of the structure motion on their excitation source is an acceptable simplification, but for many others it is not. Sommerfeld (1904) was the first to study the phenomenon of this interaction, later called the Sommerfeld Effect, making an experiment of an elastic base supporting an unbalanced machine. A few years later this experiment was replicated by Kononenko and Korablev [1], who had their work re-analyzed by Nayfeh and Mook [2].

Non-ideal systems are those in which the structural motion influences its source of excitation. These systems can be linear, or nonlinear, regardless of its excitation. In general, the more the power supply is limited, the more the system moves further away from the ideal system, and the greater the machine-structure interaction is. Mathematically it is imperative to include to the model an equation that describes the dynamics of the motor. Therefore, an additional degree of freedom is required to model non-ideal systems [1,2,3,4,5].

In this work, we develop a non-ideal system model of a supported machine with an unbalanced rotor. This non-ideal system is composed of a rigid foundation block directly supported by springs and dashpots.

This work aims to present ongoing research of the machine-foundation interactions. The mathematical development of the proposed non-ideal system is carried out via Lagrange’s equations. In Sect. 2, the physical model representing the foundation structure and its driver source, the machine, will be presented. Next, Sect. 3 presents the mathematical model composed of equations that describe the displacements and velocities of the physical model, obtained using Lagrange’s equations. Numerical simulations and graphical displays are presented in Sect. 5, using assumed stiffness, mass and damping parameters. Sections 5 and 6 will present the final discussion and conclusions.

2 Physical Model

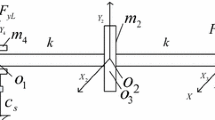
The proposed physical model considers the machine and structure interaction and consists of four degrees of freedom: the two translations (vertical and horizontal), one rotation (about the axis of the foundation) and the last one associated with the motor shaft. This additional degree of freedom is typical of the so-called non-ideal systems, as can be seen in Fig. 1.

Fig. 1
figure 1

Model of a foundation structure with unbalanced excitation source

Full size image

\({C}_{i}\hspace{1em}(i\hspace{0.33em}=\hspace{0.33em}1,\hspace{0.33em}2, 3)\) and \({K}_{i}\hspace{1em}(i\hspace{0.33em}=\hspace{0.33em}1,\hspace{0.33em}2, 3)\) are, respectively, conveniently adopted damping and stiffness coefficients of the machine foundation.

3 Mathematical Model

In this mathematical model, time functions \({q}_{1}, {q}_{2}\) and \({q}_{3}\) are, respectively, the generalized coordinates related the horizontal, vertical, and rotational motions of the block foundation, while time function \({q}_{4}\) is the angular displacement of the motor shaft. The eccentricity \(e\) is obtained through the quality of the balance of the rotating machine, while \(h\) is the height between the motor shaft and the foundation axes (Fig. 1).

Unbalanced mass \(({{\varvec{M}}}_{{\varvec{r}}})\)

The coordinates and velocities of the unbalanced mass from Fig. 1 are:

$$\begin{array} {c}{x}_{r}= {q}_{1}-h {q}_{3}+e \mathrm{cos} {q}_{4} \end{array} \begin{array} {cccc}{y}_{r}= {q}_{2}+e \mathrm{sin} {q}_{4}+h \end{array}$$
(1)
$$\begin{array} {c}{\dot{x}}_{r}= {\dot{q}}_{1}-h{\dot{q}}_{3}-e {\dot{q}}_{4}\mathrm{sin}{q}_{4} \end{array} \begin{array} {cccc}{\dot{y}}_{r}= {\dot{q}}_{2}+e {\dot{q}}_{4} \mathrm{cos} {q}_{4} \end{array}$$
(2)

Mass of the foundation block \(({{\varvec{M}}}_{{\varvec{b}}})\)

The coordinates and velocities of the machine foundation block mass presented in the Fig. 1 are:

$$\begin{array}{c}{x}_{b}= {q}_{1} \end{array} \begin{array} {cccc}{y}_{b}= {q}_{2}\end{array}$$
(3)
$$\begin{array} {c}{\dot{x}}_{b}= {\dot{q}}_{1}\end{array} \begin{array} {cccc} {\dot{y}}_{b}= {\dot{q}}_{2} \end{array}$$
(4)

Motor mass \(({{\varvec{M}}}_{{\varvec{m}}})\)

The coordinates and velocities of the mass of the motor are:

$$\begin{array}{c}{x}_{m}= {q}_{1}-h {q}_{3}\end{array} \begin{array} {cccc} {y}_{m}= {q}_{2}+h \end{array}$$
(5)
$$\begin{array} {c}{\dot{x}}_{m}= {\dot{q}}_{1}-h{\dot{q}}_{3} \end{array} \begin{array} {cccc} {\dot{y}}_{m}= {\dot{q}}_{2} \end{array}$$
(6)

Kinetic Energy \(({\varvec{T}})\)

The kinetic energy of this model is obtained as follows:

$$T = 1/2 \left[ {\begin{array}{*{20}c} {M_b \left( {\dot{q}_1^2 + \dot{q}_2^2 } \right) + M_m \left[ {\left( {\dot{q}_1 - h\dot{q}_3 } \right)^2 + \dot{q}_2^2 } \right]} \\ { + J_b \dot{q}_3^2 + M_r \left( {\dot{q}_1 - h\dot{q}_3 - \dot{q}_4 e \sin q_4 } \right)^2 } \\ { + M_r \left( {\dot{q}_2 + \dot{q}_4 e\cos q_4 ) + J_m \dot{q}_4^2 } \right)^2 } \\ \end{array} } \right]$$
(7)

in which \({J}_{m}\) is the moment of inertia of the machine rotor and \({J}_{b}\) the moment of inertia of foundation block.

Strain energy \(({\varvec{U}})\)

In this case the strain energy can be obtained by:

$$U=1/2({K}_{1}{q}_{1}^{2}+{K}_{2}{q}_{2}^{2}+{K}_{3}{q}_{3}^{2})$$
(8)

in which \({K}_{i} (i=1, 2, 3)\) are the stiffness coefficients.

Work of conservative forces \(({\varvec{W}})\)

The work of the weight forces is given by:

$$W= -g[\left({M}_{b}+{M}_{m}+{M}_{r}\right){q}_{2}+{M}_{r}\left({q}_{2}+e sin{q}_{4}\right)]$$
(9)

in which \(g\) it is the acceleration due to gravity.

Total Potential Energy \(({\varvec{V}})\)

The total potential energy will be determined by:

$$V=U-W$$
(10)

Lagrange’s equation

In this model, Lagrange’s equation can be presented as:

$$\frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial {\dot{q}}_{i}}\right)-\frac{\partial \mathcal{L}}{\partial {q}_{i}}= {N}_{i} (i=1, 2, \mathrm{3,4})$$
(11)

in which \(\mathcal{L}=T-V\) is the Lagrangean function and \({N}_{i}\) are the non-conservative generalized forces.

Equations of Motion

First degree of freedom

For the first degree of freedom the equation of motion is:

$$\left({M}_{b}+{M}_{m}+{M}_{r}\right){\ddot{q}}_{1}+{C}_{1}{\dot{q}}_{1}+{K}_{1}{q}_{1}= \left({M}_{m}+{M}_{r}\right){h\ddot{q}}_{3}+{M}_{r} e \left({\ddot{q}}_{4} \sin {q}_{4}\right) +{ M}_{r} e \left({\dot{q}}_{4}^{2} \cos {q}_{4}\right)$$
(12)

Second degree of freedom

For the second degree of freedom the equation of motion is:

$$\left({M}_{b}+{M}_{r}+{M}_{m}\right){\ddot{q}}_{2}+{C}_{2}{\dot{q}}_{2}+{K}_{2}{q}_{2}= -g\left({M}_{b}+{M}_{r}+{M}_{m}\right)-{M}_{r}e\left({\ddot{q}}_{4} \cos{q}_{4}-{{\dot{q}}_{4}}^{2} \sin{q}_{4}\right)$$
(13)

Third degree of freedom

For the third degree of freedom the equation of motion is:

$$\left({M}_{m}{h}^{2}+{M}_{r}{h}^{2}+{J}_{b}\right){\ddot{q}}_{3}+{C}_{3}{\dot{q}}_{3}+{K}_{3}{q}_{3}= \left({M}_{b}+{M}_{m}\right)h{\ddot{q}}_{1}-{M}_{r}he\left({\ddot{q}}_{4} \sin{q}_{4}-{{\dot{q}}_{4}}^{2} \cos{q}_{4}\right)$$
(14)

Fourth degree of freedom

For the fourth degree of freedom the equation of motion is:

$${M}_{r}e\left({\ddot{q}}_{1} \mathrm{sin}{q}_{4}+{\ddot{q}}_{2} \mathrm{cos}{q}_{4}+h{\ddot{q}}_{3} \mathrm{sin}{q}_{4}\right)+\left({M}_{r}{e}^{2}+{J}_{m}\right){\ddot{q}}_{4}=L\left({\dot{q}}_{4}\right)-H\left({\dot{q}}_{4}\right)+{M}_{r}eg\mathrm{cos}{q}_{4}$$
(15)

in which \(L({\dot{q}}_{4})\) is the total torque of the rotor and \(H({\dot{q}}_{4})\) is its the motor damping torque due to internal friction.

Matrix formulation

Let us re-write the equations of motion (12 to 15) in matrix form:

$$\left[M\right]\left\{\ddot{q}\right\}+\left[C\right]\{\dot{q}\}+\left[K\right]\left\{q\right\}=\left\{p\right\}$$
(16)

where

$$\left[M\right]=\left[\begin{array}{c}{M}_{b}+{M}_{r}+{M}_{m}\\ 0\\ -({M}_{m}+{M}_{r})h\\ -{M}_{r} e \sin{q}_{4}\end{array}\begin{array}{c}0\\ {M}_{b}+{M}_{r}+{M}_{m}\\ 0\\ {M}_{r} e \cos{q}_{4}\end{array}\begin{array}{c}-({M}_{m}+{M}_{r})h\\ 0\\ ({M}_{m}+{M}_{r})h^{2}+{ J}_{b}\\ {M}_{r} h e \sin{q}_{4}\end{array}\begin{array}{c}-{M}_{r} e \sin{q}_{4}\\ {M}_{r} e \cos{q}_{4}\\ {M}_{r} h e \sin{q}_{4}\\ {M}_{r}{ e}^{2}+{J}_{m}\end{array}\right]$$
(17)
$$\left\{\ddot{q}\right\}=\left\{\begin{array}{c}{\ddot{q}}_{1}\\ {\ddot{q}}_{2}\\ {\ddot{q}}_{3}\\ {\ddot{q}}_{4}\end{array}\right\}$$
(18)
$$\left[C\right]=\left[\begin{array}{cc}\begin{array}{cc}{C}_{1}& 0\\ 0& {C}_{2}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}{C}_{3}& 0\\ 0& 0\end{array}\end{array}\right]$$
(19)
$$\left\{\dot{q}\right\}=\left\{\begin{array}{c}\begin{array}{c}{\dot{q}}_{1}\\ {\dot{q}}_{2}\end{array}\\ \begin{array}{c}{\dot{q}}_{3}\\ {\dot{q}}_{4}\end{array}\end{array}\right\}$$
(20)
$$\left[K\right]=\left[\begin{array}{cc}\begin{array}{cc}{K}_{1}& 0\\ 0& {K}_{2}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}{K}_{3}& 0\\ 0& 0\end{array}\end{array}\right]$$
(21)
$$\left\{q\right\}=\left\{\begin{array}{c}\begin{array}{c}{q}_{1}\\ {q}_{2}\end{array}\\ \begin{array}{c}{q}_{3}\\ {q}_{4}\end{array}\end{array}\right\}$$
(22)
$$\left\{p\right\}=\left\{\begin{array}{c}\begin{array}{c}-{M}_{r} e {{\dot{q}}_{4}}^{2}\mathrm{cos}{q}_{4}\\ -{M}_{r} e {{\dot{q}}_{4}}^{2}\mathrm{sin}{q}_{4}-\left({M}_{b}+{M}_{m}+{M}_{r}\right)g\\ -{M}_{r} h e {{\dot{q}}_{4}}^{2}\mathrm{cos}{q}_{4}\end{array}\\ L({\dot{q}}_{4})-H({\dot{q}}_{4})+{M}_{r}eg\mathrm{cos}{q}_{4}\end{array}\right\}$$
(23)

Equations of this type are difficult to solve in closed form, so is convenient to transform the second order differential equation system into a first order differential equations system and then choose a numerical method to solve the problem, as the Runge–Kutta method implemented in Matlab®.

4 Torque Relationships

A steady state constant motor frequency condition is given by the torque relationship

$$S\left({\dot{q}}_{4}\right)=H\left({\dot{q}}_{4}\right)+R\left({\dot{q}}_{4}\right)$$
(24)

In Eq. (21), remembering that torque and energy have the same unities, \(S\left({\dot{q}}_{4}\right)\) is the total energy dissipated by the motor/structure system and \(R\left({\dot{q}}_{4}\right)\) the energy dissipated by damping of the support structure, given by

$$R\left({\dot{q}}_{4}\right)=\sum_{i=1}^{3}\frac{{C}_{i}}{2{q}_{4}}{\omega }_{i}^{2}{a}_{i}^{2}$$
(25)

where \({\omega }_{i}\) are the undamped frequencies of vibration of the support structure (rad/s). The amplitudes of vibration of these three modes are

$${a}_{i}=\frac{{M}_{r}e}{Mode mass}{D}_{i}{\beta }_{i}^{2}$$
(26)

where the nondimensional Coefficients of Dynamic Amplification are

$${D}_{i}=\frac{1}{\sqrt{{\left(1-{\beta }_{i}^{2}\right)}^{2}+{\left(2{\xi }_{i}{\beta }_{i}\right)}^{2}}}$$
(27)

defining the nondimensional relationships

$${\beta }_{i}=\frac{{q}_{4}}{{\omega }_{i}} {\xi }_{i}=\frac{{C}_{i}}{2\left(Mode mass\right){\omega }_{i}}$$
(28)

5 Numerical Simulations

Next, numerical parameters are adopted: \({M}_{b}+{M}_{r}+{M}_{m}\) = 2 t, K1 = 50,000 KN/m, K2 = 100,000 KN/m, K3 = 75,000 KNm/rad, \({M}_{r}\) = 0.1 t, e = 0.01 m, \({\xi }_{1}={\xi }_{2}={\xi }_{3}=0.05\), \({J}_{m}\) = 1.7 × 10–4 tm2, \(H\left({\dot{q}}_{4}\right)=4\mathrm{x}{10}^{-4}{\dot{q}}_{4}\) KNm. Figure 2 displays the \(S\left({\dot{q}}_{4}\right)\) energy dissipation curve of this system (in black), from Eq. (21), and three possible \({L}_{k}\left({\dot{q}}_{4}\right)\) available torque characteristic curves of the motor (in red, green and blue), for three different possible energy levels, considered as linear, in KNm,

Fig. 2
figure 2

\(S\left({\dot{q}}_{4}\right)\) curve, in black, \({L}_{1}\left({\dot{q}}_{4}\right)\) line, in red, \({L}_{2}\left({\dot{q}}_{4}\right)\) blue and \({L}_{3}\left({\dot{q}}_{4}\right)\) blue line, in green

Full size image
$${L}_{1}\left({\dot{q}}_{4}\right)=0.25-0.0009{\dot{q}}_{4} {L}_{2}\left({\dot{q}}_{4}\right)=0.35-0.0009{\dot{q}}_{4}$$
$${L}_{3}\left({\dot{q}}_{4}\right)=0.30-0.0009{\dot{q}}_{4}$$

Figure 2 displays only the first two resonance peaks of this system. The third one, related to the roll mode of the foundation block is not of interest for the adopted parameters.

The computed stable steady state constant motor frequencies (rad/s) and corresponding torques, for positive increase of the motor power (KNm) are: P1 \(\cong\) (152; 0.11), P2 \(\cong\) (214; 0.16) and P3 \(\cong\) (204; 0.11).

Next, it is performed a time step-by-step numerical integration of the equations of motion, using Runge–Kutta’s 4th and 5th order algorithm, implemented in Matlab® software. The first steady state regime, P1, is displayed in Fig. 3, the second, P2, is displayed in Fig. 4 and P3, displayed in Fig. 5.

Fig. 3
figure 3

Steady state constant motor frequency regime, P1

Full size image
Fig. 4
figure 4

Steady state constant motor frequency regime, P2

Full size image
Fig. 5
figure 5

Steady state constant motor frequency regime, P3

Full size image

In Figs. 3, 4 and 5, a fairly good agreement with Fig. 2 results is obtained. As expected, the effect of gravity on \({m}_{r}\) leads to a complex steady state behavior, as is possible to see in Fig. 6, a zoom of part of Fig. 3.

Fig. 6
figure 6

Zoom of steady state constant motor frequency P1

Full size image

6 Discussion

Let us discuss simulations results presented in Figs. 2, 3, 4 and 5.

In steady state P1, the amount of energy provided by the motor through torque curve \({L}_{1}\left({\dot{q}}_{4}\right)\), in red, is not enough to surpass the first resonance peak of the energy dissipation curve, resulting in stagnation of the angular speed regime of the machine.

If some more energy is provided, through torque curve \({L}_{3}\left({\dot{q}}_{4}\right)\), in green, the system reaches a point at this first resonance peak and jumps to far away point P3 where a steady state regime is again possible, no stable steady states in between. This is the so called Sommerfeld Effect.

Finally, if more energy is applied, through torque curve \({L}_{2}\left({\dot{q}}_{4}\right)\), in blue, it is possible to reach higher steady state angular velocity regimes as point P2.

7 Conclusions

Studies of models considering non-ideal systems are important for a better practice of engineering, but are not usually done, being replaced by approximations. The system of differential equations of the model studied here is coupled, nonlinear and of second order, quite difficult to solve analytically. So, it is necessary to use a numerical method.

Among the possible solver methods to this model, the solution for this model was carried out in the Matlab® program using the ode45 function, that uses a combination of fourth and fifth order Runge Kutta methods. The implementation of this algorithm requires the transformation of the of second-order differential equations into a first order system [6, 7].

A study of non-ideal behavior of a four degrees of freedom support structure for a limited power unbalanced motor was presented. The expected Sommerfeld Effect of rotation frequency stagnation near resonances was observed, as well as a jump phenomenon due to instability. Modeling of this type of foundation as non-ideal systems can be of importance in practice.