Keywords

1 Introduction

The key component of production management for modern enterprises is effective production planning and scheduling. It is of great significance for reducing production costs, shortening production cycle and improving production efficiency. The job shop scheduling problem has the major characteristics including modeling complexity, computer complexity, dynamic randomness, multiple constraints, and multi-objectiveness.

The production planning and scheduling problem is to arrange the production tasks delivered on the equipment according to the sequence. It discusses how to arrange the processing resources and sequence of the operations under the premise of satisfying the processing constraints, aiming to minimize the product manufacturing time and the consumption cost. Due to the complexity of the production operation management system and various real-world constraints, the production scheduling problem becomes a NP-hard problem [6]. The classical job shop scheduling problem (JSP) assumes that there is no flexibility of the resources (including machines and tools) for each operation of the corresponding job. In another word, the problem requires that one machine only processes one type of the operation. However, in the real world application, many flexible manufacturing systems are used to improve the production efficiency in modern manufacturing enterprises [14].

In the light of this, the FJSP attracts increasing attentions from both research and industrial areas [2]. The FJSP can be divided into two sub-problems: the machine selection (MS) and the operations sequencing (OS), adding a more complicated scenario MS to the conventional JSP problem. Many methods have been proposed to solve this problem so far, including exact algorithm [3], dispatching rules [1], evolutionary algorithm (EA) [18], local search algorithms [7] and so on. For exact algorithm, Torabi et al. proposed a mixed integer nonlinear program for deterministic FJSP [16]. Roshanaei et al. presented two MILP models [13]. However, exact algorithm cannot obtain good results for large scale FJSP. So Tay and Ho used dispatching rules for multi-objective FJSP [15]. Ziaee proposed a construction procedure based heuristic for FJSP [19]. As for EA, the most used method is genetic algorithm, Pezzella et al. integrated GA with different strategies to solve FJSP [10]. Driss et al. proposed a new chromosome representation method and some novel crossover and mutation strategies for FJSP [4]. However, EA is lack of local search ability. So local search method is used in FJSP and tabu search (TS) is the most effective method for FJSP. Vilcot and Billaut used TS for the objective of minimum makespan and maximum lateness [17]. Jia and Hu proposed a TS based pathrelinking algorithm for multi-objective FJSP [7].

The remainder of this paper is structured as follows: the problem formulation of FJSP is discussed in Sect. 2, followed by the three compared algorithms that are briefly introduced in Sect. 3, where the encoding and decoding method are also given. Experimental studies and the corresponding discussion are reported in Sect. 4. Finally, Sect. 5 concludes the paper.

2 Problem Formulation

The formulation of FJSP is described as follows: Assuming that there are M machines in the workshop, which need to process N jobs within the overall time period. Each job consists of a series of operations that allows them to be processed in a set of available machines. In this paper, the objective function is to minimize the maximal completion time, i.e. makespan (\(C_{max}\)), which is denoted as follows:

Notations for the formulation:  

i:

number of jobs

j:

operations of the jobs

k:

number of machines

\(B_{ijk}\):

starting time of operation j of job i on machine k

\(P_{ijk}\):

processing time of operation j of job i on machine k

\(F_{ijk}\):

completion time of operation j of job i on machine k

\(F_i\):

completion time of job i

 

Objective function: Minimize \(C_{max}\)

Constraints:

  • Jobs are independent and preemption or cancellation of jobs is not permitted.

    $$\begin{aligned} B_{ijk}+P_{ijk}=F_{ijk} \end{aligned}$$
    (1)
    $$\begin{aligned} \sum \limits _k{B_{ijk}}\ge \sum \limits _k{F_{i(j-1)k}} \end{aligned}$$
    (2)

  • Every machine can only process one job at a time.

    $$\begin{aligned} B_{ik}+P_{ik}\le B_{(i+1)k} \quad \forall j \end{aligned}$$
    (3)

  • One operation of each job can be processed by only one machine at a time.

    $$\begin{aligned} B_{ij}+P_{ij}\le B_{i(j+1)} \quad \forall k \end{aligned}$$
    (4)

  • All jobs and machines are available at time zero and the transmission time between machines is ignored.

    $$\begin{aligned} B_{ijk}\ge 0 \end{aligned}$$
    (5)
    $$\begin{aligned} F_{ijk}\ge 0 \end{aligned}$$
    (6)

  • Processing time is deterministic and includes other elements of set-up, transportation and inspection. the makespan is the maximal completion time of all jobs.

    $$\begin{aligned} F_i\ge F_{ij} \quad \forall j \end{aligned}$$
    (7)
    $$\begin{aligned} C_{max}\ge F_i \quad \forall i \end{aligned}$$
    (8)

3 Three Algorithms for FJSP

3.1 Algorithm Introduction

Moth-Flame Optimization Algorithm. Moth-flame optimization algorithm is a modern intelligent bio-inspired optimization algorithm proposed in 2015 [8]. It mimics the navigation mechanism of the moth in the space during the flight. Several advantages could be found in the algorithm design. First of all, due to that several flames is formulated and moths are considered flying around the individual flame and do not interfere with each other, the parallel optimization ability of the algorithm is strong. In addition, due to the spiral wrap path of the moth is assumed in the algorithm, as the number of iterations increases, it gradually approaches the contemporary flame center with a certain random amount. Such scheme avoids the whole population to be easily falling into the local optimal solution, and therefore guarantees the global optimal solution of the algorithm with excellent search performance and robustness.

The position update mechanism of each moth relative to the flame can be expressed by an equation:

$$\begin{aligned} M_i=S(M_i,F_j) \end{aligned}$$
(9)

where \(M_i\) represents the ith moth, \(F_j\) represents the jth flame, and S represents the spiral function. The spiral function of the moth flight path is defined as follows:

$$\begin{aligned} S(M_i,F_j)=D_ie^{bt}\cos (2\pi t)+F_j \end{aligned}$$
(10)

where \(D_i\) represents the linear distance between the ith moth and the jth flame, b is the defined logarithmic spiral shape constant, and the path coefficient t is a random number in [−1, 1]. The expression of \(D_i\) is as follows:

$$\begin{aligned} D_i=|F_j-M_i| \end{aligned}$$
(11)

In order to reduce the number of flames in the iterative process and balance the global search ability and local development ability of the algorithm in the search space, an adaptive mechanism for the number of flames is proposed. The formula is as follows:

$$\begin{aligned} flame.number=round(N-G*\frac{N-1}{Gm}) \end{aligned}$$
(12)

where G is the current number of iterations, N is the initial maximum number of flames, and Gm is the maximum number of iterations. Due to the reduction in flames, the moths corresponding to the reduced flames in each generation update their position based on the flame with the worst fitness value.

Teaching-Learning-Based Optimization Algorithm. The optimization algorithm based on ‘teaching and learning’ simulates the interaction of student-teacher in a class, which is a group intelligent optimization algorithm proposed in 2011 [12]. The improvement of the grades of students in the class requires the teacher’s ‘teaching’. In addition, the students need to ‘learn’ to promote the absorption of knowledge. Among them, teachers and students are both individuals in the evolutionary algorithms, and the teacher is the best individual in each iteration. The following formula shows the process of ‘teaching’:

$$\begin{aligned} X_i^{new}=X_i^{old}+difference \end{aligned}$$
(13)
$$\begin{aligned} difference=r_i*(X_{best}-F_i*Popmean) \end{aligned}$$
(14)

where \(X_i^{old}\) and \(X_i^{new}\) represent the values of the ith student before and after learning; \(X_{best}\) is the student who gets the best grades, e.g. the teacher; \(Popmean=\frac{1}{N}\sum \limits _{i=1}^{N}{(X_i)}\) is the average value of all students; N is the number of students; the teaching factor \(F_i=round[1+rand(0,1)]\) and the learning step \(r_i=rand(0,1)\). After the ‘teaching’ phase is completed, the students are updated according to their grades e.g. fitness value. In the process of ‘learning’, for each student \(X_i\), a learning object \(X_j(j\not =i)\) in the class is randomly selected, and \(X_i\) adjusts himself by analyzing the difference between himself and the student \(X_j\), with the formula is as follows:

$$\begin{aligned} X_i^{new}=\left\{ \begin{array}{ll} X_i^{old}+r_i*(X_i-X_j) &{} \quad {f(X_j)<f(X_i)}\\ X_i^{old}+r_i*(X_j-X_i) &{} \quad {f(X_i)<f(X_j)} \end{array}\right. \end{aligned}$$
(15)

Also the students are updated according to their fitness values.

Rao-2 Algorithm. Rao-2 algorithm is a simple metaphor-less optimization algorithm proposed in 2019 for solving the unconstrained and constrained optimization problems [11]. The algorithm is based on the best and worst solutions obtained during the optimization process and the random interactions between the candidate solutions. The algorithm requires only common control parameters like population size and number of iterations and does not require any algorithm-specific control parameters. The individuals are updated according to the following formula:

$$\begin{aligned} \begin{aligned} X_{j,k,i}^{new}=X_{j,k,i}+r_{1,j,i}*(X_{j,best,i}-X_{j,worst,i}) \\ +\, r_{2,j,i}*(\left| X_{j,k,i} or X_{j,h,i}\right| -\left| X_{j,h,i} or X_{j,k,i}\right| ) \end{aligned} \end{aligned}$$
(16)

where \(X_{j,best,i}\) and \(X_{j,worst,i}\) are the value of the variable j for the best and worst candidate during the ith iteration. \(X_{j,k,i}^{new}\) is the updated value of \(X_{j,k,i}\). \(r_{1,j,i}\) and \(r_{2,j,i}\) are the two random numbers for the jth variable in the range [0, 1]. \(X_{j,k,i}\) and \(X_{j,h,i}\) are the candidate solution k and any randomly picked candidate solution h. If the fitness value of the kth solution is better than that of the hth solution, the term ‘\(X_{j,k,i} or X_{j,h,i}\)’ becomes \(X_{j,k,i}\). And if the fitness value of the hth solution is better than that of the kth solution, the term ‘\(X_{j,h,i} or X_{j,k,i}\)’ becomes \(X_{j,k,i}\).

Then update the individuals according to their fitness values.

3.2 Encoding and Decoding

The method of encoding is shown as follows:

  • The individuals are corresponding to the solutions of the FJSP, where each individual is a matrix of m rows and n columns, m is the number of the jobs, n is the number of operations for each job.

  • Each element in the individual represents the machine used in the corresponding process.

  • Initialize the individuals by selecting from the alternative machines randomly.

  • During the iterations of the algorithm, each row of the individual is treated as a variable.

The procedure of decoding is as follows:

  • Step 1: Obtain the best individual which has the information on which machine to use for each operation of each job.

  • Step 2: Determine the allowable starting time for each operation which satisfies all the constrains mentioned above. Specifically, the starting time is the completion time of previous job processed on the same machine, but if the completion time of the last operation for the same job is longer than the completion time of previous job processed on the same machine, the starting time should be the completion time of the last operation.

  • Step 3: Determine the completion time for each operation, which should be the sum of starting time and processing time.

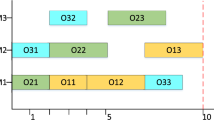
  • Step 4: Use the set of starting and completion time to paint the Gantt chart. The ith occurrences of the job number in the square represents the ith operation of the job.

4 Experimental Results and Discussions

The objective of this paper is to minimize the maximal completion time. The comparisons among the three algorithms and other algorithms are provided to compare the optimization performance. These algorithms are compared on one medium and one large size FJSP (MFJS01 and MFJS10). MFSJ01 represents that this problem has 5 jobs with 3 operations and 6 machines, MFSJ10 represents that this problem has 12 jobs with 4 operations and 8 machines. The algorithm terminates when the number of iteration reaches to the maximum generation value. The parameters for the two experiments are shown in Table 1.

Table 1. The parameters settings of optimization algorithms and benchmark
Full size table

The data of the experiment is adopted from literature [5]. Table 2 shows the experimental results and comparisons of these algorithms. To eliminate the randomness, 10 independent run is implemented for each problem. ‘Best’ represents the minimum value of makespan, and ‘Mean’ represents the average value of makespan. The results of HSA/SA, HSA/TS, HTS/TS, HTS/SA, ISA and ITS are adopted from literature [5] and [9]. The results with * are the best result for the given problem among these algorithms.

Table 2. The statistical results obtained by algorithms
Full size table
Fig. 1.
figure 1

Convergence results of the makespan for all the compared algorithms

Full size image
Fig. 2.
figure 2

Gantt chart of problem MFSJ01 of MFO

Full size image
Fig. 3.
figure 3

Gantt chart of problem MFSJ10 of MFO

Full size image

It could be found in the Table 2 that MFO obtains all the best results for the two problems. Although other 7 algorithms can obtain the same results for problem MFSJ01 by 469, the average value may not as good as MFO. MFO also obtains the best result for problem MFSJ10. The results of TLBO for MFSJ10 is outperformed by MFO, but its result is better than other algorithms. In terms of the performance of Rao-2, it obtains the same best result for MFSJ01 as several other algorithms, it does not perform well in solving MFSJ10. This means that MFO has both good effectiveness and high efficiency for solving FJSP. Figure 1 shows the convergence results of the makespan of each algorithm in a featured run. It again shows that MFO converges fast and obtains the best result. Figures 2 and 3 illustrate the Gantt charts of the optimal solution obtained by MFO for problem MFSJ01 and MFSJ10 respectively.

5 Conclusion

In this paper, three algorithms including MFO, TLBO and Rao-2 are used for solving flexible job shop scheduling problem in comparing the optimization performance. FJSP is more complicated than the classical JSP with more constraints considered whereas more flexibility is endowed. The corresponding encoding and decoding methods is illustrated and two featured scales FJSP is introduced as the benchmarks to make the comparison. Through comprehensive results comparison of the three selected algorithms and some other popular method, MFO gets the best results for both problem MFSJ01 and MFSJ10, followed by TLBO. Rao-2 get the best result for problem MFSJ01 while performs pool in the larger scale problem MFSJ10. Future research will be addressing the further improvement for the algorithms variants and constraint handling methods, and more realistic objectives would be comprehensively considered.