A genetic algorithm embedded with a concise chromosome representation for distributed and flexible job-shop scheduling problems

Abstract

This paper proposes a genetic algorithm $GA\_JS$ for solving distributed and flexible job-shop scheduling (DFJS) problems. A DFJS problem involves three scheduling decisions: (1) job-to-cell assignment, (2) operation-sequencing, and (3) operation-to-machine assignment. Therefore, solving a DFJS problem is essentially a 3-dimensional solution space search problem; each dimension represents a type of decision. The $GA\_JS$ algorithm is developed by proposing a new and concise chromosome representation ${\varvec{S}}_{{\varvec{JOB}}}$, which models a 3-dimensional scheduling solution by a 1-dimensional scheme (i.e., a sequence of all jobs to be scheduled). That is, the chromosome space is 1-dimensional (1D) and the solution space is 3-dimensional (3D). In $GA\_JS$, we develop a 1D-to-3D decoding method to convert a 1D chromosome into a 3D solution. In addition, given a 3D solution, we use a refinement method to improve the scheduling performance and subsequently use a 3D-to-1D encoding method to convert the refined 3D solution into a 1D chromosome. The 1D-to-3D decoding method is designed to obtain a “good” 3D solution which tends to be load-balanced. In contrast, the refinement and 3D-to-1D encoding methods of a 3D solution provides a novel way (rather than by genetic operators) to generate new chromosomes, which are herein called shadow chromosomes. Numerical experiments indicate that $GA\_JS$ outperforms the IGA developed by De Giovanni and Pezzella (Eur J Oper Res 200:395–408, 2010), which is the up-to-date best-performing genetic algorithm in solving DFJS problems.

Introduction

This research examines the distributed and flexible job-shop scheduling (DFJS) problems. The DFJS problem addresses a manufacturing system comprising several sub-systems (also called manufacturing cells); each cell is a flexible job-shop. Each job shall be processed in one cell (i.e., cross-cell production is prohibited). DFJS examples can be a multi-factory network in which factories are geographically distributed, and can be a multi-cell plant where several manufacturing cells are located in the same plant. To reduce overall completion time, the assignment of jobs to cells is very important because it shall affect cell loading profiles.

As stated, each cell in a DFJS system is a flexible job-shop, which denotes that an operation of a job can be processed by more than one machine. Therefore, assigning an operation to a different machine yields a different process route. The operation-to-machine assignment decision is very important in scheduling because it shall affect machine loading profiles.

In a flexible job-shop, after the operation-to-machine assignment decision has been made, each machine may have several operations to be processed. Operations assigned to the same machine must be sequenced in using the machine capacity. Therefore, operation-sequencing decision has an effect on job completion time and is very important in scheduling.

In summary, a DFJS problem involves three scheduling decisions: (1) job-to-cell assignment, (2) operation-sequencing, and (3) operation-to-machine assignment. Two degenerated DFJS problems are studied in literature. One is called flexible job-shop scheduling (FJS) problem, in which only one manufacturing cell exists in the DFJS system. The other is called distributed job-shop scheduling (DJS) problem, in which each job has a fixed route. Therefore, the job-to-cell assignment decision is not concerned in the FJS problem while the operation-to-machine assignment decision is not concerned in the DJS problem.

DJS problems are more complicated than classical job-shop scheduling (JS) problems which are NP-hard (Garey et al. 1976). Many prior studies developed genetic algorithms to solve DJS problems. For example, Jia et al. (2003) developed a genetic algorithm, which is further enhanced by Jia et al. (2007). Chan et al. (2005) developed an adaptive genetic algorithm with dominated genes. Some other prior studies attempted to solve dynamic DJS problems which include unexpected events. For example, Zhang et al. (2008) developed a multi-agent genetic algorithm and Chou and Cheng (2010) developed an agent-based method.

FJS problems are strongly NP-hard (Garey et al. 1976). Some studies developed mathematical programming approach (Bruker and Schlie 1990; Jinyan et al. 1995; Kim and Egbelu 1999; Choi and Choi 2002). Some other studies (e.g., Hmida et al. 2010) developed tree search method. And many other studies developed meta-heuristic algorithms in two approaches. One approach is making the two scheduling decisions in a hierarchical manner. That is, the operation-to-machine assignment decision is firstly made; then the operation-sequencing decision is subsequently made by meta-heuristic algorithms (Brandimarte 1993; Tung et al. 1999; Kacem et al. 2002a, b; Bożejko et al. 2010). The other approach is making the two decisions simultaneously by meta-heuristic algorithms, which include tabu search algorithms (Hurink et al. 1994; Dauzère-Pérès and Paulli 1997; Mastrolilli and Gambardella 2000; Jia and Hu 2014), genetic algorithm (Ho and Tay 2004; Pezzella et al. 2008; Tay and Wibowo 2004; Zhang et al. 2011), simulated annealing (Baykasoǧlu 2002), and hybrid meta-heuristic algorithms (Xia and Wu 2005; Gao et al. 2008; González et al. 2013; Xing et al. 2010; Yuan and Xu 2013; Gutiérrez and García-Magariño 2011).

In solving DFJS problems, two studies (Chan et al. 2006; De Giovanni and Pezzella 2010) developed genetic algorithms (GAs); and Ziaee (2014) developed a heuristic algorithm. A mathematical formulation of DFJS problems can be referred to Chan et al. (2006). The GA developed by De Giovanni and Pezzella (2010) is called IGA, which is the up-to-date best-performing algorithm for solving DFJS problems and is taken as the benchmark of this research. To facilitate comparison, the chromosome representations used in Chan et al. (2006) is called ${\varvec{S}}_{{\varvec{C}}}$ and that used in De Giovanni and Pezzella (2010) is called ${\varvec{S}}_{{\varvec{G}}}$ hereafter.

This paper proposes a genetic algorithm $GA\_JS$ for solving DFJS problems. The $GA\_JS$ algorithm is developed by proposing a new and concise chromosome representation ${\varvec{S}}_{{\varvec{JOB}}}$, which models a 3-dimensional DFJS scheduling solution by a 1-dimensional scheme (i.e., a sequence of all jobs to be scheduled). That is, the chromosome space is 1-dimensional (1D) and the solution space is 3-dimensional (3D).

In $GA\_JS$, we develop a 1D-to-3D decoding method to convert a 1D chromosome into a 3D solution. In addition, given a 3D solution, we use a refinement method to improve the scheduling performance and subsequently use a 3D-to-1D encoding method to convert the refined 3D solution into a 1D chromosome. The 1D-to-3D decoding method is designed to obtain a “good” 3D solution which tends to be load-balanced. In contrast, the refinement and 3D-to-1D encoding methods of a 3D solution provides a novel way (rather than by genetic operators) to generate new chromosomes, which are herein called shadow chromosomes. Numerical experiments indicate that $GA\_JS$ outperforms the IGA developed by De Giovanni and Pezzella (2010).

The remaining of this paper is organized as follows. “Comparison of chromosome representations” section compares the proposed chromosome representation ${\varvec{S}}_{{\varvec{JOB}}}$ against the two prior ones ${\varvec{S}}_{{\varvec{C}}}$ and ${\varvec{S}}_{{\varvec{G}}}$. “$GA\_JS$ algorithmic framework” section describes the algorithmic framework of $GA\_JS$. “Decoding of ${\varvec{S}}_{{\varvec{JOB}}}$ chromosomes” section presents the 1D-to-3D decoding method for converting a 1D ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome into a 3D scheduling solution. “Refinement and encoding of 3D solutions” section describes the refinement and 3D-to-1D encoding methods for obtaining a shadow chromosome from a 3D solution. “$GA\_JS$ algorithm” section summarizes the proposed algorithm $GA\_JS$. “Numerical experiments” section reports experiments of comparing $GA\_JS$ against IGA. Concluding remarks are in last section.

Comparison of chromosome representations

This section compares the proposed chromosome representation ${\varvec{S}}_{{\varvec{JOB}}}$ against two prior ones ${\varvec{S}}_{{\varvec{C}}}$ and ${\varvec{S}}_{{\varvec{G}}}$, in which ${\varvec{S}}_{{\varvec{C}}}$ is proposed by Chan et al. (2006) and ${\varvec{S}}_{{\varvec{G}}}$ is proposed by De Giovanni and Pezzella (2010). The three chromosome representations are explained by referring to a DFJS problem shown in Table 1(a), in which there are 3 jobs and 2 cells and each job has 3 operations. Then, the three chromosome representations are examined in terms of eight encoding principles (or properties) proposed in prior research (Gen et al. 2008; Gen and Cheng 1997; Raidl and Julstrom 2003; Lin and Gen 2006).

Table 1 A DFJS example (a) Job-Cell-Op table, (b) Job-Cell table

$S_{C}$ chromosome representation

As shown in Fig. 1a, an ${\varvec{S}}_{{\varvec{C}}}$ chromosome (represented by a sequence of genes) denotes a sequence of all operations. In the example DFJS problem, there are 9 operations in total; thus an ${\varvec{S}}_{{\varvec{C}}}$ chromosome involves 9 genes. Each gene models an operation by a 5-tuple vector. See the figure, the first gene is in which the $3^{\mathrm{rd}}$ and $4^{\mathrm{th}}$ elements are used to identify the operation $O_{31}$ (the $1^{\mathrm{st}}$ operation of Job $J_{3})$. Moreover in the vector , the $1^{\mathrm{st}}$ element denotes the job-to-cell assignment decision, and the $2^{\mathrm{nd}}$ denotes the operation-to-machine assignment decision. That is, job $J_{3}$ is assigned to cell $U^{2}$, and operation $O_{31}$ is assigned to machine $M^{22}$. Finally, the $5^{\mathrm{th}}$ element in the vector is a binary variable, in which 1 denotes that the gene is a dominated gene and 0 denotes that the gene is a non-dominated one. While applying genetic operators to generate new chromosomes, only dominated genes can be changed and non-dominated genes shall keep unchanged.

Fig. 1

a ${\varvec{S}}_{{\varvec{C}}}$ chromosome representation, b ${\varvec{S}}_{{\varvec{G}}}$ chromosome representation, and c ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome representation

In summary, ${\varvec{S}}_{{\varvec{C}}}$ chromosome representation explicitly models the three DFJS scheduling decisions: (1) job-to-cell assignment, (2) operation-sequencing, and (3) operation-to-machine assignment. As a result, the use of ${\varvec{S}}_{{\varvec{C}}}$ chromosomes results in a 3D chromosome space while developing a GA.

$S_{G}$ chromosome representation

As shown in Fig. 1b, an ${\varvec{S}}_{{\varvec{G}}}$ chromosome also denotes a sequence of all operations (i.e., each gene models an operation). Therefore, an ${\varvec{S}}_{{\varvec{G}}}$ chromosome also involves 9 genes in the example DFJS problem. Each gene models an operation by a 2-tuple vector. See the figure, the first gene is (2,3) in which the $1^{\mathrm{st}}$ element denotes a cell $(U^{2})$, and the $2^{\mathrm{nd}}$ element denotes a job $(J_{3})$. This implies that job $J_{3}$ is assigned to cell $U^{2}$. Moreover, the first appearance of job $J_{3}$ implies that this gene denotes operation $O_{31}$ (i.e., the $1^{\mathrm{st}}$ operation of job $J_{3})$. Operation $O_{31}$ and the others can be identified accordingly.

Out of the three DFJS scheduling decisions, ${\varvec{S}}_{{\varvec{G}}}$ chromosome representation models only two ones: (1) job-to-cell assignment and (2) operation-sequencing. And the operation-to-machine assignment decision is obtained by a heuristic rule (De Giovanni and Pezzella 2010). As a result, the use of ${\varvec{S}}_{{\varvec{G}}}$ chromosomes results in a 2D chromosome space while developing a GA.

$S_{JOB}$ chromosome representation

As shown in Fig. 1c, an ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome denotes a sequence of all jobs (i.e., each gene models a job). Now an ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome involves only 3 genes in the example DFJS problem. See the figure, the chromosome (3,2,1) denotes that a job sequence $J_{3} \rightarrow J_{2} \rightarrow J_{1}$. By developing a decoding method which involves three heuristic rules (Fig. 2), we can convert an ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome into a DFJS scheduling solution. In the proposed $GA\_JS$ algorithm, the use of ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome representation results in a 1D chromosome space.

Fig. 2

The decoding method for converting a ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome into a 3D scheduling solution

In summary, solving a DFJS problem is a 3D solution space search problem. In developing a GA, the use of ${\varvec{S}}_{{\varvec{C}}}$ results in a 3D chromosome space; the use of ${\varvec{S}}_{{\varvec{G}}}$ results in a 2D chromosome space; and the use of ${\varvec{S}}_{{\varvec{JOB}}}$ results in a 1D chromosome space.

Chromosome properties examinations

According to prior research (Gen et al. 2008; Gen and Cheng 1997; Raidl and Julstrom 2003; Lin and Gen 2006), eight principles (or properties) have been proposed to evaluate an encoding scheme. In the following, the three chromosome representations (${\varvec{S}}_{{\varvec{C}}}$, ${\varvec{S}}_{{\varvec{G}}}$, and ${\varvec{S}}_{{\varvec{JOB}}})$ are examined in terms of the eight properties, in which $m$ denotes the total number of all job operations and $n$ denotes the total number of jobs; therefore $m>n$ substantially because a job has many operations.

Property 1

(Space): Chromosomes should not require extravagant amounts of memory. The ${\varvec{S}}_{{\varvec{C}}}$ chromosome represents a solution by $5m$ integers ($m$ genes and each gene involves 5 integers). The ${\varvec{S}}_{{\varvec{G}}}$ chromosome represents a solution by $2m$ integers ($m$ genes and each gene involves 2 integers). The ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome represents a solution by $n$ integers ($n$ genes and each gene involves 1 integer). In terms of memory requirement, the proposed ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome is the most concise.

Property 2

(Time): The time complexity of executing evaluation, recombination and mutation on chromosomes should be small. In terms of chromosome evaluation, ${\varvec{S}}_{C}$ requires less computation time than ${\varvec{S}}_{{\varvec{G}}}$; and ${\varvec{S}}_{{\varvec{G}}}$ requires less time than ${\varvec{S}}_{{\varvec{JOB}}}$. This is due to that ${\varvec{S}}_{C }$ requires no decoding, while ${\varvec{S}}_{{\varvec{JOB}}}$ requires three decoding rules and ${\varvec{S}}_{{\varvec{G}}}$ requires only one decoding rule. Yet, in terms of recombination and mutation on chromosomes, ${\varvec{S}}_{{\varvec{JOB}}}$ requires the least in computation time because its gene length is the shortest.

Property 3

(Feasibility): A chromosome corresponds to a feasible solution. The ${\varvec{S}}_{{\varvec{C}}}$ chromosome may yield an infeasible solution; for example if operation $O_{32}$ precedes $O_{31}$. The ${\varvec{S}}_{{\varvec{G}}}$ chromosome may also yield an infeasible solution; for example, if one job $(J_{3})$ is assigned to two different cells ($U^{1}$ and $U^{2}$); that is genes (1, 3) and (2, 3) appear simultaneously. In contrast, the proposed ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome always yields feasible solutions.

Property 4

(Legality): Any permutation of a chromosome corresponds to a solution. In ${\varvec{S}}_{{\varvec{C}}}$ chromosomes, a permutation may results in an infeasible solution; while in ${\varvec{S}}_{{\varvec{G}}}$ and ${\varvec{S}}_{{\varvec{JOB}}}$ chromosomes, any permutation always results in a feasible solution.

Property 5

(Completeness): Any solution has a corresponding chromosome. In ${\varvec{S}}_{{\varvec{C}}}$ chromosomes, any solution indeed has a corresponding chromosome. In ${\varvec{S}}_{{\varvec{G}}}$ and ${\varvec{S}}_{{\varvec{JOB}}}$ chromosomes, not all solution has a corresponding chromosome due to the use of decoding rules. For example, decoding the ${\varvec{S}}_{{\varvec{G}}}$ chromosome in Fig. 1b by a heuristic rule shall yield only one operation-to-machine assignment decision; yet there are many other alternatives.

Property 6

(Uniqueness): The mapping from chromosomes to solution may belong one of the following three cases: 1-to-1 mapping, n-to-1 mapping, and 1-to-n mapping. We consider the solution space as the set of all the decision portfolios, each portfolio represents an alternative of the three scheduling decisions. Then, ${\varvec{S}}_{{\varvec{C}}}$ is 1-to-1, ${\varvec{S}}_{{\varvec{G}}}$ and ${\varvec{S}}_{{\varvec{JOB}}}$ are both $n$-to-1.

Property 7

(Heritability): Offspring of simple crossover (i.e., one-cut point crossover) should correspond to solutions which combine the basic feature of their parents. The three chromosomes ${\varvec{S}}_{{\varvec{C}}}$, ${\varvec{S}}_{{\varvec{G}}}$, and ${\varvec{S}}_{{\varvec{JOB}}}$ have different degrees of heritability. ${\varvec{S}}_{{\varvec{G}}}$ has the highest degree of heritability by completely keeping job-to-cell assignment and partially keeping operation-sequencing, ${\varvec{S}}_{{\varvec{JOB}}}$ ranks 2 by partially keeping job sequence, and ${\varvec{S}}_{{\varvec{C}}}$ ranks the last because a simple crossover will very likely yield an infeasible solution.

Property 8

(Locality): A mutated chromosome should usually represent a solution similar to that of its parent. ${\varvec{S}}_{{\varvec{C}}}$ has the highest degree of locality due to substantially keeping operation-to-machine assignment and operation-sequencing; ${\varvec{S}}_{{\varvec{G}}}$ ranks 2 due to substantially keeping operation sequence, and ${\varvec{S}}_{{\varvec{JOB}}}$ ranks the last due to substantially keeping job sequence.

$GA\_JS$ algorithmic framework

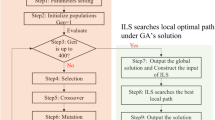
The proposed $GA\_JS$ algorithmic framework is shown in Fig. 3. As stated, the chromosome space is 1D and the solution space is 3D. To justify the “goodness” of a 1D chromosome, we have to develop a 1D-to-3D decoding method for converting a 1D chromosome into a 3D scheduling solution. Details of the decoding method shall be presented in “Decoding of ${\varvec{S}}_{{\varvec{JOB}}}$ chromosomes” section.

The $GA\_JS$ attempts to find out a best-ever solution by an evolutionary search process. That is, $GA\_JS$ firstly generates a finite set of chromosomes (called chromosome population) and iteratively updates the chromosome population in order to find a best-ever 3D scheduling solution. The $GA\_JS$ is distinguished in proposing a new way of generating new chromosomes (called shadow chromosomes).

Fig. 3

The algorithmic framework of $GA\_JS$

See Fig. 3, the chromosome population in $GA\_JS$ is updated by two ways: (1) genetic operators and (2) shadow chromosomes. The basic idea of genetic operators is a 1D-to-1D chromosome generation; that is, a new 1D chromosome is generated from one or two existing 1D chromosome. The genetic operators in the $GA\_JS$ include crossover and mutation operators, which are essentially adapted from prior GA studies.

In contrast, the basic idea of shadow chromosomes is a 3D-to-1D chromosome generation. That is, given a 3D scheduling solution, we firstly use a refinement method to improve the scheduling performance; the outcome is called the refined 3D solution. Secondly, we use a 3D-to-1D encoding method to generate a new chromosome from the refined 3D solution. Such a newly generated chromosome is called a shadow chromosome. Notice that shadow chromosomes are generated by a novel way rather than genetic operators. Details of the refinement and 3D-to-1D encoding methods shall be presented in “Refinement and encoding of 3D solutions” section; and the $GA\_JS$ procedure is summarized in “$GA\_JS$ algorithm” section.

Decoding of ${\varvec{S}}_{{\varvec{JOB}}}$ chromosomes

In the proposed $GA\_JS$, the use of ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome results in a 1D chromosome space; yet a DFJS problem is concerned with a 3D solution space. We develop a decoding method to convert an ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome into a DFJS scheduling solution. The 1D-to-3D decoding method involves three heuristic rules (H1, H2, and H3) as shown in Fig. 2. Each heuristic rule is respectively explained below by referring to the example DFJS problem in Table 1(a) and the example ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome $(J_{3}\rightarrow J_{2}\rightarrow J_{1})$ in Fig. 1c. Notation used for explaining $GA\_JS$ and the three heuristic rules and are listed below.

Notation

$J_i$::

job $i,i=1,\ldots ,n$

$O_{ij}$::

$j\hbox {th}$ operation of job $i,j=1,\ldots ,n_i$

$U^{l}$::

cell $l,l=1,\ldots ,q$

$M^{l\mathrm{k}}$::

$k\hbox {th}$ machine in cell $l,k=1,\ldots , H_l$

$d_i^l$::

transportation time required to move job $i$ in and out cell $l$

$p_{ij}^{lk}$::

processing time of operation $O_{ij}$ on machine $M^{lk}$

J::

set of all jobs

U::

set of all cells

M::

set of all machines

Decoding rule H1: job-to-cell assignment

See Fig. 2, given a ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome, heuristic rule H1 is developed to determine the job-to-cell assignment decision. The idea of rule H1 is to balance the workload of each cell. The H1 procedure involves two steps with its pseudo codes listed below followed by an example.

We now use an example to explain the H1 procedure. Step 1 is designed to estimate the average processing time $p_i^l$ for each job $(J_{i})$ in each cell $(U^{l})$ to obtain a Job-Cell table (Table 1(b)). Each element $(p_i^l )$ in Table 1(b) is obtained by the formula: ${p_{i}^{l}} = {\sum }_j \overline{p_{\imath \jmath l}}$, where $\overline{p_{\imath \jmath l}} = \frac{{\sum }_k p_{ij}^{lk}}{H_l}$ denotes the average processing time of operation $O_{ij}$ in cell $U^{l}$. See Table 1(a), $\overline{p_{111}} = (6 + 2) / 2 = 4$ indicates that the average processing time of operation $O_{11}$ in cell $U^{1}$ is 4. Accordingly, we can obtain $\overline{p_{121}} = 2.5$ and $\overline{p_{131}} = 2$. As a result, $p_1^1 = {\sum }_j \overline{p_{1 \jmath 1}} = \left( {\overline{p_{111}} + \overline{p_{121}} + \overline{p_{131}}} \right) = \left( {4+2.5+2} \right) =8.5$. Each element $\left( {p_i^l} \right)$ in Table 1(b) can be accordingly obtained.

Step 2 is designed to assign each job to a particular cell. Firstly, ${\varvec{S}}_{{\varvec{JOB}}}$ is used to determine the sequence of assigning jobs; for example, the three jobs in Fig. 4 shall be assigned to cells by following the sequence $J_{3} \rightarrow J_{2} \rightarrow J_{1}$. Then, the Job-Cell table (Table 1(b)) is used to assign each job to a cell by a try-and-select approach. That is, a job is assigned to each possible cell, and we shall select the cell whose “expected makespan” is the minimum one. The “expected makespan” is the sum of the cell workloads and the job transportation time. For example, in Fig. 4a, job $J_{3}$ is tried to be assigned to cells $U^{1}$ and $U^{2}$ which shows that the expected makespan of $U^{1}$ is longer than that of $U^{2}$; as a result, $J_{3}$ is assigned to cell $U^{2}$. Accordingly, the job assignment result can be obtained in Fig. 4. Notice that minimizing “expected makespan” in making job-to-cell assignment decision tends to balance the workload of each cell.

Fig. 4

An example of implementing heuristic rule H1

See Fig. 2, decoding the example ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome $(J_{3} \rightarrow J_{2}\rightarrow J_{1})$ by applying heuristic rule H1 results in a job-to-cell assignment decision, in which $\{J_{2}\}$ is assigned to cell $U^{1}$ and $\{J_{3}\rightarrow J_{1}\}$ is assigned to cell $U^{2}$.

Decoding rule H2: operation-sequencing

See Fig. 2, heuristic rule H2 is used to determine the operation-sequencing decision for each cell. The idea of rule H2 is to give higher priority to the job with longer remaining processing time with its pseudo codes listed below followed by an example.

We now explain heuristic rule H2 by referring to Table 2, in which job $J_{1}$ and $J_{3}$ both have been assigned to cell $U^{2}$ by applying rule H1. In Step 1, we sequence the first operations ($O_{31}$ and $O_{11}$) of all jobs in the cell $(U^{2})$ by following the job sequence $J_{3} \rightarrow J_{1}$ in Fig. 1c. See Table 2(a), the resulting operation sequence is $O_{31} \rightarrow O_{11}$.

Table 2 An example of implementing heuristic rule H2

In Step 2, we attempt to sequence the remaining operations. See Table 2(b), of all remaining operations, now only the leading operations ($O_{32}$ and $O_{12}$) of each job can be selected as the next one of the present operation sequence ($O_{31} \rightarrow O_{11}$). This implies that we need to select one job in the cell; once a job is selected, its leading operation is selected. For all jobs in the cell, we select the one whose remaining load is the longest. See Table 2(b), the remaining load of $J_{3}$ is 4.0 and that of $J_{1}$ is 8.0. Therefore, $J_{1}$ (its leading operation $O_{12}$) shall be selected; and the operation sequence becomes $O_{31} \rightarrow O_{11} \rightarrow O_{12}$. Herein, the remaining load of a job denotes the sum of the average processing time (APT) of all its remaining operations. For example, for job $J_{3}$ in Table 1(a), the APT of $O_{32}$ is $p_{32}^{22} =2$ and that of $O_{33}$ is $(p_{33}^{21} +p_{33}^{22} )/2 = (1 + 3) / 2 = 2$; as a result, the remaining load of job $J_{3}$ is $2 + 2 = 4$. Accordingly, we can obtain that the remaining load of job $J_{1}$ is 8.0. See Table 2(e), repeatedly following the above step, we can obtain the ultimate operation sequence $O_{31} \rightarrow O_{11} \rightarrow O_{12} \rightarrow O_{32} \rightarrow O_{13} \rightarrow O_{33}$.

The idea of rule H2 is intended to give higher dispatching priorities to those jobs which have longer remaining processing times. The reason is that jobs with longer remaining processing times tend to be completed later. To reduce total completion time, operations of these jobs are thus given higher priorities while allocating machine capacity to operations.

See Fig. 2, decoding the example ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome $(J_{3} \rightarrow J_{2} \rightarrow J_{1})$ by successively applying heuristic rules H1 and H2 results in the following outcomes. Jobs $\{J_{3} \rightarrow J_{1}\}$ is assigned to cell $U^{2}$, and the operation-sequencing decision in cell $U^{2}$ is $O_{31} \rightarrow O_{11} \rightarrow O_{12} \rightarrow O_{32} \rightarrow O_{13} \rightarrow O_{33}$.

Decoding rule H3: operation-to-machine assignment

Heuristic rule H3 is used to make the operation-to-machine assignment decision for each cell. The idea of rule H3 is to balance the workload of each machine by adopting a try-and-select approach. That is, we try to assign an operation $(O_{ij})$ to each possible machine in the cell; and the machine which has the lowest cumulative load is selected. The cumulative load of a machine is the total processing times of all assigned operations and the presently tried operation $O_{ij}$. Based on the idea, the pseudo code of H3 is presented below followed by an example.

We now explain procedure H3 by the example DFJS problem shown in Table 1(a). By applying rules H1 and H2, job $J_{1}$ and $J_{3}$ now have been assigned to cell $U^{2}$; and the operation sequence in cell $U^{2}$ is $O_{31} \rightarrow O_{11} \rightarrow O_{12} \rightarrow O_{32}\rightarrow O_{13}\rightarrow O_{33}$. Detail steps of applying rule H3 to assign the six operations in cell $U^{2}$ are shown in Table 3.

Table 3 An example of implementing heuristic rule H3

In Table 3, the operation sequence ($O_{31}\rightarrow O_{11}\rightarrow O_{12}\rightarrow O_{32}\rightarrow O_{13}\rightarrow O_{33})$ forms the first column. The $1^{\mathrm{st}}$ row indicates that the cumulative loads (C_Load) for the two machines are initially both 0. The $2^{\mathrm{nd}}$ row indicates that operation $O_{31}$ is assigned to machine $M^{22}$ because machine $M^{21}$ cannot process $O_{31}$. The 3$^{\mathrm{rd}}$ row updates the C_Load of each machine after assigning $O_{31}$ to $M^{22}$. The $4^{\mathrm{th}}$ row indicates that operation $O_{11}$ is assigned to machine $M^{22}$ because machine $M^{21}$ cannot process $O_{11}$. The $5^{\mathrm{th}}$ row updates the C_Load of each machine after assigning $O_{11}$ to $M^{22}$. The $6^{\mathrm{th}}$ row indicates that operation $O_{12 }$ is assigned to machine $M^{12}$ due to having lower C_Load. Repeatedly applying the above procedure, each row in Table 3 can be obtained. Notice that in the procedure a random selection method is used for resolving the tie-breaking issue. The resulting operation-to-machine assignment decision is shown in the last column of the table.

See Fig. 2, by successively applying heuristic rules H1, H2, and H3 to decode the example ${\varvec{S}}_{{\varvec{JOB}}}$ chromosome $(J_{3}\rightarrow J_{2}\rightarrow J_{1})$. Its three DFJS scheduling decisions (job-to-cell assignment, operation-to-machine assignment, and operation-sequencing) can be revealed. Based on three DFJS scheduling decisions, we can generate its Gantt chart (i.e., the exact scheduling solution) as shown in Fig. 5a.

Fig. 5

Gantt chart of ${\varvec{S}}_{{{\mathbf {JOB}}}}$ chromosome a before applying refinement method b after applying refinement method

The ideas underlying the above three heuristic rules are summarized below. Rule H1 attempts to balance the workload of each cell. Rule H3 attempts to balance the workload of each machine. Rule H2 attempts to give higher priority to the operations which tend to have a higher impact on the overall completion time.

Refinement and encoding of 3D solutions

This section presents the cell refinement method and 3D-to-1D encoding method shown in Fig. 3. Given a 3D scheduling solution as input, the cell refinement method is used to generate a refined 3D solution for obtaining better scheduling performance. In turn, the 3D refined solution is encoded to obtain a new chromosome (i.e., shadow chromosome). The pseudo code for each of the two methods is presented below and followed by examples.

Cell refinement method

Adapted from De Giovanni and Pezzella (2010), the cell refinement method is designed to improve the scheduling performance of the critical cell by changing the operation-sequencing as well as the operation-to-machine assignment in the cell. Notice that the critical cell is the cell with maximum makespan; for example, cell $U^{2}$ is the critical cell in Fig. 5a.

Notice that the Gantt chart of cell $U^{2}$ is implicitly determined by the operation sequence within the cell. See Fig. 2, the application of rule H2 yields the operation sequence within cell $U^{2}(O_{31}\rightarrow O_{11}\rightarrow O_{12}\rightarrow O_{32}\rightarrow O_{13}\rightarrow O_{33})$; in turn, the application of rule H3 yields the operation-to-machine assignment decision. These two decisions result in the Gantt chart of Fig. 5a. That is, changing the operation sequence within the cell shall change the Gantt chart (i.e., scheduling performance).

The refinement method is designed to exhaustively swap any two operations on the operation sequence $(O_{31}\rightarrow O_{11}\rightarrow O_{12}\rightarrow O_{32}\rightarrow O_{13}\rightarrow O_{33})$ within critical cell $U^{2}$ in order to obtain better scheduling performance. To avoid infeasible swapping, we model the operation sequence by replacing each operation by its associated job. Accordingly, operation sequence $O_{31}\rightarrow O_{11}\rightarrow O_{12}\rightarrow O_{32}\rightarrow O_{13}\rightarrow O_{33}$ is represented by $J_{3}\rightarrow J_{1}\rightarrow J_{1}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{3}$. Notice that each job appears several times in the sequence, in which the $n$th appearance of a job denotes its $n$th operation. Now, assume the first two operations are swapped; this yields a new sequence $J_{1}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{3}$ which can be interpreted as $O_{11}\rightarrow O_{31}\rightarrow O_{12}\rightarrow O_{32}\rightarrow O_{13}\rightarrow O_{33}$.

With sequence representation $O_{31}\rightarrow O_{11}\rightarrow O_{12}\rightarrow O_{32}\rightarrow O_{13}\rightarrow O_{33}$, the swapping of $O_{31}$ and $O_{32}$ is infeasible and shall be prohibited. Yet, with sequence representation $J_{3}\rightarrow J_{1}\rightarrow J_{1}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{3}$, the swapping of $O_{31}$ and $O_{32}$ shall be interpreted as the swapping of $J_{3}$ and $J_{3}$, which is an unchanged swapping (i.e., not meaningful swapping) and needs not to be carried out.

The operation swapping is carried out in an exhaustive and dynamic-updating manner. Consider the operation sequence $J_{3}\rightarrow J_{1}\rightarrow J_{1}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{3}$ which is a 6-element array (i.e., the value of each element denotes an operation). A swap denotes a pair of two elements. An exhaustive swapping theoretically involves C(6,2) = 15 swaps in total. See Fig. 6, each of these 15 swaps is indexed in a predefined sequence and carried out accordingly. In performing these swaps, if a swap is not meaningful, we just skip it. While a swap is meaningful, we compute the resulting makespan. If the makespan improves, the swap is regarded as “dominant”; and the operation sequence must be updated; then the remaining swaps are carried out on the updated operation sequence.

Fig. 6

Define the sequence of operation swapping in the refinement method

Example input and output of the refinement methods are illustrated below. See Fig. 5a, the input is an operation sequence $J_{3}\rightarrow J_{1}\rightarrow J_{1}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{3}$ whose resulting makespan is 14. See Fig. 5b, after exhaustively carrying out the 15 swaps, we find that the output of the refinement method yields an operation sequence $J_{1}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{3}$ whose resulting makespan is 12.

Noticeably, after carrying out the refinement method, the makespan of the critical cell may be reduced. As a result, another cell may turn out to be the new critical cell. Then, the refinement method must be accordingly performed on the new critical cell. This refinement procedure is iteratively carried out until the ultimate critical cell is determined and its minimum makespan is obtained.

Encoding method for generating shadow chromosomes

The 3D-to-1D encoding method attempts to convert a 3D scheduling solution obtained by the aforementioned refinement method into a 1D chromosome (called shadow chromosome). The pseudo code of the 3D-to-1D encoding method is listed below and followed by an example.

We now use an example to explain the 3D-to-1D encoding method by considering the 3D scheduling solution in Fig. 5b, which is the output of the refinement method. Its operation sequence within cell $U^{2}$ is $O_{11}\rightarrow O_{31}\rightarrow O_{12}\rightarrow O_{32}\rightarrow O_{13}\rightarrow O_{33}$; and its operation sequence within cell $U^{1}$ is $O_{21}\rightarrow O_{22}\rightarrow O_{23}$.

Firstly, we form an “aggregated” operation sequence by placing the operation sequence of the critical cell $(U^{2})$ in the first block and successively place the operation sequences of the other cells $(U^{1})$ in the remaining blocks. This yields an aggregated operation sequence . Secondly, we keep only the first operation of each job and yield a concise sequence ; in turn each operation is replaced by its associated job. As a result, this yields a job sequence $J_{1}\rightarrow J_{3}\rightarrow J_{2}$ which is called a shadow chromosome.

The reason why we generate shadow chromosomes in such a way is explained below. Remind that the shadow chromosome $J_{1}\rightarrow J_{3}\rightarrow J_{2}$ indirectly derives from the chromosome $J_{3}\rightarrow J_{2}\rightarrow J_{1}$ in Fig. 1c by the following steps. Firstly, the chromosome $J_{3}\rightarrow J_{2}\rightarrow J_{1}$ is decoded and yields a 3D scheduling solution in Fig. 2, whose job-to-cell assignment decisions are $U^{1}\leftarrow \{J_{2}\}$ and $U^{2}\leftarrow \{ J_{3}, J_{1}\}$. Secondly, given the job-to-cell assignment decision, the refinement method attempts to improve the scheduling performance by changing the operation-sequencing and the operation-to-machine assignment decisions. Namely, the refinement method is designed to obtain a near-optimum schedule for the job-to-cell assignment decision.

Now to further improve the scheduling performance, we need to change the job-to-cell assignment decision. And the way of generating a shadow chromosome $(J_{1}\rightarrow J_{3}\rightarrow J_{2})$ is for providing a new job-to-cell assignment decision. Applying heuristic rule H1 to decode the shadow chromosome $(J_{1}\rightarrow J_{3}\rightarrow J_{2})$, we tend to place $\{J_{1}, J_{3}\}$ which are originally in the critical cell $U^{2}$ to different cells. That is, following the job sequence $J_{1}\rightarrow J_{3}\rightarrow J_{2}$, job $J_{1}$ tends to be the first allocated job of one cell; and job $J_{3}$ tends to be the first allocated job of another cell. This implies that we attempt to “break” the critical cell and generate a new job-to-cell assignment decision; as a result, we may come out a new critical cell with better scheduling performance.

Herein we explain why such a new chromosome is named as a shadow chromosome. The term “shadow” is adopted from the “shadow cabinet” in British political system. As known, a shadow cabinet intends to criticize the policies of the government and offer alternative policies. Likewise, the shadow chromosome is designed to offer an alternative job-to-cell allocation policy by “breaking” the critical cell.

$GA\_JS$ algorithm

In this section, we present the procedure of the proposed algorithm $GA\_JS$, in which $N, \rho _{c}, \rho _{m}, k_{b}, \phi _f$, and $\phi _{max}$ are given parameters and a job in a chromosome is called a gene.

The crossover operator, designed to generate two new chromosomes from two existing chromosomes (i.e. parent chromosomes), is a one-point crossover (Gen and Cheng 1997). As shown in Fig. 7a, it randomly divides the two parent chromosomes ($A$, $B$) into two substrings ($A_{1}, A_{2}, B_{1}, B_{2}$) and two new chromosomes are generated by two steps. Consider parent chromosome $A$ as an example. In step 1, the first substring $(A_{1})$ is maintained $(J_{2}\rightarrow J_{3}\rightarrow J_{1})$. In step 2, the gene value sequence $(J_{4}\rightarrow J_{5})$ in the second substring $(A_{2})$ is modified into a new sequence $(J_{5}\rightarrow J_{4})$, which is obtained by following the gene value sequence $(J_{5}\rightarrow J_{4}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{2})$ of the other parent chromosome $(B)$. As a result, a new chromosome $A'$ (i.e., $J_{2}\rightarrow J_{3}\rightarrow J_{1}\rightarrow J_{5}\rightarrow J_{4}$) is generated. Accordingly, the other new chromosome $B'$ can be generated by the crossover operation.

Fig. 7

a Crossover operator, b mutation operator

The mutation operator is designed to generate one new chromosome from one existing chromosome (i.e. parent chromosome). It randomly chooses two genes and exchanges their gene values. As shown in Fig. 7b, two genes are randomly selected from the parent chromosome and their gene values are exchanged to generate a new chromosome .

Numerical experiments

This section compares the empirical performance of the proposed algorithm $GA\_JS$ against IGA which is proposed by De Giovanni and Pezzella (2010). Notice that the completion time of all jobs (called makepan) in the DFJS problems is taken as the performance measure.

Experiment design

To make a compatible comparison, we repeat the 2-cell, 3-cell and 4-cell experiments reported in De Giovanni and Pezzella (2010). Each of these three experiments includes 23 DFJS instances; 15 replicates are carried out for each DFJS instance in the $GA\_JS$. Genetic parameters of $GA\_JS$ are set the same as that of IGA in each experiment (Table 4).

Table 4 Genetic parameters

Algorithm $GA\_JS$ is implemented in C++ and run on a personal computer equipped with a 3.0 GHz AMD Athlon(tm) II*4640 processor and 4GB RAM. In contrast, IGA is implemented in C++ and run on a personal computer equipped with 2.0 GHz Intel Core2 processor and 2 GB RAM.

The three experiment results are shown in Table 5. Each column in the table is explained below. See Table 5, the first three columns respectively give (1) the name of instance, (2) the number of jobs, and (3) the number of operations per job. The $4^{\mathrm{th}}$ column LB reports a lower bound proposed by De Giovanni and Pezzella (2010). The formula for determining the LB is as shown below.

$$\begin{aligned} LB = \mathop {max}\limits _{i\in {\varvec{J}}} \left\{ {\mathop {min}\limits _{l\in {\varvec{U}}} \left\{ {\sum \limits _{j=1}^{n_i} \mathop {min}\limits _{k\in {\varvec{M}}} \left\{ {p_{ij}^{l\mathrm{k}}} \right\} +d_i^l} \right\} } \right\} \end{aligned}$$

The $5^{\mathrm{th}}$ column MK denotes the best makespan of all replicates in an instance. The $6^{\mathrm{th}}$ column Av. denotes the average makespan of all replicates in an instance. The $7^{\mathrm{th}}$ column $T(s)$ denotes the average computation time in seconds. The $8^{\mathrm{th}}$ column $Gap\% =\frac{MK-LB}{LB}$ reports the gap between MK and LB, and the remaining columns in the table are defined accordingly.

Table 5 Performance comparison of $GA\_JS$ against IGA in 2, 3, and 4-cell scenarios

Performance comparison

We first compare $GA\_JS$ against IGA in terms of Gap%. See Table 5, $GA\_JS$ outperforms IGA in each of the three experiments. In 2-cell experiment, the Gap% of of $GA\_JS$ is 10.1 % better than that of IGA (12.4 %). In 3-cell experiment, the Gap% of $GA\_JS$ is 0.9 % better than that of IGA (2.0 %). In 4-cell experiment, the Gap% of $GA\_JS$ is 0.0 % better than that of IGA (0.2 %).

We then compare $GA\_JS$ against IGA in terms of average solution quality (Av.). To statistically justify the performance difference, we use Wilcoxon signed rank test. In 2-cell experiment, $GA\_JS$ outperforms IGA with $p\hbox {-value} = 0.002 < 0.05$. In 3-cell experiment, $GA\_JS$ outperforms IGA with $p\hbox {-value} = 0.018 < 0.05$. In 4-cell experiment, the difference between $GA\_JS$ and IGA is not statistically significant with $p\hbox {-value} = 0.091 > 0.05$.

We further compare $GA\_JS$ against IGA in terms of computation time. Such a comparison is for reference only because these two algorithms as stated above are run on different computers. See Table 5, $GA\_JS$ requires less computation time than IGA in each of the three experiments. In 2-cell experiment, the average computation time of $GA\_JS$ is 38.4 s, faster than that of IGA (79.6 s). In 3-cell experiment, the average computation time of $GA\_JS$ is 15.1 s, faster than that of IGA (27.9 s). In 4-cell experiment, the average computation time of $GA\_JS$ is 9.9 s, faster than that of IGA (16.2 s).

Analysis of experiment results

According to experiment results, $GA\_JS$ appears to outperform IGA. Yet, their performance differences become smaller when we increase the number of cells. In 2-cell experiment, the difference of Gap% is $2.3\,\% = 12.4\,\%$–$10.1\,\%$. In 3-cell experiment, the difference of Gap% is $1.1\,\% = 2.0\,\%$–$0.9\,\%$. In 4-cell experiment, the difference of Gap% is $0.2\,\% = 0.2\,\%$–$0.0\,\%$.

The reason why the performance differences between $GA\_JS$ and IGA monotonically decrease against the number of cells is explained below. As stated, we have 23 DFJS instances in the experiments. In each DFJS instance, the number of jobs and the number of operations are always kept the same, even in different cell environment. This implies that the cell loading becomes lower while we increase the number of cells. That is, in 4-cell environment, the capacity supply may become much higher than the capacity demand. As a result, $GA\_JS$ can find out the lower bound (LB) solution in 23 instances; and IGA can find out LB solutions in 22 instances. Therefore, the reported comparison in 3-cell/4-cell is concerned with light-loading cases. To make a comparison in high-loading cases for 3-cell/4-cell environments, we need to increase the number of jobs and operations. However, the high-loading experiment results of IGA for 3-cell/4-cell environments are not reported in literature and cannot be compared.

Concluding remarks

This paper proposes a genetic algorithm $GA\_JS$ for solving distributed and flexible job-shop scheduling (DFJS) problems. A DFJS problem involves three scheduling decisions: (1) job-to-cell assignment, (2) operation-sequencing, and (3) operation-to-machine assignment. Therefore, solving a DFJS problem is essentially a 3D solution space search problem, in which each dimension represents a type of decision.

The ${ GA}\_{ JS}$ algorithm is developed by proposing a new and concise chromosome representation ${\varvec{S}}_{{\varvec{JOB}}}$, which models a 3D scheduling solution by a 1-dimensional scheme (i.e., a sequence of all jobs to be scheduled). That is, the chromosome space is 1D and the solution space is 3D. In $GA\_JS$, we develop a 1D-to-3D decoding method to convert a 1D chromosome into a 3D solution. In addition, given a 3D solution, we use a refinement method to improve the scheduling performance and subsequently develop a 3D-to-1D encoding method to convert the refined 3D solution into a 1D chromosome.

The 1D-to-3D decoding method is designed to obtain a “good” 3D solution which tends to be load-balanced in terms of job-to-cell assignment and operation-to-machine assignment decisions. The refinement method is designed to find a near-optimum schedule for a given job-to-cell assignment decision. In contrast, the 3D-to-1D encoding method is deigned to change the job-to-cell assignment decision by “breaking” the critical cell for generating a new chromosome (called shadow chromosomes).

Numerical experiments reveal that $GA\_JS$ outperforms IGA (the up-to-date best-performing genetic algorithm in solving DFJS problems) in 2-cell and 3-cell environments. However, $GA\_JS$ and IGA appear to perform equally well in 4-cell environment. This is due to that the 4-cell experiments reported in prior studies are concerned with light-loading cases.

In future research, we attempt to develop a brand-new chromosome representation or extend the ${\varvec{S}}_{{\varvec{JOB}}}$ representation to solve a DFJS problem which includes the decision of when to carry out preventive maintenance (PM). Such a scheduling problem is in essence a 4-dimensional solution space search problem. How to model the PM decision as well as the three DFJS scheduling decisions makes room for further study.