1 Introduction

In many optimization problems, in regression methods and when solving over-determined systems of equations, it is often necessary to determine a sparse solution, that is, a solution with the minimum number of nonzero components. This kind of problems are known as sparse approximation problems and arise in different fields. In Machine Leaning, the Feature Extraction problem requires, for a given problem, to eliminate as many features as possible, while still maintaining a good accuracy in solving the assigned task (for example, a classification task). Sparse solutions are also required in signal/image processing problem, for example in sparse approximation of signals, image denoising, etc. [4, 12, 36].

In these cases the \(l_0\) pseudo-norm is utilized. This pseudo-norm counts the number of nonzero elements of a vector. Problems utilizing the \(l_0\) pseudo-norm have been considered by many researchers, but they seem “to pose many conceptual challenges that have inhibited its widespread study and application” [4]. Moreover, the resulting problem is NP–hard and, in order to construct a more tractable problem, various continuously differentiable concave approximations of the \(l_0\) pseudo-norm are used, or the \(l_0\) pseudo-norm is replaced by the simpler to handle 1–norm. In [27] two smooth approximations of the \(l_0\) pseudo-norm are proposed in order to determine a vector that has the minimum \(l_0\) pseudo-norm.

Recently, Sergeyev proposed a new approach to infinitesimals and infinitiesFootnote 1 based on the numeral \(\textcircled {1}\), the number of elements of \(\mathrm{{\mathrm I}}\!\mathrm{{\mathrm N}}\), the set of natural numbers. It is crucial to note that \(\textcircled {1}\) is not a symbol and is not used to perform symbolic calculations. In fact, the \(\textcircled {1}\) is a natural number, and it has both cardinal and ordinal properties, exactly as the “standard”, finite natural numbers. Moreover, the new proposed approach is different from non–Standard Analysis, as demonstrated in [33]. A comprehensive description of the grossone–based methodology can also be found in [32].

The use of \(\textcircled {1}\) and the new approach to infinite and infinitesimals has been beneficial in several fields of pure and applied mathematics including optimization [6,7,8,9, 14, 15, 17,18,19, 23], numerical differentiation [29], ODE [1, 22, 34], hyperbolic geometry [25], infinite series and the Riemann zeta function [28, 30], biology [31], and cellular automata [13].

Moreover, this new computational methodology has been also utilized in the field of Machine Learning allowing to construct new spherical separations for classification problems [2], and novel sparse Support Vector Machines (SSVMs) [16].

In this chapter we discuss the use of \(\textcircled {1}\) to obtain new approximations for the \(l_0\) pseudo-norm, and two applications are considered in detail. More specifically, the chapter is organized as follows. In Sect. 2 some of the most utilized smooth approximations of the \(l_0\) pseudo–norm proposed in the literature are discussed. Then, in the successive Sect. 3 it is shown how to utilize \(\textcircled {1}\) for constructing approximations of the \(l_0\) pseudo-norm. Finally, in Sect. 4, mostly based on [16], two relevant applications of the newly proposed approximation scheme for the \(l_0\) pseudo norm are discussed in detail: the elastic net regulation problem and sparse Support Vector Machines.

We briefly describe our notation now. All vectors are column vectors and will be indicated with lower case Latin letter (i.e. x, y, \(\ldots \)). Subscripts indicate components of a vector, while superscripts are used to identify different vectors. Matrices will be indicated with upper case Roman letter (i.e. A, B, \(\ldots \)). The set of natural and real numbers will be denoted, respectively, by \(\mathrm{{\mathrm I}}\!\mathrm{{\mathrm N}}\) and \(\mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}\). The space of the n–dimensional vectors with real components will be indicated by \(\mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\). Superscript \(^T\) indicates transpose. The scalar product of two vectors x and y in \(\mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\) will be denoted by \({x}^T{y}\). Instead, for a generic Hilbert space, the scalar product of two elements x and y will be indicated by \(\left\langle x,y \right\rangle \). The Euclidean norm of a vector x will be denoted by \(\left\| x \right\| \). The space of the \(m\times n\) matrices with real components will be indicated by \(\mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^{m\times n}\). For a \({m \times n}\) matrix A, \(A_{ij}\) is the element in the ith row, jth column.

In the new positional numeral system with base \(\textcircled {1}\), a gross-scalar (or gross–number) C has the following representation:

$$\begin{aligned} C= C^{(p_{m})} {\textcircled {1}}^{p_{m}}+ \cdots + C^{(p_{1})} {\textcircled {1}}^{p_{1}}+ C^{(p_{0})} {\textcircled {1}}^{p_{0}}+ C^{(p_{-1})} {\textcircled {1}}^{p_{-1}}+\cdots +C^{(p_{-k})} {\textcircled {1}}^{p_{-k}}, \end{aligned}$$
(1)

where \(m,k\in \mathrm{{\mathrm I}}\!\mathrm{{\mathrm N}}\), for \(i=-k, -k+1,\ldots ,-1,0, 1,\ldots ,m-1,m\), the quantities \(C^{(p_{i})}\) are floating-point numbers and \(p_{i}\) are gross-numbers such that

$$\begin{aligned} p_{m}>p_{m-1}>\cdots>p_{1}>p_{0}=0>p_{-1}>\cdots>p_{-k+1}>p_{-k}. \end{aligned}$$
(2)

If \(m=k=0\) the gross-number C is called finite; if \(m>0\) it is called infinite; if \(m=0\), \(C^{(p_0)}=0\) and \(k>0\) it is called infinitesimal; the exponents \(p_{i}\), \(i=-k, -k+1,\ldots ,-1,0, 1,\ldots ,m-1,m\), are called gross-powers.

2 The \(l_0\) Pseudo-norm in Optimization Problems

Given a vector \(x=(x_1,x_2,\dots ,x_n)^T\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\), the \(l_0\) pseudo-norm of x is defined as the number of its components different from zero, that is:

$$\begin{aligned} \left\| x \right\| _0 = \text{ number } \text{ of } \text{ nonzero } \text{ components } \text{ of } x = \sum _{i=1}^{n} 1_{x_i}, \end{aligned}$$
(3)

where \(1_a\) is the characteristic (indicator) function, that is, the function which is equal to 1 if \(a \ne 0\) and zero otherwise.

Note that \(\left\| \cdot \right\| _0\) is not a norm and hence is called, more properly, pseudo-norm. In fact, for a non zero vector \(x \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\), and a not null constant \( \lambda \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}\), we have:

$$\begin{aligned} \left\| \lambda x \right\| _0 = \left\| x \right\| _0 . \end{aligned}$$

Consequently \(\left\| \lambda x \right\| _0 = \left| \lambda \right| \left\| x \right\| _0 \), \(\lambda \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}\), if and only if \(\left| \lambda \right| = 1\).

The \(l_0\) pseudo-norm plays an important role in several numerical analysis and optimization problems, where it is important to get a vector with as few non-zero components as possible. For example, this pseudo-norm has important applications in elastic-net regularization, pattern recognition, machine learning, signal processing, subset selection problem in regression and portfolio optimization. For example, in signal and image processing many media types can be sparsely represented using transform-domain methods, and sparsity of the representation is fundamental in many highly used techniques of compression (see [4] and references therein). In [20, 26] the cardinality-constrained optimization problem is studied and opportunely reformulated. In [5] the general optimization problem with cardinality constraints has been reformulated as a smooth optimization problem.

The \(l_0\) pseudo-norm is strongly related to the \(l_p\) norms. Given a vector \(x=(x_1,x_2,\dots ,x_n)^T\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\), the \(l_p\) norm of x is defined as

$$ \left\| x \right\| _p :=\left( \sum _{i=1}^n \left| x_i \right| ^p \right) ^{\frac{1}{p}}. $$

It is not too difficult to show that

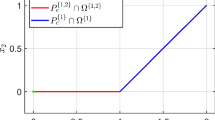
$$ \left\| x \right\| _0 = \lim _{p \rightarrow 0} \left\| x \right\| _p^p = \lim _{p \rightarrow 0}\sum _{i=1}^n \left| x_i \right| ^p. $$

In Fig. 1 the behavior of \(\left| \sigma \right| ^p\) (\(\sigma \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}\)) for different values of p is shown (see also [4]). Note that, as the figure suggests, for \(0< p < 1\), the function \(\left\| x \right\| _p\) is a concave function.

Fig. 1
figure 1

The value of \(\left| \sigma \right| ^p\) for different values of p

Full size image

It must be noted that the use of \(\left\| x \right\| _0 \) makes the problems extremely complicated to solve, and various approximations of the \(l_0\) pseudo-norm have been proposed in the scientific literature, For example, in [27] two smooth approximations of the \(l_0\) pseudo-norm are proposed in order to determine a particular vector that has the minimum \(l_0\) pseudo-norm.

In [24], in the framework of elastic net regularization, the following approximation of \(\left\| x \right\| _0\) is studied:

$$\begin{aligned} \left\| x \right\| _{0,\delta } := \sum _{i=1}^{n} \frac{x_i^2}{x_i^2 + \delta }, \end{aligned}$$
(4)

where \(\delta \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}},\ \delta >0\), and a small \(\delta \) is suggested in order to provide a better approximation of \(\left\| x \right\| _0\).

Instead, in the context of Machine Learning and Feature Selection [3], the following approximation of \(\left\| x \right\| _0\):

$$\begin{aligned} \left\| x \right\| _{0,\alpha } := \sum _{i=1}^n \left( 1 - e^{-\alpha \left| x_i \right| } \right) , \end{aligned}$$
(5)

where \(\alpha \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}\), \(\alpha >0\), is proposed, and the value \(\alpha =5\) is recommended.

By using \(\textcircled {1}\), in [16] a new approximation of \(\left\| x \right\| _0\) has been suggested. In the next section we discuss in detail this approximation and we also propose other approximations that use the new numeral system based on \(\textcircled {1}\). Moreover, we provide the connections between \( \left\| x \right\| _0\) and the new approximations.

Note that the approximation introduced in [16] has been used in connection to two different applications. The first application is an elastic net regularization. The second application concerns classification problems using sparse Support Vector Machines. These two applications are extensively reviewed in Sect. 4.

3 Some Approximations of the \(l_0\) Pseudo-norm Using \(\textcircled {1}\)

The first approximation of the \(l_0\) pseudo-norm in terms of \(\textcircled {1}\) was proposed in [16], where, following the idea suggested in [24] of approximating the \(l_0\) pseudo-norm by (4), the following approximation has been suggested:

$$\begin{aligned} \left\| x \right\| _{0,\textcircled {1},1}:=\sum _{i=1}^{n} \frac{x_i^2}{x_i^2 + \textcircled {1}^{-1}}. \end{aligned}$$
(6)

In this case, we have that

$$\begin{aligned} \left\| x \right\| _{0,\textcircled {1},1} = \left\| x \right\| _0 + C \textcircled {1}^{-1}, \end{aligned}$$
(7)

for some gross-number C which includes only finite and infinitesimal terms. Therefore, the finite parts of \( \left\| x \right\| _0 \) and \(\left\| x \right\| _{0,\textcircled {1},1} \) coincide.

To this scope, let

$$\begin{aligned}&\psi _1(t)=\frac{t^2}{t^2 + \textcircled {1}^{-1}}, \quad t\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}. \end{aligned}$$
(8)

We have that \(\psi _1(0)=0\) and \(\psi _1(t)=1-\textcircled {1}^{-1}S\), when \(t\ne 0\), where S is a gross-number such that

$$\displaystyle 0<S=\frac{1}{t^2+\textcircled {1}^{-1}}<\frac{1}{t^2}.$$

Therefore, S has only finite and infinitesimal terms. Moreover,

$$\begin{aligned} \sum _{i=1}^{n} \frac{x_i^2}{x_i^2 + \textcircled {1}^{-1}}=\sum _{i=1}^{n} \psi _1(x_i)=\sum _{i=1, x_i\ne 0}^n\psi _1(x_i)=\left\| x \right\| _0 + C \textcircled {1}^{-1}, \end{aligned}$$
(9)

where

$$ C =\left\{ \begin{array}{cc} \displaystyle -\sum _{i=1, x_i\ne 0}^n S_{i},&{} \quad \mathop {\mathrm{when}} \left\| x \right\| _0\ne 0,\\[6mm] 0,&{} \quad \mathop {\mathrm{otherwise}}, \end{array} \right. $$

and \(S_{i}\) is a gross-number such that

$$\displaystyle 0<S_{i}=\frac{1}{x_{i}^2+\textcircled {1}^{-1}}<\frac{1}{x_{i}^2}, \quad x_i\ne 0, \quad i=1, \ldots , n.$$

Hence C is a gross-number with only finite and infinitesimal terms and the finite part of of \( \left\| x \right\| _0 \) and \(\left\| x \right\| _{0,\textcircled {1},1} \) are the same.

A different proof of this result is provided in [16]. For \(i=1,\ldots ,n\), let assume that

$$\begin{aligned} x_{i} = x^{(0)}_{i} + R_i \textcircled {1}^{-1} , \end{aligned}$$

where \(R_i\) includes only finite and infinitesimal terms.

When \(x_i^{(0)} = 0\):

$$ \psi _1(x_i) = \frac{R_i^2\textcircled {1}^{-2}}{R_i^2\textcircled {1}^{-2} +\textcircled {1}^{-1} } = \textcircled {1}^{-1} \frac{R_i^2}{R_i^2\textcircled {1}^{-1} + 1 } = 0 \; \textcircled {1}^{0} + R_i' \textcircled {1}^{-1} ,$$

where \(R_i'\) includes only finite and infinitesimal terms.

When, instead, \(x_i^{(0)} \ne 0\):

$$ \psi _1(x_i) = \frac{\left( x^{(0)}_{i} + R_i\textcircled {1}^{-1}\right) ^2 }{\left( x^{(0)}_{i} + R_i\textcircled {1}^{-1}\right) ^2 +\textcircled {1}^{-1} } = 1 - \frac{\textcircled {1}^{-1}}{\left( x_i^{(0)} + R_i\textcircled {1}^{-1}\right) ^2 +\textcircled {1}^{-1} }= 1 + R_i' \textcircled {1}^{-1},$$

where, again, \(R_i'\) includes only finite and infinitesimal terms. Therefore,

$$ \left\| x \right\| _{0,\textcircled {1},1} = \sum _{i=1}^{n} \psi _1(x_i) = \left\| x \right\| _{0} + S \textcircled {1}^{-1} $$

where S includes only finite and infinitesimal terms and hence \(\left\| x \right\| _{0,\textcircled {1},1}\) and \(\left\| x \right\| _{0}\) coincide in their finite part.

Following the idea suggested in [3], we now propose three novel approximation schemes of the \(l_0\) pseudo-norm all based on the use of \(\textcircled {1}\). In [3] the authors proposed to approximate the \(l_0\) pseudo-norm using (5) and suggest to take a fixed value for \(\alpha \), i.e. \(\alpha =5\), or an increasing sequence of values of \(\alpha \).

Based on this idea, we propose the following approximation formula for \(\left\| x \right\| _0\):

$$\begin{aligned}&\left\| x \right\| _{0,\textcircled {1},2}:= \sum _{i=1}^n\left( 1-\textcircled {1}^{-\alpha \vert x_i\vert }\right) , \quad \alpha >0. \end{aligned}$$
(10)

Also in this case, the finite parts of \( \left\| x \right\| _0 \) and \(\left\| x \right\| _{0,\textcircled {1},2} \) coincide. More precisely, let us show that

$$\begin{aligned} \left\| x \right\| _{0,\textcircled {1},2} = \left\| x \right\| _0 -\textcircled {1}^{-\alpha m_x}C, \end{aligned}$$
(11)

where

$$\begin{aligned}&m_x=\left\{ \begin{array}{ll} \min \Bigl \{\vert x_i\vert \ :\ x_i\ne 0 \Bigr \}, &{} \quad \mathop {\mathrm{when}} x\ne 0, \\ 0, &{} \quad \mathop {\mathrm{otherwise}}, \end{array}\right. \end{aligned}$$
(12)

and C is a gross-number which is null when \( \left\| x \right\| _0 =0\) and, otherwise, includes only finite and infinitesimal terms.

Let us define

$$\begin{aligned}&\psi _2(t)=1-\textcircled {1}^{-\alpha \vert t\vert }, \quad t\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}. \end{aligned}$$
(13)

Since \(\psi _2(0)=0\), we have:

$$\begin{aligned} \left\| x \right\| _{0,\textcircled {1},2}= & {} \sum _{i=1}^n\left( 1-\textcircled {1}^{-\alpha \vert x_i\vert }\right) =\nonumber \\= & {} \sum _{i=1}^n\psi _2(x_i)=\sum _{i=1, x_i\ne 0}^n\psi _2(x_i)=\nonumber \\= & {} \vert \vert x\vert \vert _0-\sum _{i=1, x_i\ne 0}^n\textcircled {1}^{-\alpha \vert x_i\vert }=\vert \vert x\vert \vert _0-\textcircled {1}^{-\alpha m_x}C. \end{aligned}$$
(14)

It is easy to see that \(C=0\) when \( \left\| x \right\| _0=0 \). Instead, if \( \left\| x \right\| _0 \ne 0\) then C has only finite and infinitesimal terms. This shows that \( \left\| x \right\| _0 \) and \(\left\| x \right\| _{0,\textcircled {1},2} \) coincide in their finite part.

Another approximation of the \(l_0\) pseudo–norm is given by:

$$\begin{aligned}&\left\| x \right\| _0 \approx \left\| x \right\| _{0,\textcircled {1},3}:= \sum _{i=1}^n\left( 1-e^{-\textcircled {1}\vert x_i\vert }\right) . \end{aligned}$$
(15)

In this case, it is possible to show that

$$\begin{aligned} \left\| x \right\| _{0,\textcircled {1},3} = \left\| x \right\| _0 -e^{-\textcircled {1} m_x} C, \end{aligned}$$
(16)

where, as in the previous cases, C is a gross-number which includes only finite and infinitesimal terms and is null when \(\left\| x \right\| _0=0\). Hence, also in this case we have that the finite parts of \( \left\| x \right\| _0 \) and \(\left\| x \right\| _{0,\textcircled {1},3} \) coincide.

To prove the above result, let

$$\begin{aligned}&\psi _3(t)=1-e^{-\textcircled {1}\vert t\vert }, \quad t\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}. \end{aligned}$$
(17)

Since \(\psi _3(0)=0\), we have:

$$\begin{aligned} \left\| x \right\| _{0,\textcircled {1},3}= & {} \sum _{i=1}^n\left( 1-e^{-\textcircled {1}\vert x_i\vert }\right) =\nonumber \\= & {} \sum _{i=1}^n\psi _3(x_i)=\sum _{i=1, x_i\ne 0}^n\psi _3(x_i)=\nonumber \\= & {} \vert \vert x\vert \vert _0-\sum _{i=1, x_i\ne 0}^ne^{-\textcircled {1}\vert x_i\vert }=\vert \vert x\vert \vert _0-e^{-\textcircled {1} m_x}C, \end{aligned}$$
(18)

where \(m_x\) is defined in (12) and C is a gross-number with only finite and infinitesimal terms. Moreover, C is null when \(\left\| x \right\| _0=0\).

Finally, another approximation of the \(l_0\) pseudo–norm, always in the spirit of (5), is given by:

$$\begin{aligned}&\left\| x \right\| _{0,\textcircled {1},4}:=\sum _{i=1}^n\left( 1-\textcircled {1}^{-\textcircled {1}\vert x_i\vert }\right) . \end{aligned}$$
(19)

In this last case, let

$$\begin{aligned}&\psi _4(t)=1-\textcircled {1}^{-\textcircled {1}\vert t\vert }, \quad t\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}. \end{aligned}$$
(20)

Since even in this circumstance \(\psi _4(0)=0\), we have:

$$\begin{aligned} \left\| x \right\| _{0,\textcircled {1},4}= & {} \sum _{i=1}^n\left( 1-\textcircled {1}^{-\textcircled {1}\vert x_i\vert }\right) =\nonumber \\ {}= & {} \sum _{i=1}^n\psi _4(x_i)=\sum _{i=1, x_i\ne 0}^n\psi _4(x_i)=\nonumber \\= & {} \vert \vert x\vert \vert _0-\sum _{i=1, x_i\ne 0}^n\textcircled {1}^{-\textcircled {1}\vert x_i\vert }=\vert \vert x\vert \vert _0-\textcircled {1}^{-\textcircled {1} m_x}C, \end{aligned}$$
(21)

where \(m_x\) is again defined in (12) and C is a gross-number with only finite and infinitesimal terms that is null when \(\vert \vert x\vert \vert _0=0\). As in the previous cases we have that

$$\begin{aligned} \left\| x \right\| _{0,\textcircled {1},4} = \left\| x \right\| _0 -\textcircled {1}^{-\textcircled {1} m_x}C, \end{aligned}$$
(22)

and, therefore, the finite parts of \(\left\| x \right\| _0 \) and \(\left\| x \right\| _{0,\textcircled {1},4 }\) coincide.

We have presented a number of different approximation schemes for the \(l_0\) pseudo-norm. We want to stress that in all the cases the value of \(\left\| x \right\| _0 \) and its approximation coincide in their finite part and may only differ for infinitesimals quantities.

In the next section we will discuss some utilization of these approximating schemes in two extremely important problems: regularization and classification.

4 Applications in Regularization and Classification Problems

In this section we review some interesting uses of the proposed \(l_0\) pseudo–norm approximations in two classes of optimization problems: elastic net regularization problems and sparse Support Vector Machine classification problems. These two applications are deeply studied in [16].

4.1 Elastic Net Regularization

There are many important applications where we want to determine a solution \(x\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\) of a given linear system \(Ax = b\), \(A \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^{m\times n}\), \(b \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^m\), such that x has the smallest number of nonzero components, that is

$$\begin{aligned} \begin{array}{lc} {\displaystyle \mathop {\mathrm{min}}_{x}} &{} {\left\| x \right\| _0,} \\ * {\mathop {\mathrm{subject \, to}}} &{} {\begin{array}{c} Ax=b. \end{array}} \end{array} \end{aligned}$$

To this problem it is possible to associate the following generalized elastic net regularization:

$$\begin{aligned} \min _x \frac{1}{2}\left\| Ax - b \right\| _2^2 + \lambda _0 \left\| x \right\| _0 + \frac{\lambda _2}{2} \left\| x \right\| _2^2, \end{aligned}$$
(23)

where \(\lambda _0 > 0\) and \(\lambda _2 > 0\) are two regularization parameters (see [24] for details).

In [24] a suitable algorithm for the solution of Problem (23) with \(\left\| x \right\| _{0,\delta }\) (defined in (4)) instead of \(\left\| x \right\| _0\) is proposed. The corresponding solution approximates the solution of (23) and depends on the choice of \(\delta >0\) in (4).

Following the idea suggested in [24], we look for the solution of the following minimization problem:

$$\begin{aligned} \min _x f_1(x), \end{aligned}$$
(24)

where

$$\begin{aligned} f_1(x) :=\frac{1}{2}\left\| Ax - b \right\| _2^2 + \lambda _0 \left\| x \right\| _{0,\textcircled {1},1} + \frac{\lambda _2}{2} \left\| x \right\| _2^2. \end{aligned}$$
(25)

Note that Problem (24)–(25) is obtained from Problem (23) by substituting \(\left\| x \right\| _{0,\textcircled {1}, 1}\) to \(\left\| x \right\| _0\).

In [16] we proved that the corresponding solution coincides with the solution of the original Problem (23) apart from infinitesimal terms. In particular, in [16], the following iterative scheme for the solution of Problem (24)–(25) has been proposed: given an initial value \(x^0 \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\), for \(k = 0, 1, \ldots \), compute \(x^{k+1}\) by solving

$$\begin{aligned} \Biggl (A^T A + \lambda _2 I + \lambda _0 D(x^k) \Biggr ) x^{k+1} = A^T b , \end{aligned}$$
(26)

where \(I \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^{n\times n}\) is the identity matrix and \(D \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^{n\times n}\) is the following diagonal matrix:

$$\begin{aligned} D_{ii}(x) = \frac{2 \textcircled {1}^{-1}}{\left( \left( x_i\right) ^2 + \textcircled {1}^{-1} \right) ^2}, \qquad D_{ij}(x) = 0,\; i \ne j. \end{aligned}$$
(27)

The convergence of the sequence \(\{x^k\}\) to the solution of Problem (24)–(25) is ensured by Theorem 1 in [16]. In particular, when \(\mathcal {L} :=\{x: f_1(x) \le f_1(x^0) \}\) is a compact set, the above constructed sequence \(\{x^k\}_{k}\) has at least one accumulation point, \(x_k\in \mathcal {L}\) for each \(k=1,\dots \), and each accumulation point of \(\{x^k\}_{k}\) belongs to \(\mathcal {L}\) and is a stationary point of \(f_1\).

In [24] a similar algorithm was proposed, where \(\left\| x \right\| _0\) was substituted by (4). However, in this latter case, the quality of the final solution (in terms of being also a solution of Problem (24)–(25) strongly depends on the value of \(\delta \) that is utilized. In our approach, instead, taking into account that \(\left\| x \right\| _0\) and our approximation with \(\textcircled {1}\) only differ for infinitesimal terms, the final solution solves also Problem (24)–(25).

The results presented here are relative to the first of the four approximation schemes for \(\left\| x \right\| _0 \) discussed in Sect. 3.

Considering the minimization of the following functions

$$\begin{aligned} f_i(x) :=\frac{1}{2}\left\| Ax - b \right\| _2^2 + \lambda _0 \left\| x \right\| _{0,\textcircled {1},i} + \frac{\lambda _2}{2} \left\| x \right\| _2^2, \end{aligned}$$
(28)

\(\text{ with } \,\,\, i=2 \, \mathop {\mathrm{or}} \, i= 3 \, \mathop {\mathrm{or}} \, i=4,\) and computing the corresponding first order optimality conditions, new iterative schemes similar to (26) can be obtained and studied.

4.2 Sparse Support Vector Machines

The grossone \(\textcircled {1}\) and the different approximations of \(l_0\)-pseudo norm can be also used in Sparse Support Vector Machines.

Given empirical data (training set) \((x^i, y_i), \) \(i = 1, \ldots , {l},\) with inputs \(x^i \in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n,\) and outputs \(y_{i} \in \{-1,1\}\), \(i = 1, \ldots , {l}\), we want to compute a vector \(w\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\) and a scalar \(\theta \) (and hence an hyperplane) such that:

$$\begin{aligned}&{w}^T{x^i} + \theta > 0 \text{ when } y_i = 1 , \nonumber \\&{w}^T{x^i} + \theta < 0 \text{ when } y_i = -1. \nonumber \end{aligned}$$

The classification function is

$$\begin{aligned} h(x) = \text {sign}\left( {w}^T{x} + \theta \right) . \end{aligned}$$

Given

$$\begin{aligned} \phi : \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n \mapsto \mathcal {E}, \end{aligned}$$

where \(\mathcal {E}\) is an Hilbert space with scalar product \(\left\langle \cdot ,\cdot \right\rangle \), the optimal hyperplane can be constructed by solving the following (primal) optimization problem (see [10, 11, 35] and references therein for details):

$$\begin{aligned} \begin{array}{lc} {\displaystyle \mathop {\mathrm{min}}_{w, \theta , \xi }} &{} {\frac{1}{2}\left\langle w,w \right\rangle + C {e}^T{\xi },} \\ * {\mathop {\mathrm{subject \, to}}} &{} {\begin{array}{c} y_i \left( \left\langle w,\phi (x^i) \right\rangle + \theta \right) \ge 1 - \xi _i,\quad i = 1, \ldots , {l}, \\ \xi _i \ge 0, \quad i = 1, \ldots , {l}, \end{array}} \end{array} \end{aligned}$$
(29)

where \(e\in \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^l\) is a vector with all elements equal to 1 and C is a positive scalar.

The dual of (29) is

$$\begin{aligned} \begin{array}{lc} {\displaystyle \mathop {\mathrm{min}}_{\alpha }} &{} {\frac{1}{2}{\alpha }^T{Q\alpha } - {e}^T{\alpha },} \\ * {\mathop {\mathrm{subject \, to}}} &{} {\begin{array}{c} {y}^T{\alpha } = 0 ,\\ 0 \le \alpha \le Ce, \end{array}} \end{array} \end{aligned}$$
(30)

where

$$ Q_{ij} = y_i y_j K_{ij}, \quad K_{ij}= K(x^i, x^j) :=\left\langle \phi (x^i),\phi (x^j) \right\rangle ,\quad i,j=1,\dots ,l, $$

and \(K: \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n\times \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}^n \rightarrow \mathrm{\mathrm{I}}\!\mathrm{\mathrm{R}}\) is the kernel function.

We note that, this dual problem and the classification function depend only on \(K_{ij}=\left\langle \phi (x^i),\phi (x^j) \right\rangle \). In fact, from the Karush–Kuhn–Tucker conditions we have

$$\begin{aligned}&w = \sum _{i=1}^{l}\alpha _i y_i \phi (x^i), \end{aligned}$$
(31)

and the classification function reduces to

$$ h(x) = \text {sign}\Bigl (\left\langle w,\phi (x) \right\rangle + \theta \Bigr )= \text {sign}\left( \sum _{i=1}^{l}\alpha _i y_i \left\langle \phi (x^i),\phi (x) \right\rangle + \theta \right) . $$

In [21], the authors consider an optimization problem based on (29) where \(\frac{1}{2}\left\langle w,w \right\rangle \) is replaced with \(\left\| \alpha \right\| _0\) (and, then, this term is approximated by \(\frac{1}{2}\alpha \Lambda \alpha \) for opportune values of a diagonal matrix \(\Lambda \)) and use the expansion (31) of w in terms of \(\alpha \).

Furthermore, in [16] the quantity \(\left\| \alpha \right\| _0\) is replaced by \(\left\| \alpha \right\| _{0,\textcircled {1},1}\), and the following \(\textcircled {1}\)–Sparse SVM problem is defined:

$$\begin{aligned} \begin{array}{lc} {\displaystyle \mathop {\mathrm{min}}_{\alpha , \theta , \xi }} &{} { \frac{\textcircled {1}}{2} \left\| \alpha \right\| _{0,\textcircled {1},1} + C {e}^T{\xi },} \\ * {\mathop {\mathrm{subject \, to}}} &{} {\begin{array}{c} y_i \Bigl [{K_{i.}}^T{\alpha }+ \theta \Bigr ] \ge 1 - \xi _i,\;\;\; i = 1, \ldots , {l},\\ \xi \ge 0, \end{array}} \end{array} \end{aligned}$$
(32)

where \(K_{i.}\) denotes the column vector that corresponds to the ith row of the matrix K.

The algorithmic scheme, originally proposed in [21] and revised in [16], starting from \(\lambda ^0_r=1\), \( r = 1, \ldots , {l},\)  requires, at each iteration, the solution of the following optimization problem:

$$\begin{aligned} \begin{array}{lc} {\displaystyle \mathop {\mathrm{min}}_{\alpha , \theta , \xi }} &{} { \displaystyle \frac{1}{2}\sum _{r=1}^{l} \lambda ^k_r \alpha _r^2 + C {e}^T{\xi },} \\ * {\mathop {\mathrm{subject \, to}}} &{} {\begin{array}{c} y_i \Bigl [{K_{i.}}^T{\alpha }+ \theta \Bigr ] \ge 1 - \xi _i,\;\;\; i = 1, \ldots , {l},\\ \xi \ge 0, \end{array}} \end{array} \end{aligned}$$
(33)

and then the update of \(\lambda ^k\) with a suitable formula.

From the Karush–Kuhn–Tucker   conditions for Problem (32), it follows that

$$\begin{aligned} \displaystyle \frac{1}{\displaystyle \left( \alpha _r^2 + \textcircled {1}^{-1}\right) ^2} \alpha _r = {\bar{K}_{r.}}^T{\beta }, \quad r = 1, \ldots , {l} , \end{aligned}$$
(34)

where \(\bar{K}_{r.}\) is the r–th row of the matrix \(\bar{K}\) with \( \bar{K}_{rj} = y_j K_{jr}\), for \(r,j = 1, \ldots , {l}\).

The Conditions (34) above suggest the more natural updating formula:

$$\begin{aligned} \lambda ^{k+1}_r = \displaystyle \frac{1}{\displaystyle \left( \alpha _r^2 + \textcircled {1}^{-1}\right) ^2}, \quad r = 1, \ldots , {l}. \end{aligned}$$
(35)

Moreover, by considering the expansion of the gross-number \(\alpha \), it is easy to verify that formula (35) well mimics the updating formulas for \(\lambda ^k\) proposed in [21], also providing a more sound justification for the updating scheme.

We note that the algorithm proposed in [16], and briefly described here, is based on the first of the approximations of \(\left\| \alpha \right\| _0\) discussed in Sect. 3. Using the other different approximations introduced in the same section, new different updating formulas for \(\lambda ^{k+1}\) can be obtained.

5 Conclusions

The use of the \(l_0\) pseudo–norm is pervasive in optimization and numerical analysis, where a sparse solution is often required. Using the new approach to infinitesimal and infinite proposed by Sergeyev, four different approximations of the \(l_0\) pseudo–norm are presented in this chapter. In all cases, we proved that the finite value of the \(l_0\) pseudo–norm and and its approximation coincide, being different only for infinitesimal terms. The use of such approximations is beneficial in many applications, where the discontinuity due to the use of the \(l_0\) pseudo–norm is easily eliminated, by using one of the four proposed approaches presented in this chapter.