Abstract
We introduce partial sessions and partial (multiparty) session types, in order to deal with open systems, i.e., systems with missing components. Partial sessions can be composed, and the type of the resulting system is derived from those of its components without knowing any suitable global type nor the types of missing parts. Incompatible types, due to e.g. miscommunications or deadlocks, are detected at the merging phase. We apply these types to a process calculus, for which we prove subject reduction and progress, so that well-typed systems never violate the prescribed constraints. Therefore, partial session types support the development of systems by incremental assembling of components.
Work supported by the Italian MIUR project PRIN 2017FTXR7S IT MATTERS (Methods and Tools for Trustworthy Smart Systems).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
(Multiparty) session types (MPST) are a well-established theoretical and practical framework for the specification of the interactions between components of a distributed systems [10, 12, 15,16,17, 26]. The gist of this approach is to first describe the system’s overall behaviour by means of a global type, from which a local specification (local type) for each component can be derived. The system will behave according to the global type if each component respects its local type, which can be ensured by means of, e.g., static type checking [18, 24]. Therefore, session types support a top-down style of coding: first the designer specifies the behaviour from a global perspective, then the programmers are given the specifications for their modules. On the other hand, these session types do not fit well bottom-up programming models, where systems are built incrementally by composing existing reusable components, possibly with dynamic bindings. In these situations, components could offer “contracts” in the form of, e.g., session types; then, when these components are connected together, we would like to derive the contract for the resulting system from components’ ones. The system becomes a new component which can be used in other assemblies, and so on.
To this end, we need to infer the type for an open system (i.e., where some parts may be still missing) using the types of the known components, in a compositional way and without knowing any global type. This is challenging. As an example, let us consider a protocol from [10] with three participants: a server s, an authorization server a and some client c. First, s sends to c either a request to login, or to cancel. In the first case, c sends a password to a, and a sends a boolean to s (telling whether c is authorized). In the second case, c tells a to quit. Using the syntax of [10], the two server processes have the following types:
Let us suppose that we have implementations a and s for \(S_a,S_s\). To prevent miscommunications, we would like to verify that these two processes work well together; e.g., we have to ensure that a can send the message auth(Bool) to s iff s is waiting for it. This corresponds to see these two processes as a single system a|s, and to check that a|s is well-typed without knowing the behaviour of clients; more precisely, we have to figure out a session type for a|s from \(S_a\) and \(S_s\). This is difficult, because the link that propagates the choice made by s to a is the missing client c, so we have to “guess” its role without knowing it.
In this paper, we address this problem by introducing partial sessions and partial (multiparty) session types. Partial session types generalise global types with the possibility to type also partial (or open) sessions, i.e., where some participant may be missing. The key difference is that while a global type is a complete, “platonistic” description of the protocol, partial session types represent the subjective views from participants’ perspectives. We can merge two sessions with the same name but from two different “point of views”, whenever their types are compatible; in this case, we can compute the new, unified, session type from those of the components. In this way, we can guarantee important properties (e.g., absence of deadlocks) about partial session without knowing all participants beforehand, and without a complete global type. In fact, the distinction between local and global types vanishes: local types correspond to partial session types for sessions with a single participant, and global types correspond to finalized partial session types, i.e., in which no participant is missing.
Defining “compatibility” and how to merge partial session types is technically challenging. Intuitively, the semantics of a partial session type is the set of all possible execution traces (which depend on internal and external choices). We provide a merging algorithm computing a type covering all the possible synchronizations of these traces. Incompatible types, due to, e.g., miscommunications or deadlocks, are detected when no synchronization is possible. Also the notion of progress has to be revisited, to accommodate the case when a partial session cannot progress not due to a deadlock, but due to some missing participant.
The rest of the paper is organized as follows. In Sect. 2 we introduce a formal calculus for processes communicating over multiparty sessions. Partial session types are presented in Sect. 3, and the type system is in Sect. 4. Central to this type system is the merging algorithm, which we describe in Sect. 5. Subject reduction and progress are given in Sect. 6. Finally, comparison with related work are in Sect. 7, and conclusions are in Sect. 8.
A prototype implementation of the merging algorithm can be found at https://github.com/cstolze/partial-session-types-prototype.
2 A Calculus for Processes over Multiparty Sessions
Our language for processes is inspired by [10], in turn inspired by [28]; as in those works, we consider synchronous communications. We note \(p, q, p_1, p', \ldots \) for participant names, belonging to some set \(\mathfrak {P}\); \(\tilde{p}\) for a finite non-empty set of participants \(\{p_1, \ldots , p_n\}\). The syntax of processes is as follows:
The process \(\overline{x}^{p \tilde{q}}\triangleright \mathrm {in}_i. P\) sends label \(\mathrm {in}_i\) in session x, as participant p, to \(\tilde{q}\), and proceeds as P. This label is received by processes of the form \(x^{q p}\triangleleft (Q_1, Q_2)\), which then proceeds as \(Q_i\). The process \(\overline{x}^{p \tilde{q}}(y). P\) creates a fresh subsession handler y, sends it to \(\tilde{q}\), and proceeds as P. This handler is received by processes of the form \(x^{q p}(y). (Q \parallel R)\) which forks a process Q (dedicated to y) in parallel to the continuation R (on x)Footnote 1. We compose the processes P and Q through session x with \(P \mid _x Q\). \(\mathrm {close}(x)\) is the neutral element for \(\mid _x\), while \(\mathrm {wait}(x). P\) closes session x when all the other participants are gone. \((\nu x) P\) is the standard restriction, and \(P + Q\) is the standard non-deterministic choice.
The session name y is bound in expressions of the form \((\nu y) P\), \(\overline{x}^{p \tilde{q}}(y). P\), and \(x^{p q}(y). (P \parallel Q)\). Free names of a process P (noted \(\mathrm {fn}(P)\)) are the set of free names of sessions appearing in P.
In order to define the operational semantics, we first introduce the usual notion of contextual equivalence.
Definition 2.1
(Contexts). \( \mathcal C[\_] \;{:}{:=}\; \_ \mid (\nu x) \mathcal C[\_] \mid (\mathcal C[\_] \mid _x P) \mid (P \mid _x \mathcal C[\_]) \)
Definition 2.2
(Equivalence \(\equiv \)). The relation \(\equiv \) is the smallest equivalence relation closed under contexts (that is, \(P \equiv Q \Rightarrow \mathcal C[P] \equiv \mathcal C[Q]\)) satisfying the following rules (we suppose that x, y and z are different session names):
We can see that processes have the structure of a commutative monoid, thus we will use \(\varPi ^z_i P_i\) as a shorthand for \(P_1 \mid _z \dots \mid _z P_n\).
Definition 2.3
(Reductions for processes). The actions \(\alpha \) for processes are defined as:
We may write \(x : \gamma \) for either \(x : p \rightarrow \tilde{q} : \langle \cdot \rangle \) or \( x : p \rightarrow \tilde{q} : \& \mathrm {in}_i\).
We note \(P \overset{\alpha }{\longrightarrow } Q\) for a transition from P to Q under the action \(\alpha \). This relation is defined by the rules in Fig. 1.
Note that the typing rules will ensure x does not escape its scope when reducing \((\nu x) (\mathrm {wait}(x).P)\) into P.
Example 2.1
As a running example, let us consider three participants p, q, r. p chooses whether to send a message to r or not; this choice is communicated to r through an intermediate participant q.
Here is an example of execution:
Notice that p can start the session with just q and then wait for input from r:
3 Partial Multiparty Session Types
Partial multiparty session types (or just “session types”) define the behaviour of a partial session. Their syntax is as follows (where \(i \in \{1,2\}\)):
The set of participant names appearing in G is denoted by \(\mathrm {fn}(G)\).
Informally, \(p \rightarrow \tilde{q} : m; G\) means that the participant p sends the message m to the participants in \(\tilde{q}\), then the session continues with G. The message&in\(_{i}\) is a label, while \(\langle G \rangle \) is a fresh session handler of type G. \(\mathrm {end}\) means that the session ends and the process survives, while \(\mathrm {close}\) means that the session and the process end. \(G_1 \oplus G_2\) (resp. \( G_1 \; \& \;G_2\)) denotes an internal (resp. external) choice. Internal choices are made by local participants of the session, contrary to external choices; notice that, in contrast with standard practice, sending or receiving a label &in\(_{i}\) is unrelated from the choices done with \(\oplus \) or \( \; \& \;\). Finally, we add the empty type \(0\), which denotes no possible executions (and it is the unit of \(\oplus \)), and the inconsistent type \(\omega \), which denotes an error in the session.
Example 3.1
Continuing our running Example 2.1, the following should be the types of each participant.
These types are actually assigned to \(P_p, P_q, P_r\) by the type system we will present in Sect. 4. But moreover, we would like to be able to type also compositions of these processes; e.g. the types of \(P_p \mid _x P_q\) and \(P_q \mid _x P_r\) should be the following:
Moreover, notice that \(G_{p,q}\) describes also the behaviour of \(P_p \mid _x P_q \mid _x P_r\). As we will see in the next section, these types can be inferred from \(G_p\), \(G_q\), \(G_r\) in a compositional way. \(\square \)
A chain of communications is a type of the form \(C_1; C_2; \ldots ; C_n\). Messages m and communications C are defined as follows:
The communications \(\mathrm {end}\), \(\mathrm {close}\), \(0\), \(\omega \) are also types and they are called terminal; the only non-terminal communications are \(p \rightarrow \tilde{q} : m\) and 1, the latter representing any communication which is not observable from the current process. As such, we can prefix 1 to any session type G by defining \(1; G := G\). We denote by \(\mathfrak {C}_\omega \) the set of all communications, and by \(\mathfrak {C}= \mathfrak {C}_\omega \setminus \{\omega , 0\}\) the set of executable communications. We pose \(\mathfrak {G}_{\omega }\) the set of all session types, and \(\mathfrak {G}\) the set of session types where there is no occurence of \(0\) and \(\omega \). By default, we will use \(\mathfrak {G}_{\omega }\), while \(\mathfrak {G}\) will be used to type processes in Sect. 4.
In the following, we denote by \(S, S_1, \ldots \) sets of participants, and we use the shorthand \(S_1 \mathrel {\sharp }S_2\) for \(S_1 \cap S_2 = \varnothing \). A set of participant S will be called viewpoint.
Definition 3.1
(Independence relation). We define the independence of communications relative to a set of participants S as the smallest symmetric relation \(\mathrel {I_{S}}\) such that \(C \mathrel {I_{S}} 1\) for any C, and \((p \rightarrow \tilde{q} : m) \mathrel {I_{S}} (p' \rightarrow \tilde{q}' : m')\) whenever \((\{p\} \cup \tilde{q}) \cap (\{p'\} \cup \tilde{q}') \mathrel {\sharp }S\).
Informally, \(C_1 \mathrel {I_{S}} C_2\) means that the common participants of \(C_1\) and \(C_2\) are not in S. This independence is relative to the viewpoint of S, because when \(C_1 \mathrel {I_{S}} C_2\), the viewpoint of S cannot discriminate between \(C_1; C_2; G\) and \(C_2; C_1; G\), as is shown in Eq. (1) below. In fact, we can define an equivalence relation between session types relative to S:
Definition 3.2
(Equivalence relation). For any set of participants S, we define the relation \(\simeq _S\) on session types as the smallest congruence verifying the following properties:
We can see that the operations \(\oplus \) and \( \; \& \;\), together with the constants \(0\) and \(\omega \), form a unital commutative semiring. We note \(\bigoplus \{G_1,\ldots ,G_n\}\) for \(G_1 \oplus \ldots \oplus G_n\), and  for \( G_1 \; \& \;\ldots \; \& \;G_n\). In particular, \(\bigoplus \varnothing = 0\), and
for \( G_1 \; \& \;\ldots \; \& \;G_n\). In particular, \(\bigoplus \varnothing = 0\), and  . Equation (1) allows for the “out of order” execution of independent communications. Notice that in general \(G \oplus \omega \not \simeq _S \omega \) because the behaviour of a process of type \(G \oplus \omega \) is not necessarily always inconsistent.
. Equation (1) allows for the “out of order” execution of independent communications. Notice that in general \(G \oplus \omega \not \simeq _S \omega \) because the behaviour of a process of type \(G \oplus \omega \) is not necessarily always inconsistent.
The fact that choices \(G_1 \oplus G_2\) or \( G_1 \; \& \;G_2\) are unrelated from the action of sending a choice allows us to move these operators around without changing the meaning. Hence, we can consider disjunctive normal forms of session types.
Definition 3.3
(Disjunctive Normal Form). A session type G is in Disjunctive Normal Form (DNF), if it is of the form  with the \(A_i\) being sets of chains of communications where every message \(\langle G' \rangle \) is in DNF.
with the \(A_i\) being sets of chains of communications where every message \(\langle G' \rangle \) is in DNF.
In DNF a type can be seen as a set of sets of traces (sequences of communications), the intuition being that a trace describes a single possible interaction of a process. A set of traces defines a deterministic strategy followed by a single process P, describing how P reacts for any possible choice from other processes. A set of sets of traces describes all the possible strategies that P can follow once it has selected all its possible internal choices. So, describing a behaviour in DNF is like saying that a process P starts by anticipating all possible internal choices for all possible interactions during execution. After that, P becomes deterministic and reacts in a single possible way to communications of other processes.
The equivalence relation on types allows us to rewrite any type in a DNF.
Proposition 3.1
For any type G and set of participants S, we can compute a \(G'\) in DNF such that \(G'\simeq _S G\).
4 Type System
In this section we introduce the type system for processes. A key point is that the type of a session are relative to the participants of that session.
Definition 4.1
(Environment). A typing declaration for session x is a triple \(x : \langle G \mid S \rangle \) where \(G \in \mathfrak {G}\) and \(S \subseteq \mathfrak {P}\). S is the set of local participants of x.
An environment \(\varGamma \) is a finite set of typing declarations \(\varGamma = x_1 : \langle G_1 \mid S_1 \rangle , \ldots , x_n : \langle G_n \mid S_n \rangle \), such that \(x_1, \ldots x_n\) are all distinct.
The main differences between our environments and those in [10] are that session types replace local types, and each session is endowed with a set of local participants, in addition to its session type.
Definition 4.2
(Equivalent environments). We define \(\simeq \) on environments as the smallest equivalence relation satisfying the following rule:

The typing judgment is \(P \vdash \varGamma \), whose rules are shown in Fig. 2.
Rules (send), (recv), \((sel_i)\), and (case) deal with communication. Differently from most type systems (see e.g. [10]), the send and receive actions are typed by the same global type, and not by dual types: in our approach the duality is given by the set of participants, which is either the sender or the receiver.
Rules (close) and (wait) correspond respectively to the 1 and \(\bot \) rules in linear logic, and they both assume there is no named participant, therefore the set of inner participants in the conclusion is empty.
Rule \((+)\) types an internal choice between two processes, but this internal choice is not done for a single session but for the whole process, hence we need to add \(\oplus \) to every type. If the internal choice is irrelevant for some session x, that is, we have \(x : \langle G \mid S \rangle \) in the two premises, then in the conclusion we would have \(x : \langle G \oplus G \mid S \rangle \), which is equivalent to the former. We can of course rewrite types into equivalent ones with rule \((\simeq )\).
Rule \((\nu )\) allows us to create a local, restricted session. To correctly type the local session, we need to check that the its type is complete, since no other participants will be able to join that session afterward. To this end, we introduce the notion of finalized session type. Intuitively, a type is finalized for a given viewpoint (i.e., a set of participants) if all participants involved in the session are in the viewpoint, there are no occurence of \(\omega \) or \(\mathrm {close}\) (because we need to avoid deadlocks and miscommunications), and that the end of the session is not the end of the process (because we are within a subsession).
Definition 4.3
(Finalized session type). The judgment \(G \downarrow S\), meaning that the session type G is finalized for the set of participants S, is defined as follows:
Rule \((\mid )\) is one of the key novelties of this type system. This rule allows us to connect two processes through a shared session merging their respective types. The shared session has a merged type, computed by  . The definition of this operator is quite complex and is postponed to Sect. 5. For the time being, it is enough to know that
. The definition of this operator is quite complex and is postponed to Sect. 5. For the time being, it is enough to know that  may not be in \(\mathfrak {G}\), e.g. when \(G_1, G_2\) are not compatible. To guarantee that only valid types are used for the merged session, we have to find some \(G_3 \in \mathfrak {G}\) such that
may not be in \(\mathfrak {G}\), e.g. when \(G_1, G_2\) are not compatible. To guarantee that only valid types are used for the merged session, we have to find some \(G_3 \in \mathfrak {G}\) such that  .
.
The (extra) rule allows us to add participants which actually do not interact with the sessions; this is needed for the Subject Reduction.
Remark 4.1
Our rule for parallel composition is similar to a cut rule for linear logic. It may be interesting to compare our rule with the cut rule for linear logic [14], that for binary session types [28], and that for multiparty session types [10]:

Each of these rules corresponds to the applications of two rules of our system: the rule \((\mid )\) which merges partial sessions, and the rule \((\nu )\) which closes the session. For instance, if we assume that \(A_1, A_2\), and B are suitable session types, we have the following derivation:

In the case of a multiparty session involving n participants, we would apply \((\mid )\) \(n-1\) times, and then the \((\nu )\) rule to close the session. This correspondence (in a logical setting and for binary choreographies) have been previously observed in [9], where the cut rule above is split into two rules (called (Conn) and (Scope)).
5 Merging Partial Session Types
The central part of the type system is the merging algorithm that infers the result of interaction of two partial session types. In this section, we will define the merge function  , where \(G_1,G_2\) describe the behavior of a session from the viewpoint of the local participants found in the set \(S_1\) and \(S_2\), respectively.
, where \(G_1,G_2\) describe the behavior of a session from the viewpoint of the local participants found in the set \(S_1\) and \(S_2\), respectively.  then describes the behaviour of the session from the unified viewpoint \(S_1 \cup S_2\). In particular, if \(G_1\) and \(G_2\) are intuitively incompatible, then
then describes the behaviour of the session from the unified viewpoint \(S_1 \cup S_2\). In particular, if \(G_1\) and \(G_2\) are intuitively incompatible, then  should contain some occurrence of \(\omega \).
should contain some occurrence of \(\omega \).
To merge two types, we can consider them in DNF; in this way we can recursively reduce the problem to merging chains of communications. Informally, we merge two sequences of communications by considering all possible reorderings which are compatible with each other. This give us a set of all possible merged behaviours, which we glue together using external choices (&). Thus, two types are compatible if they can agree on at least a pair of merged sequences of communications, whatever their internal choices; if no such sequences exist, we get \(\omega \) as result. Extra complexity is given by the fact that a single communication in the form \(p \rightarrow \tilde{q} : \langle G \rangle \) contains a general type; therefore, the function \(\mathsf {mcomm}_{S_1,S_2}(C_1,C_2)\) for merging single communications and the function  for merging session types are mutually recursive.
for merging session types are mutually recursive.
We also need the following helper functions:
-
the partial function \(\mathsf {cont}_S(G,C)\) takes a chain of communications G and a communication C as input, and returns a type that corresponds to what remains in G after having executed C (up to \(\simeq _S\))
-
the decidable predicate
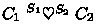 tells us whether \(C_1\) and \(C_2\) are mergeable (from their respective viewpoints \(S_1,S_2\))
tells us whether \(C_1\) and \(C_2\) are mergeable (from their respective viewpoints \(S_1,S_2\)) -
the total function \(\mathsf {sync}_{S_1,S_2}(G_1,G_2)\) takes two chains of communications \(G_1\) and \(G_2\) as input, and returns all possible tuples \((C_1,G'_1,C_2,G')\) such that \(C_1;G'_1 \simeq _{S_1} G_1\), \(C_2; G'_2 \simeq _{S_2} G_2\) and \(C_1\) and \(C_2\) are mergeable
-
finally, the partial function \(\mathsf {map}_{S_1,S_2}(f)(G_1,G_2)\) takes a (partial) function \(f : \mathfrak {C}\times \mathfrak {C}\rightharpoonup \mathfrak {C}\) and two session types in DNF as arguments, and maps f on the pair \((G_1,G_2)\).
We can then define the partial function \(\mathsf {mcomm}_{S_1,S_2}(C_1,C_2)\) and the total function  . These functions are actually non-deterministic, but
. These functions are actually non-deterministic, but  is deterministic up to \(\simeq \).
is deterministic up to \(\simeq \).
In order to prove termination of these functions, we define the length l of session types; besides, we define also the height h of communications and session types as the maximal number of nested subsessions. Formally, we have:
5.1 Mapping Merging Functions over Session Types
Definition 5.1
(\(\mathsf {cont}\)). The partial function \(\mathsf {cont}_S(G,C)\) takes as input a chain of communications G and a communication C, and returns some \(G'\) in DNF such that \(G \simeq _S C; G'\). It is undefined if such \(G'\) does not exist.
Intuitively, \(\mathsf {cont}_S(G,C)\) is a kind of Brzozowski derivative that tells us what happens in G after the communication C.
Proposition 5.1
The function \(\mathsf {cont}\) is computable, and moreover \(l(C;G') = l(G)\) and \(h(C;G') = h(G)\).
Note that \(\mathsf {dom}(\mathsf {cont}_S(G,\_))\) is finite, and can be computed using Eq. (1) repeatedly.
Definition 5.2
(Function \(\mathsf {sync}\)). Let \(G_1,G_2\) be chains of communications in DNF. Let \(A_1 = \{ (C, G') \mid C \in \mathsf {dom}(\mathsf {cont}_S(G_1,\_)), G' = \mathsf {cont}_S(G_1,C) \}\), and \(A_2 = \{ (C, G') \mid C \in \mathsf {dom}(\mathsf {cont}_S(G_2,\_)), G' = \mathsf {cont}_S(G_2,C) \}\). We then define:
Intuitively, \(\mathsf {sync}_{S_1,S_2}(f)(G_1,G_2)\) returns a set containing all possible pairs of communications that can be merged, as well as their continuations.
It is important to know whether a communication \(C_1\) (from the viewpoint \(S_1\)) and a communication \(C_2\) (from the viewpoint \(S_2\)) can correspond to the same communication; in this case, we say that they are mergeable. Formally, this notion is defined by the following relation.
Definition 5.3
(Mergeability). We define  as follows:
as follows:

The first rule deserves some explanations. In the first hypothesis, \(G_1\) and \(G_2\) describe sessions whose participants can be only in \(\{p\} \cup \tilde{q}_1 \cup \tilde{q}_2 \); if all these participants are in \(S_1\cup S_2\), then after the merge all the participants are present and therefore the communication must be safe, because no other participant may join later. This means that, in this case, we have to check that the merge of \(G_1\) and \(G_2\) is finalized. The second hypothesis (and dually the third one) corresponds to the fact that in the (send) rule of Fig. 2, the sender specifies all receiving participants, while in (recv) a receiver may not know about other receivers; therefore, if \(p \rightarrow \tilde{q}_1 : \langle G_1 \rangle \) describes the communication from the point of view of the sender (i.e., \(p\in S_1\)), then \(\tilde{q}_2\) is a set of receivers only, and must be contained in \(\tilde{q}_1\). The fourth (and dually the fifth) hypothesis means that if a participant which is known to a process (i.e., in \(S_1\)) appears as receiver for other process (i.e., in \(\tilde{q}_2\)), then it must appear as a received also by the first process.
Proposition 5.2
 is decidable.
is decidable.
Definition 5.4
(Function \(\mathsf {map}\)). Let \(S_1,S_2\) be two sets of participants, two types \(G_1,G_2\in \mathfrak {C}\) and a (partial) function \(f : \mathfrak {C}\times \mathfrak {C}\rightharpoonup \mathfrak {C}\) such that
-
\(G_1\) and \(G_2\) are in DNF
-
for any \(C_1\), \(C_2\), we have that \(f(C_1,C_2)\) is a terminal communication iff it is defined and both \(C_1\) and \(C_2\) are terminal
-
if \(f(C_1,C_2)\) is defined, then either both \(C_1\) and \(C_2\) are terminal, or none of them are.
Then, \(\mathsf {map}_{S_1,S_2}(f)(G_1, G_2)\) is defined recursively over \(G_1,G_2\) as follows:
-
First cases:
$$\begin{aligned} \begin{array}{rcl} \mathsf {map}_{S_1,S_2}(f)(G_1 \oplus G_2, G_3) &{} := &{} \mathsf {map}_{S_1,S_2}(f)(G_1, G_3) \oplus \mathsf {map}_{S_1,S_2}(f)(G_2, G_3) \\ \mathsf {map}_{S_1,S_2}(f)(G_1, G_2 \oplus G_3) &{} := &{} \mathsf {map}_{S_1,S_2}(f)(G_1, G_2) \oplus \mathsf {map}_{S_1,S_2}(f)(G_1, G_3) \\ \end{array} \end{aligned}$$ -
If neither of the cases above apply, then we have:
$$ \begin{aligned} \begin{array}{rcl} \mathsf {map}_{S_1,S_2}(f)(G_1 \; \& \;G_2, G_3) &{} := &{} \mathsf {map}_{S_1,S_2}(f)(G_1, G_3) \; \& \;\mathsf {map}_{S_1,S_2}(f)(G_2, G_3) \\ \mathsf {map}_{S_1,S_2}(f)(G_1, G_2 \; \& \;G_3) &{} := &{} \mathsf {map}_{S_1,S_2}(f)(G_1, G_2) \; \& \;\mathsf {map}_{S_1,S_2}(f)(G_1, G_3) \\ \end{array} \end{aligned}$$ -
If \(G_1\), \(G_2\) are both chains of communications and at least one of them is not a terminal communication, we pose \(B := \mathsf {sync}_{S_1,S_2}(f)(G_1,G_2)\) and we have:
-
If \(G_1\) or \(G_2\) ends with \(0\), \(\mathsf {map}_{S_1,S_2}(f)(G_1,G_2) := 0\).
-
If \(G_1\) or \(G_2\) ends with \(\omega \), or if \(B = \varnothing \), then \(\mathsf {map}_{S_1,S_2}(f)(G_1,G_2) := \omega \).
-
Otherwise:

-
-
If \(G_1\) and \(G_2\) are both terminal communications, then:
$$\begin{aligned} \mathsf {map}_{S_1,S_2}(f)(G_1, G_2) := {\left\{ \begin{array}{ll} 0&{} \text{ if } G_1 \text{ or } G_2 \text{ is } 0\\ f(G_1,G_2) &{} \text{ if } f(G_1,G_2) \text{ is } \text{ defined } \\ \omega &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$
The two conditions on f guarantee that \(\mathsf {map}_{S_1,S_2}(f)(G_1, G_2)\) is well-defined in the last two cases, when f is applied to \(G_1,G_2\) or to the chains \(C_1, C_2\).
Proposition 5.3
Termination of \(\mathsf {map}\) is ensured by induction on \(l(G_1) + l(G_2)\).
Note that, when we computing \(\mathsf {map}_{S_1,S_2}(f)(G_1,G_2)\), every application of f is of the form \(f_{S_1,S_2}(C_1,C_2)\), where \(h(C_1) + h(C_2) \leqslant h(G_1) + h(G_2)\).
5.2 Merging Communications and Session Types
We now define the partial function \(\mathsf {mcomm}_{S_1,S_2}(C_1,C_2)\) which merges compatible communications \(C_1\) (from the viewpoint \(S_1\)) and \(C_2\) (from the viewpoint \(S_2\)) and returns, if possible, the new communication from the merged viewpoints \(S_1 \cup S_2\). We also define by mutual recursion the merging function for session types, which is just a shorthand for \(\mathsf {map}\) applied to \(\mathsf {mcomm}\):

We suppose that \(G_1\) and \(G_2\) are in DNFs, but it can be applied to any session types by rewriting them in DNF.
Definition 5.5
(Function \(\mathsf {mcomm}\)). If  , then:
, then:

Otherwise, \(\mathsf {mcomm}_{S_1,S_2}(C_1,C_2)\) is undefined.
Proposition 5.4
Termination is ensured by induction on \(h(C_1) + h(C_2)\).
Example 5.1
Continuing Example 3.1, let us recall the types of participants p, r:
We have that:
As a consequence, we have for instance that: \( \mathsf {sync}_{\{p\},\{q\}}(G_1,G'_1) = \{ (p \rightarrow q : \& \mathrm {in}_1, 1, (p \rightarrow r : \langle \mathrm {end} \rangle ; \mathrm {close}), G'_1), (1, q \rightarrow r : \& \mathrm {in}_1, G_1, (p \rightarrow r : \langle \mathrm {close} \rangle ; \mathrm {close}))\}\).
We have that:

6 Subject Reduction and Progress
In this section we state two main properties of session types, subject reduction and progress, which guarantee that “well-typed systems cannot go wrong”. To this end, we first define a reduction semantics for partial session types.
Definition 6.1
(Reductions for session types). Actions \(\gamma \) for session types are defined as
We write \(G_1 \overset{\gamma }{\longrightarrow }_S G_2\) for a transition from \(G_1\) to \(G_2\) from the viewpoint of S under the action \(\gamma \). This relation is defined as follows:

Note that transitions are not deterministic, in particular \(G \simeq _S G \oplus G\), therefore we always have \(G \overset{+}{\longrightarrow } G\), which is useful in case we are reducing an internal choice which is irrelevant for G.
Definition 6.2
(Reduction for environments). Reductions for environments are labelled by actions for processes \(\alpha \), and are defined as follows:
The type system enjoys the following properties:
Theorem 6.1
(Subject equivalence). If \(P \vdash \varGamma \) and \(P \equiv Q\), then \(Q \vdash \varGamma \).
From now on, we can consider processes equal modulo \(\equiv \).
Theorem 6.2
(Subject reduction). If \(P_1 \vdash \varGamma _1\) and \(P_1 \overset{\alpha }{\longrightarrow } P_2\), then for some \(\varGamma _2\), we have \(P_2 \vdash \varGamma _2\) and \(\varGamma _1 \overset{\alpha }{\longrightarrow } \varGamma _2\).
Remark 6.1
In earlier work about MPST, usually subject reduction requires some consistency condition over the typing environment \(\varGamma \) (see, e.g., [26]). In our development, this condition is not explicitly needed because the type rules for processes ensure that environments are consistent; hence, the derivability of \(P_1 \vdash \varGamma _1\) implies that no session in \(\varGamma _1\) has the type \(\omega \).
Progress. In usual session types, the progress property means that well-typed systems can always proceed, and in particular they are deadlock-free. In our case, well-typed systems can still contain processes which cannot proceed not due to a deadlock or miscommunication but due to some missing participant.
Example 6.1
Let us consider \( P = \overline{x}^{p q}\triangleright \& \mathrm {in}_1.\mathrm {close}(x)\). This process is typable (\( P \vdash x:\langle p \rightarrow q : \& \mathrm {in}_1;\mathrm {close} \mid \{p\} \rangle \)), yet it is stuck. It can be completed into a redex \( P \mid _x Q\), with \(Q = x^{q p}\triangleleft (Q_1,Q_2)\). In fact, P can be seen as the restriction of \(P \mid _x Q\) on session x with participants in \(\{p\}\). Hence, P is preempted by x and so it can be considered a correct process, waiting for the missing participant.
Therefore, in order to define the progress property for our system, we need to define the restriction of a process to a given set of local participants.
Definition 6.3
(Restriction). We define the restriction of a term P on session x with participants in S (noted \(P \downharpoonleft _{S} x\)) as follows:
Definition 6.4
(Preemption). We say that a session x with type \(G \in \mathfrak {G}\) and local participants S preempts P (noted \(x : \langle G \mid S \rangle \gg _{\mathrm {g}} P\)) when one of these condition occurs:
-
\(x : \langle p \rightarrow \tilde{q} : \langle G_1 \rangle ; G_2 \mid S \rangle \gg _{\mathrm {g}} ((\overline{x}^{p \tilde{q}}(y). R \mid _x \varPi ^x_i (x^{q_i p}(y). (P_i \parallel Q_i))) \downharpoonleft _{S} x) \mid _x P\) if \(G_2 \simeq _S C\) where C is terminal, or \(x : \langle G_2 \mid S - \{p, \tilde{q}\} \rangle \gg _{\mathrm {g}} P\)
-
\( x : \langle p \rightarrow \tilde{q} : \& \mathrm {in}_i; G \mid S \rangle \gg _{\mathrm {g}} (\overline{x}^{p \tilde{q}}\triangleright \mathrm {in}_i. R \mid _x \varPi ^x_j x^{q_j p}\triangleleft (P_{1,j}, P_{2,j}) \downharpoonleft _{S} x) \mid _x P\) if \(G_2 \simeq _S C\) where C is terminal, or \(x : \langle G \mid S - \{p,\tilde{q}\} \rangle \gg _{\mathrm {g}} P\)
-
\(x : \langle \mathrm {close} \mid S \rangle \gg _{\mathrm {g}} \mathrm {close}(x)\)
-
\(x : \langle \mathrm {end} \mid S \rangle \gg _{\mathrm {g}} \mathrm {wait}(x).P\)
-
\(x : \langle G_1 \oplus G_2 \mid S \rangle \gg _{\mathrm {g}} U\) if \(x : \langle G_1 \mid S \rangle \gg _{\mathrm {g}} P\) or \(x : \langle G_2 \mid S \rangle \gg _{\mathrm {g}} P\)
-
\( x : \langle G_1 \; \& \;G_2 \mid S \rangle \gg _{\mathrm {g}} P\) if \(x : \langle G_1 \mid S \rangle \gg _{\mathrm {g}} P\) and \(x : \langle G_2 \mid S \rangle \gg _{\mathrm {g}} P\)
-
\(x : \langle G \mid S \rangle \gg _{\mathrm {g}} P\) if \(x : \langle G \mid S \rangle \gg _{\mathrm {g}} P'\) and \(P \equiv P'\)
Definition 6.5
(Contextual preemption). We define \(x : \langle G \mid S \rangle \gg _{\mathrm {c}} P\) if for some \(\mathcal C[\_]\), \(P'\), we have that \(P \equiv \mathcal C[P']\), \(x \not \in \mathrm {fn}(\mathcal C[\_])\), and \(x : \langle G \mid S \rangle \gg _{\mathrm {g}} P'\).
Intuitively, \(x : \langle G \mid S \rangle \gg _{\mathrm {c}} P\) means that every local participant in S is ready to trigger its respective communication described in G. As a consequence, there is no deadlock for x: if all the concerned participants are present there is a redex, otherwise we are blocked due to the absence of some sender or receiver. The following lemma states that if a session is finalized and preempted, then the process (with the session restricted) contains a redex.
Lemma 6.1
-
1.
If \(G \downarrow S\) and \(x : \langle G \mid S \rangle \gg _{\mathrm {g}} P\), then \((\nu x) P\) has a redex.
-
2.
If \(G \downarrow S\) and \(x : \langle G \mid S \rangle \gg _{\mathrm {c}} P\), then \((\nu x) P\) has a redex.
Theorem 6.3
(Progress). If \(P \vdash \varGamma \) then there is a redex in P, or for some \(x : \langle G \mid S \rangle \in \varGamma \) we have \(x : \langle G \mid S \rangle \gg _{\mathrm {c}} P\).
7 Related Work
The problem of composing session types has been faced in several related work. Compositional choreographies are discussed in [23], with the same motivations as ours, but from a different perspective. The authors manage to compose choreographies using global types, but the global type of shared channels has to be the same. This is in contrast with our approach, where the processes may have different session types that we merge during the composition. Moreover, also their typing judgments use sets of participants (there called roles); more precisely, the types for channels keep track of the “active” role, the set of all roles in the global type, and the roles actually implemented by the choreography under typing. On the other hand, we do not need to specify neither the complete set of participants nor the “active” role, in typing sessions.
Synthesis of choreography from local types has been studied also in [21], but with no notion of “partial types” and no distinction between internal/external choice. Graphical representations of choreographies (as communicating finite-state machines) and global types have been used in [22], where an algorithm for constructing a global graph from asynchronous interactions is given.
An interesting approach based on gateways has been investigated in [2,3,4,5]: two independent global types \(G_1\) and \(G_2\) with different participants can be composed through participant h in \(G_1\) and k in \(G_2\) where h and k relay the message they receive to each other. Therefore, in this approach the two session types \(G_1,G_2\) are connected by the gateway but not really merged, as in our approach. Finally, [26] do not use global types altogether: behaviours of systems are represented by sets of local types, over which no consistency conditions are required, and behavioural properties can be verified using model checking techniques.
A problem similar to ours is considered in [8], where the authors introduce a type system for the Conversation Calculus, a model for service-oriented computing. Conversation types of parallel processes can be merged like in our approach, but the underlying computational model is quite different.
Semantics of concurrent processes can be given using Mazurkiewicz trace languages [25]. Semantics can also be defined using event structures, as in [11], where they are used for defining equivalent semantics for processes and their global types. Interestingly, the semantics for global types proposed in [11] is similar to the representation of Mazurkiewicz trace languages as event structures given in [25]. Mazurkiewicz trace languages have been also used to characterize testing preorders on multiparty scenarios [13]. A denotational semantics based on Brzozowski derivatives that corresponds to bisimilarity is given in [20].
Another semantics of processes (but for binary session types) that records exchanged informations is given in [1]. This semantics is similar to the relation-based model of linear logic [6], and not based on traces. It would interesting to investigate if this alternative semantics can be extended to MPST and to interpret the merge operation. The relationship between category theory and session types has been investigated also in [19, 27].
8 Conclusions
In this paper, we have introduced partial sessions and partial (multiparty) session types, extending global session types with the possibility to type also sessions with missing participants. Sessions with the same name but observed by different participants can be merged if their types are compatible; in this case, the type for the unified session can be derived compositionally from the types of components. To this end we have provided a merging algorithm, which allows us to detect incompatible types, due to miscommunications or deadlocks, as early as possible; this differs from usual session type systems which delay all the checks to when the system is completed (i.e., at the restriction rule). Therefore, in this theory the distinction between local and global types vanishes. We have also generalised the notion of progress to accommodate the case when a partial session cannot progress not due to a deadlock, but to some missing participant.
Future Work. An interesting application of partial session types would be in the verification of composition of components, like e.g. containers a la Docker; to this end, we can think of defining a typing discipline similar to the one presented in this paper, but tailored for a formal models of containers, like that in [7].
We claim that for the type system presented in this paper both type checking and type inference are decidable. The idea is that, in order to be typable, the structure of a process has to match the structure of the type(s), up-to type equivalence; hence, the typing derivation is bounded by the complexity of process terms. At worst, this bound is exponential, as in the application of type equivalence rule we have to explore a possibly exponential space of equivalent types; however, this limit could be improved by some algorithmic machinery concerning the normal form of types, which we leave to future work.
The current merging algorithm returns types that may contain many equivalent subterms; a future work could be to define shorter and more efficient representations. Another interesting aspect of this algorithm is that it is defined by two functions (\(\mathsf {map}\) and \(\mathsf {mcomm}\)), which can be updated separately in future variations; in particular, adding recursion only requires to update the function \(\mathsf {map}\), while adding new kinds of communication, or changing how communications are merged, only requires to update the function \(\mathsf {mcomm}\). The correctness of this algorithm can be proved with respect to a categorical semantics for session types based on traces, which we leave to the extended version of this work.
In this paper we have considered a calculus with synchronous multicast, along the lines of [10, 28] and others. However, it would be interesting to extend the definitions and results of this paper to an asynchronous version of the calculus. This is not immediate, as it requires non-trivial changes in the typing systems and especially in the (already quite complex) merging operation.
Following the Liskov substitution principle, we could define a subtyping relation by seeing \( \; \& \;\) and \(\oplus \) as the meet and join operator of a lattice, respectively. However, a semantical understanding of this subtyping relation is not clear yet.
One intriguing possible extension would be to add some form of encapsulation. For instance, if we have the type \(p \rightarrow q : m_1;q \rightarrow r : m_2;p \rightarrow r : m_3; \mathrm {close}\) from the viewpoint of \(\{q,r\}\), then we could be tempted to “erase” the communication \(q \rightarrow r : m_2\), since this communication is purely internal, but this erasure would not be compatible with equivalence:
How to add a form of encapsulation to our type system is an open question.
Finally, to guarantee the correctness of most complex proofs and definitions of this paper, it would be useful to formalise them in a proof assistant, like Coq.
Notes
- 1.
From a computational point of view, this “parallel input” corresponds to the programming practice to selectively share sessions between processes. This constructor allows us to enforce a discipline on the shared sessions in order to avoid deadlocks between processes. Moreover, it is motivated by connections with linear logic [10, 28].
References
Atkey, R.: Observed communication semantics for classical processes. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 56–82. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_3
Barbanera, F., Dezani-Ciancaglini, M.: Open multiparty sessions. In: Proceedings of the ICE. EPTCS, vol. 304, pp. 77–96 (2019)
Barbanera, F., Dezani-Ciancaglini, M., Lanese, I., Tuosto, E.: Composition and decomposition of multiparty sessions. J. Log. Algebraic Methods Program. 119, 100620 (2021)
Barbanera, F., Lanese, I., Tuosto, E.: Composing communicating systems, synchronously. In: Margaria, T., Steffen, B. (eds.) ISoLA 2020. LNCS, vol. 12476, pp. 39–59. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-61362-4_3
Barbanera, F., de’ Liguoro, U., Hennicker, R.: Global types for open systems. In: Proceedings of ICE. EPTCS, vol. 279, pp. 4–20 (2018)
Barr, M.: *-autonomous categories and linear logic. Math. Struct. Comput. Sci. 1(2), 159–178 (1991). https://doi.org/10.1017/S0960129500001274
Burco, F., Miculan, M., Peressotti, M.: Towards a formal model for composable container systems. In: Hung, C., Cerný, T., Shin, D., Bechini, A. (eds.) SAC 2020: The 35th ACM/SIGAPP Symposium on Applied Computing, pp. 173–175. ACM (2020). https://doi.org/10.1145/3341105.3374121
Caires, L., Vieira, H.T.: Conversation types. Theoret. Comput. Sci. 411(51–52), 4399–4440 (2010)
Carbone, M., Montesi, F., Schürmann, C.: Choreographies, logically. Distrib. Comput. 31(1), 51–67 (2018)
Carbone, M., Montesi, F., Schürmann, C., Yoshida, N.: Multiparty session types as coherence proofs. Acta Informatica 54(3), 243–269 (2017)
Castellani, I., Dezani-Ciancaglini, M., Giannini, P.: Event structure semantics for multiparty sessions. In: Boreale, M., Corradini, F., Loreti, M., Pugliese, R. (eds.) Models, Languages, and Tools for Concurrent and Distributed Programming. LNCS, vol. 11665, pp. 340–363. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21485-2_19
Coppo, M., Dezani-Ciancaglini, M., Yoshida, N., Padovani, L.: Global progress for dynamically interleaved multiparty sessions. Math. Struct. Comput. Sci. 26(2), 238–302 (2016)
De Nicola, R., Melgratti, H.: Multiparty testing preorders. In: Ganty, P., Loreti, M. (eds.) TGC 2015. LNCS, vol. 9533, pp. 16–31. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-28766-9_2
Girard, J.Y.: Linear logic. Theoret. Comput. Sci. 50(1), 1–101 (1987)
Honda, K., Vasconcelos, V.T., Kubo, M.: Language primitives and type discipline for structured communication-based programming. In: Hankin, C. (ed.) ESOP 1998. LNCS, vol. 1381, pp. 122–138. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0053567
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. In: Necula, G.C., Wadler, P. (eds.) Proceedings of the POPL 2008, pp. 273–284. ACM (2008). https://doi.org/10.1145/1328438.1328472
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. J. ACM 63(1), 9:1–9:67 (2016). https://doi.org/10.1145/2827695
Jespersen, T.B.L., Munksgaard, P., Larsen, K.F.: Session types for rust. In: Proceedings of the 11th ACM SIGPLAN Workshop on Generic Programming, pp. 13–22 (2015)
Keizer, A.C., Basold, H., Pérez, J.A.: Session coalgebras: a coalgebraic view on session types and communication protocols. In: ESOP 2021. LNCS, vol. 12648, pp. 375–403. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-72019-3_14
Kokke, W., Montesi, F., Peressotti, M.: Better late than never: a fully-abstract semantics for classical processes. Proc. ACM Program. Lang. 3(POPL) (2019). https://doi.org/10.1145/3290337
Lange, J., Tuosto, E.: Synthesising choreographies from local session types. In: Koutny, M., Ulidowski, I. (eds.) CONCUR 2012. LNCS, vol. 7454, pp. 225–239. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32940-1_17
Lange, J., Tuosto, E., Yoshida, N.: From communicating machines to graphical choreographies. In: POPL, pp. 221–232. ACM (2015)
Montesi, F., Yoshida, N.: Compositional choreographies. In: D’Argenio, P.R., Melgratti, H. (eds.) CONCUR 2013. LNCS, vol. 8052, pp. 425–439. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40184-8_30
Neubauer, M., Thiemann, P.: An implementation of session types. In: Jayaraman, B. (ed.) PADL 2004. LNCS, vol. 3057, pp. 56–70. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24836-1_5
Nielsen, M.: Models for concurrency. In: Tarlecki, A. (ed.) MFCS 1991. LNCS, vol. 520, pp. 43–46. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-54345-7_47
Scalas, A., Yoshida, N.: Less is more: multiparty session types revisited. Proc. ACM Program. Lang. 3(POPL), 1–29 (2019)
Toninho, B., Yoshida, N.: Polymorphic session processes as morphisms. In: Alvim, M.S., Chatzikokolakis, K., Olarte, C., Valencia, F. (eds.) The Art of Modelling Computational Systems: A Journey from Logic and Concurrency to Security and Privacy. LNCS, vol. 11760, pp. 101–117. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31175-9_7
Wadler, P.: Propositions as sessions. J. Funct. Program. 24(2–3), 384–418 (2014)
Acknowledgments
We are grateful to Mariangiola Dezani-Ciancaglini, Marco Peressotti and the anonymous reviewers for their useful remarks on the preliminar version of this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Stolze, C., Miculan, M., Di Gianantonio, P. (2021). Composable Partial Multiparty Session Types. In: Salaün, G., Wijs, A. (eds) Formal Aspects of Component Software. FACS 2021. Lecture Notes in Computer Science(), vol 13077. Springer, Cham. https://doi.org/10.1007/978-3-030-90636-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-90636-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-90635-1
Online ISBN: 978-3-030-90636-8
eBook Packages: Computer ScienceComputer Science (R0)






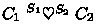 tells us whether
tells us whether 