Abstract
Multiparty session types (MPST) are a formal specification and verification framework for message-passing protocols without central control: the desired interactions at the scale of the network itself are specified into a session (called global type). Global types are then projected onto local types (one for each participant), which describe the protocol from a local point of view. These local types are used to validate an application through type-checking, monitoring, and code generation. Theory of session types guarantees that local conformance of all participants induces global conformance of the network to the initial global type. This paper provides a very gentle introduction of the simplest version of multiparty session types for readers who are not familiar with session types nor process calculi.
Work partially supported by EPSRC projects EP/K034413/1, EP/K011715/1, EP/L00058X/1, EP/N027833/1 and EP/N028201/1.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 A Gentle Introduction to Multiparty Session Types
Backgrounds. Session types were introduced in a series of papers during the 1990s [8, 10, 18] in the context of pure concurrent processes and programming. Session types have since been studied in many contexts over the last decade—see the surveys of the field [4, 13].
A basic observation underlying session types is that a communication-based application often exhibits a highly structured sequence of interactions involving, for example, sequencing, choices and recursion, which as a whole form a natural unit of session. The structure of a session is abstracted as a type through an intuitive syntax, which is then used for validating programs through associated language primitives.
Multiparty session types generalise the binary session type theory to the multiparty case, preventing deadlock and communication errors in more sophisticated communication protocols involving any number (two or more) of participants. The central idea is to introduce global types, which describe multiparty conversations from a global perspective and provide a means to check protocol compliance. The theory [11, 12] was born by transforming the industry idea developed during designing a protocol description language, Scribble [17], which was presented by Kohei Honda in [9] (see the historical background [20]). This original work was extended in various ways and applied to many different programming languages and tools, some of which use Scribble. The reader who is interested in programming languages can find the tools and papers at Mobility Reading Group Home Page.
Binary Session Types. As a first example, consider a scenario where a customer tries to conclude a deal with a travel agency. We associate a process with the customer (\(\mathtt {Customer}\)) and one with the agency (\(\mathtt {Agency}\)). The task involves synchronisation in the communication between the customer and the agency. Synchronisation is obtained through the exchange of messages.
Specifically, the protocol works as follows.
-
1.
The customer sends an order to the agency, namely the place they desire to visit in their next travel (let us say \( Hawaii \)). On receiving the request, the agency looks up the price relative to that travel and sends a quote (\( quote \)) back to the customer.
-
2.
When the customer receives the \( quote \), they make a decision (choice): either to \( accept \) or to \( reject \) the offer. The customer communicates their decision to the agency, which is waiting for such a message.
-
3.
In case of acceptance, the agency waits that the customer communicates their address (\( address \)), then sends a confirmation date (\( date \)) for the trip back to the customer and the protocol terminates.
-
4.
In case of rejection, the deal is not made and the protocol immediately terminates.
The multiparty session types methodology is as follows. First, define a global type that gives a shared contract of the allowed pattern of message exchanges in the system. Second, project the global type to each end-point participant to obtain a local type: an obligation on the message sends and receipts for each process that together ensure that the pattern of messages are allowed by the global type. Finally, check that the implementation of each process conforms to its local type.
In our protocol, from a global perspective, we expect to see the following pattern of message exchanges, encoded as a global type for the communication:
The type describes the global pattern of communication between \(\mathtt {Customer}\) and \(\mathtt {Agency}\) using message exchanges, sequencing, and choice. The basic pattern \(\mathtt {Customer}\rightarrow \mathtt {Agency}:\!{m}{(S)}\) indicates a message with label m sent from the \(\mathtt {Customer}\) to the \(\mathtt {Agency}\), together with an element of sort \(S\). The communication starts with the customer sending the message \( Hawaii \) to the agency, then the agency sends the \( quote \) label together with a natural number and at this point the customer either sends an \( accept \) or a \( reject \) message. In case of \( reject \), the protocol ends (type \(\mathtt {end}\)); otherwise, the communication continues with the sequential exchange of an \( address \) (from the customer to the agency) and a \( date \) (from the agency to the customer). The operator “.” denotes sequencing, the “, ” separates possible continuations for the protocol.
The global type states what are the valid message sequences allowed in the system. When we implement \(\mathtt {Customer}\) and \(\mathtt {Agency}\) separately, we would like to check that their composition conforms to the global type. Since there are only two participants, projecting to each participant is simple. From the perspective of the \(\mathtt {Customer}\), the communication can be described by the type:
where !m denotes a message with label m sent to \(\mathtt {Agency}\), ?m denotes a message with label m received from \(\mathtt {Agency}\), and \(\oplus \) denotes an internal choice. Thus the type states that, \(\mathtt {Customer}\) after sending the message with label \( Hawaii \), waits for a natural number for the \( quote \) and, after receiving it, decides either to send \(! accept (\mathtt {bool}). \; ! address (\mathtt {nat})\), wait for a natural number for the \( date \) and then exit, or to send just \( reject (\mathtt {bool})\) and exit.
From the viewpoint of \(\mathtt {Agency}\), the same global session is described by the dual type
in which & means that a choice is offered externally.
We can now individually check that the implementations of the customer and the agency conform to these local types.
Multiparty Session Types. In the case of two parties, the safety can be checked given the local type (2) since its dual (3) is unique (up to unfolding recursions).
However, for applications involving multiple parties, the global type and its projection to each participant are essential to provide a shared contract among all participants.
For example, consider a simple ring protocol, where, after the customer’s acceptance, the agency needs to forward some details to the hotel, before a direct communication starts between the hotel and the customer. Namely, \(\mathtt {Customer}\) sends a message \( details \) to \(\mathtt {Agency}\), which forwards the message to \(\mathtt {Hotel}\). After receiving the message, \(\mathtt {Hotel}\) sends an acknowledgement \( ok \) to \(\mathtt {Customer}\). We start by specifying the global type as:
As before, we want to check each process locally against a local type such that, if each process conforms to its local type, then the composition satisfies the global type. The global type in (4) is projected into the three local types:
where \(\mathtt {Agency}! details (\mathtt {nat})\) means “send to \(\mathtt {Agency}\) a \( details \) message,” and \(\mathtt {Hotel}? ok (\mathtt {bool})\) means “receive from \(\mathtt {Hotel}\) an \( ok \) message.” Then each process is type-checked against its own endpoint type. When the three processes are executed, their interactions automatically follow the stipulated scenario.
If instead we only used three separate binary session types to describe the message exchanges between \(\mathtt {Customer}\) and \(\mathtt {Agency}\), between \(\mathtt {Agency}\) and \(\mathtt {Hotel}\), and between \(\mathtt {Hotel}\) and \(\mathtt {Customer}\), respectively, without using a global type, then we lose essential sequencing information in this interaction scenario. Consequently, we can no longer guarantee deadlock-freedom among these three parties. Since the three separate binary sessions can be interleaved freely, an implementation of the \(\mathtt {Customer}\) that conforms to \(\mathtt {Hotel}? ok (\mathtt {bool}).\mathtt {Agency}! details (\mathtt {nat}).\mathtt {end}\) becomes typable. This causes the situation in which each of the three parties blocks indefinitely while waiting for a message to be delivered.
In what follows we will start from giving more examples in Sect. 2, which will be used as running examples throughout the whole paper. In Sect. 3 we will introduce a formal process calculus powerful enough to describe multiparty communication protocols, such as the ones from above. Finally in Sect. 4, we will introduce a type system; we will show how multiparty session types work by examples and present the key properties of typed processes.
2 Examples, Intuitively
Multiparty session types are aimed at enabling compositional reasoning about communication among different parties. In this section we present informally some essential communication protocols that can be handled with this methodology.
Let us for example consider the basic protocol from the previous section. This simple protocol for a travel agency is synthetically displayed by Fig. 1a. A more interesting protocol could be the one shown in Fig. 1b. Here the customer is allowed to try again and again to obtain the new quote, should they not like the first one. We will see that our calculus (Sect. 3) is endowed with recursion, which can model an indefinite number of iterations.
Let us consider a specification in Fig. 2, which describes a simple communication protocol among three parties. Bob is waiting for a message from Alice, non-deterministically allowing for messages with two different labels (l1 and l2). Alice sends the message with label l1 and the communication continues with Bob sending a message message1 to Carol and finally Carol returning a message answer to Alice, which depends on the previous communication, including the choice of the label for the original message from Alice to Bob.
In the following sections, we model these protocols by a simple multiparty session calculus, and give types to processes modelling these protocols.
3 Synchronous Multiparty Session Calculus
This section introduces the syntax and semantics of a synchronous multiparty session calculus from [7], which simplifies the calculus in [14] by eliminating both shared channels for session initiations and session channels for communications inside sessions.
Notation 01 (Base sets). We use the following base sets: values, ranged over by \(\mathsf {v},\mathsf {v}',\ldots \); expressions, ranged over by \(\mathsf {e},\mathsf {e}',\ldots \); expression variables, ranged over by \(x,y,z\dots \); labels, ranged over by \(\ell ,\ell ',\dots \); session participants, ranged over by \(\mathsf{p},\mathsf{q},\ldots \); process variables, ranged over by \(X,Y,\dots \); processes, ranged over by \(P,Q,\dots \); and multiparty sessions, ranged over by  .
.
Syntax. A value \(\mathsf {v}\) can be a natural number \(\mathsf {n}\), an integer \(\mathsf {i}\), or a boolean \(\mathsf {true}\)/\(\mathsf {false}\). An expression \(\mathsf {e}\) can be a variable, a value, or a term built from expressions by applying the operators \(\mathtt{succ}, \mathtt{neg}, \lnot , \oplus ,\) or the relation \(>.\) An evaluation context \(\mathcal {E}\) is an expression with exactly one hole. The operator \(\oplus \) models non-determinism: \(\mathsf {e}_1 \oplus \mathsf {e}_2\) is an expression that might yield either \(\mathsf {e}_1\) or \(\mathsf {e}_2\).
The processes of the synchronous multiparty session calculus are defined by:
The output process \(\mathsf{p} ! \ell \langle \mathsf {e} \rangle . Q\) sends the value of expression \(\mathsf {e}\) with label \(\ell \) to participant \(\mathsf{p}\). The sum of input processes (external choice) \(\sum _{i\in I} \mathsf{p} ? \ell _i(x_i) .P_i\) is a process that can accept a value with label \( \ell _i \) from participant \( \mathsf{p}, \) for any \( i\in I\). According to the label \(\ell _i\) of the received value, the variable \(x_i\) is instantiated with the value in the continuation process \( P_i\). We assume that the set I is always finite and non-empty.
The conditional process \(\mathsf {if}~ \mathsf {e} ~\mathsf {then} ~P ~\mathsf {else}~Q \) represents the internal choice between processes \( P\) and \( Q\). Which branch of the conditional process will be taken depends on the evaluation of the expression \( \mathsf {e}\). The process \(\mu X.P\) is a recursive process. We assume that the recursive processes are guarded. For example, \(\mu X.\mathsf{p} ? \ell (x) .X\) is a valid process, while \(\mu X.X\) is not. We often omit \(\mathbf {0}\) from the tail of processes.
We define a multiparty session as a parallel composition of pairs (denoted by \(\mathsf{p} \triangleleft P\)) of participants and processes:

with the intuition that process \(P\) plays the role of participant \(\mathsf{p}\), and can interact with other processes playing other roles in  . A multiparty session is well formed if all its participants are different. We consider only well-formed multiparty sessions.
. A multiparty session is well formed if all its participants are different. We consider only well-formed multiparty sessions.
Example 1
We now show how to encode, in the above calculus, processes respecting the protocols informally presented in Fig. 1. Note that we picked one different label for each destination (that can be either Hawaii or France), as well as for each action (as “accept”, “reject”, ...).
Let us start with processes in Fig. 1a.

The customer here would ask for Hawaii as a destination, they will receive a quote that will be too expensive (\(5000>1000\)) and, thus, they will end up rejecting the offer (via sending \(\mathsf {true}\) with label \( reject \)).
In what follows instead we will extend the above processes, giving to the customer the opportunity to retry, as suggested by the diagram in Fig. 1b.

In the example above, we have highlighted the syntactic construct allowing the customer to retry the purchase and obtain a new quote. In \(P_\mathtt {Customer}\) the only occurrence of the label \( retry \) is within a deterministic choice (\(\mathsf {if}~ \_ ~\mathsf {then} ~\_ ~\mathsf {else}~\_\) construct): if the quote is too high, the customer will communicate to the agency that they would like a different quote for a different destination. More interesting is how \(P_\mathtt {Agency}\) handles the \( retry \) request, namely by recursion on X: the recursive call is activated each time the agency receives a \( retry \) request from the customer.
Operational Semantics. The value \(\mathsf {v}\) of expression \(\mathsf {e}\) (notation \(\mathsf {e} \downarrow \mathsf {v}\)) is computed as expected, see Table 1. The successor operation \(\mathtt{succ}\) is defined only on natural numbers, the negation \(\mathtt{neg}\) is defined on integers, and \(\lnot \) is defined only on boolean values. The internal choice \(\mathsf {e}_1\oplus \mathsf {e}_2\) evaluates either to the value of \(\mathsf {e}_1\) or to the value of \(\mathsf {e}_2\).
The computational rules of multiparty sessions are given in Table 3. They are closed with respect to the structural congruence defined in Table 2. In rule [r-comm], the participant \(\mathsf{q}\) sends the value \(\mathsf {v}\) choosing the label \(\ell _j\) to participant \(\mathsf{p}\), who offers inputs on all labels \(\ell _i\) with \(i\in I\). In rules [t-conditional] and [f-conditional], the participant \(\mathsf{p}\) chooses to continue as \(P\) if the condition \(\mathsf {e}\) evaluates to \(\mathsf {true}\) and as \(Q\) if \(\mathsf {e}\) evaluates to \(\mathsf {false}\). Rule [r-struct] states that the reduction relation is closed with respect to structural congruence. We use \(\longrightarrow ^*\) with the standard meaning.
We adopt some standard conventions regarding the syntax of processes and sessions. Namely, we will use \(\prod _{i\in I} \mathsf{p}_i \triangleleft P_i\) as short for \(\mathsf{p}_1 \triangleleft P_1~|~\ldots ~|~\mathsf{p}_n \triangleleft P_n,\) where \(I=\{1,\ldots ,n\}\). We will sometimes use infix notation for external choice process. For example, instead of \(\sum _{i\in \{1,2\}} \mathsf{p} ? \ell _i(x) .P_i,\) we will write \(\mathsf{p} ? \ell _1(x) .P_1+\mathsf{p} ? \ell _2(x) .P_2 . \)
Example 2
We now show the operational semantics in action. Consider the following multiparty session with three participants, \( \mathtt {Alice},\) \(\mathtt {Bob}\) and \( \mathtt {Carol}: \)

where
This multiparty session reduces to
after three communications occur. First, \( \mathtt {Alice}\) sends to \( \mathtt {Bob}\) natural number 50 with the label \( \ell _1 \). \( \mathtt {Bob}\) is able to receive values with labels \( \ell _1 \) and \( \ell _4 .\) Next, the only possible communication is between \( \mathtt {Bob}\) and \( \mathtt {Carol}.\) So, \( \mathtt {Carol}\) receives natural number 100 from \( \mathtt {Bob}. \) The value 100 is substituted in the continuation process. Finally, since \(\mathtt{succ}(100) \downarrow 101 \), \( \mathtt {Carol}\) sends 101 to \( \mathtt {Alice}. \) We can then reduce the session to, for example, \( \mathtt {Alice} \triangleleft \mathbf {0}\), but not further.
Exercise 1
Prove the following:
-
1.
\(\mathtt {Customer} \triangleleft P'_\mathtt {Customer}~|~\mathtt {Agency} \triangleleft P'_\mathtt {Agency}\) reduces to \(\mathtt {Customer} \triangleleft \mathbf {0}~|~\mathtt {Agency} \triangleleft \mathbf {0}\);
-
2.
\(\mathtt {Customer} \triangleleft P_\mathtt {Customer}~|~\mathtt {Agency} \triangleleft P_\mathtt {Agency}\) reduces to \(\mathtt {Customer} \triangleleft \mathbf {0}~|~\mathtt {Agency} \triangleleft \mathbf {0}\).
From the end of Example 2, we can see that a session  always has at least one participant, since we do not have neutral element for the parallel composition. In Sect. 4, we will introduce a type system ensuring that if a well-typed multiparty session has only one participant, then the corresponding process is \(\mathbf {0}\) — hence, the participant’s process has no inputs/outputs to perform.
always has at least one participant, since we do not have neutral element for the parallel composition. In Sect. 4, we will introduce a type system ensuring that if a well-typed multiparty session has only one participant, then the corresponding process is \(\mathbf {0}\) — hence, the participant’s process has no inputs/outputs to perform.
The most crucial property is that when a multiparty session contains communications that will never be executed.
Definition 1
A multiparty session  is stuck if
is stuck if  and there is no multiparty session
and there is no multiparty session  such that
such that  A multiparty session
A multiparty session  gets stuck, notation
gets stuck, notation  if it reduces to a stuck multiparty session.
if it reduces to a stuck multiparty session.
The multiparty session  in Example 2 does not get stuck. A similar multiparty session, where instead of \( P_\mathtt {Alice}\) we take \( P_\mathtt {Alice}' = \mathtt {Bob} ! \ell _1\langle 50 \rangle . \mathtt {Carol} ? \ell _5(x) .\mathbf {0}\), gets stuck because of label mismatch.
in Example 2 does not get stuck. A similar multiparty session, where instead of \( P_\mathtt {Alice}\) we take \( P_\mathtt {Alice}' = \mathtt {Bob} ! \ell _1\langle 50 \rangle . \mathtt {Carol} ? \ell _5(x) .\mathbf {0}\), gets stuck because of label mismatch.
4 Type System
This section introduces a type system for the calculus presented in Sect. 3 (the formulation is based on [7]). We formalise types and projections (Sect. 4.1), the subtyping relation (Sect. 4.2), and the typing rules and their properties (Sect. 4.3). All stated results in this paper are proved in [7].
4.1 Types and Projections
Global types provide global conversation scenarios of multiparty sessions, with a bird’s eye view describing the message exchanges between pairs of participants.
Definition 2
(Sorts and global types). Sorts, ranged over by \(S\), are defined as:

Global types, ranged over by \(\mathsf {G}\), are terms generated by the following grammar:

We require that \(\mathsf{p}\ne \mathsf{q}\), \(I\ne \emptyset ,\) and \(\ell _i \ne \ell _j\) whenever \(i \ne j,\) for all \(i,j\in I\). We postulate that recursion is guarded. Unless otherwise noted, global types are closed: a recursion variable \(\mathbf {t}\) only occurs bounded by \(\mu \mathbf {t}.\ldots \)
In Definition 2, the type  formalises a protocol where participant
formalises a protocol where participant  must send to
must send to  one message with label
one message with label  and a value of type
and a value of type  as payload, for some
as payload, for some  ; then, depending on which
; then, depending on which  was sent by
was sent by  , the protocol continues as
, the protocol continues as  . Value types are restricted to sorts, that can be natural (
. Value types are restricted to sorts, that can be natural ( ), integer (\(\mathtt {int}\)) and boolean (\(\mathtt {bool}\)). The type \(\mathtt {end}\) represents a terminated protocol. Recursive protocol is modelled as
), integer (\(\mathtt {int}\)) and boolean (\(\mathtt {bool}\)). The type \(\mathtt {end}\) represents a terminated protocol. Recursive protocol is modelled as  , where recursion variable \(\mathbf {t}\) is bound and guarded in
, where recursion variable \(\mathbf {t}\) is bound and guarded in  — e.g.,
— e.g.,  is a valid global type, whereas
is a valid global type, whereas  is not. We take the equi-recursive viewpoint, i.e. we identify
is not. We take the equi-recursive viewpoint, i.e. we identify  .
.
We define the set of participants of a global type  , by structural induction on
, by structural induction on  , as follows:
, as follows:

We will often write  instead of
instead of  .
.
A local session type describes the behaviour of a single participant in a multiparty session.
Definition 3
(Local Session Types). The grammar of session types, ranged over by \({\mathsf T}\), is:

We require that \(\ell _i \ne \ell _j\) whenever \(i \ne j\), for all \(i,j\in I\). We postulate that recursion is always guarded. Unless otherwise noted, session types are closed.
Note that, according to the previous definition, labels in a type need to be pairwise different. For example, \( \mathsf{p}?\ell (\mathtt {int}).\mathtt {end} \& \mathsf{p}?\ell (\mathtt {nat}).\mathtt {end}\) is not a type.
The session type \(\mathtt {end}\) says that no further communication is possible and the protocol is completed. The external choice or branching type  requires to wait to receive a value of sort \(S_i\) (for some \(i \in I\)) from the participant \(\mathsf{p}\), via a message with label \(\ell _i\); if the received message has label \(\ell _i\), the protocol will continue as prescribed by \({\mathsf T}_i\). The internal choice or selection type \(\oplus _{i\in I}\mathsf{q}!\ell _i(S_i).{\mathsf T}_i\) says that the participant implementing the type must choose a labelled message to send to \(\mathsf{q}\); if the participant chooses the message \(\ell _i\), for some \(i\in I,\) it must include in the message to \(\mathsf{q}\) a payload value of sort \(S_i\), and continue as prescribed by \({\mathsf T}_i\). Recursion is modelled by the session type \(\mu \mathbf {t}.{\mathsf T}\) We adopt the following conventions: we do not write branch/selection symbols in case of a singleton choice, we do not write unnecessary parentheses, and we often omit trailing \(\mathtt {end}\)s.
requires to wait to receive a value of sort \(S_i\) (for some \(i \in I\)) from the participant \(\mathsf{p}\), via a message with label \(\ell _i\); if the received message has label \(\ell _i\), the protocol will continue as prescribed by \({\mathsf T}_i\). The internal choice or selection type \(\oplus _{i\in I}\mathsf{q}!\ell _i(S_i).{\mathsf T}_i\) says that the participant implementing the type must choose a labelled message to send to \(\mathsf{q}\); if the participant chooses the message \(\ell _i\), for some \(i\in I,\) it must include in the message to \(\mathsf{q}\) a payload value of sort \(S_i\), and continue as prescribed by \({\mathsf T}_i\). Recursion is modelled by the session type \(\mu \mathbf {t}.{\mathsf T}\) We adopt the following conventions: we do not write branch/selection symbols in case of a singleton choice, we do not write unnecessary parentheses, and we often omit trailing \(\mathtt {end}\)s.
The set \(\mathtt {pt}\{{\mathsf T}\}\) of participants of a session type \({\mathsf T}\) is defined inductively as follows

In what follows we introduce the concept of projection of a global type onto a participant, didactically into two steps: first we give the simpler version of the projection from [11, 12], then we extend it with the merging operation. The second definition will extend the domain of the projection as a partial function on global types, i.e., the second version of the projection will be well-defined on a wider range of global types.
Definition 4
The projection (no-merging version) of a global type onto a participant \(\mathsf{r}\) is defined by recursion on  :
:

We describe the clauses of Definition 4:
-
[proj-end,proj-var] give the behaviour of projections on \(\mathtt {end}\) and type variables;
-
[proj-rec-1,proj-rec-2] give the behaviour of projections on recursive types; in particular [proj-rec-2] is needed: if we applied only [proj-rec-1] to any recursive type, we will obtain
 , namely we will allow for unguarded occurrences of \(\mathbf {t}\), which we do not accept as valid;
, namely we will allow for unguarded occurrences of \(\mathbf {t}\), which we do not accept as valid; -
[proj-in] (resp. [proj-out]) states that a global type
 starting with a communication from \(\mathsf{p}\) to \(\mathsf{r}\) (resp. from \(\mathsf{r}\) to \(\mathsf{q}\)) projects onto an external (resp. internal) choice
starting with a communication from \(\mathsf{p}\) to \(\mathsf{r}\) (resp. from \(\mathsf{r}\) to \(\mathsf{q}\)) projects onto an external (resp. internal) choice  (resp.
(resp.  ), provided that the continuations of
), provided that the continuations of  (resp.
(resp.  ) are also projections of the corresponding global type continuations
) are also projections of the corresponding global type continuations 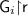 .
. -
[proj-cont’] states that if
 starts with a communication between
starts with a communication between  and
and  , and we are projecting
, and we are projecting  onto a third participant
onto a third participant  , then we need to make sure that continuation is the same on all branches; just below we will see how this restriction can be relaxed.
, then we need to make sure that continuation is the same on all branches; just below we will see how this restriction can be relaxed.
Example 3
We now show an example of some projections of global types. Consider the global type (where \(\mathsf{p}\), \(\mathsf{q}\) and \(\mathsf{r}\) are pairwise distinct):

We have:

Note that  is well defined only because the continuation of the communication after the exchange
is well defined only because the continuation of the communication after the exchange  is equal, namely
is equal, namely  , in both branches.
, in both branches.
In the following Definition 5, we give a more permissive definition of projection, that handles also cases in which the continuation is not the same in all branches, but the types are somehow “compatible”, namely they can be merged. Our definition follows [7], which extends [11, 12], along the lines of [19] and [2]. i.e., it uses a merging operator \(\sqcap \).
Definition 5
The projection of a global type onto a participant \(\mathsf{r}\) is defined by recursion on  :
:

Above, \(\sqcap \) is the merging operator, that is a partial operation over session types defined as:

Proposition 1
The merging operation is associative, i.e.:  .
.
By Definition 5, merging a type with itself results in itself (rule [mrg-id]). Moreover, Definition 5 allows to combine different external choices (rule [mrg-id]) if and only if common labels have identical sorts and identical continuations, as formalised in Proposition 2 below and illustrated in Examples 4 to 6.
Proposition 2
For two types \( {\mathsf T}' = \& _{i \in I} \mathsf{p}'?\ell _i(S_i){.{\mathsf T}_i}\) and \( {\mathsf T}'' = \& _{j \in J} \mathsf{p}''?\ell _j(S_j){.{\mathsf T}_j}\), we have that \({\mathsf T}' \sqcap {\mathsf T}''\) is defined if and only if  and, whenever \(\ell _i = \ell _j\) (for some \(i \in I\) and \(j \in J\)), \(S_i = S_j\) and \({\mathsf T}_i = {\mathsf T}_j\).
and, whenever \(\ell _i = \ell _j\) (for some \(i \in I\) and \(j \in J\)), \(S_i = S_j\) and \({\mathsf T}_i = {\mathsf T}_j\).
Example 4
We now give some small examples that illustrate the definition of the merging operator (here, \(i \ne j\) implies \(\ell _i \ne \ell _j\)):

Now we understand better how clause [proj-cont] works: it states that if  starts with a communication between \(\mathsf{p}\) and \(\mathsf{q}\), and we are projecting
starts with a communication between \(\mathsf{p}\) and \(\mathsf{q}\), and we are projecting  onto a third participant \(\mathsf{r}\), then we need to (1) skip the initial communication, (2) project all the continuations onto \(\mathsf{r}\), and (3) merge the resulting session types, using the merging operator \(\sqcap \).
onto a third participant \(\mathsf{r}\), then we need to (1) skip the initial communication, (2) project all the continuations onto \(\mathsf{r}\), and (3) merge the resulting session types, using the merging operator \(\sqcap \).
As a result, clause [proj-cont] of Definition 5 allows participant \(\mathsf{r}\) to receive different messages (from a same participant \(\mathsf{p}'\)) in different branches of a global type, as shown in Example 5 below.
Example 5
We demonstrate interesting points of Definition 5. First, we show some projections of global types. Consider the global type:

We have:

Note that in  , \(\mathsf{q}\) could output different messages towards \(\mathsf{r}\), depending on whether \(\mathsf{p}\) sends \(\ell _1\) or \(\ell _2\) to \(\mathsf{q}\); therefore, in
, \(\mathsf{q}\) could output different messages towards \(\mathsf{r}\), depending on whether \(\mathsf{p}\) sends \(\ell _1\) or \(\ell _2\) to \(\mathsf{q}\); therefore, in  , the possible inputs of \(\mathsf{r}\) in
, the possible inputs of \(\mathsf{r}\) in  and
and  are merged into a larger external choice that supports all possible outputs of \(\mathsf{q}\).
are merged into a larger external choice that supports all possible outputs of \(\mathsf{q}\).
Importantly, by Definition 5, there exist global types that cannot be projected onto all their participants. This is because  might describe meaningless protocols, that cause the merging operation \(\sqcap \) in clause [proj-cont] to be undefined, as shown in Example 6 below.
might describe meaningless protocols, that cause the merging operation \(\sqcap \) in clause [proj-cont] to be undefined, as shown in Example 6 below.
Example 6
We show two global types that cannot be projected according to the Definition 5. Consider the global type  , with
, with  and
and  . Then,
. Then,

Intuitively, when \(\ell _3 \ne \ell _4\),  is undefined because in
is undefined because in  , depending on whether \(\mathsf{p}\) and \(\mathsf{q}\) exchange \(\ell _1\) or \(\ell _2\), \(\mathsf{r}\) is supposed to send either \(\ell _3\) or \(\ell _4\) to \(\mathsf{q}\); however, \(\mathsf{r}\) is not privy to the interactions between \(\mathsf{p}\) and \(\mathsf{q}\), and thus,
, depending on whether \(\mathsf{p}\) and \(\mathsf{q}\) exchange \(\ell _1\) or \(\ell _2\), \(\mathsf{r}\) is supposed to send either \(\ell _3\) or \(\ell _4\) to \(\mathsf{q}\); however, \(\mathsf{r}\) is not privy to the interactions between \(\mathsf{p}\) and \(\mathsf{q}\), and thus,  provides an invalid specification for \(\mathsf{r}\). Instead, if \(\ell _3 = \ell _4\), then by Definition 5 we have
provides an invalid specification for \(\mathsf{r}\). Instead, if \(\ell _3 = \ell _4\), then by Definition 5 we have  .
.
Now, consider the global type  , with
, with  and
and  . Then,
. Then,

Here,  is undefined because in
is undefined because in  , depending on whether \(\mathsf{p}\) and \(\mathsf{q}\) exchange \(\ell _1\) or \(\ell _2\), \(\mathsf{r}\) is supposed to receive either one or two messages \(\ell _3\) from \(\mathsf{q}\); however, as in the previous example, \(\mathsf{r}\) is not aware of the interactions between \(\mathsf{p}\) and \(\mathsf{q}\), and thus,
, depending on whether \(\mathsf{p}\) and \(\mathsf{q}\) exchange \(\ell _1\) or \(\ell _2\), \(\mathsf{r}\) is supposed to receive either one or two messages \(\ell _3\) from \(\mathsf{q}\); however, as in the previous example, \(\mathsf{r}\) is not aware of the interactions between \(\mathsf{p}\) and \(\mathsf{q}\), and thus,  provides an invalid specification for \(\mathsf{r}\). This example could be fixed, e.g., by replacing \(\ell _3\) with \(\ell ' \ne \ell _3\) in
provides an invalid specification for \(\mathsf{r}\). This example could be fixed, e.g., by replacing \(\ell _3\) with \(\ell ' \ne \ell _3\) in  , or by letting
, or by letting  : both fixes would make
: both fixes would make  defined, similarly to Example 5.
defined, similarly to Example 5.
4.2 Subtyping
The subtyping relation \(\leqslant \) is used to augment the flexibility of the type system (introduced in Sect. 4.3): by determining when a type \({\mathsf T}\) is “smaller” than \({\mathsf T}'\), it allows to use a process typed by the former whenever a process typed by the latter is required.
Definition 6
(Subsorting and subtyping). Subsorting  is the least reflexive binary relation such that
is the least reflexive binary relation such that  .
.
Subtyping  is the largest relation between session types coinductively defined by the following rules:
is the largest relation between session types coinductively defined by the following rules:

Intuitively, the session subtyping \(\leqslant \) in Definition 6 says that \({\mathsf T}\) is smaller than \({\mathsf T}'\) when \({\mathsf T}\) is “less liberal” than \({\mathsf T}'\) — i.e., when \({\mathsf T}\) allows for less internal choices, and demands to handle more external choices.Footnote 1 A peculiarity of the relation is that, apart from a pair of inactive session types, only inputs and outputs from/to a same participant can be related (with additional conditions to be satisfied). Note that the double line in the subtyping rules indicates that the rules are interpreted coinductively [15, Chapter 21]
-
[sub-end] says that \(\mathtt {end}\) is only subtype of itself.
-
[sub-in] relates external choices from the same participant \(\mathsf{p}\): the subtype must support all the choices of the supertype, and for each common message label, the continuations must be related, too; note that the carried sorts are contravariant: e.g., if the supertype requires to receive a message \(\ell _i(\mathtt {nat})\) (for some \(i \in I\)), then the subtype can support \(\ell _i(\mathtt {int})\) or \(\ell _i(\mathtt {nat})\), since
 and
and  .
. -
[sub-out] relates internal choices towards the same participant \(\mathsf{p}\): the subtype must offer a subset of the choices of the supertype, and for each common message label, the continuations must be related, too; note that the carried sorts are covariant: e.g., if the supertype allows to send a message \(\ell _i(\mathtt {int})\) (for some \(i \in I\)), then the subtype can allow to send \(\ell _i(\mathtt {int})\) or \(\ell _i(\mathtt {nat})\), since
 and
and  .
.
Lemma 1
The subtyping relation \(\leqslant \) is reflexive and transitive.
4.3 Type System
We now introduce a type system for the multiparty session calculus presented in Sect. 3. We distinguish three kinds of typing judgments:

where \(\varGamma \) is the typing environment:
i.e., a mapping that associates expression variables with sorts, and process variables with session types.
We say that a multiparty session  is well typed if there is a global type
is well typed if there is a global type  such that
such that  . If a multiparty session is well typed, we will sometimes write just
. If a multiparty session is well typed, we will sometimes write just 
The typing rules for expressions are given in Table 4, and are self-explanatory. The typing rules for processes and multiparty sessions are content of Table 5:
-
[t-sub] is the subsumption rule: a process with type \({\mathsf T}\) is also typed by the supertype \({\mathsf T}'\);
-
 says that a terminated process implements the terminated session type;
says that a terminated process implements the terminated session type; -
[t-rec] types a recursive process \(\mu X.P\) with \({\mathsf T}\) if \(P\) can be typed as \({\mathsf T}\), too, by extending the typing environment with the assumption that X has type \({\mathsf T}\);
-
[t-var] uses the typing environment assumption that process X has type \({\mathsf T}\);
-
[t-input-choice] types a summation of input prefixes as a branching type. It requires that each input prefix targets the same participant \(\mathsf{q}\), and that, for all \(i \in I\), each continuation process \(P_i\) is typed by the continuation type \({\mathsf T}_i\), having the bound variable \(x_i\) in the typing environment with sort \(S_i\). Note that the rule implicitly requires the process labels \(\ell _i\) to be pairwise distinct (as per Definition 3);
-
[t-out] types an output prefix with a singleton selection type, provided that the expression in the message payload has the correct sort \(S\), and the process continuation matches the type continuation;
-
[t-choice] types a conditional process with \({\mathsf T}\) if its sub-processes can be typed by \({\mathsf T}\) and expression \(\mathsf {e}\) is boolean.
-
[t-sess] types multiparty sessions, by associating typed processes to participants. It requires that the processes being composed in parallel can play as participants of a global communication protocol: hence, their types must be projections of a single global type
 . The condition
. The condition  allows to also type sessions containing \(\mathsf{p} \triangleleft \mathbf {0}\): this is needed to assure invariance of typing.
allows to also type sessions containing \(\mathsf{p} \triangleleft \mathbf {0}\): this is needed to assure invariance of typing.
Example 7
We show that the multiparty session  from Example 2 is well typed. Consider the following global type:
from Example 2 is well typed. Consider the following global type:

We show that participants \( \mathtt {Alice},\) \(\mathtt {Bob}\) and \( \mathtt {Carol}\) respect the prescribed protocol  , by showing that they participate in a well-typed multiparty session. Applying rules from Table 5, we derive
, by showing that they participate in a well-typed multiparty session. Applying rules from Table 5, we derive
where:
Now, let:
Since it holds that \( {\mathsf T}_\mathtt {Alice}\leqslant {\mathsf T}_\mathtt {Alice}' \), and the projections of  to the participants are
to the participants are

we conclude:

Example 8
Let us consider processes \(P_\mathtt {Customer}\) and \(P_\mathtt {Agency}\) from Example 1. As a suitable global type for the session
we pick the following.

Observe the recursive behaviour over \(\mathbf {t}\). Now, let us project  onto its participant \(\mathtt {Agency}\) (there is no need to merge types here, namely we can use Definition 4):
onto its participant \(\mathtt {Agency}\) (there is no need to merge types here, namely we can use Definition 4):

Also this projection presents a recursive behaviour as expected. The reader will now be able to derive:

Exercise 2
This exercise is intended to guide the reader to obtain the final result (using the same notation as in Examples 1 and 8):

Let us proceed step by step following Example 7.
-
1.
Given the global type
 and its projection
and its projection  , derive
, derive  .
. -
2.
Then derive
 and
and  .
.
Hint 1. The reader might want to use the identification of  and
and  (this holds both for global and session types), namely the possibility to unfold any recursive construct for types.
(this holds both for global and session types), namely the possibility to unfold any recursive construct for types.
Hint 2. In order to prove points 2. and 3. the reader might want to proceed in two steps: first, finding appropriate session types \({\mathsf T}_\mathtt {Customer}\) and \({\mathsf T}_\mathtt {Agency}\) for processes \(P_\mathtt {Customer}\) and \(P_\mathtt {Agency}\) respectively, and second, proving  and
and  .
.
Exercise 3
Prove that:  .
.
The proposed type system for multiparty sessions enjoys two fundamental properties: typed sessions only reduce to typed sessions (subject reduction), and typed sessions never get stuck. The remaining of this section is devoted to the proof of these properties.
In order to state subject reduction, we need to formalise how global types are modified when multiparty sessions reduce and evolve.
Definition 7
(Global types consumption and reduction). The consumption of the communication \(\mathsf{p}\xrightarrow {\ell }\mathsf{q}\) for the global type  (notation
(notation  ) is the global type coinductively defined as follows:
) is the global type coinductively defined as follows:

The reduction of global types is the smallest pre-order relation closed under the rule: 
Example 9
We show that a projection of a global type before the consumption might require to support more external choices than the projection after the consumption. Take  , its subterm
, its subterm  , from Example 5, and their types denoted as
, from Example 5, and their types denoted as  and
and  , respectively. Also take the projection:
, respectively. Also take the projection:

and recall the explanation on how  above merges all the possible inputs that \(\mathsf{r}\) might receive from \(\mathsf{q}\), depending on whether \(\mathsf{p}\) first sends \(\ell _1\) or \(\ell _2\) to \(\mathsf{q}\).
above merges all the possible inputs that \(\mathsf{r}\) might receive from \(\mathsf{q}\), depending on whether \(\mathsf{p}\) first sends \(\ell _1\) or \(\ell _2\) to \(\mathsf{q}\).
We have:

and we obtain  . The reason is that, after the transition from
. The reason is that, after the transition from  to
to  , there is no possibility for \(\mathsf{q}\) to send \(\ell _4\) to \(\mathsf{r}\), hence \(\mathsf{r}\) does not need to support such a message in its projection.
, there is no possibility for \(\mathsf{q}\) to send \(\ell _4\) to \(\mathsf{r}\), hence \(\mathsf{r}\) does not need to support such a message in its projection.
Note that a process that plays the role of \(\mathsf{r}\) in  , and is therefore typed by
, and is therefore typed by  , has to support the input of \(\ell _4\) from \(\mathsf{q}\), by rule [t-input-choice] in Table 5. After the transition from
, has to support the input of \(\ell _4\) from \(\mathsf{q}\), by rule [t-input-choice] in Table 5. After the transition from  to
to  , the same process is also typed by
, the same process is also typed by  , by rule [t-sub] — but will never receive a message \(\ell _4\) from \(\mathsf{q}\).
, by rule [t-sub] — but will never receive a message \(\ell _4\) from \(\mathsf{q}\).
We can now prove subject reduction.
Theorem 1
(Subject Reduction). Let  For all
For all  , if
, if  , then
, then  for some
for some  such that
such that  .
.
Theorem 2
(Progress). If  , then either
, then either  or there is
or there is  such that
such that 
As a consequence of subject reduction and progress, we get the safety property stating that a typed multiparty session will never get stuck.
Theorem 3
(Type Safety). If  , then it does not hold
, then it does not hold 
Proof
Direct consequence of Theorems 1, 2, and Definition 1.
Finally the reader wishes to learn more about the full asynchronous multiparty session types (which includes channel passing, asynchrony (FIFO queues), shared names and parameterised recursion) can proceed to [1]. The article [16] also discusses type soundness of various MPST calculi.
Notes
- 1.
Readers familiar with the theory of session types might notice that our subtyping relation is inverted w.r.t. the original binary session subtyping, introduced in the works of [3, 6]. In such works, smaller types have less internal choices, and more external choices: this is because they formalise a “channel-oriented” notion of subtyping, while we adopt a “process-oriented” view. For a thorough analysis and comparison of the two approaches, see [5].
References
Coppo, M., Dezani-Ciancaglini, M., Padovani, L., Yoshida, N.: A gentle introduction to multiparty asynchronous session types. In: Bernardo, M., Johnsen, E.B. (eds.) SFM 2015. LNCS, vol. 9104, pp. 146–178. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-18941-3_4
Deniélou, P., Yoshida, N., Bejleri, A., Hu, R.: Parameterised multiparty session types. Log. Methods Comput. Sci. 8(4) (2012). https://doi.org/10.2168/LMCS-8(4:6)2012
Gay, S., Hole, M.: Subtyping for session types in the pi calculus. Acta Informatica 42(2/3), 191–225 (2005). https://doi.org/10.1007/s00236-005-0177-z
Gay, S., Ravera, A. (eds.): Behavioural Types: From Theory to Tools. River Publishers (2017)
Gay, S.J.: Subtyping supports safe session substitution. In: Lindley, S., McBride, C., Trinder, P., Sannella, D. (eds.) A List of Successes That Can Change the World. LNCS, vol. 9600, pp. 95–108. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-30936-1_5
Gay, S., Hole, M.: Types and subtypes for client-server interactions. In: Swierstra, S.D. (ed.) ESOP 1999. LNCS, vol. 1576, pp. 74–90. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-49099-X_6
Ghilezan, S., Jaksic, S., Pantovic, J., Scalas, A., Yoshida, N.: Precise subtyping for synchronous multiparty sessions. J. Log. Algebr. Meth. Program. 104, 127–173 (2019). https://doi.org/10.1016/j.jlamp.2018.12.002
Honda, K.: Types for dyadic interaction. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 509–523. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-57208-2_35
Honda, K., Mukhamedov, A., Brown, G., Chen, T.-C., Yoshida, N.: Scribbling interactions with a formal foundation. In: Natarajan, R., Ojo, A. (eds.) ICDCIT 2011. LNCS, vol. 6536, pp. 55–75. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19056-8_4
Honda, K., Vasconcelos, V.T., Kubo, M.: Language primitives and type discipline for structured communication-based programming. In: Hankin, C. (ed.) ESOP 1998. LNCS, vol. 1381, pp. 122–138. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0053567
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. In: POPL, pp. 273–284. ACM Press (2008). https://doi.org/10.1145/1328438.1328472
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. J. ACM 63, 1–67 (2016)
Hüttel, H., et al.: Foundations of session types and behavioural contracts. ACM Comput. Surv. 49(1) (2016). https://doi.org/10.1145/2873052
Kouzapas, D., Yoshida, N.: Globally governed session semantics. In: D’Argenio, P.R., Melgratti, H. (eds.) CONCUR 2013. LNCS, vol. 8052, pp. 395–409. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40184-8_28
Pierce, B.C.: Types and Programming Languages. MIT Press (2002)
Scalas, A., Yoshida, N.: Less is more: multiparty session types revisited. ACM Program. Lang. POPL (2019). https://doi.org/10.1145/3290343
Scribble home page. http://www.scribble.org
Takeuchi, K., Honda, K., Kubo, M.: An interaction-based language and its typing system. In: Halatsis, C., Maritsas, D., Philokyprou, G., Theodoridis, S. (eds.) PARLE 1994. LNCS, vol. 817, pp. 398–413. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58184-7_118
Yoshida, N., Deniélou, P.-M., Bejleri, A., Hu, R.: Parameterised multiparty session types. In: Ong, L. (ed.) FoSSaCS 2010. LNCS, vol. 6014, pp. 128–145. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12032-9_10
Yoshida, N., Hu, R., Neykova, R., Ng, N.: The scribble protocol language. In: Abadi, M., Lluch Lafuente, A. (eds.) TGC 2013. LNCS, vol. 8358, pp. 22–41. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-05119-2_3
Acknowledgements
We would like to thank Fangyi Zhou for their carfeul proofreading and detailed comments on the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Yoshida, N., Gheri, L. (2020). A Very Gentle Introduction to Multiparty Session Types. In: Hung, D., D´Souza, M. (eds) Distributed Computing and Internet Technology. ICDCIT 2020. Lecture Notes in Computer Science(), vol 11969. Springer, Cham. https://doi.org/10.1007/978-3-030-36987-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-36987-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36986-6
Online ISBN: 978-3-030-36987-3
eBook Packages: Computer ScienceComputer Science (R0)








 , namely we will allow for unguarded occurrences of
, namely we will allow for unguarded occurrences of  starting with a communication from
starting with a communication from  (resp.
(resp.  ), provided that the continuations of
), provided that the continuations of  (resp.
(resp.  ) are also projections of the corresponding global type continuations
) are also projections of the corresponding global type continuations 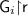 .
. starts with a communication between
starts with a communication between  and
and  , and we are projecting
, and we are projecting  onto a third participant
onto a third participant  , then we need to make sure that continuation is the same on all branches; just below we will see how this restriction can be relaxed.
, then we need to make sure that continuation is the same on all branches; just below we will see how this restriction can be relaxed. and
and  .
. and
and  .
. says that a terminated process implements the terminated session type;
says that a terminated process implements the terminated session type; . The condition
. The condition  allows to also type sessions containing
allows to also type sessions containing  and its projection
and its projection  , derive
, derive  .
. and
and  .
.