First-Principles Modeling of Non-covalent Interactions in Molecular Systems and Extended Materials

Abstract

The intermolecular non-covalent interactions through van der Waals or dispersion forces are pervasive in nature and play a fundamental role in regulating the structure and function of molecular systems ranging from solid state materials to biological systems. The atomistic modeling of non-covalent interactions is incredibly difficult, as they often require exact treatment of long-range electron correlation which in turn demand to go beyond second-order perturbation theory. As for example, the prediction of induction that stems from the response of a molecular system to a permanent multipole necessitate the precise evaluation of molecular polarizabilities. The computation of dispersion interaction also appears to be a formidable task as they involve Coulomb interaction between the instantaneous correlated fluctuations of electrons. Therefore, a systematic and unified theoretical framework for isolating non-covalent interactions is essentially required to reliably model the structure, energetics, and reactivities of realistic molecular systems. In this review, the fundamental theoretical principles and computational aspects for the estimation of strong and weak non-covalent interactions are discussed by emphasizing studies of classic examples such as hydrogen bonding and related properties of small water clusters, halide-water clusters, fatty acid dimers and their amides; several gas-phase and dihydrated cation-π complexes comprising benzene, p-methylphenol, and 3-methylindole as the π-donor systems and Mg²⁺, Ca²⁺, and NH₄ ⁺ cations as the acceptor units; the π-π interactions between benzene and monosubstituted benzenes in parallel face-to-face stacking configuration, as well as the supramolecular complexes. A comprehensive picture of the accuracy of the most widely used first-principles approaches including dispersion-corrected density functional approximations, second order Møller-Plesset and symmetry-adapted perturbation theory, as well as non-canonical coupled cluster theory in predicting van der Waals and dispersion interactions has also been presented. The discussion culminates through the conceptual and mathematical ingredients required to establish structure-property relationships e.g., the correlation between hydrogen-boning and the vibrational modes, impact of electrostatic interactions on charge transfer to solvents, and the relation between Hammett substituent constants and the dispersion interactions in extended π-systems.

3.1 Introduction

Various kind of forces are associated with the formation of molecular structures and crystals. They can be generally classified in terms of strong and weak interactions. The strong interactions are responsible for the formation of molecular frame and are generally classified as covalent and electrostatic forces. There are, of course, two sub-classes of these two forces and are characterized in terms of co-ordinate and metallic bonding. Pure electrostatic bond is generally considered as stronger than the co-ordinate and metallic bonds, while a covalent bond can be much stronger than these three forces. Such a comparison is, of course, purely qualitative and the magnitude of such binding forces can vary depending on the bonding condition. The weak interactions, on the other hand, exert much weaker forces (than these four strong forces) and are responsible for the shape and properties of various molecular systems (as well as crystals) and, like strong interactions, are important forces of nature.

The natures of strong forces are quite well-defined using bonding theories of quantum chemistry. The covalent bonding, for example, was explained from Pauling’s hybridization theories [1], and through molecular orbital (MO) theories [2]. The MO theories were later modified in present day quantum chemistry for very accurate description of molecular systems in relation to their shape and bonding characteristics. These are mostly based on Hartree-Fock (HF) theories [3] with the inclusion of basis set concepts of Roothan and Hall [3, 4]. More accurate HF based theories, for example Møller-Plesset perturbation theories [5,6,7], coupled-cluster theories [6, 8], and configuration interaction (CI) techniques [3, 6, 8] include electronic correlation effect and are widely used for present-day structure and bonding analysis of molecular systems. The alternative density functional theory (DFT) based approaches, which are based on Kohn-Sham variational principle [9, 10], are also very successful and widely used techniques to explain molecular structures in gas-phase, solvated conditions, and their excited state properties [6, 11, 12]. The DFT techniques find further importance in calculating the structures and electronic properties of solid systems and in present days are widely used in the field of materials science research. All the techniques described above are well developed and could be used directly to explain the nature of the four major strong forces occurring in different forms of the molecular systems. These are, of course, not in the purview of the present article. In the present review, we will discuss the nature of weak interactions, and the use of the present-day theories (MP, CC, DFT etc. theories) to assess the various structural and binding characteristics of the weakly-bonded species.

Weak interactions, also called non-covalent interactions in chemistry, usually occur between two molecular species. Some molecular systems, for example inert gas dimers (He₂, Ar₂ etc.) are also weakly bonded as such. These interactions are of medium to long range in nature and arise from the charge distribution patterns around a molecule (or an atom). Such a charge distribution is not constant and fluctuates due to movement of electrons. In the case of weakly interacting systems, the transient asymmetry of the charge distribution around one of the component species can induce a complementary asymmetry in the electronic distribution around the neighboring partner through electrostatic interactions and produce a weak attractive force to hold them together. This force of attraction is operative up to a certain distance r between these two systems and at smaller distance (with respect to r), the forces become repulsive because of the overlap of the outer electron clouds. Thus, this attractive force is of long range in nature, but at sufficiently large separation between the two species (much larger than r), it disappears due to simple electrostatic law. The important point related to the weakly bound system is that the individual components retain their characteristics more or less unchanged. This is a very qualitative oversimplified way to explain the origin of weak interactions. The actual situation is more complex when someone would try to identify the nature of such forces through proper quantitative analysis of the operating forces.

The origin of weak interactions, as introduced here, are special forms of electron-correlation effects and fall under the category of van der Waals interactions. Dipole-dipole, dipole-induced dipole, and London dispersion forces (r ^–6 dependent forces) are mostly responsible for such van der Waals interactions. Although these terms have their common classical mechanics definitions, they could be explicitly treated in quantum chemical methods through introduction of electron correlation effects. Formation of hydrogen boded systems, e.g., water, methanol, ammonia etc. are mostly due to the van der Waals interactions arising from dipole-dipole interactions effects, since the individual molecular components in these systems have permanent dipole moments. The interactions inside the H₂-He or noble gas dimers, on the other hand, has binding forces arising purely through London dispersion types. The forces are generally weak in nature (0.1–0.2 kcal/mol), although hydrogen bonding interactions are much stronger (e.g., 2–5 kcal/mol for hydrogen bonding involving N-H and O-H units).

Long-range π-π and cation-π are two different type of non-covalent interactions, which are usually stronger than regular hydrogen bonds. In both the cases dispersion interactions are generally operative, but the interaction-nature cannot be explained so simply. In the case of cation-π interactions, dipole-induced dipole and higher order quadrupole-dipole, quadrupole-quadrupole interactions etc. interactions are also operative. These types of interactions were predicted initially by Kier and coworkers [13, 14] and, almost 20 years later, were fully established by Dougherty and coworkers [15, 16]. These interactions have emerged as a very common binding force to interpret binding nature between cation and aromatics in various biomolecular systems including proteins, receptor-ligand complexes, molecular recognition, drug actions and protein folding [15,16,17,18,19,20,21]. The π-π dispersion interactions are long known, and this type of weak interactions are important in many naturally occurring materials. The most common example is graphite, and multilayered graphene sheets.

The present review is primarily oriented around the quantification of these non-covalent weak interactions. These would be based on various case specific analyses to understand the energetics of such interactions. There are, of course, several other characteristics of such systems which are available through experimental and theoretical analyses. Low-frequency vibrations along with the high frequency vibrational modes were found to modulate the strength of hydrogen bonds in several hydrogen-bonded systems [22]. Furthermore, the weakly bound systems demonstrate several molecular properties e.g., additive properties of interaction energies and charge transfer to solvents (CTTS, in halide-water clusters) [23]. In the case of π-π interactions, Hammett equation criteria was found to be important to understand the nature of interactions in specific cases, when various π-derivative systems were allowed to interact with a specific π-scaffold [24]. These properties have been experimentally studied in weakly bound systems using finite sized weak clusters [25]. The non-covalent interactions are also the building blocks for the artificial designing of several bioinspired materials [26]. The present review will also address these properties of the weakly bound systems with specific examples. A brief review related to the theoretical background of the energy quantification, both classical and quantum mechanical, would be presented prior to the discussion of the individual type of non-covalently bound systems.

3.2 Theoretical Models of Non-covalent Interactions

Non-covalent interactions between atoms or molecules could be treated through regular molecular interaction calculations. The only difference is that the interaction energy values are low because of the larger separation of the interacting systems. Electrostatic interactions are central to all these attractive forces, but it cannot account for the whole interaction energies. Interactions between the noble gas atoms are typical examples, since they have no dipole moment or higher moments. On the other hand, there must be some clear interactions between these atoms. The molecular beam experiments [27, 28] were used to measure interactions between the noble gas atoms and Fig. 3.1 schematically shows the nature of such interactions in the case of argon dimer. The computed interaction energy surface reaches a minimum at 3.8 Å (i.e., it shows an attractive nature) and this energy tends to vanish at a very large separation [29]. At shorter distances, this interaction energy curve shows repulsive character. This trend of non-covalent interactions has already been discussed in Sect. 3.1 and such an energy curve is general for all the noble gas atoms dimers also. The force between the atoms, which could be defined as the negative of the potential energy derivative with respect to the interatomic distances (r) (shown schematically in Fig. 3.1), also shows similar trend with respect to r.

Fig. 3.1

Schematic diagram of the intermolecular energy and the force between two argon (Ar) atoms

The curves in Fig. 3.1 are considered as a balance between two forces viz., attractive dispersive force and the repulsive force of exchange type. Both forces have their quantum mechanical origin. The dispersive force arises from the generation of instantaneous dipole from the fluctuating electron clouds. This instantaneous dipole can induce a dipole in the neighboring molecule producing an attractive inductive effect. The dispersive force could be developed from Drude model based on traditional Schrödinger equation. For two interacting molecules, the Drude model generates interaction energy of the form,

$$ E(r)=-\frac{1}{2}\frac{\alpha^4\mathrm{\hbar}\omega }{{\left(4\pi {\varepsilon}_0\right)}^2{r}^6} $$

(3.1)

Where α is the polarizability, ω/2π is the frequency of an isolated Drude molecule, r is the separation between the two molecules, and ħ(=h/2π) is the Planck’s constant. In three dimensions, this energy is given by,

$$ E(r)=-\frac{3}{4}\frac{\alpha^4\mathrm{\hbar}\omega }{{\left(4\pi {\varepsilon}_0\right)}^2{r}^6} $$

(3.2)

The complete derivation of the interaction energies is not needed in this review. Interested readers can see the ref. [30] for the complete derivation. The Drude model described here considers only dipole-dipole interaction term. If higher order terms arising from dipole-quadrupole, quadrupole-quadrupole etc. interactions are included, the interaction energy from Drude model could be represented as [30, 31]

$$ E(r)=\sum_n\frac{A_n}{r^n}\kern0.75em \left(n=6,8,10,\dots \dots \right) $$

(3.3)

The determination of the coefficients (A _n) is discussed in detail in ref. [31]. These coefficients are negative due to attractive nature of the interaction terms. If just A ₆ term is included for Ar case, the computed dispersion is ~25% smaller with respect to the total interaction energies from experiment.

The interaction energy curve in Fig. 3.1 shows that slight decrease in interatomic distance between Ar-atoms (~3 Å) causes a large increase in energy to the repulsive region. This increase has quantum mechanical origin and could be explained from Pauli’s principle. It formally prevents two electrons in a system having same set of quantum numbers. The short-range repulsive force here, is arising from electrons with same spin, and is referred to as exchange forces (also known as overlap forces). At short r, the interaction energy varies as 1/r due to nuclear repulsion and at larger r, the energy decays exponentially as $\exp \left(-\frac{2r}{a_0}\right)$ (a ₀ : Bohr Radius).

3.2.1 Modeling van der Waals Interactions

The dispersive and repulsive (exchange-repulsion) interactions between atoms and molecules could be calculated through quantum mechanics. These calculations are far from trivial and require electron correlation with large basis sets. We will discuss such methods in connection with the non-covalent interactions in DFT calculations. The simpler form of the van der Waals interaction as would be outlined here are the basis for the interpretation of non-covalent interactions computed through more complicated quantum-mechanical calculations.

The basic criteria of the dispersive and repulsive forces in a non-covalent interaction between two molecules or atoms should fit to the general functional form,

$$ {E}_{VW}\left({r}^{IJ}\right)={E}_{repulsive}\left({r}^{IJ}\right)-\frac{C^{IJ}}{{\left({r}^{IJ}\right)}^6} $$

(3.4)

It is not possible to classically derive the functional form of the repulsive interactions. The interaction energy should go to zero as (r ^IJ) → ∞ and should approach zero faster than (r ^IJ)⁻⁶ term.

The most popular potential, which satisfy this requirement, is the Lennard-Jones (LJ) potential [32]. Here, the repulsive part has (r ^IJ)⁻¹² dependence,

$$ {E}_{LJ}(r)=\frac{C_1}{{\left({r}^{IJ}\right)}^{12}}-\frac{C_2}{{\left({r}^{IJ}\right)}^6} $$

(3.5)

where, C ₁ and C ₂ are suitable constants. The alternative form of LJ potential has the following form,

$$ {E}_{LJ}(r)=\varepsilon \left[{\left(\frac{r_0}{r^{IJ}}\right)}^{12}-2{\left(\frac{r_0}{r^{IJ}}\right)}^6\right] $$

(3.6)

Where, r ₀ is the minimum distance, and ε is the depth of the minimum. There is no theoretical basis for the choice of the repulsive part, this is purely for computational convenience. Sometimes exponent of 9 or 10 can generate better results.

Considering the exponential decay of the repulsive term, a E _VW potential, known as Buckingham or Hill type potential [33] was developed in the following form,

$$ {E}_{VW}(r)={C}_1\mathit{\exp}\left(-{C}_2{r}^{IJ}\right)-\frac{C_3}{{\left({r}^{IJ}\right)}^6} $$

(3.7)

Here, C ₁, C ₂ and C ₃ are suitable constants. Equation (3.7) is sometimes written in the following convoluted form also.

$$ {E}_{VW}(r)=\zeta \left[\frac{6}{\alpha -6}\mathit{\exp}\left\{\alpha \left(1-\frac{r^{IJ}}{r_0}\right)\right\}-\frac{\alpha }{\alpha -6}{\left(\frac{r_0}{r^{IJ}}\right)}^6\right] $$

(3.8)

Where, α is a force parameter and choosing α = 12, Eq. (3.8) generates LJ potential. Figure 3.2 schematically shows the attractive part of the LJ(12-6), LJ(9-6) and Buckingham potentials for the H₂–He interactions. The Buckingham potential shows a better description of the attractive part with respect to the other two potentials, which may be due to the presence of three parameters (Eq. 3.7) in the potential. The LJ-potentials have only two adjustable parameters in this respect.

Fig. 3.2

Schematic representations of Buckingham, Lennard-Jones (12-6) and Lennard-Jones (9-6) potentials

The hydrogen bond interaction potential can also be represented in terms of LJ potentials, but this potential needs some adjustments in the attractive part, as the interaction energies are stronger in such cases. The function form of E _VW(r) is commonly represented in such cases through the following 12-10 potential (Eq. 3.9).

$$ {E}_{HB}=\varepsilon \left[{\left(\frac{r_0}{r^{IJ}}\right)}^{12}-6{\left(\frac{r_0}{r^{IJ}}\right)}^{10}\right] $$

(3.9)

E _HB represents the hydrogen bond potential. In some cases of hydrogen bond potential, directional terms like (1 −  cos θ) or simply cosθ [34] (θ : a HB angle) are multiplied with the distance dependent part of Eq. (3.9). The various E _VW terms discussed here comprise only the basic form of the potentials to be used in molecular mechanics (MM) or more commonly known force field calculations. These force fields are central to the classical molecular dynamics (MD) simulations and there are many different forms of such force fields in dealing with diverse molecular systems including simple molecules to more complex systems like proteins, enzymes, nucleic acids, membranes, polysaccharides etc. This is not a place to discuss these large collection of force fields applicable to various diverse systems, since they are not the objective of the present review article. We will discuss only several forms of dispersion potentials related to their use in combination with quantum chemical methods to show the diversity of the force field parameters.

Let us start with the rare gas interaction cases. The interactions between the rare gas atoms are usually very weak. The potential energy for interactions varies from 0.08 kcal/mol (1.29 × 10⁻⁴ a. u.) for He₂ to 0.78 kcal/mol (12.5 × 10⁻⁴ a. u.) for the Rn₂ dimers. Such interaction energy calculations need specially designed van der Waals potentials to account for the binding distance and energies of such dimers. In recent times, Tang-Toennies (TT) potentials were developed [35] to account such interactions. The potential has usual attractive and repulsive parts. The repulsive potential part is short-ranged Born-Mayer type, while the long-range attractive potential is added as damped dispersion series [36]. Mathematically, it is written as,

$$ {E}_{VW}(r)={E}_{rep}+{E}_{att}=A{e}^{-b{r}^{IJ}}-\sum_{n=3}^N{f}_{2n}\left(b{r}^{IJ}\right)\frac{C_{2n}}{{\left({r}^{IJ}\right)}^{2n}} $$

(3.10)

where C _2n terms are dispersion coefficients. The term b is the Born-Mayer range parameter and the only parameter in the damping function f _2n(br ^IJ). This function can be expressed as

$$ {f}_{2n}\left(b{r}^{IJ}\right)=1-{e}^{-b{r}^{IJ}}\sum_{i=0}^{2n}\frac{{\left(b{r}^{IJ}\right)}^i}{i!} $$

(3.11)

This function can be computed from incomplete gamma function also [35]. It is to be noted that the function has some similarity with the Eq. (3.3) originating from Drude model. With proper knowledge of the parameters in Eq. (3.10), potential energy curves for the rare atom dimers could be very accurately computed. The example related to the dimers He₂ through Rn₂ are shown in Fig. 3.3. The details related to the other different rare gas atom interactions are also available in ref. [35].

Fig. 3.3

Potential energy curves of the homogeneous rare gas dimers calculated with the Tang–Toennies (TT) potential model (reprinted from ref. [35], with the permission of AIP Publishing)

3.2.2 Quantum Chemical Approaches for Non-covalent Interactions

The calculations of non-covalent interaction energies between two interacting systems A and B to form the weakly bound complex is straightforward and given by,

$$ \Delta {E}_{AB}={E}_{AB}-{E}_A-{E}_B $$

(3.12)

Since the binding energy is experimentally observable quantity (negative of the experimentally measured dissociation energy), the E _AB, E _A and E _B should be calculated for the lowest energy structures of the individual species for its measurement. Moreover, because of the weak nature of the binding force, the energies should have basis set superposition energy (BSSE) correction, if large basis sets (preferably triple zeta type) are not used in the energy computations. The energy should further be zero-point energy (ZPE) corrected. Thus, Eq. (3.12) would be like Eq. (3.13) in the final form,

$$ \Delta {E}_{AB}={E}_{AB}-{E}_A-{E}_B-\Delta BSSE-\Delta ZPE $$

(3.13)

There is, of course, one caveat in such strategy. If the techniques involved do not provide dispersion energy effect, the results from Eq. (3.13) will not provide proper ∆E _AB value with respect to the experiments. Pure HF and Kohn-Sham density functional theories (KS-DFT) do not have dispersion correction to the total interaction energies. Generally, higher order HF-wavefunction based techniques involving perturbation theory, e.g., MP2, CC-techniques (CCSD, CCSD(T)) etc., include high electron-correlation effects (consequently dispersion effects), and could be directly used for such computations. The DFT-calculations become successful when a proper density functional is augmented with empirical dispersion term. The quantum chemical methods also provide the techniques to breakdown the total interaction energies in terms of dispersion, exchange, electrostatic etc. to understand the role of such interaction energy components to shape up a non-covalently bound system. In the following subsections we will discuss these features in more detail.

3.2.3 Dispersion Computations in DFT

The KS-DFT functionals mostly include Grimme’s D2 [37], D3 [38], or D3BJ [39] dispersion terms to compute dispersion energy part in DFT calculations. The total energy through any dispersion modified density functional could be expressed as,

$$ E\left( DFT-D\right)=E\left( KS- DFT\right)+{E}_D $$

(3.14)

Here, E(KS − DFT) is usual Kohn-Sham energy as obtained from a chosen density functional, and E _D is the empirical dispersion correction.

The D2, D3 or D3BJ empirical dispersion terms are similar to TT-potentials, as discussed earlier, but generate the dispersion part of the non-covalent molecular interactions in a different way. The D2 dispersion correction is written as [37],

$$ {E}_D=-{S}_6\sum_{I=1}^{N_{atom}-1}\sum_{J=I+1}^{N_{atom}}\frac{C_6^{IJ}}{{\left({r}_{IJ}\right)}^6}f\left({r}_{IJ}\right) $$

(3.15)

Here, N _atom is the number of atoms in the system; ${C}_6^{IJ}$ is the dispersion coefficient for the atom pair IJ; S ₆ is the global scaling factor (that depends on the density functional used) and r _IJ is the distance between the atom pair I and J. The f(r _IJ) term is a damping function, and it is important to avoid near-singularities for small r _IJ. The f term is expressed as,

$$ f\left({r}_{IJ}\right)=\frac{1}{1+{e}^{-d\left(\frac{r_{IJ}}{R}-1\right)}} $$

(3.16)

Where, R is the sum of atomic van der Waals radii. The term d is a preset parameter and d = 20 is usually set here to provide larger corrections at intermediate distances and generating negligible dispersion energy at covalent binding region.

Further developments of these dispersion potentials in DFT calculations were introduced later in the D3 and D3BJ techniques [38, 39]. The basic equation is the same as Eq. (3.14); only the dispersion calculations were modified. The D3 calculation [37] uses the following form of E(D),

$$ E(D)={E}^{(2)}+{E}^{(3)} $$

(3.17)

The E ⁽²⁾ and E ⁽³⁾ are the two-body and three-body dispersion interaction terms, respectively. The philosophy for using such equation comes from the definition of interaction energies in terms of many body interactions [40].

The term E ⁽²⁾ and E ⁽³⁾ are usually expressed as follows,

$$ {E}^{(2)}=\sum_{IJ}\sum_{n=6,8,10\dots }{S}_n\frac{C_n^{IJ}}{r_{IJ}^n}{f}_{d,n}\left({r}_{AB}\right) \vspace*{-18pt}$$

(3.18)

$$ {f}_{d,n}\left({r}_{AB}\right)=\frac{1}{1+6{\left(\frac{r_{IJ}}{S_{r,n}{r}_0^{IJ}}\right)}^{-{\alpha}_n}} \vspace*{-18pt}$$

(3.19)

$$ {E}^{(3)}=\sum_{IJK}{f}_{d,(3)}\left({r}_{IJK}\right){E}^{IJK} $$

(3.20)

f terms in Eqs. (3.18) and (3.20) are damping terms and the terms given in Eq. (3.19). The nonadditive dispersion term E ^IJK in Eq. (3.20) is computed from the third-order perturbation theory for the three atoms I, J, K and is discussed in detail in the ref. [38]. The three-body term is insignificant for small molecular systems, and usually has some contribution when the system is quite large. The D3BJ potential is similar to D3 potential. It differs from D3 only in the contribution of damping factor [39]. The detailed discussions related to these methods are available in the respective papers, and they include the determination of such factor (S _n) and assignment of the proper values of ${C}_n^{IJ}$ and ${r}_0^{IJ}$ terms. We will discuss below only the basic features of the D3BJ potential to show its difference with D3.

Becke and Johnson (BJ) [41] proposed a rational damping procedure for the dispersion potential in the following form,

$$ E(D)=-\frac{1}{2}\sum_{I\ne J}\frac{C_n^{IJ}}{r_{IJ}^n+ const.} $$

(3.21)

Based on such a damping approach, the modified form of DFT-D3 method could be represented in the following form of Eqs. (3.22) and (3.23).

$$ E(D)=-\frac{1}{2}\sum_{I\ne J}{S}_6\frac{C_6^{IJ}}{r_{IJ}^6+f{\left[{r}_0^{IJ}\right]}^6}+{S}_8\frac{C_8^{IJ}}{r_{IJ}^8+f{\left[{r}_0^{IJ}\right]}^8} $$

(3.22)

with

$$ f\left({r}_0^{IJ}\right)={x}_1{r}_0^{IJ}+{x}_2 $$

(3.23)

Where, x ₁ and x ₂ are the fit parameters introduced by BJ [40]. The BJ-damping leads to a constant contribution of E(D) to the total correlation energy for each bonded atom-pairs. This damping procedure seems theoretically more justified over a normal zero-damping [42], although it was found to change the thermochemical description of the underlying density functional (DF). Adjustment of standard correlation functionals are required to overcome such a problem. The related computer codes are usually equipped with these parameters for the computation of the dispersion terms for the proper thermochemical description of DF. It has been shown that, although the damping procedures in D3BJ differs from D3, both the procedures produce almost equivalent results [39].

3.2.4 Dispersion Computation Through MP2 and Higher Correlation Methods

The binding energy of non-covalently bound complexes could be computed through MP2, CCSD, CCSD(T) etc. type of quantum chemical techniques using Eq. (3.13). In such techniques, it is not needed to include the dispersion term separately. This energy is already included in these methods through higher electron-correlation effects. Let us consider, the case of MP2 method. We begin with the consideration of the effect of perturbation $\lambda \hat{V}$ on the generalized Hamiltonian ${\hat{H}}_{\lambda }$.

$$ {\hat{H}}_{\lambda }={\hat{H}}_0+\lambda \hat{V} $$

(3.24)

Here, ${\hat{H}}_0$ is the unperturbed HF Hamiltonian. The Rayleigh-Schrödinger perturbation theory tells us that the effect of perturbation renders the following expansion effect on the wave function (ψ _λ) and energy (E _λ) corresponding to ${\hat{H}}_{\lambda }$.

$$ {\psi}_{\lambda }={\psi}^{(0)}+\lambda {\psi}^{(1)}+{\lambda}^2{\psi}^{(2)}+\dots\vspace*{-18pt} $$

(3.25)

$$ {E}_{\lambda }={E}^{(0)}+\lambda {E}^{(1)}+{\lambda}^2{E}^{(2)}+\dots $$

(3.26)

The Møller-Plesset (MP) energy up to the first order perturbation term is the HF-energy. The second order contribution (E ⁽²⁾) to the MP-energy could be written as [5,6,7],

$$ {E}^{(2)}=\sum_{i<j}^{occ}\sum \sum_{a<b}^{virt}\sum \frac{{\left\langle \left. ij\right|| ab\right\rangle}^2}{\left({\varepsilon}_a+{\varepsilon}_b-{\varepsilon}_i-{\varepsilon}_j\right)} $$

(3.27)

Here, ε terms are orbital energies of the occupied (i, j) and virtual (a, b) orbitals and ⟨ij|| ab⟩ is a two-electron integral over spin-orbitals (and obviously involves double substitution). Now, if we consider non-covalent interactions between two molecular systems or atoms, E ⁽²⁾ is the correlation correction to the HF-energy and represents the effect of dispersion energy (with higher correlation terms). The dispersion interaction energy at the MP2 level could then be written as [43, 44],

$$ {\varepsilon}_{MP}^{(2)}={E}_{AB}^{(2)}-{E}_A^{(2)}-{E}_B^{(2)} $$

(3.28)

Where, AB is the overall system generated from the species A and B. The Pure HF-interaction energy in such a case could be written as

$$ \Delta {E}_{HF}={E}_{HF}^{AB}-{E}_{HF}^A-{E}_{HF}^B $$

(3.29)

This ΔE _HF could be partitioned further into Heitler-London $\left(\Delta {E}_{HL}^{ex}\right)$ energy components as

$$ \Delta {E}_{HL}^{ex}={\varepsilon}_{EL}^{(10)}+{\varepsilon}_{EX}^{(10)} $$

(3.30)

where ${\varepsilon}_{EL}^{(10)}$ and ${\varepsilon}_{EX}^{(10)}$ are the electrostatic and exchange contribution to the $\Delta {E}_{HL}^{ex}$. The difference between ΔE _HF and ΔE _HL generates the delocalization component of the total HF interaction energies. Thus,

$$ \Delta {E}_{HF}^{del}=\Delta {E}_{HF}-\Delta {E}_{HL}^{ex} $$

(3.31)

Such partitioning implies that total MP2 interaction energy ΔE _MP2 could be partitioned into four components in the following way [43, 44].

$$ \Delta {E}_{MP2}={\varepsilon}_{EL}^{(10)}+{\varepsilon}_{EX}^{(10)}+\Delta {E}_{HF}^{del}+{\varepsilon}_{MP}^{(2)} $$

(3.32)

The ${\varepsilon}_{EL}^{(10)}$ can further be divided into short-range penetration and long-range multipolar components [44]. Thus, in quantum chemical analysis, the interaction energies can not only be computed with accuracy but also the various energy components affecting the interactions can be deduced from energy-component analysis as outlined here. The details of such analyses are available in the refs. [43, 44]. The coupled cluster level of computations can be used for binding energy calculations through Eq. (3.13) for additional accuracy, and energy components can also be measured for the total interaction energies through symmetry adopted perturbation analysis (SAPT) [45]. In recent times, SAPT analysis has also been developed for energy component measurements for DFT techniques [46]. The DFT energy component analysis computes total interaction energy as the sum of ΔE _D + ΔE _ex + ΔE _ind (ΔE _ex: exchange component; ΔE _ind: induction component). The ΔE _ex in DFT and $\Delta {E}_{HL}^{ex}$ in the MP2 energy component analysis [as in Eq. (3.32)] are similar. The $\Delta {E}_{HF}^{del}$ in Eq. (3.31) and ΔE _ind in DFT-SAPT calculations are closely related. The difference is, while $\Delta {E}_{HF}^{del}$ is associated with the relaxation of electron densities of monomers upon interactions restrained by Pauli principle [47] (charge delocalization with charge transfer interactions), ΔE _ind represents interactions arising from the charges due to deformation of the monomer units.

We have so far narrated a brief description of the various quantum chemical techniques used to analyze the non-covalent interactions between two molecular units. The rest part of the review article would be devoted to various non-covalent weak interaction analysis based on techniques described in this section.

3.3 Non-covalent Interactions in Hydrogen-Bonded (HB) Systems

A hydrogen bond is formed when hydrogen atom covalently bound to an electronegative atom or group, generally termed as donor (D) group that interacts with another electronegative atom with lone pair of electrons (the so-called acceptor (A) group) forming a non-covalent interaction of the type D-H…A. The hydrogen bond formed is often described as electrostatic (dipole-dipole type), although it has some features of covalent bonding. The interaction distance is usually shorter than the sum of the van der Waals radii of the interacting components. The hydrogen bond strength depends on the electronegativities of D and A, and such bond could be as strong as 38.6 kcal/mol [48]. Examples of very weak hydrogen bond are also found in cases of S, Cl and C (~1.0 kcal/mol) [48, 49]. They are also ubiquitous and have importance in control of receptor-ligand interactions in medicinal chemistry, and intra-/intermolecular interactions in materials science [50, 51]. Most common examples of hydrogen bonding are found in water, ammonia, hydrogen fluoride, organic fatty acids, alcohols etc. Hydrogen bonding in such solvent systems is important in manifestation of several physical properties viz., melting point, boiling point, solubility, viscosity, and azeotropic properties of solvent mixtures. Such interactions are also one of the most important building blocks in various polymeric materials including DNA, proteins, cellulose, synthetic polymers, and the bonding features in these systems are explored mostly through crystallography, NMR, and IR experiments [52, 53].

Quantum chemical (QC) techniques and molecular dynamics (MD) simulations are important in silico methods to understand the nature of hydrogen bonding. The theoretical findings are important in explaining various experimental observations in this context. Small clusters are usually important to understand such interaction phenomenon, since these clusters are generated in recent times in gas phase and their structural and bonding features could be observed through IR spectra. For example, gas phase IR spectroscopic techniques viz., extensive terahertz laser vibration-rotation-tunneling (VRT) spectra and mid-IR laser spectra [54,55,56,57] were used to understand the origin of hydrogen bond formation in small water clusters. QC-techniques are very effective in elucidating structural behavior and in the present section we will discuss two such examples. The discussions would be oriented around the structural, binding, and spectroscopic properties of several small water clusters and fatty acid dimers. The discussions on water clusters would also include the effect of inclusion of halide ions in several of such water clusters and their charge transfer properties to solvent (CTTS) [23]. The fatty acid dimers were generated in gas phase and apart from their binding properties, they have unique low and high frequency vibrational modes which are involved in the relative stability of such clusters [22]. Furthermore, these fatty acid clusters have unique fragment energy additive properties, which could be used to predict the binding energies of higher fatty acids. This characteristic is unique to such fatty acids and were not explored before.

3.3.1 Hydrogen Bonding and Related Properties of Small Water Clusters

The change of structural and spectroscopic properties of small water clusters with increasing cluster size have been investigated through theory and experiments for a long time [23, 54,55,56,57,58,59,60,61,62,63]. The primary objectives of such instigations were to understand the nature of hydrogen bonding in such clusters, how such changes are related to their vibrational characteristics, effect of adding halide ions to such clusters [23, 64] and related changes in hydrogen bonding and spectroscopic properties. Experimental structure analysis of the small water clusters, (H₂O)_n, n = 2–6, have been reported from the VRT spectroscopy [54,55,56,57], while the vibrational spectra of n = 1–8 water clusters bound the benzene and water clusters of n = 7–10 are available for their O-H vibrational modes [59, 60, 63]. The water dimer is linearly hydrogen bonded [65], while water trimer to pentamer are cyclic rings [61, 62]. The higher clusters starting from n = 8 and above are multiring types [59, 60]. These structures were ascertained from the theoretical and experimental results. The low-energy structures of water hexamer and heptamer are also mostly multiring type, although they can have two-dimension (2D) and three-dimensional (3D) structures. A 3D-cage structure of (H₂O)₆ is believed to be the lowest energy structure from both theory and experiments [57, 58, 61]. On the other hand, extensive QC calculations on water hexamer has also suggested the presence of open-book like structure [65].

With this brief resumé on the structural aspect of the small water clusters, we turn our attention to the more specific properties related to the hydrogen bonding, i.e., relative stabilities and IR characteristics arising from hydrogen bonds. We are taking the specific example of water heptamer, as the low energy water clusters formed in this case show various structural possibilities including directional hydrogen bond properties due to the formation of 3D structures. The small water clusters fall under two broad structural types viz., 2D ring and 3D cage (e.g., prism, or cube). Furthermore, the water monomers inside a water cluster could be of single proton donor–single acceptor (da), single donor–double acceptor (daa), double donor–single acceptor (dda), and double donor–double acceptor (ddaa) types. In the water hexamer, for example, these types of water monomers were found to be related to the O–H spectra [66]. Water clusters presented in Fig. 3.4 tries to explain these features through specific examples of (H₂O)₇-clusters [67]. It contains twelve optimized water heptamer structures (C to R7, all in C₁-symmetry) together with four stable hexamer (cage, prism, book, and ring in C₁-symmetry) [66] and two stable octamer clusters (D2d, S4) [59, 60]. These hexamer and octamer structures are shown here, since they are geometrically related to the heptamer structures for their formation. The cage and prism structures of (H₂O)₆-clusters can generate the C, D, E, and F structures through addition of a water molecule. The octamer structure could also affect these structure formations in an alternative way. The global minima D2d and S4 octamers are degenerate and contain dda and aad types of water monomers. Exclusion of these water molecules from S4 would generate the C and D structures, whereas removal of similar water molecules from the D2d cluster would be responsible for the E and F cluster formation. The formation of the G and H structures could similarly be explained from the S4 structure. The ring structures R5, R4 and R7 could be generated from the ring and book structures of water hexamers through addition of one water molecule [67].

Fig. 3.4

The optimized geometries of water heptamer (C–R7), hexamer (ring, book, cage, and prism), and octamer (D2d and S4) clusters. All the structures are in C₁ symmetry except D2d, S4, and ring (S6). The sequential numbers in each figure represent the direction of the unidirectional H orientations (reprinted from ref. [67], with the permission of AIP Publishing)

The number of hydrogen bonds (HBs) play a major role in relative stability and strength of hydrogen bond in water clusters. As a result, such properties together with the polarity of hydrogen bonds can influence the observed –OH frequencies of these clusters. The number HBs in C, D, E, F, G, and J are ten, while they are nine in H, I, and K, eight in R5, R4, and seven in R7. The average HB distances vary between 2.84 Å (cluster F) to 2.76 Å (cluster R4). These results were available from the fully optimized structures of these clusters (MP2/TZ2P++ calculations) and are slightly shorter than the normal O…O distance (2.98 Å) in water. These average bond distances of the individual clusters together with the number of hydrogen bonds determine the following relative stability order of the clusters.

$$ { {\begin{array}{ll}{C}_{10}^{2.82}>{D}_{10}^{2.82}>{G}_{10}^{2.83}>{H}_9^{2.83}>{E}_{10}^{2.83}>{F}_{10}^{2.84}>{J}_{10}^{2.82}>{I}_9^{2.80}>R{5}_8^{2.76}>R{4}_9^{2.76}\end{array}}} $$

The subscripts in the cluster notation indicate the number of HBs, and the superscript represents average HB-length in Å (in terms of O-H-O distance). There are few deviations in the above stability order in relation to the aforementioned hypothesis. This could be attributed to the strain in the structure (Fig. 3.4), which alters the stability order in terms of average HB-number and length considerations. The relative stability order was verified through Gibbs free energy change measurements in molecular beam experiments [54,55,56,57,58]. The energy difference between C and D is only 0.5 kcal/mol and the other clusters except R7 and K are within 2.5 kcal/mol. The average HB energies for the lowest energy clusters C and D were found to be 3.8 and 3.7 kcal/mol respectively (MP2/TZ2P++) and these values are weaker than normal hydrogen bond energy in water (~5.0 kcal/mol). The average HB-energy in other clusters is all within 4.2 kcal/mol (MP2//B3LYP/6-311++G** level) [67].

Unidirectionality of HBs also determine the relative stability of the water clusters. The low-energy clusters C, D, and R5 in Fig. 3.4 show that their HB orientations are unidirectional. This is also true for the hexa- and octamer (n = 6, and n = 8) clusters in Fig. 3.4. The lower clusters with n = 3, 4 and 5 with unidirectional HBs (cyclic structures) are the most stable [61]. This is also true for the n = 9, and 10 clusters with nine- and ten-membered cyclic rings [60].

3.3.2 Nature of O-H Stretching Modes

The proton donor and acceptor properties of water monomers inside a water cluster controls the O-H stretching modes of a (H₂O)_n cluster. Generally, most of the O-H stretching modes in a water cluster are red shifted with respect to the water monomer stretching modes. This is because these donor-acceptor properties of water monomers in a cluster control the HB-strengths. We will discuss this case for the low-energy water clusters with n = 6, 7, and 8. Figure 3.5 shows the calculated vibrational spectra of these clusters (B3LYP/6-311++G**) [67]. The spectra are presented with respect to the water monomer frequencies computed at the same level of theory (3921 cm^–1, 3816 cm^–1, and 1603 cm^–1). As it could be seen from the spectra (Fig. 3.5), the H₂O)_n clusters have n number of asymmetric (n ₃) and symmetric (n ₁) O-H stretching modes. Most of these peaks are red shifted with respect to the monomer frequencies, except one (slightly blue shifted). The classification of water monomers based on their donor-acceptor properties in n = 7 cluster, as discussed earlier, are as follows: C, D, E, F, G (1 da, 3 aad, and 3 daa); H, I (3 da, 2 aad, 2 daa); J (2 da, 2 aad, 2 dda, 1 ddaa); K (5 da, 2 ddaa); R5, R4 (5 da, 1 aad, 1 dda); R7 (7 da). The general principle is that the n ₃-band of the dda or ddaa types are lower (in energy) than those of the da types. On the other hand, in the case of n ₁-band, the dda and ddaa type O-H stretches are higher than those of the da and aad types. The spectral shifts in the whole spectral data in Fig. 3.5 can be explained from this principle.

Fig. 3.5

Computed IR spectra for various low energy clusters of the water heptamer, hexamer, and octamer at the B3LYP/6-311++G** level of theory (reprinted from ref. [67], with the permission of AIP Publishing)

The experimental determination of the IR spectra of (H₂O)₇-cluster [63] indicated two structural isomers. These are based on the number of experimental peaks These peaks in terms of frequency shift with respect to the experimental average O-H stretching frequencies of the water monomers, are –757 (2), –627 (2), 397, 287 (2), –147 (4), –57, and 13 cm^–1) (the numbers within parentheses are splitting pattern of the peaks). These spectral shifts are similar to the calculated shifts of the mixture of C and D isomers (Fig. 3.4), indicating the presence to two competitive lowest energy structures of the water heptamer. It is to be mentioned in this connection that the computed absolute values of frequencies were not in very good agreement with experiment, since anharmonicity effect was not explicitly considered in such calculations. The anharmonicity effect, of course, do not alter the binding energy (also the HB-energy) of these clusters, as was found in a later study for n = 2–10 clusters [68].

3.3.3 Effect of Halide Ion Interactions with Small Water Clusters

The structural characteristics of the halide ion inclusions in water clusters were monitored effectively through photoelectron spectroscopy (PES) [69, 70]. The PES analysis showed that X(H₂O)_n (X = F^–, Cl^–, Br^–, and I^–), surface structures are favored for X= Cl^–, and Br^– form small n. On the other hand, for X = I^–, the n = 6 cluster has an internal state with first solvation layer of 6. The QC calculations on X(H₂O)_n (X = Cl^–, Br^–, and I^–) [64, 71] indicated that for n = 2–6, the Cl^–, and Br^– ions resides on the surface of the cluster, while the I^– resides on the surface for n = 2–5, but for the n = 6 cluster, the I^– tends to move from the surface to the interior site. The F^–(H₂O)_n clusters are different from the other halide-water clusters, since the F^– ion interactions are much stronger than the rest of the halide ions. Because of the exceptionality of HB-interactions, we have chosen to discuss the structural features and binding characteristic of such clusters in more details. Moreover, all these halide-water clusters show CTTS properties [23]. These special features of X(H₂O)_n (n = 1–4) would also be reviewed here.

The F^–(H₂O)_n (n = 1–6) clusters were analyzed through QC calculations using various approaches, and F^–-binding energies of these clusters are experimentally available. Figures 3.6 and 3.7 contain different structural possibilities of these clusters in different QC calculations [72]. There were not many disagreements related to the cluster properties, and most of the calculations agreed on the minimum energy structures, and these are important to compute the parameters related to experiments. We have chosen to discuss the results based on DFT/B3LYP and MP2 calculations using large basis sets (6-311++G**). The results do not differ much with respect to the higher level MP2 (and larger basis set) and CCSD(T) [72, 73] computations. Figure 3.6 shows the cluster arrangements for n = 1–5, while Fig. 3.7 contains the structural possibilities for n = 6. The F^– ion in the higher clusters could orient on the surface or inside the cluster. A specific (n₁ + n₂) notation is chosen, together with the overall molecular symmetries, to represent such possibilities of F^– ion arrangements. The numbers n₁ and n₂ represent the number of water molecules in the primary and secondary hydration shells, and when n₂ = 0, the structure is simple represented as n₁. As it could be seen from the structures of (H₂O)₆ clusters (Fig. 3.4), the insertion of F^– ion changes the structural patterns. This is true for the other clusters (different n) also.

Fig. 3.6

Optimized geometries of the F^–(H₂O)n, n = 1–5, clusters obtained by using MP2 method (reprinted from ref. [72], with the permission of AIP Publishing)

Fig. 3.7

Optimized geometries of the F^–(H₂O)₆ clusters predicted by employing MP2 method (reprinted from ref. [72], with the permission of AIP Publishing)

The lowest energy clusters of F^–(H₂O)_n (n = 1–6) are 1(C_s) (n = 1), 2(C₂) (n = 2), 3(C₃) (n = 3), 4(C₁) (n = 4), 5(C₁) (n = 5), and (4 + 2)(C₂) (n = 6) (Figs. 3.6 and 3.7). The clusters with higher symmetry are mostly high-energy or transition states. The smaller sized clusters (n ≤ 3) show very small energy difference between the low-lying isomers (~0.2 kcal/mol). The cases of n = 3 and 4 are quite interesting. The 3(C_3h) isomer of n = 3 has slightly lower energy than 3(C₃), although careful analysis showed that the higher symmetry structure is a transition state. The 4(C₁) (n = 4) cluster, on the other hand, is not an unambiguous global minimum. The (3 + 1)(C_s) is actually a competitive minimum energy isomer. In the case of higher clusters (N = 5, 6), global minimum (as assigned above) is unambiguous through both DFT and MP2 analysis [72], and in more recent calculations also [73]. Further details of the energetics of these isomers are available in ref. [72].

The F…H, F…O, and O-H distances and related H-O-H bond angle are important parameters to understand the strength of F^– ion interactions in these F^–(H₂O)_n clusters. The variations of these parameters with increasing n represent how F^– ion interacts with the water cluster part. Figure 3.8 represents such variations with respect to the cluster size (n). The variations are related to the lowest energy clusters of different n. The graphs containing the variations of different bond-lengths reflect the variation of F^– ion interactions. The shortest F…H, F…O and O-H bond lengths represent higher interactions in this respect. The variation of the H-O-H angle with respect to the cluster size is a result of such interactions, and this angle is always smaller than free water.

Fig. 3.8

Variation of the lengths r(F…H), r(F…O), and r(O–H) and H–O–H angle [θ(H–O–H)] with increasing water molecules in clusters F^–(H₂O)_n. The parameters are chosen for the minimum energy (MP2) geometries of each cluster. The dotted lines indicate the values for the minimum energy n₁ cluster (n₂ = 0) of n = 5 and 6 clusters (reprinted from ref. [72], with the permission of AIP Publishing)

The actual variations of F^–-ion binding energies with respect to the cluster size are presented in Fig. 3.9 in terms of enthalpy (ΔH^298K) and Gibbs free energy (ΔG^298K) of binding. These are MP2-level data and are compared with the experimental results from two different sources (marked as Expt. a [74] and Expt. b [75]), and the trends of both types of estimations are consistent. The MP2 results (6-3111++G**) are presented with both BSSE-corrected and uncorrected ways, and it could be observed that BSSE-corrected values somewhat underestimate the binding energies for n ≥ 4. The interactions could also be analyzed through many-body interaction theories [72], since they are quite important for bigger systems (especially n = 5 and 6 clusters) to estimate interactions as well as binding energies. Both 2-body and 3-body interactions contribute to the total binding energies in these clusters. The higher body interactions (4 and above) are not important. These are in nut-shell the nature of F^–-ion non-covalent interactions in F^–(H₂O)_n clusters. Such interactions have significant effect on the ionization potential and O-H vibrational characteristics of these clusters. A specific effect is the higher red-shift of the O-H stretching frequencies more than the normal water clusters. The detailed discussion is available in ref. [72]. We will conclude this section after a general discussion of the CTTS properties of halide-water cluster as HB-properties influence such CT-spectra.

Fig. 3.9

Plots of experimental and calculated (MP2) ΔH and ΔG values of F^–(H₂O)n clusters with increasing n (n = 1–6) (reprinted from ref. [72], with the permission of AIP Publishing)

3.3.4 CTTS Properties of Halide-Water Clusters

The UV-spectra of halide ions in water demonstrates a unique type of charge-transfer spectra. These specific spectral characteristics occur due to the electron injection from the halide to the solvent in the UV region and generated excited state is known as CTTS state. Thus, it is not the property of halide ion itself. The bound CTTS state is created due to the stabilizing potential of the surrounding solvent molecules. The non-covalent interactions of halide ions with the surrounding solvent are an operative factor for such a CTTS phenomenon. For example, the aqueous solution of iodine exhibits broad charge transfer band due to electron ejection from iodide to the solvent. The spectrum consists of two bands at ~ 2100 Å separated by characteristic spin-orbit splitting (0.94 eV) of neutral iodine [76].

The measurements of the CTTS bands of I^–(H₂O)_n (n = 1–4) through photo-detachment spectra [77], and studies on the dynamics of electron solvation in the photo excited states of the I^–(D₂O)_n (n = 4–6) and I^–(H₂O)_n (n = 2–4) [78] unraveled the importance of water-cluster…halide ion interactions. The experimental CTTS spectra of Cl^–, and Br^– are only available in bulk water [79]. The theoretical calculations determined the CTTS spectra of X^–(H₂O)_n (X = F, Cl, Br, I; n = 1–4) using their lowest energy clusters [80, 81]. The excited state calculations at the TD-DFT level produced sufficiently accurate results. The first excited singlet state (S₁) of these clusters were found to represent the CTTS states through computed charge transfer (Δq) data from S₀ → S₁ states (Table 3.1). The computed CTTS states were verified with respect to the experiment for the case of I^–(H₂O)_n (n = 1–4) clusters (Table 3.1). The minimum energy clusters used in such calculations have halide ions on the surface of the water cluster networks. All these structures are similar to the those of F^–(H₂O)_n (n = 1–4) clusters in Fig. 3.4. The only difference is that the F^–(H₂O)₂ cluster is a 2(C₂) isomer, while the rest of the minimum energy n = 2 halide-water clusters are 2(C₁) isomers (Table 3.1). The further details of these structures are available in ref. [81].

Table 3.1 Computed vertical transition energies [∆E ^VT(S ₁), eV], experimental ∆E _CTTS(eV), enthalpy of binding (∆H,  kcal/mol), dipole moment (μ, Debye) and charge transfer from S ₀ to S ₁ (∆q, a. u.) for the clusters X ⁻(H ₂ O)_n (X = F, Cl, Br, I; n = 1 − 4)

The CTTS bands of I^–(H₂O)_n (n = 1–4) show blue-shift with respect to the stepwise increment of n (Table 3.1) in both experiment and theoretical calculations. The computed CTTS bands of other halide-water clusters also show similar trends, indicating the role of water…halide interactions in such spectra. It has been argued that CTTS bands of iodide-water cluster correspond to the excitation of electron from an orbital localized in I^– to a delocalized state with support from the water network. Generally, a neutral molecule with around 2.5 D dipole moment can bind an electron in a dipole-state through exchange repulsion between excess electron and electrons in molecules [82, 83]. Considering the dipole moments of water molecules induced by halide (Table 3.1), it can be safely assumed that the initial upper state of I^–(H₂O)_n (n = 1–4) cluster could be a short-lived I(³P₂).[(H₂O)_n]^– (n = 1–4) state in pump-pulse experiment. Here electron is transferred from iodide to the dipole-bound state of the water network. This argument could also be generally applied to the CTTS spectra other halide-water clusters. The formation of X.[(H₂O)_n]^– actually might take place through several steps involving dissociation of X^–(H₂O)_n to X^– and (H₂O)_n, followed by recapture of electron from X^– to the water network. A thermodynamic cycle was proposed [23] in this respect and was found to work well to interpret CTTS spectral positions [80]. This is a way to interpret the CTTS bands (vertical S₁-state energy) through its dissociation into several thermodynamic components, indicating the importance of non-covalent interactions of halide-water clusters in such phenomena.

3.3.5 Effect of Low-Frequency Vibrations of HBs in Fatty Acid Dimers and Their Amides

HB is associated with interesting vibrational properties in molecular systems. They are related to the relative stabilities of various hydrogen bonded isomers generated through intermolecular interactions between the monomers of the same species. Generally, high-frequency vibrations of the O-H/N-H bond, associated with HB formation, are considered to influence the HB-strengths. Specific low-frequency vibrations of several molecular systems, forming polymeric hydrogen bonded systems through OH/NH bonds, were also found to correlate with the HB-strengths/binding energies (ΔE^B) of such systems through coupling with the with the associated high-frequency modes. These correlations could be verified in systems where several hydrogen bonded isomers could be identified. Small organic fatty acids like, formic acid, acetic acid and their amides form hydrogen bonded dimers. Involvement of low-frequency mode/s in the stabilities of such dimers were identified through experiments and QC calculations [22, 84,85,86]. These correlations further facilitated the development of a local fragment energy-based (related to the HB) additive property to predict binding energies of such dimers. The concept is extendable to other homologs of these acids, e.g., propionic, and n-butyric acids [86].

Formic acid monomer predominantly exists in trans-form [87,88,89], although the less common rotamer cis-form has also been characterized [89]. This conformational behavior of formic acid has opened up the possibilities of this molecule to form several dimeric forms through hydrogen bonding. These include trans-trans, trans-cis, and cis-cis combination of monomers, and experiments based on the vibrational excitations of ground state trans-formic acid has detected most of these isomers [90,91,92]. Acetic acid, like formic acid, exhibits rotational isomerism through C-OH bond. Trans-form is the predominant rotamer, while the less probable cis-variety also exists in the gas-phase [93, 94]. The cis-form is ~5.3 kcal/mol above the trans-form with trans to cis conversion barrier of 13.2 kcal/mol. Thus, this cis-form is unlikely to take part in dimer formation. Six dimers in trans-trans combination could be constructed, three of them were found to exist through experiments [84, 95].

QC calculations are available on the various trans-trans and trans-cis isomers of formic acid dimer and the global minimum was ascertained to be trans-trans (TT-1, Fig. 3.10) [85]. This structure is similar to the other theoretical results [96] and experiment [22, 90]. As it could be seen from Fig. 3.10, most of the isomers have dihydrogen bond with a few exceptions (TC-3 and TC-4). High level QC calculations are usually needed for accurate estimation of the ΔE^B of such hydrogen bonded dimers. A ΔE^B value of 13.4 kcal/mol (MP2/aug-cc-pVTZ) [85] was found to be comparable with the experiment (14.2 ± 0.2 kcal/mol) [97]. The theoretical result was estimated using anharmonicity corrections and CCSD(T) (aug-cc-pVTZ) calculations in this respect also generated satisfactory answer (13.23 kcal/mol). The trans-trans dimer of acetic acid (AA-1, Fig. 3.11), out of the six probable isomers, is of lowest energy [86]. This isomer was also found to be the most stable isomer through experiment [84, 98]. All these probable acetic acid dimers have dihydrogen bonds, i.e., they form a closed ring system. The computed ΔE^B at different theoretical levels using aug-cc-pVTZ basis sets generate similar results (DFT/B3LYP: –14.7 kcal/mol, MP2: –14.4 kcal/mol, CCSD(T): –14.8 kcal/mol). The observed dissociation energy in this context is a combined theoretical and experimental data (16.2 kcal/mol) [98]. It has been argued that if experimental thermal contribution (~0.7 kcal/mol) is considered, the computed values would be compatible with experiment.

Fig. 3.10

Optimized structures of formic acid dimers (at the CCSD level) with the computed hydrogen-bond distances (Å). These dimers are formed through trans–trans (TT-1 to TT-6) and trans–cis (TC-1 to TC-5) combinations of the monomers (reprinted with permission from ref. [85] Copyright (2013) American Chemical Society)

Fig. 3.11

Optimized structures of acetic acid dimers (at the MP2/aug-cc-pVDZ level) with the computed hydrogen-bond distances (Å). These dimers are formed through trans–trans (AA-1 to AA-6) combinations of the monomers (reproduced from ref. [86] with permission from the PCCP Owner Societies)

The amides of these fatty acids do not possess the rotamerism properties of the corresponding acids. The situation limits the formation of the hydrogen-bonded dimers to five [85, 86]. In the case of formamide, two of the constructed structures have been characterized through IR spectra (FMAD-A and FMAD-C, Fig. 3.12) [99], the rest of them are predicted structures. These isomers, like formic acid dimers, are mostly formed through dihydrogen bond (except FMAD-D). The FMAD-A is the minimum energy isomer and the computed ΔE^B (MP2/aug-cc-pVTZ: –12.86 kcal/mol, CCSD(T)/aug-cc-pVTZ: –12.92 kcal/mol) is close to that of AA-1 (Fig. 3.11). The weaker NH…O HB-strength (with respect to O-H…O) is reflected in these ΔE^B values. The experimental binding energy of formamide dimer is not known. The presence and abundance of FMAD-A isomer was predicted from strong red-shift of the n _s(NH₂) (~387 cm^–1) and n _as(NH₂) (~171 cm^–1) modes with respect to the monomer frequencies [99]. Acetamide dimer also does not have experimental ΔE^B values. Five possible isomers (Fig. 3.13) were assigned as the probable acetamide dimers, and AMD-1 was found to be the most abundant isomer from the strong red-shift data of n _s(NH₂) (~299 cm^–1) and n _as(NH₂) (~37 cm^–1) modes with respect to the corresponding monomer frequencies [100]. The computed red-shift data of the AMD-1 (n _s(NH₂): ~299 cm^–1) and n _as(NH₂) : ~37 cm^–1) compares [86] well with the experiment, and this isomer was found to be the global minimum also. The ΔE^B values (MP2/aug-cc-pVTZ: –12.5 kcal/mol, CCSD(T): –14.3 kcal/mol) are close to the formamide dimer. The structural details related to the other isomers of formic acid, acetic acid, formamide and acetamide dimers are available in refs. [85, 86]. We will discuss only the effect of vibrational frequencies on the relative stabilities of these dimers through the ΔE^B values.

Fig. 3.12

Optimized structures of formamide dimers (at the CCSD level) with the computed hydrogen-bond distances (Å). These dimers are formed through different orientations of the monomers (FMAD-A to FMAD-E) (reprinted with permission from ref. [85] Copyright (2013) American Chemical Society)

Fig. 3.13

Optimized structures of acetamide dimers (at the MP2/aug-cc-pVDZ level) with the computed hydrogen-bond distances (Å). These dimers are formed through different orientations of the monomers (AMD-1 to AMD-4) (reproduced from ref. [86] with permission from the PCCP Owner Societies)

The primary characteristics of formic acid, acetic acid and their amide dimers is that they form dihydrogen bonded ring structures in their lowest energy geometry and except a few cases all the isomeric forms of these dimers maintain this HB geometry. These specific non-covalent interaction patterns among these isomers generate unique vibrational characteristics related to their relative stabilities and provide information about the local properties of the hydrogen bonded groups. The computed stretching vibrational data of –OH (n(OH)) group of the acid dimers (TT-1 and AA-1) and –NH₂ (n _s(NH₂)) group of their amide dimers (FMAD-A and AMD-1) are presented in Table 3.2. These data show that these frequencies are red shifted with respect to the acid (trans-formic and acetic acids) and amide (formamide and acetamide) monomers. The intensities (I) of such modes are substantially enhanced in these respects (Table 3.2), and the computed values are compatible with respect to the experimental vibrational data [85, 86]. The vibrational data for the rest of the isomers of these dimers (not discussed here) are available in refs. [85, 86], and they have the same characteristics of the minimum energy isomers in Table 3.2. These modes are usually called marker bands for such dimers as their intensities decrease regularly with respect to their binding characteristics (ΔE^B) and main linear correlations (Eqs. 3.33–3.36).

$$ \mathrm{Formic}\ \mathrm{acid}\ \mathrm{dimers}:I=-164.0\Delta {E}^B-359.0\kern0.75em R=0.97 \vspace*{-18pt}$$

(3.33)

$$ \mathrm{Acetic}\ \mathrm{acid}\ \mathrm{dimers}:I=-248.0\Delta {E}^B-729.0\kern1em R=0.98 \vspace*{-18pt}$$

(3.34)

$$ \mathrm{Formamide}\ \mathrm{dimers}:I=-107.0\Delta {E}^B-333.0\kern0.75em R=0.96 \vspace*{-18pt}$$

(3.35)

$$ \mathrm{Acetamide}\ \mathrm{dimers}:I=-233.0\Delta {E}^B-1150.0\kern0.75em R=1.00 \vspace*{-12pt}$$

(3.36)

Table 3.2 –OH and NH₂ stretching modes (ν(OH) and ν _S(NH ₂) cm^–1) of the lowest energy isomers of TT-1, FMAD-A, AA-1, and AMD-1. The table also includes intensities (I, KM/MOL), red-shift (Δν, cm^–1) and change of intensity (ΔI) of each mode with respect to monomers of formic acid, acetic acid, formamide and acetamide

These correlations are at the MP2 level. It could be seen from the regression coefficients (R) that these correlations are quite convincing to predict linear correlations.

Experimentally six low-frequency vibrational modes were observed for formic acid lowest energy dimer TT-1 [22]. The modes with u-symmetry (two A_u and one B_g) are IR-active and three g-symmetry modes (two A_g and one B_g) are Raman active. These low-frequency modes were determined theoretically for TT-1 isomer through anharmonicity corrections, since these vibrations were experimentally assigned as the lowest fundamentals of the overtone band. For example, n ₁ band was determined as the lowest fundamental (n ₁, A_u) of the experimentally assigned overtone band ([2n ₁], A_g). Table 3.3 contains all these six low-frequency fundamentals along with their theoretically determined values (MP2 level). The computed values for the rest of the isomers are available in ref. [85]. It is only important to note here that the intensities of the in-plane-bending mode (n ₃), related to the low-frequency OH-bending of various formic acid dimers, show regular change with respect to their ΔE^B through the following linear correlation (Eq. 3.37).

$$ I=-4.62\Delta {E}^B-8.49\kern0.75em R=0.96 \vspace*{-14pt} $$

(3.37)

Table 3.3 Low frequency vibrations of TT-1 and FMAD-A (ν ₁ − ν ₆), AA-1 and AMD-1 (ν ₁ − ν ₈) dimers. The intensities (I, KM/MOL) of the vibrational modes responsible for hydrogen bonding are also included. The results are presented at the MP2/6-311++G** level and the values within parentheses are experimental data

Formamide dimer (FMAD-A) also have six low-frequency modes and only the intensities of the stretch-bend mode (n ₃, B_u) (related to the n _s(NH₂) mode) (Table 3.3) together with the intensities of the similar modes of the other isomers [85] show linear correlation with their ΔE^B,

$$ I=-9.54\Delta {E}^B-34.8\kern0.75em R=0.99 $$

(3.38)

These correlations were validated using other high-level QC techniques including DFT/B3LYP, G4MP2, CBS-QB3, and G2MP2 methods [85].

Acetic acid dimers have eight such low-frequency vibrational modes [84, 86], and these modes with their symmetries are shown in Table 3.3 for the lowest energy AA-1 isomer. These bands are either IR-active (u-symmetry) or Raman-active (g-symmetry). The acetamide dimer do not have any experimental data and six such modes (instead of eight) could be computationally assigned through theoretical computations (Table 3.3). They are also IR and Raman active and shown in Table 3.3 for the lowest energy AMD-1 isomer. The data for the other isomers of acetic acid and formic acid dimers are available in ref. [86]. Analysis of such data revealed that the in-plane-bending or stretch-bend (in plane) modes of AA-1 (Raman active n ₇(A_g) and n ₈(A_g) and the IR-active n ₄(B_u)) modes showed importance in hydrogen bonding. The n ₇ and n ₈ bands have very low intensities, while the n ₄ band have quite large intensity (Table 3.3). The n ₄ band also showed regular change of intensities for various acetic acid dimers and maintain a linear correlation with corresponding ΔE^B values (Eq. 3.39, MP2 results).

$$ I=-2.52\Delta {E}^B-6.41\kern1em R=0.99 $$

(3.39)

Similar analysis for the acetamide dimers generated the following correlation (Eq. 3.40, MP2) using intensities of the IR-active n ₅ band.

$$ I=-5.79\Delta {E}^B-22.5\kern0.75em R=0.91 $$

(3.40)

These correlations, like formic acid and formamide dimers, were validated using similar high-level QC techniques [86].

3.3.6 Empirical Additive Relations of ΔE^B for Fatty Acid and Amide Dimers

The important aspect of the individual linear correlations between the ΔE^B of the fatty acid (and amides) dimers and intensities (I) of the high frequency n(OH)-modes, as discussed above, could be extended for their combined cases. For example, the I-values of both trans-trans formic acid (TT-1–TT-5, Fig. 3.10) and acetic acid (AA-1–AA-6, Fig. 3.11) dimers, when combinedly plotted against their respective ΔE^B values, a linear correlation is again prevailed (R= 0.97, MP2 results). Similar linear correlation was also observed for the formamide and acetamide dimers (R = 0.96; for the I [n _s(NH₂)] and ΔE^B plot: MP2 results). The low-frequency hydrogen bonding mode also showed similar features [85, 86]. These linear dependencies led to an empirical additivity relation of ΔE^B among these dimers due to transferable local character of the individual hydrogen bonding fragments. Such relations were established through analysis of the local hydrogen-bonding/binding energies of the fragments (E_X…Y) (X and Y are the atoms or groups involved in hydrogen bonding). It is assumed that the ΔE^B values are originating solely due to the contribution of E_X…Y terms and they are also transferable. In the case of formic acid and acetic acid dimers these fragments are OH…O, CH…O, OH…O(H), and CH…O(H), while for formamide and acetamide dimers these fragments are NH…O and CH…O (see Figs. 3.10, 3.11, 3.12, and 3.13 for the definition of these fragments). The hydrogen within parentheses belong to the O-H group not involved in hydrogen bonding. The E_X…Y values of the fragments could be evaluated by inspecting the nature of HB interactions and ΔE^B values of an individual dimer and setting a simple additive relation from these data. The procedure could be explained using the following examples of the different dimers.

In the case of formic acid dimers, the hydrogen bonds in TT-1 and TT-5 isomers are solely due to OH…O and CH…O fragment interactions (Fig. 3.10). Thus E_OH…O and E_CH…O fragment energies in these cases are simply half of their ΔE^B values. The evaluations of the E_OH…O(H) and E_CH…O(H) fragment energies could be computed directly from the following relations for TT-4 and TT-6 isomers (Eqs. 3.41 and 3.42)

$$ {E}_{CH\dots O}+{E}_{OH\dots O(H)}=\Delta {E}^B\left( TT-4\right) \vspace*{-18pt}$$

(3.41)

$$ {E}_{CH\dots O}+{E}_{CH\dots O(H)}=\Delta {E}^B\left( TT-6\right) $$

(3.42)

Once the fragment energies are known, the ΔE^B values of the other dimers could be easily evaluated using these key E_X…Y values. In the case of trans-cis dimers, the trans- to cis-formic acid conversion energy (E_TC) would be needed to evaluate the binding energies. The following Eq. (3.43) could be used as an example for the use of E_TC data to compute ΔE^B of TC-1 isomer (Fig. 3.10).

$$ {E}_{CH\dots O}+{E}_{O\dots HO}+{E}_{TC}=\Delta {E}^B\left( TC-1\right) $$

(3.43)

The predicted ΔE^B values (MP2 level) of the isomers TT-2 (–8.28 kcal/mol), TC-1 (–4.20 kcal/mol), TC-3 (–2.60 kcal/mol = TC-4), and TC-5 (–1.66 kcal/mol) were within 0.5 kcal/mol of the computed results at the MP2/aug-cc-pVTZ level. The computed E_TC value of 4.08 kcal/mol (MP2 level) was used in such calculations for the trans-cis isomers [85].

The acetic acid dimers (Fig. 3.10), like formic acid dimers, have OH…O (AA-1), CH…O (AA-5), and OH…O(H) (AA-4) fragments involved in hydrogen bonding. The evaluations of the related fragment energies, like formic acid dimers, are quite straight forward. These values are not the same with respect to the formic acid dimers due to the difference of ΔE^B values. The AA-3 dimer in this respect presents a special hydrogen bonding situation. Here, O-H center on fragment is bound to O (O-H…O) and O-H (HO…HO) centers of the second fragment (Fig. 3.11). This HO…HO fragment is not like OH...O(H) fragment of AA-4 and is marked as OH…O₁. The ΔE^B of AA-3 isomer is used to evaluate the OH…O₁ fragment energy using the value of E_OH…O(H) in the following relation (3.44).

$$ {E}_{OH\dots {O}_1}+{E}_{OH\dots O(H)}=\Delta {E}^B\left( AA-3\right) $$

(3.44)

These known values of fragments energies predict the ΔE^B AA-2 and AA-6 isomers within 1.0 kcal/mol of the computed values using MP2/aug-cc-pVTZ technique [86]. These additive relations were used in cases of formamide and acetamide dimers also. They needed knowledge of the fragment energies of NH…O and CH…O fragment energies from the structural patterns of formamide (FMAD-A and FMAD-E) and acetamide (AMD-1, and AMD-4) dimers. These fragment energy values differ slightly because of the differences of structures, and ΔE^B values of these two different amides. The predicted values for the other isomers using these fragment values were quite satisfactory [85, 86].

The results discussed so far are not restricted to the dimers of specific fatty acids and their amides. The idea was found to be useful to other homologs also, provided they have similar hydrogen bonding features. The propionic acid and n-butyric acid dimers have similar dihydrogen bonded structures of AA-1. They differed only in the size of the alkyl group (-C₂H₅ for propionic acid and –C₃H₇ for n-butyric acid). Considering the difference of binding energies of TT-1 (–13.4 kcal/mol) and AA-1 (–14.4 kcal/mol) isomers at the MP2/aug-cc-pVTZ level [85], the fragment energy of two –CH₃ $\left({E}_{CH_3}\right)$ is estimated to be 1.0 kcal/mol (since rest parts of the two dimers are similar). Assuming the fragment energies –C₂H₅ and –C₃H₇ to be equivalent to two and three –CH₃ groups, the ΔE^B of propionic acid and n-butyric acid dimers could be predicted to be –15.4 and –16.4 kcal/mol [86]. These results are very impressive against the respective experimental values of 15.2 ± 0.2 and 17.2 ± 0.8 kcal/mol. Thus, the additive nature of binding energies, as discussed here, seems quite natural for such dimers. It shows some predictive nature on binding energies in a homologous series as well.

3.4 Molecular Modeling of Strong and Weak Cation-π Interactions

The cation-π interactions, which were fundamentally coined by Kier and coworkers [13, 14] as a non-covalent interaction mediated by ion-induced dipole foreseeable via the molecular modeling of acetylcholinesterase inhibition reactions and subsequently rationalized by Dougherty and coworkers [15, 16] in diverse chemical and biological systems, have appeared as a very prevalent restraining force to explicate the crucial factor responsible for non-covalent binding in small gas-phase ion–molecule complexes as well as macromolecular protein-ligand systems. There are mainly two types of cation-π interactions that falls into the category of weak and strong interactions for the sake of essence of electrostatics in molecular fragments. The quantitative estimation of such cation-π interactions in biological systems is the paramount concern to comprehend the underlying factors for the molecular recognition processes. To interpret the molecular recognition pattern contributed by the cation-π interactions stemming from the side chain of phenylalanine, tyrosine, and tryptophan with arginine and lysine in 1718 typical protein structures, Minoux and Chipot [17] performed quantum mechanical calculations by accounting the interactions of ammonium and guanidinium ions with the toluene, p-cresol, and methyl-indole as prime models of large molecular assemblies. The inclusion of polarization effects in predicting cation-π interactions seems to be indispensable, as evident by the computed binding energies with the basis-set superposition error (BSSE)-corrected MP2/6-311++G(d,p)//MP2/6-31G(d,p) level of approximation. Furthermore, the commercial force field such as Amber is demonstrated to be a reliable and efficient approach for evaluating the cation-π interactions in macromolecular assemblies of biological concern. The trends in calculated binding energies for the non-covalent interactions of toluene, p-cresol, and methyl-indole with the ammonium and guanidinium ions using the Amber force field compare well with the MP2 results even though the molecular mechanics method based on Amber force field predicts shorter interaction distances between the cations and the centroid of the aromatic ring with respect to the quantum mechanical calculations.

The cation-π interactions also play a critical role in stabilizing the coordination complexes of alkali-metal cations together with the aromatic systems. Nicholas et al. [101] have estimated the strength of cation-π interaction between the alkali-metal cations (Li⁺ to Cs⁺) and the benzene ring by accounting the consequences of incomplete basis sets within the framework of restricted Hartree-Fock (RHF) and second-order Møller-Plesset perturbation theory (MP2) levels. The predicted binding energies for the three heavier cations at the SVWN/TZ94p level are found to be 15–20% higher compared to the MP2 results, while the computed binding energies using BP96/TZ94p level are shown to be ~20% reduced when compared with the MP2 data. For such cation-π interactions, the binding enthalpies are usually underestimated compared to the experimental measurement, albeit the calculated binding enthalpies using BP96/TZ94p level are in accordance with the MP2 results. In another study by Sunner et al. [102], the ion-quadrupole and ion-induced dipole attractions due to the interaction between the potassium ion and benzene were evaluated by performing ab initio calculations (at the STO-3G level) as well as the classical electrostatic calculations, and the consideration of quadrupole moment of the aromatic ring is suggested to be the pivotal parameter to describe the electrostatics of cation-π interaction. In practice, the total electrostatic interaction could be judged as the sum of charge–charge, charge-dipole, charge–quadrupole, charge–octupole, and higher order terms. Kim et al. [103] have estimated charge-dipole, charge–quadrupole and charge-polarizability interactions using MP2 level in conjunction with 6-311+G(d,p) basis sets, to comprehend the nature of cation-π interactions for the binding of ammonium and tetramethylammonium cations with benzene and water. The obtained results clearly demonstrate that the interaction between tetramethylammonium cation and benzene ring is crucially contributed by the charge-quadrupole and charge-polarizability interactions. However, the contribution of other electrostatic terms has not been properly accounted in such cation-π interactions involving charged amino group or metal ions and aromatic systems.

The pertinency of computing various multipolar electrostatic energy terms in describing both the strong and weak cation-π interactions has been critically analyzed by Kadlubanski et al. [104]. The nature of cation-π interactions is assessed via the comprehensive survey of two-body interaction energy decomposition components of several gas-phase and dihydrated cation-π complexes comprising benzene, p-methylphenol, and 3-methylindole as the π-donor systems and Mg²⁺, Ca²⁺, and NH₄ ⁺ cations as the acceptor units by implementing a hybrid variational–perturbational interaction energy decomposition scheme. The first-order electrostatic and higher order delocalization energy components of the interaction energy are indicated to be the critical parameters in elucidating the strong and weak binding of cation-π complexes. To ascertain the reliability of the computational approach for evaluating the energetics of cation-π interactions, the computed interacting distances between the donor and acceptor units, binding energies, and thermochemical properties such as enthalpy and Gibbs free energy of binding for each complex using local DFT method at the B3LYP level after the counterpoise (CP) and zero-point energy (ZPE) corrections are further compared with those obtained from the G4MP2 and CCSD(T) level of theory in combination with the aug-cc-pVDZ basis sets. The calculated binding energies and thermochemical properties for the gas-phase cation-π complexes using DFT/B3LYP level are in the immediate vicinity of the G4MP2 results. However, in case of dihydrated cation-π complexes, the predicted binding energies using G4MP2 method are usually lowered by 3–7 kcal/mol compared to those obtained by the DFT/B3LYP level, which is in accordance with the calculated shorter interaction distance using G4MP2 method. The binding energies are further improved by the CCSD(T) level of approximation especially for the binding of dihydrated Ca²⁺ ion with benzene and 3-methylindole. The Mulliken population analysis manifests that a significant amount of electronic charge is transferred from the aromatic systems to the Mg²⁺ and Ca²⁺ ions. Furthermore, a linear correlation between the calculated binding energy and the charge transport is obtained, thereby, indicating identical provenance of electrostatics of the cation-π interactions and demanding meticulous assessment of diverse electrostatic interaction components to untangle the dominating factors for the strong and weak cation-π interactions. Within the framework of Onsager reaction field model, the total energy of such a cation-π complex in the presence of a homogeneous electric field (V) induced by the acceptor atoms of the complex could be expressed as,

$$ {{\begin{array}{ll}\displaystyle E=&{E}_0-{\mu}_i^0{V}_i-\frac{1}{2}{\alpha}_{ij}{V}_i{V}_j-\frac{1}{3!}{\beta}_{ij k}{V}_i{V}_j{V}_k-\frac{1}{4!}{\gamma}_{ij k l}{V}_i{V}_j{V}_k{V}_l\dots\\ &\displaystyle \frac{1}{3}{A}_{i, jk}{V}_i\nabla {V}_{jk}\dots -\frac{1}{6}{B}_{ij, kl}{V}_i{V}_j\nabla {V}_{kl}\dots -\frac{1}{15}{C}_{i, jk l}{V}_i{\nabla}^2{V}_{jk l}\end{array}}} $$

(3.45)

where E ₀ refers to the energy of the molecular system in the absence of external perturbation; μ ⁰ and α are the dipole moment and polarizability, and β and γ represent the higher-order polarizabilities, respectively. A _{i, jk} defines the dipole–dipole-quadrupole hyperpolarizability. The dipole–quadrupole and dipole–octupole polarizabilities are denoted by B _{ij, kl} and C _{i, jkl}, respectively.

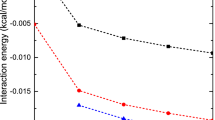
The essence of total electrostatic interaction energies (T-El) and the multipolar components of electrostatic terms including charge–charge (C–C), dipole-charge (D–C), quadrupole-charge (Q–C), and octupole–charge (O–C) as a function of interacting distance (r) in the cation-π complexes of Mg²⁺, Ca²⁺, and NH₄ ⁺ are delineated in Figs. 3.14 and 3.15. The T-El curves corresponding to the cation-π complexes of Mg²⁺ exhibit a minimum, while those curves are dispersive in nature for the binding of Ca²⁺ ion with benzene and 3-methylindole (Fig. 3.14). The stabilities of strong and weak cation-π complexes of these ions are substantially guided by the repulsive or attractive contributions of the Q–C and O–C components, as manifested by the calculated curves of multipolar components of the Mg²⁺- and Ca²⁺-complexes shown in Fig. 3.14. The distinct nature of cation-π interactions for the NH₄ ⁺-complexes is certainly evident by the T-El curves as well as anisotropic potential expansion of the multipolar components around the equilibrium distance r as displayed in Fig. 3.15. The contribution of multipolar components of the interaction energy is further demonstrated to be intrinsically linked to the cation-π vibrational modes specifically the intramolecular stretching frequency (S _z) assigned to the back-and-forth motion of the cation coupled with out-of-plane twisting mode of the aromatic moiety, and the out-of-plane C-H bending mode of the π-system (ν _opCHb). The augmentation of IR intensity of a particular mode in a cation-π complex could be further estimated from the alteration in dipole derivative expressed as

Fig. 3.14

Plots of total electrostatic interaction energies (T-El) and its other multipolar components as a function of r for the complexes of Mg²⁺ and Ca²⁺ ions with benzene (Bz), p-methylphenol (PMP), and 3-methylindole (3MI). Panels a and b represent the curves for the Mg²⁺ complexes, while panels c and d are for the Ca²⁺ ion complexes. In the figures, C–C, D–C, Q–C, and O–C represent the multipolar electrostatic interaction energy components (C–C, charge–charge; D–C, dipole–charge; Q–C, quadrupole–charge; O–C, octopole–charge) (reprinted with permission from ref. [104] Copyright (2013) American Chemical Society)

Fig. 3.15

Plots of total electrostatic interaction energies (T-El) and their multipolar components as a function of r for the complexes of NH₄ ⁺ ion with benzene (Bz) (a), p-methylphenol (PMP) (b), and 3-methylindole (3MI) (c) (reprinted with permission from ref. [104] Copyright (2013) American Chemical Society)

$$ \partial \left(\frac{\partial \mu }{\partial Q}\right)={\left(\frac{\partial \mu }{\partial Q}\right)}_{complex}-{\left(\frac{\partial \mu }{\partial Q}\right)}_{isolated} $$

(3.46)

where Q corresponds to the normal coordinates of the cation–π mode; and the dipole derivative for a given vibrational mode of the molecular system could be computed by neglecting higher order induced moment terms as follows,

$$ \left(\frac{\partial {\mu}_i}{\partial Q}\right)=\left(\frac{\partial {\mu}_i^0}{\partial Q}{+}\frac{\partial {\alpha}_{ij}}{\partial Q}{V}_j+\frac{1}{2}\frac{\partial {\beta}_{ij k}}{\partial Q}{V}_j{V}_k\dots \right)+\left({\alpha}_{ij}\frac{\partial {V}_i}{\partial Q}+{\beta}_{ij k}\frac{\partial {V}_i}{\partial Q}{V}_k+\dots \right) $$

(3.47)

The predicted intramolecular stretching mode of the respective cation-π complex corroborates well with the binding strength of the studied systems (Fig. 3.16a). The increase in IR intensities of these vibrational modes is found to correlate well with the multipolar electrostatic comportment of cation-π interactions as anticipated from the computed higher order quadrupolar and octupolar terms (Fig. 3.16c, d), albeit the linear correlation between the calculated blue shift of the C-H bending mode with respect to the isolated π-system (Δν _opCHb) and the binding energy (ΔE _B) shows strong dependence on the nature of π-system (Fig. 3.16b).

Fig. 3.16

(a, b) Correlation of ΔE_B with the intermolecular stretching (S_z, panel a) and blue-shifted out-of-plane CH bending mode of aromatic moiety (Δν_opCHb, panel b) modes of various cation–π complexes. (b) Red, blue, and green lines respectively, represent the complexes of the cations with benzene, p-methylphenol, and 3-methylindole. (c, d) Correlation of ΔE_B with IR_I for the respective Sz (panel c) and the intensity enhancement for the respective Δν_opCHb (panel d) modes of the various cation–π complexes. The red line in panel c represents the correlation with all the complexes, while the blue line represents correlation excluding the hydrated metal ions. The red, blue, and green lines in panel d represent correlations for the similar cases in panel b (reprinted with permission from ref. [104] Copyright (2013) American Chemical Society)

3.5 Molecular Modeling of π-π Interactions

The estimation of non-covalent interaction between π-systems constitute a basis for understanding binding mechanism of protein-ligand systems [105, 106]. The arene-arene interactions resulting from the edge-to-face or the parallel-displaced stacking orientations are found to play a leading role in stabilizing organic heterostructures and bio-macromolecules [107,108,109]. The high-level quantum mechanical calculations [110,111,112,113,114,115] anticipate that these arene-arene interactions are primarily assisted by the dispersion forces, although an earlier investigation led by Hunter and Sanders demonstrated that the essential contributions to the π-π interactions emanate from the electrostatic interactions [116]. A detailed theoretical investigation of the interactions between benzene and monosubstituted benzenes in parallel face-to-face stacking configuration revealed that the computed binding energies using hybrid DFT method correlate well with the Hammett σ_m values for the substituents. The parity of stacking interaction energies with the σ_m parameters could be further explicated from the direct electrostatic and dispersive interactions of the benzene and substituted benzene systems as evident by the symmetry-adapted perturbation theory (SAPT) results. Recently, the influences of electrostatic and dispersive interactions in establishing the correlation between binding energies and Hammett σ-parameters for the offset face-to-face (OSFF) stacking interactions of diverse nitrobenzene derivatives with the model graphene systems have been assessed by Khan et al. [117]. An extensive comparative study of the arene-arene interactions is conducted for the interactions of substituted nitrobenzene dimers, X–C₆H₄–NO₂ (X= H, CH₃, OCH₃, OC₂H₅, Cl, Br, I, OH, CN, and NH₂ substituents at m- and p-positions) as well as di- and tri-substituted nitrobenzene derivatives [3-NO₂-4-OH, 3,5-di-NO₂-4-OH, and 3,5-di-NO₂-4-CH₃] with the model 5,5-graphene (GR) and its B- and N-doped scaffolds (3BGR and 3NGR) within the framework of DFT using M06 exchange-correlation functional and accounting the impact of large basis sets namely cc-pVDZ, cc-pVTZ and sp-aug-cc-pVTZ. The calculated BSSE- and ZPE-corrected binding energies (∆E _B) and related thermodynamic parameters ($\Delta {H}_B^0$ and $\Delta {G}_B^0$) using DFT methods are further compared with those obtained from the MP2 level. Albeit the estimated binding energies at higher basis sets and the perturbative MP2 technique are found to be somewhat lower compared to the results derived from the M06/cc-pVDZ level, the predicted trends in ∆E _B values at diverse levels closely resemble to each other. The computed values of ∆E _B for the interaction of m- and p-substituted nitroaromatics with GR/BGR/NGR are revealed to be remarkably higher than that of benzene as well as pristine nitrobenzene. The changes in $\Delta {H}_B^0$ and $\Delta {G}_B^0$ are shown to be enhanced with the rise in the number of substituents in the nitroaromatic ring. It is noteworthy to mention that the predicted values of $\Delta {G}_B^0$ for the adsorption of nitrobenzene, m-nitrobenzene, and p-nitrotoluene on the graphene surface compare well with the experimental results obtained from the Freundlich and Langmuir isotherms. The small disagreement in magnitude with respect to the experimental adsorption free energies is mainly attributable to the overestimated CP correction via double-ζ basis set. The robust interaction of these extended π-systems stems from the electrostatic and dispersion interactions, as manifested by the molecular electrostatic potential (MEP) maps. The correlation between computed binding energy and Hammett parameter (∑|σ _m| or ∑|σ _p|) is further illustrated in Fig. 3.17a, b. The values of calculated ∆E _B using M06/cc-pVDZ level of theory are in conformity with the ∑|σ _m| for all the nitroaromatics involved in π-π interactions with the GR/3BGR/3NGR scaffold, and the estimated correlation coefficient is found to be > 0.92 for each scaffold. The correspondence between ∆E _B and ∑|σ _m| is retained to a greater or lesser extent for using diverse DFT methods and MP2 approach. The linear correlation between ∆E _B and ∑|σ _p| parameters is also conserved but to a slightly lesser extent compared to the ∑|σ _m| parameters especially for the interaction of nitrobenzene derivatives with the 3NGR. Similar correlations are maintained for the computed thermodynamic parameters $\Delta {H}_B^0$ and $\Delta {G}_B^0$ with the Hammett constants ∑|σ _m| and ∑|σ _p|, as portrayed in Fig. 3.18.

Fig. 3.17

Correlations of ΔE_B with Σ|σ_m| (panel a) and Σ|σ_p| (panel b) for the interactions between GR, 3BGR, and 3NGR with various m-, p- and several di- and tri-substituted nitrobenzene derivatives at the DFT/M06/cc-pVDZ level. Panel a: correlations of GR (blue line and black dots; r = 0.9), 3BGR (red line; r = 0.91) and 3NGR (green line; r = 0.87) (r: correlation coefficient) interacting with m-, and other higher substituted nitrobenzene derivatives. Panel b: correlations of GR (blue line; r = 0.91), BGR (red line; r = 0.91) and NGR (green line; r = 0.80) interacting with p-, and other higher substituted nitrobenzene derivatives (reprinted with permission from ref. [117] (https://pubs.acs.org/doi/10.1021/acsomega.7b01912), Copyright (2018) American Chemical Society; “Further permissions related to the material excerpted should be directed to the ACS”)

Fig. 3.18

Correlations of ΔH_B ⁰ and ΔG_B ⁰ with Σ|σ_m| (panels a and b) Σ|σ_p| (panels c and d) for the interactions of GR, 3BGR, and 3NGR with various m-, p- and several di- and tri-substituted nitrobenzene derivatives at the DFT/M06/cc-pVDZ level. Correlations in panel (a): GR…nitrobenzenes (blue): r = 0.93; 3BGR…nitrobenzenes (red): r = 0.92; 3NGR…nitrobenzenes (green): r = 0.92. Correlations in panel (b): GR…nitrobenzenes (blue): r = 0.93; 3BGR…nitrobenzenes (red): r = 0.94; 3NGR…nitrobenzenes (green): r = 0.95. Correlations in panel (c): GR…nitrobenzenes (blue): r = 0.85; 3BGR…nitrobenzenes (red): r = 0.90; 3NGR…nitro-benzenes (green): r = 0.86. Correlations in panel (d): GR…nitrobenzenes (blue): r = 0.86; 3BGR…nitrobenzenes (red): r = 0.92; 3NGR…nitrobenzenes (green): r = 0.95 (reprinted with permission from ref. [117] (https://pubs.acs.org/doi/10.1021/acsomega.7b01912), Copyright (2018) American Chemical Society; “Further permissions related to the material excerpted should be directed to the ACS”)

Moreover, the dominant contribution of dispersion and electrostatic components to the ∆E _B is justified from the multiple regression analysis by accounting the molar refractivity (∑M _r) or the changes in polarizability (∆α) (with respect to benzene) in conjunction with the ∑|σ _m| and ∑|σ _p| parameters. The contributions of electrostatic $\left({E}_{el}^{(10)}\right)$, and dispersive interactions (∆E _disp: obtained from MP2) together with empirical dispersion stemming from the M06/cc-pVDZ level are further evaluated to explicate the nature of π-π interaction due to the attachment of nitroaromatics on the surface of GR, 3BGR and 3NGR, as represented in Fig. 3.19. The involvement of ${E}_{el}^{(10)}$ and ∆E _disp terms appear to be substantial in stabilizing offset face-to-face stacking interactions in such extended π-systems. The ${E}_{el}^{(10)}$ term is found to increase with the stronger electron-withdrawing and electron-donating substituents and furnish approximately equal contribution when compared with the sum of energy components emanating from the ∆E _disp, the delocalization term $\left(\Delta {E}_{del}^{HF}\right)$, and the repulsive Heitler–London exchange term $\left({E}_x^{HL}\right)$. The energy decomposition analysis further anticipates that the ${E}_{el}^{(10)}$ contribution crucially originates from the charge–charge interactions even though the higher-order energy components associated with the dipole–dipole, dipole–quadruple, and quadruple–quadruple interactions are found to be important to determine the stabilizing factors for the π-π interactions. Thus, the obtained results substantiate the necessity of ∑M _r and ∆α together with the ∑|σ _m| or ∑|σ _p| parameters in the multiple regression analysis to evaluate the binding energies in extended π-systems in gas phase.

Fig. 3.19

Bar chart graphs comparing the contributions of E_el ⁽¹⁰⁾ and ΔE_disp in GR (panel a)/3BGR (panel b)/3NGR (panel c) interactions with various m- and several di- and tri-substituted nitrobenzene derivatives through energy decomposition analysis. The red and blue bars respectively represent ΔE_disp (MP2) and E_el ⁽¹⁰⁾ contributions. The empirical dispersion contributions at the M06/cc-pVDZ level (green bars) are also included for comparison (reprinted with permission from ref. [117] (https://pubs.acs.org/doi/10.1021/acsomega.7b01912), Copyright (2018) American Chemical Society; “Further permissions related to the material excerpted should be directed to the ACS”)

3.6 Modeling Non-covalent Interactions in Bio-inspired Supramolecular Systems

Hierarchical molecular self-assembly, also called supramolecular polymerization, is prevalent in nature, and the molecular recognition pattern of such naturally occurring biomolecules can be exploited convincingly in vitro to generate functional nanomaterials with distinctive electronic, mechanical, and biological properties [118,119,120,121,122,123]. The potential applications of supramolecular assemblies in diverse fields including nanotechnology, biotechnology, and medicine necessitate a comprehensive understanding of the mechanism of molecular assembly [124,125,126,127,128]. Experimental techniques such as electron microscopy (scanning and transmission), nuclear magnetic resonance (NMR), X-ray diffraction (XRD), and in situ atomic force microscopy (AFM) fail to provide a detailed overview of the atomic interactions and the molecular driving forces that essentially promote the formation of macroscopic structures [129]. The design of tailored hierarchical soft materials using molecular dynamics simulations is also a formidable task, since a broad array of conformational sampling is necessary for the convergence of thermodynamic and structural quantities. The supramolecular polymerization is assisted by the delicate balance of attractive forces between the building blocks including hydrogen bonding and van der Waals interactions.

By performing atomistic MD simulations for a cylindrical nanofiber comprising 144 peptide amphiphile (PA) molecules (Fig. 3.20a) in water with physiological ion concentration and employing CHARMM force field, Schatz and co-workers have shown that the self-assembly of PAs into nanofiber is aided by the electrostatic interaction between the PAs and the sodium counterions as well as the van der Waals interaction between the PA units (Fig. 3.20b) [130]. Furthermore, the formation of β-sheets parallel to the fiber axis through the hydrogen-bonding network is predicted to be the critical factor for the ordered structure of cylindrical nanofiber. In another study [131], the pertinency of plane-wave (PW)-based DFT computations in determining the driving forces for the experimentally perceived cooperativity in the hydrogen-bond-mediated supramolecular polymerization of C3-symmetrical trialkylbenzene-1,3,5-tricarboxamides (BTAs) has been assessed by analyzing the function of electrostatic interactions on the total cooperativity. The calculated interaction energy for the BTA dimer derived from PW-DFT using PBE functional is found to be –38.7 kJ/mol, which further enhances to –116 kJ/mol for the BTA oligomer holding seven monomers, and thereby leading to the total cooperative effect of 200%. The escalation of binding strength for the higher oligomers corroborates well with the shortening of hydrogen-bond length. The key interactions accounted for the cooperativity include long-range dipole-dipole interactions, short-range polarization, and resonance-assisted hydrogen bonding. The contribution of long-range dipole-dipole interactions for the self-assembled supramolecular polymer comprising seven BTA monomers is predicted to be 43% within a framework of pairwise dipole-dipole model. The remainder 71% of the interaction energy was assigned to the short-range polarization and resonance-assisted hydrogen bonding accompanied by electron redistribution along the BTA chain. The electron-density difference maps further manifest that the polarization of electron density alters substantially around the amide hydrogen bond with the augmentation of chain length of BTA oligomer, as delineated in Fig. 3.21.

Fig. 3.20

(a) Snapshot of self-assembled PAs at 40 ns. The hydrophobic core is represented by a blue surface: R-helixes are in red, β-sheets are in yellow, turns are in cyan, and coils are in gray. (b) Intermolecular interaction energies between PAs are shown in the left column, and interaction energies between sodium ion and PA are shown in the right column. The sum of electrostatic (open blue circle) and van der Waals energies (open red circle) is shown as a filled purple circle (adapted with permission from ref. [130] Copyright (2011) American Chemical Society)

Fig. 3.21

Electron-density differences calculated (a) by subtracting the electron density of the individual monomers from the electron density of the constituting oligomer (dimer, trimer, and hexamer) and (b) by subtracting the electron density of two trimers within a hexamer from the electron density of the constituting hexamer. Values are in electrons/ų. Red regions denote accumulation of electron density, and blue regions correspond to depletion of electron density upon formation of the hydrogen-bond complex (reprinted with permission from ref. [131] Copyright (2010) American Chemical Society)

Later, by performing classical MD simulations, Kang et al. [132] have demonstrated the impact of both the π-π stacking and the hydrogen bonding network on the growth of chiral filaments through the self-assembly of a peptide-drug conjugate, where a β-sheet forming peptide (CGVQIVYKK, or Tau) is conjugated with the anticancer drug camptothecin (CPT) by dint of disulfide linker (disulfylbutyrate, buSS). As revealed by the MD simulations, the π-π stacking between the CPT moieties, that emanates from the planar pentacyclic structure of the drug molecules, harnesses the initial phases of self-assembly process. The π-π stacking of the planar drug molecules of the neighboring peptide-drug conjugate is diverse in nature and exhibits both the displaced parallel and sandwiched configurations. The preassembled system accommodates a higher proportion of van der Waals interactions (31%) and lower contribution of electrostatic interactions (69%) between the drug amphiphiles (DAs) in contrast to the random system even though the calculated total interaction energies per DA are found to be comparable. Moreover, the fraction of intermolecular hydrogen bonds is found to escalate from 46% in the random system to 77% in the preassembled system, leading to a substantial cooperative rearrangement of the hydrogen bonding network prior to the commencement of nanofilament structure.

3.7 Conclusions

The non-covalent interactions play a significant role in diverse chemical and biological systems as well as the rational design of functional nanomaterials and drug discovery. The structure and conformational dynamics of complex molecular systems are influenced by the delicate interplay of non-covalent interactions encompassing hydrogen bonding, dipole-dipole interactions, steric repulsion, and London dispersion. The interaction of non-polar molecules is impacted by the dispersive forces, while the interaction of charged or highly polar molecules is chiefly emerged from the electrostatic interaction including Coulombic interaction and induction. The energetics of hydrogen-bonded systems, especially where polymeric hydrogen-bonding network are formed via O-H/N-H bonds, are demonstrated to be influenced by the specific low-frequency vibrations of the molecular systems in combination with the high-frequency modes. The reckoning of non-covalent interactions of halide ions with the surrounding solvent is turned out to be important to interpret the CTTS bands that are characteristics of charge-transfer spectra of halide-water clusters. As evident by the numerous theoretical investigations, the quantitative characterization of dispersion-dominated interactions such as the π-π and the cation-π interactions demand advanced correlated ab initio methods or empirical treatment. The understating of origin of cation-π interactions relies on the accurate description of the dipole-induced dipole as well as higher order terms like quadrupole-dipole, quadrupole-quadrupole interactions etc. The Hammett substituent constants are manifested to be critical parameters to comprehend the nature of interactions and their impact in predicting reaction thermodynamics for those molecular systems which are stabilized by the π-π interactions. The stability of the self-assembled structure in proteins and protein-mimetic materials is mainly attributable to the subtle balance between different non-covalent interactions like electrostatic, hydrophobic, hydrogen bonding, and van der Waals as revealed by the atomistic MD simulations; and the ability to estimate and comprehend the nature of non-covalent interactions is thus essential to elucidate the structure and function of hybrid materials.

The high-level wave function-based methods such as CCSD(T) or MP2 together with large basis sets like aug-cc-pVTZ and anharmonicity corrections are found to yield reliable predictions of weak and strong non-covalent interactions. However, the practical implementations of such approximate methods for large molecular systems are categorically hindered by their slow convergence with the basis set size and associated large basis set superposition errors. The dispersion-corrected DFT-based methods or range-separated functionals with a long-range correlation contribution from wave function methods followed by ZPE and BSSE corrections appear to be effective approach to trade-off between computational cost and accuracy.