Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

Van der Waals Interactions in DFT

In line with increasing use of density functional theory (DFT) in quantum chemistry, it is presently employed in more than 80 % of van der Waals calculations. Since most van der Waals calculations target at large-scale systems such as biomolecules and nanomaterials, it is natural to use DFT having features of both high speed and high accuracy. Nevertheless, it has been reported that DFT provides poor van der Waals bonds for many years [1]. For example, until recently, no exchange-correlation functional gives meaningful potential energy curves for the van der Waals bonds of rare gas dimers in Kohn–Sham calculations [1]. The main cause for the poor DFT results of van der Waals bonds is the neglect of van der Waals interactions in conventional exchange-correlation functionals [2].

By definition, van der Waals interaction is the collective term of dipole–dipole, dipole–induced dipole, and dispersion interactions [3]. The dipole–dipole interaction is the electrostatic interaction between permanent dipoles in polar systems. For the interactions between systems A and B, the corresponding potential is given classically as

$$ {V}_{\mu -\mu }(r)=-\frac{{\mu }_{A}{\mu }_{B}}{{R}_{AB}{}^{3}}$$
(1)

where μ X is the permanent dipole of system X and R AB is the distance between systems A and B. Note that atomic units (ℏ = e = m e = 1 ∕ (4π ε 0) = 1, energies are in hartree, and distances are in bohr) are used in all equations of this review. In the Kohn–Sham equation [4], which is usually the main equation of DFT, this interaction is contained as a part of Coulomb interactions. The dipole–induced dipole interaction is the interaction between polar and nonpolar systems. Assuming the permanent dipole moment of polar system A as μ A and the polarizability, the linear response for electric field producing induced dipole moment, of nonpolar system B as α B, the classical potential of this interaction is given as [3]

$$ {V}_{\mu -\alpha }(r)=-\frac{{\mu }_{A}^{2}{\alpha }_{B}}{{R}_{AB}{}^{6}}$$
(2)

Since this interaction is very weak, it causes the low solubility of polar molecules in nonpolar solvents. This interaction is also incorporated in Kohn–Sham SCF calculations. The dispersion interaction is a universal interaction, which acts even between the bodies of neither charge nor multipole moment. As a classical expression, the potential function between two heterogeneous bodies, which London developed using perturbation theory, is used [5],

$$ \begin{array}{c}{V}_{disp}^{London}(r)=-\frac{3}{2}\frac{{\alpha }_{A}{\alpha }_{B}}{{R}_{AB}{}^{6}}\frac{{I}_{A}{I}_{B}}{{I}_{A}+{I}_{B}}\end{array}$$
(3)

where I X is the ionization potential of partial system X. This dispersion interaction is interpreted as the interaction between an instantaneous dipole moment by the fluctuation of electron distribution and an induced dipole moment by the electric field formed of the instantaneous dipole moment. That is, two spatially separated electron distributions fluctuate around these equilibrium distributions by electron correlation to produce interactions between two bodies. Therefore, dispersion interaction is a pure electron correlation between two bodies, which cannot be incorporated by one-body mean-field approximation, and it is long-range correlation explicitly acting between distant electrons. This dispersion interaction is the only van der Waals interaction that is not incorporated in Kohn–Sham calculations using conventional correlation functionals.

Although dispersion interaction should be included in correlation functionals, it has usually been not taken into consideration in conventional correlation functionals. Conventional generalized-gradient-approximation (GGA) correlation functionals are classified into two types: density gradient expansion-type and Colle–Salvetti-type correlation functionals. In density gradient expansion-type correlation functionals, local density approximation (LDA) correlation functionals are corrected using the functionals of density gradient. For example, Perdew–Wang 1991 (PW91) [6] and Perder–Burke–Ernzerhof (PBE) [7] correlation functionals are involved in these functionals. However, since electron density and its gradient are essentially one-electron functions, these functionals cannot give dispersion interactions, which are explicit long-range electron–electron interactions as shown in Eq. (3). Colle–Salvetti-type correlation functionals [8] are derived from correlation wavefunctions, in which uncorrelated wavefunctions are multiplied by the factor of correlation holes. Lee–Yang–Parr (LYP) [9] and one-parameter progressive (OP) correlation functionals [10] are included in these functionals. Since these functionals contain only short-range correlation resulting from correlation holes, long-range correlations including dispersion interactions are neglected in these functionals. Naturally, Kohn–Sham calculations using these GGA correlation functionals have almost always failed with no dispersion interaction to give van der Waals bonds even qualitatively. It is, therefore, reasonable to consider that dispersion interaction should be explicitly supplemented in conventional correlation functionals.

π-Stacking Interactions

π-Stacking interaction is one of the dispersion interactions and often significantly contributes to the structures of large-scale systems. The name “π-stacking” comes from the structures of π-stacked systems, in which π orbitals seem to overlap. However, it is theoretically revealed that π orbitals do not play a special role in π-stacking interactions [11], as implicated by experimental phase-change studies. That is, π-stacking interactions are nothing more than usual dispersion interactions. π-Stacking interactions have also been interpreted by various models: e.g. solvophobic (entropic interaction), donor–acceptor (charge transfer interaction), and atomic charge (electrostatic interaction between uneven charge distributions) models [12]. However, these classical models have been disconfirmed both experimentally and theoretically [12]. Hunter suggested a model, in which the repulsive electrostatic interactions of quadrupole moments are balanced with attractive dispersion interactions [13]. However, as clearly shown in section “Long-Range Exchange Interactions”, long-range exchange interactions are actual repulsions against the attractions of long-range dispersion correlations in π-stacking bonds [14]. In most cases, π-stacking interactions indicate the noncovalent interactions between aromatic rings. π-Stacking interactions have three types of conformations: parallel, T-shaped, and parallel-displaced configurations (Fig. 1). As anticipated from the above discussion, similar potential energy curves are given for the bond dissociations of parallel and T-shaped configurations, although parallel configurations tend to give shorter bond distances with smaller binding energies than those of T-shaped configurations [14]. Therefore, most theoretical studies have assumed that π-stacking interactions are accurately reproduced by appropriate methods giving correct dispersion interactions.

Fig. 1
figure 1

Three conformation types of benzene dimer

Full size image

So far, it has been experimentally reported that π-stacking interactions play important roles in various large systems: e.g., carbon nanomaterials (stackings on fullerene, graphene, and nanotube available in hydrogen storage materials [15], drug-delivery vehicles [16] and biochemical sensors [17, 18]), biomolecules (DNA stackings [19, 20] and protein foldings [21, 22]), and supramolecules (molecular recognitions [23, 24], crystal packings [25, 26], and host–guest interactions [27, 28]). Therefore, past theoretical investigations have also mainly approached the π-stacking natures of these large systems. Carbon nanomaterials having polycyclic structures use π-stackings to solvate in organic sovents. In DNA, π-stacking interactions form stacking bonds between the bases to build up the double-helical structure [29]. Protein foldings are also critically affected by the π-stacking of aromatic rings in proteins. For supramolecules, π-stackings are usually used to self-assemble π-conjugated molecules [30]. On the other hand, π-stacking interactions hardly contribute to chemical reactions. For the substitution reaction of benzene dimer shown in Fig. 2, Wheeler and Houk suggested that even for the reaction of π-stacked benzene derivatives, the substituent group (X) directly interacts with the aromatic ring to proceed the reaction with no contribution of the π-stacking [31]. This is analogous to Diels–Alder reactions, in which dispersion interactions between π orbitals hardly affect the reaction enthalpies [32]. However, it is also found that dispersion interactions clearly decrease reaction barriers of these Diels–Alder reactions [32]. We, therefore, suppose that π-stackings may contribute to reactivities in reactions of π-stacked systems, although they may not directly affect reaction mechanisms.

Fig. 2
figure 2

The displacement reaction of benzene dimer

Full size image

As described above, π-stackings essentially consist of dispersion interactions. Dispersion effects should, therefore, be explicitly taken into consideration to calculate π-stackings. However, many conventional DFT calculations have used exchange-correlation functionals containing no explicit dispersion interaction such as pure LDA and GGA functionals and consequently have provided poor results in π-stacking calculations. To open the door to quantitative discussions of van der Waals bonds including π-stackings, a wide variety of dispersion corrections have been developed in the field of DFT. In this review, we will briefly explain major dispersion corrections for DFT exchange-correlation functionals on their basic concepts in section “Dispersion Corrections in DFT”. We will then list past DFT applications to π-stacking systems with mentioning their limitations in section “DFT Calculations of π-Stacking Systems”.

Dispersion Corrections in DFT

So far, various types of dispersion corrections have been suggested. These dispersion corrections are generally classified to five types: classical dispersion corrections, combinations with perturbation theories, linear-response theories, van der Waals (dispersion) functionals, and semiempirical dispersion-corrected functionals. Besides these dispersion corrections, long-range exchange interactions and correlation functionals are also significant in calculating van der Waals bonds. In this section, these dispersion corrections and the effects of long-range exchange interactions and correlation functionals are briefly reviewed.

Classical Dispersion Corrections

The simplest dispersion correction may be the empirical correction for the Kohn–Sham energy using the London’s classical interatomic dispersion energy,

$$ \begin{array}{c}{E}_{disp}^{London}=-{\displaystyle \sum _{A>B}\frac{{C}_{6}{}^{AB}}{{R}_{AB}{}^{6}}{f}_{damp}({R}_{AB})}\end{array}$$
(4)

where A and B are usually the labels of atoms and C 6 AB is the interatomic dispersion coefficient parameterized, and f damp is a damping function for cutting off unnecessary short-range interactions. The feature of this correction method is much less computational time required in dispersion calculations than those of other dispersion corrections. Since this classical correction also accurately reproduces experimental results with well-calibrated dispersion coefficients, it is the most widely used dispersion correction in classical molecular dynamics (MD) simulations. It is, however, difficult to apply this correction to the calculations of new uninformed systems due to the empirically parameterized dispersion coefficient and it has been reported that this correction gives much different results dependent on exchange-correlation functionals combined. Therefore, the right-hand side of Eq. (4) is usually multiplied by adjusted parameters dependent on exchange-correlation functional combined as seen in DFT-D (section “Semiempirical Dispersion-Corrected Functionals”). However, these methods are too empirical to be appropriate for a wide variety of systems. To solve this problem, Becke developed the exchange-hole dipole moment (XDM) method [33, 34], in which the C 6 AB coefficient in Eq. (4) is calculated by

$$ {C}_{6}^{AB}=\frac{{\langle {d}_{x}^{2}\rangle }_{A}{\langle {d}_{x}^{2}\rangle }_{B}{\alpha }_{A}{\alpha }_{B}}{{\langle {d}_{x}^{2}\rangle }_{A}{\alpha }_{B}+{\langle {d}_{x}^{2}\rangle }_{B}{\alpha }_{A}}$$
(5)
$$ {\langle {d}_{x}^{2}\rangle }_{A}={\displaystyle \sum _{\sigma }{\displaystyle \int {d}^{3}r{\rho }_{\sigma }(r){d}_{x\sigma }^{2}(r)}}$$
(6)

and

$$ {d}_{x\sigma }(r)=\left\{\frac{1}{{\rho }_{\sigma }(r)}{\displaystyle \sum _{ij}\left[{\displaystyle \int {d}^{3}{r}^{\prime }{r}^{\prime }{\varphi }_{i\sigma }({r}^{\prime }){\varphi }_{j\sigma }({r}^{\prime })}\right]}{\varphi }_{i\sigma }(r){\varphi }_{j\sigma }(r)\right\}-r$$
(7)

Although this method is also empirical, it has a physical meaning at least in the dispersion coefficient and gives more accurate dispersion interactions than those of the London’s classical dispersion energy.

Combination with Perturbation Theories

Perturbation theories such as the second-order Møller–Plesset perturbation (MP2) method [35] have been appreciated as ab initio wavefunction theories reproducing dispersion interactions with relatively short computational time. Therefore, dispersion interactions can be incorporated in the Kohn–Sham method by combining with the perturbation theories in principle. One of the methods based on this concept is DFT symmetry-adapted perturbation theory (DFT-SAPT), which uses Kohn–Sham orbitals to calculate the perturbation energies [36]. In contrast to ab initio SAPT calculating both inter- and intra-molecular electron correlations, only intermolecular electron correlations are calculated as a dispersion correction for the Kohn–Sham method in DFT-SAPT. Consequently, this drastically reduces the computational cost to tenths or hundredths of an ab initio SAPT one with similar accuracies. Although DFT-SAPT is a promising dispersion calculation method for clearly separated systems, it cannot reproduce intramolecular dispersion interactions. Moreover, despite the drastically reduced computational time, DFT-SAPT calculations need much more computational time than those of Kohn–Sham calculations even for the lowest-order DFT-SAPT2. Therefore, these are consequently applicable to systems containing only up to several dozens of atoms with current commercial computer performance. As another method combining DFT with perturbation theories, there are double-hybrid functionals, which mix perturbation energies in correlation functionals at a constant rate [37]. That is, these functionals extend hybrid functionals by mixing correlation functionals with MP2 perturbation energies such as

$$ \begin{array}{c}{E}_{\text{xc}}=(1-{a}_{\text{x}}){E}_{\text{x}}+{a}_{x}{E}_{\text{HF}}+(1-{a}_{\text{c}}){E}_{\text{c}}+{a}_{\text{c}}{E}_{\text{MP2}}\end{array}$$
(8)

where E MP2 is MP2 electron correlation energy. B2PLYP functional [38] is one of the double-hybrid functionals. Although this method gives middle-range electron correlations, it is not appropriate for dispersion calculations because of the incomplete dispersion interactions incorporated.

Linear-Response Theories

By using linear-response theories, dispersion interactions can be calculated directly in the framework of the Kohn–Sham method. Adiabatic connection/fluctuation-dissipation theorem (AC/FDT) method is a linear-response theory for calculating dispersion interactions based on the Kohn–Sham method [39]. In this AC/FDT method, electron correlation is calculated as the energy response quantity for the spontaneous fluctuations of electronic motions coming from the perturbation of interelectronic interactions as

$$\displaystyle\begin{array}{rcl} E_\mathrm{{c}}^\mathrm{AC/FDT}& =& -\int _{0}^{1}d\lambda \int \!\!\!\int {d}^{3}\mathbf{r}{d}^{3}{\mathbf{r}}^{{\prime}} \frac{1} {\vert \mathbf{r} -{\mathbf{r}}^{{\prime}}\vert } \times \left [\frac{1} {2\pi }\int _{0}^{\infty }\!\!\!du\left \{\chi _{\lambda }\left (\mathbf{r},{\mathbf{r}}^{{\prime}},\mathrm{i}u\right ) -\chi _{ 0}\left (\mathbf{r},{\mathbf{r}}^{{\prime}},\mathrm{i}u\right )\right \}\right ],{}\end{array}$$
(9)

where r and r ′ are the position vectors of electrons. In this equation, χ λ and χ 0 are density response functions for interacting and independent electrons, respectively, and these are obtained by solving the Dyson equation as

$$\displaystyle\begin{array}{rcl} \chi _{\lambda }\left (\mathbf{r},{\mathbf{r}}^{{\prime}},\omega \right )& =& \chi _{ 0}\left (\mathbf{r},{\mathbf{r}}^{{\prime}},\omega \right ) +\int \!\!\!\int \!\! {d}^{3}\mathbf{r}_{ 1}{d}^{3}\mathbf{r}_{ 2}\chi _{0}\left (\mathbf{r},\mathbf{r}_{1},\omega \right ) \\ & & \times \left \{ \frac{\lambda } {\vert \mathbf{r}_{1} -\mathbf{r}_{2}\vert } + f_{\mathrm{xc}}^{\lambda }\left (\mathbf{r}_{1},\mathbf{r}_{2},\omega \right )\right \}\chi _{\lambda }\left (\mathbf{r}_{2},{\mathbf{r}}^{{\prime}},\omega \right ),\qquad {}\end{array}$$
(10)

where f xc λ is the exchange-correlation integral kernel for interacting systems. Since the electron correlation in Eq. (9) contains dispersion interactions as the long-range correlation, the long-range part of this correlation energy is often used as a dispersion correction, which is called “RPAx” [40]. Analogously to the time-dependent response Kohn–Sham (TDKS) method, the correlation energy is calculated by solving the TDKS matrix equation. Although this AC/FDT method is obviously the most superior dispersion correction from a physical point of view, this method requires an enormous amount of computational time, which is more than thousand times the time needed in Kohn–Sham calculations, unless drastic approximations would be adopted.

Van der Waals (Dispersion) Functionals

Van der Waals (dispersion) functionals have been developed to reduce the enormous computational time required in the AC/FDT method with keeping the accuracies and to be easy-to-use like the London’s classical potential. Lundqvist and coworkers proposed a dispersion functional called Andersson–Langreth–Lundqvist (ALL) functional by using a local density approximation for the electron density response function of the AC/FDT method [41],

$$\displaystyle{ E_\mathrm{{disp}}^\mathrm{ALL}\left [\rho \right ] = - \frac{6} {{4\pi }^{3/2}}\int _{\mathrm{V}_{1}}\!\!\!{d}^{3}\mathbf{r}_{ 1}\!\!\!\int _{\mathrm{V}_{2}}\!\!\!{d}^{3}\mathbf{r}_{ 2} \frac{\sqrt{\rho (\mathbf{r} _{1 } )}\sqrt{\rho (\mathbf{r} _{1 } )}} {\sqrt{\rho (\mathbf{r} _{1 } )} + \sqrt{\rho (\mathbf{r} _{1 } )}} \frac{1} {r_{12}^{6}}. }$$
(11)

As almost the same functional, Dobson and coworkers independently suggested a dispersion functional based on local density approximation in the same year [42]. Note that explicit numerical two-electron integrals, which usually take long computational time to be calculated, are included in the formulations of these functionals. However, in actual calculations, the computational time is usually less than that of the Kohn–Sham calculation, because spatial regions of small momentum variations and core regions can be neglected in the integral calculations. On the other hand, these functionals are applicable only to two-body systems having well-separated electron distributions and need damping functions f damp shown in Eq. (4) for short-range electron–electron distances. To solve this problem, many researchers have attempted to develop dispersion functionals applicable to the regions of overlapped electron distributions. Lundqvist and coworkers also proposed a dispersion functional available for such electronic regions [43]. This functional has a complicated form using ϕ(r 1, r 2) function containing the spatial coordinates of two electrons and the electron density and its gradient at these coordinates,

$$ {E}_{\text{disp}}^{\text{DRSLL}}\left[\rho \right]={\displaystyle \int {d}^{3}}{r}_{1}{\displaystyle \int {d}^{3}}{r}_{2}\rho ({r}_{1})\varphi ({r}_{1},{r}_{2})\rho ({r}_{2}),$$
(12)
$$ \varphi ({r}_{1},{r}_{2})=\frac{2}{{\pi }^{2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}d}a{a}^{2}{\displaystyle \int d}b{b}^{2}W(a,b)T\left({\nu }_{1}(a),{\nu }_{1}(b),{\nu }_{2}(a),{\nu }_{2}(b)\right),$$
(13)
$$ T(w,x,y,z)=\frac{1}{2}\text{}\left[\frac{1}{w+x}\text{}+\text{}\frac{1}{y+x}\right]\text{}\left[\frac{1}{(w+y)(x+z)}\text{}+\text{}\frac{1}{(w+z)(y+x)}\right],$$
(14)

and

$$ \begin{array}{l}W(a,b)=\frac{2}{{a}^{3}{b}^{2}}[(3-{a}^{2})b\ \mathrm{cos}\ b\ \mathrm{sin}\ a\ +(3-{b}^{2})a\ \mathrm{cos}\ a\ \mathrm{sin}\ b\\ \text{}+({a}^{2}+{b}^{2}-3)\ \mathrm{sin}\ a\ \mathrm{sin}\ b\ -3ab\ \mathrm{cos}\ a\ \mathrm{cos}\ b],\end{array}$$
(15)

where

$$ \begin{array}{c}{\nu }_{i}(y)={y}^{2}/2\left(1-\mathrm{exp}(-4\pi {y}^{2}/9{d}_{i}^{2})\right),\end{array}$$
(16)

and

$$ \begin{array}{c}{d}_{i}={r}_{12}{q}_{0}({r}_{i}).\end{array}$$
(17)

In Eq. (17), q 0 is given using the Fermi momentum, k F = (3π 2 ρ)1 ∕ 3, as

$$ \begin{array}{c}{q}_{0}(r)={k}_{\text{F}}(r)\left[1+0.09434{\left(\frac{\rho (r)}{2{k}_{\text{F}}(r)\rho (r)}\right)}^{2}\right].\end{array}$$
(18)

This functional requires no damping function, because it naturally approaches zero for short electron–electron distance. Therefore, this functional can reproduce intramolecular dispersion interactions. This dispersion functional is used in, e.g., vdW-DF dispersion correction [43] combining with revPBE or another GGA functional. As other interesting dispersion functionals, Vydrov–van Voorhis 2009 (VV09) functional [44], which uses the dielectric model smoothing the real-space cutoff, and local response dispersion (LRD) functional [45], which combines the local response approximation functional of Dobson and coworkers [42] with the real-space cutoff [44], are also suggested. Combining with long-range corrected DFT, this LRD functional has succeeded to reproduce various kinds of reaction energy diagrams and photochemistries, which have been poorly given by conventional DFTs, as mentioned in section “Long-Range Exchange Interactions”.

Semiempirical Dispersion-Corrected Functionals

Semiempirical dispersion-corrected functionals intend to reproduce accurate properties including van der Waals interaction energies by using dispersion terms with many adjusted semiempirical parameters like CHARMM [46] and Amber [47] molecular force fields in classical MDs of biological systems. DFT-D functionals such as BLYP-D, B3LYP-D, and B97-D functionals [48] and Mx-series functionals such as M05-2x and M06-2x functionals [49] are included in these semiempirical dispersion-corrected functionals. In DFT-D functionals, there are three versions, DFT-D1, -D2, and -D3, based on the level of dispersion corrections. For deep understanding of dispersion corrections, it is interesting to show the highest-level DFT-D3 functional [50],

$$ \begin{array}{c}{E}^{\text{DFT-D3}}\end{array}={E}^{\text{KS}}-{E}_{\text{disp}}^{(\text{2})}-{E}_{\text{disp}}^{(\text{3})}$$
(19)
$$ {E}_{\text{disp}}^{(\text{2})}=-{\displaystyle \sum _{\text{A}>\text{B}}{\displaystyle \sum _{n=6,8,10,\cdots }{s}_{n}}}\frac{{C}_{n}^{\text{AB}}}{{R}_{\text{AB}}{}^{n}}{f}^{n}{}_{\text{damp}}({R}_{\text{AB}}),$$
(20)
$$ \begin{array}{c}{E}_{\text{disp}}^{(\text{3})}\end{array}=-{\displaystyle \sum _{\text{A}>\text{B}>\text{C}}\frac{{C}_{9}^{\text{ABC}}\left(3\mathrm{cos}{\theta }_{a}\mathrm{cos}{\theta }_{b}\mathrm{cos}{\theta }_{c}+1\right)}{{\left({R}_{\text{AB}}{R}_{\text{BC}}{R}_{\text{CA}}\right)}^{3}}}{f}_{\text{damp}}^{(\text{3})}({\overline{R}}_{\text{ABC}}),$$
(21)

where A, B, and C are atomic labels, θ a , θ b , and θ c are the internal angles of ABC triangle, and \( {\overline{R}}_{\text{ABC}}\) is geometrically averaged radii. The damping functions are given by

$$ \begin{array}{c}{f}_{\text{damp}}^{n}({R}_{\text{AB}})\end{array}=\frac{1}{1+6{\left({R}_{\text{AB}}/({s}_{r,n}{R}_{0}^{\text{AB}})\right)}^{-{\alpha }_{n}}},$$
(22)

and

$$ \begin{array}{c}{f}^{(\text{3})}{}_{\text{damp}}({\overline{R}}_{\text{ABC}})\end{array}=\frac{1}{1+6{\left({\overline{R}}_{\text{ABC}}/(4{R}_{0}^{\text{ABC}}/3)\right)}^{-16}},$$
(23)

All the remaining parameters are semiempirical: R 0 AB and R 0 ABC are cutoff radii adjusted to each atomic pairwise and three-body. Coefficients s n (n = 8, 10, ⋯ ) are fitted in benchmark calculations depending on functionals combined, while s 6 is one or an adjusted value less than 1. For dispersion coefficients, C n AB and C 9 ABC, time-dependent DFT (TDDFT) and recursion relations are used to determine the values for each atomic pairwise and three-body. The lowest-order C 6 AB is expressed in the Casimer–Polder formula [51],

$$ \begin{array}{c}{C}_{6}^{\text{AB}}=\frac{3}{\pi }{\displaystyle \underset{0}{\overset{\infty }{\int }}d\omega {\alpha }^{\text{A}}}(i\omega ){\alpha }^{\text{B}}(i\omega ),\end{array}$$
(24)

where α A(i ω) is the averaged dipole polarizability of atom A at imaginary frequency. Other C n AB coefficients are derived by the recursion relations [52] as

$$ \begin{array}{c}{C}_{8}^{\text{AB}}\end{array}=3{C}_{6}^{\text{AB}}\sqrt{{Q}_{\text{A}}{Q}_{\text{B}}},$$
(25)
$$ \begin{array}{c}{C}_{10}^{\text{AB}}\end{array}=\frac{49}{40}\frac{{({C}_{8}^{\text{AB}})}^{2}}{{C}_{6}^{\text{AB}}},$$
(26)

and

$$ \begin{array}{c}{C}_{n+4}^{\text{AB}}\end{array}={C}_{n-2}^{\text{AB}},{\left(\frac{{C}_{n+2}^{\text{AB}}}{{C}_{n}^{\text{AB}}}\right)}^{3}$$
(27)

with

$$ \begin{array}{c}{Q}_{\text{A}}=\end{array}\sqrt{{Z}_{\text{A}}}\frac{{\langle {r}^{4}\rangle }_{\text{A}}}{{\langle {r}^{2}\rangle }_{\text{A}}},$$
(28)

where Z A is the nuclear charge of atom A and ⟨r 4⟩A and ⟨r 2⟩A are the expectation values derived from the electron density of atom A. The remaining triple–dipole C 9 ABC coefficient is given by

$$ \begin{array}{c}{C}_{9}^{\text{ABC}}\end{array}=\frac{3}{p}{\displaystyle \underset{0}{\overset{\infty }{\int }}d\omega {\alpha }^{\text{A}}}(i\omega ){\alpha }^{\text{B}}(i\omega ){\alpha }^{\text{C}}(i\omega )\approx -\sqrt{{C}_{6}^{\text{AB}}{C}_{6}^{\text{BC}}{C}_{6}^{\text{CA}}}.$$
(29)

These coefficients are determined by TDDFT calculation for each atomic pairwise and three-body. Since these values are fixed after one TDDFT calculation, these dispersion calculations are not the bottleneck of DFT-D3 calculations. For DFT-D3 functionals, BLYP-D3 and B2PLYP-D3 functionals are suggested [50]. In Mx-series and other semiempirical dispersion-corrected functionals, dispersion interactions are incorporated in the similar manner, although only the C 6 AB term is usually contained. This type of dispersion corrections is obviously efficient, because dispersion interactions are easily incorporated with high accuracy only by using functionals. However, it has been reported that the calculated results depend on the parameters used and the R  − 6 decay of dispersion interaction cannot be reproduced.

Long-Range Exchange Interactions

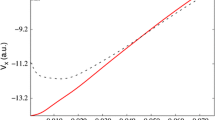
Although only dispersion corrections have so far been presented in this section, we should notice that repulsions balanced with dispersion attractions are equivalently significant in dispersion calculations. As seen in the Lennard–Jones potential (section “Biomolecules: DNA and Proteins”), the repulsions have been interpreted to come from long-range exchange interactions. Nevertheless, long-range exchange interactions have been neglected in conventional exchange functionals similarly to dispersion interactions in conventional correlation functionals. Figure 3a displays the dissociation potential energy curves of Ar dimer, which are calculated using various exchange functionals [1]. It is well known that the bond of Ar dimer consists only of dispersion interactions. This figure clearly indicates that the dissociation potentials of van der Waals bonds are significantly affected by exchange functionals used: LDA, Becke 1988 GGA (B88), and Perdew–Burke–Ernzerhof GGA (PBE) exchange functionals give qualitatively different potential energy curves, despite these functionals have been combined with dispersion corrections mentioned above. In contrast, the figure shows that long-range correction clearly makes these potential energy curves close to each other. Therefore, this figure reveals that the different potential energy curves of GGA functionals mainly come from the lack of long-range exchange interactions.

Fig. 3
figure 3

Dissociation potential energy curves of argon dimer calculated with (a) various pure and long-range corrected (LC) functionals and (b) LC functionals combined with ALL dispersion functional. The curves of CCSD(T) and other dispersion-corrected DFT are also shown for comparison

Full size image

Tsuneda and coworkers suggested the long-range correction, in which exchange interactions are divided into short- and long-range parts, and then the short-range part of a general exchange functional is combined with the long-range part of the Hartree–Fock (HF) exchange integral [53]. In this correction, the two-electron operator 1 ∕ r 12 is divided by the error function as

$$ \begin{array}{c}\frac{1}{{r}_{12}}=\frac{1-\text{ erf}(\mu {r}_{12})}{{r}_{12}}+\frac{\text{ erf}(\mu {r}_{12})}{{r}_{12}}.\end{array}$$
(30)

Since usual exchange functionals, however, have no corresponding density matrices, the short-range part of exchange functionals are derived assuming that all the difference in exchange functionals is reflected to the momentum k σ as

$$ \begin{array}{c}{E}_{\text{x}}^{\text{LC}(\text{sr})}=-\frac{1}{2}{\displaystyle \sum _{\sigma }{\displaystyle \int {d}^{3}}}r{\rho }_{\sigma }^{4/3}{K}_{\sigma }\left\{1-\frac{8}{3}{a}_{\sigma }\left[\sqrt{\pi }\text{ erf}\left(\frac{1}{2{a}_{\sigma }}\right)+2{a}_{\sigma }\left({b}_{\sigma }-{c}_{\sigma }\right)\right]\right\},\end{array}$$
(31)

where a σ , b σ , and c σ are given as

$$ \begin{array}{c}{a}_{\sigma }\end{array}=\frac{\mu }{2{k}_{\sigma }}=\frac{\mu {K}_{\sigma }^{1/2}}{6\sqrt{\pi }{\rho }_{\sigma }^{1/3}},$$
(32)
$$ \begin{array}{c}{b}_{\sigma }\end{array}=\mathrm{exp}\left(-\frac{1}{4{a}_{\sigma }^{2}}\right)-1,$$
(33)

and

$$ \begin{array}{c}{c}_{\sigma }\end{array}=2{a}_{\sigma }^{2}{b}_{\sigma }+\frac{1}{2}.$$
(34)

A dimensionless coefficient K σ is defined in usual GGA exchange functional form as

$$ \begin{array}{c}{E}_{x}=-\frac{1}{2}{\displaystyle \sum _{\sigma }{\displaystyle \int {d}^{3}}}r{\rho }_{\sigma }^{4/3}{K}_{\sigma }.\end{array}$$
(35)

The significant feature of this correction is to use the following momentum k σ , which becomes the Fermi momentum when combined with the LDA exchange functional,

$$ \begin{array}{c}{k}_{\sigma }={\left(\frac{9\pi }{{K}_{\sigma }}\right)}^{1/2}{\rho }_{\sigma }^{1/3}.\end{array}$$
(36)

This momentum makes long-range corrected (LC) LDA functional identical to the form that Savin previously proposed as a long-range correction for LDA exchange functional, which is called range-separation hybrid (RSH) functional [54]. For the long-range part of the HF exchange integral, the two-electron operator is simply replaced with the error function such as

$$\displaystyle\begin{array}{rcl} E_\mathrm{{x}}^\mathrm{LC(lr)} = -\frac{1} {2}\sum \limits_{\sigma }\!\sum \limits_{i}^{n}\!\sum \limits_{ j}^{n}\int \!\!\!\int \!\!{d}^{3}\mathbf{r}_{ 1}{d}^{3}\mathbf{r}_{ 2}\phi _{i\sigma }^{{\ast}}(\mathbf{r}_{ 1})\phi _{j\sigma }^{{\ast}}(\mathbf{r}_{ 1})\frac{\mbox{ erf}\left (\mu r_{12}\right )} {r_{12}} \phi _{i\sigma }(\mathbf{r}_{2})\phi _{j\sigma }(\mathbf{r}_{2}).& &{}\end{array}$$
(37)

The only parameter μ is determined for each exchange functional: e.g., for B88 [55] and PBE [7] exchange functionals, μ = 0. 33 in response property calculations [56] and 0.47 in ground-state property calculations [57] are adopted. The computational time needed in LC-DFT calculations is almost the same as that in B3LYP calculations. Nevertheless, it has been reported that long-range correction solves or improves various problems in conventional DFT calculations: e.g., charge transfers, Rydberg excitations, and oscillator strengths in TDDFT [56], optical response properties of long-chain molecules [58] and diradicals [59], and orbital energies of valence molecular orbitals [60]. Due to its high applicabilities, many types of LC functionals have been developed: e.g., CAM-B3LYP [61], LC-ωPBE [62], and ωB97X [63] functionals. By using this long-range correction, long-range exchange interactions are naturally incorporated in exchange functionals.

Figure 3b illustrates the potential energy curves of LC-DFT combining with a dispersion functional (ALL functional in section “Van der Waals (Dispersion) Functionals”). As shown in the figure, LC functionals give very accurate potential energy curves, which are close to ab initio coupled-cluster singles, doubles, and perturbative triples (CCSD(T)) one [64], in contrast to those of a dispersion-corrected semiempirical functional (mPW1PW91) and a classical dispersion-corrected one (B3LYP+vdW). In addition, it was suggested that long-range exchange interactions play a determinant role in van der Waals bond angles [65]. Besides ALL dispersion functional, LC functionals have been combined with various dispersion corrections: e.g., LRD dispersion functional (section “Van der Waals (Dispersion) Functionals”) [45], AC/FDT dispersion energy (section “Linear-Response Theories”) [40], semiempirical functionals (section “Semiempirical Dispersion-Corrected Functionals”) such as ωB97X-D [66], and perturbation energies (section “Combination with Perturbation Theories”) such as ωB97X-2 [67]. Actually, LC functionals can be easily combined with any dispersion correction.

Effects of Correlation Functionals

In DFT calculations of dispersion interactions, the choice of correlation functionals is also important. Figure 3a also compares the dissociation potential energy curves of Ar dimer for using one-parameter progressive (OP) [10] and Lee–Yang–Parr (LYP) [9] correlation functionals, which are both Colle–Salvetti-type correlation functionals [8]. The Colle–Salvetti-type correlation functionals are derived from correlated wavefunctions, in which uncorrelated wavefunctions such as the HF wavefunction are multiplied by a correlation factor (Jastrow factor) satisfying the correlation cusp condition for short-range interelectrons. Therefore, these functionals essentially contain only short-range electron correlations and neglect long-range electron correlations including dispersion interactions. Nevertheless, artificial van der Waals bonds are given using the LYP correlation functional with no dispersion interaction. This is attributed to the inappropriate behavior of this functional. To give appropriate weak bonds like van der Waals bonds, correlation functionals have to obey the high-density-gradient low-density (HDGLG) limit condition for correlation energy [68, 69],

$$ \begin{array}{c}\underset{x\to \infty }{\mathrm{lim}}{\rho }^{-1}{\overline{E}}_{\text{c}}\end{array}=0,$$
(38)

where x =  | ∇ ρ | ∕ ρ 4 ∕ 3. However, the LYP functional does not satisfy this condition differently from the OP functional [1]. The Kohn–Sham method using a correlation functional violating this condition usually overstabilizes van der Waals bonds. Therefore, we should carefully select a correlation functional satisfying the HDGLG limit condition in DFT calculations of dispersion interactions.

DFT Calculations of π-Stacking Systems

In this section, past DFT studies on π-stacking interactions are briefly reviewed. Except for small benchmark molecules, the most frequently raised π-stacked systems are carbon nanomaterials including nanotube and graphene, biomolecules including DNA and proteins, and supramolecules. Summarizing previous dispersion-corrected DFT calculations of these π-stacked systems, we will anticipate the future trend of DFT studies on π-stacking interactions.

Small π-Stacked Systems

The applicabilities of dispersion corrections have so far been examined by calculating small weakly bonded systems including π-stacked systems. In particular, benzene and naphthalene dimers have been used as test targets of dispersion corrections for π-stacking interactions [14, 70, 71], because these dimers are the simplest systems for discussing three conformations shown in Fig. 1. For clarifying the reproducibilities of π-stacking interactions, it is one of the best strategies to calculate the dissociation potential energy curves of these dimers. Figure 4 illustrates the dissociation potential energy curves of benzene dimer for the parallel conformation calculated with (a) pure LDA and GGA functionals and LC functionals and (b) LC functionals with ALL dispersion functional. As shown in Fig. 4a, traditional DFTs using pure LDA and GGA functionals give much different dissociation potential energy curves for benzene dimer [14] similarly to the curves of rare-gas dimers [1]. This difference is also attributed to the lack of long-range exchange interactions in exchange functionals (section “Long-Range Exchange Interactions”) and the poor HDGLG limit of some correlation functionals (section “Effects of Correlation Functionals”) [14]. Figure 4b indicates that all LC exchange functionals with OP correlation functional, which gives the correct HDGLG limit, produces very accurate potential energy curves close to CCSD(T) one by combining with a dispersion functional. Since similar curves are obtained for naphthalene dimer [14], this indicates that besides dispersion corrections, long-range exchange interactions should be included with an appropriate correlation functional satisfying the HDGLG limit condition in DFT calculations of dispersion interactions. Nonetheless, further quantitative validation is required, because some other dispersion-corrected DFTs also give correct potential energy curves for benzene dimer with no long-range correction [70, 72].

Fig. 4
figure 4

Dissociation potential energy curves of benzene dimer for the parallel conformation calculated using (a) various pure and long-range corrected (LC) functionals and (b) LC functionals combined with ALL dispersion functional. The curves of CCSD(T) and other dispersion-corrected DFT are also shown for comparison

Full size image

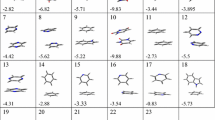
As a benchmark set for the quantitative validation of dispersion corrections, Hobza and coworkers suggested the S22 set [73], which contains 22 dimers including benzene dimer and other π-stacked systems (Fig. 5). This S22 benchmark set provides interaction energies of hydrogen-bonded, dispersion-bonded, and mixed complexes, which are the calculated results of the CCSD(T) method at the complete basis set (CBS) limit [74]. Due to its convenience, this benchmark set has been used not only in testing the accuracies of dispersion corrections but also in determining the adjustable parameters of semiempirical dispersion-corrected functionals. Table 1 displays the mean absolute deviations (MAD) of various dispersion-corrected DFT calculations for the S22 benchmark set in the ascending order. This table clearly shows that independent of dispersion corrections combined, LC functionals give better accuracies than those of semiempirical functionals and vdW functionals. In contrast, relatively poor results are given by vdW-DF functionals, which combine pure functionals such as revPBE or the HF exchange integral with a vdW functional. Therefore, this table obviously supports the above suggestion that long-range exchange interactions should be included to reproduce van der Waals bonds. It is interesting to note that some dispersion-corrected DFTs give more accurate results than those of the MP2 method at the CBS limit. In this connection, it is reported that DFT-SAPT (section “Combination with Perturbation Theories”) gives close accuracies at the CBS limit to those of M06-2x and BLYP-D for the S22 set, although it is not listed in this table due to the unrecording of MAD [74]. These accuracies may be taken as poorer-than-expected, because perturbation theories have been believed to give highly accurate dispersion interactions. However, these results are reasonable because the poor interaction energies in MP2 calculations have been found for several π-stacked dimers having near-degenerate orbitals that usually cause instability in perturbation calculations [65].

Table 1 Mean absolute deviations (MAD) of DFT calculations using various types of dispersion corrections for the S22 benchmark set in ascending order (kcal/mol). The MAD of the MP2 method at complete basis set (CBS) limit is also displayed for comparison. For each method, the section giving an explanation in this chapter is appended
Full size table
Fig. 5
figure 5

The S22 benchmark set of weakly bonded systems

Full size image

Carbon Materials: Nanotube and Graphene

Besides benzene and naphthalene dimers, various carbon materials have also attracted attentions in the context of π-stacking interactions. The most frequently targeted systems are nanotube and graphene for their electronic, adsorptive, and reactive properties. So far, many DFT studies have been reported especially for single-walled carbon nanotube (SWCNT) and graphene in the fields of both quantum chemistry and solid state physics.

For SWCNT, some studies focus on the π-stacking-mediated solubility in organic solvent (Fig. 6). SWCNT is a promising multifunctional material to be an efficient gas storage element, a sensor, and a drug-delivery agent. However, it is well known in the field of carbon materials that SWCNT is hardly dissolved in any solvent. This may impose restrictions on industrial or medical use. For solving this problem, many DFT calculations have been performed to suggest organic molecules solvating SWCNT by π-stacking interactions. The π-stacking on SWCNT has been examined with various model systems of SWCNT for the adsorptions of various organic molecules: e.g., planar organic molecules [77], liquid crystal molecules [78], and benzene derivatives [79]. SWCNT has also attracted attentions as gas storage materials [15]. Therefore, DFT studies have also focused on the adsorptions of various small molecules [80]: e.g., hydrogen [81] and methane [82] molecules, on SWCNT. These studies have reported that conventional DFTs provide reasonable interaction energies. However, further investigations are required for approaching to the adsorptive properties of SWCNT, because most conventional calculations have used unreliable dispersion-uncorrected functionals such as pure LDA and GGA functionals for evaluating the dispersion interactions. The adsorptive property of SWCNT is, therefore, still a challenge in DFT calculations.

Fig. 6
figure 6

An example of the π-stacking of single-walled carbon nanotube

Full size image

Graphene is also one of the most frequently studied π-stacking systems in carbon materials because of its high carrier mobility, high thermal and electronic conductivity, and strong material behavior. For graphene, the adsorptive property has been explored in the π-stacking calculations of its model systems such as coronene [83, 84]. Dispersion-corrected DFTs have provided accurate π-stacking interaction energies between these graphene models, if appropriate dispersion corrections are incorporated. Therefore, graphene models are usually used as trial systems for examining dispersion corrections. These calculations have consequently revealed the adsorptive properties of planar polyaromatic systems. For example, π-stacking interaction energies of these systems are found to increase as a function of the number of hydrogen atoms at the edge [84]. Graphene is also theoretically investigated for the adsorption of biomolecules such as DNA in the context of drug delivery, molecule immobilization, and biosensor [85, 86]. As a result, it is suggested that the nucleobases of DNA form weak hydrogen-bond-like interactions with graphene between the pyramidal amino groups of the bases and the π-center of graphene [86]. Graphene is also well known as a semiconductor, which has zero band gap in the electronic state. In association with this unique electronic state, band gap calculations are also performed for the π-stacking of aromatic systems on graphene to develop high performance nanodevices [87]. Since graphene is attractive for its unique electronic properties, we expect that the π-stacking of graphene would be much more investigated from the viewpoint of electronic structure.

Biomolecules: DNA and Proteins

π-Stackings have also been attracted attentions in the field of biological science. Besides π-stacking effects on the structures of DNA and proteins, there are various DFT studies on π-stackings of biomolecules: e.g., DNA-nanotube [88] and DNA-graphene [86] stackings. However, most DFT studies have drawn attentions to the base stackings of DNA and protein foldings in this field.

The base stackings in DNA have been studied using the hydrogen-terminated models of five nucleobases (Fig. 7), i.e. guanine, cytosine, adenine, thymine, and uracil, in DFT calculations. For the base stackings, there is even a benchmark set in JSCH-2005 database [73], which contains hydrogen-bonded DNA base pairs, stacked base pairs, and amino acid pairs besides S22 set mentioned above, for examining the applicabilities of dispersion corrections. However, this benchmark set has been calculated only with DFT-D (section “Semiempirical Dispersion-Corrected Functionals”) [89] in dispersion-corrected DFTs, while this set is frequently calculated using semiempirical molecular orbital theories combined with semiempirical dispersion corrections. This is due to the computational cost needed in the calculation of this set containing 143 complexes. Most dispersion-corrected DFT calculations of DNA focus only on the stackings of five nucleobases. So far, DFT-D [38], vdW-DF (section “Van der Waals (Dispersion) Functionals”) [90], and DFT-SAPT (section “Combination with Perturbation Theories”) [91] have been applied to the base-stacking calculations and consequently have provided accurate interaction energies. For the stacked bases, excited state calculations have also been performed by TDDFT using LC functionals (section “Long-Range Exchange Interactions”) [92, 93]. We see that dispersion-corrected DFT studies of DNA would shift attentions from base-stacking structures to electronic properties.

Fig. 7
figure 7

DNA nucleobases

Full size image

In most dispersion calculations of proteins, folding structures have been discussed with no particular attention to π-stackings. These folding structure calculations are carried out by classical MDs using empirical potentials such as CHARMM [46] and Amber [47]. In these empirical potentials, dispersion interactions are incorporated by London’s classical dispersion energy in Eq. (4) multiplied by an empirical parameter in the Lennard–Jones potential (Fig. 8). Note that exchange interaction is also incorporated as the repulsion term in this potential as supported by the above discussion. Most dispersion-corrected DFT studies of proteins have used hydrogen-terminated small amino acid residues to discuss π-stackings in proteins [49], because DFT calculations are too time consuming to determine the folding structures of proteins. In practice, since protein structures are essentially not so sensitive to the quality of calculation methods, classical potential calculations may be the best way to obtain the structures. However, proteins would be further investigated for the electronic structures in near future at the request of drug discovery field. We, therefore, suppose that dispersion-corrected DFT becomes more important even in the research field of proteins.

Fig. 8
figure 8

The Lennard–Jones potential and empirical potential of argon dimer

Full size image

Supramolecules

Recently, supramolecules become one of the hottest π-stacked systems in DFT calculations. In supramolecules, molecules self-assemble with weak bonds such as hydrogen and van der Waals bonds. We should notice that optimized structures do not always provide enough information to design new materials. Material design often requires the detailed information on electronic properties, which are not given in classical MD calculations. Dispersion-corrected DFTs are best suited to obtaining this information. Fullerene is one of the most frequently used constituent materials in π-stacking supramolecules. In particular, C60 fullerene has been studied for its π-stacking with polycyclic organic molecules to produce supramolecules such as buckycatcher (Fig. 9) [94, 95]. Self-assembled nanowires are also frequently raised systems in DFT calculations. For example, the nanowires of azaadamantanetrione [96] and cyclic oligothiophene [97] have been calculated. Moreover, metal complexes self-assembling to huge structures are noteworthy. That is, many metal complexes coordinating aromatic ring molecules are π-stacked to form huge systems. Dispersion-corrected DFTs are promising even in determining the structures of these metal complexes, because it is hard to optimize the geometries of metal-contained systems in classical MD calculations. Actually, several calculations are recently performed [98]. DFT calculations have also been used for other self-assembled systems to analyze their electronic states. Since most of these calculations have been carried out in recent 5 years, the use of dispersion-corrected DFTs may keep increasing in the calculations of supramolecules.

Fig. 9
figure 9

Buckycatcher

Full size image

Conclusions

π-Stacking is a dispersion interaction between cyclic compounds such as aromatic rings. Since π-stacking often determines the structures of significant large systems such as carbon nanomaterials, biomolecules, and supramolecules, it currently draws attentions in a wide variety of scientific and industrial fields. Although the name “π-stacking” implies the contribution of π orbitals, it is confirmed that π orbitals play no particular role in π-stackings. Namely, π-stacking is nothing but usual dispersion interaction. Dispersion interaction is the only van der Waals interaction that the Kohn–Sham SCF calculation using conventional exchange-correlation functionals cannot reproduce. Therefore, an explicit dispersion correction is required for functionals to investigate π-stackings on the Kohn–Sham SCF calculations.

Various dispersion corrections have, so far, been developed in the field of DFT. Fortunately, these corrections are generally classified into only five categories: classical dispersion corrections, combinations with perturbation theories, linear-response theories, van der Waals (dispersion) functionals, and semiempirical dispersion-corrected functionals. Naturally, these corrections have both advantages and disadvantages as explained in the text. However, due to practical reasons such as computational time and user-friendliness, only van der Waals and semiempirical dispersion-corrected functionals seem to be frequently used in current DFT calculations. What should not be overlooked is the repulsion, which balances with the dispersion attraction in van der Waals bonds. In the Lennard–Jones potential, this repulsion appears as the R  − 12 term, which is interpreted to come from long-range exchange interaction. Note that this long-range exchange interaction is also deficient in conventional functionals.

The significance of the long-range exchange interaction is also numerically shown in the potential energy curves of small π-stacked benzene and naphthalene dimers and the dispersion interaction energies of the S22 benchmark set. As a result of these calculations, long-range corrected (LC) DFTs, in which long-range exchange interactions are complemented to exchange functionals, give the best performance in all dispersion-corrected DFTs. Nevertheless, LC-DFTs have not been applied to significant π-stacked systems that various dispersion-corrected DFTs have been examined: nanotube, graphene, DNA, protein, and supramolecule. However, the use of other dispersion-corrected DFTs is also not so common in the calculations of these systems. Since this is mainly due to the high computational cost required in the calculations, we expect that dispersion-corrected DFTs become one of the main tools for investigating these systems theoretically.