Keywords

1 Introduction

Vibration energy harvesting has become the need of the hour for realizing autonomous systems in fields such as structural health monitoring without relying much on the hazardous and exhaustible batteries. Among all the mechanisms available for harnessing vibration from the environment, piezoelectric energy harvesting is the most sought after one, which is mainly due to its higher power densities [1]. Harvesters based on linear resonance work efficiently only when the excitation frequency is in close proximity to the natural frequency. This makes the linear harvester susceptible to the uncertain variations in the ambient environment. Introducing deliberate nonlinearities into the harvesting system as a means to harvest power over a broadband of frequencies has garnered more attention in the recent times as it aids in overcoming the major shortcoming of the linear harvester [2].

Harvesters with intentional nonlinearities have been reported to display improved bandwidth of power in comparison to the linear harvesters under both deterministic and random excitation (Litak [3] and Friswell [4]). Also, several works in the literature demonstrate the potential of exciting multiple modes of piezoelastic system for broadband performance [5]. Internal resonance can occur in multi-modal nonlinear harvesters when the natural frequencies of the system are commensurable [6]. Energy transfer occurs between the modes under internal resonance, and this phenomenon can be made use of to harvest electrical power over a broad band of frequencies.

Geometrically, nonlinear beams are commonly idealized as cubic oscillators with symmetric potential wells. For such oscillators, significant energy transfer between the modes is found to occur when their corresponding natural frequencies are tuned to the ratio of 1:3 [6]. The dynamics of such systems boast modulated responses in the vicinity of the primary resonances [7]. The experimental work carried out by Guillot et al. [8] on a piezoelectric system with 1:3 internal resonance under harmonic excitation demonstrated the possibility of using internal resonance toward broadband energy harvesting.

The motivation of carrying out this work comes from the prospect of utilizing large responses of 1:3 resonant systems near the fundamental resonance for wideband power extraction. To this end, studies are carried out in the present work to characterize the performance of a piezoelectric harvester with 1:3 internal resonance under harmonic excitation.

2 Harvester Model

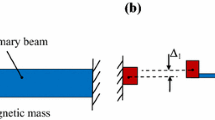
The schematic representation of the harvester is shown in Fig. 1. An inverted cantilever beam of length L b constitutes the harvester system. The material properties, namely the density and the modulus of elasticity of the beam, are represented by ρ b and E b, respectively. The width and thickness of the beam are correspondingly taken to be b b and d b. A concentrated mass M t with a corresponding mass moment of inertia I t is lumped at a distance L t from the fixed end of the beam. Piezoelectric patches of length L p, width b p, and thickness d p are attached onto both faces of the beam. The cross-sectional area as well as the second moment area of the beam and piezoelectric patch are denoted as [A b, A p] and [I b, I p], respectively. The geometrical and electrical properties of the piezoelectric patches considered in the study are taken from [9]. The damping ratios of the first two modes are represented by ξ 1 and ξ 2, respectively. The harvester system is set to steady-state motion by a harmonic base displacement of the form z = z 0 cos(Ωt).

Fig. 1
figure 1

Schematic representation of the harvesting system

Full size image

Let u p and v p be the vertical and horizontal displacements of any given point P at a distance s from the fixed end along the neutral axis of the beam as shown in Fig. 1. In addition to these displacements, the cross-section of the beam also undergoes rotation at point P that is denoted by ϕ p the corresponding curvature of which is represented as κ p. Assuming the beam to be inextensible, ϕ p, κ p, and u p can be expressed in terms of v p as given in [4]. This chapter employs Galerkin discretization to obtain an approximate solution for the horizontal displacement at any point, v p along the beam that is given by

$$\displaystyle \begin{aligned} v_p(s,t) = \sum_{h=1}^{N} q_h(t)\bigg[\varPhi_{h}^c (s)H_c(s)+\varPhi_{h}^b (s)H_b(s)\bigg], {} \end{aligned} $$
(1)

where \(\varPhi _{h}^c(s)\) and \(\varPhi _{h}^b(s)\) are the cantilever beam modes of the piezoelectric and non-piezoelectric domains of the harvester, respectively. N corresponds to the total number of modes considered for the analysis. q h(t) denotes the generalized coordinate of the h th mode. H c(s) and H b(s) correspond to the piezoelectric and non-piezoelectric regions.

Using the expressions given in [4] for the kinetic as well as potential energies and the work done by harvester in extracting electrical power, the following governing mechanical equation can be obtained.

$$\displaystyle \begin{aligned} &\alpha_{hh}\ddot{q}_h+c_h\dot{q}_h+\gamma_{hh}q_h+ \sum_{i,j,k,l=1}^{N}\beta_{hjkl}\bigg(q_kq_l\ddot{q}_l+ q_j\dot{q}_k\dot{q}_l\bigg)+\bigg(\lambda_{ijhl}q_iq_l+\lambda_{hjkl}q_kq_l\bigg)q_j \notag\\ &\quad -\varTheta_{1,h}V -\frac{1}{2}\sum_{i,j,k=1}^{N}\bigg(\varTheta_{2,hjk}q_jq_k+2\varTheta_{2,ijh}q_iq_j\bigg)V=\varPsi_h\ddot{z}\qquad h=1,2,...,N, {} \end{aligned} $$
(2)

where

$$\displaystyle \begin{aligned} \alpha_{hj}&=\rho_c A_c \varDelta_{hj}^c+\rho_b A_b \varDelta_{hj}^b+M_t\psi_{hj}+I_t N_{hj} \end{aligned} $$
(3a)
$$\displaystyle \begin{aligned} \gamma_{hj}&=E_bI_c\mu_{hj}^c+E_bI_b\mu_{hj}^b-\rho_cA_cg\varGamma_{hj}^c-\rho_b A_b g \varGamma_{hj}^b-M_t g \chi_{hj} \end{aligned} $$
(3b)
$$\displaystyle \begin{aligned} \beta_{hjkl}&=\rho_cA_c\varLambda_{hjkl}^c+\rho_b A_b\varLambda_{hjkl}^b+M_t \sigma_{hjkl}+I_t \varXi_{hjkl} \end{aligned} $$
(3c)
$$\displaystyle \begin{aligned} \lambda_{hjkl}&=E_bI_c\eta_{hjkl}^c+E_bI_b \eta_{hjkl}^b \end{aligned} $$
(3d)
$$\displaystyle \begin{aligned} \varPsi_h&=-(\rho_cA_c\upsilon_h^c+\rho_b A_b\upsilon_h^b+M_t\tau_h). \end{aligned} $$
(3e)

The constants in Eq. (3) are functions of the mode shapes integrated from 0 to L b. For the definition of constants in Eq. (3), the reader can refer to [10]. The harvester takes the monostable configuration if M t < M tb and bistable configuration if M t > M tb where M tb is the buckling mass. In this chapter, studies are carried out to probe the behavior of monostable harvester in the presence of internal resonance.

Similarly, the governing differential equation of the electrical front of the harvester is obtained to be

$$\displaystyle \begin{aligned} C_p \dot{V} + \frac{V}{R_L} + \sum_{i=1}^{N}\varTheta_{1,i}\dot{q}_i + \frac{1}{2}\sum_{i,j,k=1}^{N}\varTheta_{2,ijk}\bigg(2q_i\dot{q}_jq_k +\dot{q}_iq_jq_k\bigg) = 0, {} \end{aligned} $$
(4)

where Θ 1 and Θ 2 are the electromechanical coupling coefficients obtained as a function of the mode shape of the piezoelectric patch. R L is the load resistance.

3 Approximate Solutions Using Perturbation Approach

In order to understand the performance of the harvester near its fundamental resonance, the system Eqs. (2) and (4) with weak nonlinearities (β hjkl → 𝜖β hjkl, λ hjkl → 𝜖λ hjkl) and damping (c h → 𝜖c h) under soft excitation (z → 𝜖z) is analyzed where 𝜖 is a perturbation constant that is very small.

Solutions for q and V  are assumed to be of the following asymptotic form [6]:

$$\displaystyle \begin{aligned} q_{h}(t;\epsilon)=q_{h_0}(T_0,T_1)+\epsilon q_{h_1}(T_0,T_1)+O(\epsilon^2) \end{aligned} $$
(5a)
$$\displaystyle \begin{aligned} V(t;\epsilon)=V_{0}(T_0,T_1)+\epsilon V_{1}(T_0,T_1)+O(\epsilon^2), \end{aligned} $$
(5b)

where T 0 = t, T 1 = 𝜖t are the time scales used in the present work. The temporal derivatives in the governing equations can be written in terms of T 0 and T 1 as

$$\displaystyle \begin{aligned} \frac{d}{dt}=D_0+\epsilon D_1+O(\epsilon^2);~ \frac{d^2}{dt^2}=D_0^2+2\epsilon D_0 D_1+O(\epsilon^2), \end{aligned} $$
(6)

where \(D_0=\frac {\partial }{\partial T_0};~ D_1=\frac {\partial }{\partial T_1}\).

The zeroth-order solution of q h is given by

$$\displaystyle \begin{aligned} q_{h_0}=C_h(T_1)e^{\mbox{i}\omega_hT_0}+{C_h}^*(T_1)e^{-\mbox{i}\omega_hT_0}. {} \end{aligned} $$
(7)

The two terms in the above solution represent the complex conjugate pair, where C h is the complex amplitude to be found out and its complex conjugate term is represented by (∗) in the superscript. Using \(q_{h_0}\), the zeroth-order solution of the generated voltage, V 0, can be obtained as

$$\displaystyle \begin{aligned} V_0={{\tilde{{{V}}}}}_0+{{{\tilde{{{V}}}}}_0}^*. {} \end{aligned} $$
(8)

The term \(\tilde {V_0}\) in Eq. (8) is obtained to be

$$\displaystyle \begin{aligned} {{\tilde{{{V}}}}}_0= \sum_{i=1}^{N} R_i \varTheta_{1,i}C_ie^{\mathrm{i}\omega_iT_0}, {} \end{aligned} $$
(9)

where \(R_i=-\alpha _{ii}\frac {\bigg (\omega _i^2C_pR_L^2+\mathrm {i}\omega _iR_L\bigg )}{1+\omega _i^2C_p^2R_L^2}\).

This chapter only considers the first two primary modes commensurable with a ratio of 1:3. To denote the proximity of ω 2 to 3ω 1 and Ω to ω 1, the following terms are defined.

$$\displaystyle \begin{aligned} \omega_2=3\omega_1+\epsilon\sigma_0,\quad \varOmega=\omega_{1}+\epsilon\sigma_1, {} \end{aligned} $$
(10)

where σ 0 and σ 1 are the internal detuning parameters. Making use of the above relation, the O(𝜖) term of the excitation force is given by

$$\displaystyle \begin{aligned} O(\epsilon):\psi_h\ddot{z}=-\omega_h^2z_0\psi_h\cos{}(\omega_{1}T_0+\sigma_1T_1). {} \end{aligned} $$
(11)

Eliminating the secular terms of O(𝜖) to zero and setting the temporal derivatives with respect to T 1 to zero, the following stationary equations for amplitudes and phases when Ω ≈ ω 1 are obtained.

$$\displaystyle \begin{aligned} &8\omega_1 a_1(\sigma_1)+4\mathrm{Re}(Z_1)a_1+\big[\mathrm{Re}(W_{12})\cos\eta_1-\mathrm{Im}(W_{12})\sin\eta_1\big]a_1^2a_2+a_1\sum_{i=1}^{2}\mathrm{Re}(W_{ii})a_i^2\notag\\ &\quad =-4{\psi}_{1}\omega_1^2z_0\cos\eta_2 {} \end{aligned} $$
(12)
$$\displaystyle \begin{aligned} &4\mathrm{Im}(Z_1)a_1+\big[\mathrm{Im}(W_{12})\cos\eta_1+\mathrm{Re}(W_{12})\sin\eta_1\big]a_1^2a_2+a_1\sum_{i=1}^{2}\mathrm{Im}(W_{ii})a_i^2\notag\\ &\quad =4\psi_{1}\omega_1^2z_0\sin\eta_2 {} \end{aligned} $$
(13)
$$\displaystyle \begin{aligned} &8\omega_2a_2\big(3\sigma_1-\sigma_0\big)+4\mathrm{Re}(Z_2)a_2+\big[\mathrm{Re}(P_{21})\cos\eta_1+\mathrm{Im}(P_{21})\sin\eta_1\big]a_1^3\notag\\ &\quad +a_2\sum_{i=1}^{2}\mathrm{Re}(P_{ii})a_i^2=0 {} \end{aligned} $$
(14)
$$\displaystyle \begin{aligned} 4\mathrm{Im}(Z_2)a_2+\big[\mathrm{Im}(P_{21})\cos\eta_1-\mathrm{Re}(P_{21})\sin\eta_1\big]a_1^3+a_2\sum_{i=1}^{2}\mathrm{Im}(P_{ii})a_i^2=0, {} \end{aligned} $$
(15)

where a 1 and a 2 are the modal amplitudes. η 1 = φ 2 + σ 0 T 1 − 3φ 1 and η 2 = σ 1 T 1 − φ 1 are the phase shifts of the second modal response and excitation frequency with respect to the first modal response, respectively.

To obtain the steady-state solutions of the amplitudes and phases, the terms \(\dot {a_i}\) and \(\dot {\varphi _i}\) are set to be equal to 0 in Eqs. (12)–(15).

The harvested power, P, is given by

$$\displaystyle \begin{aligned} P=\frac{|V_0|{}^2}{R_L}, \end{aligned} $$
(16)

where the expression for V 0 is given in Eq. (8).

4 Results and Discussion

Table 1 provides the values of the parameters for which the numerical simulations are carried out in this work. The value of 𝜖 is taken to be 0.01 in this chapter. The lumped mass, M t, is varied to realize 1:3 internal resonance in the harvesting system. The critical value of lumped mass (M cr=19.1 g) corresponds to the value at which commensurability of the natural frequencies is realized. The first two natural frequencies pertaining to M cr are 16.51 rad/s and 49.52 rad/s, respectively. The internal detuning parameter, σ 0, is negative for M t > M cr and positive for M t < M cr. Stable and unstable branches of the stationary solutions are represented by solid and dashed lines, respectively. Solid dot markers and black colored asterisk in the responses represent the Hopf (HP) and Saddle-Node (SN) points, respectively.

Table 1 Description of parameters used in the model
Full size table

The frequency responses of first two modal amplitudes (a 1, a 2) and harvested power, P, for σ 0 = 0 under different excitation amplitudes are shown in Fig. 2. Despite a 2 taking a non-zero value, the frequency response of a 1 resembles a single-mode response for an excitation amplitude (z 0) of 2 mm. Loops emerge in the frequency response of a 2 indicating the existence of internal resonance in the system [6]. The amplitude of the loop-like branch increases considerably with increase in z 0, which can be observed from Fig. 2b. This gives rise to an additional coexistent stable branch in the power curve (2.4 ≤ σ 1 ≤ 3.2 for z 0 = 15 mm). The influence of higher mode response on the harvested power can be perceived from the observation that the magnitude of harvested power due to loop-like branch (P ≈ 2.5 mW) is of the same order as that of the primary hardening branch (P ≈ 5 mW) in the range of σ 1 considered for this chapter as can be seen from Fig. 2c.

Fig. 2
figure 2

Frequency response curves of modal amplitudes and harvested power when Ω ≈ ω 1, σ 0 = 0, R L = 1 MΩ. Violet and green lines correspond to z 0 = 2 mm and 15 mm, respectively

Full size image

For z 0 = 15 mm, the time histories and frequency spectra obtained using fast Fourier transform (FFT) plots of voltage corresponding to σ 0 = 0, R L = 1 MΩ at two different values of σ 1 (1.8, 2.5) are shown in Fig. 3. Two frequencies dominate the responses, and expectedly, those frequencies pertain to first (f 1 = 2π∕ω 1) and second (f 2 = 3f 1 = 2π∕ω 2) natural frequencies of the system. The predominant contribution to the voltage from the first modal response, a 1, is clearly evident for the case of σ 1 = 2.5, which could be observed from the FFT plot given in Fig. 3a. The significant energy transfer between the modes can be observed when σ 1 = 2.5 where the voltage generation due to loop-like branch surpasses that of a 1 although Ω ≈ ω 1 as can be observed from the time history in Fig. 3b.

Fig. 3
figure 3

Frequency spectra and time histories of generated voltage, V , for z 0 = 15 mm, R L = 1 MΩ, σ 0 = 0. Black and blue lines denote responses at σ 1 = 1.8 and σ 1 = 2.5, respectively

Full size image

The variation of harvested power with detuning parameter, σ 0, is shown in Fig. 4. For σ 0 = −10, the frequency response of P boasts a loop-like branch existing over a broader frequency range (0.45 ≤ σ 1 ≤ 4.1) with an appreciable magnitude of power as compared to other coexisting stable branches. The magnitude of power decreases tremendously when σ 0 is not very close to 0. This inference is well supported by the observation of the absence of loop-like branches when σ 0 = −20. Thus, the stable branch yielding higher power output can be realized by the appropriate tuning of internal detuning parameter (σ 0).

Fig. 4
figure 4

Variation of the harvested power with σ 0 when for R L = 1 MΩ and z 0 = 15 mm. Gray and orange lines denote the responses for σ 0 = −10 and σ 0 = −20, respectively

Full size image

To understand the feasibility of activating higher power yielding branches, basins of attraction are studied when σ 0 = −10 and z 0 = 15 mm, which are presented in Fig. 5. The power outputs of 2.35 mW,1.12 mW, and 32 μW are represented by yellow, cyan, and violet basins, respectively, as shown in Fig. 5a. Similarly, violet and yellow basins in Fig. 5b denote the power outputs of 20 μW and 4.28 mW, respectively. The complex loop response is realized at σ 1 = 3 only if the initial values of a 2 are significantly large for values of a 1 belonging to the range 3.6e-3≤ a 1 ≤ 7.7e-3. Yellow basin is preferred for a small set of initial conditions when σ 1 = 6 where a 1 is markedly larger than a 2. Figure 5b demonstrates that the magnitude of power is significantly low for low values of a 1. Hence, the harvesting efficiency in the required frequency band can be improved by operating the harvester with externally perturbed initial conditions.

Fig. 5
figure 5

Basins of attraction of harvested power for z 0 = 15 mm and σ 0 = −10 at (a) σ 1 = 3, (b) σ 1 = 6

Full size image

The role of excitation amplitude on influencing the energy transfer between the modes, and consequently, the harvested power is shown in Fig. 6 when σ 1 = 1.8. A monotonic increase in the magnitude of harvested power is observed when σ 0 = 0 with an increase in z 0. In contrast to the above, three stable branches coexist in the range 6.4 ≤ z 0 ≤ 19.5 when σ 0 = −10. The magnitude of power harvested can be increased notably by activating higher stable branch in the above specified amplitude range through suitable initial conditions. Saturation in the magnitude of power can be observed beyond a particular value of z 0 as seen in Fig. 6.

Fig. 6
figure 6

Effect of excitation amplitude on harvested power at σ 1 = 1.8. Green and gray lines correspond to the responses when σ 0 = 0 and σ 0 = −10

Full size image

5 Conclusions

This chapter studies the role of 1:3 internal resonance toward broadband piezoelectric energy harvesting. The method of multiple scales is employed to obtain the asymptotic solutions of the governing equations in the neighborhood of fundamental resonance. Results presented in this chapter show that the higher mode positively influences the magnitude and bandwidth of power generation near the fundamental resonance. The work also reports the effect of suitable tuning of the lumped mass in amplifying the energy transfer between the modes that in turn enhances the power output. The outcomes of the present study demonstrate that the performance of piezoelectric harvester can be significantly improved by realizing 1:3 internal resonance between the first two modes.