1 Introduction

Harvesting surrounding waste kinetic energy to run low-powered electronics has emerged as a prominent research area and continues to grow at a rapid pace. As a promising approach, piezoelectricity has been used to convert ambient vibrations into useful electrical energy. There are several excellent and comprehensive survey monographs and papers, notably Elvin and Erturk [1], Erturk and Inman [2], Tang et al. [3], Zhu et al. [4], reviewing the state of the art in different time phases of investigations related to piezoelectric energy harvesting.

Vibration-based energy harvesters are generally based on the principle of resonance. Therefore, the energy harvesters operate only for surrounding vibrations with their frequencies in a small range. However, in many practical circumstances, the ambient vibrations are frequency-varying or random with a wide or narrow frequency spectrum. Hence, it is a challenging problem to increase the working frequency range of vibration-based energy harvesters. In previous works, nonlinearity enhances vibration-based energy harvesting by producing softening or hardening stiffness effects as well as bistable systems. Challa et al. [5] investigated a vibration energy harvester of bidirectional resonance frequency with a magnetic force tuning technique. Erturk et al. [6] investigated numerically and experimentally the response to harmonic excitations and found that the bistable energy harvester produced consistently the larger output power than the linear counterpart, except the excitation frequency near the natural frequency of the linear energy harvester. Mann and Sims [7] proposed a novel energy harvesting using magnetic levitation to produce electricity, derived the approximate analytical expressions of the frequency–amplitude curves for the steady-state responses via the multiple scales method, and validated the response amplitudes with experiments. Stanton et al. [8] applied the method of harmonic balance to characterize quantitatively the beam and electrical network oscillation amplitudes and validated the response amplitudes of numerical simulations predicated by experiments. Liu and Yuan [9] presented a nonlinear magnetic levitation energy harvester that uses diamagnetism and obtained a harvester that can potentially be preferred in the low frequency range. Hajati and Kim [10] employed an ultra-wide bandwidth piezoelectric energy harvesting to exploit nonlinear stiffness. Stanton et al. [11] investigated the response of harvesting energy as a nonlinear oscillator and demonstrated that the bistability may be used to improve energy harvesting. Zhu and Zu [12] presented a buckled-beam piezoelectric energy harvester that uses a midpoint magnetic force to improve the efficiency of output voltage. Zhao et al. [13] reported numerical and experimental investigations of a bistable piezomagnetoelastic energy harvester using rotatable magnets. Arrieta et al. [14] proposed a novel piezoelectric energy harvester of bistable plate and studied the output voltage and power by experiments.

Despite the success of the deterministic approach, randomness, inherent in most real-world circumstances, may significantly change the behavior of vibration-based energy harvesters. There is some research into stochastic approaches. Cottone et al. [15] found numerically and experimentally that nonlinear oscillators can outperform linear ones under stochastic excitation. Gammaitoni et al. [16] revealed that nonlinear oscillators can outperform linear ones under noise excitation in monostable configurations. Litak et al. [17] calculated the response of a nonlinear piezomagnetoelastic energy harvester under stationary Gaussian white noise. Blarigan et al. [18] reported an energy harvesting device to enhance output voltage, and validated the output power via experiments. Daqaq [19] demonstrated that a monostable Duffing oscillator does not provide any enhancement over the typical linear oscillators under white Gaussian and colored excitations. Wickenheiser and Garcia [20] designed a cantilevered energy harvester using magnetic tip mass, and demonstrated multiple-order-of-magnitude power harvesting performance improvement at low frequencies by numerical simulations. Khovanova and Khovanov [21] investigated numerically the output power under Poisson white noise excitations and found the bistable energy harvester producing consistently the larger output power than the linear system. Daqaq [22] derived an approximate expression for the mean power under exponentially correlated noise and demonstrated the existence of an optimal potential shape maximizing the output power. Green et al. [23] reported that Duffing-type nonlinearities can reduce the size of energy harvesting devices without affecting their power output, and verified the result using the technique of equivalent linearisation.

The resonance referred in all available investigations on energy harvesters is external resonance. In multi-degree-of-freedom nonlinear vibrations, internal resonance may occur if the linearized frequencies are commensurable or nearly commensurable. Internal resonance leads to modal interactions, an energy exchange, or a coupling among the modes [24]. In conservative systems, internal resonance results in the formation of a dense set of resonance layers that destroy KAM surface so that stochastic layers are no longer isolated [25]. Therefore, internal resonance plays a crucial role in dynamics of a vibrating system. Internal resonance has been employed in some applications, such as prediction of instability in non-neutral plasmas [26], reduction of transition cost in near-integrable Hamiltonian systems [27], nonlinear vibration absorbers [28], coupling between different modes in atomic force microscopy [29], and improvement of sensing in non-contact atomic force microscopy [30]. However, the effects of internal resonance on energy harvesting have never been investigated. In the following, internal resonance will be proposed as a mechanism to enhance energy harvesting. The methodology is demonstrated via a conceptual design of an internal resonance energy harvester.

The paper is organized as follows. Section 2 presents the design schematic of an energy harvester based on internal resonance. Section 3 calculates the output voltages under various random vibrations via numerical simulations. Section 4 ends the paper with concluding remarks.

2 A design of an energy harvester based on internal resonance

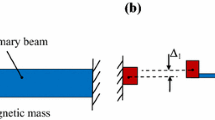
Figure 1 depicts schematically a two-degrees-of-freedom (2-DOF) mechanical model of a single modal piezoelectric energy harvester. Two masses with relative displacement, \(x_{1}\) and \(x_{2}\), measured from its static equilibrium positions are connected by a spring with stiffness \(k_{2}\) and a viscous damping with coefficient \(c_{2}\). Mass \(m_{1}\) is also connected to the vibrating enclosure by a spring with stiffness \(k_{1}\) and a viscous damping with coefficient \(c_{1}\). There are three magnets, two fixed to the enclosure and one attached to mass \(m_{1}\), and their action directions are shown in Fig. 1. The piezoelectric part, resulting in voltage output \(\upsilon \), is represented by the piezoelectric leakage resistance \(R_{\mathrm{l}}\), capacitance \(C\), and electromechanical coupling coefficient \(\theta \). The system is essentially a conventional piezoelectric energy harvester subjected to nonlinear magnetic actions and attached to an additional linear mass-spring-damper oscillator. In the following, the design of the additional system will be explored.

Fig. 1
figure 1

Schematic of the two-degrees-of-freedom model of an energy harvester

Full size image

The mass \(m_{1}\) with a magnet moves in the field of two magnets fixed on the vibrating frame. The nonlinear action between magnets can be described by \(f_{\mathrm{m}}=ax_{1}+bx_{1}^{3}\) [7, 11]. Then the dynamic equation of the system shown in Fig. 1 is

$$\begin{aligned}&m_1 \ddot{x}_1 +\left( {c_1 +c_2 } \right) \dot{x}_1 -c_2 \dot{x}_2 +\left( {k_1 +k_2 +a} \right) x_1 \nonumber \\&\quad -k_2 x_2 +bx_1^3 -\theta \upsilon (t)= m_1 f\left( t \right) , \end{aligned}$$
(1)
$$\begin{aligned}&m_2 \ddot{x}_2 -c_2 \dot{x}_1 +c_2 \dot{x}_2 +k_2 x_2 -k_2 x_1 =m_2 f(t), \end{aligned}$$
(2)
$$\begin{aligned}&R_\mathrm{l} C\dot{\upsilon }(t)+\upsilon (t)+\theta R_\mathrm{l} \dot{x}_1 =0, \end{aligned}$$
(3)

where \(f\left( t \right) =-\ddot{x}_b \). It should be recognized that, in short-circuit conditions, Eqs. (1) and (2) define a two-degrees-of-freedom oscillator with a cubic nonlinear term. Neglecting the nonlinear term and exciting terms in Eqs. (1)–(3), one derives the system frequency equation as

$$\begin{aligned} a_0 \lambda ^{5}+a_1 \lambda ^{4}+a_2 \lambda ^{3}+a_3 \lambda ^{2}+a_4 \lambda +a_5 =0, \end{aligned}$$
(4)

where \(a_0 =R_\mathrm{l} Cm_1 m_2\), \(a_1 =R_\mathrm{l} C[m_1 c_2 +m_2 (c_1 +c_2 )]+m_1 m_2\), \(a_2 =R_\mathrm{l} C[m_1 k_2 +m_2 (k_1 +a+k_2 )+c_2 c_1 ] +m_1 c_2 +m_2 (c_1 +c_2 +R_\mathrm{l} \theta ^{2})\), \(a_3 =R_\mathrm{l} C[k_2 c_1 +(k_1 +a)c_2 ]+(c_1 +R_\mathrm{l} \theta ^{2})c_2 +m_1 k_2 +m_2 (k_1 +a+k_2 )\), \(a_4 =R_\mathrm{l} C[(k_1 +a)k_2 ]+(c_1 +R_\mathrm{l} \theta ^{2})k_2 +(k_1 +a)c_2\), and \(a_5 =(k_1 +a)k_2 \). Equation (5) has five roots, a negative real root, and two pairs of conjugate complex roots with negative real parts. The two imaginary parts of the conjugate complex roots are the natural frequencies that are denoted as \(\omega _1\) and \(\omega _2\,(\omega _1 <\omega _2 )\). In cubic nonlinear system defined by Eqs. (1)–(3), if \(\omega _2 =3\omega _1 \), there will be the internal resonance. It should be noted that the internal resonance addressed here is in the coupled system consisting of not only the mechanical part, but also the electric part.

3 Energy harvested from various random vibrations

To highlight the advantage of the internal resonance, the averaged root-mean-square voltage \(V_{\mathrm{rms}} =\sqrt{E[\upsilon ^{2}]-(E[\upsilon ])^{2}}\) is calculated for different designs under various types of random excitations. The following investigations focus on five designs, three sets of 2-DOF systems and two sets of 1-DOF systems. Let \(m_{1}=1.0, \,m_{2}=0.2,\, k_{1}=1.0,\,c_{1}=0.01,\,c_{2}=0.005,\,a=1.0,\,b=0.5,\, \theta =0.05,\,R_{\mathrm{l}}=200\), and \(C=0.1\). Vary \(k_{2}\) to tune the internal resonance. The 1:3 internal resonance occurs for \(k_{2}=2.403\) with \(\omega _{1}=1.2822, \,\omega _{2}=3.8469\). In the other two designs, \(\omega _{1}:\omega _{2}\) is away from any integers. For \(\omega _{2}\) is smaller than \(3\omega _{1}\), choose \(k_{2}=0.65\) with \(\omega _{1}=1.2169,\,\omega _{2}=2.1080\) and \(\omega _1 :\omega _2 \approx 1:\sqrt{3}\). For \(\omega _{2}\) is larger than \(3\omega _{1}\), choose \(k_{2}=4.098\) with \(\omega _{1}=1.2896,\,\omega _{2}=4.9950\) and \(\omega _1 :\omega _2 \approx 1:\sqrt{15}\). Removal of the additional mass-spring-damper system attached to mass \(m_{1}\) (set \(m_{2}=0,\,k_{2}=0\), and \(c_{2}=0\)) leads to a 1-DOF system with mass \(m_{1}\) and only one undamped linearized frequency \(\omega _{1}=1.4230\). Fixing mass \(m_{2}\) on mass \(m_{1}\) (mathematically set \(k_2 \rightarrow \infty \) and \(c_{2}=0\)) yields another 1-DOF system with mass \(m_{1}+ m_{2}\) and undamped linearized frequency \(\omega _{1}=1.2990\). In the calculations, initial conditions are set at the stable equilibrium positions, namely, \(x(0)=0,\dot{x}(0)=0,\upsilon (0)=0\). Equations (1)–(3) are integrated via the fourth order Runge–Kutta algorithm [31] for stochastic ordinary differential equations.

In the first case, random excitation \(f(t)\) is the Gaussian white noise [17, 22] with standard deviation \(\sigma _f\). Figure 2 shows the averaged root-mean-square output voltage varying with the standard deviation. It can be found that the internal resonance leads to the largest output voltage except \(\sigma _f\) near 0.14 and 0.20.

Fig. 2
figure 2

The averaged root-mean-square output voltage versus the standard deviation of Gaussian white noise for several designs

Full size image

In the second case, random excitation \(f(t)\) is the colored noise defined by a second-order filter [19, 32]

$$\begin{aligned} \ddot{f}+\beta \dot{f}+\varOmega ^{2}f=\varOmega \sqrt{\beta }\xi \left( t \right) , \end{aligned}$$
(5)

where \(\varOmega \) is the center frequency, \(\beta \) is the bandwidth, \(\xi (t)\) is the Gaussian white noise with zero mean and a specified variance. As a leading factor, the center frequency changes significantly the averaged root-mean-square output voltage, and the changing trend is shown in Fig. 3 with \(\sigma _\xi =0.12\) and \(\beta =0.5\). For different designs, the linearized frequency varies between 1.2169 and 1.4230. As shown in Fig. 3, the output voltage produced by the internal resonance design is larger than that of other designs near the first (external) resonance for \(1.0<\varOmega <2.0\), and the advantage preserves beyond the second (external) resonance until \(\varOmega =4.5\). For any given \(V_{\mathrm{rms}}\) larger enough (for example \(V_{\mathrm{rms}}>0.2\)), the internal resonance yields the largest center frequency bandwidth on which the output voltage is larger than the given value. With \(\varOmega =2.0\) and \(\beta =0.5\), Fig. 4 shows the output voltage for the changing intensity of the colored noise, measured by the standard deviation of the excitation \(\xi (t)\) in Eq. (5). The results demonstrate that the internal resonance leads to largest output voltage except a small deviation range [0.005, 0.007]. The bandwidth of the colored noise is also an influential factor. Its effects on the output voltage are shown in Fig. 5. Except a small bandwidth range between 0.20 and 0.35, the internal resonance produces largest output voltage, and this advantage is especially significant for the bandwidth between 0.75 and 0.95.

Fig. 3
figure 3

The averaged root-mean-square output voltage versus the center frequency of colored noise (5) for several designs

Full size image
Fig. 4
figure 4

The averaged root-mean-square output voltage versus the intensity of colored noise (5) for several designs

Full size image
Fig. 5
figure 5

The averaged root-mean-square output voltage versus the bandwidth of colored noise (5) for several designs

Full size image

In the third case, random excitation \(f(t)\) is the narrow-band noise in the form [33]

$$\begin{aligned} f(t)=A\cos \left( {\varOmega t+\rho W\left( t \right) } \right) , \end{aligned}$$
(6)

where \(A>0\) is a deterministic amplitude, \(\varOmega \) is the center frequency, \(\rho \) is the frequency bandwidth, \(W (t)\) is a standard Wiener process satisfying \(\dot{W}(t)=\xi (t)\), and \(\xi (t)\) is the Gaussian white noise with zero mean and a specified variance. Figure 6 highlights the effect of center frequency \(\varOmega \) on averaged root-mean-square output voltage \(V_{\mathrm{rms}}\) for five different designs with \(\rho =0.18\) and \(A=0.8\). The internal resonance design possesses the largest frequency range on which the external resonance occurs, and the range covers the external resonance bandwidths of both the two sets of single-degree-of-freedom designs and the two other sets of two-degree-of-freedom designs without internal resonance. In addition, for the varying center frequency, the internal resonance yields the largest output voltage with a few exceptions. Figure 7 plots averaged root-mean-square output voltage \(V_{\mathrm{rms}}\) varying with frequency bandwidth \(\rho \) for five different designs with \(\varOmega =2\) and \(A=0.8\). The voltage produced by the internal resonance design is larger than that by other designs for most frequency bandwidth.

Fig. 6
figure 6

The averaged root-mean-square output voltage versus the center frequency of narrow-band colored noise (6) for several designs

Full size image
Fig. 7
figure 7

The averaged root-mean-square output voltage versus the frequency bandwidth of narrow-band colored noise (6) for several designs

Full size image

In the last case, random excitation \(f(t)\) is the exponentially correlated noise defined by the Ornstein–Uhlenbeck equation [22]

$$\begin{aligned} \dot{f}+\gamma f=\xi (t), \end{aligned}$$
(7)

where \(\gamma \) is the bandwidth of the noise, and \(\xi (t)\) is Gaussian white noise with zero mean and a specified correlation function. The intensity of the excitation is indicated by the standard deviation of \(\xi (t)\). The effect of excitation intensity \(\sigma _\xi \) on averaged root-mean-square output voltage \(V_{\mathrm{rms}}\) for five different designs is shown in Fig. 8 with \(\gamma =0.5\). The internal resonance design produces the largest voltage except the case of the very small excitation intensity. Fixed \(\sigma _\xi =0.2\), The internal resonance design still produces the largest voltage for varying bandwidth \(\gamma \), as shown in Fig. 9.

Fig. 8
figure 8

The averaged root-mean-square output voltage versus the intensity of exponentially correlated noise for several designs

Full size image
Fig. 9
figure 9

The averaged root-mean-square output voltage versus the bandwidth of exponentially correlated noise for several designs

Full size image

The above simulations reveal that the internal resonance increases the operating bandwidth and the output voltage for different types of random excitations. Further calculations can be performed for other types of colored noises [34–37]. Internal resonance has a main merit over the considerations on external resonance. It can be achieved through choosing suitable parameters and is independent of any external excitation. The proposed methodology can works on other occasions. For example, the magnetic oscillator in Ref. [38] may be designed at internal resonance. Besides piezoelectric energy harvesters, magnetic levitation energy harvesters [7, 8] may be attached to a mass-spring-damper oscillators designed via the proposed methodology.

4 Conclusions

In summary, this paper proposes a new possibility to enhance energy harvesting by tuning harvesters at their internal resonance. A prototype of an internal resonance energy harvester is conceptually designed. The output voltages are calculated under the Gaussian white noise, the colored noise defined by a second-order filter, the narrow-band noise, and exponentially correlated noise. Numerical experiments demonstrate the superiority of internal resonance design over other designs.