Keywords

1 Introduction

Vortex-induced vibration (VIV) is a nonlinear resonant fluid–structure interaction phenomenon due to the synchronization of vortex shedding frequency with one of the natural frequencies of the structure. In engineering projects, VIV is usually studied as a problem to be mitigated, as it is a factor of great impact in fatigue analysis. Nevertheless, this phenomenon may be approached from a different perspective, within the context of energy harvesting. In this case, the objective is a controlled amplification of the response, to be used for obtaining electric energy. As an example, [1] present the concept of VIVACE (Vortex-Induced Vibration Aquatic Clean Energy), a device based on a series of cylinders in tandem arrangement that uses electromagnetic transducers to convert structural kinetic energy into electricity.

Many of the classical studies of VIV phenomena concern rigid cylinders mounted on an elastic base. However, from the low-power-energy-harvesting perspective, the phenomenon on flexible cylinders with orthotropic bending stiffness may be considered an interesting endeavor, since VIV leads to self-excited and self-limited oscillations and, in this particular case, higher amplitudes are maintained for a broad band of frequencies. First observed in [2] and later confirmed in [3], experiments with flexible cylinders with larger stiffness in the in-line direction compared to the cross-flow ones showed a new branch of response, called by the authors high-speed mode. This new branch observed is stable and extends, with high-frequency response, to large incoming flow velocities. The in-line and cross-wise amplitudes obtained in this study for the first two bending vibration modes of a cantilever of frequency ratio 4:1 are shown in Fig. 1, represented by their dominant intrinsic mode function (IMF); see [4] for the definition of an IMF within the empirical mode decomposition and [5] for their application in VIV analysis. This phenomenon has been thought to be primarily caused by twisting–bending coupling, triggered by VIV.

Fig. 1
figure 1

Modal VIV response branches for orthotropic stiffened flexible cantilevered cylinder: experimental set-up, in-line and cross-wise modal amplitudes as functions of reduced velocity (adapted from [3])

Full size image

Concerning energy conversion, piezoelectric energy harvesting is a useful solution for reduced power demanded by electronic devices. Experimental and numerical studies on piezoelectric flexible cantilevered beams are found in [6, 7] and [8].

As a theoretical approach, this chapter derives a reduced-order model for studying a cantilevered piezoelectric harvester with orthotropic bending stiffness under VIV. The equations of motion coupling mechanical and electrical subsystems, as well as the wake-oscillator model for the fluid–structure interaction, are addressed in Sect. 2. Numerical simulations at chosen scenarios illustrate the problem in Sect. 3.

2 Mathematical Model

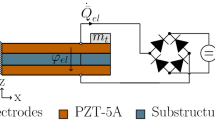
The system modelled in this chapter is represented in Fig. 2. The harvester is composed of a cantilevered flexible polymeric cylinder molded over a flat bar constituted by a metallic substrate between two piezoelectric material layers connected in series to an electrical resistance.

Fig. 2
figure 2

Schematic representation of the energy harvesting system

Full size image

For the mathematical modelling, the Bernoulli–Euler’s cantilever model is taken. A fixed frame XY Z with origin at the clamped end of the beam is adopted, with X parallel to the incident flow direction, Y  parallel to the cross-wise direction, and Z aligned with the beam axis. The displacements in each of these directions are U, V , and W, respectively (see Fig. 2). The extended Hamilton’s principle for dissipative systems then reads

$$\displaystyle \begin{aligned} \int_{t_1}^{t_2} \! \Big[ \delta\mathcal{T}-\delta\mathcal{V}+\left( \delta\mathcal{W}_{nc} + \delta\mathcal{W}_{i,e}\right)\Big] \, \mathrm{d}t=0 . \end{aligned} $$
(1)

Being μ the mass per unit length, J p the mass moment of inertia around Z, and θ the twist angle, the variation of the kinetic energy is given as

$$\displaystyle \begin{aligned} \int_{t_1}^{t_2} \! \delta\mathcal{T} \, \mathrm{d}t=-\int_{t_1}^{t_2} \! \int_0^L \! \Big[\mu\left(\ddot{u}\delta u+\ddot{v}\delta v+\ddot{w}\delta w\right)+J_p\ddot{\theta}\delta\theta\Big] \, \mathrm{d}Z \, \mathrm{d}t . \end{aligned} $$
(2)

The potential energy \(\mathcal {V}\) can be divided into a portion due to external potential fields, a portion due to strain energy, and a portion corresponding to the electric field in the piezoelectric layers, namely \(\mathcal {V}=\mathcal {V}_f+\mathcal {V}_k+\mathcal {V}_e\). Since the external conservative forces are weight and buoyance, it follows that:

$$\displaystyle \begin{aligned} \delta \mathcal{V}_f=-\int_0^L \!\gamma\delta w \, \mathrm{d}Z , \end{aligned} $$
(3)

with γ being the immersed weight per unit length. Following, the variation of the strain energy, considering a linear-elastic and piezoelectric behavior for the materials, is written as

$$\displaystyle \begin{aligned} \delta \mathcal{V}_k=\int_0^L \! \iint_A \! \Big[ E\varepsilon_{zz}\delta\varepsilon_{zz}+G\left(\gamma_{xz}\delta\gamma_{xz}+\gamma_{yz}\delta\gamma_{xz}\right)\Big] \, \mathrm{d}A \, \mathrm{d}Z , \end{aligned} $$
(4)

with ε zz being the axial strain, while γ xz and γ yz are the distortions in the cross-section plane. In turn, E and G are the Young and Shear moduli, respectively. Since the cross-sections are composed of different materials, the area integrals must be carried out for each element. In order to proceed with a formulation that takes into account axial extensibility, torsion, and bending in both transversal directions, the relations presented in [9] for the axial strain and the distortions are used for each element of the cross-section. These relations are correct up to second order, leading to a model correct up to nonlinearities of third order. Substituting those relations and adding up terms from different elements of the cross-sections lead to

$$\displaystyle \begin{aligned} \delta \mathcal{V}_k&=\int_0^L \! \left[EA\left(w'+\frac{\left(u'\right)^2}{2}+\frac{\left(v'\right)^2}{2}\right)+\frac{EI_p}{2}\left(\theta '\right)^2\right]\left[\delta w'+u'\delta u'+v'\delta v'\right] \, \mathrm{d}Z \\ &\quad +\int_0^L \! \left[EI_p\left(w'+\frac{\left(u'\right)^2}{2}+\frac{\left(v'\right)^2}{2}\right)\theta '+\frac{EI_4}{2}\left(\theta '\right)^3\right]\delta \theta ' \, \mathrm{d}Z\\ &\quad +\int_0^L \! EI_X v''\delta v''+EI_Y u''\delta v''+GI_p \theta '\delta \theta ' \, \mathrm{d}Z . \end{aligned} $$
(5)

The stiffness products are taken in the whole cross-section, which requires the contribution of each element to be added up. The area moment of inertia around axis X and Y  are I X and I Y, respectively, while I p = I X + I Y is the polar moment of inertia, I t is the torsional moment of inertia, and I 4 is an area integral given by

$$\displaystyle \begin{aligned} I_4=\iint_A \! \left(X^2+Y^2\right)^2 \, \mathrm{d}A . \end{aligned} $$
(6)

Now, for the electric component of the deformation in the bimorphic piezoelectric layers, following [8], the variation of the piezoelectric potential energy is given by

$$\displaystyle \begin{aligned} \delta\mathcal{V}_{e}= - \int_0^L \! \left( \frac{e_{31}}{2h_p}M_X\overline{V}\delta v''+\frac{e_{31}}{2h_p}M_Xv''\delta\overline{V} \right) \, \mathrm{d}Z . \end{aligned} $$
(7)

Only the coupling between the displacements v and the voltage \(\overline {V}\) appears since the static moment of each piezoelectric layer with respect to the Y  axis is zero. Equation (7) already added up both piezoelectric layers. The absolute value of the static moment of each piezoelectric layer is M X, h p is the thickness of each layer, and e 31 is the constant of piezoelectric coupling. Finally, completing the conservative terms, the variation of the generated electric energy is given as [8]:

$$\displaystyle \begin{aligned} \delta\mathcal{W}_{i,e}=\int_0^L \! \left( \frac{e_{31}}{2h_p}M_X\overline{V}\delta v''+\frac{e_{31}}{2h_p}M_Xv''\delta\overline{V}+\frac{\overline{E}A_p}{2h_p^2}\overline{V}\delta\overline{V} \right) \, \mathrm{d}Z . \end{aligned} $$
(8)

To close the mathematical model, the variation of the work of non-conservative forces is given as

$$\displaystyle \begin{aligned} \delta\mathcal{W}_{nc}=\int_0^L \! \Big[ \left(f_u-c_u\dot{u}\right)\delta u+\left(f_v-c_v\dot{v}\right)\delta v \Big] \, \mathrm{d}Z+Q\delta\overline{V} , \end{aligned} $$
(9)

with Q being the electric charge output of the electrical system, c u and c v are the linear structural damping coefficients in the X and Y  directions, respectively, while f u and f v are the hydrodynamic forces in those same directions. Collecting all variational terms in the extended Hamilton’s principle (Eq. 1), developing the appropriate algebraic operations, and deriving the equation of the electric charge with respect to time, one obtains the following system of nonlinear partial differential equations of motion:

$$\displaystyle \begin{aligned} &\mu\ddot{w}-EA\left(w''+u'u''+v'v''\right)-EI_p\theta'\theta''-\gamma=0 ; \end{aligned} $$
(10)
$$\displaystyle \begin{aligned} &\mu\ddot{u}+c_u\dot{u}+EI_Yu''''-\left[EAu'\left(w'+\frac{\left(u'\right)^2}{2}+\frac{\left(v'\right)^2}{2}\right)+\frac{EI_p}{2}u'\left(\theta'\right)^2\right]'=f_u ; \end{aligned} $$
(11)
$$\displaystyle \begin{aligned} &\mu\ddot{v}+c_v\dot{v}+EI_Xv''''-\left[EAv'\left(w'+\frac{\left(u'\right)^2}{2}+\frac{\left(v'\right)^2}{2}\right)+\frac{EI_p}{2}v'\left(\theta'\right)^2\right]'\\ &-\frac{e_{31}M_X}{h_p}\overline{V}''=f_v ; \end{aligned} $$
(12)
$$\displaystyle \begin{aligned} & J_p\ddot{\theta}-GI_t\theta''-\left[EI_p\theta'\left(w'+\frac{\left(u'\right)^2}{2}+\frac{\left(v'\right)^2}{2}\right)+\frac{EI_4}{2}\left(\theta'\right)^3\right]'=0 ; \end{aligned} $$
(13)
$$\displaystyle \begin{aligned} &\int_0^L \! \frac{e_{31}}{h_p}M_X\dot{v}'' \, \mathrm{d}Z+\frac{\overline{E}A_pL}{2h_P^2}\dot{\overline{V}}+\frac{\overline{V}}{R}=0 . \end{aligned} $$
(14)

To complete the set of equations of motion, the hydrodynamic forces are adapted from the model presented in [10]. Here, the wake variable q is taken as a continuous variable that may vary with Z. The hydrodynamic forces are then written as

$$\displaystyle \begin{aligned} f_u&=-\mu_a\ddot{u}-\frac{1}{2}\left(\frac{qC_{L}}{2}\right)\rho D\dot{v}\sqrt{\left(U_\infty-\dot{u}\right)^2+\dot{v}^2}\\ &\quad +\frac{1}{2}C_{D}\rho D\left(U_\infty-\dot{u}\right)\sqrt{\left(U_\infty-\dot{u}\right)^2+\dot{v}^2}\\ &\quad +\frac{1}{2}\alpha\left(\frac{qC_{L}}{2}\right)^2\rho D\left(U_\infty-\dot{u}\right)\sqrt{\left(U_\infty-\dot{u}\right)^2} \end{aligned} $$
(15)
$$\displaystyle \begin{aligned} f_v&=-\mu_a\ddot{v}+\frac{1}{2}\left(\frac{qC_{L}}{2}\right)\rho D\left(U_\infty-\dot{u}\right)\sqrt{\left(U_\infty-\dot{u}\right)^2+\dot{v}^2}\\ &\quad -\frac{1}{2}C_{D}\rho D\dot{v}\sqrt{\left(U_\infty-\dot{u}\right)^2+\dot{v}^2}. \end{aligned} $$
(16)

The coefficients C L and C D are the amplitude of oscillation of the lift coefficient for a stationary cylinder and the mean drag coefficient for a stationary cylinder, respectively. In turn, μ a is the potential added mass for the cross-section and α is a coefficient related to the drag amplification during VIV. The wake variable follows the forced van der Pol equation:

$$\displaystyle \begin{aligned} \ddot{q}+\varepsilon_v\omega_s\left(q^2-1\right)\dot{q}+\omega_s^2q - \frac{\kappa}{D} \ddot{u}q =\frac{A_v}{D}\ddot{v}, \end{aligned} $$
(17)

with ω s being the vortex shedding frequency, while ε v and A v are, respectively, a van der Pol equation parameter and a coupling coefficient, both determined experimentally [10]. In order to numerically integrate the mathematical model, a Galerkin projection is made on the systems defined by Eqs. (11)–(14) and Eq. (17). For the trial functions, the first three modes of vibration of the cantilever beam are taken for the transversal displacements together with one mode for the axial displacement and one for the angle of twist. For the wake variable, the three modal shapes for transversal vibrations are also adopted as projection functions. Due to the presence of the square root dependency on the velocity of each cross-section in the hydrodynamic forces, the reduced-order model does not show up a closed mathematical expression. This leads the projection for those terms to be made at every time step of a numerical simulation.

Aiming at concluding the description of the mathematical modelling, a discussion is needed on the adopted wake-oscillator model. The model was taken from [10], where the parameters ε v and A v are dependent on the reduced velocity that is related to the incident flow, as U r = U∕f n D, being f n the natural frequency corresponding to the transversal oscillations of a rigid cylinder mounted on an linear-elastic 2-dof system. Herein, an ad hoc assumption is made to extend this dependency to the case of a flexible cylinder, by taking f n as the natural frequency related to vibration modes dominated by transversal oscillations. It is assumed that these parameters are independent for each component of q obtained after the Galerkin projection, being taken as ε v,i and A v,i, with i being the mode number of the component, ranging from one to three in the present work. With those assumptions, and using a Heaviside function to represent that the electric tension output occurs only at the clamped end as in [8], after some cumbersome algebraic work, the equations for the reduced-order model are

$$\displaystyle \begin{aligned} & m^{w}\ddot{w}_1+\beta^{w}w_1+\sum_{k=1}^3\sum_{l=1}^3\beta_{k,l}^{uu}u_ku_l+\sum_{k=1}^3\sum_{l=1}^3\beta_{k,l}^{vv}v_kv_l+\beta^{\phi\phi}\phi_1^2=0; \end{aligned} $$
(18)
$$\displaystyle \begin{aligned} & m_{i}^{u}\ddot{u}_i+c_{i}^{u}\dot{u}_i+\sum_{l=1}^3\beta_{i,l}^{u}u_l+\sum_{l=1}^3\beta_{i,l}^{uw}u_lw_1+\sum_{j=1}^3\sum_{k=1}^3\sum_{l=1}^3\beta_{i,j,k,l}^{uuu}u_ju_ku_l\\ &\quad +\sum_{j=1}^3\sum_{k=1}^3\sum_{l=1}^3\beta_{i,j,k,l}^{uvv}u_jv_kv_l+\sum_{l=1}^3\beta_{i,l}^{u\phi\phi}u_l\phi_1^2=f_{i}^{u} ; \end{aligned} $$
(19)
$$\displaystyle \begin{aligned} & m_{i}^{v}\ddot{v}_i+c_{i}^{v}\dot{v}_i+\sum_{l=1}^3\beta_{i,l}^{v}v_l+\sum_{l=1}^3\beta_{i,l}^{vw}v_lw_1+\sum_{j=1}^3\sum_{k=1}^3\sum_{l=1}^3\beta_{i,j,k,l}^{vuu}v_ju_ku_l\\ &\quad +\sum_{j=1}^3\sum_{k=1}^3\sum_{l=1}^3\beta_{i,j,k,l}^{vvv}v_jv_kv_l+\sum_{l=1}^3\beta_{i,l}^{v\phi\phi}v_l\phi_1^2+d_{i}\overline{V}=f_{i}^{v} ; \end{aligned} $$
(20)
$$\displaystyle \begin{aligned} & m^{\phi}\ddot{\phi}_1{+}\beta^{\phi}\phi_1{+}\beta^{w\phi}w_1\phi_1{+}\beta^{\phi\phi\phi}\phi_1^3{+}\sum_{k=1}^3\sum_{l=1}^3\beta_{k,l}^{uu\phi}u_ku_l\phi_1{+}\sum_{k=1}^3\sum_{l=1}^3\beta_{k,l}^{vv\phi}v_kv_l\phi_1=0 ; \end{aligned} $$
(21)
$$\displaystyle \begin{aligned} &\ddot{q}_i+\epsilon_{v,i} \left[\sum_{j=1}^3 \sum_{k=1}^3 \sum_{l=1}^3 Q^{i,j,k,l}q_jq_k\dot{q}_l \right]-\epsilon_{v,i} St U_r\dot{q}_i + \left(St U_r\right)^2q_i=A_{v,i}\ddot{v}_i ;{} \end{aligned} $$
(22)
$$\displaystyle \begin{aligned} &\dot{\overline{V}} + \eta\overline{V} +\sum_{l=1}^3\zeta_{l}\dot{v}_l=0,{} \end{aligned} $$
(23)

with u i, v i, and w i being the degrees of freedom relative to the projections of u, v, and w, respectively. The index i refers to each of the three modal components adopted for displacements u and v. The twist is ϕ, S t is the Strouhal number, and U r = U ∞∕f y1 D is the reduced velocity according to the frequency of the first natural mode in the Y  direction.

3 Results and Discussion

A case study is presented aiming at illustrating simulations based on the proposed mathematical model. An aluminum flat bar of dimensions 10 mm × 40 mm gives the structure with a frequency ratio close to 4:1 between in-line and cross-wise directions. The structural and electric parameters considered are presented in Table 1, where the index a refers to the aluminum bar, s to the silicon cylinder, and p to the piezoelectric material. In order to analyze the response including the three transverse modes in the Galerkin projection, reduced velocities up to 75 were considered. Practical design aspects such as intensity of incoming flow velocity and the structure strength were not considered in the present simulations.

Table 1 Simulation parameters
Full size table

Equations (18)–(23) were numerically integrated under two different conditions: (i) steady states obtained from a step-by-step increase in reduced velocity; (ii) continuously increasing or decreasing the reduced velocity linearly with time. In case (ii), a very slow increasing (or decreasing) rate is applied, at a time scale much longer than the typical shedding periods, such that the ratio between them lies in the interval 195 < ratio < 3500, being always of order 100 or larger. Hilbert–Huang analyses were undertaken for the in-line and cross-wise displacements time series; [3,4,5]. An empirical mode decomposition (EMD) algorithm is applied to each of the modal time series, obtaining their respective intrinsic mode functions (IMF) as exemplified in Fig. 3. A Hilbert transform is then calculated for these IMF, obtaining the instantaneous amplitude modulation and response frequency of the system.

Fig. 3
figure 3

Cross-wise modal displacements and respective IMF, normalized with respect to the cylinder diameter, as a function of reduced velocity based on the first transversal mode natural frequency in still water. Reduced velocity linearly increasing with time at a rate U r = αt, α = 0.01

Full size image

Typical response amplitudes were calculated from the peak of the obtained spectra, which are dominated by a single frequency value at each time instant. The sum of the modal responses is presented in Fig. 4. Results for the simulation run with linearly increasing velocities are represented in blue and for decreasing velocities in red. Markers (*) are steady-state amplitude responses obtained from series simulated at those respective reduced velocities.

Fig. 4
figure 4

Cross-wise and in-line amplitudes, normalized with respect to the cylinder diameter, as a function of reduced velocity based on the first transversal mode natural frequency in still water. Continuous line: varying current speed slowly; in blue: increasing velocity; in red: decreasing velocity. Modal amplitudes are determined by taking the Hilbert transform of the dominant IMF, within a EMD scheme [3, 4]. Dots represent amplitudes measured after a steady-state response is attained

Full size image

As seen in Fig. 4, the transverse amplitudes exhibit three locked-in responses, corresponding to the transverse natural frequencies of the structure. A hysteresis loop, a phenomenon commonly present in experimental VIV studies, can be identified as jumps between coexisting modes, where dynamic bifurcations show up clearly. Such a jump phenomenon is clearly depicted in the interval 55 < U r < 75, where the transversal modes 2 and 3 coexist. As for the in-line response, a first peak of amplitude is observed at reduced velocities around U r = 5.5, along with the transverse lock-in peak. The first in-line mode lock-in is also observed at higher reduced velocities, close to U r = 15.

When compared to the results presented in Fig. 1, the model herein developed shows good qualitative results for typical VIV response. However, the high-energy response branch, clearly observed in the experimental campaigns [2, 3], was not captured by the proposed mathematical model. In addition, amplitudes in longitudinal direction are considerably smaller than the ones obtained experimentally. As a matter of fact, the high-speed (energy) response branch was thought to be caused by the structure dynamics, through the twisting–bending coupling. As this coupling has been taken into account, with twisting terms considered up to third order, it appears that, so far, the fluid–structure interaction phenomenon has not been modelled properly, at least not sufficiently well. Further investigation is surely needed regarding the nature and the modelling of this intriguing fluid–structure interaction phenomenon.

Even not capturing the high-speed (energy) response branch and assuming the present reduced-order model as valid, an estimate for the electric power harvested from the system was carried out. The results are presented in Fig. 5.

Fig. 5
figure 5

Electric power harvested. Measure given in Watts. See Fig. 4 caption, for explanation on lines and dots

Full size image

The power generated increases at a very strong rate with the vibration frequency of the system, varying from very low values (of order of a few mW) at small reduced velocities, close to the first mode lock-in peak, to low ones (of order of 1W) harvested at higher modes of vibration.

4 Concluding Remarks

A 3D mathematical model was proposed for the representation of a flexible piezoelectric energy harvester under VIV, coupling structural, electrical, and hydrodynamics effects. The structural part of the model derived in this chapter is robust including, besides bending, axial displacements and torsion. For the fluid–structure interactions, represented by a wake-oscillator model, qualitative VIV aspects were recovered, including hysteresis loops at reduced velocity ranges where vibration modes switching occurs. However, the high-energy branch experimentally observed has not been captured by the present model yet. Therefore, the forms of the equations of the phenomenological model, alongside the calibration of its parameters, are objects of further work. In turn, as expected, the electric power harvested is highly dependent on the frequency of the system. Considering the results obtained by this model, the system presents a potential for energy harvesting, in different scales, at lower and higher modes, with distinct applications for each case. An experimental campaign on this subject is planned to be carried out in the near future.