Investigation of a nonlinear piezoelectric energy harvester with advanced electric circuits with the finite element method

Abstract

In this contribution, a system simulation method based on the finite element method (FEM) is applied to simulate a strongly coupled bimorph piezoelectric vibration-based energy harvester (PVEH) with various nonlinear, non-ideal and active circuits: The standard circuit, the synchronized switch harvesting on inductor circuit and the synchronized electric charge extraction circuit are considered. Furthermore, nonlinear elastic behavior of the piezoelectric material is taken into account and harmonic base excitations of different magnitudes at a fixed frequency are applied. The holistic FEM-based system simulation approach solves the complete set of piezoelectric equations together with the equation of the electric circuit such that all electromechanical coupling phenomena are taken into account. This fully coupled numerical analysis enables the detailed evaluation of the influences of the electric circuits on the vibrational behavior and the harvested energy of the PVEH with respect to the magnitude of base excitation. Results from literature on the efficiency of electric circuits are confirmed and interactions between mechanical and electrical nonlinearities of PVEHs are revealed.

Article highlights

• System simulations of a mechanically and electrically nonlinear piezoelectric energy harvester are performed using only one software tool.

• The infuence of electric circuits on the vibration behavior and the effciency of an energy harvester are investigated in detail.

• Interactions between mechanical and electrical nonlinearities of an energy harvester are revealed.

1 Introduction

A piezoelectric vibration-based energy harvester (PVEH) is composed of an electromechanical structure along with an electric circuit. The objective of such a device is converting otherwise unused mechanical energy into electrical energy to power e.g. wireless sensors. The piezoelectric effect, used as the energy conversion principle, describes the generation of electric voltage when the piezoelectric material is mechanically deformed and vice versa.

In vibration-based energy harvesting, beam type electromechanical structures under base excitation are mostly used due to their simple production and efficiency [1]. In a unimorph or bimorph configuration, one or two active piezoelectric layers are glued to a passive substrate. The energy generation is maximized when the resonance frequency of the electromechanical structure matches the excitation frequency. A mass is often added to the tip of the beam to improve the energy output. There are various possible sources of nonlinearities in vibration-based energy harvesting regarding the electromechanical structure: geometric nonlinearities caused by large deformations [2], nonlinear constitutive behavior caused by nonlinear damping or nonlinear elasticity [3], and others [4, 5].

The electric circuit is used to extract energy from an electromechanical structure. The optimal choice of the electric circuit depends on the electromechanical coupling, the excitation signal, and the electric load among others. Because of the piezoelectric effect the behavior of the electric circuit influences the mechanical behavior of the electromechanical structure and vice versa. Strongly coupled PVEHs are characterized by a pronounced interaction of electrical and mechanical quantities. In this case, there is a significant influence of the electric circuit on the electromechanical structure and the energy output of the PVEHs. To improve the energy harvesting efficiency, various electric circuits have been developed [6].

During vibration, the electromechanical structure generates an AC signal, while charging an electric storage component requires a DC signal [7]. The electric circuit has to provide AC-DC conversion and needs to be nonlinear for practical PVEHs. The passive standard circuit is the simplest electric circuit and it was reported, that active circuits like the synchronized switch harvesting on inductor (SSHI) circuit and the synchronized electric charge extraction (SECE) circuit can significantly increase the efficiency of a PVEH compared to the standard circuit [8, 9]. The aim of this contribution is to simulate and compare the energy output of a strongly coupled PVEH with standard, SSHI and SECE circuits for different magnitudes of base excitations. Nonlinear elasticity becomes important for large magnitudes of base excitation and has to be taken into account in the simulations [3]. Because the electric circuit and the electromechanical structure influence each other, an accurate simulation of a PVEH requires accurate modelling of both the nonlinear electromechanical structure and the nonlinear electric circuit.

The simulation approaches for PVEHs presented in literature are mainly restricted to model either nonlinearities of the electromechanical structure or of the electric circuit [10]. An overview of simulation methods for PVEHs, which are limited to the linear modeling of electromechanical structures but consider nonlinear electric circuits, can be found in [11]. Bistable PVEHs with different electric circuits are considered e.g. in [12,13,14], however, the present work focuses on the influence of material nonlinearities. In [10], a bimorph PVEH with a standard circuit is considered and a lumped parameter model of the system is derived. Material nonlinearities are considered, and the method of harmonic balances is applied to solve the lumped parameter model. The method of harmonic balances allows the quick simulation of the steady state response of the system but is restricted to periodic solutions.

Often the finite element method (FEM) is applied to simulate PVEHs. It can account for arbitrarily shaped geometries and nonlinear material behavior [15, 16]. FEM based simulation methods are either restricted to linear electric circuit elements [17,18,19] or do not consider nonlinearities of the electromechanical structure [20,21,22]. Recently, the authors presented a FEM simulation method, which simultaneously accounts for nonlinear electromechanical structures and nonlinear electric circuits [23]. The possibly nonlinear influence of the electric circuit on the electromechanical structure is considered via the vector of external forces and an implicit time integration scheme is used. This method allows for efficient and flexible simulations of PVEHs considering nonlinearities of both the electric circuit and the structure and is applied within this contribution to analyze and compare the influences of various advanced electric circuits on the efficiency of PVEHs.

In the next section, the relevant equations of piezoelectricity are presented and then discretized in space and time. After the introduction of various electrical circuits, the system simulation method of [23] is described and the FEM modeling of the SECE circuit is developed. Finally, numerical simulations of a PVEH with various electric circuits and at different magnitudes of excitation are performed and the results are carefully discussed.

2 Governing equations of piezoelectricity

Within this contribution, index notation in accordance with [24] is applied. The linear strain tensor $S_{ij}$ and the electric field $E_i$ are defined as

$$\begin{aligned} S_{ij}=\frac{1}{2}\left[ u_{i,j}+u_{j,i}\right] \quad \text { and } \quad E_{i}=-\varphi _{,i} \end{aligned}$$

(1)

Here, $u_i$ is the mechanical displacement and $\varphi$ is the electric voltage. The mechanical and the electric equations for the piezoelectric behavior in a body $\Omega$ are given by the balance of linear momentum and Gauss’ law, considering that piezoelectric materials are insulating, as

$$\begin{aligned} T_{ij,i}=\rho \ddot{u}_j \quad \text { and } \quad D_{i,i}=0 \end{aligned}$$

(2)

Here, $\rho$ is the material density, $D_i$ is the dielectric displacement and $T_{ij}$ are the components of the mechanical stress. A constitutive law that specifies the material behavior must be introduced. In [3], the influences of elastic, electroelastic, geometric and damping nonlinearities were analyzed for cantilevered bimorph electromechanical structures made of PZT-5A, similar to those used later in the simulations. Nonlinear elasticity was identified as the primary source of nonlinearity and a material model was postulated to account for nonlinear elasticity in a 1D setting. We extended this nonlinear elasticity model later in [23] to allow for 3D FEM simulations. This model is also used in this contribution and reads as

$$\begin{aligned} T_{{ij}} = & c_{{ijkl}}^{E} S_{{kl}} - e_{{kij}} E_{k} + c_{4} \left[ {S_{{mn}} A_{{mn}} } \right]^{3} A_{{ij}} \\ & + c_{6} \left[ {S_{{mn}} A_{{mn}} } \right]^{5} A_{{ij}} \\ \end{aligned}$$

(3)

$$\begin{aligned}&D_i=e_{ikl}S_{kl}+\varepsilon ^{S}_{ij}E_j \end{aligned}$$

(4)

with the structural tensor ${A_{ij}}={a_i a_j}$ and the vector ${a_i}={e}_{1i}$ being equal to the Cartesian basis vector pointing in the direction with the nonlinear elastic behavior. The components of the elasticity tensor at constant electric field are denoted as $c_{ijkl}^{E}$, $e_{ikl}$ is the piezoelectric constant tensor and $\varepsilon _{ij}^{S}$ is the dielectric constant at constant strain. Nonlinear elastic behavior is thus only introduced in 1-direction, which is a reasonable approach since this is the direction of the largest stresses and strains. This elastic model, specified in Eq. (3) with the parameters given in Appendix 1, is only applicable to similar problems, where the largest stresses and strains occur in $e_{1i}$ direction and the material is polarized in $e_{3i}$ direction. The piezoelectric problem can be solved with appropriate boundary conditions

$$\begin{aligned} u_i \!&= {{\bar{u}}}_i \text { on } \partial \Omega _{Du}\quad \varphi&= {\bar{\varphi }} \text { on } \partial \Omega _{D\varphi } \nonumber \\ T_{ij}n_j \!&= {{\bar{t}}}_i \text { on } \partial \Omega _{Nu} \quad D_i n_i \!&= \! {-{{\bar{Q}}}} \text { on } \partial \Omega _{N\varphi } \end{aligned}$$

(5)

whereby $n_i$ denotes the normal vector. The prescribed surface traction ${{\bar{t}}}_i$ and the free surface charge density ${{\bar{Q}}}$ are introduced. The boundary $\partial \Omega$ of $\Omega$ consists of subsets that do not overlap, such that $\partial \Omega _D \cup \partial \Omega _N=\partial \Omega$ and $\partial \Omega _D \cap \partial \Omega _N=\emptyset$.

3 Discretization of the equations

A fundamental step of the FEM is to transform the partial differential equations from their strong formulation into their weak formulation. To obtain the weak formulation, Eq. 2 are essentially multiplied by test functions ${\eta _j}$ and $\xi$ and subsequently, integration by parts is applied and the boundary conditions are introduced. The weak form is given as

$$\begin{aligned} \underbrace{ \int _\Omega \rho \eta _j \ddot{u}_j \ dV}_{\rightarrow {\varvec{f}}^{dyn,u}} +\underbrace{\int _\Omega \eta _{j,i}T_{ij} \ dV}_{\rightarrow {\varvec{f}}^{int,u}}- & {} \underbrace{\int _{\partial \Omega _{Nu}} \eta _j {{\bar{t}}}_j\ dA}_{\rightarrow {\varvec{f}}^{ext,u}}= 0\end{aligned}$$

(6)

$$\begin{aligned} \underbrace{ \int _\Omega \xi _{,i}D_i \ dV}_{\rightarrow {\varvec{f}}^{int,\varphi }}+ & {} \underbrace{\int _{\partial \Omega _{N\varphi }} \xi {{\bar{Q}}} \ dA}_{\rightarrow {\varvec{f}}^{ext,\varphi }}=0 \end{aligned}$$

(7)

The particular integral terms of the weak form result after the FE discretization in the force terms specified below the brackets. Thereby, ${\varvec{f}}^{dyn,u}$ is the mechanical inertial force, ${{\varvec{f}}^{int,u}}$ is the internal mechanical force, ${{\varvec{f}}^{ext,u}}$ is the mechanical external force, ${{\varvec{f}}^{int,\varphi }}$ is the electric internal force and ${{\varvec{f}}^{ext,\varphi }}$ is the electric external force. The FEM subdivides the domain $\Omega$ into small discrete elements and approximates the unknown solutions namely the mechanical displacement and the electric voltage elementwise by means of polynomial ansatz functions and nodal degrees of freedom. Thus, two coupled vector-valued equations for the unknown nodal displacements and electric voltage values result as

$$\begin{aligned} {\varvec{f}}^{dyn,u}+{\varvec{f}}^{int,u}-{\varvec{f}}^{ext,u}&={\varvec{0}} \end{aligned}$$

(8)

$$\begin{aligned} {\varvec{f}}^{int,\varphi }+{\varvec{f}}^{ext,\varphi }&={\varvec{0}} \end{aligned}$$

(9)

The coupling to an electric circuit is easier if the electric surface current $-\dot{\bar{ {Q}}}$ appears in the equation. Therefore, the time derivative of Eq. (9) is used for the system simulations. Furthermore, a mechanical damping force ${\varvec{f}}^{damp,u}$ is introduced to model Rayleigh-type damping. The resulting system of equations thus becomes

$$\begin{aligned} {\varvec{f}}^{dyn,u}+{\varvec{f}}^{damp,u}+{\varvec{f}}^{int,u}-{\varvec{f}}^{ext,u}&={\varvec{0}} \end{aligned}$$

(10)

$$\begin{aligned} \dot{{\varvec{f}}}{}^{int,\varphi }-\dot{{\varvec{f}}}{}^{ext,\varphi }&={\varvec{0}} \end{aligned}$$

(11)

Equations (10) and (11) are solved with the implicit Bossak-Newmark method for direct time integration introduced in [25]. In each time step the nonlinear system of equations is iteratively solved with Newton’s method.

4 Electric circuits

In this section, the standard, the SSHI and the SECE circuit are introduced, along with the bimorph electromechanical structure from [26].

4.1 Standard circuit

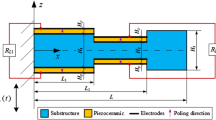
The simplest way of an AC-DC converter is to use a diode bridge and supply the rectified voltage to an energy storage element. Figure  1 presents this standard circuit coupled to a bimorph electromechanical structure, and the typical waveforms of $\varphi _{el}$ and $\dot{{{\bar{Q}}}}_{el}$ under harmonic excitation are illustrated in Fig. 2.

Fig. 1

Bimorph electromechanical structure coupled to a standard circuit

Fig. 2

Typical waveforms of $\varphi _{el}$ and $\dot{\bar{Q}}_{el}$ arising from the standard circuit under a harmonic base excitation of the electromechancial structure

Here, $\varphi _{el}$ and $\dot{\bar{Q}}_{el}$ are the voltage and current values at the electrode of the electromechanical structure. If the absolute value of the piezoelectric voltage $|\varphi _{el}|$ is smaller than the conductive voltage $V_C$, the electromechanical structure is in open circuit mode and there is no current $\dot{\bar{Q}}_{el}$ leaving the electrode. The conductive voltage $V_C$ results from the drop voltage of the diodes $V_{D}$ and the constant voltage $V_{DC}$ as $V_C=2V_D+V_{DC}$. When $|\varphi _{el}|$ reaches $V_C$ the diode bridge conducts and an electric current $\dot{{{\bar{Q}}}}_{el}$ charges the battery. The harvested energy can be computed as

$$\begin{aligned} {{\mathcal {E}}}=\int _{0}^{t}|\dot{{\bar{Q}}}_{el}|V_{DC} \ d\tau \end{aligned}$$

(12)

4.2 SSHI circuit

The SSHI circuit was introduced in [8] and adds a switch and an inductor (L) to the standard circuit. Figure 3 presents the SSHI circuit coupled to a bimorph electromechanical structure and Fig. 4 shows the typical waveforms of $\varphi _{el}$ and $\dot{{{\bar{Q}}}}_{el}$ under harmonic excitation of the structure.

Fig. 3

Bimorph electromechanical structure coupled to an SSHI circuit

When $|\varphi _{el}|$ starts to decrease, the switch is closed, and only the inductor is connected to the electromechanical structure. Since closing the switch creates an electric resonant circuit consisting of the electromechanical structure as a capacitance and the inductor, the voltage is inverted. When the electric current in the inductor is zero-crossing, the switch is opened again. Equation (12) can also be applied to compute the harvested energy of the SSHI circuit.

4.3 SECE circuit

The SECE circuit was introduced in [9] and consists of a diode rectifier bridge and a buck-boost DC-DC converter circuit composed of a switch, an inductor and a diode. To emulate an ideal energy storage device a constant voltage $V_{DC}$ is assumed. During operation of the SECE circuit different phases can be distinguished [27]:

• Extraction phase. When the electric voltage $\varphi _{el}$ reaches its maximum value, the switch is closed and thus only the inductance is connected to the electromechanical structure. Because the piezoelectric capacitance and the inductor form an electric resonance circuit, the electric voltage and the electric current start to oscillate as soon as the switch is closed. When the switch is closed, the energy stored in the piezoelectric capacitance is transferred to the inductor. When the electric current in the inductance reaches its maximum value, the switch is opened again. During the extraction phase the absolute value of the piezoelectric voltage $|\varphi _{el}|$ drops to $\pm 2V_D$. Because the electrical frequencies are usually by orders higher than the mechanical frequencies, the extraction process happens almost instantaneously.

• Open circuit and freewheeling phase. The energy stored in the inductor is transferred via the freewheeling diode to the battery. The electrical frequencies are usually by orders higher than the mechanical frequencies and the current in the inductor falls to zero in every cycle. Because the switch is opened, the electromechanical structure is in open circuit mode and the electric current $\dot{{{\bar{Q}}}}_{el}$ vanishes.

The inductor is connected either to the electromechanical structure or to the battery, therefore, the electromechanical structure is decoupled from the electric load. Figure 5 presents the SECE circuit coupled to a bimorph electromechanical structure and Fig. 6 illustrates the typical waveforms of $\varphi _{el}$, $\dot{{{\bar{Q}}}}_{el}$ and ${\dot{Q}}_{c}$ under harmonic excitation of the structure. The harvested energy of the SECE circuit can be computed as

$$\begin{aligned} {{\mathcal {E}}}=\int _{0}^{t}|\dot{{\bar{Q}}}_{el} |\left[ |\varphi _{el}|-2V_D\right] \frac{V_{DC}}{V_{DC}+V_D} \ d\tau \end{aligned}$$

(13)

Fig. 4

Typical waveforms of $\varphi _{el}$, and $\dot{\bar{Q}}_{el}$ arising from the SECE circuit under a harmonic base excitation of the electromechanical structure

Fig. 5

Bimorph electromechanical structure coupled to an SECE circuit.

In the computation of the harvested energy the dissipation of the diodes is considered, for details please see [27].

5 FEM system simulation

The system simulation method introduced in [23] is applied to simulate a PVEH with a standard, an SSHI and an SECE circuit. Applying the FEM to model an electrode on a surface means to prescribe that all voltage degrees of freedom have the same value $\varphi _{el}$ on this surface. One reference degree of freedom ${\mathcal {F}}$ is introduced for the voltage of the electrode. Furthermore, one electrode is assumed to be grounded. Hence, the voltage difference between the electrodes of a PVEH is just the electrical voltage $\varphi _{el}$ of the non-grounded electrode with the corresponding degree of freedom ${\mathcal {F}}$. The electric boundary conditions for the grounded electrode is therefore a homogeneous Dirichlet boundary condition with ${\bar{\varphi }}=0$. The electric circuit is coupled to the electromechanical structure via the boundary condition of the non-grounded electrode. To account for the influence of the electric circuit on the electromechanical structure, the surface current ${\dot{{\bar{Q}}}}_{el}$ leaving the electrode is prescribed. It can be constructed via an inhomogeneous Neumann boundary condition

$$\begin{aligned} {\dot{{\bar{Q}}}}_{el}=\int _{\partial \Omega _{Electrode}} \!\!\!\!\!\!\!\!\!\!\!\! {\dot{D}}_in_i \ \text {dA} \end{aligned}$$

(14)

Both, $\varphi _{el}$ and ${\dot{{\bar{Q}}}}_{el}$ correspond to the same reference degree of freedom ${\mathcal {F}}$ of the non-grounded electrode. The electric current ${\dot{{\bar{Q}}}}_{el}$ appears in Eq. (11) and is introduced in $\dot{{\varvec{f}}}{}^{ext,\varphi }$ in the entry for the reference degree of freedom ${\mathcal {F}}$ as

$$\begin{aligned} \dot{{\varvec{f}}}{}^{ext,\varphi }= {\left\{ \begin{array}{ll} {\dot{{\bar{Q}}}}_{el} &{} \text {for degree of freedom}={\mathcal {F}}\\ 0 &{} \text {for degree of freedom}\ne {\mathcal {F}} \end{array}\right. } \end{aligned}$$

(15)

To consider the coupling of various electric circuits with the FE simulation, the relation between the electric current ${\dot{{\bar{Q}}}}_{el}$ and the voltage of the non-grounded electrode $\varphi _{el}$ has to be specified. The implementation of the standard and SSHI circuits are described in detail in [23]. In the following, only the implementation of the SECE circuit is specified.

During operation of the SECE circuit two cases are possible:

Case 1: This is the open circuit case when the switch is opened, and the inductor is not connected to the electromechanical structure. Hence, the electric current $\dot{{\bar{Q}}}_{el}$ vanishes and this situation can be modeled via a homogeneous Neumann boundary condition in the FE simulation

$$\begin{aligned} {\dot{{\bar{Q}}}}_{el}=0 \end{aligned}$$

(16)

Case 2: In this case, the switch is closed, and the inductor is connected to the electromechanical structure. The influence of the inductor on the electromechanical structure is considered via an inhomogeneous Neumann boundary condition. Depending on the sign of $\varphi _{el}$ the relation is specified as

$$\begin{aligned} {\ddot{{\bar{Q}}}}_{el}= {\left\{ \begin{array}{ll} \frac{\varphi _{el}-2V_D}{L} &{} \text { if } \varphi _{el}>0\\ \frac{\varphi _{el}+2V_D}{L} &{} \text { if } \varphi _{el}<0 \end{array}\right. } \end{aligned}$$

(17)

In Eq. (15) the electric current appears, therefore, equation (17) is numerically integrated to obtain the electric current. In Fig.  7 the logic of the SECE circuit, i.e. the conditions how to switch between cases 1 and 2, is illustrated.

It must be prevented in the simulation that the switch is triggered at inappropriate times. After closing the switch, $\varphi _{el}$ decreases rapidly because the electrical oscillation frequency is usually by orders higher than the mechanical excitation frequency. The rapid decrease of $\varphi _{el}$ acts like an actuation on the structure, which leads to higher order oscillations of $\varphi _{el}$ and the electromechanical structure. To prevent that the switch is triggered due to these higher order oscillations of $\varphi _{el}$, a time span $t_{ns}$ is introduced during which closing the switch is prohibited. Moreover, $\varphi _{el}$ flutters during the instationary settling process when the mechanical excitation starts. Therefore, a time span $t_{switch}$ is defined during which closing of the switch is prohibited at the beginning of the simulation.

Fig. 6

Typical waveforms of $\varphi _{el}$, $\dot{\bar{Q}}_{{el}}$ and $\dot{\bar{Q}}_{c}$ arising from the SECE circuit under a harmonic base excitation of the electromechanical structure

6 Application example

As an application example the bimorph electromechanical structure introduced in [26] coupled to the three different electric circuits is simulated. The bimorph cantilever has a mass mounted on its tip and consists of two layers of PZT-5A bracketing a layer of a passive substructure. The piezoceramic layers are poled in opposite directions. For the substructure, a linear elastic material behavior is assumed and for the PZT-5A the nonlinear piezoelectric constitutive law (Eqs. (3) and (4)) is applied. Figure 5 presents the considered PVEH and the appendix provides its parameters. A harmonic base acceleration a(t) with a frequency of 48.7 Hz, which is close to the open circuit resonance frequency of the electromechanical structure for small excitations, is applied. Three different magnitudes of the base acceleration of 0.5, 1 and 9.81 m/s$^2$ are chosen and the harvested energy and the electric voltage are compared for the standard, the SSHI and the SECE circuit. Some of these results for the standard and SSHI circuits have already been discussed in [23], but here, for the first time, the results for all three circuits are carefully analyzed and compared for different excitation magnitudes.

In order to avoid that the switch is triggered at inappropriate times $t_{ns}=4$ ms and $t_{switch}=10.8$ ms are chosen. The bimorph PVEH is discretized with 90 quadratic hexahedral elements. During the extraction phase when the switch is closed the time step size of the Bossak-Newmark time integration scheme is set to $10^{-5}$ ms since it happens almost instantaneously. After the switch is opened the time step size is set to $10^{-3}$ ms within a time span $t_{osc}=3$ ms to precisely capture the higher order oscillation of the electromechanical structure. For the remaining time period a time step size of $10^{-1}$ ms is used. The system simulation method is implemented based on the open source C++ software library deal.ii targeted at the computational solution of partial differential equations [28]. Most components of the FEM based system simulation method have been validated in [23]. The results of this validation are summarized in Appendix 1.

6.1 Harmonic base acceleration with a magnitude of 0.5 m/s$^2$

Firstly, a magnitude of 0.5 m/s$^2$ of the harmonic base acceleration is applied. Figure  8 presents the results for $\varphi _{el}$ and Fig. 8 shows the harvested energy of the standard, the SSHI and the SECE circuit. The considered time period is 0 to 200 ms. The standard circuit harvests around 0.0014 mJ which is approximately 128% of the energy harvested by the SECE circuit and around 300% of the amount of energy harvested by the SSHI circuit. As shown in Fig. 9, the SSHI circuit rapidly changes the electric voltage when the switch is closed by a much larger amount than the SECE circuit. Therefore, the excitation of high frequency vibration modes is more significant for the SSHI circuit, and the energy dissipation is higher than for the SECE circuit. Moreover, the advantage of the SSHI circuit is usually to extend the time during which the diode rectifier is conducting. But in this case, due to the higher order vibration modes, the conduction time is actually shorter than for the standard circuit which can be seen in the zoom-in of the diagram in Fig. 8. Because of the higher dissipation due to the high frequency vibrations and the short conduction time, the SSHI circuit is the least effective here and harvests the least amount of energy. For a base acceleration of 0.5 m/s$^2$ the passive standard circuit, that does not excite high frequency vibration modes, is more efficient than the SSHI and SECE circuits.

Fig. 7

Logic for the definition of boundary conditions for the FE simulation of an electromechanical structure with an SECE circuit

Fig. 8

Electrode voltage $\varphi _{el}$ of the bimorph PVEH with standard, SSHI and SECE circuit under a harmonic base acceleration of 0.5 m/s$^2$ and a frequency of 48.7 Hz

6.2 Harmonic base acceleration with a magnitude of 1 m/s$^2$

Figure 10 presents the results for $\varphi _{el}$ and Fig. 11 shows the harvested energy when a magnitude of 1 m/s$^2$ of harmonic base acceleration is applied. The considered electric circuits harvest nearly the same amount of energy within a time period of 200 ms namely around 0.006-0.007 mJ. The change of $\varphi _{el}$ caused by the switching events of the SSHI and the SECE circuit are in the same order and therefore approximately an equal amount of energy is dissipated by the high frequency vibration modes. Furthermore, when a magnitude of 1 m/s$^2$ of harmonic base excitation is applied, the SSHI circuit extends the time fraction during which the diode bridge conducts compared to the standard circuit, as shown in the zoom-in in Fig. 10. The standard circuit does not excite high frequency vibration modes and has nearly the same efficiency for the considered PVEH like the SSHI and SECE circuits. While the standard and the SSHI circuits limit the piezoelectric voltage $\varphi _{el}$ to $\pm V_C$, the SECE circuit does not limit $\varphi _{el}$ and therefore the highest values of $\varphi _{el}$ are reached.

Fig. 9

Harvested energy ${\mathcal {E}}$ of the bimorph PVEH with standard, SSHI and SECE circuit under a harmonic base acceleration of 0.5 m/s$^2$ and a frequency of 48.7 Hz

6.3 Harmonic base acceleration with a magnitude of 9.81 m/s$^2$

Figure 12 presents the results for the electrode voltage $\varphi _{el}$ and Fig. 13 shows the harvested energy for the standard, SSHI and SECE circuits when a harmonic base acceleration with a magnitude of 9.81 m/s$^2$ is applied. In contrast to small base excitations, considering nonlinear elasticity becomes important for high base excitations because the nonlinear material behavior of PZT-5A strongly influences the harvested energy [23]. The SECE circuit harvests approximately 0.35 mJ during 200 ms, which is around three times the amount of energy harvested by the standard or the SSHI circuit. The high level of applied base acceleration would lead to high open circuit piezoelectric voltages compared to the conductive voltage $V_C$ of the standard and the SSHI circuits, which limit $\varphi _{el}$ to $\pm V_C$. Therefore, the actuation of the electromechanical structure caused by voltage inversion for the SSHI circuit and, thus, the related dissipation of energy, are relatively small. However, because of the high level of mechanical base acceleration the advantage of the SSHI circuit, namely to extend the conduction time of the diode bridge, does not significantly improve the efficiency compared to the standard circuit, as is shown in the zoom-in in Fig. 12. Therefore, both the standard and SSHI circuits harvest nearly the same amount of energy, around 0.09 mJ. In contrast, when the SECE circuit is used the harvested energy is independent of the applied electric load. Therefore, the SECE circuit is more efficient than the standard and the SSHI circuits for this high level of base acceleration. To optimize the harvested energy of the standard and SSHI circuits for this setting a DC-DC converter must be applied after the diode bridge to regulate the conductive voltage $V_C$. A DC-DC converter allows the flexible adjustment of $V_C$ to the current conditions and the efficiency of the respective electric circuit can be significantly improved [29].

Fig. 10

Electrode voltage $\varphi _{el}$ of the bimorph PVEH with standard, SSHI and SECE circuit under a harmonic base acceleration of 1 m/s$^2$ and a frequency of 48.7 Hz

Fig. 11

Harvested energy ${\mathcal {E}}$ of the bimorph PVEH with standard, SSHI and SECE circuit under a harmonic base acceleration of 9.81 m/s$^2$ and a frequency of 48.7 Hz

Fig. 12

Electrode voltage $\varphi _{el}$ of the bimorph PVEH with standard, SSHI and SECE circuit under a harmonic base acceleration of 9.81 m/s$^2$ and a frequency of 48.7 Hz

Figure 14 shows the SSHI circuit with a DC voltage regulation stage consisting of a DC-DC converter and a smoothing capacitor $C_C$. For the standard circuit, a similar architecture regarding the load adaption is considered.

To dynamically adapt $V_{a}$, and therefore $V_C=V_{a}+2V_{drop}$, to its optimum value a control unit is necessary. Here, the energy consumption of the control unit is neglected, and the DC-DC converter is assumed to be perfect. Furthermore, it is assumed that the capacitor $C_C$ is much larger than the capacitance of the electromechanical structure. Hence, the voltage $V_{DC}$ is independent of the piezoelectric voltage $\varphi _{el}$ and the capacitor $C_C$ is replaced in the model by a flexible voltage source, whose current value is controlled by the control unit. However, here for the prescribed harmonic base excitation with a constant magnitude a constant conductive voltage $V_{C}=15$ V ($V_{a}=13.8$ V) is chosen for both load adapted circuits. Figure 15 presents the piezoelectric voltage $\varphi _{el}$ and Fig.  16 shows the harvested energy of the load adapted standard and SSHI circuits and of the SECE circuit. The results for the SECE circuit are similar to the results in Figs. 12 and 13. The PVEH with SSHI circuit harvests about 0.6 mJ of energy, which is approximately 170% of the energy harvested by the PVEH with SECE circuit. The PVEH with standard circuit harvests around 0.4 mJ of energy until 200 ms. The energy generations of the load adapted standard and SSHI circuits increase significantly compared to the non-load adapted configurations.

Fig. 13

Harvested energy ε of the bimorph PVEH with standard, SSHI and SECE circuit under a harmonic base acceleration of 9.81 m/s² and a frequency of 48.7Hz.

Fig. 14

Bimorph electromechanical structure coupled to an SSHI circuit with a DC-DC converter for load adaption

Fig. 15

Electrode voltage $\varphi _{el}$ of the bimorph PVEH with load adaption standard, load adaption SSHI circuit, and SECE circuit under a harmonic base acceleration of 9.81 m/s$^2$ and a frequency of 48.7 Hz

Fig. 16

Harvested energy ${\mathcal {E}}$ of the bimorph PVEH with load adaption standard, load adaption SSHI circuit, and SECE circuit under a harmonic base acceleration of 9.81 m/s$^2$ and a frequency of 48.7 Hz

6.4 Discussion of the simulation results

Different magnitudes of a harmonic base excitation at a fixed frequency were considered. For small base excitations of 0.5 and 1 m/s$^2$ the fixed excitation frequency is close to the resonance frequency of the electromechanical structure. Therefore, consistently with the literature, the standard circuit is more efficient than the SECE and the SSHI circuit [6, 30,31,32,33]. In contrast, the result, that the load adapted SSHI circuit harvests more energy than the load adapted standard circuit for a base excitation of 9.81 m/s$^2$, is explained as follows: The excitation frequency of 48.7 Hz is only close to the resonance frequency of the electromechanical structure for small base excitations when nonlinear elasticity can be neglected. The stiffness of the PVEH is influenced by the nonlinear constitutive law if large strains occur in the structure. Consequently, the resonance frequency of the PVEH shifts for high excitations and is no longer close to 48.7 Hz. Consistently with the literature, the SSHI circuit is more efficient than the standard circuit in this non-resonance case [31, 34]. While oscillating in resonance, a structure moves with a particular pattern, called normal mode. Disturbances of the normal mode, e.g. caused by switching events of the SSHI and SECE circuits, depart the state of the system from resonance. High frequency modes are excited and lead to significant damping. In the non-resonance case these effects become increasingly unimportant, because the oscillation of the electromechanical structure is a superimposition of its normal modes already. That leads to the presented results, that the further away the excitation frequency of the PVEH is from its resonance frequency, the more efficient become the SSHI and SECE circuit compared to the standard circuit.

7 Conclusion

The FEM based system simulation method introduced in [23] is here applied and extended to include the SECE circuit. A strongly coupled PVEH with three different electric circuits, a standard, an SSHI and an SECE circuit, is considered and the efficiency of the electric circuits is compared. Nonlinear elasticity of the electromechanical structure is taken into account and different magnitudes of a harmonic base acceleration at a fixed frequency are considered. The simulation results confirm the advantage of the SECE circuit namely the independence of the harvested energy on the electric load. The efficiency of the standard and the SSHI circuits decreases without an additional load adaption stage compared to the SECE circuit for high levels of base acceleration. Moreover, consistently with the literature, the SECE circuit and the SSHI circuit dissipate energy compared to the standard circuit through higher order vibration modes caused by switching events. This additional dissipated energy reduces the efficiency of the respective electric circuits in particular when the electromechanical structure is in resonance. In this case, the efficiency of the standard circuit is superior to the efficiency of the SECE and SSHI circuit. Because the harvested energy is independent of the electric load, the SECE circuit is more efficient than the considered standard circuit and the SSHI circuit without an additional DC-DC converter for high levels of base accelerations. When a DC-DC converter is applied, the efficiency of the standard and SSHI circuit is significantly improved. Consistently with the literature, for non-resonance excitations, which are here related to high base excitations, the standard circuit becomes less efficient compared to the SSHI circuit. Therefore, the efficiencies of the standard, SSHI and SECE circuits depend also on the magnitude of base excitation. By taking electrical and mechanical nonlinearities into account, the obtained results demonstrate the applicability of the system simulation method of [23] to develop or improve PVEHs. Interactions between the harvesting efficiency of advanced electric circuits, mechanical nonlinearities and the magnitude of base excitation are revealed with the simulations.

Appendices

Appendix A Parameters

The parameters of the electromechanical structure from [26] are specified in Table 1.

Table 1 Parameters of the PVEH

The material parameters for PZT-5A are defined as

$$\begin{aligned}&{\varvec{c}}^{E} =\begin{bmatrix} 120.3 &{} 75.2&{} 75.1 &{} 0 &{} 0 &{} 0\\ 75.2 &{} 120.3 &{} 75.1 &{} 0 &{} 0 &{} 0\\ 75.1 &{} 75.1 &{} 110.9 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 21.1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 21.1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 22.6\\ \end{bmatrix} \text {GPa}\end{aligned}$$

(A1)

$$\begin{aligned}&{\varvec{e}}=\begin{bmatrix} 0&{} 0&{} 0 &{} 0 &{} 12.3&{} 0\\ 0 &{} 0&{} 0 &{} 12.3&{} 0 &{} 0\\ -5.4 &{} -5.4&{} 15.8 &{} 0 &{} 0 &{} 0\\ \end{bmatrix} \frac{{\text {C}}}{{\text {m}}^2}\end{aligned}$$

(A2)

$$\begin{aligned}&{\varvec{\varepsilon }}^{{S}}=\begin{bmatrix} 813.7 & 0& 0 \\ 0 &813.7& 0 \\ 0 & 0& 731.9 \\ \end{bmatrix} \times 10^{-11} \frac{{\text {F}}}{{\text {m}}} \end{aligned}$$

(A3)

The coefficients in equation (3) for the nonlinear piezoelectric constitutive law were identified for the considered PZT-5A material in [3] as $c_4=-9.7727\times 10^{17}$ Pa and $c_6=1.4700\times 10^{26}$ Pa.

Appendix B Validation

The same FEM-based system simulation method as used in [23] is also applied for the simulations in this contribution. In the following the validation of the FEM framework as presented in [23] is summarized.

Figure 17 presents the results obtained in [23] for the simulation of a linear unimorph electromechanical structure with SSHI circuit introduced in [35]. The results are compared against results reported in [21]. Overall, a good agreement between the simulation results can be observed confirming that the FEM framework provides accurate results.

The simulation of an SSHI circuit requires similar boundary conditions as the standard and SECE circuits. Particularly simulations of the SSHI and SECE circuit require similar boundary conditions when the switch is closed and the inductor is connected to the electromechanical structure. It is therefore confirmed that the FEM-based system simulation method gives accurate results for the standard and SECE circuits. For more details about this validation example please see [23].

Fig. 17

Comparison of the piezoelectric voltage $\varphi _{el}$ in Hegendörfer et al. [23] against the results reported in Gedeon and Rupitsch (2018) [21] for the SSHI circuit and a unimorph electromechanical structure

In contrast to the previous example, in this contribution a bimorph PVEH with tip mass is considered, which is experimentally analyzed in [26]. An FEM simulation of the linear bimorph electromechanical structure gives the first open circuit eigenfrequency as 48.95 Hz, while this frequency is experimentally determined in [26] as 48.4 Hz. This relative error of around 1% between the experimental data and the simulation confirms the accuracy of the presented FEM simulation for the bimorph structure. Overall, all components of the FEM code are validated.