Introduction

One of the most important objectives in the interpretation of gravity data is to define characterization the size, shape, and location of different types of subsurface structures for various purposes like exploration, mining, and subsurface geologic mapping. Subsurface geologic structures can often be adequately modeled from gravity data as simple geometric shapes such as spherical, cylindrical, or tabular bodies. Parameters that control a geometric model’s shape and position, such as depth, length, and radius, are estimated and the parameters that result in a model that best estimates the gravitational anomaly are considered good models.

The interpretation of gravity anomalies as idealized geometric shapes has a wide range of applications (e.g., Grant and West 1965; Nettleton 1976; Beck and Qureshi 1989; Hinze 1990; Lafehr and Nabighian 2012; Hinze et al. 2013; Long and Kaufmann 2013; Lasmar et al. 2014). Various techniques can be used to invert gravity data and estimate the parameters of the idealized source bodies, including graphical methods (e.g., Nettleton 1962, 1976), Fourier transform (e.g., Odegard and Berg 1965; Sharma and Geldart 1968), Euler de-convolution (e.g., Thompson 1982), Mellin transform (e.g., Mohan et al. 1986), ratio methods (e.g., Bowin et al. 1986; Abdelrahman et al. 1989), neural networks (e.g., Elawadi et al. 2001), least-squares minimization approaches (e.g., Gupta 1983; Lines and Treitel 1984; Abdelrahman and Sharafeldin 1995a), Werner de-convolution (e.g., Hartmann et al. 1971; Jain 1976; Kilty 1983), Walsh Transformation (e.g., Shaw and Agarwal 1990), fair function minimization (e.g., Asfahani and Tlas 2012), depth to extreme point (e.g., Fedi 2007), continual least-squares methods (e.g., Abdelrahman and Sharafeldin 1995b; Abdelrahman et al. 2001a, b; Essa 2012, 2013), simultaneous regularized inversion methods (e.g., Mehanee 2014), and very fast simulated annealing method (Biswas 2015).

The global particle swarm optimization (GPSO) algorithm was introduced two decades ago by Eberhart and Kennedy (1995) but the method has been applied in limited applications to geophysics (Alvarez et al. 2006; Shaw and Srivastava 2007; Sweilam et al. 2008; Juan et al. 2010; Toushmalani 2013a, b; Pekşen et al. 2014). The method has been applied to hydrological problems (Chau 2008), seismic wavelet inversion (Sanyi et al. 2009), and self-potential modeling (Monteiro Santos 2010; Pekşen et al. 2011). GPSO methods are commonly considered simple to apply because they are easy to understand and code, and computationally efficient (Eberhart and Shi 2001). In the present case study, a basic implementation of GPSO is used to estimate the parameters of idealized bodies (spheres and horizontal and vertical cylinders) that would generate a given gravity anomaly, using both noise-free and noisy synthetic data. The method is further applied to five field examples and compared with other interpretations made using various inversion and interpretation techniques.

Formulation of the Forward Problem

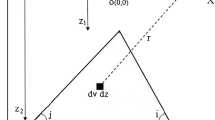
The common expression of a gravity anomaly V(x) for a sphere, horizontal cylinder, and vertical cylinder-like structure at any point on the free surface along the principal profile in a cartesian coordinate system (Fig. 1) is given as (e.g., Gupta 1983; Telford et al. 1990; Abdelrahman et al. 2001a, b; Essa 2007, 2013)

Figure 1
figure 1

A schematic diagram showing the cross-sectional views, geometries, and parameters of a sphere (left), horizontal cylinder (center), and a vertical cylinder (right)

Full size image
$$ V(x) = k\left[ {\frac{z}{{\left\{ {(x - x_{0} )^{2} + (z)^{2} } \right\}^{q} }}} \right], $$
(1)

where q = 1.5 and \( k = \frac{4}{3}\pi G\sigma R^{3} \) for a sphere; 1 and k = 2πGσR 2 for a horizontal cylinder, and 0.5 and \( k = \frac{{{{\pi G\sigma R}}^{2} }}{\text{z}} \) for a vertical cylinder.

In Eq. (1), k is the amplitude coefficient, z is the depth from the surface to the center of the body (sphere or horizontal cylinder) or the depth from the surface to the top of the object (vertical cylinder), q is the geometric shape factor, x 0 (i = 1,…,N) is the horizontal position coordinate, σ is the density contrast between the anomalous body and the host rock, G is the universal gravitational constant, and R is the radius of the buried structure.

The expression for the gravity anomaly forward problem can be represented generally in discrete form as

$$ d^{\text{cal}} = f(m), $$
(2)

where f is a forward modeling operator, which is non-linear in the present work, m = (R, σ, x 0, z, and q)T is a model parameter vector, and d cal is a predicted data vector. With measured data d obs the conventional way of solving an ill-posed inverse problem for m in Eq. (2) is based on the minimization data misfit functional, which is written as

$$ \phi \left( m \right)^{\text{NRMSE}} = \left( {\frac{{\sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left( {d_{i}^{\text{obs}} - d_{i}^{\text{cal}} } \right)^{2} } } }}{{d_{\hbox{max} }^{\text{obs}} - d_{\hbox{min} }^{\text{obs}} }}} \right), $$
(3)

where N is the total number of data point in d obs and ϕ(m)NRMSE is the normalized root-mean square error. The latter is often expressed as a percentage, where lower values indicate less residual variance. The following constrained multivariate problem is solved using particle swarm optimization algorithm:

$$ \begin{aligned} {\text{Minimize}}\phi \left( m \right)^{\text{NRMSE}} \hfill \\ {\text{Subject to}}\;R \ge 0,z \ge 0 \hfill \\ 0 \le q \le 2, \hfill \\ - \infty < \sigma < \infty \;\;{\text{and}} \hfill \\ - \infty < x_{0} < + \infty \hfill \\ \end{aligned}. $$

The Particle Swarm Optimization (PSO) Method

The PSO algorithm is based on the argument that social sharing of information among members of a species offers an evolutionary advantage (Kennedy and Eberhart 1995). It is inspired by the apparent behavior of a flock of birds collectively searching for food in their habitat. In implementation of the algorithm, birds are represented by “particles” and each particle consists of (a) a location vector in parameter space and (b) an associated velocity vector. Particles change position at each time step of the algorithm. The velocity vector helps determine the location of a particle at the next time step. As the algorithm progresses, PSO stores historical data for particles from previous time steps: (a) the best individual position obtained by each particle so far and (b) the best global position obtained by all particles so far.

Hence by knowing the above two parameters, the collection of all particles (the “swarm”) coordinates their movements in such a way that they progressively move toward the global optimum. Like many optimization algorithms, PSO can become trapped in a local optimum or can display non-convergent behavior. A constriction factor (Shaw and Srivastava 2007) can be used to mitigate these problems by gradually contracting the search space as the algorithm progresses. This helps the algorithm to surpass the local minima early in the search, and avoid non-convergence later in the search. The remainder of this section describes the PSO algorithm as implemented in this work.

Mathematical Formulation of GPSO

The particle swarm process is stochastic in nature; it uses the velocity vector and location of the best local and global values to update the current model parameters of each particle in the swarm and find the corresponding optimization function value at that location. The velocity vector associated with each particle is updated based on the history of each particle’s model parameters and misfit-function value. This history represents the “knowledge” gained by each particle, conceptually resembling an autobiographical memory, as well as the “knowledge” gained by the swarm as a whole (Eberhart and Kennedy 1995). Thus, the misfit-function value of each particle in the swarm is updated based on the social behavior of the swarm, which adapts to its environment by returning to promising regions of the solution space previously discovered and searching for optimal misfit-function values over time. Numerically, the value of an ith model parameter for the jth particle in the swarm at iteration k + 1 is updated as

$$ m_{i,j}^{k + 1} = m_{i,j}^{k} + v_{i,j}^{k + 1} \Delta t, $$
(4)

where \( v_{i,j}^{k + 1} \) is the corresponding updated velocity vector, and Δt is the time step value, typically considered as unity (Shi and Eberhart 1998). The velocity vector of each value of model parameter is calculated as

$$ v_{i,j}^{k + 1} = wv_{i,j}^{k} + c_{1} r_{{_{1,j} }}^{k} \frac{{\left( {p_{{i,{\text{best}}}}^{k} - m_{i,j}^{k} } \right)}}{\Delta t} + c_{2} r_{{_{2,j} }}^{k} \frac{{\left( {p_{{i,g{\text{best}}}}^{k} - m_{i,j}^{k} } \right)}}{\Delta t}, $$
(5)

where \( v_{i,j}^{k + 1} \) is the velocity vector of the ith model parameter for the jth particle in the swarm at iteration k; \( m_{i,j}^{k} \) is the value of the ith model parameter for the jth particle in the swarm at iteration k; \( p_{{i,{\text{best}}}}^{k} \) is the value of the ith model parameter for the personal best misfit-function value recorded by the jth particle in the swarm, from initialization through iteration k; \( p_{{i,g{\text{best}}}}^{k} \) is the ith model parameter of the global best misfit-function value recorded by the swarm, from initialization through iteration k; w is the inertia weight; \( r_{1,j}^{k} \) and \( r_{1,j}^{k} \) each represents a random number in the interval [0, 1] at iteration k; c1 and c2 are the positive acceleration constants which are used to weight the contribution of the cognitive parameter and social parameter, respectively.

Figure 2 illustrates updating the value of ith model parameter and velocity for jth particle of the swarm using Eq. (4). Note that the updated model parameter is affected not only by the local and global optimal parameters, but also by the magnitude of the cognitive parameter \( c_{1} \), social parameter \( c_{2} \) and inertia weight \( w \). Figure 3 shows that each particle is evaluated at step k, and the personal best value \( p_{{i,{\text{best}}}} \) of that particle, as determined by the misfit function, is recorded. In addition, the particle that has the lowest value of all the personal best values is denoted as \( p_{{i,{\text{best}}}} \), and is recorded.

Figure 2
figure 2

GPSO model parameters and velocity update (modified from Perez and Behdinan 2007)

Full size image
Figure 3
figure 3

Flow chart for the GPSO algorithm

Full size image

The implementation of PSO in this paper uses the following parameters: swarm size (number of particles), number of iterations, velocity components, acceleration coefficients, and inertia weights. These are discussed briefly in turn.

Swarm Size and Number of Generations

Swarm size or population size is the set of particles in the swarm. A small set of particles may reduce the number of generations needed to obtain a good optimization result. In contrast, a large population size increases the computational complexity. Table 1 shows the marginal benefit of dramatically increasing the swarm size; the number of generations to convergence is reduced by about 20% due to 15× increase in swarm size time to convergence. The number of generations needed to obtain a good result is also problem dependent. A too low number of generations may stop the search process prematurely, while a too large number of generations have the consequence of unnecessarily added computational complexity and more time needed (Perez and Behdinan 2007).

Table 1 Effect of population size over computation time
Full size table

Velocity Components

The velocity components are very important for updating particle’s velocity. There are three terms of the particle’s velocity as shown in Eq. (5):

  • The term \( v_{i,j}^{k} \) is the inertia component that provides a memory of the previous swarm direction (i.e., movement in the immediate past). This component represents a momentum that prevents (a) drastic change in the direction of the particles and (b) bias toward the current direction.

  • The term \( c_{1} r_{{_{1,j} }}^{k} \frac{{\left( {p_{{i,{\text{best}}}}^{k} - m_{i,j}^{k} } \right)}}{\Delta t} \) is the cognitive component that measures the performance of the particles relative to past performances. This component represents an individual memory of the position that was the best for the particle. The effect of the cognitive component is the tendency of particles to return to positions that satisfied them most in the past. The cognitive component referred to as the nostalgia of the particle.

  • The term \( c_{2} r_{{_{2,j} }}^{k} \frac{{\left( {p_{{i,g{\text{best}}}}^{k} - m_{i,j}^{k} } \right)}}{\Delta t} \) is the social component that measures the performance of the particles relative to a swarm. The effect of this component is that each particle move toward the best position found by the particle’s neighborhood.

Initialization

Particles are randomly initialized across the entire domain of the misfit function. This is to ensure, as much as possible given the population size, that the entire misfit-function domain has the potential to be searched, and no region is left unexplored. This increases the chances of finding the global optimum, if it exists. The domain is defined by m min and m max, which represent the minimum and maximum ranges of m for the ith model parameter, respectively. Initialize a set of model parameters \( m_{i,j}^{0} \) and velocities \( v_{i,j}^{0} \) randomly distributed throughout the model space bounded by specified limits as

$$ m_{1,j}^{0} = m_{\hbox{min} ,j} + r_{1,j} \left( {m_{\hbox{max} ,j} - m_{\hbox{min} ,j} } \right), $$
(6)
$$ v_{i,j}^{0} = \frac{{m_{1,j}^{0} = m_{\hbox{min} ,j} + r_{1,j} \left( {m_{\hbox{max} ,j} - m_{\hbox{min} ,j} } \right)}}{\Delta t}, $$
(7)

where m min,j and m max,j represent the lower and upper model parameter variables bounds, respectively, and r represents a random number in the interval [0, 1].

Acceleration Coefficient and Inertia Weight

Perez and Behdinan (2007) demonstrated that a particle swarm is stable only if the following conditions are satisfied:

$$ 0\,<\,c_{1} + c_{2} \,< \,4 $$
(8)
$$ \left( {\frac{{c_{1} + c_{2} }}{2}} \right) - 1 < w < 1. $$
(9)

If the above conditions are satisfied, the system is guaranteed to converge to a local optimum value. However, it is not guaranteed to converge to the global optimum value, and its acceptability as a solution should be verified by misfit functional (i.e., the convergence criterion set by the user). The final term, w, is the inertia weight, which scales the current velocity vector. This controls the influence of the current velocity vector on the updated velocity vector. Large inertia weights increase the magnitude of the updated velocity vector, allowing the algorithm to explore the solution model space globally (Perez and Behdinan 2007), and reduce the influence of the local and global velocity terms, increasing the inertia of the current velocity vector term. Conversely, small inertia values reduce the inertia of the current velocity vector, so that the updated velocity vector is influenced by the local and global terms and concentrates updated searches in the nearby regions of the model space. A variation of inertia weight has been proposed by decreasing linearly at each iteration as (Shi and Eberhart 1998)

$$ w_{k + 1} = w_{\hbox{max} } - \left( {\frac{{w_{\hbox{max} } - w_{\hbox{min} } }}{{k_{\hbox{max} } }}} \right)k, $$
(10)

where \( w_{\hbox{max} } \) and \( w_{\hbox{min} } \) are the maximum and minimum values of inertia weight, respectively, \( k_{\hbox{max} } \) is the maximum iteration number, and k is the current iteration number.

A desktop PC with Intel Core2Duo was used to execute in the present work. To obtain the result, the present GPSO approach took around 0.8 s in which five number of model parameter has been optimized. The program was developed in Window 7 environment using MATLAB (R2015a).

Results

In the present work, the same PSO parameters were used for synthetic (noise-free and contaminated) and field data. The experiments were conducted with 20 tests using the following parameters: population size = 40, the number of generation = 200, and c 1 and c 2 were 1.2 and 1.7, respectively. The maximum and minimum values of inertia weight were 0.9 and 0.4, respectively.

Synthetic Examples

The GPSO optimization, as described in “The Particle Swarm Optimization (PSO) Method” section, was applied to interpret noise-free and noisy synthetic residual gravity anomaly data. Forward models of the residual gravity anomaly were calculated for a sphere, horizontal, and vertical cylinder-type model, with zero noise and with 10% Gaussian noise added. In the first application of GPSO to the synthetic gravity anomaly data, all model parameters were optimized for each dataset. Subsequently, the shape factor was fixed to its known value, 1.5 for sphere, 1.0 for horizontal cylinder, and 0.5 for vertical cylinder, and the GPSO was repeated for these values.

Model 1 (Sphere)

Synthetic data were generated using Eq. (1) for a spherical model (Table 2). Next, 10% Gaussian noise was added to the synthetic data, yielding a total of two synthetic gravity anomaly datasets. GPSO was then performed to estimate the (known) parameters (R, σ, x 0, z, and q) of the idealized bodies, using Eq. (3) as the objective function. Initially, a wide suitable search range for the various model parameters was selected and GPSO was executed. Figure 4 shows the convergence pattern of various model parameters and the normalized root-mean square error (NRMSE) after GPSO for a single solution. The mean of the (local) particle best values (blue curves) converge to the best global value (red curves), because the best global value initially has only one particle and then over time other particles converge to the region. Therefore, the mean of all the best individual particle values has a greater spread and initially underestimates (for a local maximum) the best value, gradually converging to the best value as more particles converge on the global best value. If the shape factor (q) is free, the standard deviations of the various model parameters (Table 2) tend to be higher than if the shape factor (q) is fixed. If the shape factor is fixed to its actual value, the misfit of the model parameters with the actual value decreases and the final model parameters are close to the actual value (Fig. 5). If the shape factor (q) is free, the frequency distributions of the different parameters for sphere show a wide range of solutions for R, σ, and z (Fig. 6). However, the location of the body can be precisely determined and the shape factor shows that it is within the range of actual value. If the shape factor (q) is fixed, the depth of the body and its location are more precisely determined; however, the radius and the density have wide frequency distributions (Fig. 7). This implies that the radius and the density cannot be determined very precisely and the parameters remain uncertain even if the shape factor is fixed. In order to analyze the effect of errors in the data for estimating the model parameters by using the GPSO, we generated the cross-plots (Fig. 8) between various model parameters if two parameters are kept free and the remaining parameters are fixed. The cross-plot between density and radius shows a wide range of solution suggesting that these two parameters are ambiguous. However, the cross-plots show that the other parameters can be determined very precisely. The cross-plots indicate that except for density and radius model parameters converge toward the global minimum of the corresponding model.

Table 2 Comparison of actual and GPSO-estimated parameters for a spherical model of noise-free synthetic data and synthetic data with 10% Gaussian noise
Full size table
Figure 4
figure 4

Convergence pattern for model parameters radius (R), density contrast (σ), depth (z), location (x 0), and shape factor (q) for sphere—(Model 1) when shape factor (q) is free

Full size image
Figure 5
figure 5

Convergence pattern for the model parameters radius (R), density contrast (σ), depth (z), location (x 0), and shape factor (q) for sphere—(Model 1) when shape factor (q) is fixed

Full size image
Figure 6
figure 6

Frequency distribution of model parameters (i.e., radius (R), density contrast (σ), depth (z), location (x 0), and shape factor (q) for sphere—(Model 1) when shape factor (q) is free

Full size image
Figure 7
figure 7

Frequency distribution of model parameters (i.e., radius (R), density contrast (σ), depth (z), and location (x 0) for sphere—(Model 1) with noise-free synthetic data when shape factor (q) is fixed

Full size image
Figure 8
figure 8

Cross-plots for sphere—(Model 1) when two of five parameters are variable, rest of them are fixed, for noise-free data. a Vicinity of variation of R and σ (R = 50 m, σ = 2 g/cc). b Variation of R and z (R = 50 m, z = 100 m). c Variation of σ and z (σ = 2 g/cc, z = 100 m). d Variation of σ and x 0 (σ = 2 g/cc, x 0 = 250 m). e Variation of z and x 0 (z = 100 m, x 0 = 250 m). f Variation of x 0 and q (x 0 = 250 m, q = 1.5)

Full size image

Next, GPSO was applied to the noisy data (10% Gaussian). The results of the noisy data were worse with respect to noise-free data but the results have less than 10% error. Adding some Gaussian noise to the data results in some ambiguous model parameters. The frequency distributions of the model parameters show that the exact points are shifted from the global minimum (Fig. 9), which results in some ambiguity of the model parameters. The error level directly affects the area of the global minimum of corresponding model parameters as can be seen from the cross-plots diagram (Fig. 10). Figure 11 depicts a comparison between the observed and the mean model data for noise-free and noisy synthetic data.

Figure 9
figure 9

Frequency distribution of model parameters radius (R), density contrast (σ), depth (z), and location (x 0) for sphere—(Model 1) when shape factor (q) is fixed for synthetic data with 10% Gaussian noise

Full size image
Figure 10
figure 10

Cross-plots for sphere—(Model 1) when two of five parameters are variable, rest of them are fixed. For synthetic with 10% Gaussian noise. a Vicinity of variation of R and σ (R = 50 m, σ = 2 g/cc). b Variation of R and z (R = 50 m, z = 100 m). c Variation of σ and z (σ = 2 g/cc, z = 100 m). d Variation of σ and x 0 (σ = 2 g/cc, x 0 = 250 m). e Variation of z and x 0 (z = 100 m, x 0 = 250 m). f Variation of x 0 and q (x 0 = 250 m, q = 1.5)

Full size image
Figure 11
figure 11

Observed data and GPSO solution for sphere—(Model 1): noise-free synthetic data (top) and synthetic data with 10% Gaussian noise (bottom)

Full size image

Model 2 (Horizontal Cylinder)

For the synthetic model of a horizontal cylinder a forward model was generated without noise (Table 3), as well as with an addition of 10% Gaussian noise. The convergence patterns for each of the parameters of Model 2 are similar to those of Model 1 (Figs. 4, 5), but the figures are not shown here for brevity and because of page limitations. The parameter q was estimated in the first application of GPSO, and then was fixed for subsequent applications, as in the spherical case. The frequency distribution of each model parameter (depth and location) converges toward actual value (Fig. 12) however, the other two parameters remain uncertain when the shape factor is fixed. The frequency distribution of model parameters using the noisy data (10% Gaussian) (Fig. 13) are similar to those for the sphere model (Fig. 9). The cross-plot analyzed for horizontal cylinder model was also similar to those of sphere model (Figs. 8, 10) and are not shown here for brevity and because of page limitations. The final horizontal cylinder model parameters from those of noise-free and noisy data are compared in Table 3. Figure 14 illustrates the difference between the observed and the mean model data for noise-free and noisy synthetic data.

Table 3 Comparison of actual and GPSO-estimated parameters for a horizontal cylindrical model of noise-free synthetic data and synthetic data with 10% Gaussian noise
Full size table
Figure 12
figure 12

Frequency distribution of model parameters for horizontal cylinder—(Model 2) when shape factor (q) is fixed for noise-free synthetic data

Full size image
Figure 13
figure 13

Frequency distribution of model parameter for horizontal cylinder—(Model 2) when shape factor (q) is fixed for synthetic data with 10% Gaussian noise

Full size image
Figure 14
figure 14

Observed data and GPSO solution for Horizontal cylinder—(Model 2): noise-free synthetic data (top) and synthetic data with 10% Gaussian noise (bottom)

Full size image

Model 3 (Vertical Cylinder)

The theoretical noise-free and noisy data inversions were also carried out for Model 3 (vertical cylinder) keeping the shape factor free as well as fixed to interpret the model parameters. The convergence patterns for each of the parameters for Model 3 are similar to those of Model 1 (Figs. 4, 5) and are not shown here for brevity and because of page limitations. The frequency distribution of the model parameters obtained from the noise free for the vertical cylinder model (Fig. 15), when the shape factor is fixed, are similar to those for the sphere and horizontal cylinder models. The frequency distributions of the model parameters obtained from the noisy data for the vertical cylinder model (Fig. 16), when the shape factor is fixed, are similar to those for the sphere and horizontal cylinder models. The final vertical cylinder model parameters from the noise-free and noisy data are compared in Table 4. Figure 17 illustrates the difference between the observed and the mean model data for noise-free and noisy synthetic data.

Figure 15
figure 15

Frequency distribution of model parameters for vertical cylinder—(Model 3) when shape factor (q) is fixed for noise-free synthetic data

Full size image
Figure 16
figure 16

Frequency distribution of model parameter for vertical cylinder—(Model 3) when shape factor (q) is fixed synthetic data with 10% Gaussian noise

Full size image
Table 4 Comparison of actual and GPSO-estimated parameters for a vertical cylindrical model of noise-free synthetic data and synthetic data with 10% Gaussian noise
Full size table
Figure 17
figure 17

Observed data and GPSO-optimized solution for vertical cylinder—(Model 3): noise-free synthetic data (top) and synthetic data with 10% Gaussian noise (bottom)

Full size image

Field Examples

Humble Dome Anomaly, Houston, Texas, USA

Residual gravity data over the Humble Dome near Houston (Texas) were taken from Nettleton (1976). Humble Dome is a geological feature that has been studied for its oil and gas potential. Nettleton (1976) analyzed the residual gravity data and estimated the depth and dimensions of the geologic body causing a significant negative gravity anomaly over the Humble Dome. The gravity anomaly over this dome was also interpreted by several authors (Shaw and Agarwal 1990; Abdelrahman et al. 2001a; Salem and Ravat 2003; Salem et al. 2003, 2004; Tlas et al. 2005; Asfahani and Tlas 2012; Mehanee 2014, Biswas 2015), all of whom assumed a spherical structure for the geological body generating the anomaly. Optimization methods that have been used for interpretation of residual gravity anomaly include adaptive simulated annealing (Tlas et al. 2005), fair function minimization (Asfahani and Tlas 2012), simultaneous regularized inversion (Mehanee 2014), and very fast simulated annealing (Biswas 2015). Parameters for the spherical source of the anomaly based on these optimization techniques are summarized in Table 5. We applied GPSO to estimate optimal parameters for a spherical source (fixed q). The anomaly is obtained by digitizing at 610 m interval based on the earlier literature. The estimated parameters are shown in Table 5. The results reveal that GPSO yields results similar to those obtained using the other optimization methods. The observed data and GPSO-predicted anomaly are shown in Figure 18a. It must be mentioned that we consider the radius and the density as model parameters in this work instead of a combined amplitude coefficient (k) as mentioned in Eq. (1). However, the main model parameters for exploration study are to determine precisely the location and depth of the source body along with its radius and density.

Table 5 Search range and estimated parameters for a spherical source body, Humble Dome Anomaly, Houston, Texas, USA
Full size table
Figure 18
figure 18

Agreements between observed data and GPSO solution using a spherical source body for the Humble Dome Anomaly, Houston, Texas, USA; b vertical cylindrical source body for the Leona Anomaly, South Saint-Louis, Western Coastline, Senegal; c horizontal cylindrical source body for the Karrbo Gravity Anomaly, Sweden; d horizontal cylindrical source body for the Offshore Louisiana Salt Dome Anomaly, USA; and (e) horizontal cylindrical source body for the Mobrun Anomaly, Noranda, Quebec, Canada

Full size image

Leona Anomaly, South Saint-Louis, Western Coastline, Senegal

Residual gravity data along a profile length of 30 km over an anomaly in the west coast of Senegal (West Africa) were taken from Nettleton (1976). The anomaly has been studied for its oil and gas potential. The anomaly was digitized with an equal interval of 500 m. This anomaly has also been previously interpreted as a spherical source body (Tlas et al. 2005; Asfahani and Tlas 2012) and as a vertical cylindrical source body (Mehanee 2014; Biswas 2015). The parameters of the source body estimated in the previous study are summarized in Table 6. The present study assumes that the source body is a vertical cylinder. The GPSO results agree well with the results of Mehanee (2014) and Biswas (2015), strengthening the interpretation of the source body as a vertical cylinder. The observed data and GPSO vertical cylinder model are shown in Figure 18b. The GPSO algorithm converges toward a vertical cylindrical body and consistently yielded better results for vertical cylindrical body. Moreover, the results estimated using a vertical cylindrical body is more accurate for vertical cylinder as compared to a spherical body.

Table 6 Search range and estimated parameters for the Leona Anomaly, South Saint-Louis, Western Coastline, Senegal
Full size table

The Karrbo Gravity Anomaly, Sweden

Residual gravity data along a profile of 25.6 m over a pyrrhotite ore body at Karrbo (Vastmanland, Sweden) were taken from Shaw and Agarwal (1990). This geologic feature has been studied for its iron ore and sulfide mineral potential. Results of previous analysis and the present analysis are shown in Table 7. The observed data and interpreted mean model response from this present study are shown in Figure 18c. The depth of the body assessed by the present study is 4.70 m. The depths obtained by Tlas et al. (2005) were 4.82 m, using adaptive simulated annealing and Asfahani and Tlas (2012) was 4.84 m using fair function minimization. The results are also in good agreement with the other results as shown in Table 7. The estimated misfit based on GPSO is very low.

Table 7 Search range and estimated parameters for the Karrbo Gravity Anomaly, Sweden
Full size table

Offshore Louisiana Salt Dome Anomaly, USA

Residual gravity data over a salt dome offshore Louisiana (USA) was taken from Nettleton (1976) and Roy et al. 2000. This geologic feature has been studied for its oil and gas potential. The results from the previous and present studies are shown in Table 8. The observed field data and interpreted mean model response in this study are shown in Figure 18d. The depth of the body estimated in the present study is 2874.8 m with a misfit of about 7%. The depths obtained by Mehanee (2014) using regularized inversion and by Biswas (2015) using very fast simulated annealing were 2899 and 2702 m, respectively.

Table 8 Search range and estimated parameters for the Offshore Louisiana Salt Dome Anomaly, USA
Full size table

Mobrun Anomaly, Noranda, Quebec, Canada

Residual gravity anomaly data over a massive sulfide ore body in the Noranda Mining District (Quebec, Canada) were taken from previous studies (Siegel et al. 1957; Grant and West 1965; Roy et al. 2000). The results from previous and present studies are shown in Table 9. The observed field data and interpreted mean model response from the present study are shown in Figure 18e. The depth of the body estimated in the present study is 46.69 m. which is very close to the depths obtained by Mehanee (2014) and Biswas (2015).

Table 9 Search range and estimated parameters for the Mobrun Anomaly, Noranda, Quebec, Canada
Full size table

Discussion

Standard geometrical shapes of gravity anomalies such as sphere, horizontal cylinder, vertical cylinder, or sheet-type structures, cannot be found in natural conditions. Hence, modeling and inversion of gravity data from field surveys using standard geometrical formulation may not give the actual subsurface structure. If the geologic data suggest that subsurface bodies are irregularly shaped (e.g., complexly folded and faulted), then modeling the subsurface shape of such bodies as idealized spheres or cylinders is not likely to yield meaningful results. In such a case, the multi-dimensional objective (misfit/error) function will be complex and, thus, application of a simple iterative inversion approach may fail to demonstrate the actual subsurface structure. Hence, global optimization is needed to deal with such a case. Moreover, it must be emphasized that irregular-shaped bodies cannot be determined very accurately using any interpretation method unless there is a good knowledge about the geology of the area and log data.

The GPSO method consistently yields lower misfit for theoretical and field examples. The field examples show that the method is robust and can be applied effectively with default parameters, whereas other methods may not be so. When low to moderate misfits are acceptable, it is appropriate to let GPSO estimate the shape factor. This is demonstrated from the results with synthetic data which yield near-true value of the shape factor. When data are noisy, as is the case from the field examples, we do not know what type of noise is added in the data. However, as demonstrated from the results with noisy data, finding global minimum is somewhat critical but certainly not hard to find. In some cases, we may get results within local minima that are close to the actual global minima. In such situation, both solutions are viable but the final interpretation would be misleading. Hence, it is preferable to estimate the shape factor and then fix the shape factor to decide on the nature of the body. This way we can also reduce the error in the final interpretation. Also, from the noisy data, the resulting misfit is less than 1–10%, which is also acceptable along with the field examples.

When using regional gravity data to predict large structures, such as depth and configuration of sedimentary basins, a misfit of <10% would be an excellent result. This is because modeling results are sensitive to small lateral changes in density, and the distribution of density in the subsurface is largely unknown at the scale of structural basins. Depending on the application, a misfit of <10% is acceptable and it is appropriate to model the shape factor as well as the other parameters. This is especially true in places where all information of geologic evidence does not provide enough clue as to what the shape factor is. Hence, it is prudent to first estimate the shape factor and, depending on the interpretation of the type of structure, to fix the shape factor to its actual value. This provides the advantage of finding the least error solution. The GPSO solutions obtained in this study are very optimal and compare very well with solution obtained by other interpretation methods. The convergence rate of the GPSO is even faster than the other methods as applied for the interpretation of gravity data. In comparison, the results of the GPSO in this study with results from previous studies using other interpretation methods, the equation for the objective function or the misfit error is different than in other interpretation methods and hence the errors measured from the previous studies are different and not shown in Tables 5, 6, 7, 8, and 9.

Conclusions

The results obtained using GPSO from field gravity data showed good agreement with the results obtained using other inversion methods in previous studies. The results of the implementation of the GPSO algorithm developed in the present study for the interpretation of residual gravity anomaly data are comparable to results using other inversion algorithms in terms of computation time and misfit error. However, the GPSO provides impressive convergence rate curves with the ability to find low-misfit geophysical models much faster than other interpretation methods when using the same initial population and search space.