Analytical Methods in the Interpretation of Self-Potential Anomalies—A Comprehensive Review

Abstract

The self potential (SP) method is one of the simple, elegant and economical geophysical tools that has many diverse applications in the subsurface exploration for minerals, ground water etc. It is a passive method based on the natural occurrence of electrical field ranging from less than a milli volt to a maximum of one or two volts on/under the surface of earth. The surface measurements of SP caused by subsurface targets can be estimated in terms of its size, dimension, depth, width, inclination etc. often by qualitative methods directly from the shape of the anomalies. In this, the profile shape, amplitude, polarity and contour pattern are also considered. In addition, the target/source is assumed to lie directly below the minimum of the anomaly. On the other hand, a large number of quantitative methods that are in vogue approximate the subsurface targets as regular geometrical shapes such as cylinder, sphere etc. These quantitative methods are mostly based on mathematical transforms such as Fourier, Hartley, Hilbert transforms and some of their modifications in addition to a few soft computing tools like artificial neural network (ANN) etc. In this chapter, some of these methods are illustrated with theoretical examples and also exemplified with real field data. A simplified mathematical treatment of these techniques, the merits of the methods are also included.

1.1 General Introduction

The self-potential (SP) method is one of the oldest methods that was proposed in the beginning of nineteenth century (1830) by Robert Fox) who carried out SP experiments with mines in UK. The SP method is a passive method similar to gravity and magnetic methods that measures the natural electrical potential observed on/in the subsurface due to geological/hydrogeological and geochemical reasons which usually cause potential difference between any two measuring points. The major factor for the origin of SP is ground water and is sensitive to the flow of the ground water and to the chemistry of both the pore water and the pore water mineral interface. The SP is also known as Static potential or Spontaneous potentials that are usually caused by charge separation in clay or other minerals, due to the presence of semi-permeable interface impeding the diffusion of ions through the pore space of rocks, or by natural flow of a conducting fluid through the rocks. In most cases, the SP measured is only related to the electrochemical potential. The potentials are measured in millivolts (mV) relative to a reference point (base station), where the potential is assumed to be zero volts. SP can range from less than a milli volt (mv) to over one volt and the sign of the potential is an important diagnostic factor in the interpretation of SP anomalies.

Further, there exist two different types of SP anomalies namely mineral potential and background potential. The mineral potential is due to sulphide ore bodies—generally –ve in the range of a few 100 mv and it is the most important in mineral exploration associated with massive sulphide ore bodies. It is characterized by large negative SP anomalies (100–1000 mV) that can be observed particularly over deposits of pyrite, chalcopyrite, pyrrhotite, magnetite,and graphite. The potentials are almost invariably negative over the top of the deposit and are quite stable in time. Also, mineral potential is constant and unidirectional due to electrochemical processes. Background potential is due to geochemical process, bioelecric activity, ground water movement and topography, either + ve or –ve and ranges from less than 300 mv except in the case of topography wherein it varies up to −2 V. Background potentials fluctuate with time caused by different processes ranging from AC currents induced by thunderstorms.

Variations in Earth’s magnetic fields, effects of heavy rainfalls etc. also fluctuate  background potentials. Generally to measure SP, two non polarisable porous pot electrodes are connected to a high precision multi meter with an impedance >10⁸ Ω and capable of measuring to at least 1 mv.Each electrode is made up of a copper (cu). Electrodes dipped in a saturated solution of copper sulphate (CuSo₄) which can penetrate through the porous base to the pot in order to make electrical contact with the ground. Zinc & silver electrodes and their respective sulphate solutions can also be used.

There are two techniques by which SP can be measured and they are known as potential gradient and potential amplitude. In potential gradient method, two electrodes at a fixed separation (5–10 m) between which the potential difference- pd- measured is divided by the electrode separation results potential gradient in mv/m. The point to which this observation applied is the mid point between two electrodes. The electrodes are moved along the traverse and the pd measured every time and recorded. On the other hand, in potential amplitude method, one electrode is fixed at a base station on a mineralized ground and to measure the pd, the second electrode is moved along the traverse. Depth of investigation ranges approximately 30–100 m depending upon the depth to targets as well nature of overburden.

Generally, SP consists of two different components of potentials known as Static and Variable potential. Static part of SP is called signal and the variable part of SP is termed as noise. The variable part is due to atmospheric effect which is in the range of 5–10 Hz and at best be minimized by repeated measurements along the profile and averaged for further interpretation. Electrical noise may incur if the measurements are made too soon after heavy rain or near running water. Best be avoided by suspending the SP work during rainy days. Topography also causes minor variation and hence require correction.

Further, SP measured over a large area may have a regional trend due to “telluric current” of 100 mv/km. Mineral potential may be superimposed upon this regional gradient. Prior to interpretation of the anomaly which is due to the source/target, it has to be isolated from regional gradient as is done in gravity regional and residual separation (R/R) separation. Topography causes potential variation particularly at the highly elevated locations, the SP anomaly is –ve for which a minor correction need to be applied prior to interpretation.

1.2 Interpretation of SP Anomalies

Usually, interpretation consists of looking for the order of magnitude of anomalies in the range 0–20 mv as normal variation, 20–50 mv possibly of interest, especially if observed over a fairly large area, more than 50 mv as definite anomaly and 400–1000 mv as very large anomalies. Generally, SP anomalies are interpreted by means of “qualitative method”, wherein the target/source is assumed to lie directly below the minimum of the anomaly. The anomaly half width provides a rough estimate of depth. The symmetry or asymmetry of anomaly provides the attitude of the body. The presence and type of over burden can have strong effect on the presence or absence of SP anomaly. For example sand has very little effect where as a clay cover may mask the SP anomaly of the subsurface source/target.

In quantitative interpretation of SP anomalies, generally it is assumed that the causative bodies to be regular geometrical shapes that can be described with appropriate analytical formulas. Logarithmic-curve matching (Murty and Haricharan 1984), the method of characteristic points (Rao et al. 1970), and the method of nomograms (Bhattacharya and Roy 1981) all involve many approximations. The method of least squares necessitates a series of trials to minimize the error between the observed and calculated values. Spectral analysis is reliable only for very long profiles. Whereas the ease of use and accuracy of results vary with the specific interpretation technique, they are all subject to many constraints. None of these methods yields a precise location of origin of the source of the anomaly, which is a prerequisite for meaningful interpretation.

Some of the analytical methods of self potential anomaly interpretation based on mathematical tools and techniques employing Hilbert transform, modified Hilbert transform/Sundararajan transform, Fourier transform/Hartley transform, Mellin transform etc.besides soft computing tools such as artificial neural networks (ANN) etc.play a significant role to realize reliable estimation of source parameters of subsurface targets. In this chapter, a brief review of these mathematical tools and the process of interpretation are given as hereunder.

During early 1990s, Sundararajan et al. (1990, 1998), Sundararajan and Chary (1993) suggested the use of Hilbert transforms for the interpretation of SP anomalies because this method is effective in the presence of random noise. This method is based on using the real roots of the anomaly and its Hilbert transform/modified Hilbert transform, horizontal and vertical derivatives, avoids many of the drawbacks listed above. In addition, a precise location of origin is achieved by using the Hilbert transform and its modified version by means of amplitude of analytic signal. The method is simple, elegant, straightforward, and above all is free from any assumptions. It also can be automated easily. Theoretical and field examples illustrate the method in the following section of some selected models and well known field anomalies.

1.3 Hilbert Transforms

The Hilbert transform (HT) and its modified version in geophysical data processing and interpretation has gained importance over the last more than half a century (Nabhigian 1972; Mohan et al. 1982; Sundararajan et al. 1998, 2000; Sundararajan and Srinivas 2010). In these methods, the parameters of the causative bodies are evaluated as functions of some characteristic points of the anomaly and its Hilbert transform. The HT can physically be realized as a 90° (270° in the case of MHT) phase shifter is not only useful in extracting the parameters such as depth, inclination, width etc. of the causative bodies but also plays a significant role in exact spatial location of the subsurface sources. The modified Hilbert transform is also known as ‘Sundararajan transform’ in literature (Sundararajan et al. 2000). In this section, it is illustrated some basic concepts of HT and how they are applied in the interpretation of self potential anomalies of certain simple geometrical structures such as 2-D horizontal circular cylinder, sphere, inclined sheet etc.

The Hilbert transform HT(x) and modified Hilbert transform MHT(x) of self potential anomalies represented by any real function SP(x) can be defined as

$$HT1\left( x \right) = ~~\frac{1}{\pi }~\int_{0}^{\infty } {[Im~SP\left( \omega \right){\text{cos}}(\omega x) - ReSP\left( \omega \right){\text{sin}}\left( {\omega x} \right)]} d\omega$$

$$HT2\left( x \right) = ~~\frac{1}{\pi }~\int_{0}^{\infty } {[Im~SP\left( \omega \right){\text{cos}}(\omega x) + ReSP\left( \omega \right){\text{sin}}\left( {\omega x} \right)]} d\omega$$

where ${\text{ImSP}}\left({\upomega } \right)$ and ${\text{ReSP}}\left({\upomega } \right)$ are the imaginaray and real components of the Fourier transform of ${\text{SP}}({\text{x}})$ implying that the HT can be computed via the Fourier transform.

Alternatively, the HT can also be computed in space domain as convolution of SP(x) with $1/\pi x$ given by

$${\text{HT}}({\text{x}}) = (1/\pi x)*SP\left( x \right)$$

where * is the convolution operator.

Yet another way by which the Hilbert transform can be conceived is the horizontal and vertical derivatives of SP(x) that form a Hilbert transform pair. That is,

$$SP_{{x~}} \left( x \right)\left\langle { - - - - - } \right\rangle \,SP_{{z~}} \left( x \right)$$

Here $SP_{{z~}} \left( x \right)$ is the vertical derivative and  SPx(x) is the horizontal  derivative of the SP anomaly SP(x) which form the Hilbert transform pair.

1.4 Analytic Signal and Amplitude

Locating the origin is of paramount importance in the interpretation of all geophysical anomalies, that can be achieved with utmost accuracy by the amplitude of analytical signal in a couple of ways as discussed hereunder.

The analytic signal of a self potential represented by SP(x) can be expressed as:

$${\text{AS}}({\text{x}}) = {\text{SP}}({\text{x}}) - {\text{iHT}}({\text{x}})$$

where HT(x) is the Hilbert transform of SP(x). The amplitude of analytic signal can be deciphered as:

$${\text{A}}({\text{x}}) = \sqrt {SP\left( x \right)^{2} + ~HT\left( x \right)^{2} ~~}$$

In general, the amplitude A(x) of analytic signal attains its maximum exactly over the subsurface targets/source in structures whose width is less than the depth. On the other hand, for the structures whose width is greater than the depth, A(x) results two peaks flanked by a minimum at the centre. In this case, the minimum corresponds to the centre of the source/target and the distance between the two peaks yields the width of the target. Further, if the modified Hilbert transform HT2(x) is used for the extraction of parameters, then in the above relation, HT(x) can be replaced with its modified version HT2(x). This can be defined as under while using Hilbert transform or modified Hilbert transform (Nabhigian 1972; Sundararajan et al. 1998; Sundararajan and Srinivs 2010)

$${\text{A}}1({\text{x}}) = \sqrt {SP\left( x \right)^{2} + ~HT1\left( x \right)^{2} }$$

and

$${\text{A}}2({\text{x}}) = \sqrt {SP\left( x \right)^{2} + ~HT2\left( x \right)^{2} ~~}$$

Alternatively, the intersection of the HT1(x) and HT2(x) also corresponds to the origin (Fig. 1.1). Similarly, the amplitudes as defined above A1(x) and A2(x) do intersect over the origin (Fig. 1.2).

Fig. 1.1

Hilbert transform and its modified version

Fig. 1.2

Amplitudes A1(x) and A2(x) of analytic signal

1.5 2-D Horizontal Circular Cylinder

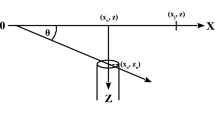
The geometry of obliquely polarized 2-D horizontal circular cylinder with radius is shown in Fig. 1.3. In the Cartesian coordinate system, ‘O’ is the origin which is on the surface at a point vertically above the center of the cylinder. The axis of the cylinder is parallel to the y-axis. AA′ is the axis of polarization. It makes an angle ‘α’ with the x-axis. P is the point of observation at a distance ‘x’ from the origin, ‘$\alpha$’ is the angle between the axis of polarization and the line passing through the centre of the sphere and P and Po is the point where the potential is zero. Therefore, the potential at a point P on the surface is given (Sundararajan and Srinivas 1996) as:

Fig. 1.3

Geometry of the 2-D horizontal circular cylinder

The self potential due to such a cylindrical structure can be expressed as (Sundararajan and Srinivas 1996):

$$SP1\left( x \right)~ = ~~~\frac{{A[~x~{\text{cos}}\left( \alpha \right) - ~zsin\left( \alpha \right)}}{{\left( {x^{2} + ~z^{2} } \right)}}$$

where z-is the depth to the centre of the cylinder, ‘α’ is the angle between the horizontal axis and the axis of polarization and A is a constant comprising the polarization current (I) and the resistivity $(\rho ).$

In this case, the computation of Hilbert transform HT1(x) and its modified version HT2(x) can be realized via the Fourier transform and therefore, the real and imaginary components of the Fourier transform of SP1(x) are derived as:

$$\text{ReSP} 1(\omega ) = K\pi ~sin\left( \alpha \right)e^{{ - \omega z}}$$

$$\text{lmSP} 1(\omega ) = K\pi ~cos\left( \alpha \right)e^{{ - \omega z}}$$

Using these ReSP1 $(\omega )$ and ImSP1 $(\omega )$ components in the equations of HT and the MHT, the Hilbert transform and its modified version can be obtained as:

$$HT1\left( x \right)~ = ~~~\frac{{A[~z~{\text{cos}}\left( \alpha \right) + {\text{}}~x~sin\left( \alpha \right)}}{{\left( {x^{2} + ~z^{2} } \right)}}$$

$$HT2\left( x \right) = \frac{{A[~z~{\text{cos}}\left( \alpha \right) - ~x~sin\left( \alpha \right)}}{{\left( {x^{2} + ~z^{2} } \right)}}$$

The graphical plots of SP1(x) and HT1(x) or [SP1(x) and HT2(x)] intersect at one point since SP1(x) and HT1(x) or H2(x) are of first degree in x and at this point of intersection say $x_{1}$, the following holds good:

$${\text{SP}}1({\text{x}}) = {\text{HT}}1({\text{x}})\,{\text{at}}\,{\text{x}} = x_{1}$$

$${\text{SP}}1({\text{x}}) = {\text{HT}}2({\text{x}})\,{\text{at}}\,{\text{x}} = x_{1}$$

That is, when

$${\text{SPl}}({\text{x}}) = {\text{HT}}1({\text{x}})$$

$$i,e\quad \frac{{A[~x~{\text{cos}}\left( \alpha \right) - ~zsin\left( \alpha \right)}}{{\left( {x^{2} + ~z^{2} } \right)}} = \frac{{A[~z~{\text{cos}}\left( \alpha \right) + {\text{~}}~x~sin\left( \alpha \right)}}{{\left( {x^{2} + ~z^{2} } \right)}}\,{\text{at}}\,{\text{x}} = x_{1}$$

On simplification it results, the depth ‘z’ as

$${\text{z}} = x_{1} \left[ {~\frac{{\sin \alpha - cos\alpha }}{{\sin \alpha + cos\alpha }}} \right]$$

This solution for depth ‘z’ is dependent in ‘α’ which itself is an unknown to be evaluated and therefore to be ignored. On the other hand, the following results the depth independently as a function of the abscissa as illustrated hereunder.

$${\text{SP}}1({\text{x}}) = {\text{HT}}2({\text{x}})$$

$$i,e\quad \frac{{A[~x~{\text{cos}}\left( \alpha \right) - ~zsin\left( \alpha \right)}}{{\left( {x^{2} + ~z^{2} } \right)}} = \frac{{A[~z~{\text{cos}}\left( \alpha \right){\text{~}} - ~x~sin\left( \alpha \right)}}{{\left( {x^{2} + ~z^{2} } \right)}}\,{\text{at}}\,{\text{x}} = x_{1}$$

Further simplification lead to the required solution for depth ‘z’ as,

$${\text{z}} = x_{1}$$

This implies that the depth is directly equal to the point of intersection of the SP anomaly SP1(x) and its modified Hilbert transform HT2(x). Once the depth is evaluated, the angle of polarization ‘α’ can be determined from the SP anomaly SP1(x) and its modified Hilbert transform HT2(x) as:

$$\alpha = \tan ^{{ - 1}} \frac{[{zSP1\left( x \right) - ~xHT2\left( x \right)]}}{{\left[ {xSP1\left( x \right) - ~zHT2\left( x \right)} \right]}}$$

A more accurate solution for ‘α’ can be obtained as an average taken over several values of ‘x'. Finally, the constant term consisting of I (the polarization current) and $\rho$ (resistivity) can be evaluated at x = 0 from equations SP1(0) and HT2(0) as under:

$${\text{A}} = \sqrt {SP1\left( 0 \right)^{2} + HT2\left( 0 \right)^{2} }$$

By knowing either current or the resistivity, the other quantity may fairly well be determined. Thus, the depth ‘z’, the polarization angle ‘α’ and the constant term can be estimated based on the above analysis.

Theoretical and Field Examples: The interpretation procedure elucidated above is illustrated with a theoretical model and exemplified with a field data of Sulleymonkey anomaly of length 260 m in the Ergani copper district, Turkey. The Hilbert and the modified Hilbert transforms HT1(x) and HT2(x) and the SP anomaly SP1(x) are computed and shown in Fig. 1.4 in the case of theoretical model. The point of intersection of Hilbert transform and the modified Hilbert transform yield precisely the origin, and the abscissa results the depth to the centre of the cylinder. The other parameters are evaluated as discussed in the text. Similarly, the Hilbert transform and its modified versions in addition to the amplitudes of field Sulleymonkey anomaly are computed and shown in Fig. 1.5a–c. The evaluated parameters in both theoretical as well as field examples are presented in Table 1.1 and compared with the other available methods.

Fig. 1.4

The self potential anomaly due to a 2-D horizontal circular cylinder, the Hilbert transform and the modified Hilbert transform of a theoretical model

Fig. 1.5

a The self potential field of Sulleymonkey anomaly in the Ergani copper District, Turkey, and the modified Hilbert transform b The Hilbert transform of the anomaly and its modified version and c The amplitudes A1(x) and A2(x)

Table 1.1 SP interpretation of theoretical model of 2-D horizontal circular cylinder and field self potential Sulleymonkey anomaly, Ergani copper district, Turkey

1.6 Spherical Structures

The geometry of the obliquely polarized sphere with radius ‘a’ is considered for the analysis and shown in Fig. 1.6. In the Cartesian coordinate system, ‘O’ is the origin, on the surface at a point vertically above the centre of the sphere. The axis of the sphere is parallel to the y-axis and AA’ is the axis of polarization, ‘$\theta$’ is included between the polarization and x-axis. P is the point of observation at a distance ‘x’ from the origin, ‘α’ is the angle between the axis of polarization and the line passing through the centre of the sphere and P. Q is the point where the potential is zero. The potential at a point P on the surface is given as (Sundararajan and Chary 1993):

$${\text{SP}}2({\text{x}}) = C\left[\frac{{z\cos \left( \theta \right) + ~x~{\text{sin}}\left( \theta \right)}}{{\left( {x^{2} + ~z^{2} } \right)^{{1/2}} }}\right]$$

Fig. 1.6

Geometry of the spherical structure

where ‘z’ is the depth to the centre of the sphere, ‘$\theta$’ is the angle of polarization and ‘C’ is constant comprising the current density (I) and the resistivity $(\rho )$ of the surrounding medium given by C = I $\rho$/2π.

As stated earlier, the horizontal and vertical derivatives of SP2(x) are obtained as:

$$~~SP_{{x~}} 2\left( x \right)~~ = {\text{}}C\left[ {~\frac{{(z~^{{2~~}} - ~2x^{2} )\sin \left( \theta \right) - ~3xzcos\left( \theta \right)}}{{\left( {x^{2} + ~z^{2} } \right)^{{\frac{5}{2}}} }}} \right]$$

$$SP_{{z~}} 2\left( x \right)~~ = {\text{}}C\left[ {~\frac{{(x~^{{2~~}} - ~2z^{2} )\cos \left( \theta \right) - ~3xzsin\left( \theta \right)}}{{\left( {x^{2} + ~z^{2} } \right)^{{\frac{5}{2}}} }}} \right]$$

At x = 0, the horizontal and vertical derivatives reduce to,

$$SP_{{x~}} 2\left( 0 \right)~~~ = Csin\left( \theta \right)/z^{3}$$

and

$$SP_{z~} 2\left( 0 \right) = - 2Ccos\left( \theta \right)/z^{3}$$

From the above relations, the angle of polarization ‘$\theta$’ can be determined as:

$$\theta = \tan ^{{ - 1}} [ - 2SP_{x~} 2\left( 0 \right)/SP_{z~} 2\left( 0 \right)]$$

Further, the derivatives $SP_{{x~}} 2\left( x \right)~$ and $SP_{{z~}} 2\left( x \right)$ are of second degree in x, they have two real roots say $x_{1}$ and $x_{2}$ and therefore it can be written as,

$$SP_{{x~}} 2\left( x \right)~~ = ~~SP_{{z~}} 2\left( x \right)\,{\text{at}}\,{\text{x}} = x_{1} \,{\text{and}}\,x_{2}$$

i, e $C\left[ {~\frac{{(z~^{{2~~}} - ~2x^{2} )\sin \left( \theta \right) - ~3xzcos\left( \theta \right)}}{{\left( {x^{2} + ~z^{2} } \right)^{{\frac{5}{2}}} }}} \right] = C\left[ {~\frac{{(x~^{{2~~}} - ~2z^{2} )\cos \left( \theta \right) - ~3xzsin\left( \theta \right)}}{{\left( {x^{2} + ~z^{2} } \right)^{{\frac{5}{2}}} }}} \right]$ at x = $x_{1}$ and $x_{2}$.

On simplification, the depth ‘z’ can be obtained as

$${\text{z}} = (x_{1} + ~x_{{2~}} )\left[ {~\frac{{\left( {\cos \left( \theta \right)~ + ~2\sin \left( \theta \right)} \right)}}{{3\left( {\sin \left( \theta \right) - \cos \left( \theta \right)} \right)}}} \right]$$

As $^{\prime } \theta ^{\prime } ,$ is known already, the depth can be evaluated from the above relation. However, it would be worth mentioning here that the depth tends to ‘∞’ at $\theta = 45~$° which is purely a hypothetical in such an analysis and that can be attributed to the fact that $(x_{1} + ~x_{{2~~}} ) = 0.~$ This introduces a catastrophe in the mathematical procedure. That is, the magnitude of the roots of the derivatives are equal and opposite in sign which is seldom encountered in practice in which case the depth further simplified as:

$${\text{z}} = x_{1} = - x_{2}$$

Finally, the constant term C can be evaluated as by squaring and adding $~SP_{{x~}}2\left( 0 \right)$ and $SP_{{z~}} 2\left( 0 \right)$ $as~$

$${\text{C}} = \frac{{2z^{3} \left[ {~SP_{{x~}} 2\left( 0 \right)^{2} ~ + {\text{}}SP_{{z~}} 2\left( 0 \right)^{2} } \right]^{1/2}{\text{}}}}{{\left( {1~ + 3cos^{2} \left( \theta \right)} \right)}}$$

Field Example: The procedure detailed above is exemplified by the well known ‘Weiss anomaly’ of the copper district in eastern Turkey. The anomaly represents the principle profile AA’ shown in the contour map (Fig. 1.7). The ‘Weiss’ anomaly is approximately 1 km north west of the Madam copper mine and is assumed to be due to spherical structure. The assumption is validated by comparing with the computed values and shown in Fig. 1.8. For further clarity, the ‘Weiss” anomaly is shown exclusively in Fig. 1.9. The horizontal derivative is obtained by the numerical differentiation and the vertical derivative is computed by the Hilbert transform. The horizontal and vertical derivatives along with amplitude of analytic signal are shown in Fig. 1.10. The depth (z) to the centre of the sphere and the angle of polarization $(\theta )$ are evaluated based on the analytical procedure discussed in the text and shown in the following Table 1.2. The depth (z) and the polarization angle $(\theta )$ obtained are compared with those of Youngal (1950) and the method of Bhattacharya and Roy (1981).

Fig. 1.7

Contour map of the self potential (Weiss) of the Ergani copper district in eastern Turkey with elevation. AA′ is the principle profile

Fig. 1.8

Measured and calculated self potential along AA’ over the Weiss anomaly, Ergani, Turkey

Fig. 1.9

Self potential anomaly (Weiss) of the Ergani copper district in eastern Turkey

Fig. 1.10

First horizontal derivative of the Weiss SP anomaly, the vertical derivative(the Hilbert transform) and their amplitude

Table 1.2 Interpreted parameters of Weiss SP anomaly, Ergani copper district of eastern Turkey

2-D Inclined Sheets.

The SP field at any given point P on the surface perpendicular to the strike of 2-D inclined sheet of infinite horizontal extent (Fig. 1.11) is given as (Murty and Haricharan 1985)

$${\text{SP}}3({\text{x}}) = \frac{{I\rho }}{{2\pi }}{\text{In}}\left[~\frac{{\left( {x - {\text{acos}}\left( \alpha \right)} \right)^{{2~}} + ~\left( {~h - {\text{asin}}\left( \alpha \right)} \right)^{{2~~}} }}{{\left( {x + {\text{acos}}\left( \alpha \right)} \right)^{{2~}} + ~\left( {~h - {\text{asin}}\left( \alpha \right)} \right)^{{2~~}} }}~\right]$$

Fig. 1.11

Geometry of the inclined sheet

where ‘h’ is the depth to the top of the sheet, $^{\prime } {\upalpha }^{\prime }$ is the inclination, ‘a’ is the half width, and ‘${\uprho }$’ is the resistivity and ‘I’ is the current density of the surrounding medium.

In this case SP3(x) is log function and hence, the partial differentiation with respect to ‘x’ frees the logarithm and yields the horizontal derivative from which the Hilbert transform and its modified version can be obtained as in the case of 2-D horizontal circular cylinder.

$$\begin{aligned} SP_{{x~}} 3\left( x \right)~ & = ~K\left[~\frac{{\left( {x - {\text{acos}}\left( \alpha \right)} \right)}}{{\left( {x - {\text{acos}}\left( \alpha \right)} \right)^{{2~}} + ~\left( {~h - {\text{asin}}\left( \alpha \right)} \right)^{{2~~}} }} \right. \\ & \qquad \;\; \left. + ~\frac{{\left( {x + {\text{acos}}\left( \alpha \right)} \right)}}{{\left( {x + {\text{acos}}\left( \alpha \right)} \right)^{{2~}} + ~\left( {~h + {\text{asin}}\left( \alpha \right)} \right)^{{2~~}} }}\right] \end{aligned}$$

The real and imaginary components of the Fourier transform of $SP_{{x~}} 3\left( x \right)$ can be obtained as:

$$\text{Re} SP_{x~} 3(\omega ) = K {\uppi }\sin (\omega \text{acos} (\alpha ))\left[ {e^{{ - \omega (h + {\text{a}}\sin (a))}} - e^{{ - \omega (h - {\text{a}}\sin (\alpha ))}} } \right]$$

$$\text{Im} SP_{x~} 3(\omega ) = K {\uppi }\cos (\omega \text{asin} (\alpha ))\left[ {e^{{ - \omega (h + {\text{a}}\sin (\alpha ))}} - e^{{ - \omega (h - {\text{a}}\sin (\alpha ))}} } \right]$$

Using these components in the equations of HT1(x) and HT2(x), the Hilbert transform and the modified Hilbert transform of $SP_{{x~}} 3\left( x \right)~$ can be obtained as:

$$\begin{aligned} {\text{HT}}1({\text{x}}) &= K\left[~\frac{{\left( {h - {\text{asin}}\left( \alpha \right)} \right)}}{{\left( {x - {\text{acos}}\left( \alpha \right)} \right)^{{2~}} + ~\left( {~h - {\text{asin}}\left( \alpha \right)} \right)^{{2~~}} }} \right. \\ & \left. \qquad + ~\frac{{\left( {h + {\text{asin}}\left( \alpha \right)} \right)}}{{\left( {x + {\text{acos}}\left( \alpha \right)} \right)^{{2~}} + ~\left( {~h + {\text{asin}}\left( \alpha \right)} \right)^{{2~~}} }}\right] \end{aligned}$$

$$\begin{aligned} {\text{HT}}2({\text{x}}) &= K\left[~\frac{{\left( {h - {\text{asin}}\left( \alpha \right)} \right)}}{{\left( {x - {\text{acos}}\left( \alpha \right)} \right)^{{2~}} + ~\left( {~h - {\text{asin}}\left( \alpha \right)} \right)^{{2~~}} }} \right. \\ & \left. \qquad + ~\frac{{\left( {h + {\text{asin}}\left( \alpha \right)} \right)}}{{\left( {x - {\text{acos}}\left( \alpha \right)} \right)^{{2~}} + ~\left( {~h + {\text{asin}}\left( \alpha \right)} \right)^{{2~~}} }} \right] \end{aligned}$$

It may be noted that the equation HT1(x) can also be obtained directly as the partial derivative of SP3(x) with respect to ‘h'.

Equations of $SP_{{x~}} 3\left( x \right)$ and HT1(x) are quadratic in x, hence we can write the following,

$$SP_{x~} 3(x) = {\text{HT}}1({\text{x}})\quad {\text{at}}\,{\text{x}} = x_{1} \,{\text{and}}\,x_{2}$$

where the roots $x_{1}$ and $x_{2}$ are nothing but, the abscissa of the points of intersection of the plots of $SP_{{x~}} 3\left( x \right)$ and HT1(x).

Further algebraic simplification results,

$$x^{2} + ~2Q~ahx + Qa^{2} - ~h^{2} ~~ = 0$$

Then, sum of the roots of this quadratic equation may be expressed as,

$$x_{1} + x_{2} = - 2{\text{Qh}}$$

where Q = $(\sin (\alpha ) - \cos (\alpha ))/(\sin (\alpha ) + \cos (\alpha ))$.

The above relation yields the depth ‘h’ once the value of ‘α’ is known.

Further, at x = 0, the equations $SP_{{x~}} 3\left( x \right)$ and HT1(x) reduce to,

$$\frac{{HT1\left( 0 \right)~~}}{{SP_{{x~}} 3\left( 0 \right)}}~ = [\frac{{(a^{{2~}} - h^{2} )}}{{(a^{{2~}} + h^{2} )}}\tan \left( \alpha \right)~ = ~S~$$

By simplifying the last three equations [quadratic in x, sum of the roots and the S], a cubic equation in $\tan \left( \alpha \right)$ is obtained as:

$${\text{A}}tan^{3} \left( \alpha \right) + Btan^{2} \left( \alpha \right) + ~C~\tan (\alpha ) + D = 0,$$

where

$${\text{A}} = 2x_{1} \cdot x_{2} ,\quad {\text{B}} = \left( {~x_{1} {\text{~}} + {\text{~}}x_{2} } \right)^{2} ~\left( {S - 1} \right) - ~A\left( {S + 2} \right)$$

$${\text{C}} = \left( {~x_{1} {\text{~}} + {\text{~}}x_{2} } \right)^{2} ~\left( {1 - S} \right) - ~A\left( {2S + 1} \right)\,{\text{and}}\,{\text{D}} = - {\text{SA}}$$

In this cubic equation in $\tan \left( \alpha \right),~$ $x_{1}$ and $x_{2}$ as well as S are known and hence ‘α’ can be determined.

Subsequently, the depth ‘h’ and the half width ‘a’ can also be evaluated as:

$${\text{h}} = \frac{{\left( {~x_{1} {\text{~}} + {\text{~}}x_{2} } \right)\left( {\cos \left( \alpha \right) + \sin \left( \alpha \right)} \right)}}{{\left( {\cos \left( \alpha \right) - \sin \left( \alpha \right)} \right)}}$$

$${\text{a}} = \sqrt {~\left( {x_{1} .x_{2} + {\text{~h}}^{2} } \right)\frac{{\left( {\cos \left( \alpha \right) + \sin \left( \alpha \right)} \right)}}{{\left( {\cos \left( \alpha \right) - \sin \left( \alpha \right)} \right)}}}$$

In evaluating ‘h’ and ‘a’, there is a singularity at $\alpha = 45$° which can be attributed to the fact that $(x_{1} + x_{2} ) = 0$ and $\left( {x_{1} .x_{2} + {\text{~h}}^{2} } \right) = ~0$ in the above equations. That is, the roots are equal and opposite. In such a case, the depth ‘h’ and the half width ‘a’are evaluated as

$${\text{h}} = x_{1} = - x_{2}$$

and

$${\text{a}} = {\text{h}} = \sqrt { - x_{1} \cdot x_{2} }$$

Finally the constant term ‘K’ ( K = I $\rho$) can be evaluated as:

${\text{K}} = \frac{{NR}}{{DR}}$ where

$${\text{NR}} = (a^{2} + ~h^{{2~}} - 2ahsin\left( \alpha \right))(\left( {a^{2} + ~h^{{2~}} - 2ahsin\left( \alpha \right)} \right)/2a$$

$${\text{DR}} = \sqrt {\left[ {~\frac{{\left( {a^{{4~~~}} + ~h^{{4~~~}} + ~2ahcos\left( {2\alpha } \right)} \right)~~}}{{SP_{{x~}} 3\left( 0 \right)^{2} + ~HT!\left( 0 \right)^{2} }}} \right]~}$$

where K being the product of polarization current (I) and the resistivity $^{\prime } \rho ^{\prime }$, with the knowledge of one of them, the other quantity can be estimated approximately. Thus, all the parameters like depth (h), half width (a), the polarization angle $(\alpha )$ and the constant term (K) can be determined from the above analysis (Sundararajan et al. 1998).

Field Example: The practicability of the method is tested on an SP profile (E −19 +100) in the Surda area of the Rakha mines Singhbhum copper belt, Bihar, India. The anomaly (Murthy and Haricharan 1984) of the profile is shown in Fig. 1.12. The first horizontal derivative is computed numerically, and the vertical derivative is obtained by means of the Hilbert transform. The derivatives, along with the amplitude, A(x) are shown in Fig. 1.13. The maximum value of the amplitude corresponds to the origin; the roots, are determined from the points of intersection of the derivatives. The parameters obtained are compared with the results of Paul (1965), Rao et al. (1970), Murthy and Haricharan (1984) and presented in Table 1.3. In the area under discussion, sulfides occur at depths ranging between 12.2 and 30.5 m. The present method yields a depth value of 27.65 m.

Fig. 1.12

SP field anomaly in Surda area of Rakha mines, Singhbhum copper belt, Bihar, India

Fig. 1.13

The horizontal and vertical derivatives with their amplitude of the SP anomaly of Rakha mines, Singhbhum copper belt, Bihar, India

Table 1.3 Hilbert transform interpretation of SP anomaly in the Surda area of the Rakha mines, Sighbhum copper belt, Bihar, India

1.7 Hartley Spectral Analysis of SP Anomalies

In general, the use of Hartley transform in geophysical data analysis has gained importance since the early 1990s (Saatcilar and Ergintov 1991, Sundararajan 1995, 1997; Sundararajan et al. 2007). The familiarity of the Fourier transforms attracts the scientists and engineers from the advantages of the Hartley transform. The Hartley and Fourier transforms are fully equivalent; however, Hartley transform differs in phase by 45° from its progenitor—the Fourier transform. The Hartley transform is purely real (Bracewell 1983; and Sundararajan 1995). The physical implication of both transforms is exactly the same and the frequency in both transforms has the same meaning. In this section, the Hartley transform is applied to a theoretical example to illustrate the method and then applied to a field example of the “Sulleymonkey” anomaly in the Ergoni copper district, Turkey to demonstrate the applicability of the method. It may be noted that the Spectral analysis of geophysical data either by Fourier transform or Hartley transform encores identical results as their amplitude spectra in 1-D are identical.

The Hartley transform H(x) of the real function V(x) is defined by Hartley (1942) as:

$$H\left( \omega \right) = ~\int_{{ - \infty }}^{\infty } {V\left( x \right)} Cas\left( {\omega x} \right)~dx$$

where

$${\text{Cas}}(\omega {\text{x}})~ = ~~Cos\left( {\omega x} \right) + ~~Sin\left( {\omega x} \right)$$

is considered as the kernel that is 45° phase-shifted sine wave. It takes the harmonics of both cosine and sine functions as real and the frequency (ω) does have the same physical meaning as that of Fourier transform (Bracewell 1983; Sundararajan 1995).

Basically, the Hartley and Fourier transforms can be related using the even and odd components with the real and imaginary components of the Fourier transform (Bracewell 1983; Sundararajan 1995) as

$$H\left( \omega \right)~ = ~~E\left( \omega \right)~ + ~~O\left( \omega \right)$$

$${\text{F}}(\omega ) = {\text{Re}} (\omega ) - {\text{iIm}} (\omega )$$

where ${\text{E}}(\omega )$ and ${\text{O}}(\omega )$ of Hartley transform ${\text{H}}(\omega )$ are numerically equal to real and imaginary parts Re($\omega$) and Im($\omega$) of the Fourier transform F($\omega$). Thus, the amplitude of the Hartley transform can be expressed as in the case of Fourier amplitude.:

$${\text{A}}(\omega )~ = ~\sqrt {E\left( \omega \right)^{2} + O\left( \omega \right)^{2} }$$

Alternatively, the amplitude spectrum can also be expressed in terms of the Hartley transform H(w) as:

$${\text{A}}(\omega )~~ = ~~~\sqrt {~\frac{{[H^{2} \left( \omega \right)~ + ~H^{2} \left( { - \omega } \right)]}}{2}}$$

Also, the phase of the Hartley transform can be expressed in the same way as that of Fourier phase as:

$$\emptyset \left( \omega \right)~~ = \tan ^{{ - 1}} \left[ { - \frac{{O\left( \omega \right)}}{{E\left( \omega \right)}}} \right]$$

Alternatively, the phase spectrum can be realized as a function of H($\omega )~$ and H($- \omega )~$

$$\emptyset \left( \omega \right)~~ = \tan ^{{ - 1}} \left[ {\frac{{H\left( { - \omega } \right) - H\left( \omega \right)~}}{{H\left( { - \omega } \right) + ~H\left( \omega \right)}}} \right]$$

The self potential due to 2-D horizontal circular cylinder given earlier can be written as:

$$SP4\left( x \right)~ = ~~~\frac{{A[~x~{\text{cos}}\left( \alpha \right) - ~zsin\left( \alpha \right)}}{{\left( {x^{2} + ~z^{2} } \right)}}$$

where ‘z’, ‘α’ and ‘A’ have same meaning as defined earlier.

The even and odd components of the Hartley transform of the SP anomaly due to horizontal circular cylinder given above can be obtained as:

$${\text{E}}(\omega )~ = ~~K\pi sin\left( \alpha \right)e^{{ - \omega z}}$$

and

$${\text{O}}(\omega )~ = ~~K\pi ~cos\left( \alpha \right)e^{{ - \omega z}}$$

Therefore, the amplitude spectrum of the Hartley transform can be obtained by squaring and adding and taking the square root as:

$${\text{A}}(\omega ) = K\pi ~e^{{ - \omega z}}$$

And the phase also can be obtained as the arctan of odd by even components of the Hartley transform as

$$\emptyset \left( \omega \right)~ = ~\alpha ~ - {\uppi }/4$$

Theoretically, it is feasible to express the amplitude at two different frequencies say $\omega _{i}$ and $\omega _{{i + 1}}$ as

$${\text{A}}(~\omega _{{i~}} ) = K\pi ~e^{{ - \omega _{{i~}} z}}$$

and

$${\text{A}}(~\omega _{{i + 1~}} ) = K\pi ~e^{{ - \omega _{{i + 1}} z}}$$

By a simple algebraic division of the above equations with i = 1 and also taking natural logarithm, the depth ‘z’ can be obtained as:

$${\text{z}} = \frac{1}{{\omega _{{1 - ~~}} \omega _{{2~~}} }}~\ln \frac{{{\text{A}}\left( {~\omega _{{1~}} } \right)}}{{{\text{A}}\left( {~\omega _{{2~}} } \right)}}$$

and the angle of polarization ‘α’ can be evaluated by dividing the even and odd as

$$\alpha = ~~\tan ^{{ - 1}} [O\left( \omega \right)/E(\omega )]$$

For a complete solution, the constant term A = I $\rho$ can be evaluated by substituting the depth ‘z’ in the equation of amplitude as:

$${\text{A}} = \frac{{{\text{A}}\left( \omega \right)}}{\pi }~e^{{\omega z}}$$

Theoretical and Field Examples

The Hartley spectral analysis of geophysical data particularly in SP interpretation is relatively a recent procedure (Al-Garni and Sundararajan 2011) in comparison with the traditional Fourier spectral analysis. It may be emphasized that both are identical in magnitude however differs in phase by 45° and therefore ensure equality in applications. But being a real tool, the computation of Hartley transform is faster than its progenitor the Fourier transform. Therefore in such studies, it makes no difference in either of the transforms. Here it is illustrated with a theoretical model and substantiated with a field data of Sulleymonkey anomaly of length 260 m in the Ergani copper district, Turkey. The even and odd components, the Hartley transform of SP4(x) and amplitude spectrum are computed and shown in Fig. 1.14a–d in the case of theoretical model. The SP field of Sulleymonkey anomaly in Ergani copper district, Turkey is shown in Fig. 1.15. On the other hand, Fig. 1.16a–d illustrate the even, odd components of field SP Sulleymonkey anomaly in addition to the Hartley transform as an algebraic sum of even and odd components and also the amplitude spectrum. All the parameters are evaluated as discussed in the text. The evaluated parameters in both theoretical as well as field examples are presented in Table 1.4 and compared with the other available methods in the literature.

Fig. 1.14

Hartley spectral analysis of theoretical model. a the even component, b the odd component, c the Hartley transform and d the amplitude spectrum

Fig. 1.15

The SP field of Sulleymonkey anomaly in Ergani copper district, Turkey

Fig. 1.16

Hartley spectral analysis of SP field of Sulleymonkey anomaly, Ergani copper district, Turkey. a even component, b odd component, c Hartley transform and d the amplitude spectrum

Table 1.4 Hartley spectral analysis of theoretical model and field self potential Sulleymonkey anomaly, Ergani copper district, Turkey

1.8 Artificial Neural Network Analysis

Soft computing tools such as artificial neural network (ANN) has been gaining importance in the recent past in the interpretation of geophysical data particularly self-potential anomalies (Bescoby et al. 2006; Bhagwan Das and Sundararajan 2016). Self-potential anomaly due to a horizontal circular cylinder can be approximated by an artificial neural network, as they are universal approximators. The universal approximation theorem for multilayer perception (MLP) was proved by several authors in the early 1980s although the results depend on how many hidden units are necessary which is yet to be known. In this section, the analysis of self- potential anomalies due to a 2D horizontal circular cylinder (the interpretation of the very same geometrical structure was carried out in the previous sections using modified Hilbert transform as well as Hartley spectral analysis) is performed using ANN-based committee machine. The soundness of the method is illustrated with the study of theoretical model and a field example.

The salient features of ANNs include that it does not require any prior knowledge about the input/output mapping that is required for model development. The fitted function is represented by the network and do not have to be explicitly defined. Further, it has the ability to model highly nonlinear as well as linear input/output mapping with good generalization, i.e., it responds correctly to new data. The interpretation of SP anomalies based on ANN approach consists of two phases namely phase-I and phase-II, in phase I, a trial-and-error method is implemented for the analysis. The trial and error method starts from assuming (i.e., trial) an initial set of different ranges for required parameters (may be far from actual values), computes the predicted data values by using the self-potential effect and compares them with the observed data. Then, corrections are applied based on error to the range of parameters so that it minimizes the misfits between calculated and observed data. The procedure is repeated until a satisfying result is obtained. This process is carried out with a mathematical algorithm and implemented in Matlab which enables an efficient way of changing the model parameters. The main purpose of phase I is to obtain a suitable and close range of parameters which in turn ensures a very few training examples that are sufficient enough to train in order to extract the parameters of the model.

In phase-II, a committee machine is a type of ANN using the divide-and-conquer strategy in which the responses of multiple experts (MLPs) are combined into a single response. A committee machine is a method in which different experts sharing a common input and whose individuals are combined to produce an overall output; such a technique is referred to as an ensemble averaging method. In phase II, initially training examples are created based on the close range of parameters obtained in phase I, and then an ANN-based committee machine is constructed by replacing each expert by MLP of the same topology (i.e., same number of layers, number of neurons in each layer). Each MLP is trained to extract exactly one parameter with examples, using the Levenberg–Marquart algorithm in batch mode. An extensive further mathematical details are given in Bhagwan Das and Sundararajan (2016).

Theoretical and Field Examples

The ANN based interpretation of SP anomalies are illustrated with a theoretical model in the case of 2-D horizontal circular cylinder and further studied on a field data of the Sulleymonkey anomaly in the Ergani copper district, Turkey. The interpreted results of both theoretical and field anomaly are presented in Table 1.5 and compared with the methods that are in vogue. All the computations are presented as illustrations in Fig. 1.17 (theoretical model) and Fig. 1.18 (Field anomaly). In addition, comparison of artificial neural network generated self potential response with that of generated by other techniques for self-potential field of the Sulleymonkey anomaly in Ergani Copper district, Turkey are shown in Fig. 1.19.

Table 1.5 ANN based interpretation of theoretical model of 2-D horizontal circular cylinder and field self potential Sulleymonkey anomaly, Ergani copper district, Turkey

Fig. 1.17

ANN based interpretation of SP anomalies due to 2-D horizontal circular cylindrical model. a Self potential anomaly of the model, b ANN-generated self-potential response and c Self potential anomaly as in (a) and ANN-generated self potential response

Fig. 1.18

ANN based interpretation of field data. a The self-potential field of the Sulleymonkey anomaly in Ergani Copper district, Turkey. b ANN-generated self-potential response and c The self potential anomaly as in (a) and ANN-generated self-potential response

Fig. 1.19

Comparison of artificial neural network generated self potential response with other techniques of the self-potential field of the Sulleymonkey anomaly in Ergani Copper district, Turkey

1.9 Noise Analysis

The effect of random noise is investigated on the interpretive process by adding various levels say 5%, 10% and 20% of white Gaussian noise (WGN) to the self-potential of the 2-D horizontal circular cylinder. In Hartely spectral analysis, the noisy anomalies were not subjected to smoothing using a statistical method such as moving average which is optional (Sundararajan and Srinivas 1996). But in Hilbert transform analysis, they show that this process should be carried out prior to the computation of Hilbert transform because their interpretation is based on the abscissa of the points of the intersection of the self-potential anomaly and the modified Hilbert transform. In the case of Hartley spectral analysis, the even and odd components, the Hartley, and the amplitude spectrum are computed from the noisy anomaly. The interpretation should be carried out earlier as in the case of prior to addition of noise. The interpreted results with and without noise did not differ much and presented (Table 1.6) for a specific case of 2-D horizontal circular cylinder model with identical assumed parameters based modified Hilbert transform and Hartley spectral analysis (Fig. 1.20). Therefore, the effect of the noise of 10% of WGN or even more on the interpretive process detailed in all the methods seem to be negligible and confirming that these methods of interpretation are not much prone to the presence of noise in the acquired data. It may be noted here that similar is the noise effect on the on interpretation of SP anomalies over spherical and 2-D cylindrical models based on the techniques of horizontal and vertical derivatives and artificial neural networks (ANN).

Table 1.6 Effect of random noise on the interpretation of theoretical SP anomalies due to 2-D horizontal circular cylinder

Fig. 1.20

Effect of random noise on the interpretation of SP anomalies due to 2-d horizontal circular cylinder a SP anomaly and its modified Hilbert transform. b Hilbert transform of SP anomaly and the modified Hilbert transform and c Hartley amplitude spectrum

1.10 Discussion

In general, all geophysical data invariably contaminated with various noise factors, including inappropriate interval measurements etc. SP data interpretation also is prone to error because of the choice of computation algorithm, assumptions etc. In this regards, the Hilbert transform/modified Hilbert transform based interpretation ensures maximum accuracy in extraction of body parameters as they are directly dependent on the real roots of the equations of SP potential of geometrical structures considered. However, the accuracy of this method depends on the accurate estimation of the abscissa of the points of intersections of the anomaly and its Hilbert transform/modified Hilbert transform or the horizontal and vertical derivatives of the SP anomaly.

The modified Hilbert transform is equal in magnitude to the Hilbert transform but differs in phase by 270°. The salient feature of the modified version of the Hilbert transform is that it facilitates in precise spatial location of subsurface targets in a couple of ways. As discussed and demonstrated, the point of intersection of the Hilbert transform of SP anomalies and modified Hilbert transform aid in determining the origin. Similar is the case with the, the amplitude of analytic signal A1(x) and A2 (x) based on Hilbert transform and the modified Hilbert transform that the point of intersection of A1(x) and A2(x) confirm the exact location of in the targets.

This procedure is an analytical one without any assumptions; however, the inherent weakness of the method while obtaining the horizontal derivative of the SP anomaly by numerical differentiation which incorporates a bit of noise in the computation, and this can be minimized by any simple statistical filtering prior to computation of the vertical derivative by means of Hilbert transform. The method of interpretation is not influenced significantly by the presence of random noise in the data as evidenced by the noise analysis.

Hartley spectral analysis is not only similar to the traditional Fourier spectral analysis of geophysical data, but also numerically identical with all merits and demerits. However, Hartley transform being real function, unlike the complex Fourier transform, ensure efficiency in computation, particularly while using a large amount of data.

Applications of artificial neural network (ANN) is seen almost in every field of science and engineering including processing and interpretation of various geophysical data. It is elegant in its mathematical frame work, however, in the extraction of parameters from potential field data including SP data, the choice of training parameters of the targets may cost large computational time if the training set differs widely from the actual ones, else ANN techniques are simple to implement and does not require any prior knowledge about the input/output mapping that is required for model development.