Software Reliability Growth Models Incorporating Software Project/Application’s Characteristics as a Power Function with Change Point

Abstract

Software Reliability is a high-handed aspect to ascertain the quality of the system, which leads to development of tools that incorporates real time set-up. One of the real time concepts is change point, which highlights on the fact that a characteristic of the model changes during the testing time duration and it is significant to incorporate its effect in the model developed to ameliorate the reliability of the system. Moreover, faults are assumed to be independent and are incurred at any arbitrary time but, in practical world, faults may occur due to many factors like the testing environment, resource allocation, code complexity, testing team skill-set etc. This rate tends to change with time and assuming it to be constant may not reflect upon an actual output. Another conundrum that is taken care of is the release time of the software project/application. The weightage that is implied by this optimization planning is due to the fact that over testing may incur high cost to the firm whereas under testing may lead to release of a project/application with high fixing cost faults affecting the manufacturer by an elevated post-release cost. In this chapter, a framework is proposed that extends error-removal phenomenon model by encapsulating the software project/application characteristics as a parameter. A realistic software development situation is also taken in account by considering the parameter not only as a constant but a time dependent function. The suggested SRGMs are also monitored under a change point scenario, which gives real-time edge to the problem, and are then utilized to develop release time policy balancing reliability and expected cost incurred by a project/an application. The models are validated using Tandem dataset and performance measures are compared quantitatively with the standard models. On comparison of the results, the proposed model outperforms other extant models with and without change point.

1 Introduction

The ambitious invention of a high performing and a high-defined quality software system has given software engineers the liability to envisage a more complex system. Software brings forth automation to a wide range of domain like medicine, banking system, business houses, academics, security etc. thus, becoming an indispensable element of any commercial or non-commercial field. With the increase in its application, there is a need of improvising software at a higher speed to balance with the requirements of the consumers, to keep up with the competitors in the market and most significantly to maintain quality. Thus, reliability models are entailed to assess and forecast the reliability of the software embedded in the system quantitatively, elevating system’s reliability (Huang et al. 1999) and are also known as Software Reliability growth models (SRGM). A SRGM that helps in rendering a balanced amalgamation in terms of expense, reliability, productivity and performance can be considered to be generic in nature and applicable to sundry software project/application.

Many versions and forms of SRGM has been developed considering different assumptions and objective of the underlying study, under perfect or imperfect debugging conditions (Okumoto and Goel 1979). However, in the real world, there are many other factors that influence the quality of the software with time for example testing environment, complexity of the code, running environment, line of codes, testability etc. Lai et al. (2011) stated past SRGMs fail to incorporate these factors into past simulation. Thus, fault-detecting rate is influenced by external factors and it would be favorable to take them into account in order to increase the performance rate of a SRGM developed using past failure rate. In this study, these external factors are included in the model developed and coined as software application/project characteristic parameter. The given parameter is not only a function of software characteristics but can also be a time dependent power function. The parameter measuring the influence of the software project/application’s characteristic may not necessarily be constant over the testing time period and is subject to change due to alteration in testing plan at some time-point. This instance of time is termed as change-point. In this chapter, SRGMs are formulated under the postulation of change point to create a real-time problem.

The main concern of the management is scheduling the testing phase and release of the project but are unaware of the latent faults remaining in the system even after the completion of testing phase (Kapur et al. 2008a). However faults in a software project/application are extensively eliminated during the testing phase of the system but excessive testing is uneconomical and impractical, thereby making the optimal release planning as a powerful decision-making aspect in a business plan (Lai et al. 2011). SRGM provides enumeration of faults that might be informative to the management to curtail development cost or to anticipate the appropriate release time of a software project/application (Huang 2005a). To précis, software release planning is a vital managerial optimization problem that involves determination of the optimal release time of the software such that the cost is minimized subject to a reliability constraint. Kapur et al. (2009a) have discussed the significance of release planning that if a product is subject early to or late release, then it may lead to either high operational cost or high testing cost which is a loss for the business. In this study, the expected number of faults obtained through SRGMs with and without change point scenarios are employed to develop optimal release plans for the respective models.

The objective of this study is condensed in three-fold. Firstly, a model is simulated taking into account of change point concept and software project/application as a power function. Secondly, models are assessed for its performance and efficiency based on a real software fault dataset and comparison is made with some extant models from the past literature. Thirdly, an optimization scheme is planned for the release of the product using the models developed. The scheme specifies an optimal combination of cost and reliability for a given software project/application, thereby focusing on a rational release policy for the same.

This chapter is divided into sections, namely, in Sect. 2 a brief summary of the past literature has been captured, following which in Sect. 3 the suggested model has been explained, in Sect. 4 the proposed model is justified with a numerical illustration, a release plan has been discussed in Sect. 5 using the developed models and lastly, Sect. 6 concludes the given study.

2 Literature Survey

In this section, an abridgment of the related literature is furnished for each research topic alluded in this study.

2.1 Software Reliability Growth Models

A SRGM follows NHPP distribution that gives an estimated count of faults for both calendar as well as running timeline. In the past literature, a vast number of SRGMs are available differentiating from each other by marginal changes in assumptions set describing or tackling a testing related problem (Lai and Garg 2012). Yamada et al. (1983) proposed an S-shaped model due the non-uniformity in reliability growth that was also a succession to Okumoto and Goel (1979) model. Kareer et al. (1990) proposed a modified S-shaped model that was based on the severity level of the faults manifesting a real time situation. Jeske and Zhang (2005) gave a realistic approach by bridging a gap between theoretical and practical application of SRGM. Many earlier SRGMs do not fit all failure datasets perfectly as stated by Chiu et al. (2008) however, incorporating learning effect into the model would enhance the results. Effects of testing skills, strategy and environment on discrete SRGMs were well captured by Kapur et al. (2008b). Kapur et al. (2009b) have presented a unified approach to evaluate a wide range of SRGMs on the basis of hazard rate. A SRGM framework demonstrated by Inoue and Yamada (2011) reflected the effect of rate of change in the testing setting. Softwares are developed in an ideal environment nonetheless, it is not the same while in the operating stage (Pham 2016). While Zhu and Pham (2018) considered single environment factor and later on taking in account the effect of multiple environmental factors on modeling and estimation (Zhu and Pham 2020).

2.2 Change Point

Zhao (1993) was motivated to apply change point concept in the field of software and hardware reliability by including it SRGM. Huang (2005b) integrated logistic testing effort and change point into the reliability modeling suggesting that the project head to invest in tools and manpower that would aid in improving the reliability of the software product. Singh et al. (2010) introduced S-shaped SRGM with change point that monitors the reliability of OSS. A discrete SRGM was modeled by Goswami et al. (2007) for different levels of bugs severity under change point. Kapur et al. (2009a) have discussed a general framework with respect to altering rate of fault detection with and without change point. In the study by Chatterjee et al. (2012), SRGM with fluctuating introduction and detection rates have been examined under change point scenario. Inoue et al. (2013) scrutinized the altering effect of testing environment on change point based SRGM. Parr-curve was deployed by Ke et al. (2014) to analyze reliability model with multiple change point. Nagaraju and Fiondella (2017) have exemplified the significance of change point modeling by assessing different SRGM with and without change point. Change point SRGMs depicts mathematically a real life situation, however, Inoue and Yamada (2018) utilized Markov process to enhance the depiction. Chatterjee and Shukla (2017) used am improvised approach to regulate the reliability assessment under change point effect.

2.3 Release Policy

SRGMs are implemented to enumerate uncertainty attached to a software system, thus aiding a software developer to achieve a highly reliable software project/application. But with increasing complexity in the software, it is hard for the software engineers to deliver fault free. At the same time, these probabilistic tools are utilized to estimate the optimal release time. The concept of optimal release policy was firstly implemented by Okumoto and Goel (1979). Following which, many researchers started implementing the optimal release time concept along with software reliability assessment as well as balancing cost parameters (Kapur and Garg 1989). Shrivastava et al. (2020) proposed an optimization model to establish the optimal release time as well as the testing stop time. Li et al. (2010) study not only deals with multiple change point and release policies but, they have also made an effort to do a sensitive analysis of the results. The failure data being uncertain and vague, pushed the researchers to indulge in fuzzy sets. Under the fuzzy environment, a release plan for the software was given by Pachauri et al. (2013). For a discrete SRGM, a release policy was proposed by Aggarwal et al. (2015). Release time decision-making can be sometime tricky when the past records are inconsistent, conversely (Chatterjee and Shukla 2017) suggested a fuzzy based release schedule. Shrivastava and Sachdeva (2019) proposed a generalized release policy under different testing environment.

3 Methodology

In this study, a SRGM has been enhanced by considering a parameter as a power function of time integrating with a change point scenario.

3.1 Notations

Symbols	Description
X	Preliminary faults existing in the software project/application in the time period (0, t]
X(t)	For a given time period, say (0, t], expected number of observed faults
p	Failure rate for a software project/application
q	Residual fault detection rate
r1	Software project/application’s characteristics measuring factor before change point
r2	Software project/application’s characteristics measuring factor after change point
k	A constant
t	Time period
τ	Change point

3.2 Assumptions

Comprehending from the past literature (Huang et al. 1999; Huang 2005a; Yamada et al. 1983; Kareer et al. 1990), in this study, SRGMs are developed, based on Non-Homogenous Poisson Process (NHPP) where, $\mathrm{X}\left(\mathrm{t}\right)$ is the mean value function or the expected number of faults in the time interval (0, t]. The proposed models are developed under the following assumptions,

• Due to the presence of the dormant faults, the software project/application is subject to fail during the operational phase.

• A fault detected in the software project/application is removed instantaneously.

• On removal of certain faults, it is assumed that some latent dependent faults are also eliminated in the process.

• The software project/application’s operational phase is considered to be as one of the phases of the lifecycle.

• The failure or fault detection phenomenon incurred by the consumer or the testing team is considered to be equivalent.

• Software project/application characteristics’ effect on the model is measured by a parameter, which might change with time.

3.3 Model Development

Kapur and Garg (1992) proposed a model that was based on the assumption that faults detected can lead to observing residual faults in the system without causing the system to fail. This model has been extended by considering a parameter that characterizes software project/application as a parameter namely, r₁. Hence, the differential equation under the given assumptions for an expected number of faults in the system is given,

$$\frac{\mathrm{dX(\mathrm{t})}}{{\mathrm{dt}}}=\mathrm{r}\left(\mathrm{t}\right)[(\mathrm{p}+\frac{\mathrm{X}\left(\mathrm{t}\right)}{\mathrm{X}}\mathrm{q})\left(\mathrm{X}-\mathrm{X}\left(\mathrm{t}\right)\right)]$$

(1)

where, $\mathrm{r}\left(\mathrm{t}\right)$ can be a constant or a time-dependent function that defines the software project/application characteristics. Zhu and Pham (2020) developed a generic model including environmental factor and on the similar lines (Inoue et al. 2013) amplified fault detection rate with the help of environment factor in their cost model. Different set up for the model in Eq. (1) has been considered in the study.

Model 1a: When $\mathbf{r}\left(\mathbf{t}\right)$ is considered to be a constant without change point (BCP)

Let us consider,

$$\mathrm{r}\left(\mathrm{t}\right)= {\mathrm{r}}_{1}$$

(2)

where, r₁ is a constant value of the above defined parameter and ${\mathrm{r}}_{1}>0$. Substituting (2) in (1), the differential equation for the expected number of faults in the system is given by,

$$\frac{\mathrm{dX}(\mathrm{t})}{\mathrm{dt}}={\mathrm{r}}_{1}[(\mathrm{p}+\frac{\mathrm{X}\left(\mathrm{t}\right)}{\mathrm{X}}\mathrm{q})\left(\mathrm{X}-\mathrm{X}\left(\mathrm{t}\right)\right)]$$

(3)

The constant ${\mathrm{r}}_{1}$ implies that each fault is uniformly affected or influenced by software project/application characteristics parameter. Solving (3), we obtain the expected number of faults in the testing time interval (0, t], given the initial condition, $\mathrm{X}\left(0\right)=0$, as,

$$\mathrm{X}\left(\mathrm{t}\right)=\frac{\mathrm{X}[1-{\mathrm{e}}^{-\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{1}\mathrm{t}}]}{[1+\frac{\mathrm{q}}{\mathrm{p}}{\mathrm{e}}^{-\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{1}\mathrm{t}}]}$$

(4)

Model 1b: When $\mathbf{r}\left(\mathbf{t}\right)$ is considered to be a constant with change point (ACP)

During the testing phase, a software project/application runs in a given environment but it is not necessarily true that parameters remain uniform throughout. The instance at which a change is observed in the pattern of the failure distribution is termed as change point. In software reliability engineering, a change point occurs due to change in testing pattern observed the testing team’s, change in resource allocation, improved learning skills of the system analyst, or programmed testing codes (Kapur et al. 2008a; Zhu and Pham 2020; Ke et al. 2014). In this study, software project/application characteristics are not considered to be homogenous during the testing phase, hence developing SRGM with a change point. Let the parameter be defined as,

$$\mathrm{r}\left(\mathrm{t}\right)=\left\{\begin{array}{c}{\mathrm{r}}_{1}, \quad t<\tau \\ {\mathrm{r}}_{2},\quad t\ge \tau \end{array}\right.$$

Considering the underlying assumptions and assuming that $\mathrm{r}\left(\mathrm{t}\right)$ does not remain homogeneous during the testing phase, the mean value function is given as,

$$\mathrm{X}\left(\mathrm{t}\right)=\left\{\begin{array}{c}X\frac{\left[1-\mathrm{exp}\left(-\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{1}\right)\right]}{\left[1+\frac{\mathrm{q}}{\mathrm{p}}\mathrm{exp}\left(-\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{1}\right)\right]} \quad t<\tau \\ X\frac{\left[1-\left(1+\frac{\mathrm{q}}{\mathrm{p}}\right)\left(1+\frac{\mathrm{q}}{\mathrm{p}}\right)\mathrm{exp}\left(-{\mathrm{r}}_{1}\mathrm{\tau }\right)\right]\left[\mathrm{exp}\left(-\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{1}\mathrm{\tau }\mathrm{ }\right)+\left(-\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{2}\left(\mathrm{t}-\mathrm{\tau }\right)\right)\right]}{\left[1+\frac{\mathrm{q}}{\mathrm{p}}\mathrm{exp}\left(-{\mathrm{r}}_{1}\mathrm{\tau }\right)\right]\left[1+\frac{\mathrm{q}}{\mathrm{p}}\mathrm{exp}\left(-{\mathrm{r}}_{2}\mathrm{t}\right)\right]} \quad t\ge \tau \end{array}\right.$$

(5)

Model 2a: When $\mathbf{r}\left(\mathbf{t}\right)$ is considered as a power function BCP

Next, let us consider as a power function of testing time which is given as,

$$\mathrm{r}\left(\mathrm{t}\right)={\mathrm{r}}_{1}{\mathrm{t}}^{\mathrm{k}}$$

(6)

The form in (6) renders the suggested models generic and adaptable in nature (Kapur et al. 2008a). Substituting (6) in (1), the differential equation is given as,

$$\frac{\mathrm{d}\mathrm{X}(\mathrm{t})}{\mathrm{d}\mathrm{t}}={\mathrm{r}}_{1}{\mathrm{t}}^{\mathrm{k}}[\mathrm{p}+\mathrm{q}\frac{\mathrm{X}\left(\mathrm{t}\right)}{\mathrm{X}}][\left(\mathrm{X}-\mathrm{X}\left(\mathrm{t}\right)\right)]$$

(7)

where, $\mathrm{k}\ge 0$ and the first component represents the varying relation between ${\mathrm{r}}_{1}$ and t with varying value of k. If $\mathrm{k}=0,$ the model reduces to Eq. (3). Taking the initial condition as $\mathrm{X}\left(0\right)=0$, we get,

$$\mathrm{X}\left(\mathrm{t}\right)=\mathrm{X}\frac{[1-\mathrm{e}\mathrm{x}\mathrm{p}(-{\mathrm{r}}_{1}\left(\mathrm{p}+\mathrm{q}\right)\frac{{\mathrm{t}}^{\mathrm{k}+1}}{\mathrm{k}+1})]}{[1+\frac{\mathrm{q}}{\mathrm{p}}\mathrm{exp}\left(-{\mathrm{r}}_{1}\left(\mathrm{p}+\mathrm{q}\right)\frac{{\mathrm{t}}^{\mathrm{k}+1}}{\mathrm{k}+1}\right)]}$$

(8)

Model 2b: When $\mathbf{r}\left(\mathbf{t}\right)$ is considered as a power function ACP

The Eq. (3) has been extended by incorporating change point and power function of r.

$$\mathrm{X}\left(\mathrm{t}\right)=\left\{\begin{array}{c}X\frac{\left[1-\mathrm{exp}\left(-\frac{\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{1}}{\mathrm{k}+1}{\mathrm{t}}^{\mathrm{k}+1}\right)\right]}{\left[1+\frac{\mathrm{q}}{\mathrm{p}}\mathrm{exp}\left(-\frac{\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{1}}{\mathrm{k}+1}{\mathrm{t}}^{\mathrm{k}+1}\right)\right]} \quad t<\tau \\ X\frac{\left[1-\left(1+\frac{\mathrm{q}}{\mathrm{p}}\right)\left(1+\frac{\mathrm{q}}{\mathrm{p}}\right)\mathrm{exp}\left(-\frac{{\mathrm{r}}_{1}}{\mathrm{k}+1}{\mathrm{\tau }}^{\mathrm{k}+1}\right)\right]\left[\mathrm{exp}\left(-\frac{\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{1}}{\mathrm{k}+1}{\mathrm{\tau }}^{\mathrm{k}+1}\right)+\left(-\frac{\left(\mathrm{p}+\mathrm{q}\right){\mathrm{r}}_{2}}{\mathrm{k}+1}{\left(\mathrm{t}-\mathrm{\tau }\right)}^{\mathrm{k}+1}\right)\right]}{\left[1+\frac{\mathrm{q}}{\mathrm{p}}\mathrm{exp}\left(-\frac{{\mathrm{r}}_{1}}{\mathrm{k}+1}{\mathrm{\tau }}^{\mathrm{k}+1}\right)\right]\left[1+\frac{\mathrm{q}}{\mathrm{p}}\mathrm{exp}\left(-\frac{{\mathrm{r}}_{2}}{\mathrm{k}+1}{\mathrm{t}}^{\mathrm{k}+1}\right)\right]} \quad t\ge \tau \end{array}\right.$$

(9)

For simplification, in this study, only one change point has been considered in both the models given by (5) and (9), however in the practical world, change points are observed more than once in a testing phase.

4 Model Validation

In this section, the SRGMs given by (3), (5), (8) and (9) have been validated on the basis of fault dataset given by Wood (1996). A change point has been observed at the 8th week of testing in the dataset and change point models given by (5) and (9) are evaluated accordingly. The parameters are estimated for each model and the performances of the respective models are recorded for comparisons.

4.1 Dataset

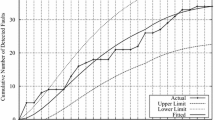
The proposed models have been validated using Tandem dataset (Wood 1996) that contains number of faults detected over a testing period of 20 weeks and cumulative sum of number of faults being 100. This dataset has been widely implemented in the past literature for example, Park and Baik (2015), Sharma (2010), Roy et al. (2014). From the data set, a change in the number of faults detected was observed at 8th week of testing. Figure 1 depicts a graph plotting tandem data set where x-axis denote the testing weeks whereas y-axis denote cumulative number of faults detected.

Fig. 1

A plot for Tandem Dataset

4.2 Parameter Estimation

The non-linear regression option in Statistical Package for social Science (SPSS) aids in obtaining least square estimates of the parameters for a given SRGM. The parameters are valued for a given testing time in weeks denoted by t and parameters X, p, q, k, r, r₁, and r₂ delineated in Sect. 3 are estimated for respective SRGM. Table 1 represents the parameter estimation for without and with change point models.

Table 1 Parameter estimations for models before and after change point scenario

In Table 1, “–” indicates null value of the parameter because they have no role play in the respective model. 35.1% and 93.7% software project/application characteristics are explained by the parameter r in model 1a and 2a respectively. However, without change point, model 1b explains 23.8% and with change point 0.91%, whereas model 2b shows the best result, combining the effect of r₁ and r₂, 98.4% characteristics are explained.

A SRGM is said to perform well when it predicts the behavior of the system accurately by using previous fault data (Roy et al. 2014). The simulations developed were assessed with the help of performance measures, co-efficient of determination (R²) and mean square of errors (MSE).

Looking at the R² and MSE values of the proposed models in Table 2, model 2b shows the best fit for the given dataset i.e. 99.7% of the variation in data is captured by the proposed model and has the lowest MSE value (2.076).

Table 2 Model comparisons with respect to performance measures

4.3 Goodness of Fit Curves

See Figs. 2 and 3.

Fig. 2

Actual versus predicted values for proposed models where r is considered constant BCP and ACP

Fig. 3

Actual versus predicted values for proposed models where r is power function of time BCP and ACP

4.4 Comparison with the Previous Models

In order to validate the robustness of the proposed model, comparisons are drawn with some conventional models, namely Goel Okumoto model (Okumoto and Goel 1979), S-shaped Yamada model (Yamada et al. 1983), Kapur Garg error removal phenomenon model (Kapur and Garg 1992) respectively using the Tandem dataset. For mathematical simplifications, the proposed model 1a has been compared with the traditional models.

Table 3 depicts the comparison values for the different SRGMs with respect to change point. Nonetheless, the MSE value is lowest for the proposed model without as well as with change point than that of GO model and S-Shaped Yamada model which implies that the proposed model has the least fitting error and hence exhibit the best performance. Since the proposed model is an extension of Kapur and Garg error phenomenon model, the comparison measure is vital for this case. For the given dataset, KG Model has MSE value 18.572 and 10.937 without and with change point respectively, while those values for model 1a are nearly half of it i.e. the suggested model has the capability to reduce the fitting error to half of that of the KG model. All in all, the extended model is a better version of KG model. Looking at the R² values, the proposed model has the highest (0.989 and 0.993) without and with change point cases in comparison to other models. Figures 4 and 5 reflects that the suggested model is the closest fit of the data set without and with change point respectively.

Table 3 Models’ performance comparison with respect to coefficient of determination

Fig. 4

A fitted curve for observed and estimated faults BCP given by proposed models and compared with some existing model

Fig. 5

A fitted curve for observed and estimated faults ACP given by proposed models and compared with some existing model

The result of the data analysis suggests that the extended version of the KG model is an effective model that enriches the data set in terms of predicting accuracy and beautifully incorporates the effect of change point under perfect debugging conditions.

5 Release Policy

With the completion of software testing phase, the software project/application is prepared for its release into the market rising to problem of optimal release policy. Protraction of testing phase implies detection of multiple faults, thus increasing the development cost, increase in the quality and delay in the release of the software project/application. The lag in release of the software may make the market restive, at the same time cause a loss to the business. On the other hand, if the testing phase is cut short, one can infer detection of a smaller number of faults implying decrease in development cost, poor quality and rapid release of the software. The accelerated release of the software may lead to loss of customers’ trust towards the firm that might incur post-release high cost. In this study, one of the objectives is to minimize software outlay with respect to a desired level of reliability, thereby obtaining the optimal software release time. The outlay parameters used to illustrate release policy is given as follows,

${\mathrm{O}}_{1}$: Outlay of fault detection BCP in the testing environment $({\mathrm{O}}_{1}>0)$

${\mathrm{O}}_{2}^{\prime}$: Outlay of fault detection ACP in the testing environment ${\mathrm{O}}_{2}^{\prime}>0)$

${\mathrm{O}}_{2}$: Outlay of fault detection in the operational environment $({\mathrm{O}}_{2}>{\mathrm{O}}_{2}^{\prime})$

${\mathrm{O}}_{3}$: Outlay of testing at arbitrary time point

T: stopping or release time of software project/application.

The expected outlay function without change point comprises of expense acquired by the software firm in order to detect fault BCP, during the operating phase and lastly, an overall expense per unit time before the software project/application’s release time, which is given by,

$$\mathrm{O}\left(\mathrm{T}\right)={\mathrm{O}}_{1}\mathrm{*}\mathrm{X}\left(\mathrm{T}\right)+{\mathrm{O}}_{2}\mathrm{*}\left(\mathrm{X}-\mathrm{X}\left(\mathrm{T}\right)\right)+{\mathrm{O}}_{3}\mathrm{*}\mathrm{T}$$

(10)

The expected outlay function with change point is composed of expense acquired by the software firm in order to detect faults BCP, ACP, during the operating phase and lastly, an overall expense per unit time before the software project/application’s release time, which is given as,

$$\mathrm{O}\left(\mathrm{T}\right)={\mathrm{O}}_{1}\mathrm{*}{\mathrm{X}}_{1}\left(\mathrm{\tau }\right)+{\mathrm{O}}_{2}^{\prime}\mathrm{*}\left({\mathrm{X}}_{2}\left(\mathrm{T}\right)-{\mathrm{X}}_{1}\left(\mathrm{\tau }\right)\right)+{\mathrm{O}}_{2}\mathrm{*}\left(\mathrm{X}-{\mathrm{X}}_{2}\left(\mathrm{T}\right)\right)+{\mathrm{O}}_{3}\mathrm{*}\mathrm{T}$$

(11)

where, X₁(t) and X₂(t) are mean value fault detection function without and with change point (τ) respectively. Henceforth, an optimization policy can be mathematically formulated as following,

$$\begin{aligned}\mathrm{Minimise}\,& \mathrm{O}\left(\mathrm{T}\right) \\ & \mathrm{subject}\,\mathrm{to}\,\mathrm{Re}(\mathrm{T})\ge {\mathrm{R}}^{\mathrm{*}}\end{aligned}$$

(12)

where, Re(T) is the reliability function and R* is the desiderated level of reliability at the release time of software project/application’s (0 < R* < 1). The software project developer establishes the desiderated reliability for the project in accordance to the market requirement.

5.1 Numerical Illustration

The formulated optimization problem is solved using MATLAB where outlay parameters are assumed on the basis of past literature (Aggarwal et al. 2015; Shrivastava and Sachdeva 2019). In order to implement the optimization problem given by (12), we have considered tandem dataset, computed parameters of the Eqs. (4), (5), (8) and (9) with the help of SPSS and given by the Table 1. The outlay parameters are assumed to be as following,

$${\mathrm{O}}_{1}=40,{\mathrm{O}}_{2}^{\prime}=50,{\mathrm{O}}_{2}=100,{\mathrm{O}}_{3}=20$$

With the help of MATLAB and Eq. (12), the expected release time and reliability is computed for the four models and given by the Table 4.

Table 4 Expected release time and reliability of a software project/application

The optimal release time for model 1a is 28.02 weeks with reliability 0.9823 and expected cost is 5111.01, and with change point (model 1b), the release time is 30.28 weeks at 0.9638 reliability and total expected cost being 9116.40. For model 2a, the optimal release time is 30.53, reliability attained is 0.9758 with the expected cost being 5340.80, however with change point, the release time decreases to 28.33 weeks and reliability reached is 0.9532 with the cost of 8901.80.

5.2 Sensitivity Analysis

The expenses involved in testing phase may vary due to various external factors like skills of developers, testing efforts, resource etc. Hence, one might be interested to know which cost parameter plays an important role to improvise the reliability for a given software project/application. Sensitivity analysis is a tool that aids in the decision making of optimal input parameters in order to obtain improvised output (Li et al. 2010). The uncertainty in failure data fails to comprehend the exact value of the outlay parameters. This methodology permits the management to evaluate the change in parameters over reliability, to assess testing strategy, to condense cost values, to attain optimal resource apportionments (Castillo et al. 2008).

For the given study, software reliability growth models given by Eqs. (4), (5), (8) and (9) have been considered, whose parameters are computed using Tandem failure data sets and with the help of SPSS. Considering a desired reliability level to be fixed at 0.95, the outlay parameters $({\mathrm{O}}_{1},{\mathrm{O}}_{2}^{\prime},{\mathrm{O}}_{2},{\mathrm{O}}_{3})$ are altered by −10 and 10%, while monitoring its effect on the reliability, total expected cost as well as release time (given by Table 5). The sensitivity of outlay parameters is analyzed by using formula given by Li and Pham (2017). The relative changes observed with respect to varying outlay parameters is given by Table 6.

Table 5 Sensitivity analysis for SRGM with respect to outlay parameters

Table 6 Relative change observed for respective model with respect to outlay parameters

For different values of ${\mathrm{O}}_{1},{\mathrm{O}}_{2}^{\prime},{\mathrm{O}}_{2},{\mathrm{O}}_{3}$, the altered release time, cost as well as reliability level are generated. Altering values of outlay parameters gives a guidance to the management to strike a balance between the cost and reliability and obtain the optimal release time. The sensitivity analysis of the stated release policy resulted in a very close release time, but in real time situation, the policy implemented by the management depends on the cost under consideration, SRGM adopted to describe the fault process, aim of the release plan and lastly constraints to be taken care of.

From Fig. 6a, it can be clearly observed that a 10% increase in cost O₁, release time decreases by 1.46%, overall cost increases by 8.52% and a marginal decrease of 0.1% has been noted. However, when cost O₂ is increased by 10%, release time increases by 3.26%, that has 0.3% and 0.2% effect on total cost and reliability respectively. On the other hand, with a 10% increase in O₃, the release time declines by 2%, increasing cost by 1% and reliability also declines by a mall fraction. The respective trend was observed exactly opposite when the costs O₁, O₂, O₃ were decreased by 10% for model 1(a) as depicted by Fig. 6b.

Fig. 6

Relative change in release time, cost and reliability with respect to a Model 1a when there is 10% increase in costs O₁, O₂ and O₃ b Model 1a when there is 10% decrease in costs O₁, O₂ and O₃ c Model 1b when there is 10% increase in costs O₁, ${\mathrm{O}}_{2}^{\prime}$, O₂ and O₃ d Model 1b when there is 10% decrease in costs O₁, ${\mathrm{O}}_{2}^{\prime}$, O₂ and O₃ e Model 2a when there is 10% increase in costs O₁, O₂ and O₃ f Model 2a when there is 10% decrease in costs O₁, O₂ and O₃ g Model 2b when there is 10% increase in costs O₁, ${\mathrm{O}}_{2}^{\prime}$ O₂ and O₃ h Model 2b when there is 10% decrease in costs O₁, ${\mathrm{O}}_{2}^{\prime}$ O₂ and O₃

Form Fig. 6c, with an increase of 10% in cost O₁, release time, expected cost and reliability increases by 2.34%, 2.79% and 0.2% respectively. However, with an increase of 10% in cost ${\mathrm{O}}_{2}^{\prime}$, release time and reliability declines by 2.29 and 0.2%, while the cost shoots up by 6.15%. On the other hand, with an increase of 10% in cost O₂, release time is majorly affected by 3.74%, but a marginal change of 0.4% and 0.3% on cost and reliability is observed. Lastly, with an increase of 10% in O₃, a decline of 2.7% and 0.2% is observed in release time and reliability along with increase in cost by 0.6%. The respective trends were seen exactly opposite when cost O₁, ${\mathrm{O}}_{2}^{\prime}$, O₂, O₃ were decreased by 10% for model 1(b) as depicted by Fig. 6d except when cost O₁ decreased by 10%, the expected cost increased by 2.8%.

From Fig. 6e, when O₁ increases by 10%, release time decreases by 1.7%, total cost does up by 8.3% and reliability decreases by 0.2%. While O₂ increases by 10%, release time, cost and relatability also increases by 3.9%, 0.4% and 0.3% respectively. Lastly, with a 10% increase in O₃, release time and reliability decreases by 2.3 and 0.2%, on the contrary, the expected cost increases by 1.1%. When the costs O₁, O₂, O₃ decreases by 10%, an exactly opposite trend is observed which is depicted by Fig. 6f for model 2a.

From Fig. 6g, when cost O₁, ${\mathrm{O}}_{2}^{\prime}$, O₂, O₃ increases by 10%, release time increase significantly by 9.8%, 9.8%, 17.3%, 9.8% respectively, while the expected cost also rises by 2.9%, 6.8%, 1.4% and 1.5%, but reliability declines by 0.3% for cost O₁, ${\mathrm{O}}_{2}^{\prime}$, and O₃, on the other hand increases by 0.3% for O₂. From Fig. 6h, it is observed that when cost cost O₁, ${\mathrm{O}}_{2}^{\prime}$, O₂, O₃ decreases by 10%, release time increases by 9.8%, 13.6%, 9.8% and 14.1% respectively, the total cost declines fpr O₁ and ${\mathrm{O}}_{2}^{\prime}$ by 2.7% and 0.5%, however increases in the case of O₂ and O₃ by 0.2% and 0.1%. Moreover, reliability decreases by 0.3% when O₁ and O₂ decreases by 10% but increases by 0.04% and 0.08%, when cost ${\mathrm{O}}_{2}^{\prime}$ and O₃ decrease by 10%.

6 Conclusion

In this chapter, a software reliability growth model has been comprehended with respect to software project/application’s characteristics under a perfect debugging environment. The stated characteristic has been considered as a constant as well as a power function of time along with assessing the model without and with change point. The parameters are estimated with the help of SPSS and comparison has been made with extant models from literature. An optimization formulation has also been proposed for all the four models with respect to desiderated reliability and with the aim of minimizing total expected outlay. Lastly, a sensitivity analysis has been provided to validate the optimal result obtained.

Looking at the results, one can state that model with change point in both cases when the software project characteristic is constant or a power function is an efficient tool in terms of providing a realistic outlook and in comparison to other previous models.

7 Future Scope

The limitation identified for the proposed model is that it has been validated on a small dataset and the under an ideal testing environment. In order to generalize the results, using large datasets would authenticate the efficiency of the proposed model. Further research work can be implemented by considering various attributes like testing effort, imperfect debugging, resource allocation etc.