Towards Interactive Transition from AOC Poset to Concept Lattice

Abstract

Efficient algorithms exist for constructing the attribute-object concept (AOC) partially-ordered set (poset) from a formal context. The atoms and co-atoms of the corresponding concept lattice can be determined from this AOC poset and horizontally ordered so as to reduce arc crossings in a layered drawing of the AOC poset initially, and ultimately of the concept lattice digraph. The remaining, abstract concepts must then be computed and progressively inserted into the AOC poset to construct the lattice digraph. This paper describes the preparation of a formal context for efficient computation of these abstract concepts, and the consequent localisation in the AOC poset digraph of any resultant insertions. In particular, it provides simple screening tests for identifying bigraph edges, and hence also any attributes and objects, which do not contribute to abstract concepts. Elimination of these bigraph elements reduces the size of the context and paves the way for dividing and conquering the enumeration of the abstract concepts. These screening tests are also used to determine ab initio which arcs in the AOC poset digraph will not be subject to subsequent transitive reduction. These arcs are visually distinguished in the line diagram to focus attention on the remaining digraph arcs where the insertion of additional concepts may yet occur, and where the graphical interpretation of meets and joins is unsafe.

1 Introduction

1.1 Formal Concept Analysis and Scalability

A formal context is a bipartite graph – henceforth bigraph – whose vertices are partitioned into objects and attributes, and whose edges are specified by a binary relation $I\subseteq G\times M$ between the sets G of objects and M of attributes. Formal Concept Analysis transforms this bigraph into a partially-ordered set – henceforth poset – of formal concepts. Each formal concept consists of a maximal set of objects, called its extent, and a maximal set of attributes, called its intent, such that each object in the extent is adjacent in the bigraph to each attribute in the intent, and vice versa. The set $g'\subseteq M$ of attributes adjacent to $g\in G$ is the intent of the corresponding object concept, and the set $m'\subseteq G$ of objects adjacent to $m\in M$ is the extent of the corresponding attribute concept. We refer to object and attribute concepts collectively as concrete concepts, and to the remainder as abstract concepts.

The set of formal concepts, partially ordered by extent set inclusion, forms a complete lattice. This concept lattice can be represented as an acyclic directed graph – henceforth digraph – whose vertices are formal concepts and whose directed edges correspond to the cover relation – the transitive reduction of the ordering relation – between concepts. A line diagram is an upward drawing of this digraph in which each object and attribute concept is labelled with the corresponding object(s) and attribute(s) respectively. Abstract concepts can be readily recognised from this diagram as those which are not labelled.

A formal context may give rise to as many as $2^{\min (|G|,|M|)}$ formal concepts, of which at most $|G|+|M|$ are concrete. Abstract concepts therefore differ quantitatively from concrete ones in that they are potentially far more numerous, and actually so in pathological cases such as the contranominal scale [1]. The potential combinatorial explosion of concepts with increasing size of the formal context poses challenges for the computation, layout and visualisation of, as well as interaction with, the lattice digraph. Contexts of even moderate size can produce a large number of resultant vertices and arcs, which compete for limited screen real estate and challenge user comprehension. On-demand construction and layout of the entire lattice digraph cannot be achieved in interactive timescales for large lattices, so either prior or user-guided construction and layout is required to support responsive interaction.

1.2 AOC Poset

Some analytic objectives, such as identifying the upper neighbours of the infimum and lower neighbours of the supremum, can be achieved without enumeration of the full concept lattice. The Attribute-Object Concept (AOC) poset [2] of a formal context consists of only the concrete concepts, once again ordered by extent set inclusion. The AOC poset therefore has at most $|G|+|M|$ elements, allowing its elements and cover relation to be computed in less time [2], and its line diagram presented using less screen real estate, than the concept lattice. For convenience, we include the supremum and infimum of the concept lattice in the AOC poset and corresponding line diagram, regardless of whether they are concrete concepts.

Applying FCA to the domain of object-oriented software engineering, Godin and Mili [5] used the term “abstract” to describe concepts lacking an object label. The analogy between abstract concepts in FCA and abstract classes in object-oriented software engineering is straighforward – an abstract class is one from which an object cannot be directly instantiated, and in this sense (only) abstracts from the properties of the classes which inherit it. Godin and Mili [5] noted the existence of concepts which have neither object nor attribute labels – for which we have reserved the term “abstract” – and described the benefits of including them in their analysis, both for domain understanding and object-oriented design. The greatest lower and least upper bounds – meet and join respectively – exist for any subset of concepts in the concept lattice, and can be “read” from the line diagram as the concepts at which downward and upward paths, respectively, from those concepts converge. Due to the absence of abstract concepts, however, these bounds are not guaranteed to exist in the AOC poset, and hence the corresponding interpretation of the line diagram is unsafe. The AOC poset is consequently insufficient for analytical tasks which rely on the existence of these bounds, such as deriving a basis for attribute implications.

1.3 Morphing AOC Poset into Concept Lattice

Pattison and Ceglar [9] therefore proposed a hybrid approach, which exploits the computational and graph drawing benefits of the AOC poset to rapidly present its line diagram to the user for familiarisation while they await computation of the abstract concepts. Progressive insertion of the abstract concepts then morphs this line diagram into that for the concept lattice, which contains all abstract concepts and delivers the attendant benefits noted by Godin and Mili [5].

The lower neighbours of the supremum and upper neighbours of the infimum in the concept lattice are referred to as atoms and co-atoms respectively. Already present in the AOC poset, these can be horizontally ordered so as to reduce arc crossings in – and hence improve the readability of – a layered drawing of the AOC poset initially, and ultimately of the concept lattice digraph [10]. The horizontal positions of the remaining concepts are derived from those of their atomic descendants and co-atomic ancestors [9]. The AOC poset with atoms and co-atoms so ordered therefore provides a suitable substrate for the subsequent progressive insertion of the remaining abstract concepts. This progressive approach to construction of the lattice digraph allows users to familiarise themselves with the line diagram of the AOC poset while the abstract concepts are being computed, and ideally to preserve their resultant mental model throughout subsequent concept insertions.

1.4 Generating only Abstract Concepts

Pattison and Ceglar [9] did not specify how, having already identified the concrete concepts and constructed the line diagram for the AOC poset, an FCA algorithm should thereafter efficiently and promptly produce only the remaining, abstract concepts. Once the AOC poset has been constructed, a conventional FCA algorithm could obviously be modified to simply discard any concepts it generates which are not abstract. However re-generating, identifying and discarding each concrete concept is not only inefficient, but also delays production of the abstract concepts awaited by the user. A second alternative is that an existing FCA algorithm might be modified to first produce the AOC poset, followed by (only) the remaining, abstract, concepts. A third alternative is that the AOC poset and its line diagram are generated by an existing algorithm such as Hermes [2], and a novel algorithm generates only the abstract concepts for subsequent insertion into the line diagram. This third option, and in particular exposition of the novel algorithm, is the focus of this paper.

The generation of abstract concepts proceeds in three stages: pre-processing of the clarified formal context to remove edges and vertices which do not satisfy necessary conditions for their participation in abstract concepts; conventional FCA of the pre-processed context; and efficient elimination of any resultant concepts which are either not valid or not abstract in the original context. The pre-processing step removes bigraph elements, and thereby ablates the formal context, while preserving all abstract concepts. Established precedents for context ablation include clarification and reduction [3], which remove selected vertices and adjacent edges from a formal context while preserving the structure of the lattice digraph. In addition to simplifying and expediting the subsequent process of Formal Concept Analysis, context ablation has the beneficial side-effect of reducing the cardinalities |G| and |M| of the context bigraph vertex sets, and thereby lowering the a priori exponential bound on the number of concepts.

In [9], the user could either await the insertion of additional abstract concepts potentially anywhere in the evolving poset digraph, or prioritise their generation by selecting existing concepts and requesting their meet or join. Thus the user may waste time waiting for, or trying to prioritise, the enumeration of abstract concepts which do not exist. If immutable arcs in the AOC poset digraph – i.e. those which will not be subject to subsequent transitive reduction – could be identified ab initio, the remainder could be visually distinguished to focus user attention on areas where the insertion of abstract concepts may yet occur, and hence where the interpretation of meets and joins is unsafe. We argue that these immutable digraph arcs include those corresponding to bigraph edges removed during our context ablation step, and demonstrate empirically that many such arcs can be identified as a by-product of context ablation.

1.5 Organisation

This paper is organised as follows. Section 2 describes the ablation of a formal context to reduce the number of bigraph elements while preserving all abstract concepts. It outlines the strategy, and details supporting theory, for the elimination of bigraph elements, illustrating their application using a worked example. Those familiar with FCA theory can start from Definition 11. Section 3 describes analysis of the ablated context to generate only abstract concepts for progressive insertion into the line diagram of the AOC poset. As the line diagram is thereby morphed into that for the concept lattice, the user’s attention is directed to where such insertions may still occur. Section 4 summarises the contribution.

2 Context Ablation

2.1 Preliminaries

Definition 1

A formal context $\mathbb {K} = (G,M,I)$ is a labelled bipartite graph, or bigraph, with object vertex set G, attribute vertex set M, and undirected edge set $I\subseteq G\times M$.

Each vertex has a unique label which derives from the domain of application. For bibliographic analysis, for example, the objects may represent publications labelled by their title and the attributes may represent authors labelled by their full name.

Definition 2

A sub-context of a formal context $\mathbb {K}=(G,M,I)$ is a formal context for which , and .

Definition 3

 

Definition 4

A biclique of the formal context $\mathbb {K}$ is a sub-context satisfying .

Definition 5

A biclique is proper if and .

Definition 6

A biclique $(\mathcal {E},\mathcal {I}, \mathcal {E}\times \mathcal {I})$ of the formal context $\mathbb {K}$ is maximal if no proper superset $\overline{\mathcal {E}}:\mathcal {E}\subset \overline{\mathcal {E}}\subseteq G$ satisfies $\overline{\mathcal {E}}\times \mathcal {I}\subseteq I$ and no proper superset $\overline{\mathcal {I}}:\mathcal {I}\subset \overline{\mathcal {I}}\subseteq M$ satisfies $\mathcal {E}\times \overline{\mathcal {I}}\subseteq I$.

Definition 7

A formal concept of the formal context $\mathbb {K}$ is an ordered pair $(\mathcal {E},\mathcal {I})$ consisting of the object set $\mathcal {E}\subseteq G$ and attribute set $\mathcal {I} \subseteq M$ of a maximal biclique.

The set $\mathcal {E}$ is called the extent of the formal concept, and the set $\mathcal {I}$ is called the intent. A formal concept may have empty intent or extent, and hence need not correspond to a proper biclique [4].

Definition 8

The intent operator maps any set $\mathcal {A}\subseteq G$ of object vertices to the maximal set $\mathcal {A}'\subseteq M$ of attribute neighbours satisfying $\mathcal {A}\times \mathcal {A}'\subseteq I$. The extent operator maps any set $\mathcal {B}\subseteq M$ of attribute vertices to the maximal set $\mathcal {B}'\subseteq G$ of object neighbours satisfying $\mathcal {B}'\times \mathcal {B}\subseteq I$.

Since it is obvious from the context which of these two operators is intended, the same symbol $'$ usually suffices for both.

Observation 1

([3]). The pair $(\mathcal {E},\mathcal {I})$ with $\mathcal {E}\subseteq G$ and $\mathcal {I}\subseteq M$ is a formal concept of $\mathbb {K}$ iff $\mathcal {I}=\mathcal {E}'$ and $\mathcal {E}=\mathcal {I}'$.

The intent $\mathcal {I}=\mathcal {E}'$ and extent $\mathcal {E}=\mathcal {I}'$ of a concept are closed under the composition $''$ of these two operators, since $\mathcal {I}=\mathcal {E}'=\mathcal {I}''$ and $\mathcal {E}=\mathcal {I}'=\mathcal {E}''$.

Definition 9

Formal concepts are partially ordered such that

$$(\mathcal {E}_{1},\mathcal {I}_{1}) < (\mathcal {E}_{2},\mathcal {I}_{2}) \iff \mathcal {E}_{1}\subset \mathcal {E}_{2} \text { and } \mathcal {I}_{1} \supset \mathcal {I}_{2}$$

The set $\mathfrak {B}$ of formal concepts of the formal context $\mathbb {K}=(G,M,I)$, partially ordered as per Definition 9, constitutes a complete lattice. The least upper bound, or supremum, and the greatest lower bound, or infimum, of $\mathfrak {B}$ are referred to collectively as the extrema.

Definition 10

The object concept for object i is $(i'',i')$, and the attribute concept for attribute j is $(j',j'')$.

Observation 2

A formal concept $(\mathcal {E},\mathcal {I})$ satisfies

$$\begin{aligned} (j',j'') \ge (\mathcal {E},\mathcal {I}) \ge (i'',i') \qquad \forall (i,j)\in \mathcal {E}\times \mathcal {I} \end{aligned}$$

(1)

Definition 11

A formal concept $(\mathcal {E},\mathcal {I})$ is abstract if $\mathcal {E}\times \mathcal {I}\ne \emptyset$ and

$$\begin{aligned} (j',j'')>(\mathcal {E},\mathcal {I})>(i'',i') \qquad \forall (i,j)\in \mathcal {E}\times \mathcal {I} \end{aligned}$$

(2)

Definition 11 excludes attribute and object concepts, to which we refer collectively as concrete concepts. It also excludes the supremum, since: the inequality is impossible – and the supremum an attribute concept – for any universal attribute $j\in \mathcal {I}$; and if instead $\mathcal {I}=\emptyset$, then $\mathcal {E}\times \mathcal {I}=\emptyset$. Definition 11 similarly excludes the infimum. $\mathfrak {B}$ can therefore be partitioned into the extrema, (other) concrete concepts and the set of abstract concepts.

Corollary 1

A formal concept $(\mathcal {E},\mathcal {I}):\mathcal {E}\times \mathcal {I}\ne \emptyset$ is abstract iff

$$\begin{aligned} |\mathcal {E}|&> k_{\mathcal E} \ge&1 \end{aligned}$$

(3a)

$$\begin{aligned} |\mathcal {I}|&> k_{\mathcal I} \ge&1 \end{aligned}$$

(3b)

where

$$\begin{aligned} k_{\mathcal E}&= \max _{i\in \mathcal {E}} |i''| \end{aligned}$$

(4a)

$$\begin{aligned} k_{\mathcal I}&= \max _{j\in \mathcal {I}} |j''| \end{aligned}$$

(4b)

Proof

This result follows from Observation 2 and Definitions 11 and 9. The constraint $\mathcal {E}\times \mathcal {I}\ne \emptyset$ is required to avoid maximisation over an empty set in Eq. 4.

We denote by $\mathfrak {B}^{*}$ the set of abstract concepts of $\mathbb {K}$, and refer to the corresponding proper maximal bicliques as abstract bicliques. We denote by $\mathbb {K}^{*}=(G^{*},M^{*},I^{*})$ the sub-context of $\mathbb {K}$ consisting of the union of all abstract bicliques.

Observation 3

$(\mathcal {E},\mathcal {I})\in \mathfrak {B}^{*}$ is a formal concept of any $\mathbb {K}':\mathbb {K}^{*}\le \mathbb {K}'\le \mathbb {K}$.

Proof

By our premise, $(\mathcal {E},\mathcal {I})$ is a proper maximal biclique in $\mathbb {K}$. It remains a proper biclique in $\mathbb {K}'\ge \mathbb {K}^{*}$ because all of its constituent edges and vertices are present in $\mathbb {K}^{*}$, and it remains maximal because all edges in $\mathbb {K}'\le \mathbb {K}$ are also in $\mathbb {K}$.

2.2 Strategy

In order to enumerate only abstract concepts, we seek a procedure which identifies and removes edges and vertices in $\mathbb {K}\setminus \mathbb {K}^{*}=(G\setminus G^{*},M\setminus M^{*},I\setminus I^{*})$. Such a procedure would ideally terminate when, and only when, $\mathbb {K}$ has been transformed into $\mathbb {K}^{*}$. The remaining subgraph $\mathbb {K}': \mathbb {K}^{*}\le \mathbb {K}'\le \mathbb {K}$ would then be divided into its connected components, the components subjected to independent FCA, and those resultant concepts which are both valid in $\mathbb {K}$ and abstract as per Corollary 1, progressively inserted into the AOC poset. Given that the elements of the AOC poset have already been enumerated, the desired procedure can use as input the properties of concrete concepts, such as intent or extent set cardinality.

Fig. 1.

Line diagram of concept lattice for InfoVis 151 omitting the extrema. Atoms (bottom) and co-atoms (top) are ordered using resistance distance, and the remaining concepts placed at the horizontal barycenter of their co-atomic ancestors and atomic descendants.

Fig. 2.

Line diagram of AOC poset for InfoVis 151 omitting the extrema. Non-black object and attribute labels are colour-coded for membership of the connected components of the context bigraph remaining after the ablation described in Example 4.

Iteration over the edges of $\mathbb {K}=(G,M,I)$ to eliminate those not involved in abstract concepts is viable provided the context is sparse. By “sparse” we mean that the cardinalities |I|, |G|, |M| of the context relation I, object set G and attribute set M satisfy $|I| \ll |G||M|$. We use as a running empirical example a sub-context of the InfoVis 2004 bibliographic data set [12] having 151 proper maximal bicliques. This clarified sub-context has 108 objects, 113 attributes and $273 \ll 108\times 113$ edges. Hereafter, we refer to this context as InfoVis 151. A drawing of the lattice digraph for this context, omitting the extrema, is shown in Fig. 1. Abstract concepts are shown with coloured fill.

2.3 Elimination of Bigraph Elements

Observation 4

Let bigraph edge (i, j) participate in an abstract concept $(\mathcal {E},\mathcal {I})$ of $\mathbb {K}$. Then

$$\begin{aligned} |j'|&> |\mathcal {E}| > |i''| \end{aligned}$$

(5a)

$$\begin{aligned} |i'|&> |\mathcal {I}| > |j''| \end{aligned}$$

(5b)

Observation 4 follows from Eq. 2 of Definition 11, and necessarily precludes $(\mathcal {E},\mathcal {I})$ from being the object concept for any $g\in i''$ or the attribute concept for any $m\in j''$. However, it might still be the object concept for some $g\in j'\setminus i''$ or the attribute concept for some $m\in i'\setminus j''$. The following corollary therefore provides a necessary but not sufficient condition for any concepts intervening between $(i'',i')$ and $(j',j'')$ to be abstract.

Corollary 2

Let edge (i, j) participate in an abstract concept of $\mathbb {K}$. Then

$$\begin{aligned} |i'|\ge & {} |j''| + 2 \end{aligned}$$

(6a)

$$\begin{aligned} |j'|\ge & {} |i''| + 2 \end{aligned}$$

(6b)

If $(i,j)\in I$ does not satisfy Eq. 6, then $(i,j)\in I\setminus I^{*}$ and can be safely eliminated without compromising any abstract maximal bicliques of $\mathbb {K}$. Eliminated bigraph edges for which $(j',j'')>(i'',i')$ correspond to arcs in the concept lattice digraph. Such arcs are already present in the line diagram of the AOC poset, and are immutable in the sense that they will not be interrupted by the subsequent insertion of the remaining (abstract) concepts.

Fig. 3.

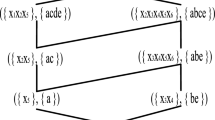
Simple context bigraph (a) and line diagrams for the corresponding AOC poset (b) and concept lattice (c). Corollary 2 eliminates the black bigraph edges. Solid edges in (a) correspond to mutable (red) and immutable (black) arcs in (b). The surviving red edges and adjacent vertices in (a) correspond to the abstract (grey) concept in (c), whose insertion interrupts the mutable arcs. (Color figure online)

Example 1

Of the 11 edges in the simple context bigraph depicted in Fig. 3a, Corollary 2 eliminates the 7 shown black. Of these, the 2 solid edges satisfy $(j',j'')>(i'',i')$, and hence correspond to lattice arcs already present in the line diagram of the AOC poset shown in Fig. 3b; the remaining 5 dashed edges do not. Solid bigraph edges correspond to mutable (red) and immutable (black) arcs in the AOC poset line diagram; dashed edges have no corresponding poset arc. The mutable (red) arcs in Fig. 3b are interrupted by the subsequent insertion of the abstract concept $(\{\mathtt {1,2}\},\{\mathtt {a,b}\})$ shown grey in Fig. 3c.

Corollary 3

Let bigraph vertex $\alpha$ participate in an abstract concept of $\mathbb {K}$. Then in $\mathbb {K}':\mathbb {K}^{*}\le \mathbb {K}'\le \mathbb {K}$, $|\alpha '| \ge 2$.

Proof

Any vertex in a biclique has at least as many neighbours as the biclique contains vertices of the opposite type. Equation 3 requires that $|\mathcal {E}|\ge 2$ and $|\mathcal {I}|\ge 2$ for an abstract biclique, so that $|\alpha '| \ge 2$ in $\mathbb {K}$. Observation 3 and Corollary 2 ensure that no edge within an abstract biclique is deleted, so that $|\alpha '| \ge 2$ also holds in $\mathbb {K}'$.

Vertices of degree less than two in $\mathbb {K}'$ can be safely deleted along with their adjacent edges, since neither can participate in an abstract concept of $\mathbb {K}$. By removing the unrealistic requirement for apriori knowledge of the elements of $\mathcal {E}$ and $\mathcal {I}$, Corollary 3 clears the way for practical application of Corollary 1 to context ablation in preparation for FCA.

Example 2

Following application of Corollary 2 to the example context in Fig. 3a, Corollary 3 eliminates objects $\{\mathtt {3,4,5}\}$ and attributes $\{\mathtt {c,d,e}\}$, leaving only the red edges and adjacent vertices. These constitute the abstract biclique $(\{\mathtt {1,2}\},\{\mathtt {a,b}\})$ corresponding to the grey vertex in Fig. 3c.

Since Corollaries 2 and 3 impose conditions on bigraph elements which are necessary but not sufficient for participation in abstract bicliques, the ablated formal context may more generally still contain superfluous elements.

The deletion of vertices and their adjacent edges from $\mathbb {K}'$ according to Corollary 3 produces a new context $\mathbb {K}'':\mathbb {K}^{*}\le \mathbb {K}''\le \mathbb {K}'\le \mathbb {K}$ to which Corollary 3 also applies. Corollary 3 should be applied iteratively, since the deletion of a vertex having a single neighbour can cause the (formerly) adjacent vertex to subsequently fail the neighbour cardinality test. In the worst case, one more iteration may be required than the longest chain of vertices of degree 2.

Example 3

Following application of Corollary 2 to InfoVis 151, 2 iterations of Corollary 3 eliminate 9 of the remaining 29 objects, 12 of 41 attributes and 20 incident edges, leaving three connected components of sizes $12\times 20$, $4\times 5$ and $4\times 4$. Additional iterations do not eliminate any further bigraph elements. FCA can be applied independently to these three components.

Whilst Corollaries 2 and 3 can be applied in either order, the cardinalities $|i'|$, $|j'|$, $|i''|$ and $|j''|$ required by the former must be calculated on the original context $\mathbb {K}$. Edge deletion may have decreased the vertex degrees $|i'|$ and $|j'|$, and, by removing the structural distinction between some vertices, increased the closure cardinalities $|j''|$ and $|i''|$. The vertex degrees $|i'|$ and $|j'|$ cannot have increased, since no edges were added to $\mathbb {K}$. Furthermore $|j''|$ and $|i''|$ cannot have decreased, since vertices which were structurally equivalent in $\mathbb {K}$ remain so in $\mathbb {K}'$.

Fig. 4.

Example illustrating that closure cardinality may be higher in $\mathbb {K}'$ than $\mathbb {K}$.

The example context in Fig. 4 contains the maximal biclique $(\{\mathtt {1,2}\},\{\mathtt {a,b}\})$. Each vertex of this biclique has an additional distinct neighbour so that the biclique edges satisfy Corollary 2. The edges $(\mathtt {1},\mathtt {c})$, $(\mathtt {2},\mathtt {d})$, $(\mathtt {3},\mathtt {a})$ and $(\mathtt {4},\mathtt {b})$ do not satisfy Corollary 2, and hence are not present in $\mathbb {K}'$. The degrees of objects $\mathtt {1}$ and $\mathtt {2}$ and attributes $\mathtt {a}$ and $\mathtt {b}$ have each decreased by 1. Object $\mathtt {1}$ is thereby rendered indistinguishable from object $\mathtt {2}$, and attribute $\mathtt {a}$ from $\mathtt {b}$. Thus for example $|\mathtt {1}''|$ is 1 in $\mathbb {K}$ but 2 in $\mathbb {K}'$.

2.4 Iterative Edge Elimination

We have seen that significant numbers of edges not involved in abstract concepts of $\mathbb {K}$ can be removed by Corollary 2 to produce $\mathbb {K}': \mathbb {K}^{*}\le \mathbb {K}'\le \mathbb {K}$. Since Corollary 2 compares the cardinalities $|i'|$, $|j'|$, $|i''|$ and $|j''|$ calculated on $\mathbb {K}$, it no longer applies to $\mathbb {K}'$, and is therefore of no further use in approaching $\mathbb {K}^{*}$. In Example 3, additional vertices and adjacent edges in $\mathbb {K}'\setminus \mathbb {K}^{*}$ were then eliminated through the iterative application of Corollary 3 to produce $\mathbb {K}'' \ge \mathbb {K}^{*}$. We now develop iterative variants of Corollary 2 which can be applied either to $\mathbb {K}'$ or to $\mathbb {K}'' \ge \mathbb {K}^{*}$, and demonstrate empirically that in the former case they can delete more edges than Corollary 3.

Observation 5

Let edge (i, j) participate in an abstract concept $(\mathcal {E},\mathcal {I})$ of the formal context $\mathbb {K}$. Then in $\mathbb {K}':\mathbb {K}^{*}\le \mathbb {K}'\le \mathbb {K}$, $(j',j'')\ge (\mathcal {E},\mathcal {I})\ge (i'',i')$.

Proof

Denote by $\mathfrak {B}'$ the set of formal concepts of $\mathbb {K}'$. Observation 3 ensures that $(\mathcal {E},\mathcal {I})\in \mathfrak {B}'$, and the result follows from Observation 2. Equalities are possible – and hence $(\mathcal {E},\mathcal {I})$ may not be abstract in $\mathbb {K}'$ – because, as a consequence of edge deletions, it may now be the object [attribute] concept for i [j].

Corollary 4

Let bigraph edge (i, j) participate in an abstract concept of the formal context $\mathbb {K}$. Then in $\mathbb {K}':\mathbb {K}^{*}\le \mathbb {K}'\le \mathbb {K}$

$$\begin{aligned} |i'|\ge & {} |j''| \end{aligned}$$

(7a)

$$\begin{aligned} |j'|\ge & {} |i''| \end{aligned}$$

(7b)

Observation 6

Let bigraph edge (i, j) participate in an abstract concept of the formal context $\mathbb {K}$. Then

$$\begin{aligned} |i'|\ge & {} |j''| + 1 \end{aligned}$$

(8a)

$$\begin{aligned} |j'|\ge & {} |i''| + 1 \end{aligned}$$

(8b)

where the derivation operators on the left- and right-hand sides are with respect to $\mathbb {K}':\mathbb {K}^{*}\le \mathbb {K}'\le \mathbb {K}$ and $\mathbb {K}$ respectively.

Proof

Let the abstract concept be $(\mathcal {E},\mathcal {I})$. From Observation 5, $|i'|\ge |\mathcal {I}|$ and $|j'|\ge |\mathcal {E}|$ in $\mathbb {K}'$ and from Observation 4, $|\mathcal {I}| \ge |j''|+1$ and $|\mathcal {E}| \ge |i''|+1$ in $\mathbb {K}$. Pairing these inequalities and noting that $\mathcal {E}$ and $\mathcal {I}$ – and hence also their cardinalities – are the same in both contexts yields the result.

Corollary 4 and Observation 6 both provide lower bounds on $|i'|$ and $|j'|$ in $\mathbb {K}'$. The greater of these two lower bounds should be applied when determining whether any additional bigraph edges can be eliminated.

In contrast with Corollary 2, which can be applied only once to $\mathbb {K}$, Corollaries 3 and 4 and Observation 6 can be applied iteratively. The removal of a non-compliant bigraph edge (i, j) in one iteration reduces $|i'|$ and $|j'|$, and can thereby cause other edges adjacent to object i or attribute j to fail Eq. 8 in the next. Since only edges in $\mathbb {K}\setminus \mathbb {K}^{*}$ are deleted, the iteration must halt when no further edges can be deleted, leaving at least the abstract concepts intact.

Example 4

Following application of Corollary 2 to InfoVis 151, 4 iterations of Observation 6 eliminated 29 additional bigraph edges, isolating an additional 11 objects and 16 attributes. No further edges were eliminated by the fifth iteration. Three connected components remained, as for Example 3, but now with sizes $10\times 17$, $4\times 5$ and $4\times 3$. The labels of the objects and attributes belonging to these connected components, and the abstract concepts to which these components give rise, are coloured in Figs. 2 and 1 respectively.

The overall context ablation procedure is listed in Algorithm 1. Corollary 2, Observation 6 and Corollary 3 are implemented in turn by the loops commencing at lines 8 and 13 and the assignments commencing at line 26 respectively. Since Corollary 2 and Observation 6 both eliminate edges adjacent to vertices of degree one, the subsequent application of Corollary 3 amounts to deleting vertices of degree zero. Their more timely deletion would confer no computational benefit, since Corollary 2 and Observation 6 both cycle through edges vice vertices. The cardinalities $|i'|, |i''| \ \forall i\in G$ and $|j'|, |j''| \ \forall j\in M$ can either be passed to Ablate() following preparation of the AOC poset, or re-calculated from the context at line 3. The values for $|i''|$ and $|j''|$ are re-used throughout Algorithm 1. Vertex k currently has Neighbours(k) neighbours, and Dirty(k) is true if one or more of its adjacent edges has been deleted during the most recent pass through the set of edges. Unless no adjacent edges remain, this flag is cleared after one complete pass through the set of edges (adjacent to “dirty” vertices) fails to delete any further adjacent edges.

3 Formal Concept Analysis of Ablated Context

Section 2 described the elimination of elements of the context bigraph $\mathbb {K}$ which cannot participate in abstract formal concepts. Examples 3 and 4 demonstrated that the resultant formal context can have considerably fewer graph elements, thereby significantly constraining the potential combinatorial explosion of abstract concepts. In this section, the remaining context $\mathbb {K}'$ is subjected to conventional FCA, and the resultant concepts screened to eliminate any which are either not valid in $\mathbb {K}$ or are not abstract. For reviews of FCA algorithms applicable to the analysis of $\mathbb {K}'$, the interested reader is referred to [7, 8, 13].

3.1 Finding Valid Abstract Concepts

For the Infovis 151 context processed as per Example 4, $\mathbb {K}'$ contains a total of 35 concepts, compared with the 151 concepts for $\mathbb {K}$. Definition 11 and Corollary 1 justify the immediate elimination of any resultant formal concepts which have extent or intent cardinality less than 2, which for Infovis 151 leaves only 14 concepts as candidate abstract concepts of $\mathbb {K}$. The more stringent form of Corollary 1 involving Eq. 4 eliminates any concepts which are valid and concrete in $\mathbb {K}$; in this instance it eliminates a further 2 concepts.

Observation 3 applies only to the abstract concepts of $\mathbb {K}$, since at least some concrete concepts must be affected by the removal of edges or vertices to form $\mathbb {K}'$. Indeed, as we have seen in the case of Infovis 151, many of the objects and attributes whose corresponding attribute and object concepts are members of the AOC poset are no longer present in $\mathbb {K}'$. For those which remain, their corresponding object and attribute concepts in $\mathbb {K}'$ may not be valid concepts in $\mathbb {K}$. Screening the concepts generated by conventional FCA of $\mathbb {K}'$ for validity in $\mathbb {K}$ according to Observation 1 can therefore eliminate some concepts which are not viable candidates for abstract concepts of $\mathbb {K}$, while preserving all abstract concepts according to Observation 3. Of the 12 remaining candidate concepts for Infovis 151, only 6 are valid in $\mathbb {K}$. In contrast, naïve application of FCA to the original Infovis 151 generates and tests the novelty of at least 151 concepts.

3.2 Dividing and Conquering

A beneficial side-effect of the context ablation described in Sect. 2 is that it allows us to divide and conquer the process of concept generation. The InfoVis 151 bigraph $\mathbb {K}$ is connected by virtue of pre-processing by the Carve algorithm [11]. However, as Examples 3 and 4 have demonstrated, deletion of some bigraph elements from $\mathbb {K}$ to form $\mathbb {K}'$ can cause the latter to be disconnected. In this case, enumeration of its formal concepts can be divided and conquered through independent FCA of each of its connected components. Pattison et al. [11] described how the lattice digraph can be constructed from the digraphs for each of these connected components. As per Example 4 for the InfoVis 151 context, which contains 108 objects and 113 attributes, three connected components with a total of 18 objects and 25 attributes can be identified following application of Corollary 2 and Observation 6. The divide and conquer approach also extends to checking of Corollary 1; for this purpose, each attribute and object should be accompanied by the cardinality of its closure from the original AOC poset.

3.3 Anticipating and Localising Change in the AOC Poset

Pattison and Ceglar [9] described an incremental approach to drawing a concept lattice whereby the elements of the attribute-object concept (AOC) poset were first identified and positioned horizontally, and then the remaining concepts progressively inserted into a two-dimensional drawing of the poset. This paper has described an efficient, divide and conquer approach for producing those remaining abstract concepts. As the line diagram for the AOC poset is morphed into that for the concept lattice, user attention can be directed to or from regions of the line diagram where the insertion of abstract concepts is still possible, and hence where the graphical interpretation of meets and joins is unsafe.

Figure 2 shows the line diagram for the AOC poset of the Infovis 151 context. The arcs shown red correspond to edges in the context bigraph which satisfy the necessary conditions in Corollary 2 and Observation 6 for participation in an abstract concept. For comparison, the line diagram for the concept lattice digraph is shown in Fig. 1, with abstract concepts shown coloured. Many of the arcs highlighted in Fig. 2 have subsequently been removed as a result of transitive reduction. However, some of these remain in Fig. 1, indicating that there may be opportunity to further refine the necessary conditions in Sect. 2 to reduce the number of such false alarms. The highlighting in Fig. 1 is for illustrative purposes only: once a connected component has been processed, and its abstract concepts inserted into the line diagram, highlighting can be removed from any of its arcs which remain highlighted.

4 Discussion and Summary

The context ablation procedure described in Sects. 2.3 and 2.4 does not require the context to have been clarified. In an unclarified context, however, some bigraph edges corresponding to immutable lattice arcs may pass the test in Eq. 6, and thereby escape elimination. This would result in the generation of additional concepts which must then be explicitly eliminated as per Sect. 3.1.

The technique described in [10] for horizontally ordering the lattice atoms and co-atoms in the AOC poset requires that these concept sets are disjoint. FCA of a formal context which does not meet this requirement can be recursively divided using the Carve algorithm [11] into sub-contexts which do. Only the resultant connected bigraphs would then be subjected to the techniques described in this paper. These may be disconnected by the context ablation in Sects. 2.3 and 2.4, and thereby further divided and conquered.

A subgraph of the context bigraph is biconnected if it remains connected upon removal of any one of its vertices, or 2-connected if a single vertex is not considered “connected”. A bridge is a biconnected component of the context bigraph containing exactly two vertices. An abstract maximal biclique of $\mathbb {K}$ is a 2-connected, bridgeless subgraph of $\mathbb {K}':\mathbb {K}^{*}\le \mathbb {K}'\le \mathbb {K}$ and hence is contained within a single biconnected component of $\mathbb {K}'$. Efficient algorithms exist for finding the biconnected components of a simple graph [6], and should be investigated for simultaneous ablation and partitioning of $\mathbb {K}$. Excluding any bridges from further analysis effectively ablates the constituent edges from, and thereby disconnects, the context bigraph.

Enumeration and visualisation of the AOC poset, vice concept lattice, scales to larger formal contexts, since the former has at most $|G|+|M|$ elements and the latter $|\mathfrak {B}|\le 2^{\min (|G|,|M|)}$. It therefore constitutes a more reliable first step for interactive, on-demand FCA. For sparse contexts, mutable poset arcs can be efficiently identified using context ablation, and the quantity

$$\min (|j'|-|i''|,|i'|-|j''|) - 1$$

calculated for each as an upper bound on the number of abstract concepts between the object concept for i and the attribute concept for j. Aggregating these bounds constrains the number of abstract concepts, from which the feasibility of interactive visualisation of the concept lattice can be assessed. The ablation and bounding steps are of course unneccessary if the results of prior, as opposed to on-demand, computation and layout of the concept lattice digraph are available. Visualisation of the AOC poset may still be appropriate in this case if the digraph size challenges user comprehension. Selection of mutable arcs might then drive on-demand insertion of any intervening abstract concepts.

Instead of morphing the line diagram for the AOC poset into that for the concept lattice, the latter could be presented to the user as a separate view. This would clearly distinguish between the line diagrams in which meets and joins are and are not guaranteed to exist. This approach would transform the challenge of maintaining the user’s mental model throughout the morph into one of acquiring the association between the two views. A comparative evaluation of the user experience will be required to decide between these two approaches.

This paper has described the ablation of a formal context to eliminate many of the concrete concepts, dividing and conquering FCA of the remaining sub-context, and screening the remaining formal concepts to produce only the required abstract concepts. These are progressively inserted into the line digram for the AOC poset, morphing it into that for the concept lattice. The user’s attention is directed to where such insertions of missing meets or joins may still occur. The potential utility of this approach has been demonstrated using a single real-world context. Empirical studies will be required to confirm and qualify its wider applicability to sparse contexts.