Uncertainty in Structural Fire Design

Abstract

Structural fire safety requirements implicitly balance up-front investments in materials (protection or element sizing) with improved performance (loss reductions) in the unlikely event of a fire. For traditional prescriptive fire safety recommendations, the underlying target safety levels are not clear to the designer, nor is the associated balancing of risk and investment costs. While easy to apply, guidance / code-based approaches to the specification of fire protection / resistance have the severe disadvantage that the level of safety investment is not tailored to the specifics of the case, resulting in large overinvestments in some cases, and possibly insufficient structural fire safety in others. This observation is a major driver for the use of performance-based design (PBD) methodologies, where the fire safety design is tailored to the needs of the building. However, it is posited in this chapter that traditional PBD in a structural fire context is deterministic, with the safety foundation premised upon the collective experience of the profession. It is separately noted that building forms are increasingly uncommon in nature, due to material choice, height, failure consequences, etc., and, as such, collective experience is increasingly a weak safety foundation. This is where probabilistic methods add value and provide a quantified / explicit basis for demonstrating the adequacy of a design. This chapter, thus, focusses on uncertainties and uncertainty quantification in the context of structural performance in the event of fire, introducing reliability and risk concepts, with supporting data and applications.

9.1 Introduction

9.1.1 Structural Design and Uncertainty

Probabilistic methods form the basis of verification of structural design under ambient conditions in most structural engineering standards around the world. Safety factors are specified based on statistical variations in load and resistance of a structure, applying reliability goals as a benchmark for verification that a structure provides an acceptable level of safety. Despite this fundamental principle, current structural fire engineering approaches are intrinsically deterministic and incorporate neither of the above two concepts of safety factors or reliability goals.

Instead, structural fire engineering analysis typically relies on the evaluation of the response of a structure to a single or very few deterministic scenarios which although often conservative do not normally account for uncertainties in the input, the modelling approach, or the output. This approach does not address in any meaningful way the amount of conservativeness inherent in a design, or provide any meaningful information about the actual level of safety. The evaluation is carried out in one of a number of ways, with verification done in either the time, the temperature, or the strength domain with the intent being simply to demonstrate that for a given scenario the fire resistance of an element or a structure is greater than or equal to the fire intensity. When verification is done in the temperature or the strength domain, this is almost always done based on the analysis of the response of the structure to one or a few design fires which represent a range of possible fires that could occur inside of that building. However, while these fires may be identified and elaborated using some risk-based technique , the analyses remain purely deterministic and the actual level of safety, margin of safety, probability of failure, or reliability is almost never calculated.

This deterministic demand/capacity evaluation in the strength or temperature domain is often termed performance-based design since the performance criteria may be set based on the unique features of the building in question and taking into account input from the various stakeholders in the project. The basic elements of performance-based design are defined in such a way as to allow the user freedom to compose any solution to a given engineering problem, allowing also the freedom to employ new techniques and technologies as they become available. The objectives must be clearly stated at the outset of the project, and any design solution which fulfils these objectives while still adhering to the performance targets of the design framework should be permitted. The effect of this on the spectrum of possible solutions available for any problem and the impact of this on verification requirements are shown in Fig. 9.1. As the design process tends towards a performance-based approach , the spectrum of possible solutions opens up, allowing more bespoke solutions to a problem.

Fig. 9.1

Expanding spectrum of solutions and verification in performance-based design

Performance-based design is a necessity where buildings fall outside of either the classification afforded by prescriptive building codes around the world or where the materials or methods of construction are such that they introduce new risks or challenge the fire strategy of buildings in ways which were unforeseen in the development of the current regulations. In such cases, the building design falls outside of the bounds by which the fire engineering community can confidently rely on the collective experience of the profession (see Sect. 9.2). It is therefore not possible to ensure safety through the application of prescriptive codes based on the nearest existent classification. Therefore, two lines of action are open to the engineer: either the building design should be modified such that it falls within the scope of the classifications available or engineering analysis has to be undertaken to demonstrate that the level of safety provided by the building is consistent with the performance that may be expected by the society.

This may result in the situation whereby although the targets in terms of life, property, and business protection may remain similar to those in prescriptive design codes, these targets should typically remain independent of the prescriptive building code performance goals. Most legislative objectives are related to preventing loss of life—either of the building occupants or of the first responders working inside of a burning building [1]—and damage to neighbouring property. However, performance-based design also opens the possibility for alternative objectives to be considered such as limiting direct or indirect financial losses to a building’s owner, limiting environmental impact, or preservation of historic structures [2].

Also, when applying performance-based design , the collective experience of the profession in applying these techniques to the specific type of structure may be insufficient to guarantee a sufficient level of safety. In those situations, an explicit verification or quantification of the resulting safety level needs to be undertaken. This is discussed in some detail elsewhere [3]. In summary, and as discussed further in Sect. 9.2, this explicit verification of the safety level aims to ensure that the uncertainties associated with the demand/capacity evaluation do not result in a too high (unknown) likelihood of the structure not fulfilling the design objectives.

9.1.2 Importance of Considering Uncertainty

The basis of demand/capacity-based design in structural engineering is that the resistance of a structure is greater than the load applied on the structure. Consider, to illustrate the concept, an axially loaded element under ambient conditions (Fig. 9.2). The linear elastic response of the system may be defined according to several very simple relationships (see Table 9.1 for definitions):

$$ \sigma =\frac{P}{A} $$

(9.1)

$$ \varepsilon =\frac{\sigma }{E}=\frac{P}{AE} $$

(9.2)

$$ \Delta L=\varepsilon L=\frac{PL}{AE} $$

(9.3)

Fig. 9.2

Simple system under axial load

Table 9.1 Sources and summary of uncertainties in the simple model described

Here, σ is the stress; P is an applied axial load; A is the cross-sectional area of the element; ε is the strain; E is the modulus of elasticity of the material; and L is the length of the element being analysed. Each of these relationships is related to the material properties, an external condition or input to the system, or a feature of the system.

Assuming some relationship between stress and strain which defines the modulus of elasticity , as well as the yield and ultimate stresses and strains as per Fig. 9.3, the failure of this system can be defined according to various different criteria, in function of the performance objective: for example, an evaluation based on a deformation criterion, i.e. ΔL > ΔL*, with ΔL* being a limiting deformation, or according to criteria based on the material response, e.g. σ > σ _y; σ > σ _u; ε > ε _y; or ε > ε _u.

Fig. 9.3

Example relationship between stress and strain at ambient

Even for this simple system, the evaluation of such criteria incorporates, to some degree or another, uncertainties. In the case of the input to the system, there are uncertainties regarding the load which is applied. In the case of the system properties, there are uncertainties with regard to the material response as well as the geometry of the system. When considering the model chosen to analyse this system, there arise model uncertainties associated with the formulation of the material in the model or any discretization or simplifications to the model made by the user. Referring to the uncertainties inherent in the system, these may largely be attributed to aleatoric uncertainties , or aleatory variability , arising from the natural randomness in a process or in the input variables. This randomness can usually be measured and quantified. For discrete variables the randomness can generally be parametrized by different probability mass functions. Uncertainties related to the modelling of the system are referred to as epistemic uncertainties . Different models inherently contain a different degree of epistemic uncertainty. With regard to these epistemic uncertainties, the impact of this on structural design under ambient conditions is well illustrated in the work by Fröderberg and Thelandersson [4]; the impact on structural fire engineering is illustrated in the work by Lange and Boström [5].

At this point, it should be clear that the simple problem presented above contains a multitude of uncertainties: aleatory uncertainty arising from the input to the model in the form of the applied force or the different properties of the system and epistemic uncertainty arising from the modelling approach adopted and any simplifications or assumptions made. As a result of the combined effect of these uncertainties, we cannot always be sure that the condition of capacity being greater than demand, under any of the failure criteria identified above, is satisfied for a given design. The implication is that some degree of risk is being adopted in the acceptance of any model of this problem.

If temperature is introduced to this problem, the nature of the uncertainties remains largely the same; however the complexity of the problem multiplies. The stress-strain relationship of the material becomes a function of temperature, and thermal expansion means that both the cross-sectional area and the length of the element change. Each of the very simple relationships presented above now becomes also a function of temperature:

$$ \sigma (T)=\frac{P}{A(T)} $$

(9.4)

$$ \varepsilon (T)=\frac{P}{A(T)E(T)} $$

(9.5)

$$ \Delta L(T)=\frac{P}{A(T)E(T)}+\alpha \Delta TL $$

(9.6)

where α denotes the coefficient of thermal expansion, and ΔT denotes a change in temperature.

Having introduced temperature to the problem, it becomes also necessary to calculate temperature. As discussed in Chap. 5, the heat transfer inside the solid is governed by Fourier’s law, while convective and radiative heat transfers are to be taken into account at the surface. Each of these processes of heat transfer, conduction, convection, and radiation, now introduces additional variable uncertainties into our system, including conductivity, convective heat transfer coefficient , and emissivity required for calculation of heat transfer by radiation. The complexity of and thus the overall uncertainty associated with this simple problem have now increased dramatically, simply by the introduction of temperature. The certainty that the capacity is always greater than the demand, for any of the criteria listed, is now diminished.

As indicated in Sect. 9.1.1, the traditional means of addressing this uncertainty in structural fire engineering has always been to overestimate the load and to underestimate the capacity, thus accounting for uncertainties by increasing the nominal margin of safety. However, this indirect approach fails to acknowledge that engineering failures occur where the distributions of demand and capacity overlap, i.e. where demand > capacity within the tails of the distributions of the demand and capacity (see Fig. 9.6). Therefore, increasing the margin of safety by increasing the distance between the average demand and the average capacity in an arbitrary way cannot ensure that failure has a probability which is acceptably low to society. Thus, when an explicit verification of the safety level is required, the uncertainties associated with the design need to be explicitly considered.

9.1.3 Sources of Uncertainty

In structural fire engineering, uncertainties arise from many sources . Referring to the process of structural fire engineering described by Buchanan and Abu [6], Fig. 9.4, sources of aleatoric uncertainty can be seen to be introduced at every stage, and epistemic uncertainty arises depending on the models used at each stage. The nature of the sources of uncertainties means that uncertainties propagate through any analysis. The uncertain input variables are propagated through uncertain models which results in uncertain outputs from models.

Fig. 9.4

Flow chart for calculating the strength of a structure exposed to fire, adopted from Buchanan and Abu [6]

When developing the fire model, uncertainties in the geometry of the fire compartment, fuel load , and fire characteristics arise. Arguably uncertainties associated with room geometry are significantly smaller than uncertainties associated with the fuel or the characteristics of the fire and can therefore be ignored. However, the fuel load and the fire characteristics are arguably very significant uncertainties in the entire process and generally cannot be ignored. In the Eurocode , uncertainties associated with the fuel load are treated by adopting some high-percentile fuel load from a distribution which varies with occupancy—increasing the demand for the design, as described above. Other uncertainties related to the fire characteristics however are not treated in any way satisfactorily; for example, the opening factor upon which the burning behaviour is largely dependent is usually treated entirely deterministically. Further uncertainty arises from the choice of fire model; as will be discussed later, different representations of fire (standard fire, parametric fire, travelling fire, zone models, field models) account for different factors related to the overall fire behaviour. The uncertainty associated with the use of these different models will be discussed later in this chapter.

Any uncertainties in the input variables to the fire model as well as uncertainties inherent in the fire model itself are propagated into an uncertainty for the thermal exposure which is an input to the heat transfer model , along with details of the geometry, the thermal properties, and the heat transfer coefficients. Element geometry is arguably similar to the room geometry in that the effects of uncertainties are likely to be relatively inconsequential compared with the uncertainties of thermal exposure, heat transfer coefficients , and material thermal properties. In this chapter, there is a discussion of the variability in thermal properties as well as heat transfer coefficients as input to the heat transfer model. Heat transfer is discussed in Chap. 5. It should be noted that any uncertainties in inputs or resulting from the modelling approach with respect to the fire model propagate through the analysis.

Uncertainties in the inputs to the heat transfer model are propagated, as well as any uncertainties in the model itself, to the structural model where the geometry, the applied loads, and the mechanical properties of the material all are subject to uncertainty. The overall effect of this propagation of uncertainty is a multiplicity of possible outcomes at every stage in the analysis process including in the final determination of the load capacity.

The above gives an overview of the many uncertainties associated with each of the steps in structural fire engineering analysis. These uncertainties can generally be parametrized by different probability distributions . The ability to do this depends to a large extent on the quality of information which is available about the specific variables. This is often cited as one of the most significant obstacles to the use of probabilistic methods in structural fire engineering that the rate of occurrence of events is typically so low that the informativeness of any resulting distributions is low. However, as will be shown in this chapter, many of the variables can be satisfactorily parametrized for a number of different applications. Where variables cannot be parametrized, or where epistemic uncertainties exist, then the sensitivity of solutions can be probed and engineering judgement can be exercised to ensure that design objectives are met.

9.2 Reliability and Risk Acceptance

9.2.1 Risk Acceptance in Structural Fire Design

As indicated in Sect. 9.1, traditional performance-based (structural) fire safety design is deterministic in nature, requiring the selection of design inputs, scenarios, and performance criteria that are deemed appropriately conservative by the engineer. In such a process, the safety level (or residual risk) associated with a given design is not evaluated, and the full spectrum of consequences and their associated probabilities are not interrogated. Instead, it is assumed that an adequate, but unquantified, level of safety is attained based upon engineering judgement and considerations: (a) that real fire events have occurred, with performance observed, and (b) that society has not expressed dissatisfaction with the levels of performance witnessed. In other words, the basis for acceptance of traditional performance-based design (or the safety foundation) is the experience of the fire safety profession (see left-hand side of Fig. 9.5) proposed in Hopkin et al. [7]. This safety foundation can only be justified where there are sufficient real fire events to observe, guide design processes, and offer society opportunities to express views on their dissatisfaction (or otherwise) of the consequences witnessed.

Fig. 9.5

(Left) assumed basis of safe design, (right) demonstrated basis of safe design where experience is not an adequate basis, Hopkin et al. [7]

Traditional (structural) fire safety design and its associated safety foundation cannot, however, be extrapolated to exceptional structures, i.e. those with atypical consequences of failure or adopting innovative materials, as it is likely that insufficient instances exist where fires have occurred and performance is witnessed. For such complex cases, there is a need to explicitly evaluate the residual risk (see right-hand side of Fig. 9.5).

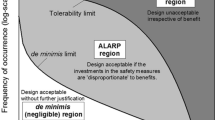
Within the framework presented by Van Coile et al. [3], there is an expectation that probabilistic risk assessment (PRA) methods be employed to demonstrate adequate safety for cases where the collective experience of the profession cannot be called upon to guide design approaches. In doing so, any design must be demonstrated to be tolerable to the society, and the residual risk as low as is reasonably practicable (ALARP). In structural safety, the full cost-benefit analysis implied by the ALARP evaluation is typically substituted by a reliability analysis , allowing to determine design acceptance based on structural failure probabilities only [3].

9.2.2 What Is Reliability?

ISO 2394:2015 [8] defines reliability as the ‘ability of a structure or structural member to fulfill the specified requirements, during the working life, for which it has been designed’. Reliability is expressed in terms of probability and can cover safety, serviceability, and durability of a structure. In the Eurocodes , no in-depth definition of reliability is given. However, in the fundamental requirements it is currently stated: ‘a structure shall be designed and executed in such a way that it will, during its intended life with appropriate degrees of reliability and in an economic way:

• Remain fit for the use for which it is required; and.

• Sustain all actions and influences likely to occur during execution and use’.

In the latter bullet point, a fire condition falls within the definition of ‘all actions’. To satisfy the above considerations in relation to reliability, Holicky [9] notes that there should be four important elements requiring consideration:

• The definition of a failure, i.e. the limit state.

• The time (reference) period under consideration.

• The reliability level, i.e. an assessment of the failure probability .

• The conditions of use (and the associated impact on the input uncertainties).

Importantly, the concept of absolute reliability does not generally exist (apart from in exceptional cases), i.e. few structures have a zero-failure probability and there must be an acceptance that there is a certain, small probability that a failure may occur within the intended lifespan of a structure [9]. This principle extends to structural design for fire safety, where structural elements or systems must have an acceptable failure probability that varies in function of the failure consequences. In the absence of such an acceptable failure probability , the drive towards absolute reliability would (sooner or later) result in grossly disproportionate costs to society, as more and more resources need to be spent to further reduce the failure probability.

In the context of structural design for fire, many fire safety objectives may exist (see Sect. 9.1.1), which are translated into functional requirements and performance criteria; see ISO 24679-1:2019 [10]. For each of the performance criteria, a reliability target can be specified, for example, a business continuity-driven performance requirement of a high certainty (reliability) of limited permanent deflection post-fire. In most common structural fire design situations, maintaining structural stability during fire is the primary functional requirement (relating, e.g., to a primary objective of life safety, possibly in conjunction with property protection). For this functional requirement , reliability in consideration of fire can be defined as the probability that the structure or structural member will maintain its load-bearing function in the event of fire, i.e. reliability is the complement of the failure probability . This definition of reliability in structural (fire) engineering will be applied herein.

Applying the above, the performance criterion can for example be specified as (i) a maximum deflection v _max being smaller than a limiting value v _lim or (ii) the load-bearing capacity of the structure R being larger than the load on the structure E (including self-weight). In the first illustrative case failure is defined by the exceedance of a (possibly deterministic) limiting deflection, while in the second case failure is defined as the exceedance of the resistance effect by the load effect . For the latter example, the failure probability definition is thus specified by Eq. (9.7). Thus, the limit defining the boundary between the failure domain and boundary of the safe domain is given by Z = R – E = 0. This is commonly referred to as the limit state corresponding with the performance criterion.

A limit state is a condition of a structure or component beyond which the structure no longer fulfils certain criteria for design. Examples of limit states in structural engineering include ultimate limit states beyond which it is expected that a structure will no longer carry the applied load and serviceability limit states beyond which it is expected that the level of comfort or confidence of the users of the building as a result of, e.g., deflections or vibrations, is no longer adequate. Ultimate limit states are of relevance for accidental actions such as fire whereas serviceability limit states have little arguable application for accidental actions.

In structural fire design situations, performance (and thus failure) is commonly evaluated given the occurrence of a fire. Consequently, the load reference period is recommended to be taken as the instantaneous load situation, i.e. an arbitrary-point-in-time load. Taking into account the specifics of the structure (i.e. the conditions of use referenced by Holicky [9]), the load and resistance effects are thus defined. A conceptual visualization of these is given in Fig. 9.6, showing the variation of the resistance effect R and the load effect E, as well as the ‘safety margin’ defined here by the difference in expected values μ _R and μ _E. As illustrated in Fig. 9.6, despite the nominal safety margin , situations of E exceeding R occur in the tails of the distribution. The acceptability of this observed failure probability now depends on the (availability of) maximum allowable failure probabilities, or in other words: target reliability levels.

$$ {P}_f=P\left[R-E<0\right] $$

(9.7)

Fig. 9.6

Concept visualization of load and resistance effects, including situations with failure (R < E ) given a nominal ‘safety margin ’

9.2.3 Target Reliability Indices for Structural Design

Defining maximum allowable (target) failure probabilities is central to the application of reliability methods. Relative to the full ALARP evaluation highlighted in Sect. 9.2.1, specified target failure probabilities allow to omit cost evaluations from the design, thus restricting the design problem to engineering considerations (and not, e.g., discount rate assessments).

Commonly, a (target) failure probability is expressed in an alternative form as a reliability index (β), with

$$ \beta =-{\varPhi}^{-1}\left({P}_f\right)={\varPhi}^{-1}\left(1-{P}_f\right) $$

(9.8)

Φ ⁻¹ is the inverse standard normal cumulative distribution function, as applied amongst others in EN 1990. For completeness, the relationship between (P _f) and (β) is as shown in Fig. 9.7. In the following subsections, target reliability indices for structural design are summarily presented both for ambient conditions and for fire.

Fig. 9.7

Relationship between reliability index and failure probability

9.2.3.1 Reliability Indices at Ambient Temperature

As noted in Sect. 9.1.1, reliability-based design has found wide application in structural engineering. For example, as the basis of the partial safety factors applied in the Structural Eurocodes , the target reliability index , β, governs everyday structural engineering practice. Different (recent) target values are, however, available from several sources [11].

Target failure probabilities (P _{f, t}) for ambient design have received much attention in the literature, e.g. see Rackwitz [12] and Fischer et al. [13]. Target values have even been included in international standards, which can be linked to the Eurocode target reliability indices . ISO 2394:1998 [14] lists ‘example’ lifetime target reliabilities as a function of the failure consequence and the relative costs of safety measures (Table 9.2). Based on the formulation in ISO 2394:1998, these values have been informed by cost optimization and calibrated against existing practice. The standard further recommends the values 3.1, 3.8, and 4.3 to be used in ultimate limit state design based on both consequence of failure and cost of safety measures. Considering the general content of the standard, these values are considered applicable at an element level.

Table 9.2 Target β-values for elements (lifetime), ISO 2394:1998

Target reliability indices specified in EN 1990 [15] as a function of the ‘reliability class’ are given in Table 9.3. The reliability classes can be associated with the consequence classes (i.e. high, medium, low). As also noted in ISO 2394:1998, considerations such as brittle or ductile failure may influence the chosen target.

Table 9.3 Target reliability index for structural elements in accordance with EN 1990:2002

The Eurocode target reliability indices are specified both for a 1-year reference period and a 50-year reference period (where 50 years equals the indicative design working life for common structures). Both sets, however, correspond with the same target reliability level, considering independence of yearly failure probabilities ; that is, irrespective of how long a structure has been standing, it is assumed that the per annum failure likelihood is constant. There is thus close agreement between β _t,50 in Table 9.3 and lifetime targets in ISO 2394:1998.

The material-specific Eurocodes apply the 50-year reliability index of 3.8 on an element basis for the definition of partial safety factors . In case of additional redundancy in the system (e.g. due to robustness considerations), this will result in a higher system reliability index.

Target values for a 1-year reference period are given in the Probabilistic Model Code developed by the Joint Committee on Structural Safety [16]; see Table 9.4. These recommended values were derived from a calibration process with respect to the existing practice and are considered compatible with cost-benefit analyses, with explicit reference to the analysis by Rackwitz [12], and can be considered to relate to an updated recommendation relative to ISO2394:1998.

Table 9.4 Target β-values for structural systems (1 year), JCSS , and adopted in ISO 2394:2015

Table 9.4 is applicable to structural systems. In case of a single-element failure mode dominating system failure, these targets are directly applicable to the structural element. The target values are given as a function of the ratio ξ of the failure plus reconstruction cost to the construction cost and an obsolescence rate on the order of 3% is considered. For very large consequences (ξ > 10) an explicit cost-benefit analysis is recommended. The target reliabilities in Table 9.4 have been incorporated into ISO 2394:2015.

It is noteworthy that the reliability targets presented previously are in some manner linked to cost optimization, where the direct and indirect consequences resulting from ‘loss of the structure’ are taken into account. Mindful of the need for potential fatalities being tolerable, as is discussed by Van Coile et al. [3], this may be considered beyond the ambit of a direct life safety evaluation, which is generally concerned only with averting fatalities. Fischer et al. [17] proposed an alternative perspective, where (societal) life safety cost optimization is concerned solely with the preservation of life through incorporation of the life quality index (LQI) ; that is, safety investments are balanced directly against the reduction in risk to life. The obtained acceptable failure probability is then considered an absolute lower bound safety requirement for further reliability assessments and more general cost optimization considerations. This acceptable failure probability is given in Eq. (9.9) for coefficients of variation in the resistance and action effects of 0.1–0.3:

$$ {P}_{f, acc}=\frac{1}{5}\frac{C_1\left({\gamma}_s+\omega \right)}{N_f\mathrm{SCCR}} $$

(9.9)

where C ₁ is the marginal safety cost, γ _s the discount rate, ω the obsolescence rate, N _f the number of fatalities in case of failure, and SCCR the societal capacity to commit resource metric.

By way of an example, taking a consequence class 3 structure from ISO 2394:2015, the expected number of fatalities in the event of structural failure is less than 50 persons. If the building were in the UK, the SCCR for a 3% discount rate is $3,665,000 ppp (purchasing power parity) according to ISO 2394:2015. For a construction cost (C ₀) of $40,000,000 ppp and a normal marginal safety cost (C ₁/C ₀) of 1%, the marginal safety cost is $400,000 ppp. Adopting an obsolescence rate of 2% and societal discount rate of 3%, the acceptable failure probability is 2 × 10⁻⁵ for a 1-year reference period. This would coincide with β = 4.1, i.e. a significantly less onerous reliability target when compared to the figures in EN 1990. This value should however be considered as an absolute lower bound, as it is (implicitly) assumed that there are no further benefits to society from the safety investment apart from averting fatalities [18]. For example, the benefit of reducing the risk of city conflagration or network resilience is not taken into account.

9.2.3.2 Reliability Targets and Fire

The application of the ambient reliability targets to structural fire design has received considerable research attention. In the Natural Fire Safety Concept (NFSC) [19], the Eurocode target reliability index of 3.8 (50-year reference), i.e. 4.7 for 1-year reference, was adopted as a starting point. By further assuming that the yearly probability of a fire-induced structural failure should be as unlikely as the yearly probability of a ‘normal-design’ structural failure, and considering fire-induced structural failures to be conditional on the occurrence of a ‘significant’ fire, the NFSC derives a target reliability index, β _t,fi, for structural fire design through Eq. (9.10), with λ _fi being the annual occurrence rate of a structurally significant fire:

$$ \varPhi \left(-{\beta}_{t, fi}\right)={P}_{f,t, fi}=\frac{P_{f,t, EN1990}}{\lambda_{fi}}=\frac{\varPhi \left(-{\beta}_{t, EN1990}\right)}{\lambda_{fi}}\Rightarrow {\lambda}_{fi}{P}_{f,t, fi}={P}_{f,t, EN1990} $$

(9.10)

Nevertheless, the NFSC goes on to consider that an acceptable target failure probability should be differentiated from that at ambient temperature in function of the building evacuation mode, in consideration that at the time of fire occurrence, in many buildings, occupants are actively encouraged to evacuate (reducing the potential number of fatalities), i.e.:

• Normal evacuation: 1.3 × 10⁻⁴ [y⁻¹].

• Difficult evacuation: 1.3 × 10⁻⁵ [y⁻¹].

• No evacuation: 1.3 × 10⁻⁶ [y⁻¹].

This concept is explored by Hopkin et al. [20] where the time-dependent failure probability of a steel structure is coupled with a stochastic evacuation timeline for a series of reference office buildings in determining so-named risk indicators.

One difficulty noted with the NFSC approach is discussed by Van Coile et al. [11] and Van Coile et al. [21]. There, it is highlighted that the Eurocode target reliability levels for ambient design which form the basis of the NFSC can be considered compatible with cost optimization considerations, as discussed above. The basic assumptions underlying the cost optimizations for ambient design conditions are however not necessarily applicable to structural fire design. Within Van Coile et al. [21] target failure probabilities are expressed in an alternative general form, in function of a damage to investment indicator (DII), expressed as

$$ DII=\frac{\xi \lambda}{b\left(\gamma +\omega \right)} $$

(9.11)

where b is the relative marginal safety investment cost, i.e. normalized to the construction cost (C ₀), as defined by Eq. (9.12); λ is the failure-instigating event occurrence rate; and ξ is the relative failure costs, i.e. also normalized to the construction cost. In the case of fire, λ would be the structurally significant fire occurrence rate. For normal design conditions, lambda is expressed as one per annum, and the corresponding reliability target is for a 1-year reference period. This formulation is compatible with the traditional formulation underlying Rackwitz [12]:

$$ \frac{d{C}_1}{C_0}=b\frac{d{P}_f}{P_f} $$

(9.12)

Figure 9.8 presents the optimal reliability indices and failure probabilities in function of DII, as proposed by Van Coile et al. [21]. This formulation confirms the scaling of the target failure probability by the occurrence rate λ as proposed conceptually in the NFSC , under the condition however that the ratio of the other parameters in the DII (i.e. the costs of failure and the costs of further safety investments) remains unchanged. Investigation into the costs and benefits of structural fire protection is an area of ongoing research. Target safety levels for structural fire resistance have been derived, e.g. by Fischer [22] for steel structural elements and by Van Coile et al. [23] for concrete slabs.

Fig. 9.8

Optimal failure probability and reliability index in function of the DII [21]

9.3 Uncertainty in Actions

Fire is an uncertain event. Depending upon building use, building size, fire strategy measures, fire safety management, etc., fire occurrence rates differ and so does the likelihood that a fire will develop to an extent that it is structurally significant. Once of an intensity to be considered structurally significant, the manifestation of the fire is uncertain and correspondingly the probability of a fire-induced structural failure. Sections 9.3.1 and 9.3.2 discuss uncertainties that arise in both the fire’s occurrence rate and development, alongside what uncertainty arises in mechanical action (load, moment, etc.). Section 9.4 speaks to uncertainty in the response of materials at elevated temperature.

9.3.1 Thermal Action

Uncertainty in the thermal action necessitates a separate consideration of the factors leading to a fire’s occurrence and its ability to become fully developed (i.e. fire occurrence rates and interventions), alongside those that influence the fire’s fully developed manifestation (i.e. fire modelling inputs). These are discussed separately in Sects. 9.3.1.1 and 9.3.1.2, respectively.

9.3.1.1 Fire Occurrence Rates and Interventions

Many events can occur between an ignition and a fire becoming fully developed. Jurisdiction-specific statistics are available which, when contrasted to building stock, give an indication of ignition rates. As fire statistics generally relate to reported fires, the thus obtained ignition frequencies should be considered to relate to fires which because of their severity, duration, or operational procedures warrant reporting.

However, subsequent to fire ignition , there will need to be a failure of numerous intervention mechanisms for the fire to become structurally significant. These could include (a) intervention of occupants via first-aid firefighting, (b) activation of automatic fire suppression systems, or (c) fire service operations.

In contributing to the development of Eurocode 1 , Part 1.2 [24], the natural fire safety concept (NFSC) project [19] explored some of the probabilistic aspects of structural fire design, with an emphasis on developing design methods that considered the relationships between early fire intervention measures and subsequent demands of the structural fire design. Table 9.5 summarizes some probabilistic factors for fire occurrence rate and differing intervention mechanisms. It should be noted that the values given likely vary significantly between jurisdictions. For sprinklers which are not installed according to standard, Schleich et al. indicate that a lower success rate (below 0.95) may be appropriate.

Table 9.5 Fire occurrence rates and intervention factors from NFSC [19]

The NFSC makes further generalizations which are subsequently adopted in EN 1991-1-2:2002, grouping building types into ‘Danger of fire activation’ classifications , ranging from low to ultra-high, as given in Table 9.6. In this table, the probability of fire occurrence is again expressed per unit area but relates to probability of ignition and subsequent unsuccessful intervention by the occupants or fire service. That is, there is no consideration of active systems, such as sprinklers.

Table 9.6 Influence of danger of fire activation on structurally significant fire occurrence rate [19]

9.3.1.2 Fire Modelling Inputs

Once the fire can develop to an extent that it can be considered structurally significant, a fire model will be required to idealize the fire’s development/behaviour. Chapter 4 discusses the various fire models that can be employed. Generally, it is found that the following key inputs need to be defined (not in all cases for all models):

• Growth/spread rate.

• Fire load.

• Ventilation conditions .

• Near-field temperature.

9.3.1.2.1 Fire Growth Rate/Spread Rate

Studies on the variability in fire growth rates are limited in literature. In a residential context, Holborn et al. [25] estimated fire growth rate based on fire investigation data, with 1991 samples, gathered in the Greater London area. Fire damage area was assumed to be consistent with the fire area, for a heat release rate density (${\dot{Q}}^{{\prime\prime} }$) of 250 kW/m². Holborn et al. [25] proposed that the average fire growth parameter α (kW/s²) could be estimated by assuming a t ² growth rate based on the area of fire damage when the fire was discovered (A ₁) compared to when the fire brigade arrived (A ₂), and the time intervals from ignition to discovery (t ₁) and ignition to fire brigade arrival (t ₂). This can be summarised as

$$ \alpha =\frac{{\dot{Q}}^{{\prime\prime}}\left({A}_1{t_1}^2+{A}_2{t_2}^2\right)}{{t_1}^4+{t_2}^4} $$

(9.13)

From this it was determined, using assumed log-normal distribution parameters , that dwelling fires had a mean fire growth rate of 0.006 kW/s², a standard deviation of 0.039 kW/s², and a 95th percentile of 0.024 kW/s².

Baker et al. [26] determined a residential growth rate distribution using zone modelling software B-RISK. A residential occupancy based on experiments undertaken in Sweden was modelled using probabilistic inputs for the ‘design fire generator’ (DFG) and by applying the Monte Carlo method. The outcome of the modelling indicated that a fire growth rate distribution could be approximated to a triangular distribution, with a minimum of 0 kW/s², a maximum of 0.412 kW/s², and a mode of 0.033 kW/s².

In a commercial and public building context, Holborn et al. [25] also computed log-normal distribution parameters for the fire growth rate. However, the sample sizes were significantly reduced compared to the residential case . Results are given in Table 9.7.

Table 9.7 Log-normal parameters characterizing the distribution of fire rates for non-residential building fires, Holborn et al. [25]

Nilsson et al. [27] computed fire growth rate distribution parameters for commercial buildings based upon the data in the Swedish fire ‘Indicators, Data and Analysis’ (IDA). The IDA is a national database recording all rescue service responses. Given 2365 commercial fires, excluding arson, Nilsson et al. [27] like Holborn et al. [25] propose a log-normal distribution for the fire growth rate, with mean 0.011 kW/s² and 95th percentile of 0.105 kW/s².

Fire spread rates have been subject to further review, albeit no commonly accepted distributions are presented in the literature. Rackauskaite et al. [28] give spread rates which are computed from a range of large-scale fire experiments or real events . These are summarized in Table 9.8. Based upon operational experiences, Grimwood [29] gives faster spread rates, particularly for large open plan offices, as shown in Table 9.9. In the case of the LA Interstate Bank Fire, Grimwood notes that the fire took 66 min to travel 142 m laterally. In comparison, the fire spread laterally 80 m in 46 min at Telstar House, London.

Table 9.8 Spread rates from Rackauskaite et al. [28]

Table 9.9 Spread rates after Grimwood [29]

9.3.1.2.2 Fire Load Density

Fire load density was subject to extensive surveys within CIB Working Group 14, led by Thomas [30]. Figures within CIB W14 influence the fire load densities adopted within the NFSC [19] and subsequently recommended in EN 1991-1-2:2002. Fire load density distributions within Eurocode 1 , Part 1.2, universally adopt a Gumbel type I distribution, with a coefficient of variation (COV) of 0.3. For different occupancy types, corresponding fire load densities are given in Table 9.10.

Table 9.10 Fire load densities from EN 1991-1-2:2002

Zalok et al. [31] present a more contemporary review of fire loadings relative to the NFSC within commercial premises. The study undertook surveys in 168 commercial premises, concluding that fire load density generally followed a log-normal distribution. A summary of findings is given in Table 9.11.

Table 9.11 Fire load densities after Zalok et al. [31]

Elhami Khorasani et al. [32] summarize the results of four fire load surveys across different countries. Data from the USA is then adopted to generate a new probabilistic model for fire load density , expressed in function of enclosure area. Equation (9.14) describes a probabilistic model for lightweight occupancies (office and clerical). Equation (9.15) gives a corresponding model for heavyweight occupancies (library, storage, file rooms):

$$ q=\exp \left[6.951-0.0047\left({A}_f\times 10.76\right)+0.5712\varepsilon \right] $$

(9.14)

$$ q=\exp \left[8.252-0.0081\left({A}_f\times 10.76\right)+0.5508\varepsilon \right] $$

(9.15)

where q is in units of MJ/m²; A _f is the room size (m²); and ε is a random variable that is in accordance with the standard normal distribution.

The proposals of Elhami Khorasani et al. [32] are further developed by Xie et al. [33] who present a fire load density model for office and residential building types. Distributions for both occupancies are said to be log-normal with mean (μ _qm – MJ/m²) and standard deviation (σ _qm – MJ/m²) varying in function of enclosure area (A _f – m²), as given in Eqs. (9.16) and (9.17) for offices, and Eqs. (9.18) and (9.19) for residential. The maximum enclosure sizes were c. 30 and 120 m² for residential and offices, respectively:

$$ {\mu}_{qm}=\frac{568}{\exp \left(0.00740{A}_f\right)} $$

(9.16)

$$ {\sigma}_{qm}=\frac{268}{\exp \left(0.00740{A}_f\right)} $$

(9.17)

$$ {\mu}_{qm}=\frac{1254}{\exp \left(0.0441{A}_f\right)} $$

(9.18)

$$ {\sigma}_{qm}=\frac{268}{\exp \left(0.0414{A}_f\right)} $$

(9.19)

9.3.1.2.3 Heat Release Rate

For fuel-controlled burning, the heat release rate density (${\dot{\mathrm{Q}}}^{{\prime\prime} }$ kW/m²) has importance. PD 7974–1:2019 [34], based on the work of Hopkin et al. [35], gives ranges for different occupancies as summarized in Table 9.12.

Table 9.12 Heat release rate density $\left({\dot{\mathrm{Q}}}^{\prime \prime}\right)$ from PD 7974–1:2019 [34]

For most cases, $\dot{Q^{{\prime\prime} }}$ corresponds with the maximum value estimated over the full duration of a fire. For hotels and industrial buildings, $\dot{Q^{{\prime\prime} }}$ corresponds with the mean value estimated over a defined period of burning.

9.3.1.2.4 Ventilation Conditions

The breakage of openings and associated probabilities has not been subject to extensive research. Studies presented by Hopkin et al. [20] have adopted a uniform distribution between a lower and upper bound of 12.5% and 100% of the total opening area. This ventilation range has no basis other than to introduce some sensitivity to ventilation conditions . Analyses underpinning British Standard BS 9999:2017 by Kirby et al. [36] also adopt a uniform distribution but expressed in function of the opening size relative to the compartment floor area. These range from 5% to 40%, with opening heights varying from 30% to 100% of the compartment height.

The Joint Committee on Structural Safety (JCSS ) [37] provides a tentative probabilistic distribution for opening factor (O = A _v√H/A _t), where

$$ O={O}_{\mathrm{max}}\left(1-\zeta \right) $$

(9.20)

with O _max being the maximum opening factor (m^0.5) assuming the failure of all non-fire-resisting external wall construction and ζ a random parameter that is log-normally distributed. The JCSS recommends that ζ have a mean of 0.2 and a standard deviation of 0.2, with any values exceeding unity suppressed so as not to generate negative opening factors.

9.3.1.2.5 Near-Field Temperature

Stern-Gottfried [38], in developing a travelling fire methodology, reviewed variability in near-field temperature at different points in time from ‘flashover’ in a limited number of large-scale fire experiments (Dalmarnock and Cardington fire tests). From this, it was determined that spatially resolved near-field temperatures followed a normal distribution. At different points in time, the mean near-field temperature varies. As such, Stern-Gottfried [38] proposes a relationship between average near-field temperature rise (ΔT _avg) and coefficient of variation (δ). The relationship is defined by Eq. (9.21):

$$ \delta =\frac{\sigma }{\Delta {T}_{\mathrm{avg}}}=1.939-0.266\ln \left(\Delta {T}_{\mathrm{avg}}\right) $$

(9.21)

Stern-Gottfried [38] notes that Eq. (9.21) could be used as a nominal expression of the standard deviation for any temperature-time curve.

In the absence of alternative data, Hopkin et al. [20] used Eq. (9.21) to describe variability in the near-field temperature of travelling fires as part of a probabilistic framework. For travelling fires, Rackauskaite et al. [28] note temperatures of the near field to be in the range of 800–1200 °C. For a conservative case, early applications of the travelling fire method (e.g [39].) adopted a deterministic near-field temperature of 1200 °C. However, structural response is highly sensitive to this input, and therefore a treatment as a stochastic variable in some manner is advocated, e.g. a uniform distribution between 800 and 1200 °C.

9.3.2 Mechanical Action

9.3.2.1 Introduction

The uncertainty in load and associated actions on structures is discussed widely in the literature, e.g. JCSS [37], Ellingwood [40], and Holicky and Sykora [41]. The study of Ellingwood is specifically focused on fire events. The mechanical actions are traditionally subdivided into permanent actions and imposed (or variable) actions, and their variability with time is an aspect of particular relevance for structural fire engineering. Other mechanical loads include wind load, snow load, and earthquake load. The joint consideration of fire and, for example, earthquake loading may be necessary for exceptional building projects with high consequences of failure, i.e. a requirement for a very high reliability. Ellingwood however adopts a de minimis risk acceptance condition of the order of 10⁻⁶ for a 1-year reference period, which is subsequently applied as a screening probability for considering combinations of loads.

In design for normal conditions, the load variability is considered by a (characteristic or design) load with a low probability of being exceeded during the lifetime of the structure. Naturally, the day-to-day probability of occurrence of such high (design) load value is low, just as for the day-to-day probability of occurrence of a significant fire. Simultaneously taking into account both events would result in very onerous fire design requirements. Hence, the reduced safety and combination factors in the Eurocode (EN 1990) and in the ASCE design format (load and resistance factor design) (ASCE 7–16) lessen the required load under consideration for structural fire design compared to normal design conditions.

Thus, when directly taking into account the uncertainty in the permanent and imposed load effects , an arbitrary point in time (APIT) load is to be considered. This differs from the stochastic load models commonly considered for normal design conditions, where distribution models for the maximum load in a long (e.g. 50 years) reference period are applied.

A recent literature review by Jovanović et al. [42] of permanent and imposed load models applied in probabilistic structural fire engineering (PSFE) studies has shown that a large variation in models is commonly applied, notably for the imposed load effect . In summary, two distinct families of probabilistic models were discerned. These are revisited in the following Sect. 9.3.2.2, together with a discussion of background studies and recommended distributions to be applied in PSFE applications .

9.3.2.2 Permanent Load Model

9.3.2.2.1 Introduction

The permanent actions result from the self-weight of the structural elements and finishes, and can be considered time invariant [37, 40]. Hence, for the stochastic model of the permanent load, the models applied for normal design qualify as APIT permanent loads. This neglects possible combustion of finishes or structure, as is a standard and conservative approximation.

9.3.2.2.2 Background

Table 9.13 gives mean values and coefficient of variation for density γ for some common structural framing materials , while Table 9.14 lists standard values for the deviation of structural elements’ dimensions from their nominal values. Considering these standard deviations, the mean volume of a structural element exceeds its nominal value. The JCSS Probabilistic Model Code (PMC) however states in a simplifying manner that the mean value of the volume can be calculated directly from the mean value of the dimensions, and that the mean dimensions can be considered equal to their nominal value [37].

Table 9.13 Mean and COV for weight density of typical materials [41]

Table 9.14 Mean values and standard deviations for deviations of cross-section dimensions from their nominal values [37]

With both γ and the volume V described by a normal distribution, the self-weight l is in principle not normally distributed. However, when the coefficients of variation (COV) of the volume and density are small (which is generally the case), the resulting self-weight loads can nevertheless be assumed to be described by a normal distribution [43]. This has also been adopted in the JCSS PMC [37]. Considering Taylor expansion, the mean value of the self-weight μ _l is given by μ _γ·μ _V. The coefficient of variation δ _l can be estimated from Eq. (9.22), with standard values listed in Table 9.13 [41]:

$$ {\delta_l}^2={\delta_V}^2+{\delta_{\gamma}}^2+{\delta_V}^2{\delta_{\gamma}}^2 $$

(9.22)

When multiple materials or components contribute with their self-weight to the permanent load effect , this corresponds with an addition of normally distributed variables. When the constituent self-weights l _i can be considered independent (with mean values μ _li and standard deviation σ _li), the overall permanent load is described by a normal distribution as well, with mean values μ _G and standard deviation σ _G given by

$$ {\mu}_G=\sum \limits_i{\mu}_{l_i} $$

(9.23)

$$ {\sigma}_G=\sqrt{\sum \limits_i{\sigma}_{l_i}^2} $$

(9.24)

9.3.2.2.3 Commonly Applied Models in Probabilistic Structural Fire Engineering

When evaluating an existing building, evaluating the load effect through Eqs. (9.23) and (9.24) can be considered reasonable, and may allow a precise assessment of the appropriate probabilistic description of the permanent load. For general reliability studies and code calibration purposes, however, generally applicable models are preferred for generality (thus avoiding assumptions with respect to, e.g., floor build-up and materials).

As elaborated by Jovanović et al. [42], two models are commonly applied for describing the permanent load effect in PSFE . On the one hand, a series of studies (e.g [44].) and Iqbal and Harichandran [45] model the permanent load effect as a normal distribution with mean value equal to 1.05 G _nom, with G _nom as the nominal permanent load, and a coefficient of variation of 0.10. These studies have the 2005 study by Ellingwood as a common point of reference. The other series of studies (e.g [46, 47].) apply a normal distribution with mean value equal to G _nom, and a COV of 0.10. These studies do not propose a differentiation of permanent load distribution by framing material.

9.3.2.2.4 Recommended Model for the Permanent Load

Considering the above, both commonly applied models agree on describing the permanent load by a normal distribution with a COV of 0.10. The normal distribution is in agreement with the background models. Taking into account Table 9.13, a COV of 0.10 can be considered a (practical) conservative assessment. Considering the discussed background information, the mean permanent load slightly exceeds its nominal value (in the order of 1% for concrete elements). It is considered preferable to neglect a 1% (order of magnitude) exceedance in accordance with the JCSS PMC recommendation than to set μ _G equal to 1.05 G _nom. This is considered to be compensated by the practical choice for a COV of 0.10.

In conclusion, the permanent load effect G is recommended to be described by a normal distribution, with mean equal to the nominal permanent load effect G _nom, and COV of 0.10.

9.3.2.3 Live Load Model

9.3.2.3.1 Introduction

The live (or imposed) loads arise from a range of components, from building occupants to their possessions and movable items, like furniture. The total live load can be broken down into two components: (1) a sustained component and (2) an intermittent or transient component [37, 40, 41].

While both vary with time, by definition, a component of the sustained load is ever present—albeit its magnitude could vary. Figure 9.9 illustrates the difference between the sustained and intermittent live load components, adapted from Ellingwood [40].

Fig. 9.9

Components of live load —sustained and intermittent, adapted from Ellingwood [40]

Normal people occupancy is generally included in the sustained load, e.g. Chalk and Corotis [48]. The intermittent live load on the other hand relates to exceptional events, such as overcrowding [48] or stacking of objects during refurbishing [37].

For PSFE , the arbitrary point in time (APIT) live load is of interest, and as the occurrence of the intermittent (transient) live load is by its conceptualization rare, it generally does not need to be taken into account simultaneously with fire exposure [40]. Ellingwood notes occurrence rates of c. 1/y and a duration of 1 day for the intermittent load. For a structurally significant fire occurrence rate of 10⁻⁶ per annum and duration of 4 h, the coincidence rate of a fire and intermittent live load is significantly below the proposed de minimis limit (10⁻⁶) leading Ellingwood to propose that the intermittent component be disregarded. While this can be considered sufficient for the general floor area of most buildings (e.g. offices, residential buildings), Jovanović et al. [42] state that care should be taken whenever the live load profile of the building has specific occurrence patterns or particular likelihood of overcrowding (e.g. sports stadia), or when considering buildings with high reliability requirements (e.g. high-rise structures). Figure 9.10 shows the coincidence rates of a 1-year returning intermittent live load and fire, for different compartment sizes and danger of activation (as defined in Table 9.6).

Fig. 9.10

Coincidence rate of intermittent live load (occurrence rate y⁻¹) and fire in function of compartment area and ‘danger of activation’

In the following, the APIT model for the sustained live load is discussed.

9.3.2.3.2 Background

The commonly applied live load models have been derived from load surveys conducted in the twentieth century.

Ellingwood and Culver [49] assessed an equivalent uniformly distributed APIT load Q from a 1974–1975 survey of US office buildings. The mean loads and COV are listed in Table 9.15 and include a nominal personnel load of 81 N/m². Ellingwood and Culver report that no significant difference with UK data published in the early 1970s could be discerned, and list a gamma distribution as the appropriate distribution model.

Table 9.15 Sustained live load in offices, US 1974–1975 survey, as reported by Ellingwood and Culver [49]

Chalk and Corotis [48] list APIT sustained live loads for different occupancy types , taking into account data from multiple surveys (Table 9.16). Comparison with the office data listed in Table 9.15 confirms the order of magnitude values. Also Chalk and Corotis applied a gamma distribution in their calculations.

Table 9.16 Sustained live load for different occupancies, as reported by Chalk and Corotis [48]

The JCSS PMC [37] tabulates live load distribution parameters as listed in Table 9.17 and recommends a gamma distribution for the APIT load . Reference is made to a limited number of documents, amongst which the 1989 CIB report [50] is of particular relevance. This report was drafted by Corotis and Sentler, which can reasonably be considered to imply a close relationship with the work presented in Table 9.16. The CIB report lists multiple surveys dating from 1893 to 1976. Looking into the PMC values for μ/Q _nom, these are comparable to those listed in Table 9.16, with all categories except warehouses resulting in a value between 0.15 and 0.20.

Table 9.17 Sustained live load parameters , as tabulated in the JCSS Probabilistic Model Code* [37]

With respect to the COV, the PMC specifies Eq. (9.25) for the standard deviation of the instantaneous imposed load. In this equation and Table 9.17, σ _V is the standard deviation of the overall load intensity, σ _U the standard deviation associated with the spatial variation of the load, A ₀ an occupancy-specific reference area, A the loaded area, and κ an influence factor (commonly between 1 and 2.4; further taken as 2.2 for agreement with Ellingwood and Culver [49]). The COV for very large loaded areas is listed in Table 9.17 as COV_inf, i.e. where the loaded area-dependent term in Eq. (9.25) reduces to zero. With the exception of the first-floor retail space, these COVs are smaller than those listed in Table 9.16. For small loaded areas, however, the COV resulting from Eq. (9.25) exceeds those in Table 9.16:

$$ {\sigma}^2={\sigma}_V^2+{\sigma}_U^2k\cdot \min \left\{\frac{A_0}{A};1\right\} $$

(9.25)

9.3.2.3.3 Commonly Applied Models in Probabilistic Structural Fire Engineering

With respect to the live load model , a wide variety of distribution models have been applied in PSFE . Not all studies however relate to APIT loads (for example using a load model for the maximum realization in a 50-year reference period instead). Limiting the discussion to APIT models, two families have been discerned in Jovanović et al. [42]:

• 1. Gamma distribution with mean value μ/Q _nom equal to 0.24 and COV of 0.60.

• 2. Gumbel distribution with mean value μ/Q _nom equal to 0.20 and COV of 1.10.

The first family has the 2005 Ellingwood study as a common point of reference. In this study, Ellingwood specifies μ/Q _nom as being in the range of 0.24–0.50. In Ellingwood’s study (2005), reference is made to the data in Tables 9.15 and 9.16 and the underlying studies.

The second family models the APIT live load by the distribution for the maximum load in a 5-year reference period (i.e. ‘5y Gumbel distribution’). In essence, it is assumed that the imposed load can be modelled by a rectangular wave renewal process with a 5-year return period [51]. The 5-year return period corresponds with the expected time between renewals (changes in use and users [37]) for office buildings [41]. The specific distribution parameters listed above apply for office buildings designed in accordance with the Eurocode-recommended nominal (characteristic) imposed load of 2–3 kN/m², considering the PMC load values , but can be used as a first approximation for other occupancies as well [41].

While both live load model families seem very distinct at first, the underlying data can reasonably be considered to be comparable, with both families linked to research by amongst others Corotis.

9.3.2.3.4 Recommended Model for the Imposed Load

The background documents agree on the use of a gamma distribution to describe the instantaneous sustained live load. Thus, it is adopted here as a recommendation based on precedent and considering the impossibility of negative values (note that the Gumbel distribution assigns a non-zero probability to negative realizations).

With respect to the distribution parameters, the background documents agree largely on the mean value μ for the sustained live load. Thus, for project-specific evaluations it is recommendable to define the mean sustained live load directly from listed data, such as the JCSS PMC [37]. The corresponding ratio μ/Q _nom depends on the guidance-specific definition of Q _nom. When defining Q _nom through EN 1991-1-1:2002-recommended values, the ratio μ/Q _nom is largely found to be in the range of 0.10–0.20. A value of 0.20 is considered reasonable for a first assessment for offices, residential areas, retail, hotels, and classrooms. A similar result is obtained for office buildings in accordance with ASCE 7–16, considering a Q _nom recommendation of 65 psf.

The COV for the sustained live load can be considered dependent on the loaded area. For large loaded areas, a COV of 0.60 is found reasonable (see Table 9.17). For smaller loaded areas the COV is higher. Project-specific evaluations are again recommended when applicable. For general reliability assessments, a COV of 0.95 is recommended. This corresponds with the COV for office areas and classrooms at approximately 120 m² loaded area. This value also results in a comparable ambient design reliability index compared to the Gumbel model with COV of 1.1 (which was used in the Eurocode background documents , i.e [47].).

In summary, for non-project-specific evaluations, excluding warehouses, the recommended model for the imposed load is given as follows:

• For a large loaded area: Gamma distribution with μ/Q _nom = 0.20, COV = 0.60.

• For a small loaded area: Gamma distribution with μ/Q _nom = 0.20, COV = 0.95.

9.3.2.4 Total Load Effect

9.3.2.4.1 Introduction and Commonly Applied Models

The models for the permanent load G and imposed load Q however do not convey the full story on the probabilistic modelling of mechanical actions. Additional stochastic factors are taken into account when combining the permanent and imposed load effects. Again, two distinct formulations are commonly applied: Eq. (9.26) with reference to Ravindra and Galambos [52] and Eq. (9.27) with reference to the JCSS PMC . Standard values for the stochastic variables are listed in Table 9.18:

Table 9.18 Load combination parameters as applied in total load models [42]

$$ w=E\left( AG+ BQ\right) $$

(9.26)

$$ w={K}_E\left(G+Q\right) $$

(9.27)

Ravindra and Galambos [52] refer to Eq. (9.26) as an assumption, and explain that A and B are to be interpreted as characterizing the difference between computed and actual internal forces in the structure, while E is intended to characterize deviations introduced by characterizing a 3D structure into elements or subsystems and other simplifying assumptions (such as boundary conditions). They however do not mention a distribution type for these variables, and indicate that the mean values and COVs (as listed in Table 9.18) were ‘chosen’ and ‘assumed’ as ‘reasonable estimates based on data and judgements’, with further reference to a 1973 Washington University report.

The total load model of Eq. (9.27) is recommended in the JCSS PMC , where a difference is made in the recommended COV for K _E in function of the considered load effect (axial load, moment). For frames, a COV of 0.1 is the higher value. Only for moments in plates the recommended value is higher at 0.2 [37]. The PMC provides no indication, however, as to the origin of these values. This formulation is nevertheless commonly applied in structural reliability calculations, and has been included in the background documents to the Eurocodes , e.g. Holicky and Sleich [47].

9.3.2.4.2 Recommended Model for the Total Load Effect

Neither of the above two models has extensive background available, and these are commonly applied based on precedent . The model of Eq. (9.27) is considered to have a greater authority considering its recommendation by the Joint Committee on Structural Safety, which is the common expert group on structural reliability of five international organizations (CEB, DIB, fib, IABSE, and RILEM).

Hence, the recommended total load model is given by Eq. (9.27) with K _E being the model uncertainty for the total load effect , described by a log-normal distribution with mean 1.0 and COV 0.10.

Taking into account the recommended models for the permanent load G and the imposed load Q as defined above, and defining the load ratio χ by Eq. (9.28) (with nominal values corresponding with the characteristic values in the Eurocode design format ), the total load w is given in Fig. 9.11 relative to the nominal total load P _nom = G _nom + Q _nom:

Fig. 9.11

Cumulative density function (CDF) and complementary CDF (cCDF) for the total nominal load w according to the recommended load models, with COV Q = 0.60 (black) and 0.95 (red), respectively

$$ \chi =\frac{Q_{nom}}{Q_{nom}+{G}_{nom}}=\frac{Q_{nom}}{P_{nom}} $$

(9.28)

9.4 Materials and Applications

As stated in Sect. 9.1, one of the uncertainties that need to be addressed during structural analysis at high temperatures relates to properties of material during fire. This section provides an overview of existing studies on the subject.

9.4.1 Concrete

Strength of concrete is one of the primary properties that are required when analysing and quantifying performance of a concrete structural element (slabs, columns, beams, and walls) at normal or elevated temperatures. This section discusses the available test data on concrete strength retention factor and related temperature-dependent probabilistic models. When analysing reinforced concrete structures, the strength of reinforcement can be modelled following the discussion in the next section on steel material.

Qureshi et al. [53] compiled a database of existing tests on calcareous and siliceous concrete strength at high temperatures, keeping the two concrete types separate following a similar approach in the available deterministic Eurocode (EC) models [54]. A total of 242 data points for siliceous and 162 data points for calcareous concrete were collected. Concrete strength at high temperatures was normalized with respect to the measured strength (or average of multiple measurements) at 20 °C. A relatively large scatter in the data was observed across all temperature ranges. Qureshi et al. [53] followed two approaches to develop probabilistic models for the concrete compressive strength retention factor :

• In the first approach, the data set was divided over different temperature groups with increments of 50 °C. Histograms for each temperature group were then constructed and compared with a number of different probability density functions (PDF) (e.g. log-normal, Weibull). The distribution that fits best over different temperature ranges and has a closed-form solution that can be implemented in computer codes was selected, and temperature-dependent functions for the parameters that would characterize the distribution were proposed.

• In the second approach, the procedure by Elhami Khorasani et al. [55] was followed where a continuous temperature-dependent logistic function is fit to the data set using a Bayesian-based maximum likelihood calculation. In this approach, the logistic function can be a function of any form or defined with an existing deterministic function as the base (such as the EC model) with correction terms added to improve the fit to the data.

One important issue to be considered in developing probabilistic models at elevated temperatures is to ensure continuity and consistency in reliability appraisals in transition between ambient and elevated temperatures; therefore, it is important to note the existing assumptions that are applied at 20 °C. Holicky and Sykora [41] recommended the mean concrete strength at ambient temperature to be defined as the characteristic concrete strength plus two standard deviations, following a log-normal distribution with a coefficient of variation (COV) varying from 0.05 to 0.18 depending on the production procedure.

Using the approaches and considerations explained above, Qureshi et al. [53] proposed a Weibull distribution with parameters λ and k for calcareous and siliceous concrete strength retention factors, given that closed-form solutions of the Weibull distribution PDF f(x; λ, k) and quantile (i.e. inverse cumulative density function) Q( p; λ, k) are available, shown in Eqs. (9.29) and (9.30). In developing the model, distribution parameters at 20 °C were constrained to closely follow Holicky and Sykora’s recommendation. The size of data points above 700 °C was limited for calcareous concrete; therefore, in order to extend the model beyond 700 °C, it was assumed that the retention factor equals to zero at 1000 °C:

$$ f\left(x;\lambda, k\right)=\frac{k}{\lambda }{\left(\frac{x}{\lambda}\right)}^{k-1}{e}^{-{\left(\frac{x}{\lambda}\right)}^k} $$

(9.29)

$$ Q\left(p;\lambda, k\right)=\lambda {\left[-\ln \left(1-p\right)\right]}^{1/k} $$

(9.30)

Figures 9.12 and 9.13 show the data set in comparison with the mean, and 5–95% quantiles of the probabilistic models based on the Weibull distribution fit for both calcareous and siliceous concrete. Eqs. (9.31)–(9.34) provide parameters of the Weibull distribution λ and k as a function of temperature T in Celsius.

Fig. 9.12

Siliceous concrete strength retention factor vs. temperature based on Weibull distribution fit

Fig. 9.13

Calcareous concrete strength retention factor vs. temperature based on Weibull distribution fit

For siliceous concrete :

$$ \lambda (T)=-8.4340\times {10}^{-7}\times {T}^2-4.0887\times {10}^{-4}\times T+1.0598 $$

(9.31)

$$ K(T)=\frac{9.7348}{0.9231+1.9787\times {10}^{-3}\times T} $$

(9.32)

For calcareous concrete :

$$ \lambda (T)=-7.3849\times {10}^{-7}\times {T}^2-2.9879\times {10}^{-4}\times T+1.0576 $$

(9.33)

$$ K(T)=\frac{27.7292}{2.5894+7.6323\times {10}^{-3}\times T} $$

(9.34)

Using the second approach explained above, Qureshi et al. [53] proposed continuous logistic functions as shown in Eqs. (9.35) and (9.36), where T is temperature in Celsius and ε is the standard normal distribution. A value of zero for ε generates the median of the function. Figures 9.14 and 9.15 show the data sets in comparison with the median and two standard deviation envelopes of the logistic functions for both calcareous and siliceous concrete.

Fig. 9.14

Siliceous concrete strength retention factor vs. temperature based on logistic function

Fig. 9.15

Calcareous concrete strength retention factor vs. temperature based on logistic function

For siliceous concrete :

$$ \frac{f_c}{f_{c,20}}=\frac{1.4\times \exp \left[0.8892-0.6319\times {10}^{-3}\times T-3.295\times {10}^{-6}\times {T}^2+0.45\times \varepsilon \right]}{1+\exp \left[0.8892-0.6319\times {10}^{-3}\times T-3.295\times {10}^{-6}\times {T}^2+0.45\times \varepsilon \right]} $$

(9.35)

For calcareous concrete :

$$ \frac{f_c}{f_{c,20}}=\frac{1.3\times \exp \left[1.142-0.0840\times {10}^{-3}\times T-3.735\times {10}^{-6}\times {T}^2+0.57\times \varepsilon \right]}{1+\exp \left[1.142-0.0840\times {10}^{-3}\times T-3.735\times {10}^{-6}\times {T}^2+0.57\times \varepsilon \right]} $$

(9.36)

Qureshi et al. [53] utilized the developed models from two approaches and evaluated probability of failure of reinforced concrete column sections under axial load. It was confirmed that the two models provide similar distribution of failure time and the results are not critically sensitive to the model choice.

9.4.2 Steel

For structural steel elements, the primary uncertainties of interest are the material properties and the variability in section profile. The former is discussed within this section, while the latter, as discussed before, carries less uncertainty compared to other random variables involved at elevated temperatures.

Elhami Khorasani et al. [55], Stephani et al. [56], and Qureshi et al. [53] presented a review of yield strength retention factors and discussed different probabilistic models for this parameter. The data set for the yield strength of steel used in the three studies was based on the data collected by the National Institute of Standards and Technology (NIST) [57]. The NIST study considered the sensitivity of stress-strain behaviour of structural steel to strain rate. Therefore, the data only include tests conducted with a strain rate that comply with the allowed strain rate in testing standards.

Steel yield strength at ambient temperature is typically defined as the 0.2% offset. However, the Eurocode (EC) retention factors at elevated temperatures [58] are based on the strength at a strain equal to 2%, which includes strain-hardening effects at lower temperatures. Such an effect is less significant at higher temperatures, where failure of a steel structure is expected to occur. Therefore, the NIST data set and existing studies, as listed above, considered measured data at both 0.2% offset and 2% strain. A total of 764 data points based on the 0.2% offset, covering a temperature range of 20–1038 °C, and 387 data points based on strain at 2% with a temperature range of 20–940 °C, were used to perform statistical analysis and quantify uncertainty of steel yield strength at elevated temperatures.

As discussed in the previous section, continuity with reliability appraisals at ambient temperature is important. Holicky and Sykora [41] recommended a log-normal distribution with mean equal to the characteristic yield strength plus two standard deviations, and COV of 0.07 to quantify uncertainty at ambient temperature. In the collected database, the retention factors were normalized based on the measured yield strength (or average strength in case of multiple measurements) at 20 °C. The majority of data points at 20 °C in the 0.2% data set are close to unity. It is hypothesized that the obtained variability at 20 °C for the 0.2% offset results from very limited intra-batch variability, together with limited inter-batch variability resulting from the different measurement sources. On the other hand, the 2% data set shows a scatter of data at 20 °C, reflecting uncertainty in material performance.

Stephani et al. [56] applied the first approach, based on a series of temperature groups and their histograms (as explained for the case of concrete material in the previous section) on the 0.2% data set. Two different statistical models , namely log-normal and a beta distribution bound by three times the standard deviation on both sides of the mean, were considered with varying means and COVs as a function of temperature. Stephani et al. coupled the proposed models with recommended statistics of steel yield strength at ambient temperature. Qureshi et al. [53] extended the work of Stephani et al. [56] by proposing continuous functions for model parameters varying with temperature where continuity at ambient temperature was also incorporated within the model. Qureshi et al. [53] proposed a log-normal distribution for 0.2% data. Equations (9.37) and (9.38) describe the model parameters ; Fig. 9.16 shows the measured data and the model. Qureshi et al. [53] applied the same approach to the 2% data, except in this case the model reflects the scatter in data at 20 °C rather than constraining the model to the recommended distributions for reliability measures at ambient temperature for 0.2% strain offset. Equations (9.39) and (9.40) describe the model parameters , and Fig. 9.17 shows the measured data and the model. In addition, Elhami Khorasani et al. [55] proposed a continuous logistic function for the 2% data. Figure 9.18 and Eq. (9.41) describe the model where T is temperature in Celsius, k _{y, θ} is the EC steel retention factor , and ε is the standard normal distribution.

Fig. 9.16

0.2% Strain steel yield strength retention factor vs. temperature based on log-normal distribution

Fig. 9.17

2% Strain steel yield strength retention factor vs. temperature based on log-normal distribution

Fig. 9.18

2% Stain steel yield strength retention factor vs. temperature based on logistic function

Parameters of log-normal distribution for 0.2% data:

$$ {\mu}_{\mathrm{ln}}=-1.45\times {10}^{-9}{T}^3-1.78\times {10}^{-6}{T}^2-2.50\times {10}^{-5}T+1.19\times {10}^{-2} $$

(9.37)

$$ {\sigma}_{\mathrm{ln}}=-1.895\times {10}^{-7}{T}^2+1.15\times {10}^{-4}T+5.62\times {10}^{-2} $$

(9.38)

Parameters of log-normal distribution for 2% data:

$$ {\mu}_{\mathrm{ln}}=-6.89\times {10}^{-9}{T}^3+1.84\times {10}^{-6}{T}^2-8.39\times {10}^{-5}T+0.148 $$

(9.39)

$$ {\sigma}_{\mathrm{ln}}=-2.41\times {10}^{-7}{T}^2+1.07\times {10}^{-4}T+9.77\times {10}^{-2} $$

(9.40)

Logistic function for 2% data:

$$ \frac{F_{Y,2\%}}{F_{Y,20}}=\frac{1.7\times e\left[{r}_{logit}+0.412-0.81\times {10}^{-3}\times T+0.58\times {10}^{-6}\times {T}^{1.9}+0.43\times \varepsilon \right]}{1+e\left[{r}_{logit}+0.412-0.81\times {10}^{-3}\times T+0.58\times {10}^{-6}\times {T}^{1.9}+0.43\times \varepsilon \right]} $$

(9.41)

with ${r}_{logit}=\ln \frac{\left({k}_{y,\theta }+{10}^{-6}\right)/1.7}{1-\left({k}_{y,\theta }+{10}^{-6}\right)/1.7}$.

The models discussed above, when applied to cases of isolated steel column subject to ISO 834 heating, gave comparable distributions of failure temperature for a particular loading condition. The logistic model (derived at 2% strain) implicitly captures the effect of strain hardening at lower temperatures, meaning that the choice of probabilistic model is important for cases where element failure could be expected at low (less than 400 °C) temperatures.

Elhami Khorasani et al. [55] also proposed a logistic function to capture uncertainty in the modulus of elasticity of steel , shown in Fig. 9.19 and Eq. (9.42) where T is the temperature in Celsius and ε is the standard normal distribution. The measured data set is from the National Institute of Standards and Technology (NIST) collected database [57]. The NIST data set can be grouped into three categories based on their measurement method: (1) static, (2) dynamic, and (3) unknown. Elhami Khorasani et al. [55] noted that previous discussions on the measurement method indicated that dynamic testing, in general, results in unconservative predictions of steel modulus. In addition, the analysis of structures under fire is equivalent to static thermal loading, and therefore, the data measured by dynamic testing were disregarded:

Fig. 9.19

Modulus of elasticity of steel vs. temperature based on logistic function

$$ \frac{E}{E_{20}}=\frac{1.1\times \exp \left[2.54-2.69\times {10}^{-3}\times T-2.83\times {10}^{-6}\times {T}^2+0.36\times \varepsilon \right]}{1+\exp \left[2.54-2.69\times {10}^{-3}\times T-2.83\times {10}^{-6}\times {T}^2+0.36\times \varepsilon \right]} $$

(9.42)

9.4.3 Timber

Timber is a graded material with highly variable properties. The material properties can be grouped into reference properties that are considered explicitly, while other properties are only assessed implicitly. Bending strength R _m, bending modulus of elasticity E _m, and density ρ are referred to as the reference material properties . JCSS [16] provides a list of expected values and coefficient of variation of timber properties such as the tension strength parallel or perpendicular to the grain, compression strength parallel or perpendicular to the grain, shear modulus, and shear strength as a function of the reference properties. For European softwood , JCSS [16] specifies a log-normal distribution for bending strength R _m and bending modulus of elasticity E _m with COVs of 0.25 and 0.13, respectively, and normal distribution with COV of 0.1 for density ρ. For glue-laminated timber , R _m follows a log-normal distribution with COV of 0.15, but E _m and ρ have similar distributions as the European softwood. More details can be found in JCSS (2006).

Three methods have been proposed in the literature on how to conduct structural analysis of timber structures at elevated temperatures. Brandon [59] discussed details of these approaches. One of these methods takes into account the mechanical properties of the material; the other two approaches calculate reduced capacity of a member during fire by reducing the cross section of the element as a function of the char layer. Charring rate is one of the basic quantities of assessment of fire resistance of wooden structural members. Due to the inherent variabilities and uncertainties involved in the fire exposure and the charring process, the charring rate is a factor with substantial uncertainty, which should be taken into account in any assessment of fire resistance of wooden members, in particular in the probabilistic approaches to assess fire resistance. In addition to the reduced dimensions from charring, the reduced cross-section method requires consideration of reduced material properties in a layer ahead of the char front, where timber has lost some strength due to increased temperature but has not charred. This layer is assumed to have zero strength in calculations.

Lange et al. [60] and Lange et al. [61] conducted a total of 32 full-scale fire tests on glulam timber beams and quantified variation in charring rate β _n,par as well as depth of zero-strength layer d ₀. The timber beams were exposed to different fire curves including two parametric fire curves and a standard fire curve. The results show that the charring rate and depth of zero-strength layer depend on the heating rate. Following a similar approach to Annex A of EN 1995-1-2 on defining the notional charring rate under parametric fire exposure β _n,par, Lange et al. [61] proposed a normal distribution with mean μ and standard deviation σ for β _n,par as shown in Eqs. (9.43) and (9.44) where β _n is 0.72, O is the opening factor, and kρc is the thermal inertia of the compartment lining. The mean μ and standard deviation σ of the zero-strength layer depth are calculated as a function of the heating rate, Γ, of the parametric fire, shown in Eqs. (9.45) and (9.46). These equations were originally expressed as a function of the opening factor:

$$ \mu \left({\beta}_{n, par}\right)=1.5\times {\beta}_n\frac{0.2\sqrt{\varGamma }-0.04}{0.16\sqrt{\varGamma }+0.08} $$

(9.43)

with$\varGamma =\frac{{\left(O/\sqrt{k\rho c}\right)}^2}{{\left(0.04/1160\right)}^2}$.

$$ \sigma \left({\beta}_{n, par}\right)=0.06\times \frac{0.45\sqrt{\varGamma }-0.2}{0.16\sqrt{\varGamma }+0.08} $$

(9.44)

$$ \mu \left({d}_0\right)=-0.94\times \varGamma +16 $$

(9.45)

$$ \sigma \left({d}_0\right)=-0.04\times \varGamma +1.07 $$

(9.46)

In a separate study, Hietaniemi [62] proposed a model for wood charring rate β (mm/min) exposed to time-dependent incident heat flux ${\dot{q}}_e^{"}(t)$, and as a function of wood density ρ, wood moisture content w, and ambient oxygen concentration ${\chi}_{o_2}$ as

$$\beta = f\left(\chi_{{02},t}\right)\cdot \frac{C.\dot{q}_{e}^{\prime\prime p}t}{\left(\rho+\rho_{0}\right)(A+B+w)}\cdot\exp \left(_{-}\frac{t}{\tau}\right)$$

(9.47)

where

$$ f\left({\boldsymbol{\chi}}_{{\boldsymbol{o}}_{\mathbf{2}}},t\right)=\xi +\left(1-\xi \right)\bullet {\left(\frac{{\boldsymbol{\chi}}_{{\boldsymbol{o}}_{\mathbf{2}}}(t)}{{\boldsymbol{\chi}}_{{\boldsymbol{o}}_{\mathbf{2}}}^{(0)}}\right)}^{0.737} $$

$$ {\boldsymbol{\chi}}_{{\boldsymbol{o}}_{\mathbf{2}}}^{(0)}=21\% $$

$$ \xi \propto U\left(0.50;0.65\right)\ \left(\mathrm{average}=0.575\right) $$

$$ A\propto U\left(505;1095\right)\kern0.5em \mathrm{kJ}/\mathrm{kg}\kern0.75em \left(\mathrm{average}=800\right) $$

$$ B\propto U\left(2430;2550\right)\kern0.5em \mathrm{kJ}/\mathrm{kg}\kern0.75em \left(\mathrm{average}=2490\right) $$

$$ C\propto \Delta \left(2.72;5.45;3.93\right)\kern0.5em \mathrm{kW}/{\mathrm{m}}^2 $$

$$ p\propto N\left(0.50;0.40\right) $$

$$ {\rho}_0\propto N\left(465;93\right)\kern0.5em \mathrm{kg}\ {\mathrm{m}}^{-3} $$

$$ \tau \propto \Delta \left(90;110;100\right)\ \min $$

$$ \vartheta \propto \Delta \left(1.026;1.387;1.162\right)\ \mathrm{kW}/{\mathrm{m}}^2 $$

In the above formulation, N(μ; σ) is the normal distribution with mean μ and standard deviation σ; Δ(x _min; x _max; x _peak) is the triangular distribution with minimum value x _min, maximum value x _max, and peak value x _peak; and U(x _min; x _max) is the uniform distribution with minimum value x _min and maximum value x _max.

9.5 Uncertainty Quantification Techniques

The acceptance of a design through consideration of reliability or risk acceptance entails explicitly taking into account the design uncertainties discussed in the above sections. A wide range of techniques for uncertainty quantification exist. Uncertainty quantification techniques can be combined as befits the situation. The methods discussed further are:

• 1. Event trees : An intuitive and computationally inexpensive method for quantifying the probability of scenarios.

• 2. Analytical solutions: Exact uncertainty quantification , but only feasible in specific situations.

• 3. Monte Carlo techniques: Uncertainty quantification based on repeated evaluation of the model, considering random sampling of input parameters. Computationally expensive, but easy to implement. Crude Monte Carlo simulations (MCS) and Latin hypercube sampling (LHS) are discussed.

• 4. FORM: Approximate evaluation of the reliability index associated with a limit state equation. Exact in specific cases. The basis of the partial factors applied for Eurocode design in normal conditions.

• 5. Maximum entropy methods: Methodology for estimating the PDF of a scalar model output variable. The ME-MDRM (MaxEnt) method is introduced as a computationally efficient method in case of a limited number of stochastic variables.

• 6. Fragility functions: Fragility functions are, in their general form, a way of representing known probabilities of exceeding a performance threshold (i.e. limit state) in function of one or more defining variables, i.e. not an uncertainty quantification technique, but a useful way of representing uncertainty. With reference to the earthquake engineering field, the concept is often applied with respect to the probability of different ‘damage states’ being exceeded in function of the magnitude of an ‘intensity measure’.

• 7. PEER PBEE: The Pacific Earthquake Engineering Research Center Performance Based Earthquake Engineering framework, or PEER framework for short, is a well-established methodology for quantifying the uncertainty in decision variables (e.g. damage cost) in function of a hazard specification. The methodology applies fragility functions to move stepwise from intensity measures, over engineering demand parameters and damage states , to the decision variables. The framework thus requires uncertainty data (fragility functions) as input, and provides a framework for aggregating these basic uncertainties.

The discussion below starts with event trees as this method is the most intuitive and easily understood. Mathematical rigor is introduced later in order not to hamper the intuitive understanding.

9.5.1 Event Trees

An event tree is used to explore the probability of different scenarios, starting from a single common initiating event, for example fire ignition . The scenarios diverge every time an additional distinction is made between the scenarios, for example [sprinklers control the fire, yes/no], or [fire load density q _F ≤ 300 MJ/m², 300 MJ/m² < q _F ≤ 700 MJ/m², or 700 MJ/m² < q _F]. This creates distinct branches of the event tree. By considering the probabilities of the differentiating events, the probability of the overall scenario is calculated.

The opposite of an event tree is a fault tree, where the different contributions leading to a single final event are explored. This approach is most common in fire investigation; see, e.g., Johansson et al. [63].

The application of an event tree is most easily introduced through an example. Consider the event tree of Fig. 9.20, applied to assess the probability of fire-induced failure of a structural element in an office building. Fire-induced failure requires a prior fire ignition , and thus fire ignition has been chosen as the initiating event. The probability p _ig of this initiating event can be determined based on fire statistics, expert judgement, or detailed analysis (such as another event tree, or a fault tree). Following the initiating event, the possibility of sprinklers controlling the fire is considered. In case sprinklers control the fire, the steel beam is not in danger of losing its load-bearing capacity (based on analyses or expert judgement). This results in scenario A with a probability of p _ig·p _ss, with p _ss being the sprinkler success probability. For this scenario A no further analysis is required, as the beam is not in danger of losing its load-bearing capacity. Sprinkler success probabilities are listed for example in BSI [64]. If sprinklers fail to control the fire, then the ability of the steel beam to maintain its load-bearing capacity till burnout is a function of the fire load density q _F; see, e.g., the fragility curves by Hopkin et al. [65] for insulated steel beams (reformatted in Fig. 9.21). Reference is made to the full paper by Hopkin et al. for further details. Based on Fig. 9.21, the failure probability of a steel beam with an intumescent paint thickness d _p of 12 mm is approximately 0 for fire loads less than 300 MJ/m². Considering the fire load density distribution listed in Table 9.10 in Sect. 9.3.1.2, the probability of actual fire load in the office compartment exceeding 800 MJ/m² is approximately 0.01. For this fire load of 800 MJ/m² and a d _p of 12 mm, Fig. 9.21 indicates a failure probability of 0.21. Combining this information in the event tree , three additional scenarios (B, C, and D) are indicated. The probabilities of the respective scenarios have been determined based on the probability density function for the fire load and are listed in Table 9.19, and the constituent probability values are listed in Table 9.20, indicating that—without further evaluation of scenario C—the annual probability of fire-induced failure is smaller than 9.3 × 10⁻⁷/year. As stated in Sect. 9.2.3.2, the maximum failure probability postulated through the Natural Fire Safety Concept is, in case of no evacuation, 1.3 × 10⁻⁶/year. The event tree analysis (using information from the fragility curve of Fig. 9.21) thus indicates that a design with d _p = 12 mm would fulfil this requirement.

Fig. 9.20

Event tree example

Fig. 9.21

Fragility curves for an insulated steel beam, denoting the probability of structural failure P _f given a fully developed fire, in function of the intumescent paint thickness d _p, for different fire load densities q _F

Table 9.19 Scenario description and probabilities

Table 9.20 Probabilities of differentiating events

An event tree thus allows to pinpoint whether the design or specific situations may need to be considered in further detail. In the example above, a simple analysis was sufficient. While intuitive and easy to use, the creation of an event tree should be done with care. Special consideration should be given to:

• The choice of differentiating events: there is no use in adding distinctions which do not influence the outcome (design decision).

• Probabilities of the differentiating events: these can be evaluated based on statistical data, expert judgement, or a separate uncertainty quantification exercise.

• The probabilities of the differentiating events are conditional probabilities: these probabilities are conditional on the preceding differentiating events. For example, when considering the event [occupants suppress the fire, yes/no], after the event [sprinklers fail to suppress the fire], in general different probabilities will apply then when considering [occupants suppress the fire, yes/no] before [sprinklers fail to suppress the fire]. In the former situation, the probability of the occupants suppressing the fire will be lower, taking into account that the fire is—for example because of its excessive growth rate—not successfully suppressed by sprinklers.

9.5.2 Analytical Solutions

In specific situations uncertainty quantification can be done through closed-form solutions. Consider Eq. (9.48) where Y is the uncertain response of interest, X the vector of stochastic input variables X _i, and h the modelled relationship. The probability of failure P _f is then given by the probability of Y being in the failure domain Ω _f, i.e. Eq. (9.49), with f _y the probability density function (PDF) of Y:

$$ Y=h(X) $$

(9.48)

$$ {P}_f=\underset{\Omega_f}{\int }{f}_y(y) dy $$

(9.49)

If Y is a linear combination of independent variables X _i, i.e. Eq. (9.50), with a _i coefficients, then the mean value of Y is given by Eq. (9.51) and its standard deviation by Eq. (9.52). Furthermore, if all X _i are normally distributed, then Y is normally distributed as well. This follows from the central limit theorem:

$$ Y=\sum \limits_i{a}_i{X}_i $$

(9.50)

$$ {\mu}_Y=\sum \limits_i{a}_i{\mu}_{X_i} $$

(9.51)

$$ {\sigma}_Y=\sqrt{\sum \limits_i{a}_i^2{\sigma}_{X_i}^2} $$

(9.52)

Similarly, if Y is a multiplicative combination , i.e. Eq. (9.53), with a _i exponents, of independent log-normally distributed variables X _i with parameters μ _lnXi and σ _lnXi as specified by Eqs. (9.54) and (9.55), then Y is also log-normally distributed with parameters given by Eqs. (9.56) and (9.57):

$$ Y=\prod \limits_i{X}_i^{a_i} $$

(9.53)

$$ {\mu}_{\ln {X}_i}=\ln \left({\mu}_{X_i}\right)-\frac{1}{2}{\sigma}_{\ln {X}_i}^2 $$

(9.54)

$$ {\sigma}_{\ln {X}_i}=\sqrt{\ln \left(1+\frac{\sigma_{X_i}^2}{\mu_{X_i}^2}\right)} $$

(9.55)

$$ {\mu}_{\ln Y}=\sum \limits_i{a}_i{\mu}_{\ln {X}_i} $$

(9.56)

$$ {\sigma}_{\ln Y}=\sqrt{\sum \limits_i{a}_i^2{\sigma}_{\ln {X}_i}^2} $$

(9.57)

The cases of the normal and log-normal distribution of Y are only two examples out of a wide set of situations for which closed-form solutions exist. The cases above are however the most common.

In cases where Y relates to an outcome defining the failure of the structure, Eq. (9.49) is to be evaluated. Here Ω _f can relate to a fixed limit value (performance criterion). For example, when Y represents the standard fire resistance of a structural element t _R, and the failure domain is given by a fixed (equivalent) standard fire duration t _E, then Eq. (9.49) can be specified to

$$ {P}_f=P\left[{t}_R\le {t}_E\right]=\underset{0}{\overset{t_E}{\int }}{f}_{t_R}\left({t}_R\right){dt}_R $$

(9.58)

If t _R is described by a normal distribution , Eq. (9.58) is directly evaluated as Eq. (9.59), with Φ the standard cumulative normal distribution function, available in common spreadsheet tools. When t _R is described by a log-normal distribution, Eq. (9.60) applies. Note that a normally distributed t _R has a non-zero probability of being negative. When this probability is not negligible, care should be taken with using a normal distribution to describe strictly positive variables :

$$ {P}_f=\varPhi \left(\frac{t_E-{\mu}_{tR}}{\sigma_{tR}}\right) $$

(9.59)

$$ {P}_f=\Phi \left(\frac{\ln \left({t}_E\right)-{\mu}_{\ln tR}}{\sigma_{\ln tR}}\right) $$

(9.60)

Alternatively, Y can relate to the value of the limit state function as defined in Sect. 9.2.2, and Ω _f then corresponds with the limit state being negative. In these situations where Y represents the limit state, P _f is given by Eq. (9.61). For Y described by a normal distribution this specifies to Eq. (9.62). Considering the definition of the reliability index β specified in Eq. (9.8), the ratio μ _Y/σ _Y directly corresponds with the reliability index. A log-normal distribution on the other hand is strictly positive, and is thus inappropriate for modelling the realization of a limit state function (with failure defined by the limit state being negative):

$$ {P}_f=\underset{-\infty }{\overset{0}{\int }}{f}_Y(y) dy $$

(9.61)

$$ {P}_f=\varPhi \left(-\frac{\mu_Y}{\sigma_Y}\right)=\varPhi \left(-\beta \right) $$

(9.62)

9.5.3 Monte Carlo Techniques

Monte Carlo techniques rely on repeated evaluation of the model for different values (realizations) of the input variables. Whereas analytical solutions are feasible in only a limited number of cases, Monte Carlo techniques are generally applicable to any problem. Their drawback is the computational expense of the repeated evaluations, making these techniques infeasible for computationally demanding models.

The resolution of the obtained results in function of the number of model evaluations N is governed by the input variables’ sampling scheme. The most simple sampling scheme is known as crude Monte Carlo simulations (abbreviated MCS), and considers a pure random sampling of the input space [66]. Thus, each model run results in a single random realization of the output variable Y. The obtained MCS realizations can be visualized in a histogram, revealing the shape of the PDF describing Y. If sufficient simulations are made (technically if N→∞), the full PDF will be perfectly approximated. As an example, Fig. 9.22 represents the histogram obtained from 10⁴ MCS of the bending moment capacity M _R,fi,t of a concrete slab considering ISO 834 standard fire exposure, as well as log-normal and mixed log-normal approximations. As indicated by the graph, assuming a specific PDF shape may not always be appropriate. Further details are given in the application example in Sect. 9.6.2.

Fig. 9.22

Observed distribution density (MCS, 10⁴ realizations), log-normal approximation (LN), and mixed log-normal approximation (mixed LN), for concrete slab considering ISO 834 standard fire exposure

MCS can also be used to directly evaluate the failure probability, i.e. Eq. (9.49). Every random realization which contributes to failure adds to the count of the number of observed failures N _f. The estimate of the failure probability is then given by

$$ {P}_f\stackrel{\wedge}{=}\frac{N_f}{N} $$

(9.63)

The estimate of P _f will only be reliable in case sufficient MCS are performed (i.e. N sufficiently large). This can be clearly observed in Fig. 9.32 further, where the estimated P _f in function of N is visualized for the fire-exposed concrete slab. As the repeated observation of failure/no failure results in a binomial distribution, the coefficient of variation of P _f is given by Eq. (9.64). The coefficient of variation indicates the relative uncertainty in the estimate of P _f (explicitly: the ratio between the standard deviation and the expected value). In order to obtain meaningful results, V _Pf should be limited to V _lim, e.g. 0.10. This results in the guideline of Eq. (9.65) for the required number of MCS realizations N. For a failure probability of 10⁻³, Eq. (9.65) thus recommends 10⁵ MCS realizations . Note that the number of samples does not depend on the number of random input variables:

$$ {V}_{Pf}=\sqrt{\frac{\left(1-{P}_f\right)}{P_fN}}\le {V}_{\mathrm{lim}} $$

(9.64)

$$ N\ge \frac{\left(1-{P}_f\right)}{P_f{V}_{\mathrm{lim}}^2} $$

(9.65)

A widely used alternative sampling scheme is known as Latin hypercube sampling , or LHS [67]. Whereas in MCS the sampling is done randomly for all input variables, the LHS scheme ensures a balanced sampling across the full input space. Thus, reliable estimates for the moments or distribution parameters of Y (e.g. μ _Y and σ _Y) can be obtained with a limited number of samples (order of magnitude: 50–200). When using LHS to estimate the output parameters, the evaluation of P _f through Eq. (9.49) will necessarily rely on an assumed shape of the PDF (e.g. normal, or log-normal). Such an assumption of the distribution type of Y introduces a bias in the assessment. LHS can however also be applied with a high number of model evaluations, in which case the distinction with MCS diminishes. When using a low number of samples in the LHS scheme , spurious correlation may be introduced (i.e. the sampling scheme may exhibit unintended correlation between the input variables). The sampling scheme can be corrected for the spurious correlation, using the procedure described in, e.g., Olsson et al. [67]. Further information on sampling schemes can be found, e.g., in Bucher [66].

9.5.4 FORM

The first-order reliability method introduced by Hasofer and Lind [68], better known as ‘FORM’ , provides an efficient way of calculating (failure) probabilities associated with a limit state. The method relies on a linearization of the limit state in standard Gaussian space at the ‘expansion point’ u* Bucher [66]. This is the point on the limit state where linearization maximizes the probability density mass in the failure domain. Equivalently, this is the point on the limit state which is closest to the origin in the standard Gaussian space (for standard situations where the realization with mean values is not in the failure domain) [68], and thus the point on the limit state with the highest probability density. The reliability index is then given by the distance from this expansion point to the origin. In case the limit state is linear in the standard Gaussian space, and the stochastic variables are independent and normally distributed, the FORM assessment of the failure probability is exact. For non-linear limit states, the linearization introduces an approximation. For stochastic variables X described by an arbitrary distribution function, a transformation to a standard Gaussian variable U is required, introducing further approximations. The variable realization x* associated with the ‘expansion point’ u* is called the ‘design point’. This is often referred to as the most probable failure point.

FORM analyses underlie the reliability formats of the Eurocode , see the Appendices of EN 1990 [15], and have been implemented in many readily available software tools. The method is appreciated for its calculation efficiency and its repeatability. The fact that the FORM assessment is invariant to the formulation of the limit state is now taken for granted, but was a major consideration at its introduction [68].

To introduce FORM , and its underlying assumptions and limitations, reference cases with increasing complexity are given in the following. For brevity, the space of the stochastic variables will be denoted the X-space, and U-space refers to the standard Gaussian space of the transformed variables.

9.5.4.1 Single Normally Distributed Variable and Failure Criterion of a Deterministic Limiting Value

In the discussion on analytical solutions above, the example was given of a prescribed (deterministic) standard fire duration t _E and a normally distributed fire resistance time t _R, with mean μ _tR and standard deviation σ _tR. For a failure criterion specified as t _R ≤ t _E, i.e. a limit state Z = t _R – t _E, the failure probability P _f was readily calculated by Eq. (9.59). A graphical representation in the domain of the stochastic fire resistance t _R is given in Fig. 9.23a, for μ _tR = 40 min, σ _tR = 5 min, and t _E = 30 min. In this figure, the shaded area corresponds with the failure probability P _f.

Fig. 9.23

(left) Failure probability and design point in the X-space; (right) failure probability and expansion point in the U-space

The same assessment can be performed in the U-space. The transformation of t _R to its equivalent u _tR in U-space is given by Eq. (9.66). The limit state equation can be transformed accordingly as shown in Eq. (9.67), and the failure probability is then given by Eq. (9.68). The expansion point on the limit state (Z = 0) is readily determined as Eq. (9.69). Figure 9.23(b) visualizes this point as well as the failure probability in the U-space. As stated in the general description of FORM above, the distance between the origin and the expansion point now corresponds with the reliability index β. For the considered case, β thus equals 2; see Fig. 9.23 (b) and Eq. (9.70). Taking into account the definition of the reliability index as listed in Eqs. (9.8) and (9.71) holds, demonstrating that the result obtained in accordance with the FORM description is exactly the same as listed in 9.5.2 as an analytical solution. For the values listed above, the failure probability is approximately 0.023; see also Fig. 9.7 for the relationship between β and P _f:

$$ {u}_{tR}=\frac{t_R-{\mu}_{tR}}{\sigma_{tR}} $$

(9.66)

$$ Z={t}_R-{t}_E={\mu}_{tR}+{u}_{tR}{\sigma}_{tR}-{t}_E $$

(9.67)

$$ {P}_f=P\left[Z<0\right]=P\left[{u}_{tR}<\frac{t_E-{\mu}_{tR}}{\sigma_{tR}}\right] $$

(9.68)

$$ {u}_{tR}^{\ast }=\frac{t_E-{\mu}_{tR}}{\sigma_{tR}} $$

(9.69)

$$ \beta =\left|{u}_{tR}^{\ast}\right|=\left|\frac{t_E-{\mu}_{tR}}{\sigma_{tR}}\right|=\left|\frac{30-40}{5}\right|=2 $$

(9.70)

$$ {P}_f=\Phi \left(-\beta \right)=\Phi \left(-\left|\frac{t_E-{\mu}_{tR}}{\sigma_{tR}}\right|\right)=\Phi \left(\frac{t_E-{\mu}_{tR}}{\sigma_{tR}}\right)=0.023 $$

(9.71)

9.5.4.2 Linear Limit State Equation with Two Normally Distributed Variables

Expanding the previous example, also the (equivalent) standard fire duration t _E is now considered stochastic, with a mean value of 27 min and a standard deviation of 3 min. Both probability density functions and (in this case, a conceptual visualization of) failure probability are illustrated in Fig. 9.24, as well as the design point values t _R^* and t _E^* as determined below. Taking into account 9.5.2, the limit state output variable Z is also described by a normal distribution with mean and standard deviation as specified in Eq. (9.72). The failure probability is thus given by Eq. (9.73) and equals 0.013 for this specific example case. Considering the definition of the reliability index , β equals 2.23:

Fig. 9.24

Probability density function (PDF) of t _R and t _E, and indication of the region associated with failure

$$ {\mu}_Z={\mu}_{tR}-{\mu}_{tE};{\sigma}_Z=\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2} $$

(9.72)

$$ {P}_f=P\left[Z<0\right]=\varPhi \left(\frac{-{\mu}_Z}{\sigma_Z}\right)=\Phi \left(-\frac{\mu_{tR}-{\mu}_{tE}}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}\right)=\varPhi \left(-2.23\right)=0.013 $$

(9.73)

The joint probability density function of t _R and t _E can be visualized more comprehensively alongside the limit state in a two-dimensional graph (Fig. 9.25(a)). Note that the different standard deviations of t _R and t _E result in an ellipsoid joint PDF in the X-space. The grey zone indicates the failure domain, and integration of the joint PDF over this failure domain is the definition of P _f. Following the specifications by Hasofer and Lind (see above), both variables as well as the limit state can also be visualized in Gaussian space; see Fig. 9.25(b). The variables u _tR and u _tE are given by Eq. (9.74), while the limit state equation is specified to Eq. (9.75). Contrary to the formulation in the X-space, the considered limit state does not go through the origin in the U-space; it is however still a linear limit state (considering a linear transformation of the variables t _R and t _E). Note that the isoprobability contours of the joint PDF are concentric circles around the origin in the U-space.

Fig. 9.25

(left) Isoprobability contours, limit state, and design point in the X-space; (right) isoprobability contours, limit state, and expansion point in the U-space

From geometric considerations, the expansion point u* is readily determined. Consider, for example, that the point p on a line a ⋅ x + b ⋅ y + c = 0 closest to the origin (in x-y-coordinate space) has coordinates as specified in Eq. (9.76). Applied to the limit state of Eq. (9.75) in the U-space, this results in the expansion point coordinates of Eq. (9.77), as visualized in Fig. 9.25(b). Alternative procedures can be thought of, for example using trigonometric considerations. The line connecting the expansion point to the origin is—by the definition of distance—perpendicular to the limit state. The distance from the identified expansion point to the origin is equal to $\sqrt{1.91^2+{1.15}^2}=2.23$, demonstrating that the distance from the expansion point to the origin indeed equals the reliability index β as calculated above from analytical considerations. Using trigonometry, it can be shown that the axis through the origin and the expansion point is the axis u _Z, i.e. the standard Gaussian transformation of the limit state variable Z. In that case, the one-dimensional case demonstrated above applies, thus proving that the distance between the expansion point and the origin indeed equals the reliability index in this 2D case; see Eq. (9.78). Using the inverse of Eq. (9.74), the design point x* in X-space is calculated and visualized in Fig. 9.25(a). The direction n _x perpendicular to the limit state is also visualized. Note that in the X-space the line connecting the design point to the centre of the joint PDF is not perpendicular to the limit state:

$$ {u}_{tR}=\frac{t_R-{\mu}_{tR}}{\sigma_{tR}};{u}_{tE}=\frac{t_E-{\mu}_{tE}}{\sigma_{tE}} $$

(9.74)

$$ Z={t}_R-{t}_E={\sigma}_{tR}{u}_{tR}+\left(-{\sigma}_{tE}\right){u}_{tE}+\left({\mu}_{tR}-{\mu}_{tE}\right) $$

(9.75)

$$ {x}_p=\frac{- ac}{a^2+{b}^2};{y}_p=\frac{- bc}{a^2+{b}^2} $$

(9.76)

$$ {u}_{tR}^{\ast }=\frac{-{\sigma}_{tR}\left({\mu}_{tR}-{\mu}_{tE}\right)}{\sigma_{tR}^2+{\sigma}_{tE}^2}=-1.91;{u}_{tE}^{\ast }=\frac{\sigma_{tE}\left({\mu}_{tR}-{\mu}_{tE}\right)}{\sigma_{tR}^2+{\sigma}_{tE}^2}=1.15 $$

(9.77)

$$ {P}_f=P\left[Z<0\right]=P\left[{u}_Z{\sigma}_Z+{\mu}_Z<0\right]=P\left[{u}_Z<-\frac{\mu_Z}{\sigma_Z}\right]=\Phi \left(-\frac{\mu_Z}{\sigma_Z}\right)=\Phi \left(-\beta \right) $$

(9.78)

The above demonstrates how in the U-space the distance between the origin and the (linear) limit state equation corresponds with the reliability index β in case of normally distributed variables. A FORM calculation procedure has, however, not yet been introduced. To this end, observe that:

• (i) The expansion point u* is by definition situated on the limit state (Z = 0).

• (ii) The vector connecting the expansion point to the origin is by definition perpendicular to the limit state (as u* is the point on the limit state closest to the origin). This vector is further denoted as β . The direction of β is specified by the vector N _U of Eq. (9.79), which results in the normalized directional vector n _U of Eq. (9.80). For both these equations, the last equality is an application for the considered case Z = t _R – t _E only. The vector n _U is the unit vector perpendicular to the limit state, facing outward from the failure region. The components of n _U are the directional cosines of β and are commonly referred to as the ‘sensitivity factors’ α _Xi as they indicate the relative importance of the variability of the underlying variable X _i in the result for β. For resistance variables, the sensitivity factor is positive, while for load variables the sensitivity factor is negative.

• (iii) The length of β is equal to the reliability index β, as specified by Hasofer and Lind:

$$ {\mathrm{N}}_{\mathrm{U}}=\left[\begin{array}{c}\frac{\partial Z}{\partial {u}_{tR}}\\ {}\frac{\partial Z}{\partial {u}_{tE}}\end{array}\right]=\left[\begin{array}{c}{\sigma}_{tR}\\ {}-{\sigma}_{tE}\end{array}\right] $$

(9.79)

$$ {\mathrm{n}}_{\mathrm{U}}=\frac{{\mathrm{N}}_{\mathrm{U}}}{\left|{\mathrm{N}}_{\mathrm{U}}\right|}=\left[\begin{array}{c}{\alpha}_{tR}\\ {}{\alpha}_{tE}\end{array}\right]=\left[\begin{array}{c}\frac{\sigma_{tR}}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}\\ {}-\frac{\sigma_E}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}\end{array}\right] $$

(9.80)

Considering the above, the vector β is given by β· n _u and thus the expansion point u* is defined by

$$ {\mathrm{u}}^{\ast }=\left[\begin{array}{c}{u}_{tR}^{\ast}\\ {}{u}_{tE}^{\ast}\end{array}\right]=-\beta \cdot {\mathrm{n}}_{\mathrm{U}}=\left[\begin{array}{c}-{\beta \alpha}_{tR}\\ {}-{\beta \alpha}_{tE}\end{array}\right] $$

(9.81)

The above allows to specify the following calculation procedure for a general linear limit state of Gaussian variables (can be readily generalized to higher dimensions):

• 1. Determine the unit vector normal to the limit state n _U, i.e. through (the multidimensional equivalent of) Eqs. (9.79) and (9.80).

• 2. Specify the expansion point u* as -β· n _U.

• 3. Substitute u* in the limit state function Z. As u* is by definition located on the limit state Z = 0, this results in a linear equation which can be solved for β.

Applying the above for the example case Z = t _R – t _E, n _U has already been listed above in Eq. (9.80), resulting in the expansion point of Eq. (9.82). Substituting u _tR^* and u _tE^* in Eq. (9.75) gives Eq. (9.83), which is readily simplified to Eq. (9.84), resulting in the same equation for β as derived from analytical considerations in Eq. (9.73):

$$ {\mathrm{u}}^{\ast }=\left[\begin{array}{c}{u}_{tR}^{\ast}\\ {}{u}_{tE}^{\ast}\end{array}\right]=\left[\begin{array}{c}-\beta \frac{\sigma_{tR}}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}\\ {}\beta \frac{\sigma_{tE}}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}\end{array}\right] $$

(9.82)

$$ Z\left({\mathrm{u}}^{\ast}\right)={\sigma}_{tR}\left(-\beta \frac{\sigma_{tR}}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}\right)+\left(-{\sigma}_{tE}\right)\beta \frac{\sigma_E}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}+\left({\mu}_{tR}-{\mu}_{tE}\right)=0 $$

(9.83)

$$ \beta =\frac{\mu_{tR}-{\mu}_{tE}}{\frac{\sigma_{tR}^2}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}+\frac{\sigma_{tE}^2}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}}=\frac{\mu_{tR}-{\mu}_{tE}}{\sqrt{\sigma_{tR}^2+{\sigma}_{tE}^2}}=2.23 $$

(9.84)

9.5.4.3 Generalized Case of a Non-Linear Limit State

The above FORM evaluation of Eqs. (9.82)–(9.84) is very straightforward thanks to the linearity of the limit state eq. Z. In case of a non-linear limit state , however, the sensitivity factors α _Xi (i.e. the directional cosines of the unit vector n _U) are not independent of the parameters X _i. In other words, the unit normal n _U to the failure domain is not constant. Consequently, a set of equations are obtained, constituted by Eq. (9.85) for the sensitivity factors α _Xi as evaluated in the expansion point u* and the limit state equation being zero in the expansion point, i.e. Eq. (9.86). Solving this set of equations gives β. As n _U is the normal vector to the limit state at the expansion point, the obtained results correspond with the result for the limit state linearized in the expansion point, and it is thus an approximation of the true failure probability:

$$ {\alpha}_{Xi}=\frac{\frac{\partial Z\left({\mathrm{u}}^{\ast}\right)}{\partial {X}_i}}{\sqrt{\sum \limits_i{\left(\frac{\partial Z\left({\mathrm{u}}^{\ast}\right)}{\partial {X}_i}\right)}^2}}\kern0.75em \mathrm{for}\ i=1..n $$

(9.85)

$$ Z\left({\mathrm{u}}^{\ast}\right)=Z\left(-\beta \cdot {\mathrm{n}}_{\mathrm{U}}\right)=0 $$

(9.86)

9.5.4.4 Generalized Case with Non-Gaussian Variables

In case of non-Gaussian variables, the transformation to the standard Gaussian space introduces difficulties. A standard approach is the application of the Rackwitz-Fiessler algorithm [69]. This algorithm transforms the distribution of X _i into a Gaussian distribution with parameters ${\mu}_{Xi}^N$ and ${\sigma}_{Xi}^N$ which at the design point has the same PDF and CDF values, i.e. Eqs. (9.87) and (9.88). Adding these equations to the set of equations listed above and solving (iteratively) result in an assessment for the reliability index β:

$$ {F}_{Xi}\left({x}_i^{\ast}\right)=\varPhi \left(\frac{x_i^{\ast }-{\mu}_{Xi}^N}{\sigma_{Xi}^N}\right) $$

(9.87)

$$ {f}_{Xi}\left({x}_i^{\ast}\right)=\frac{1}{\sigma_{Xi}^N}\phi \left(\frac{x_i^{\ast }-{\mu}_{Xi}^N}{\sigma_{Xi}^N}\right) $$

(9.88)

9.5.5 Maximum Entropy, and the MaxEnt Method

The entropy associated with a random variable gives a measure of the level of uncertainty associated with it [66]. For completeness, Eq. (9.89) gives the definition of the entropy H associated with a continuous random variable Y, with Ω _Y being the range in which Y is defined (e.g. from 0 to +∞ in case Y is described by a log-normal distribution); see Papoulis and Pillai [70]:

$$ H=-\underset{\Omega_Y}{\int }{f}_Y(y)\ln \left({f}_Y(y)\right) dy $$

(9.89)

The larger the entropy defined by Eq. (9.89), the larger the uncertainty associated with Y. Uncertainty quantification methods based on maximum entropy concepts state that, under constraints posed by available information, the PDF f _Y which maximizes the entropy is the most appropriate, as it does not introduce any subjective information (i.e. it does not introduce a bias and thus results in an unbiased estimate for f _Y).

Consider a positive variable Y (such as the load bearing capacity) for which a set of m distribution moments μ _αj, j = 1..m, are known. The formulation of f _Y which maximizes the entropy is given by Novi Inverardi and Tagliani [71]

$$ {\hat{f}}_Y(y)=\exp \left(-{\lambda}_0-\sum \limits_{j=1}^m{\lambda}_j{y}^{\alpha_j}\right) $$

(9.90)

with α _j being the exponents specifying the distribution moments ; λ _j Lagrange multipliers, for j from 1 to m; and λ ₀ a normalization factor as specified by Eq. (9.91) which ensures that the integral of the PDF over its domain equals unity. The Lagrange multipliers are determined through the boundary conditions of the known moments μ _αj. Evaluating the values of λ _j will often require numerical procedures [66]:

$$ {\lambda}_0=\ln \left(\underset{\Omega_Y}{\int}\exp \left(-\sum \limits_{j=1}^m{\lambda}_j{y}^{\alpha_j}\right) dy\right) $$

(9.91)

When the distribution moments μ _αj are assessed from a data sample through the sample moments m _αj, as calculated by Eq. (9.92), with N the number of samples and y _k the k ^th realization, Novi Inverardi and Tagliani [71] demonstrated that the Lagrange multipliers λ _j are equivalently determined by the minimization of Eq. (9.93):

$$ {m}_{\alpha_j}=\frac{1}{N}\sum \limits_{k=1}^N{y}_k^{\alpha_j} $$

(9.92)

$$ \underset{\lambda_1..{\lambda}_j..{\lambda}_m}{\min}\left[{\lambda}_0+\sum \limits_{j=1}^m{\lambda}_j{m}_{\alpha_j}\right] $$

(9.93)

When considering sample moments m _αj, there is no reason why specific values for the exponent α _j should be preferred. On the other hand, the fact that estimation errors increase with higher exponents introduces a preference for fractional moments α _j ∈ (0,1). Thus the (fractional) sample moments themselves can be part of the (bounded) optimization, resulting in [71]

$$ \underset{\alpha_1..{\alpha}_j..{\alpha}_m}{\min}\left[\underset{\lambda_1..{\lambda}_j..{\lambda}_m}{\min}\left[{\lambda}_0+\sum \limits_{j=1}^m{\lambda}_j{m}_{\alpha_j}\right]\right] $$

(9.94)

The procedure above is directly applicable in conjunction with MCS or LHS procedures for the estimation of the sample moments in Eq. (9.92). Note that it is not required to re-evaluate the model as part of the optimization of Eq. (9.94): within the optimization, the model realizations y _i are a given. Having determined the exponents α _j and coefficient λ _j, the PDF estimate of Eq. (9.90) allows to make an unbiased extrapolation to low probability quantiles of Y, consistent with the observed realizations.

Using MCS (or to a lesser degree LHS ) for the estimation of the sample moments m _αj, however, still requires a large number of model evaluations. For situations with the number of uncorrelated stochastic input variables n ≤ 10 a more efficient calculation scheme has been presented by Van Coile et al. [72], adapted from the work by Zhang [73]. This methodology is denoted as the MaxEnt method, and relies on two approximations: application of the multiplicative dimensional reduction method (MDRM) and Gaussian interpolation.

The MDRM assumes that the model formulation h of Eq. (9.48), where X is a multidimensional vector, can be approximated by the product of one-dimensional functions h _i which isolate the contribution of the different stochastic variables X _i:

$$ Y=h(X)\approx {h}_0^{1-n}\prod \limits_{i=1}^n{h}_i\left({X}_i\right) $$

(9.95)

where the one-dimensional functions are defined by Eq. (9.96), i.e. the model evaluation where all n − 1 remaining stochastic variables are set equal to their median value $\overset{\frown }{\mu }$. h ₀ then equals the model evaluation where all stochastic variables equal their median value:

$$ {h}_i\left({x}_i\right)=h\left({\hat{\mu}}_1,\dots, {\hat{\mu}}_{i-1},{x}_i,{\hat{\mu}}_{i+1},\dots, {\hat{\mu}}_n\right) $$

(9.96)

Under the above assumption, the α _j^th moment of Y is approximated by

$$ {\mu}_{\alpha_j}\approx {h}_0^{\alpha_j\left(1-n\right)}\prod \limits_{i=1}^n\underset{\Omega_{X_i}}{\int }{\left({h}_i\left({x}_i\right)\right)}^{\alpha_j}{f}_{X_i}\left({x}_i\right){dx}_i $$

(9.97)

with f _Xi the PDF of X _i.

Efficiently evaluating the integral of Eq. (9.97) is done through the approximation of Gaussian integration . For each stochastic variable X _i, L Gauss points x _i,l are considered. Together with the associated Gauss weights w _l, the distribution moment is estimated from the sampled data as

$$ {\mu}_{\alpha_j}\approx {h}_0^{\alpha_j\left(1-n\right)}\prod \limits_{i=1}^n\sum \limits_{i=1}^L{w}_i{h}_i\left({x}_{i,l}\right) $$

(9.98)

The obtained estimate for m _αj can be substituted in the optimization of Eq. (9.94). The above scheme requires L model realizations per stochastic input variable, as well as one model realization for h ₀. The total number of model realizations is thus limited to n·L. When L is odd, one of the Gauss points corresponds with the median value, and thus the number of model realizations is further limited to n·(L-1) + 1. For a standard scheme with L = 5, 4n + 1 model realizations are thus required. As long as n is limited (e.g. ≤ 10), the total required number of model evaluations will be smaller compared to common alternative sampling schemes such as MCS or LHS . An example application for the fire resistance time of a composite column is visualized in Fig. 9.26. See Gernay et al. [46] for further details and discussion. The approximations introduced by the MDRM and Gaussian interpolation may however introduce errors in the estimate. Further discussion and detailed worked examples are provided by Van Coile et al. [72].

Fig. 9.26

MaxEnt estimate for the fire resistance time of a composite column , together with an MCS validation and log-normal approximations [46]

9.5.6 Fragility

The fragility of a component or a system is another way of indicating the probability of exceedance of a limit state (i.e. performance threshold). Often this is applied to give a reflection of how likely it is to be in or have exceeded a damage state . It is typically expressed as a cumulative probability distribution , which is dependent on the intensity of some design variable or perturbation. Such curves are widely known as ‘fragility curves ’. Seismic fragility , one of the most widely used applications, was first introduced as a concept for the probabilistic assessment of nuclear structures in the energy industry.

Limit states have been introduced in Sect. 9.2.2 and indicate the conditions beyond which the structure no longer fulfils certain criteria for design. Similarly, damage states quantify the damage to components or structures as a result of a perturbation. Damage may take the form of, for example, cosmetic damage, irreversible structural damage, or collapse of the building. They can be considered different from limit states in that they may be related to a description of the physical damage to a component as opposed to a criterion for design verification and therefore are often relatable to the effort required to repair the component and return it to its original state; see Fig. 9.27.

Fig. 9.27

Damage states in earthquake engineering (adapted from [75])

The abbreviation DS is often used to denote damage state . A numerical index associated with the DS may represent consecutively more severe damage states. For example, in earthquake engineering damage state 1 (DS₁) may represent the smallest amount of damage, and the easiest to repair, requiring only for example taping and repainting of any cracks in the plasterboard. With increasing damage state , the complexity of repair increases. FEMA 273/274/356 defines damage states according to different qualitative performance levels, with DS₁ representing a condition that would not prevent immediate occupancy of a building after an earthquake. DS₂ represents a condition that could represent a risk to life. DS₃ represents a condition whereby the limit state for collapse of the structure is close to being exceeded and the corresponding margin of safety is very low. Often-cited examples of damage states in structural earthquake engineering include damage to beams, columns, or partition walls as a result of inter-storey displacements or internal member forces induced by the perturbation.

Commonly, fragility curves are applied to define the probability of a damage state being exceeded conditional on an intensity measure exceeding a given value associated to the perturbation. For each definition of fragility, the intensity measure, abbreviated IM, is typically one of many possible quantifiable expressions of the intensity of the perturbation. In earthquake engineering, many different intensity measures are used, for example, permanent ground displacement or peak ground acceleration. The fragility, F, of a structure representing the probability of exceeding a damage state is thus written as

$$ F=P\left( DS\ge {ds}_i| IM\right) $$

(9.99)

where P(.) is the probability operator . An illustrative example of fragility curves for an element with four defined damage states (DS₀–DS₄) is shown in Fig. 9.28.

Fig. 9.28

Illustrative example of fragility curves

Different classes of methods for creating fragility curves exist [76]. They may be either empirical, i.e. based on observations either from the real world or the lab; analytical, i.e. based on analyses of structural models; or based on expert judgement. The use of fragility curves in structural fire engineering is relatively uncommon, examples including Gernay et al. [77], Van Coile et al. [78], Ioannou et al. [79], and Hopkin et al. [65]. Evaluations for different damage states as in earthquake engineering are however still rare. This can at least partially be attributed to a perceived lack of the required data to generate such curves, and so recent work by Ioannou et al. [80] has relied on the use of expert elicitation, developing fragility curves for concrete exposed to fire. Cooke’s method of expert elicitation was used [81], which relies on expert judgement of the results of relatively unknown phenomenon weighted by the same experts’ response to a number of questions with known answers, accounting also for their certainty about the answer being given. This study by Ioannou et al. is discussed further in the applications section.

9.5.7 The Pacific Earthquake Engineering Research Center Performance Based Earthquake Engineering Framework

The PEER (Pacific Earthquake Engineering Research Centre) PBEE (Performance Based Earthquake Engineering) framework has seen application in several different hazards, including fire [82,83,84,85,86]. It is a comprehensive methodology that, in its original application, accounts for seismological, engineering, financial, and societal considerations to the problem of performance-based seismic engineering. The PEER framework disaggregates the problem of linking hazards to decision variables into four models: the hazard model that predicts the intensity measure, the engineering model that predicts the engineering response, the damage model that predicts the damage resulting from the response, and then the loss model that predicts the consequences of that damage from a societal or cost perspective. Each of these models builds upon and is conditional on the previous.

The framework is therefore based across three calculation ‘domains’: the hazard domain, the structural system domain, and the loss domain. These domains are linked by what may be termed ‘pinch variables’, against which each of the subsequent domains is conditioned. The framework is expressed as a triple integral, Eq. (9.100), where intensity measure is denoted as IM; the structural response to the event, the engineering demand parameter, is denoted as EDP; the estimation of damage, the damage measure, is denoted as DM; and resulting losses incurred, decision variable, are denoted as DV. In Eq. (9.100) g denotes the annual rate of exceeding a given value of one of the pinch variables, and P denotes the probability of exceeding a given value of one of the pinch variables given a value of the preceding variable:

$$ {g}_{DV}=\iiint \underset{\mathrm{Loss}\ \mathrm{Domain}}{\underbrace{P\left[ DV| DM\right] dP\left[ DM| EDP\right]}}\overset{\mathrm{Structural}\ \mathrm{System}\ \mathrm{Domain}}{\overbrace{dP\left[ EDP| IM\right]}}\underset{\mathrm{Hazard}\ \mathrm{Domain}}{\underbrace{dg_{IM}}} $$

(9.100)

Calculation in the hazard domain may be seen as analogous to the development of a ground motion hazard cover as part of a probabilistic seismic hazard analysis (PSHA), with the seismic hazard replaced with a fire hazard, i.e. a PFHA. The output of the PFHA will generally be a single parameter that defines the intensity of the fire and quantifies the rate of exceeding a given value of that intensity, i.e. g _IM = g(IM > im _i) where im _i is some value of the intensity measure. Extended frameworks which use a combination of intensity measures are however possible, i.e. vector forms of IM exist for earthquake engineering, but are not discussed here in the application to fire engineering.

In PSHA, the intensity measure chosen to represent the hazard is related to the selection of the engineering demand parameter (EDP), with common examples of the former being peak ground acceleration or some spectral response value, and an example of the latter being inter-storey drift. A good selection of the IM will have a strong correlation with the EDP of interest; that is, it will have a high efficiency [87] and therefore the uncertainty of EDP conditional on the IM will be low. Shrivastava et al. [88] explored the efficiency of a range of IMs to structural fire engineering, including maximum fire temperature; time to maximum temperature; the area under the fire curve; the total duration of the fire including cooling phase; and the cumulative incident radiation. They used maximum vertical displacement of an element of structure and showed that cumulative incident radiation was the most efficient IM in this application. Elsewhere, Devaney [82] compared both time to peak compartment temperature and peak compartment temperature as IMs and showed that for the same EDP for an uninsulated composite beam, peak compartment temperature was the most efficient IM.

Ultimately, whichever IM is chosen, the facility definition as well as limitations in either knowledge or model chosen to represent a fire will limit the number of possible scenarios which can occur and which can be modelled. For example, compartment geometry, fuel load composition and total calorific value, possible ventilation conditions , and materials chosen for the compartment boundaries will all influence the dynamics of a fire that can occur in any given volume. These fires could be generated using, e.g., Monte Carlo simulation, as discussed in Sect. 9.5.3, and used to carry out the analysis in the hazard domain.

The analysis in the structural domain requires the generation of records of structural response to a range of different fires that can occur. Additional uncertainties can and should also be incorporated into this analysis, for example, material property uncertainties and geometric uncertainties. As with the hazard analysis, the output from the structural analysis is a probabilistic measure of the response of the structure which will be related to the damage analysis which follows in subsequent stages of the framework. For example, for typical examples of the framework applied to earthquakes, the engineering demand parameter studied is the inter-storey drift and the damage measure evaluated could for example be damage to the non-structural walls. In structural fire engineering, a suitable damage measure could be, e.g., residual deflection. The structural analysis should reflect the response of the structure across the whole vector of the intensity measure.

The engineering demand parameter is expressed as a hazard curve, similar to the intensity measure, which again permits the quantification of the rate of exceedance given the intensity measure hazard curve, i.e. g _EDP =  ∫ P(EDP > edp _i|IM)dg _IM.

The calculation in the loss domain requires first the definition of one or more damage states and thus fragilities conditional on the engineering demand parameter. These damage states are denoted DS _i with i denoting a specific damage state. For example, three possible damage states may be identified: undamaged (DS ₀), lightly damaged requiring minor repair work (DS ₁), and major damage requiring demolition and replacement of the section (DS ₂). P(DM| EDP) denotes the probability of a damage measure conditional on the EDP, with the damage measure being the damage states identified.

Finally, the decision variable requires to be conditioned on the damage state. Examples of decision variables include cost to repair or downtime. Devaney in his thesis [82] uses data from the literature to derive cost and downtime distributions for different construction elements damaged by fire. In reference to the damage states identified in the previous paragraph these are shown as normalized against initial construction costs for a beam and for a column in Table 9.21.

Table 9.21 Examples of log-normal distributions of normalized cost consequence functions [82]

The framework is shown schematically in Fig. 9.29. The framework starts with the definition of the facility , including information about its design and location as may be needed for a hazard analysis, and then finishes with a decision-making process where a decision is taken as to whether or not the annual rate of exceedance of one of the decision variables is acceptable.

Fig. 9.29

PEER analysis methodology (adapted from ref. [97])

9.6 Applications

9.6.1 Event Tree

In the aftermath of an earthquake, the likelihood of fire ignition inside a building increases due to ruptured gas lines, electric arcing, toppled furniture, etc. Meanwhile, active and passive fire protections can be damaged due to earthquake shaking. Historically, it is shown that sprinkler systems could be ineffective due to breakage and leakage in the sprinkler piping. The fire compartments could be compromised due to damaged or cracked walls, ceilings, fire doors, and fire-rated linings. Finally, the passive fire protection , such as spray fire-resistant material that is used as fire protection in steel structures, may dislodge during earthquake shaking.

Figure 9.30 shows an event tree to identify post-earthquake fire scenarios inside a building and quantify the corresponding probabilities. These fire scenarios and the associated occurrence probabilities can be used by the structural engineer to evaluate damage frequency to the structure due to post-earthquake fires.

Fig. 9.30

Event tree for post-earthquake fire scenarios inside a building

The initial event, being the earthquake, may lead to a fire ignition . The probability of ignition inside a building can be quantified using the procedure discussed by Elhami Khorasani et al. [89], as a function of earthquake intensity , characteristics of the community, and building construction type. The sprinklers after the earthquake may not be functional leading to an uncontrolled fire. Some statistics of sprinkler performance as a function of ground motion acceleration (earthquake intensity) can be found in the study of LeGrone [90]. The fire can spread across and between floors in a building once it is out of control and the fire compartments are compromised. Historical data can be used to quantify damage to individual elements of fire safety systems, such as fire doors, but the overall probability of damage to the fire compartment is currently being researched and can be assigned by engineering judgement at this time. The final line of defence would be the passive fire protection on steel structural elements in a building. Severe damage to the building could be expected in case of damage to the passive fire protection while an uncontrolled fire spreads inside the building. It should be noted that taking the correlation of damage to fire compartment and passive fire protection into account, the conditional probability of having passive fire protection compromised is assumed to be higher on branches where the compartment is known to be compromised. The event tree demonstrates the conditional probabilities at different stages within a branch and finally the combined yearly occurrence probability at the end of each branch.

9.6.2 Bending Moment Capacity and Bending Failure Probability of a Concrete Slab

Introduction and Motivation

Traditionally the fire resistance of solid concrete slabs is defined through tabulated data. For example, EN 1992-1-2:2004 [54] lists minimum concrete cover and slab thicknesses in function of the required (ISO 834) standard fire resistance. For the one-way solid slab specified further in Table 9.22, the fire resistance time listed in Table 5.8 of EN 1992-1-2:2004 is 120 min. The concrete cover realized during construction is however uncertain, as is the realization of other design parameters such as the concrete compressive strength and reinforcement yield stress. The same applies to the loads acting on the slab during fire exposure. Consequently, there may be situations where the slab bending resistance during fire exposure is insufficient to resist the bending moment induced by the acting loads, and the structure is deemed to ‘fail’ prematurely.

Table 9.22 Model parameters and probabilistic models, as listed by Van Coile [51], based on Holicky and Sykora [41]

The above implies amongst others that (i) design solutions in accordance with the tables of EN 1992-1-2 have an (unknown) probability of not meeting their specified fire resistance; (ii) for structures with high requirements for structural integrity in case of fire, the failure probability associated with the tabulated design solutions of EN 1992-1-2 may be too high; (iii) for existing structures which are at first glance not compliant with the tables of EN 1992-1-2, the achieved safety level may nevertheless exceed the safety level associated with the tabulated design solutions, allowing to meet fire resistance requirements without (expensive) refurbishment; and (iv) for designs where the consequences of fire-induced structural failure are low, a higher failure probability may be allowable then as associated with the tabulated data, thus allowing for a less onerous design requirement.

In the following, the failure probability of solid concrete slabs is explored considering standard fire exposure. First the resistance and load models are introduced, as well as the limit state function for bending. These allow a direct evaluation of the failure probability through crude Monte Carlo simulations (MCS ). More insight is however obtained by studying the probability density function of the bending moment capacity . This has the further benefit of reducing computational expense when re-evaluating a given slab configuration for, e.g., a different load level and allows the use of approximate and computationally efficient reliability methods such as analytical evaluations or FORM.

Further discussions and background on the case presented here can be found in the works of Van Coile et al. [91] and Thienpont et al. [92]. Applied probabilistic models have been chosen for consistency with these references.

The structure of this section is as follows. First the considered limit state function is introduced together with models for the resistance and load effect in Sect. 9.6.2.1. Subsequently, the failure probability corresponding with the limit state function is evaluated through crude Monte Carlo simulations (MCS ) in Sect. 9.6.2.2. In Sect. 9.6.2.3, approximate distributions for the resistance are explored. These approximate distributions allow to make a direct analytical estimate of the failure probability , omitting the computational cost of MCS. This analytical failure probability estimation is demonstrated in Sect. 9.6.2.4.

9.6.2.1 The Limit State Function, and Resistance and Load Models

Limit State Function

The bending limit state function is given by Eq. (9.101), with K _R being the model uncertainty for the resistance effect, M _R,fi,t the bending moment capacity of the slab at t minutes of fire exposure, K _E the model uncertainty for the load effect , M _G the bending moment induced by the permanent load, and M _Q the bending moment induced by the imposed load:

$$ g=R-E={K}_R{M}_{R, fi,t}-{K}_E\left({M}_G+{M}_Q\right) $$

(9.101)

Model for the Resistance Effect

As models are a simplification of reality, the multiplicative model uncertainty K _R has been introduced in Eq. (9.101). The total resistance effect R thus equals K _R·M _R,fi,t. The applied probabilistic description of K _R is given in Table 9.22. While in theory the model uncertainty could be calibrated by a systematic comparison of the model for M _R,fi,t against experimental test results, the difficulty of obtaining experimental data for structural fire engineering implies that K _R is based on subjective judgement instead, informed by model uncertainties listed for normal design conditions.

In the following, uncertainties with respect to the thermal properties of the reinforced concrete slab are not taken into consideration. This relates to a situation where the performance is evaluated with respect to a standard fire exposure, both regarding the design fire conditions and the concrete thermal properties. Considering one-sided exposure to fire from below, the cross section of the slab is heated non-linearly (see further Fig. 9.31), resulting in a non-linear distribution of free thermal strains across slab depth. The temperature increase furthermore changes the concrete and reinforcing steel mechanical models (stress-strain diagrams). A simplified numerical calculation tool has been applied by Van Coile et al. [91] which evaluates the full moment-curvature diagram for a given slab cross section and fire duration. From this diagram, the bending moment capacity M _R,fi,t is defined as the maximum attainable bending moment. Van Coile et al. [91] then demonstrated that the numerical calculation can be substituted by Eq. (9.102), with parameters as listed in Table 9.22. This equation is more generally applicable for situations where both (i) the slab fails by reinforcement yielding (as is commonly the case in fire conditions as the bottom reinforcement loses its strength) and (ii) the slab is sufficiently thick so that the concrete compressive zone remains relatively cool.

Fig. 9.31

Temperature distributions in a 200 mm solid concrete slab, exposed at the bottom side to different ISO 834 standard fire durations. Comparison with data listed in EN 1992-1-2:2004 [92]

In Eq. (9.102) only the reinforcement yield stress retention factor k _fy is temperature, and thus time, dependent. The reinforcement temperature depends on the position of the reinforcement (and is thus dependent on the concrete cover realization), and is evaluated through numerical 1D heat transfer analyses [92]. In the absence of numerical evaluation, the temperatures can be directly taken from the temperature distributions for concrete slabs listed in EN 1992-1-2. Both temperatures are compared in Fig. 9.31 for specific ISO 834 standard fire durations. Background and further references for the probabilistic models for the input parameters are listed by Van Coile [51]. Here suffice it to state that the models are based on the review study by Holicky and Sykora [41], and preliminary assessments for the retention factor. Updated models for the retention factor in accordance with Sect. 9.4 of this chapter can be taken into account:

$$ {M}_{R, fi,t}={A}_s{k}_{fy}{f}_{y,20}\left(h-c-\frac{\varnothing }{2}\right)-0.5\frac{{\left({A}_s{k}_{fy}{f}_{y,20}\right)}^2}{bf_{c,20}} $$

(9.102)

Model for the Load Effect

The load effect consists of the bending moment induced by the permanent load and the (equivalent) imposed load. The probabilistic description for both is listed in Table 9.22 in function of their characteristic value. Note that the model for the instantaneous imposed load effect is the model applied by Holicky and Sleich [47] and Gernay et al. [46]; see Sect. 9.3. This has been done for consistency with the results listed by Van Coile [51]. Defining the load ratio χ by Eq. (9.103), and considering the Eurocode ambient design criterion of Eq. (9.104), with u being the ambient design utilization ≤1 and other parameters as listed in Table 9.23, the bending moments M _G and M _Q are fully defined by χ and u, for a given slab configuration.

Table 9.23 Eurocode ambient design parameters Eq. (32), EN 1990 [15]

For a statically determinate slab, the model uncertainty for the load effect included in Eq. (9.101), K _E, can be considered the same as in normal design conditions (see Table 9.22):

$$ \chi =\frac{Q_k}{Q_k+{G}_k}=\frac{M_{QK}}{M_{QK}+{M}_{GK}} $$

(9.103)

$$ {M}_{Rd}={uM}_{GK}\max \left\{{\gamma}_G+{\psi}_0{\gamma}_Q\frac{\chi }{1-\chi };{\xi \gamma}_G+{\gamma}_Q\frac{\chi }{1-\chi}\right\}\kern0.5em \mathrm{with}\ u\le 1 $$

(9.104)

9.6.2.2 Failure Probability Estimation Through MCS

For a given ISO 834 standard fire duration t _E, the temperature distribution in the slab is fully defined—as the uncertainty with respect to the thermal properties is not taken into consideration (see Sect. 9.6.2.1). For each Monte Carlo realization, the reinforcement temperature is determined from Fig. 9.31, taking into account the specific realization of the concrete cover.

In Fig. 9.32, the estimated failure probability and corresponding COV are visualized in function of the number of MCS , for t _E = 120 min, u = 0.90, and χ = 0.40 (i.e. M _Gk = 21.3 kNm and M _Qk = 14.2 kNm). These results have been obtained through a script, but a spreadsheet evaluation is possible as well (with memory constraints posing a practical limit to the number of MCS in the spreadsheet).

Fig. 9.32

Estimate for P _f and corresponding V _Pf in function of the number of MCS

The converged P _f estimate is 7.1 × 10⁻⁵ (for the specified fire exposure). This corresponds with a reliability index β = 3.8, in accordance with Eq. (9.8). This result indicates that for this specific slab—and under the constraints imposed by the model, such as no spalling—structural stability in the bending limit state will be maintained for the 120 min tabulated in EN 1992-1-2:2004 with a very high reliability.

9.6.2.3 Probability Density Function Describing the Bending Moment Capacity M _R,fi,t

Introduction

While crude MCS allows to make an assessment of the failure probability , the evaluation requires a large number of model evaluations and is thus no longer feasible when applied with a computationally expensive model. Furthermore, a pure MCS as in Fig. 9.32 requires a full recalculation whenever an aspect of the evaluation is modified (e.g. the load ratio, utilization, or nominal concrete cover).

The difficulty in evaluating the limit state of Eq. (9.101) results first and foremost from the unknown distribution of M _R,fi,t. When the distribution type is known, the parameters of the distribution can be assessed through a more limited number of model evaluations or approximate methods. A commonly assumed distribution type to represent material and cross-sectional strength is the log-normal distribution. As illustrated below however, directly assuming a distribution type without further analysis can result in an inappropriate model choice.

Observed Density Function Through MCS and Mixed Log-Normal Model

Statistical tests can be applied to determine appropriate distribution choices; see, e.g., Ang and Tang [93]. In structural engineering applications however, the appropriate description of low strength quantiles and high load quantiles is of great importance, while less importance is assigned to the close description of other quantiles (such as a very high resistance realization or exceptionally low load effect ). The Gumbel distribution commonly applied for the imposed load effect for example, see Sect. 9.3.2.3 and Table 9.22, has a non-zero probability of returning a negative load. Clearly this is an inappropriate model for the low quantiles of Q, but this is of little importance as structural failure is—in reasonable situations—associated with high quantiles of Q.

Considering the above, the engineer assessing the appropriateness of a distribution model cannot go without a visual comparison of the data against the model. In case of a model for the concrete compressive strength or other experimentally measured parameters, the term data should be understood literally. In the case under consideration here, however, the ‘data’ is the result for M _R,fi,t obtained through MCS .

In Fig. 9.33, the histogram corresponding with 10⁴ MCS realizations is visualized together with a log-normal approximation for different ISO 834 standard fire durations t _E, for the slab configuration listed in Table 9.22. Figure 9.34 visualizes similar results for a concrete cover standard deviation of 10 mm (e.g. an existing building with large uncertainty or limited quality control in production).

Fig. 9.33

Observed distribution density (MCS, 10⁴ realizations), log-normal approximation (LN), and mixed log-normal approximation (mixed LN), for the slab characteristics of Table 9.22, and different ISO 834 standard fire durations t _E

Fig. 9.34

Observed distribution density (MCS, 10⁴ realizations), log-normal approximation (LN), and mixed log-normal approximation (mixed LN), for the slab characteristics of Table 9.22, but with a concrete cover standard deviation of 10 mm instead of 5 mm, and different ISO 834 standard fire durations t _E

Figures 9.33 and 9.34 suggest that a log-normal distribution is not an appropriate choice for describing M _R,fi,t. Further study indicates that this non-standard PDF shape is the result of the concrete cover variability, and the associated non-linear change in reinforcement temperature, while for a fixed (deterministic) concrete cover c _i, M _R,fi,t,ci is described by the traditional log-normal distribution [91]. Taking this information into account, the distribution for slab bending moment capacity M _R,fi,t is described by a combination of constituent log-normal distributions, whereby each constituent log-normal distribution M _R,fi,t,ci is valid for a specific fixed concrete cover c _i, and the combination weights P _ci correspond with the (lumped) occurrence probabilities for the respective concrete covers:

$$ {M}_{R, fi,t}=\sum \limits_i{P}_{c_i}{M}_{R, fi,t,{c}_i} $$

(9.105)

$$ {P}_{c_i}=\underset{c_i-\Delta c/2}{\overset{c_i+\Delta c/2}{\int }}{f}_c(c) dc $$

(9.106)

with f _c being the PDF for the concrete cover, and Δc the lumping width for the concrete cover realizations (here: 1 mm). In conclusion, M _R,fi,t can be described by a mixed log-normal distribution. Note that the summation in Eq. (9.105) represents a combination of log-normal distributions, not a direct summation.

As the constituent distributions M _R,fi,t,ci are known to be described by a log-normal distribution, their parameters can be evaluated using more efficient sampling techniques (such as Latin hypercube sampling ; see [67]). In the current case however, the model for M _R,fi,t is given by an equation, i.e. Eq. (9.102), and a direct evaluation of the mean μ and standard deviation σ is here also possible through Taylor approximations:

$$ {\mu}_{M_{R, fi,t,{c}_i}}\cong y\left(\boldsymbol{\upmu} \right) $$

(9.107)

$$ {\sigma}_{M_{R, fi,t,{c}_i}}^2\cong \sum \limits_j{\left(\frac{\partial y\left(\boldsymbol{\upmu} \right)}{\partial {X}_i}\right)}^2{\sigma}_{X_i}^2 $$

(9.108)

where μ indicates the vector of mean values for all stochastic variables X _j in Eq. (9.1), and y(.) refers to Eq. (9.102) itself.

The evaluation of Eqs. (9.107) and (9.108) can readily be done in a spreadsheet, and so the mixed log-normal distribution for M _R,fi,t is fully specified. This mixed log-normal distribution is compared to the observed MCS histogram in Figs. 9.33 and 9.34, confirming the excellent match.

9.6.2.4 Analytical Failure Probability Estimation

Having established the mixed log-normal distribution as an appropriate modelling choice for M _R,fi,t, the failure probability can be evaluated through Eq. (9.109), where K _T is the total model uncertainty combining both the model uncertainty effects for the load and resistance effect , and the failure probability is separately evaluated for each of the log-normal constituent distributions M _R,fi,t,ci as P _f,i:

$$ {\displaystyle \begin{array}{l}{P}_f=P\left[g<0\right]=P\left[{M}_{R, fi,t}-\frac{K_E}{K_R}\left({M}_G+{M}_Q\right)<0\right]\\ {}=\sum \limits_i{P}_{ci}.P\left[{M}_{R, fi,t, ci}-{K}_T\left({M}_G+{M}_Q\right)<0\right]=\sum \limits_i{P}_{ci}.{P}_{f,i}\end{array}} $$

(9.109)

As both K _E and K _R are described by a log-normal distribution, also K _T is log-normal. Furthermore, the total load effect E = K _T (M _G + M _Q) can be approximated by a log-normal distribution as well, for which the mean and standard deviation can be assessed through Taylor approximations, i.e. Eqs. (9.110) and (9.111).

The appropriateness of the approximation is visualized in Fig. 9.35 (result of 10⁸ MCS ), shown here for the generalized dimensionless case of the load effect divided by the total characteristic load effect P _k = G _k + Q _k, for different load ratio χ. From the figure it is clear that the log-normal approximation is very good for χ = 0.3, and becomes less appropriate for higher load ratios. For χ = 0.40 as in this example, some deviation can thus be expected. As indicated in Fig. 9.35, the log-normal approximation underestimates the occurrence of large realizations of the total load effect , and will thus (for low failure probabilities) underestimate the probability of failure:

$$ {\mu}_E\cong {\mu}_{K_T}\left({\mu}_G+{\mu}_Q\right) $$

(9.110)

$$ {\sigma}_E^2\cong {\sigma}_{K_T}^2{\left({\mu}_G+{\mu}_Q\right)}^2+{\mu}_{K_T}^2\left({\sigma}_G^2+{\sigma}_Q^2\right) $$

(9.111)

Fig. 9.35

Comparison total load model K _T·(G + Q) and log-normal approximation E (MCS , 10⁸ realizations), for different load ratio χ

The introduction of an approximate log-normal total load effect E allows to evaluate Eq. (9.109) analytically. More specifically, P _f,i can be elaborated as Eq. (9.112), where Z follows a log-normal distribution (considering log-normality of both M _R,fi,t,ci and E ). The parameters of Z, i.e. μ _lnZ and σ _lnZ, are given by Eqs. (9.113) and (9.114), which are applications of Eqs. (9.56) and (9.57) in Sect. 9.5.2.

Thus, Eq. (9.115) holds and P _fi can be evaluated directly. Results for the mean and standard deviation of the constituent log-normal distributions M _R,fi,t,ci are given in Table 9.24, together with their constituent probability P _i and failure probability P _f,i (considering μ _E = 22.2 kNm and V _E = 0.21, calculated from Sects. 9.6.2.1 and 9.6.2.2). Note that the COV of the constituent M _R,fi,t,ci is quasi-constant at 0.09.

Table 9.24 Constituent models (log-normal M _R,fi,t,ci: c _i, P _i, mean, and standard deviation), corresponding failure probability P _fi, and contribution to the overall failure probability P _i·P _f,i. Calculation of the overall failure probability P _f = 4.9 × 10⁻⁵

The resulting estimate for P _f is 4.9 × 10⁻⁵, which corresponds with a reliability index β = 3.9. Despite the approximations, this result gives a correct order of magnitude evaluation of P _f, without requiring the application of specialized reliability methods. The calculation can be done in a spreadsheet. Furthermore, Table 9.24 also clearly shows how the largest contribution to the failure probability comes from the lower concrete cover realizations (i.e. the failure probability contributions of the c _i constituents up to 34.5 mm amount to 4.8 × 10⁻⁵). This example also illustrates the benefit of communicating small failure probabilities through the reliability index β, as this highlights the comparability of the approximate result with the MCS evaluation :

$$ {P}_{f,i}=P\left[{M}_{R, fi,t, ci}-E<0\right]=P\left[\frac{M_{R, fi,t, ci}}{E}<1\right]=P\left[Z<1\right] $$

(9.112)

$$ {\mu}_{\ln Z}={\mu}_{\mathrm{ln}}{M}_{R, fi,t, ci}-{\mu}_{\ln E} $$

(9.113)

$$ {\sigma}_{\ln Z}=\sqrt{\sigma_{\ln {M}_{R, fi,t, ci}}^2+{\sigma}_{\ln E}^2} $$

(9.114)

$$ {P}_{f,i}=P\left[Z<1\right]=\varPhi \left(\frac{\ln (1)-{\mu}_{\ln Z}}{\sigma_{\ln Z}}\right)=\varPhi \left(-\frac{\mu_{\ln Z}}{\sigma_{\ln Z}}\right) $$

(9.115)

9.6.3 Application of LHS

A W14x53 steel column section is part of the gravity system in a multistorey frame. Typical floor height is 3.962 m, with column ends constrained from rotation. The fire protection is designed based on the International Building Code guidelines for 2-h fire resistance, with a calculated mean fire protection thickness of 33.4 mm. The column has a characteristic yield strength of 345 MPa.

The question is to evaluate the mean and standard deviation of the column capacity (P _n) after exposure to 2 h of ASTM E119 (ISO 834), considering as single stochastic variable the yield strength of steel, in accordance with the model by Elhami Khorasani et al. [55] as presented in Sect. 9.4.2.

Solution

The problem is solved using both Monte Carlo simulations (MCS ) and Latin hypercube sampling (LHS ). The effectiveness of LHS is demonstrated by running both MCS and LHS with different number of samples and tracking the rate of convergence. The final results for the mean and standard deviation of calculated column capacity are presented in Table 9.25 using MCS and Table 9.26 using LHS.

Table 9.25 Mean and standard deviation of P_n using MCS

Table 9.26 Mean and standard deviation of P_n using LHS

Figure 9.36 shows the cumulative distribution function for the column capacity calculated using MCS and LHS with 10,000 and 500 samplings, respectively.

Fig. 9.36

CDF for column capacity calculated using MCS and LHS

9.6.4 Application of Fragility Curves

Fragility curves listing the probability of specified damage states in function of an intensity measure, as applied in earthquake engineering, have not yet been extensively developed for structural fire engineering applications. As noted in Sect. 9.5.6, a notable exception is the work by Ioannou et al. [79, 80] where expert elicitation was applied. Details of the procedure can be found in the full reference; the following gives an overview of the damage states specified and results obtained in order to clarify the concept of fragility curves .

Response measures including the presence and extent of spalling, residual capacity, span/deflection ratio, and peak rebar temperature were compared by Ioannou et al. [79, 80] with equivalent duration of standard fire exposure as an intensity measure. These response measures were linked with damage states based on the damage scale proposed by the concrete society [94], Table 9.27, resulting in the development of fragility curves for concrete slabs and concrete columns .

Table 9.27 Visual damage state classification table for reinforced concrete elements [80]

As part of the expert elicitation, 13 experts in structural fire engineering were asked to judge the relationship of these different response measures to the fire intensity, i.e. P(RM = y ∣ IM = x), for the fifth percentile, the mean, and the 95th percentile of the distribution. The intensity measure against which the response was conditioned was the time equivalence based on Ingberg’s work [95]. As part of the same exercise, the same experts were asked to judge the relationship between response thresholds and the different damage states defined in Table 9.27, i.e. P(DS ≥ ds _i ∣ RM = y), for the fifth, mean, and 95th percentiles of the distributions. Based on P(DS ≥ ds _i ∣ RM = y) a quantified damage scale for slabs and columns was created as shown in Table 9.28, accounting also for the uncertainty of the experts’ judgement.

Table 9.28 Quantified damage states for reinforced concrete slabs and columns

Fragility functions were then created through a random sampling technique which couples the relationships of response measure (RM) to intensity measure (IM) and damage state (DS) to response measure (RM). The procedure for this is described in both Ioannou et al. [80] and in more detail in Porter and Kiremidjian [96]. In summary however this involves drawing a random sample from the unit interval, which is used to select a value of RM conditioned on IM that has cumulative probability equal to this random number. Then the probability that each damage state will be reached or exceeded is determined by drawing another random sample on the unit interval to select a value of DS conditional on the RM. A large number of iterations of this is then performed to determine the probability that a building or component will sustain a damage level DS ≥ ds _i. Figure 9.37 shows the resulting fragility curves derived using this method by Ioannou et al. [80].

Fig. 9.37

Fragility curves corresponding to three damage states for (a) spalling, (b) deflection, (c) residual capacity, and (d) pear rebar temperature constructed for slabs and columns, from Ioannou et al. [80]. Note: the horizontal axis is in minutes

This same technique can be used to derive fragility functions based on relationships of DS, RM, and IM which are obtained through other means.