Investigation of the Nonlinearity Effect of the Shrouded Blade Assemblies on Their Forced Vibrations

Abstract

The paper presents the approaches to finite element studying of the forced vibrations of the shrouded blades with nonlinearity due to the interaction of contact surfaces of the shrouds and the presence of fatigue crack. The dynamic characteristics have been calculated for the developed linearized and nonlinear finite element models of the set of two blades and damaged airfoil. The comparative analysis of the obtained results shows their significant difference for the linearized and nonlinear models in both cases of study.

1 Introduction

A peculiar feature of shrouded blade assemblies, which are widely used in the design of turbine machines, is the presence of contact surfaces both between adjacent blades and in their joints with the disc (Petrov and Ewins 2006; Savchenko et al. 2018; Siewert et al. 2010; Szwedowicz et al. 2008; Zucca et al. 2012). This fact determines the nonlinearity of the blade assembly as a vibration system with a structural rotational symmetry, which can become more intense due to fatigue cracks (Dimarogonas 1996; Huang and Kuang 2006; Onishchenko et al. 2018; Shen and Chu 1992).

At present, a computational experiment with modern methods of computer modelling based on their three-dimensional models, one of which is the finite element method (FEM), becomes increasingly important in the determination of the dynamic state of blade assemblies. It is used to solve the problem of determining the dynamic stress state of the objects under investigation.

Despite the actual nonlinearity of blade assemblies, it is common to use both linear (Rzadkowski et al. 2007; Soliman 2019; Zinkovskii et al. 2016) and nonlinear (Dimarogonas 1996; Petrov and Ewins 2006; Onishchenko et al. 2018; Shen and Chu 1992; Siewert et al. 2010; Szwedowicz et al. 2008) approaches to the investigation of their vibration characteristics.

In the first case, the use of linearized finite element models is typical, where the contact conditions are replaced with kinematic constraints (Zinkovskii et al. 2016) or they are neglected (Soliman 2019). The areas with kinematic constraints are mainly specified from the results of the preliminary solution to the static contact interaction between the corresponding surfaces (Szwedowicz et al. 2008). It should be implied that the results of the linearized models often have low sensitivity and noticeable differences as compared with the experimental data.

The nonlinear analysis allows one to consider the dynamic variation in the contact between the surfaces. In turn, this leads to a qualitative and quantitative change in the vibration characteristics of the blade assemblies as compared with those obtained using linearized models, in particular, the occurrence of sub- and superharmonic resonances in the presence of fatigue cracks (Dimarogonas 1996; Matveev et al. 2010; Onishchenko et al. 2018; Shen and Chu 1992).

The analysis of some scientific papers demonstrates that the accuracy of the obtained results depends significantly on the approaches to the modelling of the contact conditions between their constituent elements. Therefore, the aim of this paper lies in the generalization of the test results in the determination of the effect of possible nonlinearity of the shrouded blade assemblies on the characteristics of their forced vibrations.

2 Approaches to Finite Element Modelling of the Object Nonlinearity

Let us consider two possible sources of the nonlinearity of the blades under study: shrouded coupling between the blades and a crack in the blade airfoil.

2.1 Shrouded Flange Coupling of the Blades

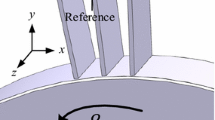
The analysis of forced vibrations of the blade assemblies is usually performed assuming that they are cyclically symmetric systems, namely all blades have identical geometric and mechanical characteristics. Here, the investigation of the blades is based on the use of their period with the appropriate boundary conditions. Such a period is assumed to have one blade. However, it is required to select a set of two blades to consider the conditions of interaction between the shrouded flanges as a period. Noteworthy is that it is also the simplest regular system that allows one to determine the influence of structural and operational force factors on the formation of its vibrations, including the frequency detuning of the blades. Therefore, for computational experiments, a set of two blades with a straight shrouded flange was chosen (see Fig. 9.1a).

Fig. 9.1

General view of the FE model of the set of blades (a) and scheme of the interaction between the contact surfaces (b)

In study (Savchenko et al. 2020), you will find a detailed description of the approaches to modelling this set of blades. Therefore, let us concentrate on the basic principles of the solution to this task.

The shrouded flanges interact on the contact surfaces K as shown in Fig. 9.1b, where α is the angle of their inclination relative to the rotation plane; t_s is the blade spacing; F_N is the resultant normal force to the contact surfaces K.

An eight-node finite element and its modifications were used to construct the finite element (FE) model of the set of blades, and a four-node contact element was used to model the contact interaction between the shrouded flanges, which make it possible to track the relative position of the corresponding contact surfaces.

2.2 Fatigue Crack

From the previous experience (Onishchenko et al. 2018), the fatigue crack was modelled in the form of a mathematical cut, which allows one to consider both its closing and opening during blade deformation. It should also be noted that the mass of the blade is the same, and only its stiffness undergoes variations on the deformation cycles. The edges of the open crack do not interact with each other. In case of a breathing crack, the mutual non-penetration of its edges is ensured by the introduction of the surface contact finite elements and the solution to the contact problem as in the modelling of the interaction between the shrouded flanges of rotor blades.

Figure 9.2 illustrates the example of the FE model of the compressor blade airfoil and its cross section with a fatigue crack.

Fig. 9.2

General view of the FE model of the compressor blade airfoil (a) and its cross section with a fatigue crack (b)

3 Calculation of the Forced Vibrations of the Blade Assemblies

As noted earlier, the dynamic variation in the contact interaction along the flanges arises under the action of structural and operational factors and leads to the nonlinearity of the assemblies. This is corroborated both by the results of the analysis of the static stress state (Szwedowicz et al. 2008) and from the data of full-scale experiments (Savchenko et al. 2018).

The matrix equation of forced vibrations of arbitrary nonlinear systems has the following form:

$$ [M]\{ \dot{u}\} + [D]\{ \dot{u}\} + ([K_{l} ] + [K_{nl} ])\{ u\} = \{ F(t)\} , $$

(9.1)

where $\left[ M \right]$, $\left[ D \right]$ are the inertia and dissipative matrices of the system, correspondingly; $\left[ {K_{l} } \right]$, $\left[ {K_{nl} } \right]$ are the linear and nonlinear components of its stiffness matrix $\left[ K \right]$; $\left\{ {F\left( t \right)} \right\}$ is the column vector of the generalized forces acting on the system $\left\{ u \right\}$; $\left\{ {\dot{u}} \right\}$ $\left\{ {\ddot{u}} \right\}$ are the column vectors of displacements, velocities and accelerations, respectively.

All matrices and column vectors of Eq. (9.1) are presented as units. The order of the matrix units is determined by the dimension of the FE mesh of the system under investigation.

The size of $\left[ {K_{nl} } \right]$, which is due to the contact interaction (Wriggers 2006), depends on the number of contact nodes where each element is presented as:

$$ \left| {\begin{array}{*{20}l} {k_{s} } \hfill & 0 \hfill & { - k_{s} } \hfill & 0 \hfill \\ 0 \hfill & {k_{n} } \hfill & 0 \hfill & { - k_{n} } \hfill \\ { - k_{s} } \hfill & 0 \hfill & {k_{s} } \hfill & 0 \hfill \\ 0 \hfill & { - k_{n} } \hfill & 0 \hfill & {k_{n} } \hfill \\ \end{array} } \right|, $$

(9.2)

where k is the coefficient in q-th node; n, s are the indexes characterizing the normal and tangential components of the stress state characteristics.

The components k_s of the stiffness coefficient k should satisfy the following conditions:

$$ \left\{ {\begin{array}{*{20}c} {k_{s} \ne 0,\mathop {}\limits^{{}} {\text{if}}\mathop {}\limits^{{}} \eta \left| {F_{n} } \right| > \left| {F_{s} } \right|;} \\ {k_{s} = 0,\mathop {}\limits_{{}} {\text{if}}\mathop {}\limits^{{}} \eta \left| {F_{n} } \right| = \left| {F_{s} } \right|,} \\ \end{array} } \right. $$

(9.3)

Here F is the internal force in the considered node; η is the friction factor of the contact surfaces of the shrouded joint.

To determine the nonlinear component $\left[ {K_{nl} } \right]$ of the stiffness matrix $\left[ K \right]$, let us use the Newton–Raphson method (Zienkiewicz 1972), which is based on the solution to the static nonlinear contact task described as follows:

$$ \left( {[K_{l} ] + [K_{BN} ]} \right)\{ u\} = \{ F(t_{i} )\} , $$

(9.4)

As a result, q and p are determined, which are in contact:

$$ F_{n} = k_{n} \left( {u_{n}^{q} - u_{n}^{p} - \Delta_{n} } \right) \ne 0;\quad F_{n} = k_{s} \left( {u_{s}^{q} - u_{s}^{p} - \Delta_{s} } \right) \ne 0, $$

(9.5)

where Δ is the parameter of the iteration process in compliance with the Newton–Raphson procedure.

Under internal and external frictions, the dissipative matrix $\left[ D \right]$ has a general view as:

$$ \left[ D \right] = \alpha \left[ M \right] + \beta \left[ K \right], $$

(9.6)

Here α and β are the coefficients characterizing the internal and external frictions, respectively.

Let us confine to considering energy dissipation due to internal friction, then Eq. (9.6) takes the following view:

$$ \left[ D \right] = \beta_{{}} \left[ K \right]. $$

(9.7)

With the vibration decrement δ, which is independent of the strain amplitude, coefficient β during vibrations of the blade by j-th mode with frequency ω_j is determined as:

$$ \beta_{j} = \frac{{\delta_{j} }}{{2\pi^{2} \omega_{j} }}, $$

(9.8)

where ω_j is the resonant j-th mode of the blade vibrations.

The total system of nonlinear differential Eq. (9.1) is solved in its integration by the Newmark method (Zienkiewicz 1972). It implies the partition of time T on N steps: Δt = T/N. Then, for each time element 0, Δt, 2Δt, …, T there is an approximate solution considering the solution for the preliminary time value at each half-step:

$$ \left\{ {\begin{array}{*{20}l} {\{ \dot{u}\}_{t + \Delta t} = \{ \dot{u}\}_{t} + \left[ {(1 - \lambda )\{ \dot{u}\}_{t} + \lambda \{ \dot{u}\}_{t + \Delta t} } \right]\Delta t;} \hfill \\ {\{ u\}_{t + \Delta t} = \{ u\}_{t} + \{ \dot{u}\} \Delta t + \left[ {\left( {\frac{1}{2} - \psi } \right)\{ \dot{u}\}_{t} + \psi \{ \ddot{u}\}_{t + \Delta t} } \right]\Delta t,} \hfill \\ \end{array} } \right. $$

(9.9)

where ψ, λ are the parameters defining accuracy and stability of integration.

The next step in solving the problem is harmonic analysis, for which the fast Fourier transformation procedure is used:

$$ u(t) = \sum\limits_{j = 1}^{\infty } {A_{(j)} \cos (\omega_{j} t - \phi_{j} )}, $$

(9.10)

Here A_(j), ω_j, φ_j are the amplitude, frequency and phase shift corresponding to the j-th harmonic of the Fourier transformation.

4 Results of the Computational Experiments

Using the developed FE models, computational investigations were performed to determine the influence of the considered nonlinearities on the characteristics of forced vibrations of the blades of the turbine machine assemblies. The calculations were carried out assuming the first flexural mode of vibrations.

A set of blades was chosen to study the nonlinearity effect due to the contact in the shrouded joint. The blades are made of heat-resistant nickel alloy with the following mechanical characteristics: E = 1.9 × 10¹¹ Pa; ρ = 8570 kg/m³; μ = 0.3. Moreover, it was assumed that the set consists of identical blades. Therefore, only in-phase vibrations are observed during kinematic excitation.

Harmonic displacement Q₀ sin (ωt) of the end elements of the blade airfoil to the plane rotation of the rotor wheel along axis 0y (amplitude Q₀ varied in the range from 0.01 to 0.1 mm) was used to model the kinematic (in-phase) excitation of the blade vibrations. The frequency of the driving force ω varied in the range of the spectrum of natural frequencies of the blade vibrations.

In accordance with the outlined method of calculating forced vibrations, the time dependences of the displacements in node A (see Fig. 9.1a) were obtained. From the results of harmonic analysis of these dependencies, which characterize the steady-state vibration mode, the amplitude-frequency characteristics (AFC) of the set of blades were constructed (see Fig. 9.3). Here, for comparison, the data obtained in the linear setting are also presented.

Fig. 9.3

Amplitude-frequency characteristics of the displacements along axis 0y for nonlinear (solid lines) and linearized (dashed lines) models of the blades

The following conclusions can be drawn:

• 1. The AFC obtained using nonlinear and linearized computational models is practically identical in the in-phase excitation of vibrations of the blades, which is consistent with the data in Larin (2010). However, the level of maximum displacement amplitudes obtained in the linear settlement is 20% lower.

• 2. The excitation frequency, when the maximum displacement amplitude is attained, is 5% lower for the linearized calculation model, which is explained by the system stiffness variation.

Based on the calculations results, the AFC of the blades in the variation of amplitude Q₀ of the kinematic displacement of the root section were determined (see Fig. 9.4).

Fig. 9.4

Amplitude-frequency characteristics of displacements along axis 0y at Q₀ = 0.01 (1), 0.05 (2), 0.07 (3), and 0.1 mm (4)

For a more detailed analysis, the values of the logarithmic decrement of vibrations δ were determined. Figure 9.5 illustrates its dependence on the excitation amplitude Q₀.

Fig. 9.5

Dependence of the logarithmic decrement of vibrations on the excitation amplitude

As seen from the results, with the increase of the excitation amplitude Q₀ within the selected range of its values, there is a linear character of the increase in the amplitude of the displacement of the blades. Here, the level of energy dissipation in the set of blades decreases more than twice with the increase of Q₀ to 0.05 mm; however, at Q₀ ≥ 0.05 mm, it does not change practically. This is due to the significant decrease of the relative displacements of the contact surfaces between the shrouded flanges, which also reduces its efficiency as the structural damper.

Next, consider the results of the calculation experiments on the determination of nonlinearity due to the presence of fatigue crack in the blade airfoil.

The two locations of the crack were investigated: on the suction side and leading edge of the blade airfoil at the height of T = 0.1L (see Fig. 9.2). Its size was 10% of the cross-sectional area of the airfoil. To simplify the numerical calculations, only the blade airfoil was considered.

A titanium alloy with the following technical characteristics was selected as the material of the blade under investigation: E = 1.15 × 10¹¹ Pa; ρ = 4500 kg/m³; μ = 0.3.

The forced vibrations were excited via the harmonic displacement Q₀ sin (ωt) of the end elements along axis 0y, which denotes the first flexural mode of vibrations within the plane of its minimum stiffness. The displacement amplitude was Q₀ = 0.01 mm.

The AFC of the blade airfoil were determined in the presence of open and breathing cracks, which are shown in Fig. 9.6. For comparison, it also illustrates the frequency response of an undamaged airfoil.

Fig. 9.6

Amplitude-frequency characteristics of the blade airfoil with open (○, □) and breathing cracks (•, ■) on the suction side (○, •) and leading edge (□, ■). Dashed line denotes the undamaged airfoil of the blade

Analysis of the data implies an insignificant decrease (less than 1%) in the frequency of vibrations of the blade with cracks, which correspond to the maximum amplitude of vibrations, as compared with the undamaged blade. At the same time, the level of the maximum vibration amplitudes of an undamaged airfoil with an open crack is also almost identical, and for the airfoil with a breathing crack, it is 10% lower. This can be explained by the fact that, due to the complex geometry of the blade airfoil, the crack type affects its stiffness considerably. It can be concluded that the model of an open crack, which does not consider the system nonlinearity, does not allow one to reliably estimate the level of vibrations of the object in question.

5 Conclusions

From the performed experiments, the following conclusions were drawn:

• In the in-phase excitation, the character of the AFC obtained using the nonlinear and linearized calculation models is almost identical. However, here, the difference in the level of the maximum amplitudes is 20%.

• The blade damage in the form of the model with a breathing crack allows one to describe the level of the maximum vibration amplitudes more accurately, as well as their corresponding frequencies, as compared with the model having an open crack. This fact enhances the efficiency of the model for the diagnostics of the presence of fatigue cracks of the blades.