Largest Small n-polygons: Numerical Optimum Estimates for n ≥ 6

Abstract

The diameter of a convex planar polygon is defined as the maximum of the distances measured between all of its vertex pairs. LSP(n), the largest small polygon with n vertices, is the polygon of unit diameter that has maximal area A(n). It has been known for almost a century that for all odd values n ≥ 3, LSP(n) is the regular n-polygon. Perhaps surprisingly, this statement is not valid for even values of n. Finding the polygon LSP(n) and A(n) for even n ≥ 6 has been a long-standing “puzzle” that can be considered as a class of global optimization problems. We present numerical solution estimates for all even values 6 ≤ n ≤ 80, using the AMPL model development environment with the LGO global–local solver engine option. Based on these results, we also present a regression model-based estimate of the optimal area sequence {A(n)}.

1 Introduction

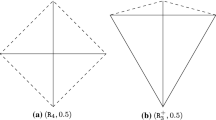
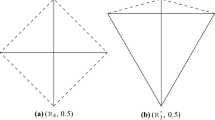
The diameter of a convex planar polygon is defined as the maximum of the distances measured between all of its vertex pairs. In other words, the diameter of the polygon is the length of its longest diagonal. The largest small polygon with n vertices is the polygon of unit diameter that has maximal area. For a given integer n ≥ 3, we will refer to this polygon as LSP(n) with corresponding area A(n). To illustrate, see Fig. 1 that depicts the largest small hexagon LSP(6); in this case, all polygon diagonals are of unit length.

Fig. 1

Largest small hexagon LSP(6)

For unambiguity, we will consider all LSP(n) instances with a fixed position corresponding to appropriate modifications of Fig. 1 for even values n ≥ 6. Specifically, we define a planar Cartesian coordinate system in which the LSP(n) polygons are positioned and express the “height” of each vertex by its coordinate on the vertical axis. Following a standard assumption, each even n-polygon considered here is symmetrical with respect to its diagonal that connects its “lowest” vertex (which is placed at the origin) with its “highest” vertex.

Reinhardt [27] proved that for all odd values n ≥ 3, LSP(n) is the regular n-polygon. Perhaps surprisingly, this statement is not valid for even values of n. For n = 4 (tetragon), the square with diameter 1 has maximum area A(4) = 0.5, but infinitely many other tetragons with diameter 1 have the same area. The case n = 6 (hexagon) was analyzed and solved by Graham [11]; the case n = 8 (octagon) was solved by Audet et al. [2]. More recently, Henrion and Messine [14] found the largest small polygons for n = 10 (decagon) and n = 12 (dodecagon) and for n ≤ 16 presented rigorous bounds for the optimum value. We refer to these studies and cited works therein for theoretical background and for further details regarding the analysis of the problem class {LSP(n)}. We will also review the results obtained by using general-purpose nonlinear optimization software, as reported in [4] and [5]. In addition to the publications cited in our study, we refer to the topical webpages [29,30,31] for concise discussions with further references.

In this work, we follow a numerical global optimization approach, in order to find LSP(n) configurations and corresponding estimated values A(n). Following this introduction, one of the standard optimization model forms is reviewed in Sect. 2. Earlier alternative solution approaches and best-known results are reviewed in Sect. 3. The AMPL model development environment [1] and the AMPL-LGO solver option [22] are briefly discussed in Sect. 4, followed by AMPL-LGO results compared to results by other researchers and using also other solvers (Sect. 5). A regression model based on our numerical results is presented in Sect. 6, together with corresponding optimum estimates {A(n)} for n ≥ 6. Conclusions are presented in Sect. 7, followed by references.

2 A Standard Optimization Model for Finding LSP(n)

Our objective is to find numerically optimized LSP(n) configurations with n ≥ 6 vertices, n being an input parameter of the general model. The model formulation presented here is cited from Bondarenko et al. [4] who refer to Gay’s model [8], discussed also in [9]. The AMPL model pgon.mod [8] refers to a GAMS model developed by Francisco J. Prieto (noting that a more accurate reference to Prieto’s original work is unknown to this author). The corresponding GAMS model library item polygon.gms [7] refers to [8, 11] and the benchmarking study [5].

Following the model formulations referred to above, we consider polar coordinates to describe LSP(n), assuming that vertex i is positioned at polar radius r_i and at angle θ_i. For unambiguity, we assume that the polygon vertices i = 1,…, n–1 are arranged (indexed) according to increasing angles θ_i. Placing the last vertex position at the origin, we have r_n = 0, θ_n = π. Please refer to Fig. 1 for the hexagon instance LSP(6) that corresponds to this standardized position.

2.1 Model Formulation

Maximize total area of the n-polygon:

$$\max \, A\left( n \right) \, = \, {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\sum\limits_{i = 1, \ldots ,n-1} {r_{i} r_{i + 1} } \sin \left( {\theta_{i + 1} - \theta_{i} } \right).$$

(1)

Bounds for pairwise distance between vertices i and j:

$$\begin{array}{*{20}{l}} {r_i^2 + r_j^2 - 2{r_i}{r_j}\cos ({\theta _i} - {\theta _j}) \le 1,} \\ {{\text{for}}\;1 \le i \le n - 2,i + 1 \le j \le n - 1.} \end{array}$$

(2)

Vertex angle ordering relations:

$$\theta _{{i + 1}} - \theta _{i} \ge 0,{\text{ for }}1 \le i \le n - 2.$$

(3)

Decision variable bounds, including the two fixed settings:

$$0 \le \theta_{i} \le \pi \,{\text{and }}0 \le r_{i} \le 1,{\text{ for }}1 \le i \le n{-}1;r_{n} = \, 0,\theta_{n} = \pi .$$

(4)

2.2 Numerical Challenges

Difficulties can be expected to arise, due to the nonconvex objective function (1) and the nonconvex constraints (2). The number of these nonlinear constraints increases quadratically as a function of n. For example, the LSP(80) model instance has 158 decision variables (since r_n and θ_n are fixed) with corresponding bound constraints; and it has 3241 constraints of which 3161 are nonconvex (adding to the 78 linear constraints (3) the two fixed value constraints from (4)). As conjectured by other researchers and numerically supported also by the present study, while the standardized LSP(n) model instances have a unique globally optimal solution, the number of local optima increases with n. Many of the local optima are close in quality to the (unknown or only approximately known) global optimum. These features make the {LSP(n)} problem-class numerically challenging, similarly to many other object configuration design problems arising e.g. in computational physics, chemistry and biology.

3 Related Earlier Studies

3.1 Analytical Approaches

Following Graham [11]—who combines geometric insight with results based on [33]—finding LSP(6) requires the exact solution of a 10th order irreducible polynomial equation. More specifically, the area A(6) of LSP(6) can be found as the second-largest real root r of the equation

$$\begin{aligned} 11993 - 78488r & + {\mkern 1mu} 144464r^{2} + {\mkern 1mu} 1232r^{3} - {\mkern 1mu} 221360r^{4} + {\mkern 1mu} 146496r^{5} \\ & + {\mkern 1mu} 21056r^{6} - {\mkern 1mu} 30848r^{7} - {\mkern 1mu} 3008r^{8} + {\mkern 1mu} 8192r^{9} + {\mkern 1mu} 4096r^{{10}} = {\mkern 1mu} 0. \\ \end{aligned}$$

Audet et al. [2], Henrion and Messine [14] follow a different approach: in their studies finding LSP(n) requires the exact solution of a corresponding nonconvex quadratic programming problem with quadratic constraints, combined with geometric analysis. These solution strategies, based on a different model from the one cited in Sect. 2, also brings the LSP(n) problem-class into the realm of global optimization.

In [14] it is conjectured that LSP(n) for all even values n ≥ 4 has a symmetry axis, as indicated by Fig. 1 for LSP(6). This conjecture was proven by Reinhardt [27] for n = 4, and by Yuan [34] for n = 6. As noted by Henrion and Messine, Graham used this conjecture to find LSP(6); the LSP(8) configuration found in [2] also supports the conjecture. The software packages SeDuMi [28], VSDP [16], and GloptiPoly [12, 13] are used in [14] to solve LSP(n) instances for 6 ≤ n ≤ 16. Henrion and Messine also discuss the current computational limitations of this approach, as runtimes increase rapidly from seconds to tens of minutes in their numerical tests.

Table 1 summarizes all currently known validated numerical results, including also the bounds reported in [14].

Table 1 Numerical results based on analytical approaches

3.2 Numerical Solution Approaches

The COPS technical report [4] by Bondarenko et al. presents comparative numerical results for several LSP(n) instances as shown in Table 2. These results were obtained by using the local nonlinear optimization software packages DONLP2, LANCELOT, LOQO, MINOS, and SNOPT (as of September 1998) linked to the AMPL modeling environment.

Table 2 Numerical results obtained by using local nonlinear optimization software [4, 5]. Best results attained by one of DONLP2, LANCELOT, LOQO, MINOS, SNOPT

Table 2 summarizes the best numerical solution—obtained by at least one of the above listed solvers—cited from the COPS report. The term best refers to the solution which has the highest objective function value, while meeting all model constraints with at least 10⁻⁸ precision. For completeness, we also added results for n = 25, 50, 75, 100 from the subsequent benchmarking study [5] in which LANCELOT, LOQO, MINOS, and SNOPT were tested: again, we cite only the best results.

Mossinghoff [17] also studied the {LSP(n)} problem-class. He describes an approach to search for polygons with an even number of sides n and fixed diameter d (here d = 1), aiming at the largest possible area. The construction is based on optimizing a parameterized polygon model, leading to an apparently difficult numerical problem to handle. For arbitrary even n ≥ 6, Mossinghoff’s construction leads to a polygon, denoted by Q_n which provably has a larger area than that of the regular polygon P_n. Mathematica, by Wolfram Research [32], has been used by Mossinghoff to find Q_n for 6 ≤ n ≤ 20: see Table 3. The required calculations are far from trivial: consult [17] for further details and alternatives. To the author’s knowledge, this approach has not been applied to find Q_n for n > 20. Arguably—and similarly to work performed by other researchers—this is due to the rapidly increasing difficulties to carry out the calculations required.

Table 3 Numerical results reported by Mossinghoff [17]

3.3 The Asymptotic Behaviour of A(n)

According to the optimization model presented in Sect. 2, the numerical solution of LSP(n) instances requires the handling of a nonlinear programming problem with O(n²) nonconvex constraints, and a nonconvex objective function. In spite of the implied difficulty, LSP(n) problems are thought not to become dramatically more difficult to handle as n increases—at least in terms of finding reasonable numerical optimum estimates. This opinion is based on the generally postulated structural similarity and symmetry of the sequence of {LSP(n)} configurations. As noted e.g., in [4], the optimal LSP(n) configurations approach the circle of unit diameter as $n \to \infty$ consult [17] for related asymptotic results. Consequently,

$$A\left( \infty \right) = \lim_{n \to \infty } A\left( n \right) = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4} \sim 0.7853981634.$$

Based on this conjectured structure, in [4, 5] “a polygon with almost equal sides” is used as the initial solution guess in all numerical tests. This approach is implemented in both the AMPL and GAMS model codes referred to earlier. Such solution strategy illustrates the point that, in optimization models good insight and resulting initial solution guess can become a valuable step towards finding credible numerical solutions efficiently. This heuristic approach, however, does not guarantee provable global optimality in many nonconvex models, including the {LSP(n)} model-class discussed here. In spite of such “hand-crafted” initial solutions, the high-quality local nonlinear solvers mentioned above often failed to find solutions, the solutions returned were typically somewhat different, and in a number of cases evidently suboptimal. For further details regarding this point, consult [4, 5], and the results presented later on in Tables 4 and 5.

4 Solving LSP Problems Numerically by AMPL-LGO

4.1 Solution Approach

In this study, we follow a numerical optimization approach, keeping in mind also the cautionary notes presented above. Specifically, using the LGO global–local optimization solver engine linked to the AMPL modeling environment, we present numerical optimum estimates for all even values 6 ≤ n ≤ 80. Our results, presented in Sect. 5, are in close agreement with the best results reported in Tables 1, 2 and 3—when comparable results are available. For comparison, we also report results obtained by using the currently available alternative solver options MINOS [18], SNOPT [10], and IPOPT [15] linked to AMPL.

4.2 The AMPL Model Development Environment

AMPL is a powerful modeling language that facilitates the formulation of optimization models. AMPL enables model development in a natural, concise, and scalable manner. AMPL also supports model analysis, the usage of different data sets for the same model, the seamless invocation of various solver engine options to handle optimization models, together with report generation and many other useful features not discussed here. AMPL has been extensively documented elsewhere: we refer to the AMPL book [6], and to the resources available at the AMPL website [1].

4.3 LGO Solver Suite for Nonlinear Optimization

Nonlinear optimization models frequently have multiple—local and global—optima: the objective of global optimization is to find the best possible solution under such circumstances. LGO is an integrated global–local solver suite for constrained nonlinear optimization. The model-class addressed by LGO is concisely defined by the vector of decision variables x ∈ Rⁿ; the explicit, finite n-vector variable bounds l and u; the continuous objective function f(x); and the (possibly absent) m-vector of continuous constraint functions g(x). Applying these notations, LGO is aimed at numerically solving models of the general form.

$$\min f\left( x \right)\,{\text{subject}}\,{\text{to}}\,x \in D: = \left\{ {l \le x \le u,\,g\left( x \right) \le 0} \right\}.$$

(5)

In (5) all vector inequalities are interpreted component-wise: l, x, u, are n-component vectors and 0 denotes the m-component zero vector. Formally more general optimization models that include also = and constraint relations and/or explicit lower and upper bounds on the constraint function values can be directly deduced to the model form (5). If D is non-empty, then the stated key analytical assumptions guarantee that the optimal solution set X* of the model is non-empty; however, finding X* could still remain a formidable analytical and/or numerical challenge. Clearly, the {LSP(n)} problem-class is encompassed by the optimization model form (5).

Without going into further details regarding LGO, we mention that the foundations of the LGO software development project are discussed by Pintér [19]; further implementation aspects are discussed e.g., in [20, 21]. Here we utilize the LGO solver option available for use with AMPL [22]; the current stand-alone LGO implementation is documented in [23]. In addition to these references, the studies [24, 25] present numerical results using LGO to solve a range of nonlinear optimization problems, from relatively simple standard test problems to well-known challenges. LGO also has been applied to handle a broad range of business, engineering and scientific optimization problems.

5 Numerical Results and Comparisons

5.1 AMPL-LGO Results

In our numerical tests reported here, the AMPL code implementation pgon.mod was used. All test runs were conducted on a several years old laptop PC with Intel Core i5-3337-U CPU @ 1.80 GHz (x-64 processor), 16 Gb RAM, running under the Windows 10 (64-bit) operating system.

The results of a single, completely reproducible run-sequence are summarized in Table 4 for all even values 6 ≤ n ≤ 80, with a single default setting of all solver options, using LGO in global search mode. In several (seemingly more difficult) cases, we received somewhat better numerical results in additional tests, at the expense of longer runtimes: however, for consistency, we did not include those results here. Let us also mention that LGO in its local search mode often found optimum estimates that are numerically identical or close to the global search-based solution, at a fraction of the runtimes reported below. (Recall the related comment from Sect. 3.3.)

The results summarized in Table 4 are directly cited from the AMPL-LGO solver output; the corresponding LSP(n) configurations can be optionally reported in the AMPL command window, and/or written to a result text file. To avoid reporting such excessive details, the optimized configurations found are not presented here. An illustrative collection of detailed results has been kept for documentation and archival purposes, and all results can be reproduced in a few minutes. The reported precision of our numerical results is set to 10 digits after the decimal point. Arguably, this is a bit of “overkill”, but it is in line with the required constraint satisfaction precision as shown below. The results reported also support an in-depth comparison with the results cited earlier, as well as with the results obtained using alternative AMPL solvers (noting that in some cases the differences between the optimum estimates found are rather small).

Table 4 AMPL-LGO numerical results

Our numerical results for n ≤ 20 are in fairly close agreement with the best results displayed in Tables 1, 2 and 3. In several cases, we found somewhat better conjectured optimum estimates compared to the earlier results in Tables 1 and 2; and our results up to n = 20 are in close agreement (up to 8 decimal digits) with those reported by Mossinghoff, see Table 3. The runtimes appear to scale rather well for 6 ≤ n ≤ 80, mostly (but not always) increasing with n. The entire sequence of the 38 optimization runs reported here took a little over 10 min.

Although AMPL-LGO seems to perform reasonably well in comparison to the other solvers tested by us or by others (as reported above), its numerical limitations start to show around n = 64 when used in a pre-set default mode. The results presented in Table 4 for n = 64, 74, and 78 are clearly suboptimal, while all other A(n) values are monotonically increasing with n, as expected. Instead of “tweaking” the LGO option parameters—e.g., by increasing the pre-set global search effort limit (which was actually reached in several cases reported above, for some of the larger n values), or increasing the runtime limit (set to 5 min for each run, but never reached)—here we very simply use linear interpolation to “adjust” the clearly suboptimal results based on the bracketing values in Table 4. For example, A(64) is estimated on the basis of the results obtained for A(62) and A(66). Applying such simple interpolation leads to the following estimated values: $A\left( {64} \right) \sim 0.7845510976,\,A\left( {74} \right) \sim 0.7847519869,\,A\left( {78} \right) \sim 0.7847919330.$

The reason to produce these simple estimates is to use them in Sect. 6, to develop a regression model for the entire sequence A(n).

5.2 An Illustrative Comparison with Results Obtained by Several AMPL Solvers

For a somewhat more comprehensive picture, we also generated a set of comparative results using several currently available AMPL solvers, namely: MINOS, SNOPT, IPOPT, and LGO. All solvers are used with their default settings. We did not include all even values 6 ≤ n ≤ 80, only a representative subset (starting from n = 30, we increased n by 10), since—based on the results obtained—the solver performance tendencies seem rather clear. Table 5 summarizes these numerical results; the LGO results are directly imported from Table 4.

In several cases, MINOS and SNOPT issued interim (runtime) warning messages—while in most runs they report optimal solutions on return—but all runs were properly terminated with the results shown in Table 5. All solvers return close, but slightly different results for n = 6 and n = 8. The first clearly notable difference appears at n = 10, where IPOPT returns a somewhat inferior result compared to the other three solvers.

Table 5 Comparative numerical results obtained by using several AMPL solvers nLSP(n) area A(n)

The numerical limitations of all tested solvers become more apparent as n increases. In several cases, MINOS returns clearly inferior results, and except for small values of n, it produces inferior results that are a few percent below the best solution returned considering all solvers. IPOPT consistently returns somewhat inferior results, but still within a few percent of the best solution returned by at least one of the solvers. SNOPT works well for the considered range of n values, in several cases returning slightly better objective function value estimates than LGO. In the other cases, LGO returns best results, with relatively little difference between LGO and SNOPT results. Let us point out that the constraint satisfaction levels attained by these solvers are a bit different, depending also on the LSP(n) instance solved: therefore, it would be inappropriate to draw far-reaching conclusions based on rather small differences in the reported objective function values.

The LSP model-class clearly poses a challenge to the high-quality solvers tested here. Arguably, the same conclusion remains valid for other solver engines which could not be considered in the present study. To support this statement, consult also [4, 5] for the numerical results included for LSP models.

6 Regression Model Development

Based on the AMPL-LGO numerical results, we present a simple nonlinear regression model that enables the estimation of the optimal area A(n), for all even values of n ≥ 6. Obviously, the same type of regression model could be used to estimate A(n) also for odd values. However, based on the optimality of regular n-polygons [27], one could exactly compute A(n) for all odd values of n.

Given that A(n) is a monotonically increasing function of n, and A(∞) = π/4, the following model form is conjectured for even values n ≥ 6:

$$A\left( n \right) = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4} - {{c_{1} } \mathord{\left/ {\vphantom {{c_{1} } n}} \right. \kern-\nulldelimiterspace} n} - {{c_{2} } \mathord{\left/ {\vphantom {{c_{2} } {n^{2} - {{c_{3} } \mathord{\left/ {\vphantom {{c_{3} } {n^{3} .}}} \right. \kern-\nulldelimiterspace} {n^{3} .}}}}} \right. \kern-\nulldelimiterspace} {n^{2} - {{c_{3} } \mathord{\left/ {\vphantom {{c_{3} } {n^{3} .}}} \right. \kern-\nulldelimiterspace} {n^{3} .}}}}$$

(6)

In (6), the parameters c₁, c₂, c₃ are expected to be positive. To calibrate this model, we use the estimated A(n) 6 ≤ n ≤ 80 values found by AMPL-LGO, substituting the three apparently suboptimal calculated A(n) values by their interpolated approximation as discussed earlier.

The regression model parameters were determined using the NonlinearModelFit function of Mathematica [32]. This leads to the following model, rounding the coefficients to five digits after the decimal point (to reflect the expected model accuracy):

$$A\left( n \right) \sim {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4} - {{0.01098} \mathord{\left/ {\vphantom {{0.01098} {n - {{2.91512} \mathord{\left/ {\vphantom {{2.91512} {n^{2} - {{5.96369} \mathord{\left/ {\vphantom {{5.96369} {n^{3} .}}} \right. \kern-\nulldelimiterspace} {n^{3} .}}}}} \right. \kern-\nulldelimiterspace} {n^{2} - {{5.96369} \mathord{\left/ {\vphantom {{5.96369} {n^{3} .}}} \right. \kern-\nulldelimiterspace} {n^{3} .}}}}}}} \right. \kern-\nulldelimiterspace} {n - {{2.91512} \mathord{\left/ {\vphantom {{2.91512} {n^{2} - {{5.96369} \mathord{\left/ {\vphantom {{5.96369} {n^{3} .}}} \right. \kern-\nulldelimiterspace} {n^{3} .}}}}} \right. \kern-\nulldelimiterspace} {n^{2} - {{5.96369} \mathord{\left/ {\vphantom {{5.96369} {n^{3} .}}} \right. \kern-\nulldelimiterspace} {n^{3} .}}}}}}$$

(7)

Applying this regression model, in Table 6 we present an illustrative set of A(n) estimates vs. the best known numerical results from Tables 1, 2, 3, 4 and 5. All values are rounded to 6-digit precision after the decimal point.

Table 6 Estimated A(n) values based on the regression model (7) vs. best known results

All estimated values shown in Table 6 are in reasonable agreement with the best numerical results presented in Tables 1, 2, 3, 4 and 5 whenever such values are available. The relative difference between the calculated best values and estimated values is less than 10^–4 in all examples included in Table 5, except for n = 30, where the relative difference approximately equals 1.3 · 10^–4.

The calculated optima shown for n = 90, 100, 200, 300, 400 were found using SNOPT. (Due to the current pre-set model size limitations of AMPL-LGO, it could not be used for doing these calculations; and the solvers MINOS and IPOPT were deemed unsuitable due to their inferior performance experienced for smaller n values). The SNOPT runtimes—which were below one second in most cases for n < 100 (reaching about 5 s for n = 100) – increased rapidly when n was sequentially set to 200, 300, and 400. SNOPT was running for more than an hour on the computer mentioned earlier to solve the n = 400 model instance. The entries ??? for n = 500, 1000, 2000 indicate that we did not attempt to calculate these, since none of the solvers used in this study seemed capable to return numerical results within an acceptable timeframe.

Let us point out that while the LSP(100) model-instance has “only” 198 decision variables and 5049 constraints (omitting the prefixed values), the LSP(400) model-instance has 798 variables, and the number of constraints is 80199. It seems clear that solving LSP(n) models directly, for arbitrarily large even values n, is beyond the capability of current (and perhaps also of future) numerical optimization tools. This aspect makes the regression model based estimation approach a simple viable alternative.

Since the data used to develop the regression model (2) are likely to be at least slightly suboptimal, one can expect that—generally speaking—the estimated A(n) values could be also suboptimal. This tendency can be observed in Table 6, but one can see also some exceptions, indicating regression model error and/or optimization inaccuracy.

Let us also note that—for the purpose of developing a regression model—the exact values {A(n)} for odd n could also be used. However, this approach would be based on “mixing” numerically exact and estimated optima, and hence would give less indication of the quality of the numerical solutions found for even values of n. For this reason, we used only the results obtained in the present study, and we did not attempt to find adjusted optimum estimates based on further information.

To support a more complete comparative analysis, first and second order regression models (with 1/n as their input argument) were also calculated, but the third order model (6) clearly resulted in a superior fit to the entire data set used. Obviously, within reason, higher order models (or perhaps other model types) could give even more precise fit to the data, but—considering also the inherent data inaccuracies—the third order model (6) already gives a fairly good fit. Figure 2 displays the model function curve defined by (7) together with the adjusted data set (represented by dots) that includes the interpolated data.

Fig. 2

The nonlinear regression model (7), vs. the adjusted data set A(n) (dots) for 6 ≤ n ≤ 80

Figure 3 displays the regression model residuals. With a few exceptions, the residual errors are less than 1⋅10^–4; the absolute value of the singularly largest estimated error is around 8 · 10^–4. All estimated error values are fairly small, compared to the approximate range [0.674981, 0.784825] of the observed data.

Fig. 3

Residuals (see dots) in the regression model (7) of A(n), for 3 ≤ n ≤ 40

One can observe that most of the residuals seem to follow an interesting cyclical pattern that—in the author’s opinion—seems more due to the inherent structure of the LSP(n) problem-class than to numerical fluctuations and other “noise” induced by the computational environment.

7 Concluding Remarks

In this study, we address the problem of finding numerically the sequence of largest small n-polygons LSP(n) with unit diameter and maximal area A(n). Finding LSP(n) and A(n) for even values of n ≥ 6 has been a long-standing challenge, leading to an interesting class of nonlinear optimization problems with different formulations by a number of researchers.

The structural properties of this problem, and of similar optimization challenges—e.g., atomic structure models, potential energy models, regular object packings, and other problems in which the goal is to find the best configuration of identical objects—often support the proposition of “credible” initial solutions and solution guesses. However, finding the true global solution typically remains difficult, as the cited earlier studies and our present work illustrate.

Using the AMPL modeling environment with the LGO solver option, we present global search based numerical solutions for all even values 6 ≤ n ≤ 80, in a matter of minutes. Our results are comparable to (and in a number of cases are somewhat better than) the best results obtained earlier by other authors and by other solver software options, before our results were produced. Based on the results obtained, we also propose a regression model that enables the simple estimation of the optimal area sequence {A(n)}, for arbitrary integer values of n.

Upon revising the manuscript of this work, it was brought to our attention by a helpful reviewer that a recently posted (September 2020) study [3] presents numerical optimum estimates which are somewhat better for n ≥ 32 than the numerical optimum estimates presented in our work. To illustrate, [3] reports for n = 32 the estimate 0.7821325276 versus our estimate 0.7818946320: the approximate ratio of these values is 0.9996958. To produce the results reported in [3] for a selection of even values n ≤ 128, a different global optimization model was used; MATLAB and CVX serve as the modeling environment, and the MOSEK Optimization Suite was used (with a default precision setting which, without delving into further details, seems to be similar to the numerical feasibility tolerance used in our study).

In response to the above, we point out that [3] cites our numerical results obtained in 2018 (and left unchanged for the present study). We never claimed more than producing credible numerical optimum estimates using off-the-shelf optimization software which returns results in seconds or minutes for the model instances discussed here.

Let us add that in a recently completed study [26] we present numerical results for an illustrative sequence of even values of n, up to n ≤ 1000. Our results are in close agreement with (or surpass) the best results reported in all earlier studies known to us, including the results presented in [3]. For completeness, we also calculated numerically optimized results for a selection of odd values of n, up to n ≤ 999. In this study, we used a tighter model formulation; to handle this model, Mathematica was used with the IPOPT solver option. Following up by corresponding regression models (similarly to our present work), we present numerical solution estimates for the entire LSP model-class.

The motto of the benchmarking studies [4, 5] is, arguably, somewhat provocative and funny, but the message is worth quoting: “COPS: Keeping optimization software honest.” In line with this message, let us conclude with some honest and pragmatic advice, not driven by unconditional “software developer’s pride”. Facing the vast universe of nonlinear optimization problems, it is advisable to refrain from confident blanket statements regarding the superiority of any particular solver software over others. Instead, it is good practice to use a repertoire of appropriate model versions and solver options whenever possible, especially since it may not be obvious a priori which model type or solver engine will work best for a novel or unusually hard optimization challenge.