Keywords

1 Hopf Bifurcation Theorem

The Hopf bifurcation theorem is one of the most famous tools to prove the existence of closed orbits for systems of ordinary differential equations. Consider the following continuous-time system:

$$\displaystyle \begin{aligned} \dot x = f (x, \mu),\, x \in R^n,\, \mu \in R. {} \end{aligned} $$
(5.1)

Assume that the system (5.1) has a fixed point x ∗ at a parameter value μ = μ H;

$$\displaystyle \begin{aligned} f(x^* , \mu_H) = 0. \end{aligned} $$
(5.2)

Furthermore, we assume that the Jacobian matrix evaluated at the fixed point x ∗,

$$\displaystyle \begin{aligned} J & = \begin{bmatrix} \frac{\partial f_1 (x^*; \, \mu)}{\partial x_1} & \frac{\partial f_1 (x^*; \, \mu)}{\partial x_2} & \cdots & \frac{\partial f_1 (x^*; \, \mu)}{\partial x_n} \\ \frac{\partial f_2 (x^*; \, \mu)}{\partial x_1} & \frac{\partial f_2 (x^*; \, \mu)}{\partial x_2} & \cdots & \frac{\partial f_2 (x^*; \, \mu)}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_n (x^*; \, \mu)}{\partial x_1} & \frac{\partial f_n (x^*; \, \mu)}{\partial x_2} & \cdots & \frac{\partial f_n (x^*; \, \mu)}{\partial x_n} \\ \end{bmatrix}, \end{aligned} $$
(5.3)

has a simple pair of pure imaginary eigenvalues and no other eigenvalues with zero real part when μ = μ H. By the implicit function theorem, this assumption implies that there is a fixed point x ∗(μ) near x ∗(μ H) which varies smoothly with μ. Since the Jacobian matrix depends on μ, each eigenvalue of the Jacobian matrix is a function of μ as well. In particular, let us express a simple pair of pure imaginary eigenvalues as a function of μ:

$$\displaystyle \begin{aligned} \lambda (\mu), \bar \lambda (\mu) = \rho (\mu) \pm \omega(\mu) i, \rho (\mu_H) =0, \, \omega (\mu_H) \neq 0, \end{aligned} $$
(5.4)

where Re λ = ρ and Im λ = ω. In the following, the existence part of the Hopf bifurcation is provided.

Theorem 5.1 (Hopf Bifurcation)

Consider the system of ordinary differential equations on an open set U ⊆ R n,

$$\displaystyle \begin{aligned} \dot x = f (x, \mu), {} \end{aligned} $$
(5.5)

where x ∈ U and μ is a real parameter varying in some open interval I ⊆ R. Suppose that for each μ in I there exists an equilibrium point x ∗ = x ∗(μ) of (5.5). Assume that the Jacobian matrix of f with respect to x, evaluated at x ∗(μ), has a pair of complex conjugate eigenvalues, λ(μ) and\( \bar \lambda (\mu ) \) , which satisfy the following (transversality conditions of the Hopf bifurcation):

$$\displaystyle \begin{aligned} \mathrm{(H1)} \,\,\, \mathrm{Re} \, \lambda (\mu_H) =0,\,\, \mathrm{Im} \, \lambda (\mu_H) \neq 0, \end{aligned}$$
$$\displaystyle \begin{aligned} \mathrm{(H2)} \,\,\, \left. \frac{d \, \mathrm{Re} \, \lambda (\mu)}{d \mu} \right|{}_{\mu = \mu_H} \neq 0, \end{aligned}$$

while Re γ(μ H) ≠ 0 for any other eigenvalues γ. Then, (5.5) has a family of non-constant, periodic solutions.

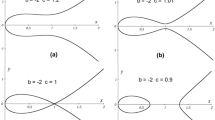
The important point to note is that there are two types of Hopf bifurcations: a supercritical Hopf bifurcation and a subcritical Hopf bifurcation. In the supercritical case, we observe a stable limit cycle around the unstable equilibrium point as μ passes through the bifurcation value μ = μ H. From the economic point of view, this case is desirable in the sense that the stable limit cycle can be considered as the representation of the actual economic fluctuations in the theory of the business cycle. This situation is shown in Fig. 5.1a, where we can detect an unstable equilibrium point E and a stable limit cycle. On the other hand, in the subcritical case, we notice an unstable limit cycle around a stable equilibrium point as μ passes through the bifurcation value μ = μ H. In this case, we cannot observe the same persistent and bounded cycles as in the supercritical Hopf bifurcation. However, this case is also important and interesting from an economic point of view. It is well known that Leijonhufvud [11] suggested the concept of “corridor stability,” which states that sufficiently large shocks advance the working of centrifugal forces in the economy, while small shocks have no persistent effects on the economy. His concept of corridor stability corresponds to the subcritical Hopf bifurcation. This circumstance is depicted in Fig. 5.1b, where we can find a stable equilibrium point E and an unstable limit cycle.

Fig. 5.1
figure 1

Two types of Hopf bifurcations. Panel (a) on the left displays a supercritical bifurcation; panel (b) on the right displays a subcritical bifurcation

Full size image

Let us now turn to another important point regarding the Hopf bifurcations. As stated above, the Hopf bifurcation theorem is explained in terms of the properties of eigenvalues. For theoretical investigations, it is useful to rewrite the conditions of eigenvalues by using the coefficients of characteristic equations. From now on, we shall deal with two-, three-, and four-dimensional systems in order.

Two-dimensional System

In the case of a two-dimensional system, the Jacobian matrix is a 2 × 2 matrix.

Theorem 5.2

The second-order polynomial equation

$$\displaystyle \begin{aligned} P(\lambda) = \lambda^2 + b_1 \lambda + b_2 = 0 \end{aligned} $$
(5.6)

has a pair of pure imaginary roots if and only if

$$\displaystyle \begin{aligned} b_1=0,\,\, b_2>0. \end{aligned} $$
(5.7)

Remark

In this case, we can easily verify that \(\lambda _{1,2} = \pm \sqrt {b_2} i\).

Three-dimensional System

When we consider the case of a three-dimensional system, the Jacobian matrix is a 3 × 3 matrix.

Theorem 5.3

The third-order polynomial equation

$$\displaystyle \begin{aligned} P(\lambda) = \lambda^3 + b_1 \lambda^2 + b_2 \lambda + b_3 = 0 \end{aligned} $$
(5.8)

has a pair of pure imaginary roots and one non-zero real root if and only if

$$\displaystyle \begin{aligned} b_2>0,\,\, b_1 b_2 -b_3=0. \end{aligned} $$
(5.9)

Remark

See Asada and Semmler [2] for a complete discussion.

Four-dimensional System

In the case of a four-dimensional system, we have the Jacobian matrix with a dimension of 4×4.

Theorem 5.4

The fourth-order polynomial equation

$$\displaystyle \begin{aligned} P(\lambda) = \lambda^4 + b_1 \lambda^3 + b_2 \lambda^2 + b_3 \lambda + b_4 = 0 \end{aligned} $$
(5.10)

has a pair of pure imaginary roots and two roots with non-zero real parts if and only if either of the following set of conditions (A) or (B) is satisfied:

$$\displaystyle \begin{aligned} \mathrm{(A)} \,\, b_1 b_3 > 0,\,\, b_4 \neq 0,\,\, \varDelta_3 = b_1 b_2 b_3 - {b_3}^2 - {b_1}^2 b_4 =0. \end{aligned} $$
(5.11)
$$\displaystyle \begin{aligned} \mathrm{(B)} \,\, b_1 = 0,\,\, b_3 = 0,\,\, b_4 < 0. \end{aligned} $$
(5.12)

Remark

See Asada and Yoshida [3] for a complete discussion.

Furthermore, we shall draw our attention to the result of Liu [12]. He developed an elegant criterion for a class of Hopf bifurcations by restricting his analysis to “simple” Hopf bifurcations, where all the eigenvalues except a pair of purely imaginary ones have negative real parts. For this reason, he could obtain a useful criterion from the Routh–Hurwitz condition, which gives the necessary and sufficient condition for all the eigenvalues of an nth-order characteristic equation to have negative real parts. In this case, we consider the following theorem:

Theorem 5.5

The characteristic equation

$$\displaystyle \begin{aligned} P(\lambda) = \lambda^n + b_1 \lambda^{n-1} + b_2 \lambda^{n-2} + \cdots + b_{n-1} \lambda + b_n = 0 \end{aligned} $$
(5.13)

has a pair of pure imaginary roots and (n − 2) roots with negative real parts if and only if

$$\displaystyle \begin{aligned} \varDelta_1 = b_1>0, \varDelta_2 &= \begin{vmatrix} b_1 & b_3 \\ 1 & b_2 \\ \end{vmatrix}>0, \,\, \varDelta_3 = \begin{vmatrix} b_1 & b_3 & b_5 \\ 1 & b_2 & b_4 \\ 0 & b_1 & b_3 \\ \end{vmatrix}>0, \ldots, \\ \varDelta_{n-1} &= \begin{vmatrix} b_1 & b_3 & b_5 & b_7 & \cdots & 0 & 0 \\ 1 & b_2 & b_4 & b_6 &\cdots & 0 & 0 \\ 0 & b_1 & b_3 & b_5 &\cdots & 0 & 0 \\ 0 & 1 & b_2 & b_4 &\cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 &\cdots & b_n & 0 \\ 0 & 0 & 0 & 0 &\cdots & b_{n-1} & 0 \\ 0 & 0 & 0 & 0 &\cdots & b_{n-2} & b_n \\ 0 & 0 & 0 & 0 &\cdots & b_{n-3} & b_{n-1} \\ \end{vmatrix}=0,\,\, b_n>0. \end{aligned} $$
(5.14)

Let us note, finally, that the condition (H2) of the Hopf bifurcation theorem is also an important factor when we apply this theorem to nonlinear systems of differential equations. This condition states that the real part of a pair of complex eigenvalues is not stationary with respect to the parameter value μ at μ = μ H. Fortunately, this condition is equivalent to

$$\displaystyle \begin{aligned} \left. \frac{\varDelta_{n-1} (\mu)}{d\mu} \right|{}_{\mu = \mu_H} \neq 0. \end{aligned} $$
(5.15)

Notice that Δ n−1 is a function of μ since every b i is a function of μ. For a complete proof of this statement, see Liu [12].

2 Two Specific Examples: Lorenz and Rössler Systems

Lorenz was a pioneer in deterministic chaos. In his paper, Lorenz [13] discovered that nonperiodic solutions could emerge in a nonlinear system of ordinary differential equations. In particular, he realized that small changes in initial conditions cause large changes in long-term outcome in his model, showing the SDIC we introduced in Definition 6.4 necessary to have a strange attractor.

The Lorenz system is a system of three differential equations as follows:

$$\displaystyle \begin{aligned} \dot x = - \sigma x + \sigma y, \end{aligned} $$
(5.16a)
$$\displaystyle \begin{aligned} \dot y = r x - y -x z, \end{aligned} $$
(5.16b)
$$\displaystyle \begin{aligned} \dot z = x y - \beta z, \end{aligned} $$
(5.16c)

where σ, r, and β are parameters. This system is algebraically simple: the right-hand side of these equations has two nonlinear terms (xz and xy). However, contrary to common sense at that time, the system produces a complex and strange behaviour as shown in Fig. 5.2. In this case, we set the parameter values as (σ, r, β) = (10, 28, 3∕8). In addition, it should be noted that we can observe various types of dynamic behaviours, depending on the parameter values. For other values, the system yields stable equilibrium points, stable limit cycles, period-doubling bifurcations, and so on.Footnote 1

Fig. 5.2
figure 2

Lorenz attractor. (a) Three-dimensional phase space. (b) Projection on the x–y plane

Full size image

The Rösller system is also a well-known system that produces chaotic motions in continuous time. Rössler [17] investigated the following system:

$$\displaystyle \begin{aligned} \dot x = - y - z, \end{aligned} $$
(5.17a)
$$\displaystyle \begin{aligned} \dot y = x + a y, \end{aligned} $$
(5.17b)
$$\displaystyle \begin{aligned} \dot z = b + z (x-c), \end{aligned} $$
(5.17c)

where a, b, and c are parameters. Note that, in comparison with the Lorenz system, the Rössler system has a simplified structure in that it takes a single quadratic nonlinearity (xz) on the right-hand side of (5.17). When (a, b, c) = (0.1, 0.3, 12), we can obtain the typical Rössler attractor, which is shown in Fig. 5.3. Depending on the parameter values, the system yields a stable equilibrium point or a stable limit cycle. Moreover, we can see period-doubling bifurcations when a specific parameter is varied.

Fig. 5.3
figure 3

Rössler attractor. (a) Three-dimensional phase space. (b) Projection on the x–y plane

Full size image

Immediate applications of the Lorenz and Rössler systems are rare in economic dynamics. An interesting and valuable exception is Goodwin [8]. He developed his own insight into modern capitalist economies by combining the ideas of Keynes, Marx, and Schumpeter and proposed several models in his book. For example, he examined the following system:

$$\displaystyle \begin{aligned} \dot v = -0.5 u + 0.15 v -0.3 z, \end{aligned} $$
(5.18a)
$$\displaystyle \begin{aligned} \dot u = 0.5v, \end{aligned} $$
(5.18b)
$$\displaystyle \begin{aligned} \dot z = 0.01 + 85 z (v-0.05). {} \end{aligned} $$
(5.18c)

Figure 5.4 shows the emergence of a chaotic attractor in the Goodwin model. We can say with fairly certainty that this system is a modified Rössler model. This is because the Goodwin model has the same quadratic term (zv) in the right-hand side of (5.18c) as in the Rössler system. Owing to this similarity, the chaotic attractor in the Goodwin system is very similar to the Rössler attractor.

Fig. 5.4
figure 4

Chaos in the Goodwin model. (a) Three-dimensional phase space. (b) Projection on the v–u plane

Full size image

3 Shilnikov’s Theorem

Numerous efforts have been made to investigate the chaotic behaviour of nonlinear dynamical systems of ordinary differential equations from the analytical point of view. The most famous transition from order to chaos is the Feigenbaum cascade, or period doubling cascade, that we have analysed in Chap. 2. Among them, it is worthwhile to take a brief look at the Shilnikov theorem.

Theorem 5.6 (The Shilnikov Theorem)

Consider the system

$$\displaystyle \begin{aligned} \dot x = \rho x - \omega y + P(x, y, z), \end{aligned} $$
(5.19a)
$$\displaystyle \begin{aligned} \dot y = \omega x + \rho y + Q(x,y,z), \end{aligned} $$
(5.19b)
$$\displaystyle \begin{aligned} \dot z = \lambda z + R(x,y,z), \end{aligned} $$
(5.19c)

where P, Q, and R vanish together with their first derivatives at the equilibrium point E = (x ∗, y ∗, z ∗). Let us assume that one of the orbits, denoted by Γ 0 , is asymptotic to E as t →±∞, being bounded away from any other singularity (Γ 0is then a homoclinic connection). Then, if

$$\displaystyle \begin{aligned} | \lambda | > | \rho | >0,\,\, \lambda \rho <0, \end{aligned} $$
(5.20)

every neighbourhood of the orbit Γ 0 contains a countable set of unstable periodic solutions of saddle type.

From (5.20), there are two essential conditions for the application of the Shilnikov theorem. For the time being, we consider the case of λ > 0. First, the system has a saddle-node equilibrium point, which means the existence of a one-dimensional unstable manifold and a two-dimensional stable manifold. This condition is easily examined from the local point of view. Second, the system has a homoclinic orbit, which connects an equilibrium point E to itself; limt→±∞ Γ(t) = E and Γ(0) ≠ E. This condition prescribes a global nature of the system. The combination of these two conditions implies topological conjugacy in a neighbourhood of the homoclinic orbit with the horseshoe dynamics that we introduced in Sect. 6.2.1.

A graphical presentation of the Shilnikov conditions is shown in Fig. 5.5. After moving away from the equilibrium point E along the one-dimensional unstable manifold, the trajectory Γ 0 returns to the identical equilibrium point on the two-dimensional stable manifold.Footnote 2

Fig. 5.5
figure 5

Homoclinic orbit in the Shilnikov scenario

Full size image

As a numerical example of the occurrence of chaos in the Shilnikov scenario, consider the following system of three differential equations:

$$\displaystyle \begin{aligned} \dot x = y, \end{aligned} $$
(5.21a)
$$\displaystyle \begin{aligned} \dot y = -x + y z, \end{aligned} $$
(5.21b)
$$\displaystyle \begin{aligned} \dot z = - z + x y +0.39, \end{aligned} $$
(5.21c)

which was reported in Sprott [23]. This system has a saddle-node equilibrium at point (0, 0, 0.39), with eigenvalues λ 1 = −1 and λ 2,3 = 0.195 ± 0.980803i. This implies that the system satisfies the local conditions of the Shilnikov theorem: |λ| > |ρ| > 0 and λρ < 0. As it is difficult to detect the existence of a homoclinic orbit from an analytical point of view, we show the numerical simulations of the initial value problem given by system (5.21). By setting the initial conditions as (x(0), y(0), z(0)) = (0.1, 0.1, 0.3), we can verify that the system displays a chaotic motion as shown in Fig. 5.6.

Fig. 5.6
figure 6

The chaotic attractor of system (5.21). (a) Three-dimensional phase space. (b) Projection on the x–y plane

Full size image

Macroeconomic applications of the Shilnikov theorem can be found in several works. Lorenz [14] investigated two macroeconomic models. One is a business cycle model with inventories; another is a linear multiplier-accelerator model with nonlinear government activity. Sportelli [22] developed a Harrodian-type macrodynamic model by considering the interactions among the actual rate of growth, the warranted rate of growth, and the fraction of income saved. Tsuzuki et al. [24] proposed an investment model and, finally, Bella et al. [4] examined the dynamics of an endogenous growth model with human capital accumulation in the dynamic optimization framework.

4 Delay-Differential Equations

This section considers two nonlinear systems of delay-differential equations investigated using numerical simulations: the Mackey–Glass system [16] and the Shibata–Saito system [18]. While the former investigated a physiological problem, the latter examined the population dynamics of two competing species with a time-delayed saturation.

It is well known that deterministic chaos occurs in the continuous-time framework only when the dimension of the dynamical system is equal to or more than three. That is, we cannot observe chaotic motions in one- and two-dimensional systems of autonomous ordinary differential equations (cf. Sect. 2.4).

If once we turn our attention towards delay-differential equations, the situation is completely different. We can observe chaotic fluctuations in the delay-differential equation with one variable. In fact, Mackey and Glass [16] provided an interesting model by using the following system:

$$\displaystyle \begin{aligned} \dot x(t) = \frac{ a x (t-\tau) }{1 + x^n (t-\tau) } - \gamma x(t), {} \end{aligned} $$
(5.22)

where a > 0, τ > 0, and γ > 0. Figure 5.7 shows chaotic motion of (5.22) with a = 3.6, τ = 1, n = 10, and γ = 2.

Fig. 5.7
figure 7

Chaotic motion of the Mackey–Glass system. (a) Time series. (b) Phase plot

Full size image

The main reason for the emergence of chaotic fluctuations is that the Mackey–Glass system has an infinite dimension. Its solution space has an infinite dimension, with a continuous function on the closed interval [−τ, 0] as the initial condition. Roughly speaking, we need an infinite number of initial conditions to solve the initial value problem of (5.22).

We shall now consider the following system of integro-differential equations:

$$\displaystyle \begin{aligned} \dot x(t) = \frac{ a y_m (t) }{1 + [y_m (t)]^n } - \gamma x(t), {} \end{aligned} $$
(5.23)

where

$$\displaystyle \begin{aligned} y_m (t) = \int_{-\infty}^t \omega(s) x (s) ds, \end{aligned} $$
(5.24)
$$\displaystyle \begin{aligned} \omega(s) = \left( \frac{m}{\tau}\right)^m \frac{(t-s)^{m-1}}{(m-1)!}e^{-(m/\tau) (t-s)},\, \tau>0. \end{aligned} $$
(5.25)

Note that m is a positive integer. Since \(\int _{-\infty }^t \omega (s) ds = 1\), we can see that the function ω(s) is a weighting function, which is identical with a density function with the mean,τ, and the variance, τ 2∕m.

If m = 1, it is the exponential distribution. For m ≥ 2, the functional shape of ω(s) has a one-humped curve with a maximum value at s = t − (m − 1)τ∕m when t is fixed. Moreover, we can obtain y m(t) = x(t − τ) if m →∞. This is because the function ω(s) becomes the Dirac delta function that appears as a sharp peak at t = τ when m →∞. Thus, we reasonably conclude that system (5.23) is equivalent to the Mackey–Glass system (5.22) when m →∞.

We shall now look at another subject related to the Mackey–Glass system. Here, we seek to transform the Mackey–Glass system into the tractable system by using MacDonald’s linear chain trick.Footnote 3 Let us define new variables:

$$\displaystyle \begin{aligned} y_j (t) = \int_{-\infty}^t \left( \frac{m}{\tau}\right)^j \, \frac{(t-s)^{j-1}}{(j-1)!}e^{-(m/\tau) (t-s)} x(s) ds,\,\, j=1, 2, \dots, m. {} \end{aligned} $$
(5.26)

By differentiating (5.26) with respect to t and using (5.23), we obtain the following system of ordinary differential equations:

$$\displaystyle \begin{aligned} \dot x(t) = \frac{ a y_m (t) }{1 + [y_m (t)]^n } - \gamma x(t), \end{aligned} $$
(5.27a)
$$\displaystyle \begin{aligned} \dot y_1 (t) = (m/ \tau)[x(t) - y_1(t)], \end{aligned} $$
(5.27b)
$$\displaystyle \begin{aligned} \dot y_j (t) = (m/ \tau)[y_{j-1}(t) - y_j(t)], \,\, j = 2, 3, \dots, m.\end{aligned} $$
(5.27c)

Consequently, this result means that we can transform the Mackey–Glass system into the system of (m + 1)-dimensional ordinary differential equations. In the course of the above argument, we arrive at the conclusion that the Mackey–Glass system corresponds to the system of infinite-dimensional ordinary differential equations by means of MacDonald’s chain trick. This property is fundamental for the generation of complex dynamics.

By using computational approaches, Farmer [7] extensively examined the properties of the chaotic attractors observed in the Mackey–Glass system. Specifically, he studied the time series, power spectra, the dimension of chaotic attractors, the spectrum of Lyapunov exponents, and so forth. In his paper, he kept the parameters a, n, and γ fixed at a = 0.2, n = 10, and γ = 0.1. On the other hand, the delay time τ is a variable parameter. For example, when τ = 17, he found that the largest Lyapunov exponent of the chaotic attractor is 0.007 and the fractal dimension is 2.13.Footnote 4

Finally, we turn to the Shibata and Saitô system, and we consider the dynamics of the system of delay-differential equations with two variables. Shibata and Saitô [18] investigated the following system:

$$\displaystyle \begin{aligned} \dot x (t) = [\varepsilon_1 -a_{11} x (t- \alpha_1) - a_{12} y (t) ] x (t), \end{aligned} $$
(5.28a)
$$\displaystyle \begin{aligned} \dot y (t) = [\varepsilon_2 -a_{21} x (t) - a_{22} y ( t - \alpha_2 ) ] y (t). \end{aligned} $$
(5.28b)

By setting a 11 = a 22 = 2, a 12 = a 21 = 1, ε 1 = ε 2 = 2, τ 1 = 1.5, and τ 2 = 0.9 for the parameters, we obtain Fig. 5.8, which shows the emergence of a chaotic attractor.

Fig. 5.8
figure 8

Chaotic attractor of the Shibata–Saitô system

Full size image

The analysis of time lags is fundamental for economics. In particular, the existence of time lags involved in the policy process has a large effect on macroeconomic stability, from both the practical and theoretical points of view. Many economists found the occurrence of complex business cycles by means of numerical simulations. For more information, see Fanti and Manfredi [6], Yoshida and Asada [25], and De Cesare and Sportelli [5].