Non-smooth Bifurcations

Abstract

In this chapter we will be interested in bifurcations that result from two “non-smooth” phenomena:

• perturbations in the sequence of impulses and

• crossings of discrete delays across impulse times.

1 Overview

In this chapter we will be interested in bifurcations that result from two “non-smooth” phenomena:

• perturbations in the sequence of impulses and

• crossings of discrete delays across impulse times.

These two situations have some elements in common, but the second of the two will typically involve explicit breaking of the overlap condition and will result in highly non-smooth bifurcations . A bifurcation involving this type of scenario will broadly be called an overlap bifurcation. The first one is slightly better behaved, and the lack of smoothness is more of a technical issue.

1.1 Bifurcations Involving Perturbations of Impulse Times

Consider the Hutchinson equation with impulsive harvesting:

$$\displaystyle \begin{aligned} \dot x&=rx(t)\left(1-\frac{x(t-\tau)}{K}\right),&t&\neq kT\\ \varDelta x&=-hx(t^-),&t&=kT, \end{aligned} $$

for $k\in \mathbb {Z}$. We will revisit this system in Chapter 2. The linearization at x = 0 has only the Floquet multipliers 0 and μ = (1 − h)e ^rT. Since x = 0 is a fixed point for all parameter values, it is reasonable to suspect that a transcritical bifurcation could occur as T crosses through the threshold period

$$\displaystyle \begin{aligned}T^*=-\frac{1}{r}\log(1-h),\end{aligned}$$

since μ = 1 when T = T ^∗. Our previous framework for parameter-dependent centre manifolds is based on taking the parameter as an additional state and in the impulses must occur at fixed times. The required transformations are therefore first a rescaling of time to map the impulses onto the integers, followed by the introduction of the new state, T. After this is completed, we get the system

$$\displaystyle \begin{aligned} \dot x&=rTx(t)\left(1-\frac{x(t-\tau/T)}{K}\right),&t&\notin\mathbb{Z}\\ \dot T&=0,&t&\notin\mathbb{Z}\\ \varDelta x&=-hx(t^-),&t&\in\mathbb{Z}\\ \varDelta T&=0,&t&\in\mathbb{Z}. \end{aligned} $$

The problem with the above system is that it contains a state-dependent delay (τ∕T). The functional that defines the vector field is not smooth in any open subset of the extended state space, so our centre manifold theory does not apply. In Sect. III.2.2 we will give one method that allows this type of non-smooth formulation to be avoided while still providing a reasonable centre manifold theory.

Remark III.2.1.1

For further justification as to why varying the period of impulse effect in an impulsive functional differential equation results in a non-smooth perturbation, consider the scalar equation without delays

$$\displaystyle \begin{aligned} \dot x&=0,&t&\neq kT\\ \varDelta x&=x,&t&=kT, \end{aligned} $$

for T ∈ (0, 2), but with the phase space $\mathcal {R}\mathcal {C}\mathcal {R}([-2,0],\mathbb {R})$. The solution from the constant initial condition x ₀ = 1 satisfies

$$\displaystyle \begin{aligned}x_t(\theta,T)=\left\{\begin{array}{ll}2^{\left\lfloor(t+\theta)/T\right\rfloor},&t+\theta>0 \\ 1 & t+\theta\leq 0, \end{array}\right.\end{aligned}$$

where we have included T as a function input to emphasize its dependence on the solution. Then for all T ∈ (0, 2), we can write

$$\displaystyle \begin{aligned}x_2(\theta,T)=2^{\lfloor(2+\theta)/T\rfloor}.\end{aligned}$$

This function (of θ) is piecewise-constant with discontinuities at $\theta \in T\mathbb {Z}-2$. Since the location of these discontinuities depends on T, the function T↦x ₂(⋅, T) is not continuous as a function from (−2, 0) into $\mathcal {R}\mathcal {C}\mathcal {R}([-2,0],\mathbb {R})$. In fact, one can show that ||x ₂(⋅, T ₁) − x ₂(⋅, T ₂)||≥ 1 whenever T ₁ ≠ T ₂. In other words, the solutions of an impulsive functional differential equation are generally not continuous (in the phase space $\mathcal {R}\mathcal {C}\mathcal {R}$) with respect to the impulse times, even for fixed initial conditions.

1.2 Bifurcations Involving Crossings of Impulse Times and Delays

The second phenomenon is most easily motivated with the following toy example:

$$\displaystyle \begin{aligned}\dot x&=\log\left(\frac{3}{2}\right)x,&t&\notin\mathbb{Z} \end{aligned} $$

(III.2.1)

$$\displaystyle \begin{aligned}\varDelta x&=-\frac{1}{2}x(t^-) + \frac{1}{4}x_{t^-}(-\omega),&t&\in\mathbb{Z}, \end{aligned} $$

(III.2.2)

where ω ∈ [0, Ω] is a real parameter. The state space is taken to be $\mathcal {R}\mathcal {C}\mathcal {R}([-\varOmega ,$ $0],\mathbb {R})$. This scalar equation essentially has a delayed jump of the form

$$\displaystyle \begin{aligned}\varDelta x=\left\{\begin{array}{ll}-\frac{1}{2}x(t^-) + \frac{1}{4}x(t-\omega), &\omega>0 \\ -\frac{1}{2}x(t^-)+\frac{1}{4}x(t^-),&\omega=0. \end{array}\right.\end{aligned}$$

When ω ∈ [0, 1], the situation is fairly simple. If we take x(t) = ϕ(t)e ^λt as a Floquet eigensolution ansatz, ϕ is a periodic solution (of period one) satisfying

$$\displaystyle \begin{aligned} \dot\phi&=\left(\log \left(\frac{3}{2}\right)-\lambda\right)\phi,&t&\notin\mathbb{Z}\\ \varDelta\phi&=-\frac{1}{2}\phi(t^-)+\frac{1}{4}e^{-\lambda\omega}\phi_{t^-}(-\omega),&t&\in\mathbb{Z}. \end{aligned} $$

Since ω ∈ [0, 1], this equation can be explicitly solved with little effort. We find

$$\displaystyle \begin{aligned} \phi(1)&=\frac{1}{2}e^{\log(3/2)-\lambda}\phi(0) + \frac{1}{4}e^{-\lambda\omega}e^{(\log(3/2)-\lambda)(1-\omega)}\phi(0)\\ &=e^{-\lambda}\left(\frac{3}{4} + \frac{1}{4}\left(\frac{3}{2}\right)^{1-\omega}\right)\phi_0 \end{aligned} $$

for each of the cases ω = 0, ω ∈ (0, 1) and ω = 1. It follows that ϕ is periodic if and only if μ = e ^λ satisfies

$$\displaystyle \begin{aligned}\mu(\omega)=\frac{1}{4}\left(3 + 1\left(\frac{3}{2}\right)^{1-\omega}\right). \end{aligned}$$

Suppose $\omega =1+\widehat \omega$ for some $\widehat \omega \in (0,1)$. Taking a Floquet ansatz again, this time the function ϕ satisfies

$$\displaystyle \begin{aligned} \dot\phi&=\left(\log \left(\frac{3}{2}\right)-\lambda\right)\phi,&t&\notin\mathbb{Z}\\ \varDelta\phi&=-\frac{1}{2}\phi(t^-)+\frac{1}{4}e^{-\lambda(1+\widehat\omega)}\phi_{t^-}(-\widehat\omega),&t&\in\mathbb{Z}. \end{aligned} $$

We can yet again solve this impulsive differential equation explicitly, and we find

$$\displaystyle \begin{aligned} \phi(1)&=\frac{1}{2}e^{\log(3/2)-\lambda}\phi(0) + \frac{1}{4}e^{-\lambda\omega}e^{(\log(3/2)-\lambda)(2-\omega)}\phi(0)\\ &=\left(e^{-\lambda}\frac{3}{4} + e^{-2\lambda}\frac{1}{4}\left(\frac{3}{2}\right)^{2-\omega} \right)\phi_0. \end{aligned} $$

In order for ϕ to be periodic, μ = e ^λ must solve the equation

$$\displaystyle \begin{aligned}\mu^2-\frac{3}{4}\mu - \frac{1}{4}\left(\frac{3}{2}\right)^{2-\omega}=0.\end{aligned}$$

This equation has two solutions, and they coincide with the nontrivial Floquet multipliers. Combining the result from the previous section, it follows that the nontrivial Floquet multipliers are

$$\displaystyle \begin{aligned}\mu(\omega) = \left\{\begin{array}{ll} \frac{1}{4}\left(3 + 1\left(\frac{3}{2}\right)^{1-\omega}\right),&\omega\in[0,1]\\ \frac{3}{8}\left(1\pm 3^{-\omega}\sqrt{3^\omega(2^{2+\omega}+3^\omega)}\right),&\omega\in(1,2) . \end{array}\right.\end{aligned}$$

Notably, μ(1) = 1, but $\mu (1^+)=\frac {3}{8}\pm \frac {1}{8}\sqrt {33} \approx \{1.093,-0.343\}$, so, in particular, the function ω↦max|μ(ω)| is discontinuous. If (III.2.1) and (III.2.2) correspond to the linearization of a particular nonlinear system at some equilibrium, a bifurcation could occur in the “smooth” regime ω → 1⁻, while crossing over into ω > 1 could completely destroy the local orbit structure. For example, consider the nonlinear system

$$\displaystyle \begin{aligned}\dot x&=\log\left(\frac{3}{2}\right)x-\frac{1}{10}x^2,&t&\notin\mathbb{Z} \end{aligned} $$

(III.2.3)

$$\displaystyle \begin{aligned}\varDelta x&=-\frac{1}{2}x(t^-) + \frac{1}{4}x_{t^-}(-\omega),&t&\in\mathbb{Z}. \end{aligned} $$

(III.2.4)

For ω ∈ (0, 1], the nontrivial Floquet multiplier is decreasing, there is a quadratic nonlinearity and x = 0 is a fixed point. It is therefore reasonable to suspect that a transcritical bifurcation might occur as ω → 1⁻. However, the fixed point x = 0 is not a bifurcation point as ω → 1⁺ since the Floquet multipliers are bounded away from 1 in absolute value. We will study the above nonlinear example in a bit more depth in Sect. III.2.3.

Roughly speaking, an overlap bifurcation is the resulting change in the orbit structure whenever a system parameter is varied causing the overlap condition to be violated. We will study some particular overlap bifurcation scenarios in Sect. III.2.3 by focusing on systems with delayed impulses, since these are slightly more amenable to analysis.

2 Centre Manifolds Parameterized by Impulse Times

In this section we consider a class of time-invariant delay differential equation systems undergoing impulses at a specific frequency $\frac {1}{p}$:

$$\displaystyle \begin{aligned} \dot x&=LSx_t+f(x_t),&t&\neq kp\\ \varDelta x&=BSx_{t^-}+g(x_{t^-}),&t&=kp, \end{aligned} $$

(III.2.5)

for $k\in \mathbb {Z}$. The following hypotheses will be needed:

• F.1 L and B are n × m matrices, and $S:\mathcal {R}\mathcal {C}\mathcal {R}([-r,0],\mathbb {R}^n)\rightarrow \mathbb {R}^m$ is a bounded linear operator possessing a representation of the form $S\phi =\int _{-r}^0 [d\eta (\theta )]\phi (\theta )$ with $\eta :[-r,0]\rightarrow \mathbb {R}^{m\times n}$ of bounded variation and right-continuous.

• F.2 There exists $p^*\in \mathbb {R}$ such that the periodic linear system

  $$\displaystyle \begin{aligned} \dot y&=LSx_t,&t&\neq kp^*,\\ \varDelta y&=BSx_{t^-},&t&=kp^* \end{aligned} $$

  has exactly d > 0 Floquet multipliers μ ₁, …, μ _d satisfying |μ ₁| = ⋯ = |μ _d| = 1, while all other Floquet multipliers μ _j satisfy |μ _j|≠ 1. Also, r < p ^∗ < r ^∗ for some r ^∗.

• F.3 There exist Z ₁(p), $Z_2(p)\in \mathbb {R}^{n\times m}$ defined in a neighbourhood of p ^∗ with the following properties:

  • Z ₁(p ^∗) = L, Z ₂(p ^∗) = B.

  • Z ₁ and Z ₂ are continuous.

  • For each p, the periodic linear system

    $$\displaystyle \begin{aligned} \dot y&=Z_1(p)Sx_t,&t&\neq kp,\\ \varDelta y&=Z_2(p)Sx_{t^-},&t&=kp \end{aligned} $$

    (III.2.6)

    has exactly d > 0 Floquet multipliers γ ₁, …, γ _d satisfying |γ ₁| = ⋯ = |γ _d| = 1.

• F.4 $f:\mathcal {R}\mathcal {C}\mathcal {R}\rightarrow \mathbb {R}^n$ and $g:\mathcal {R}\mathcal {C}\mathcal {R}\rightarrow \mathbb {R}^n$ are C ^k for some k.

Remark III.2.2.1

Hypothesis F.2 implies that the overlap condition holds at the critical period p ^∗.

2.1 Dummy Matrix System and Robustness of Spectral Separation

Given hypotheses F.1–F.4, we introduce the quasilinear dummy matrix system (DMS),

$$\displaystyle \begin{aligned} \dot x&=Z_1(p)Sx_t + M_1 Sx_t + f(x_t),&t&\neq kp\\ \dot M_1&=0,&t&\neq kp\\ \dot M_2&=0,&t&\neq kp\\ \varDelta x&=Z_2(p)Sx_{t^-}+M_2 Sx_{t^-}+g(x_{t^-}),&t&=kp\\ \varDelta M_1&=0,&t&=kp\\ \varDelta M_2&=0,&t&=kp. \end{aligned} $$

(III.2.7)

with $M_1,M_2\in \mathbb {R}^{n\times m}$. Notice that if M ₁ = L − Z ₁(p) and M ₂ = B − Z ₂(p), then the DMS coincides with (III.2.5) extended trivially to the state space $\mathcal {R}\mathcal {C}\mathcal {R}\times \mathbb {R}^{n\times m}\times \mathbb {R}^{n\times m}$.

The idea here is that since we cannot take p as a state variable, we will instead parameterize the linear part in such a way that for each fixed p ≈ p ^∗, we have a centre manifold of the appropriate dimension. The introduction of a dummy (matrix) parameter eventually allows us to recover a particular invariant manifold of the original system. Our plan is as follows:

• 1. We show that under the assumptions F.1–F.4, the spectral separation of (III.2.6) near p = p ^∗ is robust (Lemma III.2.2.3).

• 2. Using the robustness of spectral separation and the analysis of the centre manifold construction, we prove that there exist 𝜖 > 0 and a constant δ > 0 such that the DMS has, for each p ∈ (p ^∗− 𝜖, p ^∗ + 𝜖), a centre manifold that contains all small solutions of size at most δ.

• 3. We prove that there exist ν > 0 and δ > 0 such that if p ∈ (p ^∗− ν, p ^∗ + ν), the family of centre manifolds parameterized by the parameter p and evaluated at M ₁ = L − Z ₁(p) and M ₂ = B − Z ₂(p) defines a parameter-dependent centre manifold for the original system (III.2.5) and contains all small solutions of size at most δ.

We begin with some notation. For given p, let $V(p):\mathcal {R}\mathcal {C}\mathcal {R}\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}$ denote the monodromy operator V ₀ associated with the linear system (III.2.6). Also, let U(t, s;p) denote the evolution family for (III.2.6) and $C(t,s;p):\mathcal {R}\mathcal {C}\mathcal {R}\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}$ denote the evolution family associated with the linear system without impulses $\dot z=Z_1(p)Sz_t$. Finally, let PC ₀ denote the closed subspace of $\mathcal {R}\mathcal {C}\mathcal {R}$ consisting of functions that are continuous except at zero, where they have limits on the left.

Lemma III.2.2.1

Let $V_0(p):PC_0\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}$ denote the restriction of V (p) to PC ₀ . p↦V ₀(p) is strongly continuous at p ^∗ —that is, for each $\xi \in \mathcal {R}\mathcal {C}\mathcal {R}$,

$$\displaystyle \begin{aligned}\lim_{p\rightarrow p^*}||V_0(p)\xi - V_0(p^*)\xi||=0.\end{aligned}$$

Proof

From Lemma I.2.2.1,

Continuity of Z ₂ at p ^∗ ensures that the first term above converges to zero as p → p ^∗. Denote z(t) = C(t, 0;p)ξ(0). Then,

$$\displaystyle \begin{aligned}\dot z= LSz_t + (Z_1(p)-L)Sz_t,\end{aligned}$$

which implies by Theorem I.2.3.1 the decomposition

$$\displaystyle \begin{aligned}C(p,0;p) = C(p,0;p^*) + \int_0^{p} C(p,\mu;p^*)\chi_0\left[(Z_1(p)-L)SC(\mu,0;p)\right]d\mu.\end{aligned}$$

We can then make the estimate

The integral term converges to zero as p → p ^∗ due to Lemma I.2.2.1 and the continuity of Z ₁ at p ^∗. As for the other one, observe that due to hypothesis F.2, C(p, 0;p ^∗) has range in $C([-r,0],\mathbb {R}^n)$ for |p − p ^∗| small enough. In the same way we proved Lemma I.3.1.1, one can show that p↦C(p, 0;p ^∗) is compact for p ≥ p ^∗− 𝜖 for some small 𝜖 > 0. It then follows (see for instance Lemma 4.22 of [43]) that p↦C(p, 0;p ^∗) is norm continuous at p ^∗. Combining the previous convergence results, the lemma is proven. □

Lemma III.2.2.2

There exist 𝜖 > 0 and constants α < 1 < β such that for all p ∈ (p ^∗− 𝜖, p ^∗ + 𝜖), any eigenvalue λ of V (p) satisfies one of |λ| = 1, |λ| < α and |λ| > β.

Proof

Since V (p ^∗) is compact, assumption F.2 implies that its spectrum σ admits a decomposition σ = Σ _u ∪ Σ _c ∪ Σ _s, with

for some constants α ₀ and β ₀. Note that V (p) has range in PC ₀, so any eigenvalue of V (p) (and, by compactness, any nonzero element of the spectrum) must also be an eigenvalue of the restricted operator V ₀(p). But V ₀(p) is continuous at p ^∗ from Lemma III.2.2.1, so by [Theorem 4–3.16, [79]] on semicontinuity of separated parts of the spectrum, there exists 𝜖 ₁ > 0 such that if |p − p ^∗| < 𝜖 ₁, the spectrum of V (p) lies completely in the disjoint sets

for α = (1 + α ₀)∕2, and the number of eigenvalues in Σ ₂ is constant. Similarly, there exists 𝜖 ₂ > 0 such that if |p − p ^∗| < 𝜖 ₂, the spectrum of V (p) lies completely in the disjoint sets

for β = (1 + β ₀)∕2, and the number of eigenvalues in Σ ² is constant. Thus, for $\epsilon <\min \{\epsilon _1,\epsilon _2\}$, the number of eigenvalues in the annulus $\{z\in \mathbb {C}:\alpha <z<\beta \}$ is constant, and from the decomposition σ = Σ _u ∪ Σ _c ∪ Σ _s of V (p) and assumption F.3, this annulus contains only the d eigenvalues on the unit circle. □

Taking advantage of Lemma III.2.2.2, we obtain a parameter-uniform analogue of Theorem I.3.1.3. The proof is a trivial modification of the proof of the aforementioned theorem and is omitted.

Lemma III.2.2.3

There exists 𝜖 > 0 such that U(t, s;p) is uniformly spectrally separated for p ∈ (p ^∗− 𝜖, p ^∗ + 𝜖). That is, U(t, s;p) is spectrally separated for each p ∈ (p ^∗− 𝜖, p ^∗ + 𝜖) with projectors (P _s,p, P _c,p, P _u,p), the constants K, a and b appearing in Eqs. (I.1.11) – (I.1.13) can be chosen independent of p and there is a constant N independent of p such that

$$\displaystyle \begin{aligned}\sup_{t\in\mathbb{R}}\left(||P_{s,p}(t)||+||P_{c,p}(t)||+||P_{u,p}(t)||\right)\leq N.\end{aligned}$$

Denote $X=\mathbb {R}^n\times \mathbb {R}^{m\times m}\times \mathbb {R}^{m\times m}$. Let $\tilde U(t,s;p):Y\rightarrow Y$ be the evolution family associated with the linear part of the DMS (III.2.7), for $Y=\mathcal {R}\mathcal {C}\mathcal {R}([-r,0],X)$ the extended phase space. Note that this is simply

$$\displaystyle \begin{aligned}\tilde U(t,s;p)[\phi,x,y]=(U(t,s;p)\phi,x(0),y(0)),\end{aligned}$$

so in the following we will abuse notation and identify $\tilde U(t,s;p)$ with U(t, s;p). Lemma III.2.2.3 still holds for the evolution family on the extended phase space, and the projections $\tilde P_{i,p}$ (which we later identify with P _i,p) inherit block-diagonal structures $\tilde P_{i,p}=\mbox{diag}(P_{i,p},Z,Z)$, with Z = I if i = c and Z = 0 if i ≠ c.

Due to Lemma III.2.2.3, there exist $\overline \epsilon >0$ and a constant $\overline K>0$ independent of p such that for all $\eta \in (0,\min \{-a,b\})$, the Lyapunov–Perron operator $\mathcal {K}_s^{\eta ,p}:B^\eta (\mathbb {R},X)\oplus B^\eta _{kp}(\mathbb {Z},X)\rightarrow B^\eta (\mathbb {R},Y)$

(III.2.8)

is well-defined, linear and bounded with norm $||\mathcal {K}_s^{\eta ,p}||{ }_\eta \leq \overline K$, for all $p\in (p-\overline \epsilon ,p+\overline \epsilon )$.

2.2 Centre Manifold Construction

Define $\tilde f:Y\rightarrow X$ and $\tilde g:Y\rightarrow X$ to be the vector field and jump map associated with the DMS. Specifically, they are defined by

where $\varPhi :[-r,0]\rightarrow \mathbb {R}^n\times \mathbb {R}^{m\times m}\times \mathbb {R}^{m\times m}$ is split into component functions via Φ = (ψ, ϕ ₁, ϕ ₂). Following Sect. I.5.1.3, given a bump function ξ, we can define the parameter-dependent smoothed nonlinearities $\tilde F_\delta ^p$ and $\tilde G_\delta ^p$ by replacing the projections in Eqs. (I.5.5)–(I.5.6) with the appropriate parameter-dependent ones described in Lemma III.2.2.3. Due to the robustness, there is a mutual Lipschitz constant L _δ for the nonlinearities that satisfies L _δ → 0 as δ → 0, for all p ∈ (p ^∗− 𝜖 ^∗, p ^∗ + 𝜖 ^∗) for some 𝜖 ^∗ > 0. The same is true for the parameter-dependent substitution operators $\tilde R_\delta ^p$, with Lipschitz constant $\tilde L_\delta$.

Theorem III.2.2.1 (Centre Manifold: Dummy Matrix System)

There exist γ and 𝜖 > 0 such that for each p ∈ (p ^∗− 𝜖, p ^∗ + 𝜖), the dummy matrix system (III.2.7) possesses a centre manifold $\mathcal {W}_c^p$ with (d + m)-dimensional t-fibres

where $C_p:\mathbb {R}\times \mathcal {R}\mathcal {C}\mathcal {R}([-r,0],X)\rightarrow {\mathcal {R}\mathcal {C}\mathcal {R}}([-r,0],X)$ . Moreover, the following are true:

• 1. Define the map $\tilde C_p:\mathbb {R}\times (\mathcal {R}\mathcal {C}\mathcal {R}\times \mathbb {R}^{m\times m}\times \mathbb {R}^{m\times m})$ by

  

  where $\pi _{\mathcal {R}\mathcal {C}\mathcal {R}}:\mathcal {R}\mathcal {C}\mathcal {R}([-r,0],X)\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}$ is the projection onto the first component of $\mathcal {R}\mathcal {C}\mathcal {R}([-r,0],X)$ for the product $X=\mathbb {R}^n\times \mathbb {R}^{m\times m}\times \mathbb {R}^{m\times m}$ and . Then, $\pi _{\mathcal {R}\mathcal {C}\mathcal {R}}C_p = \tilde C_p$.

• 2. $\mathcal {W}_c^p$ is locally positively invariant under the process $S^p(t,s):\mathcal {M}\rightarrow Y$ associated with the dummy matrix system (III.2.7) in the sense of Theorem I.5.3.1 , for initial conditions smaller than δ.

• 3. $\mathcal {W}_c^p$ contains all mild solutions $(\phi ,y_1,y_2)=x:\mathbb {R}\rightarrow Y$ of (III.2.7) satisfying the estimate ||x||_η = ||ϕ||_η + ||y ₁|| + ||y ₂|| < γ, for any $\eta \in (0,\min \{-a,b\})$ , with a < 0 < b the spectral separation exponents from Lemma III.2.2.3.

• 4. $\mathcal {W}_c^p$ is attracting in the sense of Theorem I.5.5.1 , provided the unstable fibre bundle is empty, f is an ACR functional and the unique matrix t↦Y (t;p) satisfying P _c,p(t)χ ₀ = Φ _t,p Y (t;p) is continuous from the right with limits on the left, where Φ _t,p is an array whose columns form a basis for $\mathcal {R}(P_{c,p}(t))$ and such that Φ _t,p = U(t, s;p)Φ _s,p for t ≥ s.

• 5. $C_p(t,\cdot ):\mathcal {R}\mathcal {C}\mathcal {R}([-r,0],X)\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}([-r,0],X)$ is C ^k and uniformly (in p) Lipschitz continuous, as are its derivatives.

Proof

Choose γ > 0 small enough so that $\tilde L_\gamma \overline K<\frac {1}{2}$. Note that $\tilde L_\gamma \overline K$ is independent of p, provided |p − p ^∗| is small enough. The existence of the centre manifold then follows by the analysis preceding the statement of the theorem, together with Theorem I.5.2.1. Property 1 follows by the definition of the vector field $\tilde f$ and jump map $\tilde g$ of the DMS, while properties 2 and 3 follow by Theorem I.5.3.1 by taking the norm on X as ||(x, y, z)|| = ||x|| + ||y|| + ||z||. To prove property 4, one emulates the proof of Theorem I.5.5.1. Smoothness of property 5 follows by Theorem I.5.6.1. □

With the above lemma at hand, we are ready to construct the parameter-dependent centre manifold for the periodic system (III.2.5).

Corollary III.2.2.1 (Parameter-Dependent Centre Manifold)

Let $S^p(t,s):\mathcal {R}\mathcal {C}\mathcal {R}\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}$ denote the process associated with the periodic system (III.2.5). Consider the formal expression

$$\displaystyle \begin{aligned}C(t,\phi;p)=\tilde C_p(t,(\phi,L-Z_1(p),B-Z_2(p))).\end{aligned}$$

There exist ν > 0 and δ >  such that $C:\mathbb {R}\times \mathcal {R}\mathcal {C}\mathcal {R}\times (p^*-\eta ,p^*+\eta )\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}$ is well-defined and enjoys the following properties:

• 1. For each p ∈ (p ^∗− ν, p ^∗ + ν), the nonautonomous set $\mathcal {W}_c^p$ with t- fibres is locally positively invariant under the process $S^p(t,s):\mathcal {M}\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}[-r^*,0]$ , for initial conditions ϕ satisfying ||ϕ|| < δ.

• 2. $\mathcal {W}_c^p$ contains all mild solutions $x:\mathbb {R}\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}$ of (III.2.5) satisfying ||x||_η < δ, for any $\eta \in (0,\min \{-a,b\})$.

• 3. $\mathcal {W}_c^p$ is attracting in the sense of Theorem I.5.5.1 , provided the conditions outlined in part 4 of Theorem III.2.2.1 are satisfied.

• 4. ϕ↦C(t, ϕ;p) is C ^k and uniformly (in p) Lipschitz continuous, as are its derivatives.

Proof

Apply Theorem III.2.2.1 to obtain the centre manifold for the DMS as the nonautonomous set with fibres given by the images of (ϕ, y ₁, y ₂)↦C _p(t, ϕ, y ₁, y ₂) with (ϕ, y ₁, y ₂) ∈ Y . Recall that the DMS at M ₁ = L − Z ₁(p) := M ₁(p) and M ₂ = B − Z ₂(p) := M ₂(p) coincides with the trivial extension of the process S ^p(t, s) to the phase space Y . Restricting the domain of the centre manifold function C _p to the hypersurface , the invariance, inclusion of small mild solutions and attractivity properties of its image imply the same results for the projection onto the first component through $\pi _{\mathcal {R}\mathcal {C}\mathcal {R}}:Y\rightarrow \mathcal {R}\mathcal {C}\mathcal {R}[-r^*,0]$, where we choose 0 < η ≤ 𝜖 small enough so that $||L-Z_1(p)||+||B-Z_2(p)||<\frac {1}{2}\gamma$ for p ∈ (p ^∗− η, p ^∗ + η) and define $\delta =\frac {1}{2}\gamma$, where γ and 𝜖 are as described in Theorem III.2.2.1. By property 1 from Theorem III.2.2.1, the aforementioned projection onto the first component is precisely the image of C(t, ⋅;p). Smoothness with respect to ϕ follows from Theorem I.5.6.1. □

Remark III.2.2.2

One cannot conclude from the above construction that the parameter-dependent centre manifold is smooth (or even continuous) with respect to the parameter p, even under compatible (i.e. C ^k) conditions on Z ₁ and Z ₂. The centre manifold associated with the DMS (Theorem III.2.2.1) in the extended phase space, however, is C ^k for each fixed p.

3 Overlap Bifurcations

In this section we will be interested in systems of the form

$$\displaystyle \begin{aligned}\dot x&=Ax(t)+f(x(t)),&t&\notin\mathbb{Z} \end{aligned} $$

(III.2.9)

$$\displaystyle \begin{aligned}\varDelta x&=Bx(t^-)+Cx(t-\omega) + g(x(t^-),x(t-\omega)),&t&\in\mathbb{Z}, \end{aligned} $$

(III.2.10)

for f and g sufficiently smooth functions satisfying f(0) = g(0, 0) = 0, real n × n matrices A, B and C and ω ≥ 0.

A remark: when ω = 0, we will interpret x(t − ω) in (III.2.10) as the left-limit: x(t ⁻). Formally, the jump condition should be understood as

$$\displaystyle \begin{aligned}\varDelta x = Bx(t^-) + C\mbox{ev}_{-\omega}(x_{t^-}) + g(x(t^-),\mbox{ev}_{-\omega}(x_{t^-})),\end{aligned} $$

(III.2.11)

where ev_−ω(ϕ) = ϕ(−ω) is the evaluation functional at − ω.

We have two related problems to investigate:

• 1. Characterize the Floquet spectrum for ω ∈ (1 − 𝜖, 1), ω = 1 and ω ∈ (1, 1 + 𝜖) for small 𝜖 > 0.

• 2. Describe the local orbit structure near x = 0 for |ω − 1| < 𝜖 and small 𝜖 > 0.

System (III.2.9)–(III.2.10) is essentially finite-dimensional. Indeed, with the help of a state transformation, one can eliminate the discrete delay for each ω fixed; it is introduced in the paper [30]. We will make use of this transformation in Sect. III.2.3.3 to set the stage for studying bifurcations.

Remark III.2.3.1

The presentation of this section and the correctness of all results as stated depend crucially on the interpretation of the jump condition and on the limit convention used. For example, if the regulated left-limit $x_t^-$ is used in (III.2.11) instead of the one-point limit $x_{t^-}$, many results will change.

3.1 Floquet Spectrum

Here we will characterize the Floquet spectrum of (III.2.9)–(III.2.10) for ω ≈ 1. The analysis will be split into two stages. First, we will consider the case ω ≤ 1. Next, we look at the ω > 1 case. Neither proof is difficult.

Lemma III.2.3.1

Let ω ∈ [0, 1]. λ is a Floquet exponent for the linearization of (III.2.9)–(III.2.10) at x = 0 if and only if μ = e ^λ satisfies the equation

$$\displaystyle \begin{aligned} \det\left((I+B)e^A + Ce^{A(1-\omega)} - \mu I\right)=0. \end{aligned} $$

(III.2.12)

That is, μ is an eigenvalue of (I + B)e ^A + Ce ^A(1−ω).

Proof

Let x(t) = ϕ(t)e ^tλ be a Floquet eigensolution. If ω ∈ (0, 1], the periodic function ϕ (complex-valued with period one) satisfies

$$\displaystyle \begin{aligned} \dot \phi&=(A-\lambda I)\phi,&t&\notin\mathbb{Z}\\ \varDelta\phi&=B\phi(t^-) + e^{-\lambda\omega}C\phi(t-\omega),&t&\in\mathbb{Z}. \end{aligned} $$

At time t = 1, the solution with initial condition ϕ(0) = ϕ ₀ satisfies

$$\displaystyle \begin{aligned} \phi(1)&=\left[(I+B)e^{A-\lambda I} + e^{-\lambda\omega}Ce^{(A-\lambda I)(1-\omega)}\right]\phi_0=\left[(I+B)e^A + Ce^{A(1-\omega)}\right]e^{-\lambda}\phi_0. \end{aligned} $$

ϕ is periodic if and only if ϕ(1) = ϕ ₀. This is equivalent to μ = e ^λ satisfying

$$\displaystyle \begin{aligned}\det\left(\left[(I+B)e^A + Ce^{A(1-\omega)}\right]\mu^{-1}-I\right)=0,\end{aligned}$$

which is equivalent to (III.2.12). For the case ω = 0, we get

$$\displaystyle \begin{aligned} \dot \phi&=(A-\lambda I)\phi,&t&\notin\mathbb{Z}\\ \varDelta\phi&=B\phi(t^-) + C\phi(t^-),&t&\in\mathbb{Z}, \end{aligned} $$

so that ϕ(t) satisfies

$$\displaystyle \begin{aligned}\phi(1)=(I+B+C)e^{(A-\lambda I)}\phi_0.\end{aligned}$$

The result follows by the same argument as the previous case. □

Lemma III.2.3.2

Let ω ∈ (1, 2). λ is a Floquet exponent for the linearization of (III.2.9)–(III.2.10) at x = 0 if and only if μ = e ^λ satisfies the equation

$$\displaystyle \begin{aligned} \det\left((I+B)e^A\mu + Ce^{A(2-\omega)} - \mu^2 I\right)=0. \end{aligned} $$

(III.2.13)

Proof

Let x(t) = ϕ(t)e ^tλ be a Floquet eigensolution. The periodic function ϕ (complex-valued with period one) satisfies

$$\displaystyle \begin{aligned} \dot \phi&=(A-\lambda I)\phi,&t&\notin\mathbb{Z}\\ \varDelta\phi&=B\phi(t^-) + e^{-\lambda\omega}C\phi(t+1-\omega),&t&\in\mathbb{Z}. \end{aligned} $$

Note that 1 − ω ∈ (0, 1). At time t = 1, the solution with initial condition ϕ(0) = ϕ ₀ satisfies

$$\displaystyle \begin{aligned} \phi(1)&=\left[(I+B)e^{A-\lambda I} + e^{-\lambda\omega}Ce^{(A-\lambda I)(2-\omega)}\right]\phi_0\\ &=\left[(I+B)e^A + Ce^{A(2-\omega)}e^{-\lambda}\right]e^{-\lambda}\phi_0. \end{aligned} $$

ϕ is periodic if and only if ϕ(1) = ϕ ₀. This is equivalent to μ = e ^λ satisfying

$$\displaystyle \begin{aligned}\det\left(\left[(I+B)e^A + Ce^{A(1-\omega)}\mu^{-1}\right]\mu^{-1}-I\right)=0,\end{aligned}$$

which is equivalent to (III.2.13). □

From these two lemmas, we immediately conclude that for ω ∈ (0, 1], there are at most n nonzero Floquet multipliers counting multiplicities, whereas for ω ∈ (1, 2) there are at most n ². There does not appear to be any general connection between the Floquet multipliers at ω = 1 and the limit from the right, ω → 1⁺.

3.2 Symmetries of Periodic Solutions

One observation that will be helpful later in analyzing bifurcations of periodic solutions is the following symmetry property.

Lemma III.2.3.3

Let x(t) be a periodic solution of (III.2.9)–(III.2.10) with period one, for delay parameter ω > 0. Then, x(t) is a periodic solution for the delay parameter ω + k for any $k\in \mathbb {Z}$ such that ω + k > 0.

Proof

Since x is periodic with period one, we have x(t − ω) = x(t − (ω + k)) whenever ω + k > 0 and $k\in \mathbb {Z}$. The result follows. □

The reason for the strict inequalities ω > 0 and ω + k > 0 in the previous lemma is because when ω = 0, the jump condition (III.2.11) reduces to

$$\displaystyle \begin{aligned}\varDelta x = (B+C)x(t^-) + g(x(t^-),x(t^-)),\end{aligned}$$

but when ω = k > 0 for $k\in \mathbb {N}$, it is

$$\displaystyle \begin{aligned}\varDelta x=Bx(t^-) + Cx(t-k) + g(x(t^-),x(t-k)).\end{aligned}$$

Since x(t ⁻) ≠ x(t) = x(t − k), it is not possible to compare periodic solutions for ω = 0 with $\omega \in \mathbb {N}$.

Take a note that this lemma applies to both linear and nonlinear systems. Consequently, it implies furthermore that whenever μ = 1 is a Floquet multiplier for ω = 1 or as ω → 1⁺, the same is true for ω = k a positive integer or as μ → k ⁺.

3.3 A State Transformation that Eliminates the Delay

In order to analyze the local orbit structure near ω = 1, we will introduce a delayed state transformation that eliminates the delay, producing a truly finite-dimensional system. The result will be an impulsive system whose impulse times depend on the parameter ω. For additional background on the transformation, see [30]. The explicit state transformation will be different depending on whether ω < 1, ω = 1 or ω > 1. This should not be surprising considering the results of the previous section.

Lemma III.2.3.4 (Delayed State Transformation: ω < 1)

Suppose ω ∈ (0, 1), and consider the finite-dimensional impulsive differential equation

$$\displaystyle \begin{aligned}\dot x&=Ax(t)+f(x(t)),&t&\notin\mathbb{Z} \end{aligned} $$

(III.2.14)

$$\displaystyle \begin{aligned} \dot y&=0,&t&\notin\mathbb{Z}-\omega \end{aligned} $$

(III.2.15)

$$\displaystyle \begin{aligned} \varDelta x&=Bx(t^-)+Cy(t^-)+g(x(t^-),y(t^-)),&t&\in\mathbb{Z} \end{aligned} $$

(III.2.16)

$$\displaystyle \begin{aligned}\varDelta y&=x-y,&t&\in\mathbb{Z}-\omega. \end{aligned} $$

(III.2.17)

If $X:\mathbb {R}\rightarrow \mathbb {R}^n$ is a solution of (III.2.9)–(III.2.10), then

$$\displaystyle \begin{aligned}(x(t),y(t))=(X(t),X(\lfloor t \rfloor-\omega))\end{aligned} $$

(III.2.18)

is a solution of (III.2.14)–(III.2.17) defined for $t\in \mathbb {R}$ and vice versa. The period of the transformed system is one, with two impulses per period. Moreover, X is locally asymptotically stable (respectively stable, unstable) if and only if the same is true for the solution (III.2.18).

Remark III.2.3.2

The transformation (III.2.18) applies only to solutions that are defined on the real line, as required by the lemma. If $X:[a,\infty )\rightarrow \mathbb {R}^n$ is a solution of (III.2.9)–(III.2.10) and $a\in \mathbb {R}$ is finite, then the transformation generates a solution (x(t), y(t)) of the transformed equation that is defined for t ≥ a + ω.

Lemma III.2.3.5 (Delayed State Transformation: ω = 1)

Suppose ω = 1, and consider the finite-dimensional impulsive differential equation

$$\displaystyle \begin{aligned}\dot x&=Ax(t)+f(x(t)),&t&\notin\mathbb{Z} \end{aligned} $$

(III.2.19)

$$\displaystyle \begin{aligned} \dot y&=0,&t&\notin\mathbb{Z} \end{aligned} $$

(III.2.20)

$$\displaystyle \begin{aligned}\varDelta x&=Bx(t^-)+Cy(t^-)+g(x(t^-),y(t^-)),&t&\in\mathbb{Z} \end{aligned} $$

(III.2.21)

$$\displaystyle \begin{aligned}\varDelta y&=x + B(x(t^-)) + Cy(t^-) + g(x(t^-),y(t^-))-y,&t&\in\mathbb{Z}. \end{aligned} $$

(III.2.22)

This system enjoys the same property as the one from Lemma III.2.3.4 , but there is only one impulse per period.

Proof

Let (x, y) be a solution of (III.2.19)–(III.2.22). By construction, y(t ⁻) = x(t − 1) whenever $t\in \mathbb {Z}$. Since the continuous-time dynamics (III.2.19) are the same as those of (III.2.9)–(III.2.10), and the impulse effect (III.2.21) is also the same upon replacing y(t ⁻) with x(t − 1), we get that x(t) is a solution of (III.2.9)–(III.2.10). The converse is similar. □

Lemma III.2.3.6 (Delayed State Transformation: ω > 1)

Suppose ω ∈ (1, 2), and consider the finite-dimensional impulsive differential equation

$$\displaystyle \begin{aligned}\dot x&=Ax(t)+f(x(t)),&t&\notin\mathbb{Z} \end{aligned} $$

(III.2.23)

$$\displaystyle \begin{aligned} \dot y_0&=0,&t&\notin 2\mathbb{Z}-\omega \end{aligned} $$

(III.2.24)

$$\displaystyle \begin{aligned} \dot y_1&=0,&t&\notin 2\mathbb{Z}+1-\omega \end{aligned} $$

(III.2.25)

$$\displaystyle \begin{aligned}\varDelta x&=Bx(t^-)+Cy_{[t]_2}(t^-)+g(x(t^-),y_{[t]_2}(t^-)),&t&\in\mathbb{Z} \end{aligned} $$

(III.2.26)

$$\displaystyle \begin{aligned} \varDelta y_0&=x -y_0,&t&\in 2\mathbb{Z}-\omega \end{aligned} $$

(III.2.27)

$$\displaystyle \begin{aligned}\varDelta y_1&=x-y_1,&t&\in 2\mathbb{Z}+1-\omega. \end{aligned} $$

(III.2.28)

If $X:\mathbb {R}\rightarrow \mathbb {R}^n$ is a solution of (III.2.9)–(III.2.10), then (x(t), y ₀(t), y ₁(t)), with x(t) = X(t) and

$$\displaystyle \begin{aligned} y_0(t)&=X(k-\omega),\quad \quad t\in[k,k+2),\quad k\in 2\mathbb{Z}\\ y_1(t)&=X(k-\omega),\quad \quad t\in[k,k+2),\quad k\in 2\mathbb{Z}+1, \end{aligned} $$

is a solution of (III.2.23)–(III.2.28) defined for $t\in \mathbb {R}$ and vice versa, and their stability is equivalent. The period of the transformed system is two, and there are four impulses per period.

Proof

If (x, y ₀, y ₁) is a solution of (III.2.23)–(III.2.28), we have two observations. First, if $k\in 2\mathbb {Z}$, then x(k − ω) = y ₀(k ⁻). Second, if $k\in 2\mathbb {Z}+1$, then x(k − ω) = y ₁(k ⁻). For a solution defined for all time, this implies that at any time $t\in \mathbb {Z}$, the delayed state x(t − ω) is one of y ₀(t ⁻) or y ₁(t ⁻). The remainder [t]₂ in (III.2.26) keeps track of the correct one. The argument then follows the same lines as the proof for Lemma III.2.3.5. The converse is similar.

To see that the period is two and there are four impulses per period, observe that although the sequence of impulses can be identified with the set $\mathbb {Z}\cup (\mathbb {Z}-\omega )$, which upon sequential ordering gives a sequence t _k satisfying t _k+2 = t _k + 1—that is, period one with two impulses—the sequence of jump functions defining Eqs. (III.2.26)–(III.2.28) can be identified with a function G _k satisfying G _k+4 = G _k. As such, there are four impulses per period and the period is two, since t _k+4 = t _k + 2. □

If we are interested in locating bounded solutions—for example, periodic solutions in invariant cylinders—it is sufficient for us to study the period maps associated with the state transformed systems of the previous three lemmas. However, since the transformed system for ω ∈ (1, 2) is of period two, we will need an additional result if we wish to detect periodic solutions of period one.

Lemma III.2.3.7

Suppose ω ∈ (1, 2). (x, y ₀, y ₁) is a periodic solution of (III.2.23)–(III.2.28) with period one if and only if y ₀ = y ₁ is constant.

Proof

Suppose (x, y ₀, y ₁) is a periodic solution of period one. Then, y ₀(k ⁻) = x(k − ω) for $k\in 2\mathbb {Z}$, while y ₁(k ⁻) = x(k − ω) for $k\in 2\mathbb {Z}+1$. Since x is periodic with period one, x(k − ω) = x ^∗ is constant for $k\in \mathbb {Z}$. Since each of y ₀ and y ₁ is piecewise-constant and only has an impulse every 2 time units, we have y ₀(t) = y ₁(t) = x ^∗ for all $t\in \mathbb {R}$.

Conversely, suppose y ₀ = y ₁ = x ^∗ is constant. Then x ^∗ = y ₀(k) = x(k ⁻) for $k\in 2\mathbb {Z}$ and x ^∗ = y ₁(k ⁻) = x(k ⁻) for $k\in 2\mathbb {Z}+1$. Consequently, x(k) = (I + B)x ^∗ + Cx ^∗ + g(x ^∗, x ^∗) for all $k\in \mathbb {Z}$, whereas for t ∈ [k, k + 1), x is determined by the autonomous dynamics (III.2.23). It follows that x is periodic with period one. □

3.4 Bifurcations of Periodic Solutions

Based on the description of the Floquet spectrum from Sect. III.2.3.1, we should expect some sort of local bifurcation of periodic solutions at ω = 1 if one or both of the following occur:

• T.1 at ω = 1, there is a Floquet multiplier μ satisfying |μ| = 1;

• T.2 as ω → 1⁺, some Floquet multiplier μ satisfies |μ|→ 1.

The T.1 scenario corresponds to the situation in which some bifurcation occurs for ω ∈ (1 − 𝜖, 1]. Such a bifurcation can be detected by computing a Taylor expansion in (x, y) with ω as a parameter of the time 1 map of the transformed system (III.2.14)–(III.2.17). To bridge the gap as ω → 1⁻, we need the following lemma.

Lemma III.2.3.8

Let $P_1(\cdot ,\omega ):\mathbb {R}^n\times \mathbb {R}^n\rightarrow \mathbb {R}^n\times \mathbb {R}^n$ denote the time 1 map of (III.2.14)–(III.2.17) for parameter ω < 1. Then, $\lim _{\omega \rightarrow 1^-}P_1(\cdot ,\omega )$ is well-defined, uniformly near $0\in \mathbb {R}^n\times \mathbb {R}^n$ . The continuous extension $P_1:\mathbb {R}^n\times \mathbb {R}^n\times [0,1]\rightarrow \mathbb {R}^n\times \mathbb {R}^n$ is smooth (with the same regularity as the nonlinearities f and g) in a neighbourhood of $(0,0,1)\in \mathbb {R}^n\times \mathbb {R}^n\times [0,1]$.

It can be proven by appealing to the time 2 map and the integral representation of solutions. Interestingly, the limit described in Lemma III.2.3.8 is completely unrelated to the time 1 map of the delayed state transformation at ω = 1. We will observe this in Sect. III.2.3.5.

The second T.2 scenario suggests a possible bifurcation in the interval [1, 1 + 𝜖). Formally, this can be justified by the following lemma, whose proof we omit.

Lemma III.2.3.9

Let $P_2(\cdot ,\omega ):(\mathbb {R}^n)^3\rightarrow (\mathbb {R}^n)^3$ denote the time 2 map for (III.2.23)–(III.2.28). The limit $\lim _{\omega \rightarrow 1^+}P_2(\omega ,\cdot )$ exists uniformly in a neighbourhood of $0\in (\mathbb {R}^n)^3$ . The continuous extension $P_2:(\mathbb {R}^n)^3\times [1,2)\rightarrow (\mathbb {R}^n)^3$ is smooth (with the same regularity as the nonlinearities f and g) in a neighbourhood of $(0,1)\in (\mathbb {R}^n)^3\times [1,2)$.

For ω ∈ (1, 2) the time 2 map will be smooth with respect to all the variables. The limit property of the above lemma then justifies using bifurcation theorems in the interval [1, 1 + 𝜖).

If scenario T.1 or T.2 explicitly does not occur, all Floquet multipliers should be away from the unit circle in the relevant ω regime: (1 − 𝜖, 1] for the negation of T.1 and (1, 1 + 𝜖) for the negation of T.2. Ideally, one would want to prove that this parameter regime does not contain any small (i.e. trivializing to zero as ω → 1) bounded solutions aside from the trivial solution x = 0. This in fact follows from very general static bifurcation theory applied to the period map—see [115], Proposition 2.6 for the relevant result. Taking into account Lemma III.2.3.3, we get the following theorem.

Theorem III.2.3.1 (Overlap Bifurcation)

The following hold in a neighbourhood of the overlap point ω = 1 for the general nonlinear system (III.2.9)–(III.2.10):

• If scenario T.1 occurs, x = 0 may exhibit a bifurcation for ω ∈ (1 − 𝜖, 1] and some small 𝜖 > 0. That is, there may exist a nontrivial bounded solution x _ω satisfying x _ω → 0 as ω → 1⁻.

• If scenario T.2 occurs, x = 0 may exhibit a bifurcation for ω ∈ [1, 1 + 𝜖) and some small 𝜖 > 0. That is, there may exist a nontrivial bounded solution x _ω satisfying x _ω → 0 as ω → 1⁺.

• If scenario T.1 does not occur, there exist δ > 0 and 𝜖 > 0 such that the only bounded solution (defined for all time) contained in the ball B _δ(0) for ω ∈ (1 − 𝜖, 1] is the trivial solution x = 0.

• If scenario T.2 does not occur, there exist δ > 0 and 𝜖 > 0 such that the only bounded solution (defined for all time) contained in the ball B _δ(0) for ω ∈ [1, 1 + 𝜖) is the trivial solution x = 0.

3.5 The Introductory Example Revisited

Let us return to the system

$$\displaystyle \begin{aligned}\dot x&=\log\left(\frac{3}{2}\right)x-\frac{1}{10}x^2,&t&\notin\mathbb{Z} \end{aligned} $$

(III.2.29)

$$\displaystyle \begin{aligned}\varDelta x&=-\frac{1}{2}x(t^-) + \frac{1}{4}x_{t^-}(-\omega),&t&\in\mathbb{Z}, \end{aligned} $$

(III.2.30)

from the overview of this chapter. We saw that at ω = 1, there is a Floquet multiplier μ = 1, whereas for ω ∈ (1, 2) all Floquet multipliers have absolute value greater than one and, in particular, $\mu \nrightarrow 1$ as ω → 1⁺. This is a T.1 overlap bifurcation scenario, so we should compute a Taylor expansion for ω ∈ [1 − 𝜖, 1] from the time 1 map of the delayed state transformation. For ω < 1, the latter is

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \dot x&=\log\left(\frac{3}{2}\right)x-\frac{1}{10}x^2,&&\quad t\notin\mathbb{Z}&&\quad \quad \varDelta x&&=-\frac{1}{2}x +\frac{1}{4}y,&&\quad t\in\mathbb{Z} {} \end{array}\end{aligned} $$

(III.2.31)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \dot y&= 0,&&\quad t\notin\mathbb{Z}-\omega&&\quad \quad \varDelta y&&=x-y,&&\quad t\in\mathbb{Z}-\omega.{} \end{array}\end{aligned} $$

(III.2.32)

The time 1 map admits an expansion of the form

$$\displaystyle \begin{aligned}z\mapsto c_1(\omega)z + \frac{1}{2}c_2(\omega)z^2 + O(z^3)=P_1(x,\omega)\end{aligned}$$

for $z=[\begin {array}{cc}x&y\end {array}]^\intercal$, c ₁ a linear map and c ₂ a bilinear map, with P ₁(0, ω) = 0. From Lemma III.2.3.8, we know that the coefficients are smooth.

Computing c ₁(ω) is relatively straightforward since it is simply the monodromy matrix of the linearization at (x, y) = 0 of (III.2.32)–(III.2.31). One can check that

$$\displaystyle \begin{aligned} c_1(\omega)=\left[\begin{array}{cc}\left(\frac{3}{2}\right)^{1-\omega}\left(\frac{1}{2}\left(\frac{3}{2}\right)^{\omega} + \frac{1}{4}\right)& 0 \\ \left(\frac{3}{2}\right)^{1-\omega} & 0 \end{array}\right].{} \end{aligned} $$

(III.2.33)

For the coefficient c ₂, we have c ₂(ω) = Z(1), where Z is a symmetric bilinear map defined by Z(0) = 0 and

$$\displaystyle \begin{aligned} \dot Z[h_1,h_2]&=\!\left[\begin{array}{@{}cc@{}}\log(3/2)&0\\0&0\end{array}\right]Z[h_1,h_2]{\kern-1pt} - {\kern-1pt}\frac{2}{10}e_1 h_1^\intercal E_{11}h_2(3/2)^{2t},&t&\notin\{1,1{\kern-1pt}-{\kern-1pt}\omega\}\\ \varDelta Z[h_1,h_2]&=\left[\begin{array}{cc}0&0\\1&-1 \end{array}\right]Z[h_1,h_2],&t&=1-\omega \\ \varDelta Z[h_1,h_2]&=\left[\begin{array}{cc}-\frac{1}{2} & \frac{1}{4} \\ 0&0 \end{array}\right]Z[h_1,h_2],&t&=1. \end{aligned} $$

Computing the solution and evaluating at t = 1, we get

$$\displaystyle \begin{aligned} &c_2(\omega)[h_1,h_2]\\ &\quad =-\frac{3h_1^\intercal E_{11}h_2}{20\log(3/2)}\underbrace{\left[\begin{array}{c}\left(\frac{3}{2}\right)^\omega-1 + \frac{1}{2}\left(\frac{3}{2}\right)^{-\omega}\left(2\left(\frac{3}{2}\right)^\omega-3\right)\left(1+\frac{1}{2}\left(\frac{3}{2}\right)^{-\omega}\right) \\ \left(\frac{3}{2}\right)^{-\omega}\left(2\left(\frac{3}{2}\right)^\omega-3\right) \end{array}\right]}_{\tilde c(\omega)}. \end{aligned} $$

The quadratic-order expansion of the time 1 map therefore takes the form

$$\displaystyle \begin{aligned} \left[\begin{array}{c}x\\y\end{array}\right]&\mapsto\left[\begin{array}{cc}\left(\frac{3}{2}\right)^{1-\omega}\left(\frac{1}{2}\left(\frac{3}{2}\right)^{\omega} {+} \frac{1}{4}\right)& 0 \\ \left(\frac{3}{2}\right)^{1{-}\omega} & 0 \end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right] {-} \frac{3}{20\log(3/2)}\tilde c(\omega)x^2 {+} O(||(x,y)||{}^3), \end{aligned} $$

uniformly for 0 < 1 − ω ≪ 1. Applying the Lyapunov–Schmidt reduction, we can uniquely solve the fixed-point problem associated with the second equation

$$\displaystyle \begin{aligned}y=2^{1-\omega}x - \frac{3\left(2-3\left(\frac{3}{2}\right)^{-\omega}\right)}{20\log(3/2)}x^2 + O(||(x,y)||{}^3)\end{aligned}$$

for y = y(x, ω) near (x, ω) = (0, 1). The fixed point satisfies y(0, ω) = 0. Restricted to the curve y = y(x, 𝜖), x is a fixed point of the first equation if and only if

$$\displaystyle \begin{aligned}x= \left(\frac{3}{2}\right)^{1-\omega}\left(\frac{1}{2}\left(\frac{3}{2}\right)^{\omega} + \frac{1}{4}\right)x + e_1^\intercal \tilde c(\omega)x^2 + O(||x||{}^3)\equiv F(x,\omega)\end{aligned}$$

uniformly for |ω − 1| small. We have

and F(0, ω) = 0. A transcritical bifurcation therefore occurs at ω = 1, and the x component of the branch of nontrivial fixed points satisfies

$$\displaystyle \begin{aligned}x^* = \frac{10}{3}\left(\log\left(\frac{3}{2}\right)\right)^2(\omega-1) + O((\omega-1)^2).\end{aligned}$$

Since the time 1 map we have computed only represents the dynamics of the system (III.2.29)–(III.2.29) for ω ∈ (1 − 𝜖, 1) and some small 𝜖 > 0, the nontrivial fixed point is only guaranteed to exist in this range. With the aid of Theorem III.2.3.1 and linearized stability, we can make the following conclusion.

Lemma III.2.3.10

The trivial solution of (III.2.29)–(III.2.30) undergoes a transcritical bifurcation at ω = 1 in the interval (1 − 𝜖, 1] for some 𝜖 > 0 small. More precisely, there is a nontrivial, positive periodic solution t↦x _ω(t) of period one that exists for ω ∈ (1 − 𝜖, 1) for some 𝜖 > 0 small and satisfies x _ω(0) > 0 and $\lim _{\omega \rightarrow 1^-}x_\omega = 0$ . There exists δ > 0 such that no periodic solution apart from x _ω and the trivial solution exist in the ball B _δ(0). The nontrivial periodic solution is locally asymptotically stable for ω ∈ (1 − 𝜖, 1), while the trivial solution is unstable.

By the symmetry of Lemma III.2.3.3, we obtain the following corollary.

Corollary III.2.3.1

For each positive integer k, the trivial solution of (III.2.29)–(III.2.30) undergoes a transcritical bifurcation at ω = k in the interval (k − 𝜖, k] for some 𝜖 > 0 small.

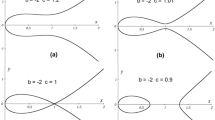
Figure III.2.1 provides the plots of numerically computed solutions of (III.2.29)–(III.2.30) for two choices of delays near ω = 1. We can see the nontrivial positive periodic solution for ω ∈ (1 − 𝜖, 1), as well as a “large” nontrivial periodic solution for ω ∈ (1, 1 + 𝜖). Performing a parameter continuation, it turns out that this “large” nontrivial periodic solution is created near ω = 2 in the transcritical bifurcation predicted by Corollary III.2.3.1. The bifurcation diagram is provided in Fig. III.2.2.

Figure III.2.1

Plots of numerical solutions from the constant initial condition x ₀ = 0.5 for the scalar equation (III.2.29)–(III.2.30) with delay ω = 0.9 (left) and ω = 1.1 (right). Inset: windowing of the numerical solutions for various time arguments, once convergence to the periodic solution is (nearly) achieved

Figure III.2.2

Bifurcation diagram of (III.2.29)–(III.2.30) for ω ∈ [0, 2]. Curves denote the mean value ($\overline x$) of a periodic solution. The nontrivial curves are asymptotically stable (solid curves), while the trivial zero fixed point is unstable (dashed line)

4 Comments

We have considered only two simple examples in this chapter of bifurcations driven by the perturbations to impulses and delay-impulse overlaps. Outside of this monograph, the former appears to have never been considered (when delays are involved). As for the later, Church and Liu [30] studied bifurcations in a logistic model with harvesting and census delay at a parameter configuration where the overlap condition was violated, but the bifurcation parameter was one of the smooth model parameters and not the delay parameter. On the whole, neither of these bifurcations—bifurcations driven by perturbations to impulse times or overlap bifurcations—is well-understood, and the methods we have developed here to analyze them are somewhat difficult to use.

In the example of Sect. 2, we needed to assume that T ^∗ > τ. If this assumption did not hold, we would be in the scope of an overlap bifurcation (if T ^∗ = τ) or at the very least need to modify the construction of the parameter-dependent centre manifold. Since the delay appears in the continuous part of the dynamics, however, the main conclusions of Sect. III.2.3 do not apply here in the case of an overlap bifurcation. How to analyze such a bifurcation scenario is unclear.