Abstract
Before starting to play a two-player board game such as Chess and Shogi (namely, Japanese chess), we have to determine who makes the first move. Players’ strategies of Chess and Shogi often rely on whether they will move first or not, and most players have their own preferences. Therefore, it would be nice if we can take their individual requests into account when determining who goes first. To this end, if the two players simply tell their preferable moves to each other, they will notice the other’s strategy. Thus, we want the players to determine the first move according to their requests while hiding any information about them. Note that this problem cannot be solved by a typical way done in Chess, namely, a coin-flipping. In this paper, we formalize this problem in a cryptographic perspective and propose a secure protocol that solves this problem using a deck of physical cards. Moreover, we extend this problem to the multi-player setting: Assume that there is a single prize in a lottery drawing among more than two players, each of who has an individual secret feeling ‘Yes’ or ‘No’ that indicates whether he/she really wants to get the prize or not. If one or more players have ‘Yes,’ we want to randomly and covertly choose a winner among those having ‘Yes.’ If all of them have ‘No,’ we want to randomly pick a winner among all the players. We solve this extended problem, which we call the “covert lottery” problem, by proposing a simple card-based protocol.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Secure multiparty computations
- Physical cryptography
- Card-based protocols
- Real-life hands-on cryptography
- Deck of cards
1 Introduction
Consider a situation where two players are about to play Chess or Shogi (namely, Japanese chess); then, they have to determine who makes the first move. In this case, one typical way is to flip a coin, i.e., to randomly choose a player who goes first. Another way is to use Rock paper scissors to choose a player who has a right to determine whether he/she makes the first move or not as he/she likes. On the other hand, in Chess or Shogi, there are many players’ strategies depending on whether they make the first move or the second move. Therefore, they want to take their favorite turn, which implies that coin flipping is not an ideal method (because their preferable choices are not taken into account at all). In addition, since individual players tend to have their own preferences about such first-move-oriented or second-move-oriented strategies, they do not want to give out the information of the move they want to take, which implies that Rock paper scissors is not an ideal method as well (because the choice of the winner of Rock paper scissors results in possibly giving out his/her strategy to the opponent). Thus, we need a more intellectual way to determine who goes first while keeping their preferences secret and taking them into account as much as possible.
More specifically, we want to have a protocol to perform the following: If two players’ preferences are different, i.e., one wants to make the first move while the other wants to make the second move, then the protocol is supposed to tell the players that the former should go first; if their preferences coincide, then the protocol randomly chooses one of the two players and tells the result. In this paper, we will construct such a protocol to solve the “Chess player’s dilemma” mentioned thus far.
1.1 Defining the Functionality for Two Players
Now we formally define the functionality that we wish to achieve.
Suppose that two players \(P_1\) and \(P_2\) have secret input bits \(x_1, x_2 \in \{0,1\}\) that represent their preferences, respectively. That is, for each player \(P_i\), \(x_i=1\) means that he/she wants to play the first move and \(x_i = 0\) means that he/she wants to play the second move. For an input \((x_1, x_2)\), the functionality \(\mathcal {F}\) outputs a single bit \(y \in \{0,1\}\). The output bit y is determined as follows. If \(x_1 \ne x_2\), i.e., they have different preferences, then y is equal to \(x_1\) which means that \(P_1\) (and also \(P_2\)) gets his/her preferred move. On the other hand, if \(x_1 = x_2\), i.e., they have the same preference, then y is chosen uniformly randomly. Thus, \(\mathcal {F} = 1\) means that \(P_1\) is going to make the first move, and \(\mathcal {F} = 0\) means that \(P_2\) is going to make the first move.
The functionality \(\mathcal {F}\) is also expressed as follows:

Here, \(\xleftarrow {\$}\) represents that the left element is randomly chosen from the right set.
We note that a player who fails to take the desired move will know that it is the case of \(x_1 = x_2\). For example, when both players wish to take the first move but \(P_1\) fails to take the first move (by the outcome of the random choice of \(\mathcal {F}\)), \(P_1\) will know that \(P_2\) also wishes to take the first move while \(P_2\) cannot distinguish whether \(x_1 = x_2\) or not. At a first glance, it seems unfair. However, we believe that this is unavoidable since when both players have the same preference, the best way is to play a coin tossing.
1.2 Defining the Functionality for Multiple Players
We moreover consider the case where the number of players is further extended to a general number of \(n \, (\ge 2)\). Specifically, consider the case where only one person is drawn from n players. For example, assume that there is a single prize in a lottery drawing among n players, each of who has an individual secret feeling ‘Yes’ or ‘No’ that indicates whether he/she really wants to get the prize or not. If one or more players have ‘Yes,’ we want to randomly and covertly choose a winner among those having ‘Yes.’ If all of them have ‘No,’ we want to randomly pick a winner among all the players. We call this extended problem the “covert lottery” problem.
Considering n players, each player \(P_i\), \(1 \le i \le n\), has a secret input bit \(x_i \in \{0,1\}\) that represents a wish. That is, \(x_i = 0\) means that \(P_i\) does not want to be the winner, and \(x_i = 1\) means that he/she wants to be the winner. First, the function \(\mathsf {True} : \{0,1\}^n \rightarrow 2^{\{1,2,...,n\}}\) is defined as:

where \(2^{\{1, 2, \ldots , n\}}\) is the power set of \(\{1, 2, \ldots , n\}\). The functionality \(\mathcal {G}_n\) for the covert lottery protocol is defined as follows:

Recall that, basically, we want to draw a lottery among players \(P_i\) with \(x_i = 1\), and if there is no such a player, a winner is randomly chosen from all players.
This functionality leaks to a player \(P_i\) who has \(x_i = 1\) and \(\mathcal {G}_n \ne i\) the fact that \(x_{\mathcal {G}_n} = 1\). Also, if \(x_i = 0\) and \(\mathcal {G}_n = i\), this problem will leak to \(P_i\) the fact that all players \(P_j\) with \(j \ne i\) also have \(x_j = 0\). However, this property is inherently owned by \(\mathcal {G}_n\), as well.
Let us show that \(\mathcal {G}_n\) is a natural extension of \(\mathcal {F}\) defined in Eq. (1). Consider the case where \(n = 2\) for \(\mathcal {G}_n\). In this case, it is obvious that \(\mathcal {G}_2 (0,0) \xleftarrow {\$} \{1,2\}, \, \mathcal {G}_2 (1,1) \xleftarrow {\$} \mathsf {True} (1,1) = \{1,2\}\), \(\mathcal {G}_2 (1,0) = 1\), and \(\mathcal {G}_2 (0,1) = 2\). Thus, \(\mathcal {G}_2\) and \(\mathcal {F}\) are essentially the same, although the formats of output are different. Therefore, \(\mathcal {G}_n\) is a generalization of \(\mathcal {F}\).
1.3 Contribution
In this paper, we propose a card-based protocol for realizing the above-mentioned functionality \(\mathcal {F}\). In particular, we construct a secure protocol for deciding the first move using a deck of physical cards. Our protocol uses only four cards and one shuffle, and its procedure is very simple.
We moreover construct a covert lottery protocol to realize the functionality \(\mathcal {G}_n\) by applying the six-card AND protocol [21]. As will be explained in more details later, the proposed protocol makes use of the extra card sequence that is not used as output in the six-card AND protocol [21].
1.4 Related Work
Card-based cryptography provides ways for secure multi-party computations using a deck of physical cards, and various protocols and their computation models have been proposed (e.g., [10,11,12, 19, 20, 27, 28, 35]) since the seminal work of Den Boer [2] in 1989. Some specific applications are three-input majority voting protocols [23, 25, 38, 39], which output a majority vote for or against three participants while keeping their input secret, millionaire protocols [14, 24, 26], which secretly compare who has the largest amount of money, ranking protocols [33, 34], which output the rich list without revealing each amount of money, a secret grouping protocol [8], which classifies players into groups, and zero-knowledge proof protocols (e.g., [3, 5, 7, 13, 15, 16, 29,30,31]), which prove the existence of a solution to a puzzle instance without revealing the solution itself.
In addition to using a deck of cards, cryptographic protocols based on various kinds of physical tools have been proposed (e.g., [1, 4, 6, 18, 22]).
2 Preliminary
In this section, we introduce basic primitives used in our protocols. In Sect. 2.1, we define a deck of cards. In Sects. 2.2 and 2.3, we present two shuffles, the random bisection cut and the pile-scramble shuffle. In Sect. 2.4, we introduce the existing six-card AND protocol.
2.1 Deck of Cards
We assume that the face of cards is either  or
or  and that their back sides are the same
and that their back sides are the same  . All cards having the same face are assumed to be indistinguishable. We call those cards of two suits binary cards. A deck of binary cards is used in our protocol presented in Sect. 3.
. All cards having the same face are assumed to be indistinguishable. We call those cards of two suits binary cards. A deck of binary cards is used in our protocol presented in Sect. 3.
Using two cards  and
and  , a single bit of information is encoded as follows:
, a single bit of information is encoded as follows:

A pair of face-down cards  is called a commitment to \(x \in \{0,1\}\) if it encodes the value x according to the above encoding rule. It is denoted by
is called a commitment to \(x \in \{0,1\}\) if it encodes the value x according to the above encoding rule. It is denoted by

We also use another type of cards called number cards. The face of each number card has a positive integer like  and their back sides are the same
and their back sides are the same  as binary cards. A deck having both binary cards and number cards is used in our protocol presented in Sect. 4.
as binary cards. A deck having both binary cards and number cards is used in our protocol presented in Sect. 4.
2.2 Random Bisection Cut
A random bisection cut [21] is a shuffle operation, which is applicable to a sequence having an even number of cards. A random bisection cut for 2m cards proceeds as follows. First, it bisects the sequence into the left m cards and the right m cards. Then, it randomly swaps the left and right piles. As a result, a sequence of 2m cards (indistinguishable to the original sequence) is obtained.
The following is an example of applying a random bisection cut to two commitments \(a \text {,} \, b \in \{0,1\}\). First, it bisects a sequence of cards into two piles of cards having the same number of cards. In this example, a sequence of four cards is divided into commitments to a and b:

Next, the left and right piles are swapped randomly. This results in two commitments to (a, b) or (b, a) with a probability of 1/2. Hereinafter, we denote a random bisection cut by \(\left[ \ \cdot \ \left| \ \cdot \ \right] \right. \) as follows:

Ueda et al. [36, 37] showed how to securely implement a random bisection cut. According to their experiments, a random bisection cut can be implemented so that nobody knows whether two piles are swapped or not.
2.3 Pile-Scramble Shuffle
A pile-scramble shuffle [9] is a shuffle operation, which is applicable to a sequence of mk cards for some positive integers m and k. A pile-scramble shuffle for m piles proceeds as follows. First, it splits a sequence of mk cards into m piles \((\mathsf {pile}_1,\mathsf {pile}_2,\ldots ,\mathsf {pile}_m)\) each having k cards. Then it randomly permutes the m piles. As a result, a sequence of m piles \((\mathsf {pile}_{\pi ^{-1}(1)},\mathsf {pile}_{\pi ^{-1}(2)},\ldots ,\mathsf {pile}_{\pi ^{-1}(m)})\) is obtained where \(\pi \) is a random permutation. A pile-scramble shuffle can be securely implemented by the use of everyday objects such as envelopes.
2.4 Six-Card AND Protocol
Mizuki and Sone [21] designed a six-card AND protocol. It takes two commitments to \(a, b \in \{0,1\}\) along with two additional helping cards  and outputs a commitment to \(a \wedge b\) as follows:
and outputs a commitment to \(a \wedge b\) as follows:

The protocol proceeds as follows.
-
1.
Place two commitments to \(a, b \in \{0,1\}\) and two binary cards
 as:
as: 
-
2.
Rearrange the sequence as:

-
3.
Apply a random bisection cut to the sequence as:

-
4.
Rearrange the sequence as:
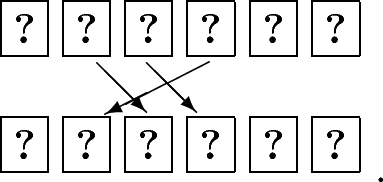
-
5.
Turn over the leftmost two cards. If they are
 , the middle pair is a commitment to \(a \wedge b\). Otherwise, the right pair is a commitment to \(a \wedge b\). The other pair is a commitment to \(\overline{a} \wedge b\) in both cases.
, the middle pair is a commitment to \(a \wedge b\). Otherwise, the right pair is a commitment to \(a \wedge b\). The other pair is a commitment to \(\overline{a} \wedge b\) in both cases. 
3 A Secure Protocol for Deciding the First Turn
In this section, we design a secure protocol for deciding the first turn. That is, our protocol should realize the functionality \(\mathcal {F}\) defined in Eq. (1) in Sect. 1.1. The protocol takes input commitments to \(x_1, x_2 \in \{0,1\}\), and outputs a commitment to \(\mathcal {F}(x_1, x_2)\) which designates whether the first player \(P_1\) takes the first move or not, as follows:

In Sect. 3.1, we explain the idea behind constructing our protocol. In Sect. 3.2, we give the protocol construction.
3.1 Idea
First, note that when \(x_1 \ne x_2\), we have \(x_1 = \overline{x_2}\); when \(x_1 = x_2\), we have \(\{x_1,\overline{x_2}\} = \{0,1\}\). Then, using \(\overline{x_2}\), Eq. (1) is rewritten as
If \(x_1 = \overline{x_2}\), \(r \xleftarrow {\$} \{x_1,\overline{x_2}\}\) always satisfies \(r = x_1 = \overline{x_2}\). Therefore, instead of Eq. (4), we can simply write
Therefore, if we have the following two commitments, it suffices to randomly choose one of them without knowing which is which:

This can be done with a random bisection cut, as seen in the next subsection.
3.2 Description
Our protocol for performing the functionality \(\mathcal {F}\) proceeds as follows.
-
1.
Place two commitments to \(x_1, x_2 \in \{0,1\}\) where \(x_i\) is \(P_i\)’s preference:

-
2.
Apply the NOT computation to the commitment to \(x_2\) by swapping the two cards:

-
3.
Apply a random bisection cut:

-
4.
The left commitment is a commitment to \(\mathcal {F}\):

Thus, our protocol surely follows Eq. (5), implying that it realizes \(\mathcal {F}\). Our protocol uses only four cards and one random bisection cut, and is very simple.
Instead of applying a random bisection cut to the four cards in Step 3, we may apply it to the first and third cards; in this case, the result will be obtained based on the encoding  and
and  .
.
4 Covert Lottery Protocol
In this section, we extend our protocol shown in the previous section: We propose a card-based covert lottery protocol that realizes \(\mathcal {G}_n\). We first present the idea behind this protocol and then show its description. Our proposed protocol takes as input n commitments to \(x_1, x_2, \ldots , x_n\) (each of which represents player’s preference) along with four binary cards and n number cards, and outputs a single number card that represents a winner \(w = \mathcal {G}_n (x_1, x_2, \ldots , x_n)\):

In Sect. 4.1, we explain the idea behind this protocol. In Sect. 4.2, we show the protocol construction completely.
4.1 Idea
Let us look back at Eq. (3). To realize \(\mathcal {G}_n\), it suffices to randomly choose a single player from the set \(\mathsf {True} (x_1, x_2, \ldots , x_n)\) if there are players who are positive to get the prize; otherwise, it suffices to randomly choose a single player from the set of all players \(\{1, 2, \ldots , n\}\). To accomplish this, we first apply a pile-scramble shuffle to the n input commitments \(x_1, x_2, \ldots , x_n\) to make the order of the inputs random. To keep track of correspondence between inputs and players, a number card  is attached to each commitment \(x_i\), \(1 \le i \le n\), before applying a pile-scramble shuffle:
is attached to each commitment \(x_i\), \(1 \le i \le n\), before applying a pile-scramble shuffle:

That is, the resulting sequence of cards after a pile-scramble shuffle is as follows:

where \((X_1, X_2, \ldots , X_n)\) is generated by permuting \((x_1, x_2, \ldots , x_n)\) with a random permutation \(\pi \).
If we turn over the commitments to \(X_1, X_2, \ldots , X_n\) one by one from left to right, the first revealed commitment to 1 deserves a randomly chosen commitment from the set \(\mathsf {True} (x_1, x_2, \ldots , x_n)\) due to the pile-scramble shuffle. Thus, it suffices to output the number card attached to it as the winner. If \(X_1= \cdots = X_n=0\), then it suffices to output the rightmost number card as a randomly chosen winner from all players. We construct the protocol based on this principle. However, of course, if we simply reveal the commitments to \(X_1, X_2, \ldots , X_n\) one by one, information about the input value of the winner and the number of 0s among (a part of) the inputs would be leaked. For example, let \(n=5\) and \((X_1, X_2, X_3, X_4, X_5) = (0, 0, 1, 0, 1)\). In this case, \(X_1\), \(X_2\), and \(X_3\) are revealed, and hence, all players learn that at least two players’ inputs are 0s and the winner’s input is 1. Let the inputs be (0, 0, 0, 0, 0) for another example. In this case, all players learn that all the inputs are 0s. To avoid this leakage, we shall perform the above computation while keeping the input values secret.
For this, we introduce a “token” commitment. A token is used to rewrite each input commitment. That is, the winner is determined by making all of the commitments correspond to 0s except for the first revealed commitment to 1. Specifically, we repeatedly perform an AND computation of an input commitment (from left to right) and the token whose initial value is 1, and replace the input commitment with the output of the AND computation (namely, it outputs 1 if and only if both the input and token are 1s). The token should remain 1 until the AND computation first outputs 1, and be 0 after it outputs 1. This computation is accomplished by performing the AND computation of the token and the negation of each input. To summarize, given an i-th input commitment to \(X_i\) and the token commitment to t, we perform the following computation and replace the i-th input commitment with a commitment to \(y_i = X_i \wedge t\) and the token commitment is updated by  \((1 \le i \le n-1)\):
\((1 \le i \le n-1)\):

where the initial value of the token is \(t = 1\). The n-th commitment is replaced with the final token.
Let us take an example. Consider the case where \((X_1, X_2, \ldots , X_5) = (0, 1, 0, 1, 1)\). In this case, \(y_i\) and t change depending on \(X_i\) and t, as shown in Table 1. First, since \(X_1 = 0\), we have \(y_1 = 0 \wedge 1 = 0\) and  . Since \(X_2 = 1\), \(y_2 = 1 \wedge 1 = 1\), we have
. Since \(X_2 = 1\), \(y_2 = 1 \wedge 1 = 1\), we have  . Since \(y_i = X_i \wedge t\) and
. Since \(y_i = X_i \wedge t\) and  , once the token t becomes 0, all of the remaining AND computations shall output 0s as shown in Table 1.
, once the token t becomes 0, all of the remaining AND computations shall output 0s as shown in Table 1.
To perform (6), it suffices to use the six-card AND protocol [21]; thus, we can implement a card-based covert lottery protocol by using the six-card AND protocol \(n-1\) times. As mentioned above, we set the final commitment to \(y_n=t\). If \(X_1,\ldots ,X_{n-1}\) are all 0s, we have \(t = 1\), and hence, \(y_n = 1\). If there is at least 1 among \(X_1,\ldots ,X_{n-1}\), we have \(t = 0\), and hence, \(y_n = 0\). Note that, aside from n input commitments, we use four binary cards for the token and the helping cards in the six-card AND protocol.
4.2 Description
The description of our proposed protocol is as follows.
-
1.
Each player secretly creates an input commitment; we now have n input commitments as follows:

-
2.
Place a number card
 above each commitment to \(x_i\) and make n piles of cards consisting of three cards:
above each commitment to \(x_i\) and make n piles of cards consisting of three cards: 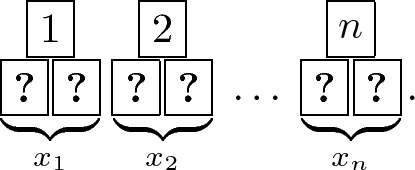
-
3.
Turn over every number card and apply a pile-scramble shuffle to the sequence of piles:

Let \(X_1 \text {,} \, X_2 \text {,} \, \ldots \text {,} \, X_n \in \{0,1\}\) be the values of the resulting commitments after the shuffle.
-
4.
Using a pair of free binary cards, make a commitment to \(t= 1\) by placing
 and turning them over.
and turning them over. -
5.
Let \(j = 1\). Perform the following computation \(n-1\) times.
-
(a)
Taking as input the commitment to \(X_j\) and the token commitment to t, perform the six-card AND protocol [21] along with the remaining pair of free cards
 to obtain the following two commitments:
to obtain the following two commitments: 
Place the former commitment to \(y_i = X_j \wedge t\) below the number card as the commitment to \(X_j\) was there. Let the latter commitment be the next token t. Note that the two face-up cards
 that were revealed to determine the output can be reused in the next AND computation.
that were revealed to determine the output can be reused in the next AND computation.
-
(a)
-
6.
Let the commitment to t be a commitment to \(y_n\).
-
7.
Apply a pile-scramble shuffle again to the sequence of n piles, each of which consists of the commitment to \(y_i\) and a number card:

Let \(Y_1, Y_2, \ldots , Y_n \in \{0,1\}\) be the values of the resulting commitments after the shuffle.
-
8.
Turn over the commitments to \(Y_1,Y_2, \ldots , Y_n\); there should be exactly one commitment to 1. Then, turn over the number card above it. We have the winner represented by the revealed number card.
4.3 Security
We claim that all face-up symbols opened in an execution of the protocol are uniformly randomly and independently distributed from the inputs and output. Face-down cards are opened in Steps 5(a) and 8 only. In Step 5(a), two cards are opened by the six-card AND protocol. From the security of the six-card AND protocol, these symbols are distributed uniformly randomly and independently from any other values. In Step 8, the commitments to \(Y_1, Y_2, \ldots , Y_n\) are opened. We note that only a single \(Y_i\) is a commitment to 1 and the others are commitments to 0. From the property of the pile-scramble shuffle, the number i is distributed uniformly randomly among \(\{1, 2, \ldots , n\}\) and independently from any other values. Therefore, all face-up symbols are uniformly randomly and independently distributed from the inputs and output.
5 Conclusion
In this paper, we formalized a novel problem that determines who makes the first move in a two-player board game such as Chess and Shogi, and designed a card-based protocol to solve this problem. Instead of randomly deciding the first move by a coin tossing, our protocol takes into account players’ preferences. Moreover, we generalized the problem into a multi-player case, and designed a “covert lottery protocol” to solve the problem.
We left to reduce the number of cards and the number of shuffles as an open problem. In card-based cryptography, they are considered to be the most important complexity measures. Our two-player protocol requires four cards and one shuffle. Our multi-player protocol requires \(3n+4\) cards and \(n+1\) shufflesFootnote 1. We note that it is possible to reduce the number of shuffles by applying the technique of the card-based garbled circuits [32]. However, in general, it is difficult to reduce both the number of cards and the number of shuffles at the same time.
Another interesting problem is to consider a different problem similar to the covert lottery protocol. For example, it is possible to generalize the covert lottery protocol into a protocol with multiple winners although our protocol has a single winner. As another example, since the covert lottery protocol can be viewed as an election with candidacies, it would be worthwhile to consider a protocol for an election that allows for nominations.
Notes
- 1.
If we make \(X_n\) be two free cards by a random bisection cut before Step 4, the number of cards can be reduced to \(3n+2\) while the number of shuffles becomes \(n+2\). If we apply the AND protocol based on the encode
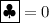 and
and 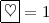 [17], we can have a \((3n+1)\)-card n-shuffle protocol or a 3n-card \((n+1)\)-shuffle protocol.
[17], we can have a \((3n+1)\)-card n-shuffle protocol or a 3n-card \((n+1)\)-shuffle protocol.
References
Abe, Y., Iwamoto, M., Ohta, K.: Efficient private PEZ protocols for symmetric functions. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11891, pp. 372–392. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36030-6_15
Boer, B.: More efficient match-making and satisfiability The five card trick. In: Quisquater, J.J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 208–217. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_23
Bultel, X., et al.: Physical zero-knowledge proof for Makaro. In: Izumi, T., Kuznetsov, P. (eds.) SSS 2018. LNCS, vol. 11201, pp. 111–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03232-6_8
Costiuc, M., MaimuŢ, D., Teşeleanu, G.: Physical cryptography. In: Simion, E., Géraud-Stewart, R. (eds.) Innovative Security Solutions for Information Technology and Communications, pp. 156–171. Springer International Publishing, Cham (2020)
Dumas, J.G., Lafourcade, P., Miyahara, D., Mizuki, T., Sasaki, T., Sone, H.: Interactive physical zero-knowledge proof for Norinori. In: Du, D.Z., Duan, Z., Tian, C. (eds.) COCOON 2019. LNCS, vol. 11653, pp. 166–177. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26176-4_14
Fagin, R., Naor, M., Winkler, P.: Comparing information without leaking it. Commun. ACM 39(5), 77–85 (1996). https://doi.org/10.1145/229459.229469
Gradwohl, R., Naor, M., Pinkas, B., Rothblum, G.N.: Cryptographic and physical zero-knowledge proof systems for solutions of Sudoku puzzles. Theory Comput. Syst. 44(2), 245–268 (2009). https://doi.org/10.1007/s00224-008-9119-9
Hashimoto, Y., Shinagawa, K., Nuida, K., Inamura, M., Hanaoka, G.: Secure grouping protocol using a deck of cards. In: Shikata, J. (ed.) ICITS 2017. LNCS, vol. 10681, pp. 135–152. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-72089-0_8
Ishikawa, R., Chida, E., Mizuki, T.: Efficient card-based protocols for generating a hidden random permutation without fixed points. In: Calude, C.S., Dinneen, M.J. (eds.) UCNC 2015. LNCS, vol. 9252, pp. 215–226. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21819-9_16
Kastner, J., et al.: The minimum number of cards in practical card-based protocols. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 126–155. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_5
Koch, A., Schrempp, M., Kirsten, M.: Card-based cryptography meets formal verification. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019. LNCS, vol. 11921, pp. 488–517. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34578-5_18
Koch, A., Walzer, S.: Foundations for actively secure card-based cryptography. In: 10th International Conference on Fun with Algorithms (FUN 2020), pp. 1–27. Leibniz International Proceedings in Informatics (LIPIcs), Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany. https://doi.org/10.4230/LIPIcs.FUN.2021.17
Lafourcade, P., Miyahara, D., Mizuki, T., Sasaki, T., Sone, H.: A physical ZKP for Slitherlink: how to perform physical topology-preserving computation. In: Heng, S.H., Lopez, J. (eds.) ISPEC 2019. LNCS, vol. 11879, pp. 135–151. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34339-2_8
Miyahara, D., Hayashi, Y., Mizuki, T., Sone, H.: Practical card-based implementations of Yao’s millionaire protocol. Theoretical Comput. Sci. 803, 207–221 (2020). https://doi.org/10.1016/j.tcs.2019.11.005
Miyahara, D., et al.: Card-based ZKP protocols for Takuzu and Juosan. In: Farach-Colton, M., Prencipe, G., Uehara, R. (eds.) 10th International Conference on Fun with Algorithms (FUN 2020). Leibniz International Proceedings in Informatics (LIPIcs), vol. 157, pp. 20:1–20:21. Schloss Dagstuhl-Leibniz-Zentrum für Informatik, Dagstuhl, Germany (2020). https://drops.dagstuhl.de/opus/volltexte/2020/12781
Miyahara, D., Sasaki, T., Mizuki, T., Sone, H.: Card-based physical zero-knowledge proof for Kakuro. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E102A(9), 1072–1078 (2019). https://doi.org/10.1587/transfun.E102.A.1072
Mizuki, T.: Card-based protocols for securely computing the conjunction of multiple variables. Theoretical Comput. Sci. 622(C), 34–44 (2016). https://doi.org/10.1016/j.tcs.2016.01.039
Mizuki, T., Kugimoto, Y., Sone, H.: Secure multiparty computations using the 15 puzzle. In: Dress, A., Xu, Y., Zhu, B. (eds.) COCOA 2007. LNCS, vol. 4616, pp. 255–266. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73556-4_28
Mizuki, T., Shizuya, H.: A formalization of card-based cryptographic protocols via abstract machine. Int. J. Inf. Secur. 13(1), 15–23 (2014). https://doi.org/10.1007/s10207-013-0219-4
Mizuki, T., Shizuya, H.: Computational model of card-based cryptographic protocols and its applications. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E100A(1), 3–11 (2017). https://doi.org/10.1587/transfun.E100.A.3
Mizuki, T., Sone, H.: Six-card secure AND and four-card secure XOR. In: Deng, X., Hopcroft, J.E., Xue, J. (eds.) FAW 2009. LNCS, vol. 5598, pp. 358–369. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02270-8_36
Murata, S., Miyahara, D., Mizuki, T., Sone, H.: Public-PEZ cryptography. In: Susilo, W., Deng, R.H., Guo, F., Li, Y., Intan, R. (eds.) Information Security, pp. 59–74. Springer International Publishing, Cham (2020)
Nakai, T., Shirouchi, S., Iwamoto, M., Ohta, K.: Four cards are sufficient for a card-based three-input voting protocol utilizing private permutations. In: Shikata, J. (ed.) ICITS 2017. LNCS, vol. 10681, pp. 153–165. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-72089-0_9
Nakai, T., Tokushige, Y., Misawa, Y., Iwamoto, M., Ohta, K.: Efficient card-based cryptographic protocols for Millionaires’ problem utilizing private permutations. In: Foresti, S., Persiano, G. (eds.) CANS 2016. LNCS, vol. 10052, pp. 500–517. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48965-0_30
Nishida, T., Hayashi, Y., Mizuki, T., Sone, H.: Securely computing three-input functions with eight cards. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E98A(6), 1145–1152 (2015). https://doi.org/10.1587/transfun.E98.A.1145
Ono, H., Manabe, Y.: Efficient card-based cryptographic protocols for the millionaires’ problem using private input operations. In: 2018 13th Asia Joint Conference on Information Security (AsiaJCIS), pp. 23–28, August 2018. https://doi.org/10.1109/AsiaJCIS.2018.00013
Ono, H., Manabe, Y.: Card-based cryptographic protocols with the minimum number of rounds using private operations. In: Pérez-Solà, C., Navarro-Arribas, G., Biryukov, A., Garcia-Alfaro, J. (eds.) DPM/CBT 2019. LNCS, vol. 11737, pp. 156–173. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31500-9_10
Ono, H., Manabe, Y.: Card-based cryptographic logical computations using private operations. New Gener. Comput. 1, 1–22 (2020). https://doi.org/10.1007/s00354-020-00113-z
Robert, L., Miyahara, D., Lafourcade, P., Mizuki, T.: Physical zero-knowledge proof for Suguru puzzle. In: Devismes, S., Mittal, N. (eds.) SSS 2020. LNCS, vol. 12514, pp. 235–247. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64348-5_19
Ruangwises, S., Itoh, T.: Physical zero-knowledge proof for numberlink puzzle and k vertex-disjoint paths problem. New Gener. Comput. 1, 1–15 (2020). https://doi.org/10.1007/s00354-020-00114-y
Sasaki, T., Miyahara, D., Mizuki, T., Sone, H.: Efficient card-based zero-knowledge proof for Sudoku. Theoretical Comput. Sci. 839, 135–142 (2020). https://doi.org/10.1016/j.tcs.2020.05.036
Shinagawa, K., Nuida, K.: A single shuffle is enough for secure card-based computation of any Boolean circuit. Discrete Appl. Math. 289, 248–261 (2021). https://doi.org/10.1016/j.dam.2020.10.013
Takashima, K., et al.: Card-based secure ranking computations. In: Li, Y., Cardei, M., Huang, Y. (eds.) COCOA 2019. LNCS, vol. 11949, pp. 461–472. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36412-0_37
Takashima, K., et al.: Card-based protocols for secure ranking computations. Theoretical Comput. Sci. 845, 122–135 (2020). https://doi.org/10.1016/j.tcs.2020.09.008
Toyoda, K., Miyahara, D., Mizuki, T., Sone, H.: Six-card finite-runtime XOR protocol with only random cut. In: Proceedings of the 7th ACM on ASIA Public-Key Cryptography Workshop, pp. 1–7. APKC 2020. ACM, New York, NY, USA. https://doi.org/10.1145/3384940.3388961
Ueda, I., Miyahara, D., Nishimura, A., Hayashi, Y., Mizuki, T., Sone, H.: Secure implementations of a random bisection cut. Int. J. Inf. Secur. 19(4), 445–452 (2019). https://doi.org/10.1007/s10207-019-00463-w
Ueda, I., Nishimura, A., Hayashi, Y., Mizuki, T., Sone, H.: How to implement a random bisection cut. In: Martín-Vide, C., Mizuki, T., Vega-Rodríguez, M.A. (eds.) TPNC 2016. LNCS, vol. 10071, pp. 58–69. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-49001-4_5
Watanabe, Y., Kuroki, Y., Suzuki, S., Koga, Y., Iwamoto, M., Ohta, K.: Card-based majority voting protocols with three inputs using three cards. In: 2018 International Symposium on Information Theory and Its Applications (ISITA), pp. 218–222 (2018). https://doi.org/10.23919/ISITA.2018.8664324
Yasunaga, K.: Practical card-based protocol for three-input majority. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E103A(11), 1296–1298 (2020). https://doi.org/10.1587/transfun.2020EAL2025
Acknowledgements
We thank the anonymous referees, whose comments have helped us to improve the presentation of the paper. We thank the anonymous reviewer at some conference who have inspired us to present the protocol shown in Sect. 3. This work was supported in part by JSPS KAKENHI Grant Numbers JP19J21153 and JP20J01192.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Shinoda, Y., Miyahara, D., Shinagawa, K., Mizuki, T., Sone, H. (2021). Card-Based Covert Lottery. In: Maimut, D., Oprina, AG., Sauveron, D. (eds) Innovative Security Solutions for Information Technology and Communications. SecITC 2020. Lecture Notes in Computer Science(), vol 12596. Springer, Cham. https://doi.org/10.1007/978-3-030-69255-1_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-69255-1_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-69254-4
Online ISBN: 978-3-030-69255-1
eBook Packages: Computer ScienceComputer Science (R0)





 as:
as: 



 , the middle pair is a commitment to
, the middle pair is a commitment to 





 above each commitment to
above each commitment to 

 and turning them over.
and turning them over. to obtain the following two commitments:
to obtain the following two commitments: 
 that were revealed to determine the output can be reused in the next AND computation.
that were revealed to determine the output can be reused in the next AND computation.
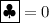 and
and 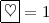 [
[