An Average Loss Control Chart Under a Skewed Process Distribution

Abstract

In the global market the quality of products is a crucial factor separating competitive companies within numerous industries. These firms may employ a loss function to measure the loss caused by a deviation of the quality variable from the target value. From the view of Taguchi’s philosophy, monitoring this deviation from the process target value is important, but in practice many quality data have distributions that are not normal but skewed. This paper thus develops an average loss control chart for monitoring quality loss variation under skewed distributions. We investigate the statistical properties of the proposed control chart and measure the out-of-control process detection performance of the proposed loss control charts by using the average run length. The average loss control chart illustrates the best performance in detecting of out-of-control loss location for a left-skewed process distribution and performs better than the existing median loss control chart.

1 Introduction

Control charts are commonly used tools in process change detection for improving the quality of manufacturing and service processes. In the past few years, more and more statistical process control techniques have been applied to the service industry, with control charts also becoming an effective tool to enhance service quality. There have been a few studies in this area of the literature, including Tsung et al. (2008), Ning et al. (2009), Yang et al. (2012), Yang and Yang (2013), Yang and Wu (2017a, b), Yang and Jiang (2019). In practice, many service quality data follow non-normal distributions. For example, the service time of a local bank branch is a critical service quality characteristic, and efficiently monitoring the location and/or dispersion of service data is an important issue to bank managers. Bank service data that have been analyzed tend to have a right-skewed distribution as shown in Yang and Wu (2017a, b). Some other examples of service quality data are fatigue symptoms of breast cancer patients Ho et al. (2014), passenger counts of Taipei’s mass rapid transit (MRT) system on a weekday basis Yang and Yang (2013), and health care costs Zhou et al. (2008). The commonly used Shewhart variables control charts, whose statistical properties depend on a normality assumption, clearly may not be suitable for monitoring service data when the variables exhibit non-normal or unknown distributions. Furthermore, McCracken and Chakraborti (2013) note that normality is often an elusive assumption, and discuss some available nonparametric schemes for jointly monitoring location and scale in overviewing control charts for joint monitoring mean and variance.

Product, service quality, and productivity loss are all crucial competitive factors of companies in numerous industries, and the loss function is a popular method for measuring the loss caused by variations in product or service quality. Taguchi (1986) proposed that target values are vital during process specification, while Sullivan (1984) emphasized the importance of monitoring deviations from the target value. Because increases in the difference between the mean and the target and/or variability are the sources of out-of-control loss, it is crucial to monitor the loss variation of a manufacturing or service process.

Scant research has been done to deal with monitoring process loss location. Existing loss-function-based control charts are based on the assumption that the in-control mean of a process quality variable equals the target value; see, for example, Zhang and Wu (2006) and Wu et al. (2009). However, in practice, the in-control process mean may not actually be the process target, and diagnosing the source of an out-of-control signal is crucial for correcting an out-of-control process loss location. Yang (2013a, b), Yang and Lin (2014) and Yang et al. (2017) proposed loss-based control charts in order to monitor the loss location that arises when quality variables deviate from target values.

A major drawback of loss-based control charts is that almost all of them are based on the assumption that the quality variable has a normal distribution. This paper focuses on discussing a loss-based control chart under non-normal distributions. We note that the sample median is more robust than the sample average for estimating the population location as the former is less affected by extreme values Graham et al. (2011). Motivated by this, Yang et al. (2017) considered using the median loss to express the quality loss function under a non-normal distribution. For this reason, the resulting loss-based control chart is called the median loss (ML) control chart throughout their paper. Their ML chart and the optimal variable sampling intervals median loss (VSI ML) chart both illustrate the best out-of-control detection performance for the left-skewed distributed process among the considered left-skewed, symmetric, and right-skewed distributions. Even under a normal distribution, they illustrated that the resulting out-of-control detection performance of the VSI ML chart is better than the VSI average loss (AL) chart in Yang (2013b) and the weighted loss (WL) control charts in Yang and Lin (2014), except for very small shifts in process mean. However, the properties of average loss (ALSN) control chart were not discussed for a non-normal distributed process. Here in this present study, we consider that both the sample size and sampling interval are fixed and will examine whether the ALSN control chart has better out-of-control detection performance than that of the ML chart under a skew-normal distributed process. Hence, we proceed to derive the ALSN control chart and discuss the out-of-control detection performances of the ALSN control chart either when the process distribution is left-skewed, symmetric, or right-skewed, respectively.

The paper is organized as follows. Section 2 introduces the sampling distribution of the median loss for a quality variable, X, with a skew-normal distribution. Section 3 illustrates the control limits of the ML chart for various sample sizes and out-of-control detection performances for small to moderate shifts in mean and variance. Section 4 derives the distribution of sample average loss, constructs the ALSN control chart, and measures its out-of-control detection performance for small to moderate shifts in mean and variance. Section 5 compares the out-of-control detection performance between the proposed ALSN chart and the ML chart in Yang et al. (2017) by considering the process with left-skewed, symmetric, and right-skewed normal distribution, respectively. Section 6 summarizes the findings and provides a recommendation.

2 The ML Control Chart

2.1 The Skew-Normal Distribution

We let the random variable X have a skew-normal distribution with location parameter $\xi _0 \in (-\infty ,\infty )$, scale parameter $a_0 \in (0,\infty )$, and shape parameter $b \in (-\infty ,\infty )$, i.e., $X\sim SN(\xi _0, a_0, b)$. From Azzalini (1985), the probability density function (pdf) of X is:

$$\begin{aligned} f_X(x) = \frac{2}{a_0} \varphi \left( \frac{x-\xi _0}{a_0}\right) \varPhi \left( b \frac{x-\xi _0}{a_0}\right) , \quad x\in (-\infty ,\infty ) \,, \end{aligned}$$

(1)

where $\varphi (\cdot )$ and $\varPhi (\cdot )$ are respectively the pdf and cumulative distribution function (cdf) of the standard normal distribution.

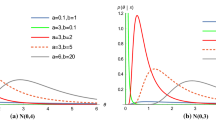
In (1) we know that if $b=0$, then the skew-normal distribution will reduce to the normal distribution with mean $\xi _0$ and standard deviation $a_0$. The distribution is right-skewed if $b>0$ and is left-skewed if $b<0$. The plot of the pdfs for $b = -2, 0, 3$ is shown in Fig. 1.

Fig. 1

The pdfs for different b

The cumulative distribution function (cdf) of the skew-normal random variable X is:

$$\begin{aligned} F_X(x) = \varPhi \left( \frac{x-\xi _0}{a_0}\right) - \frac{1}{\pi } \int _0^b \frac{\exp \left[ -\frac{1}{2} \left( \frac{x-\xi _0}{a_0}\right) ^2 (1+y^2)\right] }{1+y^2} \, dy \;,\quad x \in (-\infty , \infty ) \,. \end{aligned}$$

(2)

2.2 The Loss Function

The loss function is defined as $L = k (X-T)^2$. Let $X_i$, $i=1,2,\ldots ,n$, be a random sample from the in-control distribution of $SN(\xi , a, b)$. The sample median loss depends on the sample size being odd or even. We only consider the case where the sample size is an odd value for easier derivation of the distribution of the sample median loss.

Denote the sample statistic of median loss as $ML = (X-T)^2_{\left( (\frac{n+1}{2}\right) }$, where ML is the loss value separating the higher half from the lower half of a loss data sample. For a loss dataset, this may be thought of as the “middle” loss value.

Referring to Yang et al. (2017), the derived cdf of ML is as follows.

$$\begin{aligned} F_{ML}(t)&= \int _0^t f_M(u)\,du \nonumber \\&= \frac{n!}{\left[ \left( \frac{n-1}{2}\right) !\right] ^2} \int _0^t F_{(X-T)^2}(u)^\frac{n-1}{2} \big [ 1 - F_{(X-T)^2}(u) \big ]^\frac{n-1}{2} f_{(X-T)^2}(u) \, du \nonumber \\&= \frac{n!}{\left[ \left( \frac{n-1}{2}\right) !\right] ^2} B\left( \frac{1}{a_0\sqrt{t}} \left[ \varphi \left( \frac{\sqrt{t}+T-\xi _0}{a_0}\right) \varPhi \left( b\frac{\sqrt{t}+T-\xi _0}{a_0}\right) \ldots \right. \right. \nonumber \\&\; \left. \left. + \, \varphi \left( \frac{-\sqrt{t}+T-\xi _0}{a_0}\right) \varPhi \left( b\frac{-\sqrt{t}+T-\xi _0}{a_0}\right) \right] , \frac{n+1}{2}, \frac{n+1}{2} \right) \,, \; t > 0 \,, \end{aligned}$$

(3)

where $B(x,a,b) = \int _0^x t^{a-1} (1-t)^{b-1} \, dt$ is an incomplete beta function.

We determine the ML control chart based on the cdf of ML in order to monitor the changes in the loss location or, equivalently, to monitor the shifts in the in-control population mean (or the deviation of $\mu _0 - T$) and/or standard deviation.

Table 1 Control limits of the ML chart with ARL$_0=$370.4

2.3 The Design of a Median Loss Control Chart

We first establish the ML control chart with a specified false alarm rate $\alpha$ by using Eq. (3). The upper control limit (UCL) and the lower control limit (LCL) of the ML chart are obtained by taking the inverse cdf of ML – that is:

$$\begin{aligned} UCL = F_{ML}^{-1} (1-\alpha /2) \;,\quad LCL = F_{ML}^{-1} (\alpha /2) \,. \end{aligned}$$

(4)

The process is deemed to be out-of-control if the monitoring statistic ML is smaller than LCL or larger than UCL; otherwise, the process is considered to be in-control.

The expectation ($\mu _0$) and variance ($\sigma _0^2$) of in-control X are $\mu _0 = \xi _0 + a_0 \frac{b}{\sqrt{1+b^2}} \sqrt{\frac{2}{\pi }}$ and $\sigma _0^2 = a_0^2 \left[ 1 - \frac{2 b^2}{\pi (1+b^2)}\right]$, respectively. Let $\delta _3$ denote the dispersion parameter that satisfies $\mu _0 - T = \delta _3 \sigma _0$. For a skewed distribution, we set $\delta _3>0$.

Table 1 gives the control limits of the ML chart for various combinations of $n=5,11$, $\delta _3 = 0, 1, 2$, and $b = -500, -2, 0, 2$ and 500 under ARL$_0 = 370.4$, $\mu _0 = 0$, and $\sigma _0 = 1$. From Table 1 we can see that the widths of the control limits become narrower when n increases and b and $\delta _3$ are fixed, and the widths of the control limits become wider when $\delta _3$ increases and n and b are fixed. When $\delta _3 = 0$, the widths of the control limits are the widest for a symmetric ($b=0$) distributed quality variable. When $\delta _3>$0, the widths of the control limits become wider under an increasing b or when the distribution of the quality variable changes from left-skewed, to normal, to right-skewed.

3 Performance Measurement of the ML Chart

We fix ARL$_0$ at a desired level, for example 370.4, while for an out-of-control process average run length (ARL$_1$) being smaller is better. Here, ARL$_0$ for the ML chart is:

$$\begin{aligned} \text {ARL}_0 = 1 / \big ( 1 - P(LCL< ML < UCL\mid \text {in-control}\,{ ML})\big ) \;. \end{aligned}$$

(5)

Suppose that $X^*$ is the quality characteristic for the out-of-control process, and $X^* \sim SN(\xi ^*, a^*, b)$ has mean $\mu _1 = \mu _0 + \delta _1 \sigma _0$, $\delta _1 \ne 0$, and standard deviation $\sigma _1 = \delta _2 \sigma _0$, $\delta _2 \ge 1$. The power ($1-\beta$) is the probability that the out-of-control median loss statistic ($ML^*$) is larger than UCL or smaller than LCL – that is:

$$\begin{aligned} 1 - \beta = 1 - P(LCL< ML^* < UCL) = F_{ML^*}(LCL) + 1 - F_{ML^*}(UCL) \;. \end{aligned}$$

Hence, we obtain:

$$\begin{aligned} \text {ARL}_1 = \frac{1}{1-\beta } = \frac{1}{F_{ML^*}(LCL) + 1 - F_{ML^*}(UCL)} \;, \end{aligned}$$

(6)

where $F_{ML^*}(\cdot )$ is the cdf of the out-of-control median loss statistic.

Table 2 illustrates the out-of-control detection performance of the ML chart for the shifts in mean and standard deviation, $\delta _1 = 1.0, 2.0$, $\delta _2 = 1.0, 2.0$, the dispersion parameter, $\delta _3 = 0, 1, 2$, ARL$_0 = 370.4$, $n = 5$, $\mu _0 = 0$, $\sigma _0 = 1$, and the quality variable with the left half normal ($b = -500$), left-skewed ($b = -2$), symmetric ($b = 0$), right-skewed ($b = 2$), and right half normal ($b = 500$) distributions. In Table 2 we can see, whether $b = -500, -2, 0, 2$, or 500, that ARL$_1$ decreases when $\delta _1$ and/or $\delta _2$ are far away from $\delta _1 = 0$ and/or $\delta _2 = 1$ under a specified $\delta _3$ ($\ge 0$); the ARL$_1$ of the ML chart decreases when $\delta _3$ rises for a specified combination of ($\delta _1 > 0$, $\delta _2 > 0$, b); and the ARL$_1$s of the ML chart with the left-skewed distributed ($b < 0$) quality variable are all smaller than those of the quality variable with symmetric ($b = 0$) and right-skewed ($b > 0$) distributions. These findings suggest that the ML chart has the best performance for the left-skewed distributed quality variable.

Table 2 ARL$_1$ of the ML chart ($n=5$)

4 The Average Loss Control Chart

4.1 The Distribution of Average Loss

The Taguchi loss function is defined as $L = k (X-T)^2$. Without loss of generality, we set $k=1$. In order to design an average loss control chart, suppose that a sequence of random samples $X_1, X_2, \ldots , X_n$ of size n are taken from $SN(\xi _0, a_0, b)$. We further define the sample average loss (AL) as:

$$\begin{aligned} AL = \frac{1}{n} \sum _{i=1}^n (X_i - T)^2 = \frac{n-1}{n} S_X^2 + (\bar{X} - T)^2 \;. \end{aligned}$$

(7)

The first step to construct the ALSN chart is to find the distribution of AL when X follows a skew-normal distribution. Since the exact distribution of AL is not available, we use Edgeworth expansion (for example, see Hall 1992) to approximate the distribution of AL.

Edgeworth (1905) derived Edgeworth expansion that relates the cdf of a random variable having expectation zero and variance 1 to the cumulative density function (cdf) of the standard normal distribution using Chebyshev–Hermite polynomials.

Since the in-control $X_i$ follows $SN(\xi _0,a_0,b)$, we can obtain the first and the second moments of $L_i = (X_i - T)^2$ by using the Chebyshev–Hermite polynomials. Hence, the expectation and the standard deviation of L ($\mu _L$ and $\sigma _L$) can be obtained by the moments of L.

If we define $Z_n = \sqrt{n} (AL - \mu _L)/\sigma _L$, then we can approximate the pdf of $Z_n$ by Edgeworth expansion:

$$\begin{aligned} f_{Z_n}(z) \approx \varphi (z) - \frac{1}{\sqrt{n}} \left( \frac{1}{6} \lambda _3 \varPhi ^{(4)}(z) \right) + \frac{1}{n} \left( \frac{1}{24} \lambda _4 \varPhi ^{(5)}(z) + \frac{1}{72} \lambda _3^2 \varPhi ^{(7)}(z) \right) \;, \end{aligned}$$

(8)

where $\varPhi ^{(r)}(z) = (-1)^{r-1} H\!e_{r-1}(z) \varphi (z)$, $H\!e_{r-1}(z)$ is the Chebyshev–Hermite polynomial, and $\lambda _r$ is the $r^\text {th}$ cumulant of $(L-\mu _L)/\sigma _L$ (see Hall 1992).

We can therefore obtain the cdf of AL by the following.

$$\begin{aligned} F_{AL}(t)&= P(AL \le t) = P\left( Z_n \le \frac{\sqrt{n}(t-\mu _L)}{\sigma _L} \right) = F_{Z_n} \left( \frac{\sqrt{n}(t-\mu _L)}{\sigma _L} \right) \nonumber \\&\approx \varPhi \left( \frac{\sqrt{n}(t-\mu _L)}{\sigma _L} \right) - \frac{1}{\sqrt{n}} \left( \frac{1}{6} \lambda _3 \varPhi ^{(3)}\left( \frac{\sqrt{n}(t-\mu _L)}{\sigma _L} \right) \right) \nonumber \\&\quad + \frac{1}{n} \left( \frac{1}{24} \lambda _4 \varPhi ^{(4)}\left( \frac{\sqrt{n}(t-\mu _L)}{\sigma _L} \right) + \frac{1}{72} \lambda _3^2 \varPhi ^{(6)}\left( \frac{\sqrt{n}(t-\mu _L)}{\sigma _L} \right) \right) \,. \end{aligned}$$

(9)

The accuracy of this approximation is examined by the Pearson $\chi ^2$ goodness-of-fit test. We find when the number of random samples m is 2000 or 1000 and the sample size $n=11$ that the test reveals that the approximated cdf has no significant difference from the cdf using Monte Carlo simulation.

4.2 The Design of an Average Loss Control Chart

Using Eq. (9), the upper control limit (UCL) and lower control limit (LCL) of an average loss control chart with false alarm rate $\alpha$ are expressed as follows.

$$\begin{aligned} UCL = F_{AL}^{-1} (1-\alpha /2) \;,\quad LCL = F_{AL}^{-1} (\alpha /2) \,. \end{aligned}$$

(10)

We let the ALSN control chart represent the average loss control chart throughout the paper and estimate the control limits using Monte Carlo simulation.

Table 3 lists the control limits of the ALSN chart with ARL$_0 = 370.4$ for various combinations of $n = 5, 11$, $\delta _3 = 0, 1, 2$, $b = -500, -2, 0, 2, 500$, $\mu _0 = 0$, and $\sigma _0 = 1$. From the table we can see that the widths of the control limits become narrower when n increases and b and $\delta _3$ are fixed, and the widths of the control limits become wider when $\delta _3$ increases and n and b are fixed. When $\delta _3 = 0$, the width of the control limits is the widest for a symmetric ($b = 0$) distributed quality variable. When $\delta _3 > 0$, the widths of the control limits become wider under an increasing b or for the distribution of quality variable changing from left-skewed, to normal, to right-skewed.

Table 3 Control limits of the ALSN chart

5 Performance Measurement of the ALSN Control Chart

To measure the detection performance of the proposed ALSN control chart, we let the out-of-control mean and standard deviation be $\mu _1 = \mu _0 + \delta _1 \sigma _0$, $\delta _1 \ne 0$, and $\sigma _1 = \delta _2 \sigma _0$, $\delta _2 \ge 1$, where $\delta _1 = 1.0, 2.0$, $\delta _2 = 1.0, 2.0$, $\delta _3 = 0, 1, 2$, and $b = -500, -2. 0, 2, 500$. We estimate the ARL$_1$s using Monte Carlo simulation.

Table 4 illustrates the out-of-control detection performance of the ALSN chart for the changes in mean and standard deviation, $\delta _1 = 1.0, 2.0$, $\delta _2 = 1.0, 2.0$, the dispersion parameter, $\delta _3 = 0, 1, 2$, ARL$_0 = 370.4$, $n = 5$, $\mu _0 = 0$, $\sigma _0 = 1$, and the quality variable with the left half normal ($b = -500$), left-skewed ($b = -2$), symmetric ($b = 0$), right-skewed ($b = 2$), and right half normal ($b = 500$) distributions. In this table we can see whether $b = -500, -2, 0, 2$, or 500 that ARL$_1$ decreases when $\delta _1$ and/or $\delta _2$ are far away from $\delta _1 = 0$ and/or $\delta _2 = 1$ under a specified $\delta _3 \ge 0$); the ARL$_1$ of the ALSN chart decreases when $\delta _3$ rises for only mean changes ($\delta _1 = 1, 2$), but is almost same for $\delta _3 = 1$ and $\delta _3 = 2$; and the ARL$_1$s of the ALSN chart with the left-skewed distributed ($b < 0$) quality variable are all smaller than those of the quality variable with symmetric ($b = 0$) and right-skewed ($b > 0$) distributions, except for $\delta _1 = 1$ and $\delta _2 = 1$. These findings suggest that the ALSN chart has better performance for the left-skewed distributed quality variable.

We further compare the ARL$_1$s between the proposed ALSN chart and the existing ML chart for a process with a skew-normal distribution. From the resulting Tables 2 and 4 we can see under $b = -500, -2, 0 , 2, 500$, respectively, that the ARL$_1$s of the ALSN chart performs better than those of the ML chart whether the process has small or moderate changes in location and/or dispersion.

Table 4 ARL$_1$ of the ALSN chart ($n=5$)

6 Conclusions

In this paper we propose a new ALSN control chart to monitor the changes in process loss location or in the deviation of process mean and target and/or variance when the distribution of a process is not symmetric but left-skewed or right-skewed. We also develop the numerical approaches for calculating control limits and ARL of the ALSN control chart are developed. Through numerical analyses, the proposed ALSN chart shows reasonable and reliable detection ability compared to the ML chart. Furthermore, the proposed ALSN chart illustrates best out-of-control detection performance for the left-skewed distributed quality variable. We thus recommend the application of the proposed ALSN chart for process loss location monitoring. In the future, we suggest to study the exponentially weighted moving average ALSN control chart, adaptive control schemes and the effect of contamination by outliers.