Abstract
Default Logic refers to a family of formalisms designed to carry out non-monotonic reasoning over a monotonic logic (in general, Classical First-Order or Propositional Logic). Traditionally, default logics have been defined and dealt with via syntactic consequence relations. Here, we introduce a family of default logics defined over modal logics. First, we present these default logics syntactically. Then, we elaborate on an algebraic counterpart. We do the latter by extending the notion of a modal algebra to acommodate for the main elements of default logics: defaults and extensions. Our algebraic treatment of default logics concludes with an algebraic completeness result. To our knowledge, our approach is novel, and it lays the groundwork for studying default logics from a dynamic logic perspective.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Default Logic refers to a family of non-monotonic formalisms tailored to reasoning with incomplete knowledge, and to dealing with contradictory information. The main features of a default logic \(\mathsf {DL}\) are defaults and extensions. Defaults are used as a tool to handle reasoning from incomplete knowledge. In turn, extensions are a mechanism for reasoning in the presence of contradictory information (via consistent alternatives). Intuitively, defaults can be seen as defeasible rules of inference, i.e., rules of inference whose conclusions are subject to annulment; whereas extensions can be understood as sets of formulas closed under the application of defaults.
The history of Default Logic traces back to Reiter’s seminal work [21]. Since then, many variants of Reiter’s original ideas have been proposed – with each variant giving rise to a different default logic (see [2] for a comprehensive summary). For the most part, these variants have focused their attention on what is meant by an extension. In particular, the emphasis has been on how different interactions between defaults, and the rules of inference of the underlying proof calculus,Footnote 1 concoct different notions of an extension satisfying one or more properties of interest. This treatment of extensions carries with it the definition and analysis of a default logic from a syntactic perspective. The other side of the coin is missing. In studying a logic (of any kind), we also wish to address it from a semantic perspective via a model theory and/or a class of algebras. This yields interesting completeness results, interpolation properties, bisimulations, etc. This semantic perspective on default logics is mostly absent, making it difficult to investigate their logical properties using standard semantic tools.
Our Work. Following the tradition in Default Logic, we start with a formulation of default logics over modal logics via deducibility (i.e., syntactical consequence in the proof calculus). We rely on the notion of global deducibility for modal logics [10]. Our formulation of a default logic is parametric, and can be instantiated with any modal system from \(\mathsf {K}\) to \(\mathsf {S5}\) extended with the universal modality [4].
For each default modal logic, we make explicit how defaults interact with the rules of inference of the underlying proof calculus by integrating the use of the former into the notion of deducibility of the latter. In addition, we show how we can parametrically define for each default modal system an algebraic counterpart. We do this by extending modal algebras to accommodate for defaults and extensions. Modal algebras are Boolean algebras with additional operators for modalities, and they make up the algebraic counterpart of modal systems [12, 28].
The algebraic treatment of defaults and extensions is done as follows. We carry out a Lindenbaum-Tarski construction that acts as an algebraic canonical model for a set of permisses. We enrich this construction with an operator to deal with defaults. This operator can be thought of as “updating” the Lindenbaum-Tarski algebra w.r.t. the application of a default. The result of the update is the algebraic counterpart of an extension. On this basis we prove an algebraic completeness result.
Related Work. Our treatment of defaults and extensions enables us to think of default logics as algebraic “model changing” logics; in the sense of, e.g., public announcement logic [20].
In our case, a model update corresponds to the application of a default (a sort of inference step). The idea of updating a model dynamically to represent syntactic steps of inference can be found in several places in the literature on dynamic logics. For instance, the problem of logical omniscience in epistemic logic (see, e.g., [26]) has been thought of as a property to be achieved after the application of a dynamic operation. In [1, 7, 16, 23], omniscience is achieved by updating models containing sets of formulas. In [15, 25] the updates are performed over awareness relational models. Dynamics of evidence are presented in [24, 27] over neighbourhood models. Finally, dynamic modalities allowing to achieve introspective states over Kripke models are introduced in [8, 9].
Closer to our work is the algebraic treatment of public announcements introduced in [18]. Therein, the algebraic submodel relation induced by the announcement of a formula \(\psi \) is represented by taking the quotient algebra modulo an equivalence relation given by \(\psi \). We show that the application of a default \(\delta \) can be captured in a similar way, i.e., by taking the quotient algebra modulo the equivalence relation given by the conclusion of \(\delta \).
Motivation. Our choice of defining default logics over modal logics is not arbitrary. Modal logics provide a wide spectrum of logics which are more expressive than \(\mathsf {CPL}\), with better computational properties than \(\mathsf {FOL}\). Moreover, these logics have a well-developed algebraic theory in terms of modal algebras. In our constructions we exploit the combination of these two features. As we will see, defaults are better modeled by means of a global consequence relation, which will be captured by the use of the universal modality. While not pursued on here, building default logics on modal logics is also interesting if one has applications of the developed formalism in mind. This is particularly true in the setting of description logics – wherein it is possible to think of defaults as a way of capturing exceptions to a taxonomy of concepts modeled in a knowledge base (see [3]).
Main Contributions. We provide a syntactic and algebraic treatment of default logics built over modal logics and study their properties. Syntactically, our construction of a default modal system is parametric on a modal system and a set of defaults. We make precise how defaults interact with the rules of inference of the underlying modal system. Algebraically, we address defaults and extensions via modal algebras. This enables us to obtain an algebraic completeness result. Moreover, it enables us the use of standard algebraic tools to study metalogical properties of default modal systems. We view this work as a first step towards an algebraization of default logic, and towards a better understanding of default systems from a logical perspective. Finally, the algebraic construction for default logics over modal logics lays the groundwork to study default systems from a dynamic logic perspective.
Structure of the Article. Section 2 covers background material. Section 3 contains our main results. Section 3.1 introduces default modal systems. Section 3.2 presents default deducibility. Section 4 provides our algebraic characterization of defaults and extensions, and a completeness theorem. In Sect. 4 we discuss default modal systems from a dynamic logic perspective. In Sect. 5 we offer some final remarks.
2 Background
2.1 Boolean Algebra in a Nutshell
We introduce some definitions and notation for Boolean algebras (see, e.g., [13] for details).
Definition 1
A Boolean Algebra (BA) is a structure \(\mathbf {A}= \langle A, {*}, {-}, 1 \rangle \) satisfying a well-known set of equations. A is also denoted as \(|\mathbf {A}|\). Occasionally, we consider operations \({+}\) and 0 defined as \({a + b} = -(-a * -b)\), and \(0 = -1\).
Definition 2
Every BA \(\mathbf {A}\) brings in a partial order \(\preceq _{\mathbf {A}}\) defined as \(x \preceq _{\mathbf {A}} y\) iff \(x = {x * y}\) (sometimes we omit the subindex \(\mathbf {A}\) and write just \(\preceq \)). We write  . A filter is a non-empty subset
. A filter is a non-empty subset  s.t.:
s.t.:  and for all
and for all  ,
,  . A filter is principal if it is of the form
. A filter is principal if it is of the form  for
for  . A filter F is proper if
. A filter F is proper if  .
.
2.2 Modal Systems
We begin by making precise the set \(\mathsf {Form}\) of well formed formulas we work with.
Definition 3
Let  be a denumerable set of proposition symbols; the set \(\mathsf {Form}\) of well formed formulas (wffs, or simply formulas) is determined by the grammar
be a denumerable set of proposition symbols; the set \(\mathsf {Form}\) of well formed formulas (wffs, or simply formulas) is determined by the grammar

We use \(\bot \), \(\varphi \vee \psi \), \(\varphi \rightarrow \psi \), \({\varphi \leftrightarrow \psi }\), \(\Diamond \varphi \) and  as abbreviations defined in the usual way.
as abbreviations defined in the usual way.
The set \(\mathsf {Form}\) can be seen as an enrichment of the basic modal language with the universal modality  . We use the universal modality as a technical tool to internalize a global consequence relation.
. We use the universal modality as a technical tool to internalize a global consequence relation.
A modal system is determined by a subset of \(\mathsf {Form}\), called axioms, and the rules of inference in Definition 4.
Definition 4
The set of rules of inference of a modal system consists of

The modal system  is determined by the axioms in Definition 5.
is determined by the axioms in Definition 5.
Definition 5
The axioms of  is the smallest set of formulas which contains all instances of propositional tautologies and the schemas:
is the smallest set of formulas which contains all instances of propositional tautologies and the schemas:

We take  as our basic modal system. The rest of the modal systems we consider are constructed by enlarging the set of axioms of
as our basic modal system. The rest of the modal systems we consider are constructed by enlarging the set of axioms of  with (all instances of) any of the schemas below, or any combination thereof, as additional axioms.
with (all instances of) any of the schemas below, or any combination thereof, as additional axioms.

E.g., the system  is obtained by adding to the axioms of
is obtained by adding to the axioms of  all instances of the schema D as further axioms. Similarly, the systems
all instances of the schema D as further axioms. Similarly, the systems  and
and  are obtained by adding the schemas T and 4, and T and 5, respectively.
are obtained by adding the schemas T and 4, and T and 5, respectively.
For each modal system \(\mathsf {M} \), we define a consequence relation \(\vdash _{\mathsf {M}}\) between sets of formulas and formulas. This relation is made precise in Definition 6.
Definition 6
Let \(\mathsf {M} \) be a modal system; an \(\mathsf {M} \)-deduction of \(\varphi \) from \(\varPhi \) is a finite sequence \(\psi _1 \dots \psi _n\) of formulas such that \(\psi _n = \varphi \), and for each \(k < n\) at least one of the following conditions hold:
-
1.
\(\psi _k\) is an axiom of \(\mathsf {M} \);
-
2.
\(\psi _k\) is a premiss, i.e., \(\psi _k \in \varPhi \);
-
3.
\(\psi _k\) is obtained from two earlier formulas using \(\mathsf {mp}\), i.e., there are \({i,j} < k\) s.t. \(\psi _j = {\psi _i \rightarrow \psi _k}\);
-
4.
\(\psi _k\) is obtained from an earlier formula using \(\mathsf {u}\), i.e., there is \({j} < k\) s.t.
 .
.
We write  iff there is an \(\mathsf {M} \)-deduction of \(\varphi \) from \(\varPhi \). The relation
iff there is an \(\mathsf {M} \)-deduction of \(\varphi \) from \(\varPhi \). The relation  is commonly referred to as global consequence.
is commonly referred to as global consequence.
If there is no need to distinguish between modal systems, we simply speak of a relation \(\vdash \) and of a deduction.
We end this section by taking note of the following properties of  . Notice that the first item refers to the necessitation property in modal logics, whereas the second item refers to a version of the deduction theorem.
. Notice that the first item refers to the necessitation property in modal logics, whereas the second item refers to a version of the deduction theorem.
Proposition 1
The following properties hold:
-
1.
If
 , then,
, then,  .
. -
2.
If
 , then,
, then,  .
.
2.3 Algebraizing Modal Systems
We present the semantics of a modal system from an algebraic perspective. Following [28], and borrowing ideas and results from [12, 14], we associate with any modal system \(\mathsf {M} \) a suitable class of algebras in a way such that the properties of \(\mathsf {M} \) are in correspondence to the properties of this class.
For the case of the modal systems we consider we will use
 s. We use this algebraic treatment of modal systems to perform default reasoning from a semantic point of view. This algebraic treatment is also instrumental to viewing default reasoning as a logic of updates over algebras. But this is us getting ahead of ourselves. For now, we focus on introducing some basic concepts and results regarding
s. We use this algebraic treatment of modal systems to perform default reasoning from a semantic point of view. This algebraic treatment is also instrumental to viewing default reasoning as a logic of updates over algebras. But this is us getting ahead of ourselves. For now, we focus on introducing some basic concepts and results regarding
 s.
s.
Definition 7
The formula algebra corresponding to the set \(\mathsf {Form}\) of formulas is the structure  where: \({\lnot }\), \({\Box }\),
where: \({\lnot }\), \({\Box }\),  are unary functions on \(\mathsf {Form}\), and \({\wedge }\) is a binary function on \(\mathsf {Form}\), such that \(\lnot \) applied to \({\varphi } \in \mathsf {Form}\) returns \({\lnot \varphi } \in \mathsf {Form}\), \(\Box \) applied to \({\varphi } \in \mathsf {Form}\) returns \({\Box \varphi } \in \mathsf {Form}\),
are unary functions on \(\mathsf {Form}\), and \({\wedge }\) is a binary function on \(\mathsf {Form}\), such that \(\lnot \) applied to \({\varphi } \in \mathsf {Form}\) returns \({\lnot \varphi } \in \mathsf {Form}\), \(\Box \) applied to \({\varphi } \in \mathsf {Form}\) returns \({\Box \varphi } \in \mathsf {Form}\),  applied to \({\varphi } \in \mathsf {Form}\) returns
applied to \({\varphi } \in \mathsf {Form}\) returns  , and \(\wedge \) applied to \({\varphi ,\psi } \in \mathsf {Form}\) returns \({\varphi \wedge \psi } \in \mathsf {Form}\).
, and \(\wedge \) applied to \({\varphi ,\psi } \in \mathsf {Form}\) returns \({\varphi \wedge \psi } \in \mathsf {Form}\).
Just as Boolean algebras (as interpretation structures) and filters (as the semantic counterpart of deducibility) are fundamental for the algebraization of Classical Propositional Logic,
 s and open filters are fundamental for the algebraization of modal systems.
s and open filters are fundamental for the algebraization of modal systems.
Definition 8
A  -modal algebra is a structure
-modal algebra is a structure  where: \(\langle B, {*}, {-}, 1 \rangle \) is a Boolean algebra; and \({f^\Box }\) and
where: \(\langle B, {*}, {-}, 1 \rangle \) is a Boolean algebra; and \({f^\Box }\) and  are unary functions on B satisfying the following equations
are unary functions on B satisfying the following equations

An open filter is a subset \(F \subseteq B\) such that F is a filter in \(\langle B, {*}, {-}, 1 \rangle \), and for all \(b \in F\),  .
.
Definition 9
An interpretation of the formula algebra \(\mathbf {F}\) on a

 , a.k.a. an interpretation on \(\mathbf {M}\), is a homomorphism \(v: {\mathbf {F}\rightarrow \mathbf {M}}\) such that:
, a.k.a. an interpretation on \(\mathbf {M}\), is a homomorphism \(v: {\mathbf {F}\rightarrow \mathbf {M}}\) such that:

Proposition 2
Every interpretation v on \(\mathbf {M}\) is uniquely determined by an assignment \(v_0: \mathsf {Prop}\rightarrow |\mathbf {M}|\).
Definition 10
Let \(\mathbf {M}\) be a
 ; we define:
; we define:
-
1.
an equation is a member of \(\mathsf {Form}^2\); we write an equation \((\varphi ,\psi )\) as \(\varphi \approx \psi \);
-
2.
an equation \(\varphi \approx \psi \) is valid under an interpretation v on \(\mathbf {M}\) iff \(v(\varphi )=v(\psi )\); we write \(\mathbf {M},v\vDash \varphi \approx \psi \) if \(\varphi \approx \psi \) is valid under v;
-
3.
an equation \(\varphi \approx \psi \) is valid in \(\mathbf {M}\) iff \(\mathbf {M},v\vDash \varphi \approx \psi \) for all interpretations v on \(\mathbf {M}\); we write \(\mathbf {M}\vDash \varphi \approx \psi \) if \(\varphi \approx \psi \) is valid in v.
We are now in a position to connect
 s and modal systems.
s and modal systems.
Proposition 3
Let \(\mathsf {M} \) be a modal system; the relation \(\cong _{\mathsf {M}}^{\varPhi }\) defined as: \({\varphi \cong _{\mathsf {M}}^{\varPhi } \psi }\) iff \(\varPhi \vdash _{\mathsf {M}}{\varphi \leftrightarrow \psi }\) yields a congruence on \(\mathbf {F}\).
Definition 11
Let \(\mathsf {M} \) be a modal system; the \(\mathsf {M} \)-Lindenbaum-Tarski algebra of a set \(\varPhi \) of wffs is the structure  where:
where:  ; and
; and

The canonical interpretation v on  is defined as \(v(\varphi ) = [\varphi ]_{\cong _{\mathsf {M}}^{\varPhi }}\).
is defined as \(v(\varphi ) = [\varphi ]_{\cong _{\mathsf {M}}^{\varPhi }}\).
Proposition 4
Every \(\mathsf {M} \)-Lindenbaum-Tarski algebra is a
 .
.
Theorem 1
For every modal system \(\mathsf {M} \), \(\varPhi \vdash _{\mathsf {M}} \varphi \) iff  .
.
The algebraic completeness of a modal system \(\mathsf {M} \) w.r.t. a corresponding subclass of
 s is obtained as a corollary of Theorem 1. In other words, an \(\mathsf {M} \)-Lindenbaum-Tarski
s is obtained as a corollary of Theorem 1. In other words, an \(\mathsf {M} \)-Lindenbaum-Tarski
 acts as an ‘algebraic canonical model’ for a set of formulas in the modal system \(\mathsf {M} \), i.e., they provide a witness for \(\varPhi \not \vdash _{\mathsf {M}} \varphi \). We make full use of \(\mathsf {M} \)-Lindenbaum-Tarski
acts as an ‘algebraic canonical model’ for a set of formulas in the modal system \(\mathsf {M} \), i.e., they provide a witness for \(\varPhi \not \vdash _{\mathsf {M}} \varphi \). We make full use of \(\mathsf {M} \)-Lindenbaum-Tarski
 s in Sect. 3.3.
s in Sect. 3.3.
3 Default Modal Logic
In this section we integrate the elements of Default Logic, defaults and extensions, into modal systems. This integration yields what we call a default modal system. For each default modal system, we introduce an associated notion of default consequence and show how defaults interact with the rules of the Hilbert-style notion of deduction for the underlying modal system. Moreover, we present how a default modal system can be viewed from an algebraic perspective, and prove a completeness result using algebraic tools. Later on, we discuss how the algebraic treatment of default modal systems can be seen as an update operation on algebraic structures. This opens up the door to thinking about default systems from a dynamic logic perspective (akin to public announcements).
3.1 Default Modal Systems
The main elements of Default Logic, i.e., defaults and extensions, are given in Definitions 12 and 13, respectively. These definitions are adapted from [21]. For the rest of this section we assume that \(\mathsf {M} \) is an arbitrary but fixed modal system.
Definition 12
A default is a triple \((\pi ,\rho ,\chi )\) of formulas written as  . The formulas \(\pi \), \(\rho \), and \(\chi \), are called prerequisite, justification, and consequent.
. The formulas \(\pi \), \(\rho \), and \(\chi \), are called prerequisite, justification, and consequent.
Definition 13
Let \(\varPhi \) be a set of formulas and \(\varDelta \) a set of defaults. Let  be a function s.t. for all sets of formulas \(\varPsi \),
be a function s.t. for all sets of formulas \(\varPsi \),  is the \(\subseteq \)-smallest set of formulas which satisfies:
is the \(\subseteq \)-smallest set of formulas which satisfies:
-
(a)
 ;
; -
(b)
 ;
; -
(c)
for all
 , if
, if  and \({\lnot \rho } \notin \varPsi \), then,
and \({\lnot \rho } \notin \varPsi \), then, 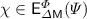 .
.
A set  is an \(\mathsf {M} \)-extension of \(\varPhi \) under \(\varDelta \) iff it is a fixed point of
is an \(\mathsf {M} \)-extension of \(\varPhi \) under \(\varDelta \) iff it is a fixed point of  , i.e., iff
, i.e., iff  . We write
. We write  for the set of all \(\mathsf {M} \)-extensions of \(\varPhi \) under \(\varDelta \).
for the set of all \(\mathsf {M} \)-extensions of \(\varPhi \) under \(\varDelta \).
Intuitively, an \(\mathsf {M} \)-extension can be thought of as a set of formulas which contains \(\varPhi \), is closed under \(\vdash _{\mathsf {M}}\), and is saturated under the application of the defaults in \(\varDelta \). When it can be clearly understood from the context, we will drop the prefix \(\mathsf {M} \) and refer to an \(\mathsf {M} \)-extension as an extension.
In the literature on Default Logic, defaults are intuitively understood as defeasible rules of inference, i.e., rules of inference whose conclusions are subject to annulment, or rules which allow us to “jump” to conclusions. In turn, extensions are intuitively understood as sets of formulas closed under the application of defaults. The next two examples illustrate two properties of extensions: multiplicity and absence of extensions.
Example 1
Let \(\varPhi =\{\Diamond p\}\) and  ; the set
; the set  of extensions of \(\varPhi \) under \(\varDelta \) consists of exactly two extensions: (1) the set
of extensions of \(\varPhi \) under \(\varDelta \) consists of exactly two extensions: (1) the set  ; and (2) the set
; and (2) the set  .
.
Each of the extensions in Example 1 corresponds to the application of each default in \(\varDelta \). Once one default has been applied, the application of the other one is blocked. This example illustrates how to handle contradictory information.
Example 2
Let \(\varPhi =\{\Diamond p\}\) and  ; the set
; the set  of extensions of \(\varPhi \) under \(\varDelta \) is empty, i.e.,
of extensions of \(\varPhi \) under \(\varDelta \) is empty, i.e.,  , i.e., there are no extensions of \(\varPhi \) under \(\varDelta \).
, i.e., there are no extensions of \(\varPhi \) under \(\varDelta \).
Example 2 highlights a subtletly in thinking of extensions as being constructed by the successive application of defaults: applying a default may result in its own annulment. To make this point clear, w.l.o.g., notice that plausible candidates for extensions are: the set  (i.e., not applying the default); or the set
(i.e., not applying the default); or the set  (i.e., result of applying the default to
(i.e., result of applying the default to  ).Neither of these sets is a fixed point of \(\mathsf {E}_{\varDelta }^{\varPhi }\), i.e.,
).Neither of these sets is a fixed point of \(\mathsf {E}_{\varDelta }^{\varPhi }\), i.e.,  and
and  . This results in
. This results in  .
.
We are now in a position to define what we mean by a default modal system. This definition arises as a natural construction over a modal system \(\mathsf {M} \).
Definition 14
A default modal system is a tuple  where \(\varDelta \) is a set of defaults and \(\mathsf {M} \) is a modal system.
where \(\varDelta \) is a set of defaults and \(\mathsf {M} \) is a modal system.
In analogy with the case in modal systems, we associate with each default modal system  a relation
a relation  between sets of formulas and formulas. This relation is based on the relation \(\vdash _{\mathsf {M}}\) and it can be understood as its default version. This is made clear in Definition 15.
between sets of formulas and formulas. This relation is based on the relation \(\vdash _{\mathsf {M}}\) and it can be understood as its default version. This is made clear in Definition 15.
Definition 15
Let  be a default modal system; define
be a default modal system; define

We use  as a shorthand for
as a shorthand for  . The relation
. The relation  is called credulous in the literature on Default Logic, because the existence of just one extension is enough to grant the inference (see [2]). The principle of monotonicity fails for
is called credulous in the literature on Default Logic, because the existence of just one extension is enough to grant the inference (see [2]). The principle of monotonicity fails for  . In other words: it is not necessarily the case that if
. In other words: it is not necessarily the case that if  , then
, then  (for an arbitrary \(\varPsi \)).
(for an arbitrary \(\varPsi \)).
Building the relation  on the underlying relation \(\vdash _{\mathsf {M}}\) raises the question of which properties of \(\vdash _{\mathsf {M}}\) are preserved at the level of
on the underlying relation \(\vdash _{\mathsf {M}}\) raises the question of which properties of \(\vdash _{\mathsf {M}}\) are preserved at the level of  . Definition 16 sets a basis on which to start answering this question.
. Definition 16 sets a basis on which to start answering this question.
Definition 16
The relation  interprets \(\vdash _{\mathsf {M}}\) iff if \(\varPhi \vdash _{\mathsf {M}} \varphi \) then
interprets \(\vdash _{\mathsf {M}}\) iff if \(\varPhi \vdash _{\mathsf {M}} \varphi \) then  .
.
Interpretability seems to be a natural requirement on  . However, as established in Example 2 (which shows that sometimes extensions do not exist) this property fails to hold in general. To overcome this problem we can go down two possible paths: (i) modify Definition 13 to guarantee the existence of extensions; or (ii) single out defaults for which extensions are guaranteed to exist. Among the most popular modifications of Definition 13 which guarantee the existence of extensions we have: justified extensions (see [17]); and constrained extensions (see [6]). For option (ii), we have the set of well-behavedFootnote 2 defaults as a very large and natural set which guarantees the existence of extensions (see [21]). Going down path (i) overburdens the definition of an extension with additional machinery which departs from the purposes of our work here. For this reason, we choose to go down path (ii); i.e., we restrict ourselves to well-behaved defaults. Interestingly, the notions of extensions, justified extensions, and constrained extensions, coincide for well-behaved defaults (see [5, 11]).
. However, as established in Example 2 (which shows that sometimes extensions do not exist) this property fails to hold in general. To overcome this problem we can go down two possible paths: (i) modify Definition 13 to guarantee the existence of extensions; or (ii) single out defaults for which extensions are guaranteed to exist. Among the most popular modifications of Definition 13 which guarantee the existence of extensions we have: justified extensions (see [17]); and constrained extensions (see [6]). For option (ii), we have the set of well-behavedFootnote 2 defaults as a very large and natural set which guarantees the existence of extensions (see [21]). Going down path (i) overburdens the definition of an extension with additional machinery which departs from the purposes of our work here. For this reason, we choose to go down path (ii); i.e., we restrict ourselves to well-behaved defaults. Interestingly, the notions of extensions, justified extensions, and constrained extensions, coincide for well-behaved defaults (see [5, 11]).
Definition 17
A default  is well-behaved, written
is well-behaved, written  , iff \(\rho = \chi \). A set of defaults \(\varDelta \) is well-behaved iff all defaults in \(\varDelta \) are well-behaved. A default modal system
, iff \(\rho = \chi \). A set of defaults \(\varDelta \) is well-behaved iff all defaults in \(\varDelta \) are well-behaved. A default modal system  is well-behaved iff \(\varDelta \) is well-behaved.
is well-behaved iff \(\varDelta \) is well-behaved.
Proposition 5
Let  be a default modal system; if
be a default modal system; if  is well-behaved, then,
is well-behaved, then,  interprets \(\vdash _{\mathsf {M}}\).
interprets \(\vdash _{\mathsf {M}}\).
We conclude this section by drawing attention to an interesting point regarding necessitation in default modal systems in Proposition 6 (cf. item 1 in Proposition 1).
Proposition 6
If  , then
, then  .
.
Proof
Suppose that  ; by definition, there is an \(\mathsf {M} \)-extension
; by definition, there is an \(\mathsf {M} \)-extension  s.t.
s.t.  . It follows that
. It follows that  . Thus,
. Thus,  .
.
The analogous to item 2 in Proposition 1, a form of the deduction theorem, i.e., if  , then,
, then,  fails to hold for an arbitrary
fails to hold for an arbitrary  (even with the presense of
(even with the presense of  ).
).
3.2 Deducibility in Default Modal Systems
We formulate a notion of  -deduction for an arbitrary but fixed well-behaved default modal system
-deduction for an arbitrary but fixed well-behaved default modal system  . This notion of a
. This notion of a  -deduction extends that of an \(\mathsf {M} \)-deduction by incorporating defaults in a natural way.
-deduction extends that of an \(\mathsf {M} \)-deduction by incorporating defaults in a natural way.
Definition 18
A  -deduction of \(\varphi \) from \(\varPhi \) is a finite sequence \(\psi _1 \dots \psi _n\) of formulas s.t. \(\psi _n = \varphi \), and for each \(k < n\) at least one of the following conditions hold:
-deduction of \(\varphi \) from \(\varPhi \) is a finite sequence \(\psi _1 \dots \psi _n\) of formulas s.t. \(\psi _n = \varphi \), and for each \(k < n\) at least one of the following conditions hold:
-
1.
\(\psi _k\) is an axiom of \(\mathsf {M} \);
-
2.
\(\psi _k\) is a premiss, i.e., \(\psi _k \in \varPhi \);
-
3.
\(\psi _k\) is obtained from two earlier formulas using \(\mathsf {mp}\), i.e., there are \({i,j} < k\) s.t. \(\psi _j = {\psi _i \rightarrow \psi _k}\);
-
4.
\(\psi _k\) is obtained from an earlier formula using \(\mathsf {u}\), i.e., there is \({j} < k\) s.t.
 .
. -
5.
\(\psi _k\) is obtained from an earlier formula using \(\varDelta \)-detachment, i.e., there is \({j} < k\) s.t.
 ;
;
A  -deduction is credulous whenever:
-deduction is credulous whenever:

We define  iff there is a credulous
iff there is a credulous  -deduction of \(\varphi \) from \(\varPhi \).
-deduction of \(\varphi \) from \(\varPhi \).
The notion of a credulous  -deduction extends the notion of \(\mathsf {M} \)-deduction with a rule of default detachment and the condition of being credulous. The rule of default detachment shows how defaults interact with the rules of the underlying proof system. The condition of being credulous in Eq. (1) captures the fact that defaults cannot be a source of inconsistency. Intuitively, a credulous
-deduction extends the notion of \(\mathsf {M} \)-deduction with a rule of default detachment and the condition of being credulous. The rule of default detachment shows how defaults interact with the rules of the underlying proof system. The condition of being credulous in Eq. (1) captures the fact that defaults cannot be a source of inconsistency. Intuitively, a credulous  -deduction of \(\varphi \) from \(\varPhi \) internalizes the construction of (part of) an extension containing \(\varphi \) together with the \(\mathsf {M} \)-deduction which witnesses this containment. This is made precise in the following result.
-deduction of \(\varphi \) from \(\varPhi \) internalizes the construction of (part of) an extension containing \(\varphi \) together with the \(\mathsf {M} \)-deduction which witnesses this containment. This is made precise in the following result.
Theorem 2
 iff
iff  .
.
3.3 Towards an Algebraic Treatment of Default Modal Systems
We turn now our attention to a characterization of defaults and extensions by means of Lindenbaum-Tarski
 s. This algebraic treatment of defaults and extensions reveals how default modal systems may be thought of as updates on
s. This algebraic treatment of defaults and extensions reveals how default modal systems may be thought of as updates on
 s. For the rest of this section, we assume that
s. For the rest of this section, we assume that  is an arbitrary but fixed well-behaved default modal system. We use \(\mathfrak {L}\) to indicate the class of Lindenbaum-Tarski
is an arbitrary but fixed well-behaved default modal system. We use \(\mathfrak {L}\) to indicate the class of Lindenbaum-Tarski
 s of \(\mathsf {M} \), i.e.,
s of \(\mathsf {M} \), i.e.,  . We drop the sub-index \(\mathsf {M} \) and use \({\varPhi }\) instead of \({\cong _{\mathsf {M}}^{\varPhi }}\) as a way of further simplifying the notation. We construct this section around the following definition.
. We drop the sub-index \(\mathsf {M} \) and use \({\varPhi }\) instead of \({\cong _{\mathsf {M}}^{\varPhi }}\) as a way of further simplifying the notation. We construct this section around the following definition.
Definition 19
Let  ; the function \(\hat{\delta } : {\mathfrak {L}\rightarrow \mathfrak {L}}\) is defined as:
; the function \(\hat{\delta } : {\mathfrak {L}\rightarrow \mathfrak {L}}\) is defined as:

Definition 19 is the algebraic counterpart of the application of a default w.r.t. a set of sentences. More precisely,  is applicable w.r.t. a set \(\varPhi \) satisfying
is applicable w.r.t. a set \(\varPhi \) satisfying  if: (a) \(\pi \in \varPhi \); and (b) \(\varPhi \cup \{\chi \} \not \vdash \bot \). Applying the default \(\delta \) results in
if: (a) \(\pi \in \varPhi \); and (b) \(\varPhi \cup \{\chi \} \not \vdash \bot \). Applying the default \(\delta \) results in  . On the algebraic side, we capture the application of a default as a transformation between Lindenbaum-Tarski
. On the algebraic side, we capture the application of a default as a transformation between Lindenbaum-Tarski
 s. More precisely, consider the Lindenbaum-Tarski
s. More precisely, consider the Lindenbaum-Tarski
 for \(\varPhi \), i.e.,
for \(\varPhi \), i.e.,  . The condition (a) of applicability of
. The condition (a) of applicability of  w.r.t.
w.r.t.  is captured in (2a) as \({[\pi ]_{\varPhi } = 1_{\varPhi }}\); and the condition (b) of applicability is captured in (2a) as
is captured in (2a) as \({[\pi ]_{\varPhi } = 1_{\varPhi }}\); and the condition (b) of applicability is captured in (2a) as  . In other words, the equivalence class of \(1_{\varPhi }\) captures the deducibility of \(\pi \) from \(\varPhi \), i.e., \(\pi \in \varPhi \), alt., \(\varPhi \vdash \pi \). In turn, the condition of being proper on the (open) filter generated by
. In other words, the equivalence class of \(1_{\varPhi }\) captures the deducibility of \(\pi \) from \(\varPhi \), i.e., \(\pi \in \varPhi \), alt., \(\varPhi \vdash \pi \). In turn, the condition of being proper on the (open) filter generated by  captures the consistency of \(\chi \) w.r.t. \(\varPhi \), i.e., \(\varPhi \cup \{\chi \} \not \vdash \bot \). Notice that if the default is applicable, the return value of \(\hat{\delta }\) incorporates \(\chi \) to
captures the consistency of \(\chi \) w.r.t. \(\varPhi \), i.e., \(\varPhi \cup \{\chi \} \not \vdash \bot \). Notice that if the default is applicable, the return value of \(\hat{\delta }\) incorporates \(\chi \) to  , i.e., it results in
, i.e., it results in  . Otherwise, \(\hat{\delta }\) has no effect on
. Otherwise, \(\hat{\delta }\) has no effect on  . When seen in this light, the operator \(\hat{\delta }\) performs an update reflecting the application of \(\delta \) on its input. The situation with \(\hat{\delta }\) is similar to the case in dynamic logics such as Public Announcement Logic [20] (in particular, in relation to the approach proposed in [18]). We retake this discussion in Sect. 4.
. When seen in this light, the operator \(\hat{\delta }\) performs an update reflecting the application of \(\delta \) on its input. The situation with \(\hat{\delta }\) is similar to the case in dynamic logics such as Public Announcement Logic [20] (in particular, in relation to the approach proposed in [18]). We retake this discussion in Sect. 4.
Having dealt with defaults we turn our attention to extensions. For well-behaved defaults, extensions can be seen as being constructed in a step-wise fashion applying defaults one at a time. From a syntactic perspective, this construction of an extension starts with a closed set \(\varPhi \), and applies the defaults \(\delta \in \varDelta \) one by one until we obtain a closed set of formulas that is saturated under the application of defaults. From the perspective of Lindenbaum-Tarski
 s we obtain the following.
s we obtain the following.
Proposition 7
Each function \(\hat{\delta }\) induces a function \({\bar{\delta }: {|\mathbf {L}| \rightarrow |\hat{\delta }(\mathbf {L})|}}\) defined as: \(\bar{\delta }([\varphi ]_{\varPhi }) = [\varphi ]_{\varPhi \cup \{\chi \}}\) if Eq. (2a) holds; or \(\bar{\delta }([\varphi ]_{\varPhi }) = [\varphi ]_{\varPhi }\) if Eq. (2b) holds. The function \(\bar{\delta }\) is a homomorphism from \(\mathbf {L}\) to \(\hat{\delta }(\mathbf {L})\).
Proof
That \(\bar{\delta }\) is a function is trivial. The proof that \(\bar{\delta }\) is a homomorphism is by cases. If Eq. (2b) holds, then, the result is obtained immediately. Otherwise:
The remaining cases are similar.
The following are some immediate properties of default operators.
Definition 20
Let  ; we write \(\mathbf {L}_1 \le \mathbf {L}_2\) iff there is a homomorphism \(h : {\mathbf {L}_1 \rightarrow \mathbf {L}_2}\); and \(\mathbf {L}_1 < \mathbf {L}_2\) iff \(\mathbf {L}_1 \le \mathbf {L}_2\) and \(\mathbf {L}_1\), \(\mathbf {L}_2\) are not isomorphic.
; we write \(\mathbf {L}_1 \le \mathbf {L}_2\) iff there is a homomorphism \(h : {\mathbf {L}_1 \rightarrow \mathbf {L}_2}\); and \(\mathbf {L}_1 < \mathbf {L}_2\) iff \(\mathbf {L}_1 \le \mathbf {L}_2\) and \(\mathbf {L}_1\), \(\mathbf {L}_2\) are not isomorphic.
Proposition 8
Every \(\hat{\delta }\) is extensive and idempotent, i.e., it satisfies \({\mathbf {L} \le \hat{\delta }(\mathbf {L})}\) and \({\hat{\delta }(\mathbf {L}) = \hat{\delta }(\hat{\delta }(\mathbf {L}))}\), resp. An arbitrary \(\hat{\delta }\) needs not satisfy monotonicity, i.e., there are  s.t. \({\mathbf {L}_1 \le \mathbf {L}_2}\) and \({\hat{\delta }(\mathbf {L}_1) \nleq \hat{\delta }(\mathbf {L}_2)}\).
s.t. \({\mathbf {L}_1 \le \mathbf {L}_2}\) and \({\hat{\delta }(\mathbf {L}_1) \nleq \hat{\delta }(\mathbf {L}_2)}\).
Proof
Extensivity follows from Proposition 7. Idempotence is proven by cases. If Eq. (2b) holds, then, the result is obtained immediately. Otherwise, Eq. (2a) holds. In this case,  . Trivially,
. Trivially,  . For a counter-example to monotonicity consider
. For a counter-example to monotonicity consider  and
and  , and
, and  .
.
The set \(\varDelta \) of defaults leads naturally to a set  . Each \(\hat{\delta }\) in this set can be seen as “taking a step” in the construction of the algebraic counterpart of an extension. To carry out this construction, we would need to compose such steps. This leads to the formulation of Definition 21.
. Each \(\hat{\delta }\) in this set can be seen as “taking a step” in the construction of the algebraic counterpart of an extension. To carry out this construction, we would need to compose such steps. This leads to the formulation of Definition 21.
Definition 21
The default monoid associated to  is the monoid \(\mathbf {D}^{*}\) freely generated by
is the monoid \(\mathbf {D}^{*}\) freely generated by  , i.e.,
, i.e.,  where:
where:
-
1.
 is the \(\subseteq \)-smallest set s.t.:
is the \(\subseteq \)-smallest set s.t.:  ;
;  ; and if
; and if  , then
, then  ;
; -
2.
 and
and  satisfy:
satisfy:  ; and
; and  .
.
Proposition 9
Every  is either: the identity, i.e.,
is either: the identity, i.e.,  ; or a composition of the form
; or a composition of the form  , where \(\delta _i \in \varDelta \).
, where \(\delta _i \in \varDelta \).
We define  ; and
; and  .
.
Definition 22
Let \(\mathbf {L}\) be a Lindenbaum-Tarski
 in
in  , and v be an assignment on \(\mathbf {L}\); for an equation \(\varphi \approx \psi \), define:
, and v be an assignment on \(\mathbf {L}\); for an equation \(\varphi \approx \psi \), define:

We write  iff
iff  for all assignments v.
for all assignments v.
Intuitively, the Lindenbaum-Tarski
 \(d(\mathbf {L})\) in Definition 22 is the algebraic counterpart of the concept of an extension. This is made clear in Theorem 3.
\(d(\mathbf {L})\) in Definition 22 is the algebraic counterpart of the concept of an extension. This is made clear in Theorem 3.
Theorem 3
 iff
iff  .
.
Proof
The interesting part is the right-to-left implication: if  , then,
, then,  . We prove the contrapositive: if
. We prove the contrapositive: if  , then,
, then,  . Let
. Let  , the proof is concluded if for all
, the proof is concluded if for all  ,
,  . We continue by induction on d. Let
. We continue by induction on d. Let  ; we must have
; we must have  ; otherwise we would obtain \(\varPhi \vdash \varphi \) (from Theorem 1); and so that
; otherwise we would obtain \(\varPhi \vdash \varphi \) (from Theorem 1); and so that  (which contradicts our assumption). For the next case, let \(d = \hat{\delta }\) for
(which contradicts our assumption). For the next case, let \(d = \hat{\delta }\) for  ; either Eq. (2b) holds or Eq. (2a) holds. If Eq. (2b) holds, \(\hat{\delta }\) behaves like
; either Eq. (2b) holds or Eq. (2a) holds. If Eq. (2b) holds, \(\hat{\delta }\) behaves like  (and we are back to the previous case). If Eq. (2a) holds,
(and we are back to the previous case). If Eq. (2a) holds,  . Assuming (i)
. Assuming (i)  leads to a contradiction. More precisely, if Eq. (2a) holds, from Theorem 1, we obtain \(\varPhi \vdash \pi \) and \(\varPhi \cup \{\chi \} \not \vdash \bot \). From (i) and Theorem 1, we obtain \(\varPhi \cup \{\chi \} \vdash \varphi \). If we place the \(\mathsf {M} \)-deduction of \(\pi \) from \(\varPhi \) in front of the \(\mathsf {M} \)-deduction of \(\varphi \) from \(\varPhi \cup \{\chi \}\), we obtain
leads to a contradiction. More precisely, if Eq. (2a) holds, from Theorem 1, we obtain \(\varPhi \vdash \pi \) and \(\varPhi \cup \{\chi \} \not \vdash \bot \). From (i) and Theorem 1, we obtain \(\varPhi \cup \{\chi \} \vdash \varphi \). If we place the \(\mathsf {M} \)-deduction of \(\pi \) from \(\varPhi \) in front of the \(\mathsf {M} \)-deduction of \(\varphi \) from \(\varPhi \cup \{\chi \}\), we obtain  . This yields the contradiction. For the inductive step, let
. This yields the contradiction. For the inductive step, let  . Suppose that
. Suppose that  . From the inductive hypothesis, we obtain
. From the inductive hypothesis, we obtain  . Assuming that
. Assuming that  leads to a contradiction using the same argument as in (i).
leads to a contradiction using the same argument as in (i).
We conclude this section by taking some steps beyond dealing with defaults and extensions in the context of Lindenbaum-Tarski
 s. In particular, we show how some of the constructions used in Sect. 3.3 can be extended to a more abstract setting via suitable congruences.
s. In particular, we show how some of the constructions used in Sect. 3.3 can be extended to a more abstract setting via suitable congruences.
Definition 23
Let  be a Lindenbaum-Tarski
be a Lindenbaum-Tarski
 and \(\chi \) a formula; define \([\varphi _1]_{\varPhi } \equiv _{\chi } [\varphi _2]_{\varPhi }\) iff
and \(\chi \) a formula; define \([\varphi _1]_{\varPhi } \equiv _{\chi } [\varphi _2]_{\varPhi }\) iff  .
.
Definition 23 is a step towards treating the application of default as a device for obtaining a
 \(\mathbf {M}\) updated by the element \([\chi ]_{\varPhi }\) in
\(\mathbf {M}\) updated by the element \([\chi ]_{\varPhi }\) in  . The updated
. The updated
 \(\mathbf {M}\) is meant to be obtained as a quotient algebra modulo the congruence \(\equiv _{\chi }\). Proposition 10 shows that \(\equiv _{\chi }\) indeed is a congruence.
\(\mathbf {M}\) is meant to be obtained as a quotient algebra modulo the congruence \(\equiv _{\chi }\). Proposition 10 shows that \(\equiv _{\chi }\) indeed is a congruence.
Proposition 10
The relation \(\equiv _{\chi }\) is a congruence on  .
.
Proof
That \(\equiv _{\chi }\) is an equivalence relation is immediate. To improve notation we drop the subscript \(_{\varPhi }\). We need to show that: if \([\varphi _1] \equiv _{\chi } [\varphi _2]\) and \([\varphi _3] \equiv _{\chi } [\varphi _4]\), then, \({[\varphi _1] * [\varphi _3]} \equiv _{\chi } {[\varphi _2] * [\varphi _4]}\); \(-[\varphi _1] \equiv _{\chi } -[\varphi _2]\); \(f^{\Box }([\varphi _1]) \equiv _{\chi } f^{\Box }([\varphi _2])\); and  . The proof continues by cases (we only show the cases \(f^{\Box }\) and
. The proof continues by cases (we only show the cases \(f^{\Box }\) and  , the rest are routine):
, the rest are routine):

Proposition 11
The quotient algebra  is isomorphic to
is isomorphic to  .
.
Proof (sketch)
Observe that  . The isomorphism between
. The isomorphism between  and
and  is given by mappings \(\iota _1\) and \(\iota _2\) defined as: \(\iota _1([[\varphi ]_{\varPhi }]_{\equiv _{\chi }}) = [\varphi ]_{\varPhi \cup \{\chi \}}\); and \(\iota _2([\varphi ]_{\varPhi \cup \{\chi \}}) = [[\varphi ]_{\varPhi }]_{\equiv _{\chi }}\).
is given by mappings \(\iota _1\) and \(\iota _2\) defined as: \(\iota _1([[\varphi ]_{\varPhi }]_{\equiv _{\chi }}) = [\varphi ]_{\varPhi \cup \{\chi \}}\); and \(\iota _2([\varphi ]_{\varPhi \cup \{\chi \}}) = [[\varphi ]_{\varPhi }]_{\equiv _{\chi }}\).
The isomorphism in Proposition 11 shows that the relation \(\equiv _{\chi }\) yields the “correct” congruence if the application of a default is to be seen as an update on a
 . Moreover, it is possible to define a function
. Moreover, it is possible to define a function  defined by \(\varepsilon ([[\varphi ]_{\varPhi }]_{\equiv _{\chi }}) = [\varphi ]_{\varPhi } *_{\varPhi } [\chi ]_{\varPhi }\). The image of \(\varepsilon \) is also isomorphic to
defined by \(\varepsilon ([[\varphi ]_{\varPhi }]_{\equiv _{\chi }}) = [\varphi ]_{\varPhi } *_{\varPhi } [\chi ]_{\varPhi }\). The image of \(\varepsilon \) is also isomorphic to  . The results discussed in this paragraph open a pathway on how to lift the constructions in Definitions 19 and 21 to the setting of arbitrary
. The results discussed in this paragraph open a pathway on how to lift the constructions in Definitions 19 and 21 to the setting of arbitrary
 s.
s.
4 On Defaults as Model Updates
We are now in a position to establish a connection between our algebraic approach for default modal systems and the algebraic treatment of Public Announcement Logic (\(\mathsf {PAL}\)) in [18]. To set up context for discussion, we briefly introduce some basic notions of \(\mathsf {PAL}\) (see, e.g., [20] for details). As a modal logic, \(\mathsf {PAL}\) extends the modal logic S5 (seen as the logic of knowledge) with a new modality \(\langle !\psi \rangle \) of announcement. Intuitively, a formula \(\langle !\psi \rangle \varphi \) states that after the truthful announcement of \(\psi \), \(\varphi \) holds. Model theoretically, the interpretation of announcing \(\psi \) relativizes the model in which \(\psi \) is announced to the submodel in which \(\psi \) holds. The formula \(\varphi \) is then evaluated on the relativized model. It is important to remark that the announcement of \(\psi \) must be truthful: it occurs only if \(\psi \) is true. Otherwise, the announcement fails and \(\langle !\psi \rangle \varphi \) evaluates to false.
There are some interesting similarities between announcements in \(\mathsf {PAL}\) and defaults. From an algebraic perspective, an announcement may be understood as a homomorphism between the modal algebra in which the announcement occurs and the modal algebra corresponding to the submodel in which the announced formula holds. The algebraic machinery introduced in Sect. 3.3 sets the basis for thinking about the application of defaults as a logic of updates between particular modal algebras (Lindenbaum-Tarski
 s). In other words, we may construe the algebraic semantics of a default as an update from the Lindenbaum-Tarski
s). In other words, we may construe the algebraic semantics of a default as an update from the Lindenbaum-Tarski
 in which the default is considered, and the one updated with the consequent of the default (if the default is applicable). Notice that a default update takes place only if the prerequisite of the default is provable and its justification does not yield an inconsistency. The situation here is similar to the case of announcements, where the update takes place only if the formula being announced is true. In both cases, that of an announcement and that of the algebraic application of a default, the update is captured by a homomorphism from the original modal algebra to an updated modal algebra (obtained as a quotient construction). There is, however, subtle difference between announcements and defaults: if the announcement of \(\psi \) is not truthful the whole formula \(\langle !\psi \rangle \varphi \) amounts to a falsity; whereas if the prerequisite of a default is not provable, or its justification is inconsistent in the modal algebra, the application of the default has no effect.
in which the default is considered, and the one updated with the consequent of the default (if the default is applicable). Notice that a default update takes place only if the prerequisite of the default is provable and its justification does not yield an inconsistency. The situation here is similar to the case of announcements, where the update takes place only if the formula being announced is true. In both cases, that of an announcement and that of the algebraic application of a default, the update is captured by a homomorphism from the original modal algebra to an updated modal algebra (obtained as a quotient construction). There is, however, subtle difference between announcements and defaults: if the announcement of \(\psi \) is not truthful the whole formula \(\langle !\psi \rangle \varphi \) amounts to a falsity; whereas if the prerequisite of a default is not provable, or its justification is inconsistent in the modal algebra, the application of the default has no effect.
The similarities between announcements in \(\mathsf {PAL}\) and defaults are even more apparent when contrasted with the proposal presented in [18]. This proposal exploits the duality between models and algebras in order to algebraize \(\mathsf {PAL}\). In particular, in [18], a formula \(\psi \) is interpreted as an element b in an \(\mathsf {S5}\) modal algebra \(\mathbf {M}= \langle B, {*}, {-}, f^{\Box } \rangle \). The result of announcing this formula is a modal algebra constructed as a quotient modulo a congruence \(\equiv _b\) defined as \(b_1 \equiv _b b_2\) iff \({b_1 * b} = {b_2 * b}\). This congruence bears a close resemblance to the one we presented in Sect. 3.3. The main difference between this congruence and ours rests on the fact that the former is presented in the setting of \(\mathsf {S5}\), whereas ours is presented in a setting where global modal consequence is taken as the basis on which to build default modal systems. This said, the approach in [18] is more abstract than ours; since it considers arbitrary modal algebras and not just Lindenbaum-Tarski modal algebras.
The discussion above offers only some first steps in understanding the relationship between defaults and updates: both in terms of a full algebraization of default modal systems, and in terms of establishing a tight connection with logics of updates. In working towards a full algebraization of default modal systems, we would like to interpret the application of a default over arbitrary modal algebras, and not only as an update over Lindenbaum-Tarski
 s. In this regard, the main challenge is how to generalize the way in which we capture the application of one default to the application of a sequence of defaults needed to build an extension. Moreover, it would also be interesting to know whether it is possible to develop a class of algebraic structures for default modal systems parallel to the class of modal algebras for modal systems. This would require an internalization of defaults as algebraic operators. In turn, in what refers to establishing a tight connection with logics of updates, it would be interesting to be able to prove a reduction result between a default modal system and a logic of announcement (or establishing a difference in expressive power between one and the other). In this case, the challenge is deciding on an adequate logic of announcement and in finding whether it is possible to faithfully translate the application of a default as a form of update in this logic. Finally, upon defining the semantics of defaults as updates, we would like to study defaults as dynamic epistemic operators. In particular, we would like to explore whether defaults can be used to represent some novel form of communication in a multi-agent setting.
s. In this regard, the main challenge is how to generalize the way in which we capture the application of one default to the application of a sequence of defaults needed to build an extension. Moreover, it would also be interesting to know whether it is possible to develop a class of algebraic structures for default modal systems parallel to the class of modal algebras for modal systems. This would require an internalization of defaults as algebraic operators. In turn, in what refers to establishing a tight connection with logics of updates, it would be interesting to be able to prove a reduction result between a default modal system and a logic of announcement (or establishing a difference in expressive power between one and the other). In this case, the challenge is deciding on an adequate logic of announcement and in finding whether it is possible to faithfully translate the application of a default as a form of update in this logic. Finally, upon defining the semantics of defaults as updates, we would like to study defaults as dynamic epistemic operators. In particular, we would like to explore whether defaults can be used to represent some novel form of communication in a multi-agent setting.
5 Final Remarks
We presented a family of default logics built over modal logics and studied some properties.
First, we presented default logics syntactically as a default modal system. For each default modal system we formulated a notion of default deducibility to make explicit how defaults interact with the rules of the underlying proof calculus. Then, we offered an algebraic treatment of defaults and extensions. The algebraic treatment enabled us to obtain an algebraic completeness result. To our knowledge, this is the first work addressing default logic algebraically.
Moreover, we discussed a connection between default modal systems and modal logics with updates. In particular, our algebraic treatment of defaults is inspired by the ideas introduced in [18] for \(\mathsf {PAL}\). We believe that considering default modal systems as logics of updates is an interesting pathway to the study of the meta-logical properties of such systems from a semantic perspective.
Notes
- 1.
- 2.
In the literature on Default Logic well-behaved defaults are called normal. We avoid using this terminology here to avoid any confusion with normality in Modal Logic.
References
Ågotnes, T., Alechina, N.: The dynamics of syntactic knowledge. J. Log. Comput. 17(1), 83–116 (2007)
Antoniou, G., Wang, K.: Default logic. In: Gabbay, D., Woods, J. (eds.) The Many Valued and Nonmonotonic Turn in Logic. Handbook of the History of Logic, North-Holland, vol. 8, pp. 517–555 (2007)
Baader, F., Hollunder, B.: Embedding defaults into terminological knowledge representation formalisms. In: Nebel, B., Rich, C., Swartout, W. (eds.) 3rd International Conference on Principles of Knowledge Representation and Reasoning (KR 1992), pp. 306–317. Morgan Kaufmann (1992)
Blackburn, P., de Rijke, M., Venema, Y. (eds.): Modal Logic. Cambridge University Press, Cambridge (2002)
Cassano, V., Fervari, R., Areces, C., Castro, P.F.: Interpolation and beth definability in default logics. In: Calimeri, F., Leone, N., Manna, M. (eds.) JELIA 2019. LNCS (LNAI), vol. 11468, pp. 675–691. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-19570-0_44
Delgrande, J., Schaub, T., Jackson, W.: Alternative approaches to default logic. Artif. Intell. 70(1–2), 167–237 (1994)
Duc, H.N.: Reasoning about rational, but not logically omniscient, agents. J. Log. Comput. 7(5), 633–648 (1997)
Fervari, R., Velázquez-Quesada, F.R.: Dynamic epistemic logics of introspection. In: Madeira, A., Benevides, M. (eds.) DALI 2017. LNCS, vol. 10669, pp. 82–97. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-73579-5_6
Fervari, R., Velázquez-Quesada, F.R.: Introspection as an action in relational models. J. Log. Algebraic Methods Program. 108, 1–23 (2019)
Fitting, M.: Modal proof theory. In: Blackburn, P., van Benthem, J., Wolter, F. (eds.) Handbook of Modal Logic, pages 85–138. Elsevier (2007)
Froidevaux, C., Mengin, J.: Default logics: a unified view. Computat. Intell. 10, 331–369 (1994)
Gabbay, D., Kurucz, A., Wolter, F., Zakharyaschev, M.: Many-Dimensional Modal Logics: Theory and Applications. Elsevier, Amsterdam (2003)
Givant, S., Halmos, P.: Introduction to Boolean Algebras. Undergraduate Texts in Mathematics. Springer, Heidelberg (2009). https://doi.org/10.1007/978-0-387-68436-9
Goranko, V., Passy, S.: Using the universal modality: gains and questions. J. Log. Comput. 2(1), 5–30 (1992)
Grossi, D., Velázquez-Quesada, F.R.: Syntactic awareness in logical dynamics. Synthese 192(12), 4071–4105 (2015). https://doi.org/10.1007/s11229-015-0733-1
Jago, M.: Epistemic logic for rule-based agents. J. Log. Lang. Inform. 18(1), 131–158 (2009)
Łukaszewicz, W.: Considerations on default logic: an alternative approach. Comput. Intell. 4, 1–16 (1988)
Ma, M.: Mathematics of public announcements. In: van Ditmarsch, H., Lang, J., Ju, S. (eds.) LORI 2011. LNCS (LNAI), vol. 6953, pp. 193–205. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24130-7_14
Mikitiuk, A., Truszczynski, M.: Constrained and rational default logics. In: Proceedings of IJCAI 1995, pp. 1509–1517 (1995)
Plaza, J.: Logics of public communications. Synthese 158(2), 165–179 (2007)
Reiter, R.: A logic for default reasoning. AI 13(1–2), 81–132 (1980)
Schaub, T.: On constrained default theories. In: 11th European Conference on Artificial Intelligence (ECAI 1992), pp. 304–308 (1992)
Solaki, A.: Steps out of logical omniscience. Master’s thesis, Institute for Logic, Language and Computation, Amsterdam (2017). MoL-2017-12
van Benthem, J., Pacuit, E.: Dynamic logics of evidence-based beliefs. Stud. Log. 99(1), 61–92 (2011)
van Benthem, J., Velázquez-Quesada, F.R.: The dynamics of awareness. Synthese (Knowl. Rational. Action) 177(Supplement 1), 5–27 (2010)
Vardi, M.Y.: On epistemic logic and logical omniscience. In: Proceedings of TARK, pp. 293–305. Morgan Kaufmann (1986)
Velázquez-Quesada, F.R.: Explicit and implicit knowledge in neighbourhood models. In: Grossi, D., Roy, O., Huang, H. (eds.) LORI 2013. LNCS, vol. 8196, pp. 239–252. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40948-6_19
Venema, Y.: Algebras and general frames. In: Blackburn et al. [4], pp. 263–333
Acknowledgment
We would like to thank the anonymous reviewers for their helpful comments and suggestions. This work is supported by projects ANPCyT-PICTs-2017-1130 and 2016-0215, Stic-AmSud 20-STIC-03 “DyLo-MPC”, Secyt-UNC, GRFT Mincyt-Cba, and by the Laboratoire International Associé SINFIN.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Cassano, V., Fervari, R., Areces, C., Castro, P.F. (2020). Default Modal Systems as Algebraic Updates. In: Martins, M.A., Sedlár, I. (eds) Dynamic Logic. New Trends and Applications. DaLi 2020. Lecture Notes in Computer Science(), vol 12569. Springer, Cham. https://doi.org/10.1007/978-3-030-65840-3_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-65840-3_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-65839-7
Online ISBN: 978-3-030-65840-3
eBook Packages: Computer ScienceComputer Science (R0)





 .
. , then,
, then,  .
. , then,
, then,  .
. ;
; ;
; , if
, if  and
and 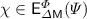 .
. .
. ;
; is the
is the  ;
;  ; and if
; and if  , then
, then  ;
; and
and  satisfy:
satisfy:  ; and
; and  .
.