Abstract
We investigate interpolation and Beth definability in default logics. To this end, we start by defining a general framework which is sufficiently abstract to encompass most of the usual definitions of a default logic. In this framework a default logic \(\mathscr {D}\mathfrak {L}\) is built on a base, monotonic, logic \(\mathfrak {L}\). We then investigate the question of when interpolation and Beth definability results transfer from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\). This investigation needs suitable notions of interpolation and Beth definability for default logics. We show both positive and negative general results: depending on how \(\mathscr {D}\mathfrak {L}\) is defined and of the kind of interpolation/Beth definability involved, the property might or might not transfer from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Interpolation and Beth definability are recognized as important properties of the meta-theory of a logic (see, e.g., [19]). Interpolation goes back to the seminal work of Craig in [11] and is, in one form, the following result: suppose that \(\varphi \vdash \psi \), there is \(\xi \) in the common language of \(\varphi \) and \(\psi \) s.t. \(\varphi \vdash \xi \) and \(\xi \vdash \psi \). In addition to its theoretical relevance, interpolation has also proven to be influential in applications in Computer Science, e.g., in the context of software specification [6, 14, 25, 34], in the construction of Formal Ontologies [23], and in Model Checking [26]. Though interpolation stands as a property in its own right, its main importance lies in the fact that it can be used to prove a result known as Beth definability via a standard argument (see, e.g., [28]). Intuitively, Beth definability implies that the syntax of the language is powerful enough to define any notion that is semantically fixed in a model. This is commonly regarded as a sign of a well behaved logic, where syntax and semantics are in harmony. Interpolation and Beth definability have received a lot less attention in non-classical and, in particular, non-monotonic logics. With this as our motivation, we investigate interpolation and Beth definability in default logics, a sub-class of the field of Non-monotonic Logic.
We start by defining a general framework which is sufficiently abstract to encompass most of the usual default logics (e.g., those introduced in [13, 24, 27, 29]), generalizing ideas presented in [17, 18]. We define a default logic \(\mathscr {D}\mathfrak {L}\) on a base, monotonic, logic \(\mathfrak {L}\) satisfying some minimal requirements. Then, we turn to the question of when interpolation and Beth definability results transfer from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\). As a result of the generality of our framework, we are able to prove far-reaching transfer results for a comprehensive class of default logics. We draw attention to the fact that interpolation and Beth definability for default logics need suitable definitions. When dealing with a non-monotonic logical consequence relation  , it may not simply be possible to define interpolation as: if
, it may not simply be possible to define interpolation as: if  , then there is \(\xi \) in the common language of \(\varphi \) and \(\psi \) s.t.
, then there is \(\xi \) in the common language of \(\varphi \) and \(\psi \) s.t.  and
and  . For starters, since
. For starters, since  is non-monotonic, it may not be transitive. Moreover, since consequence in most default logics is defined in terms of default theories, the notion of “common language”, and the left and right hand sides of
is non-monotonic, it may not be transitive. Moreover, since consequence in most default logics is defined in terms of default theories, the notion of “common language”, and the left and right hand sides of  should also be dealt with care. After discussing how to define interpolation and Beth definability in default logics, we show both positive and negative results. Depending on how \(\mathscr {D}\mathfrak {L}\) is defined and of which kind of interpolation/Beth definability property we study, the property might or might not transfer from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\). In particular, we show that the Strong Craig Interpolation Property (\(\mathsf {S}\mathsf {CIP} \)) always transfer from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\) (Proposition 6), while the Split Interpolation Property (\(\mathsf {SIP}\)) fails for any traditional \(\mathscr {D}\mathfrak {L}\) based on \(\mathfrak {L}\) extending classical propositional logic (\(\mathsf {CPL}\)), even though \(\mathsf {CPL}\) has \(\mathsf {SIP}\) (Proposition 7). Similarly, if \(\mathfrak {L}\) has \(\mathsf {SIP}\) and \(\mathscr {D}\mathfrak {L}\) is stable under substitutions, then sceptical default consequence in \(\mathscr {D}\mathfrak {L}\) has a version of the Beth definability property (Proposition 8), while this property fails for credulous default consequence in traditional \(\mathscr {D}\mathfrak {L}\) based on \(\mathfrak {L}\) extending \(\mathsf {CPL}\) (Proposition 9).
should also be dealt with care. After discussing how to define interpolation and Beth definability in default logics, we show both positive and negative results. Depending on how \(\mathscr {D}\mathfrak {L}\) is defined and of which kind of interpolation/Beth definability property we study, the property might or might not transfer from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\). In particular, we show that the Strong Craig Interpolation Property (\(\mathsf {S}\mathsf {CIP} \)) always transfer from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\) (Proposition 6), while the Split Interpolation Property (\(\mathsf {SIP}\)) fails for any traditional \(\mathscr {D}\mathfrak {L}\) based on \(\mathfrak {L}\) extending classical propositional logic (\(\mathsf {CPL}\)), even though \(\mathsf {CPL}\) has \(\mathsf {SIP}\) (Proposition 7). Similarly, if \(\mathfrak {L}\) has \(\mathsf {SIP}\) and \(\mathscr {D}\mathfrak {L}\) is stable under substitutions, then sceptical default consequence in \(\mathscr {D}\mathfrak {L}\) has a version of the Beth definability property (Proposition 8), while this property fails for credulous default consequence in traditional \(\mathscr {D}\mathfrak {L}\) based on \(\mathfrak {L}\) extending \(\mathsf {CPL}\) (Proposition 9).
Structure. In Sect. 2 we provide a general definition of a default logic. We start by defining what we require of a base logic in Sect. 2.1. We introduce default logics in Sect. 2.2, and define traditional default logics in Sect. 2.3. In Sect. 2.4 we briefly discuss strongly saturated default logics – a class of well behaved default logics generalizing traditional default logics. Section 3 investigates interpolation and Beth definability. We introduce appropriate definitions in Sects. 3.1 and 3.3. Our main results are shown in Sects. 3.2 and 3.4. Section 4 concludes the paper discussing related work and providing pointers for future research.
2 What Is a Default Logic?
Default logics are a sub-class of non-monotonic logics. Different default logics have been introduced after the originating proposal in Reiter’s seminal work [29]. These different default logics have in common the notion of a default and an extension. A default is a triple of formulas of a formal language, notation  , capturing a conditional, defeasible statement. An extension is a set of formulas making precise some constraints on \(\pi \) and \(\rho \), enabling us to detach \(\chi \) from
, capturing a conditional, defeasible statement. An extension is a set of formulas making precise some constraints on \(\pi \) and \(\rho \), enabling us to detach \(\chi \) from  . Default logics differ from one another in the conditions enabling detaching a default. Defaults and extensions are basic ingredients in what is a default logic.
. Default logics differ from one another in the conditions enabling detaching a default. Defaults and extensions are basic ingredients in what is a default logic.
2.1 Preliminary Definitions
We define default logics over a base logic. In our setting, a base logic, or a logic for short, has two ingredients: a set of formulas and a consequence relation. Formulas are defined over a language, i.e., a triple  where:
where:  is a set of non-logical symbols (the alphabet); \(\mathscr {L}\) is a set of logical symbols with corresponding arities; and \(\mathscr {G}\) are the rules of grammar. We also use \(\mathscr {F}\) for the set of all formulas of a language \(\mathscr {F}\). As usual, lowercase and uppercase Greek letters are variables for formulas and sets of formulas, resp. We restrict our attention to propositional languages, i.e., languages where
is a set of non-logical symbols (the alphabet); \(\mathscr {L}\) is a set of logical symbols with corresponding arities; and \(\mathscr {G}\) are the rules of grammar. We also use \(\mathscr {F}\) for the set of all formulas of a language \(\mathscr {F}\). As usual, lowercase and uppercase Greek letters are variables for formulas and sets of formulas, resp. We restrict our attention to propositional languages, i.e., languages where  is a set of proposition symbols. We use p, q, r, etc., for proposition symbols. For any \(\mathscr {F}\) and \(\varPhi \subseteq \mathscr {F}\),
is a set of proposition symbols. We use p, q, r, etc., for proposition symbols. For any \(\mathscr {F}\) and \(\varPhi \subseteq \mathscr {F}\),  is the alphabet of \(\varPhi \), i.e., the set of proposition symbols appearing in formulas in \(\varPhi \). We say that \(\varPhi \) is defined on an alphabet A if
is the alphabet of \(\varPhi \), i.e., the set of proposition symbols appearing in formulas in \(\varPhi \). We say that \(\varPhi \) is defined on an alphabet A if  . We define
. We define  . We use
. We use  to indicate the result of substituting every appearance of p by q in every formula in \(\varPhi \). A consequence relation \(\vdash \) is a subset of \(2^{\mathscr {F}} \times \mathscr {F}\) indicating what follows from what in a logic. We use \(\varPhi \vdash \varphi \) for \((\varPhi , \varphi ) \in {\vdash }\); and \(\vdash \varphi \) if \(\varPhi = \emptyset \) (we omit brackets for singleton sets). We make no assumptions regarding whether \(\vdash \) is defined syntactically or semantically. We do assume that \(\vdash \) satisfies reflexivity, monotonicity, cut, and structurality (see, e.g., [16]). We make precise what a logic is in the next definition.
to indicate the result of substituting every appearance of p by q in every formula in \(\varPhi \). A consequence relation \(\vdash \) is a subset of \(2^{\mathscr {F}} \times \mathscr {F}\) indicating what follows from what in a logic. We use \(\varPhi \vdash \varphi \) for \((\varPhi , \varphi ) \in {\vdash }\); and \(\vdash \varphi \) if \(\varPhi = \emptyset \) (we omit brackets for singleton sets). We make no assumptions regarding whether \(\vdash \) is defined syntactically or semantically. We do assume that \(\vdash \) satisfies reflexivity, monotonicity, cut, and structurality (see, e.g., [16]). We make precise what a logic is in the next definition.
Definition 1
(Logic). A logic is a tuple \(\mathfrak {L}= \langle \mathscr {F}, {\vdash } \rangle \) where \(\mathscr {F}\) is a language, and \({\vdash } \subseteq {2^{\mathscr {F}}\times \mathscr {F}}\) is a consequence relation s.t. \(\varphi \vdash \varphi \) (reflexivity); if \(\varPhi \vdash \varphi \) and \(\varPhi \subseteq \varPhi '\), then \(\varPhi ' \vdash \varphi \) (monotonicity); if \(\varPhi \vdash \varphi _i\) and  , then \(\varPhi \vdash \psi \) (cut); and if \(\varPhi \vdash \varphi \), then
, then \(\varPhi \vdash \psi \) (cut); and if \(\varPhi \vdash \varphi \), then  (structurality).
(structurality).
For any logic \(\mathfrak {L}\), we say that \(\varphi \) is a consequence of \(\varPhi \) iff \(\varPhi \vdash \varphi \). We define  . The operator
. The operator  is a closure operator, i.e.:
is a closure operator, i.e.:  ; if \(\varPhi \subseteq \varPhi '\), then
; if \(\varPhi \subseteq \varPhi '\), then  ; and
; and  . A set of sentences \(\varPhi \) is consistent if
. A set of sentences \(\varPhi \) is consistent if  .
.
Definition 2
An implicative logic is a logic whose logical symbols contain nullary symbols \(\top \) (verum) and \(\bot \) (falsum), and a binary symbol \(\supset \) (implication); whose set \(\mathscr {F}\) of formulas contains \(\{{\top \supset \varphi },{\varphi \supset \top },{\bot \supset \varphi },{\varphi \supset \bot },{\varphi \supset \psi }\}\); and whose consequence relation satisfies:  iff
iff  (\(\top \bot \)-def);
(\(\top \bot \)-def);  iff
iff  (\(\top \)-left-neutral); if
(\(\top \)-left-neutral); if  ,
,  (\(\supset \)-transitive); and if
(\(\supset \)-transitive); and if  ,
,  (modus ponens).
(modus ponens).
Henceforth, by a logic, we mean an implicative logic. Implicative logics play a fundamental role in our treatment of interpolation and Beth definability.
Example 1
The following are some typical cases of logics: Classical Propositional Logic (\(\mathsf {CPL}\)) [15]; Intuitionistic Propositional Logic (\(\mathsf {IPL}\)) [33]; the class of Normal Modal Logics [7]; in particular, the Basic Modal Logic \(\mathsf {K}\) with local consequence [7]; the Basic Modal Logic \(\mathsf {K}\) with global logical consequence [7]; the Modal Logic \(\mathsf {K}\mathsf {Alt}_{1}\) [7]; the Standard Deontic Logic \(\mathsf {D}\) [10, 35]; the Deontic Logic \(\mathsf {K}\)\(\mathsf {D}\)\(\mathsf {A}\) [9]; the epistemic logic \(\mathsf {S5}\) [10, 21]; and the hybrid logic \({\mathsf {H}(\mathsf {A},\downarrow )}\) [5] (which is equivalent to Classical First-Order Logic over the appropriate language).
2.2 Default Logics
We start with a general definition of a default logic.
Definition 3
(Default Logic). A default logic is a pair \(\mathscr {D}\mathfrak {L}= \langle \mathfrak {L}, \mathscr {E}\rangle \) where \(\mathfrak {L}\) is a logic and \(\mathscr {E}: {(2^{\mathscr {F}} \times 2^{(\mathscr {F}^3)}) \rightarrow 2^{(2^{\mathscr {F}})}}\) is a function s.t. for every  ,
,  for some \(\varDelta ' \subseteq \varDelta \).
for some \(\varDelta ' \subseteq \varDelta \).
\(\mathscr {D}= \mathscr {F}^3\) is the set of all defaults of a default logic.  is notation for \((\pi , \rho , \chi ) \in \mathscr {D}\). A default theory \(\Theta \) is a pair
is notation for \((\pi , \rho , \chi ) \in \mathscr {D}\). A default theory \(\Theta \) is a pair  where \({\varPhi \subseteq \mathscr {F}}\) and \({\varDelta \subseteq \mathscr {D}}\). If \(\Theta \) is a default theory,
where \({\varPhi \subseteq \mathscr {F}}\) and \({\varDelta \subseteq \mathscr {D}}\). If \(\Theta \) is a default theory,  and
and  are the sets of formulas and defaults of \(\Theta \), resp. For a default theory \(\Theta \), \(\mathscr {E}(\Theta )\) is its set of extensions. We associate with each default logic two notions of default consequence: credulous, and sceptical. Formally, \(\varphi \) is a credulous default consequence of a default theory \(\Theta \), notation
are the sets of formulas and defaults of \(\Theta \), resp. For a default theory \(\Theta \), \(\mathscr {E}(\Theta )\) is its set of extensions. We associate with each default logic two notions of default consequence: credulous, and sceptical. Formally, \(\varphi \) is a credulous default consequence of a default theory \(\Theta \), notation  , iff \(\varphi \in {\bigcup {\mathscr {E}(\Theta )}}\); in turn, \(\varphi \) is a sceptical default consequence of \(\Theta \), notation
, iff \(\varphi \in {\bigcup {\mathscr {E}(\Theta )}}\); in turn, \(\varphi \) is a sceptical default consequence of \(\Theta \), notation  , iff \(\varphi \in {\bigcap {\mathscr {E}(\Theta )}}\). If \(\mathscr {E}(\Theta ) = \emptyset \), \({\bigcup {\mathscr {E}(\Theta )}} = \emptyset \) and \({\bigcap {\mathscr {E}(\Theta )}} = \mathscr {F}\) (see [32]). Define
, iff \(\varphi \in {\bigcap {\mathscr {E}(\Theta )}}\). If \(\mathscr {E}(\Theta ) = \emptyset \), \({\bigcup {\mathscr {E}(\Theta )}} = \emptyset \) and \({\bigcap {\mathscr {E}(\Theta )}} = \mathscr {F}\) (see [32]). Define  and
and  . We use
. We use  and
and  when there is no need to distinguish between
when there is no need to distinguish between  and
and  , and
, and  and
and  , resp.
, resp.
The rest of this section illustrates how some of the most common properties of Default Logics fit into our definition. We say that a default logic \(\mathscr {D}\mathfrak {L}\) guarantees extensions iff for all \(\Theta \), \(\mathscr {E}(\Theta ) \ne \emptyset \). Default logics that guarantee extensions are supra-classical, i.e., for all  ,
,  ; and they satisfy
; and they satisfy  for all \(\Theta \). These properties are not satisfied if extensions fail to exist, i.e., if there is \(\Theta \) s.t. \(\mathscr {E}(\Theta ) = \emptyset \). Let \(\Theta _1\) and \(\Theta _2\) be default theories, define \(\Theta _1 \sqsubseteq \Theta _2\) iff \(\varPhi _{\Theta _1} \subseteq \varPhi _{\Theta _2}\) and
for all \(\Theta \). These properties are not satisfied if extensions fail to exist, i.e., if there is \(\Theta \) s.t. \(\mathscr {E}(\Theta ) = \emptyset \). Let \(\Theta _1\) and \(\Theta _2\) be default theories, define \(\Theta _1 \sqsubseteq \Theta _2\) iff \(\varPhi _{\Theta _1} \subseteq \varPhi _{\Theta _2}\) and  . We say that \(\mathscr {D}\mathfrak {L}\) is non-monotonic iff there are \(\Theta _1\) and \(\Theta _2\) s.t. \(\Theta _1 \sqsubseteq \Theta _2\) and
. We say that \(\mathscr {D}\mathfrak {L}\) is non-monotonic iff there are \(\Theta _1\) and \(\Theta _2\) s.t. \(\Theta _1 \sqsubseteq \Theta _2\) and  . We say that \(\mathscr {D}\mathfrak {L}\) is semi-monotonic iff for any two \(\Theta _1\) and \(\Theta _2\) s.t. \(\Theta _1 \sqsubseteq \Theta _2\), if \(\varPhi _{\Theta _1} = \varPhi _{\Theta _2}\), then for all \(E_1 \in \mathscr {E}(\Theta _1)\), there is \(E_2 \in \mathscr {E}(\Theta _2)\) s.t. \(E_1 \subseteq E_2\). Further, we say that \(\mathscr {D}\mathfrak {L}\) is \(\mathscr {E}\)-consistent iff for all \(\Theta \), if
. We say that \(\mathscr {D}\mathfrak {L}\) is semi-monotonic iff for any two \(\Theta _1\) and \(\Theta _2\) s.t. \(\Theta _1 \sqsubseteq \Theta _2\), if \(\varPhi _{\Theta _1} = \varPhi _{\Theta _2}\), then for all \(E_1 \in \mathscr {E}(\Theta _1)\), there is \(E_2 \in \mathscr {E}(\Theta _2)\) s.t. \(E_1 \subseteq E_2\). Further, we say that \(\mathscr {D}\mathfrak {L}\) is \(\mathscr {E}\)-consistent iff for all \(\Theta \), if  is \(\mathfrak {L}\)-consistent, then all \(E \in \mathscr {E}(\Theta )\) are \(\mathfrak {L}\)-consistent. Non-monotonocity, semi-monotonicity, and \(\mathscr {E}\)-consistency do not follow from Definition 3. Moreover, they need not be satisfied by default logics (even if they guarantee extensions); they depend on the particularities of the definition of \(\mathscr {E}\). We make no assumptions regarding whether an arbitrary default logic satisfies any of the properties above.
is \(\mathfrak {L}\)-consistent, then all \(E \in \mathscr {E}(\Theta )\) are \(\mathfrak {L}\)-consistent. Non-monotonocity, semi-monotonicity, and \(\mathscr {E}\)-consistency do not follow from Definition 3. Moreover, they need not be satisfied by default logics (even if they guarantee extensions); they depend on the particularities of the definition of \(\mathscr {E}\). We make no assumptions regarding whether an arbitrary default logic satisfies any of the properties above.
2.3 Traditional Default Logics
Definition 3 paints a general picture of what is a default logic. At the same time, it captures default logics that are, in a sense, “degenerate”. E.g., we can define a default logic s.t. for all \(\Theta \),  . This default logic ignores defaults, thus collapsing default reasoning into reasoning in the underlying logic, i.e.,
. This default logic ignores defaults, thus collapsing default reasoning into reasoning in the underlying logic, i.e.,  for all \(\Theta \). We call any default logic satisfying this condition trivial. Trivial default logics are extreme cases of little interest from a Default Logic perspective. In defining a default logic, we wish to provide a precise account of what does it mean to reason with defaults in a way such that reasoning in the underlying logic is extended non-monotonically. This is the purpose of traditional default logics. Traditional default logics encompass Reiter’s seminal work on default logic [29] and some of its major variants, e.g., [13, 24, 27, 30], summarized in [2, 12]. We introduce what we mean by a traditional default logic in Definition 8 by building on, and generalizing, definitions and results presented in [17, 18].
for all \(\Theta \). We call any default logic satisfying this condition trivial. Trivial default logics are extreme cases of little interest from a Default Logic perspective. In defining a default logic, we wish to provide a precise account of what does it mean to reason with defaults in a way such that reasoning in the underlying logic is extended non-monotonically. This is the purpose of traditional default logics. Traditional default logics encompass Reiter’s seminal work on default logic [29] and some of its major variants, e.g., [13, 24, 27, 30], summarized in [2, 12]. We introduce what we mean by a traditional default logic in Definition 8 by building on, and generalizing, definitions and results presented in [17, 18].
We begin by taking a closer look at defaults. Typically, a default  is intuitively read as: if \(\pi \) is grounded in what is known and \(\rho \) is coherent with what is known, then, detach \(\chi \) and assume it tentatively as part of what is known. Extensions formalize the set of “known things”, what is meant by grounded, coherent, and detached and assumed tentatively. How these concepts are formalized separate traditional default logics from each other, as different intuitions lead to different formalizations.
is intuitively read as: if \(\pi \) is grounded in what is known and \(\rho \) is coherent with what is known, then, detach \(\chi \) and assume it tentatively as part of what is known. Extensions formalize the set of “known things”, what is meant by grounded, coherent, and detached and assumed tentatively. How these concepts are formalized separate traditional default logics from each other, as different intuitions lead to different formalizations.
Henceforth, by consistency we mean \(\mathfrak {L}\)-consistency. Define, for all sets \(\varDelta \),  ,
,  and
and  .
.
Definition 4
(Grounded). Let \(\Theta \) be a default theory, and  ; we say that \(\varDelta _2\) is grounded in \(\varDelta _1\) iff
; we say that \(\varDelta _2\) is grounded in \(\varDelta _1\) iff  . In addition, for all
. In addition, for all  , we say that \(\varDelta \) is a closed set iff
, we say that \(\varDelta \) is a closed set iff  .
.
Definition 4 captures a standard view on what does it mean for a set of defaults to be grounded. Intuitively, if we think of the sets \(\varDelta _1\) and \(\varDelta _2\) as defaults “already considered” and defaults “to be considered”, resp., the view of grounded in Definition 4 permits only for the consequents of “already considered” defaults to be used to establish the prerequisites of “to be considered” defaults. Closed sets are sets of defaults whose prerequisites can be established from within the set.
Definition 5
(Coherence). Let \(\Theta \) be a default theory, and  ; we say that \(\varDelta _2\) is i-coherent w.r.t. \(\varDelta _1\) iff:
; we say that \(\varDelta _2\) is i-coherent w.r.t. \(\varDelta _1\) iff:
-
(1-coherent) for all \(\delta _2 \in \varDelta _2\),
 is consistent.
is consistent. -
(2-coherent) for all \(\delta _2 \in \varDelta _2\),
 is consistent.
is consistent. -
(3-coherent)
 is consistent.
is consistent. -
(4-coherent)
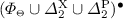 is consistent.
is consistent.
In addition, we say that \(\varDelta _2\) is self i-coherent if it is i-coherent w.r.t. itself.
Proposition 1
i-coherence implies 1-coherence, while 4-coherence implies i-coherence, for \(1 \le i \le 4\). Further, self 1-coherence implies self 2-coherence; self 3-coherence implies self 4-coherence.
A default  is normal iff \(\rho = \chi \). We use
is normal iff \(\rho = \chi \). We use  as notation for normal defaults. A default theory \(\Theta \) is normal if all
as notation for normal defaults. A default theory \(\Theta \) is normal if all  are normal.
are normal.
Proposition 2
For normal default theories, the four notions of coherence introduced in Definition 5 are equivalent.
Definition 5 captures four different views on what does it mean for a set of defaults to be coherent. The relation between these different views is made clear in Propositions 1 and 2. Again, if we think of the sets \(\varDelta _1\) and \(\varDelta _2\) as defaults “already considered” and defaults “to be considered”, resp., 1-coherence and 2-coherence require the justifications of the defaults “to be considered” to be individually consistent w.r.t. the defaults “already considered”. They differ from each other in whether or not the consequents of the defaults “to be considered” should be included in the consistency check. These takes on coherence correspond to Reiter [24, 29] and to Łukaszewicz [24], resp. In turn, 3-coherence and 4-coherence require the justifications of the defaults “to be considered” to be jointly consistent; and differ from each other in whether or not the consequents of the defaults “to be considered” should be included in the consistency check. These takes on coherence correspond to Mikitiuk and Truszczynski [27], and to Delgrande, Jackson, and Schaub [13, 30], resp. When there is no need to distinguish between the different types of coherence, we simply say that \(\varDelta _2\) is coherent w.r.t. \(\varDelta _1\).
Definition 6
(Detachment). Let \(\Theta \) be a default theory and  ; we say that \(\varDelta _2\) is detached by \(\varDelta _1\) if \(\varDelta _2\) is grounded in, and coherent w.r.t., \(\varDelta _1\). We say that \(\delta \) is detached by \(\varDelta _1\) if \(\varDelta _2 = {\varDelta _1 \cup \delta }\) is detached by \(\varDelta _1\).
; we say that \(\varDelta _2\) is detached by \(\varDelta _1\) if \(\varDelta _2\) is grounded in, and coherent w.r.t., \(\varDelta _1\). We say that \(\delta \) is detached by \(\varDelta _1\) if \(\varDelta _2 = {\varDelta _1 \cup \delta }\) is detached by \(\varDelta _1\).
Intuitively, detachment can be thought of as a version of modus-ponens for defaults. Fixing a definition of coherence, we say that detachment is: classical, justified, rational, and constrained, according to Table 1.
Remark 1
Recall that every well-ordering \(\prec \) is order-equivalent to exactly one ordinal number \(\uptau \). Such an ordinal number \(\uptau \) is the order type of \(\prec \). The precise definitions of these terms, and that of a limit ordinal, can be found in [32].
Definition 7
Let \(\Theta \) be a default theory; we say that  is regular if there is a well-ordering \(\prec \) on
is regular if there is a well-ordering \(\prec \) on  s.t. \(\varDelta = \mathsf {D}^{\scriptscriptstyle \prec }_{\scriptscriptstyle \Theta }(\uptau )\), where \(\uptau \) is the order type of \(\prec \), and for all ordinals \(\upomega \) s.t. \(0< \upomega < \uptau \), and all limit ordinals \(\uplambda \) s.t. \(\uplambda \le \uptau \), \(\mathsf {D}^{\scriptscriptstyle \prec }_{\scriptscriptstyle \Theta }\) is defined:
s.t. \(\varDelta = \mathsf {D}^{\scriptscriptstyle \prec }_{\scriptscriptstyle \Theta }(\uptau )\), where \(\uptau \) is the order type of \(\prec \), and for all ordinals \(\upomega \) s.t. \(0< \upomega < \uptau \), and all limit ordinals \(\uplambda \) s.t. \(\uplambda \le \uptau \), \(\mathsf {D}^{\scriptscriptstyle \prec }_{\scriptscriptstyle \Theta }\) is defined:

Again, Definition 7 encompasses four kinds of regularity. We say that a regular set of defaults is: classical, justified, rational, and constrained, depending on the definition of detachment it uses. Regularity captures a prescriptive view of how to cumulatively detach defaults in default theory. The function \(\mathsf {D}^{\scriptscriptstyle \prec }_{\scriptscriptstyle \Theta }\) is the closure under detachment of a set of defaults under the selection strategy defined by the well-ordering \(\prec \), and is a standard definition of a function by transfinite recursion. Example 2 illustrates the need for transfiniteness.
Example 2
In some cases, we may wish to prove that our default logic is semi-monotonic. Suppose that extensions in a default logic \(\mathscr {D}\mathfrak {L}\) are obtained through regular sets of defaults, and only those sets. This example shows that unless we allow for transfinite steps, we may fail to prove semi-monotonicity due to restrictions on the definition of \(\mathsf {D}^{\scriptscriptstyle \prec }_{\scriptscriptstyle \Theta }\). Let \(\mathscr {D}\mathfrak {L}\) be an \(\mathscr {E}\)-consistent default logic built over \(\mathsf {K}\mathsf {Alt}_{1}\Diamond ^+\) (i.e., the modal logic where \(\Diamond \) is interpreted over a weakly functional accessibility relation, and \(\Diamond ^+\) is its transitive closure, see, e.g., [7]). Let \(\Theta _1\) be a default theory s.t.  and
and  .
.  is regular for all kinds of detachment. Let
is regular for all kinds of detachment. Let  . \(E_1\) is satisfied in Kriple models in which every world has a successor. Let \(\Theta _2\) be s.t. \(\Theta _1 \sqsubseteq \Theta _2\),
. \(E_1\) is satisfied in Kriple models in which every world has a successor. Let \(\Theta _2\) be s.t. \(\Theta _1 \sqsubseteq \Theta _2\),  , and
, and  ; the formula
; the formula  describes the existence of a world reachable in a finite number of steps through the accessibility relation, which has no successors. There is no well-ordering \(\prec \) on
describes the existence of a world reachable in a finite number of steps through the accessibility relation, which has no successors. There is no well-ordering \(\prec \) on  of order type \(\upomega _0\) s.t.
of order type \(\upomega _0\) s.t.  . To see why, note that any such \(\prec \) on
. To see why, note that any such \(\prec \) on  contains
contains  at some position n. Since
at some position n. Since  is detached by any
is detached by any  , \(\mathsf {D}^{\scriptscriptstyle \prec }_{\scriptscriptstyle \Theta _2}(\upomega _0)\) detaches
, \(\mathsf {D}^{\scriptscriptstyle \prec }_{\scriptscriptstyle \Theta _2}(\upomega _0)\) detaches  in at most n steps. But as soon as
in at most n steps. But as soon as  is detached no other default in
is detached no other default in  can be detached. Thus, for all \(\prec \),
can be detached. Thus, for all \(\prec \),  is satisfied in Kripke models consisting of chains of at most n worlds; and so \(E_1 \nsubseteq E_2\). This establishes a failure of semi-monotonicity. By allowing transfinite steps, we can first detach all defaults in
is satisfied in Kripke models consisting of chains of at most n worlds; and so \(E_1 \nsubseteq E_2\). This establishes a failure of semi-monotonicity. By allowing transfinite steps, we can first detach all defaults in  , and then proceed to check whether or not
, and then proceed to check whether or not  can be detached in a transfinite step. From this, we can recover semi-monotonicity.
can be detached in a transfinite step. From this, we can recover semi-monotonicity.
Definition 8
(Traditional Default Logic). We say that a default logic \(\mathscr {D}\mathfrak {L}\) is traditional iff for all default theories \(\Theta \), \(\mathscr {E}(\Theta )\) is the smallest set s.t. for all regular and self coherent subsets \(\varDelta \) of  , there is
, there is  .
.
From Definition 8 it is possible to prove that traditional default logics encompass four distinct sub-classes of default logics. These classes are: classical default logics (classical regularity and 1-coherence); justified default logics (justified regularity and 2-coherence); rational default logics (rational regularity and 3-coherence); and constrained default Logics (constrained regularity and 4-coherence). This claim is made precise in Proposition 3.
Proposition 3
Every traditional default logic is either a classical, a justified, a constrained, or a rational default logic, and vice-versa.
It follows by construction, adapting the argument in [17, 18], that Classical Default Logic, defined by Reiter in [29], is a classical default logic. The same is true, mutatis mutandis, for Justified Default Logic, defined by Łukaszewicz in [24], Rational Default Logic, defined by Mikitiuk and Truszczynski in [27], and Constrained Default Logic, defined by Delgrande, Jackson, and Schaub in [13].
2.4 Intermediate Default Logics
Definition 3 paints a very general picture of what is a default logic. In turn, Definition 8 captures default logics whose extensions are obtained in a very prescriptive way via regular set of defaults. The obvious question is whether there are some “interesting” default logics “stricter” than those in Definition 3 but “weaker” than those in Definition 8.
Definition 9
Let \(\mathscr {D}\mathfrak {L}\) be any default logic, and \(\Theta \) be any default theory; we say that  is saturated iff for all
is saturated iff for all  , if \(\varDelta '\) is detached by \(\varDelta \), \(\varDelta ' \subseteq \varDelta \).
, if \(\varDelta '\) is detached by \(\varDelta \), \(\varDelta ' \subseteq \varDelta \).
Definition 10
We say that a default logic \(\mathscr {D}\mathfrak {L}\) is weakly saturated iff for all default theories \(\Theta \) and all \(E \in \mathscr {E}(\Theta )\), there exists a saturated  s.t.
s.t.  . In addition, we say that \(\mathscr {D}\mathfrak {L}\) is strongly saturated iff it is weakly saturated and for all default theories \(\Theta \) and all saturated
. In addition, we say that \(\mathscr {D}\mathfrak {L}\) is strongly saturated iff it is weakly saturated and for all default theories \(\Theta \) and all saturated  , if \(\varDelta \) is self coherent, then there is
, if \(\varDelta \) is self coherent, then there is  .
.
Proposition 4
Every traditional default logic is strongly saturated.
We can think of weakly saturated default logics as imposing an “upper bound” on extensions, i.e., anything that is not a saturated set of defaults cannot be an extension. On the other hand, strongly saturated default logics impose a “lower bound” on extensions, i.e., anything that is a saturated and self coherent set of defaults must be an extension. Strongly saturated default logics are an interesting generalization of traditional default logics for they simplify the proof of some results circumventing the prescriptive definition of extensions in Definition 8.
3 Interpolation and Beth Definability
As mentioned, interpolation and Beth definability are recognized as important properties of the meta-theory of a logic. Here, we investigate interpolation and Beth definability in Default Logics. More precisely, we investigate when results transfer from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\). In order to accomplish this, we first need to formulate suitable notions of interpolation and Beth definability for a default logics.
3.1 Interpolation
There is no unifying definition of interpolation in the literature, see [22]. Instead, this property comes in many flavours. In what follows, we discuss some relevant formulations of interpolation. In this discussion we assume an arbitrary logic \(\mathfrak {L}\).
Let us start with the so-called Craig Interpolation Property (\(\mathsf {CIP}\)).
Definition 11
We say that consequence in \(\mathfrak {L}\) has \(\mathsf {CIP}\) iff whenever \(\vdash {\varphi \supset \psi }\), there is \(\xi \) defined on  s.t. \(\vdash {\varphi \supset \xi }\) and \(\vdash {\xi \supset \psi }\).
s.t. \(\vdash {\varphi \supset \xi }\) and \(\vdash {\xi \supset \psi }\).
On certain occasions, in place for \(\mathsf {CIP}\), we may wish to have a stronger version.
Definition 12
We say that consequence \(\mathfrak {L}\) has the Strong Craig Inteprolation Property (\(\mathsf {S}\mathsf {CIP} \)) iff whenever \(\varPhi \vdash {\varphi \supset \psi }\), there is \(\xi \) defined on  s.t. \(\varPhi \vdash {\varphi \supset \xi }\) and \(\varPhi \vdash {\xi \supset \psi }\).
s.t. \(\varPhi \vdash {\varphi \supset \xi }\) and \(\varPhi \vdash {\xi \supset \psi }\).
A rather different formulation of interpolation, used in the standard argument for Beth Definability, is the so-called Split Interpolation Property (\(\mathsf {SIP}\)), see [31].
Definition 13
We say that consequence \(\mathfrak {L}\) has \(\mathsf {SIP}\) iff for any \(\varPhi \) and \(\varphi \) defined on an alphabet \(A_1\), and any \(\varPsi \) and \(\psi \) defined on an alphabet \(A_2\); if \({{\varPhi \cup \varPsi } \vdash {\varphi \supset \psi }}\), there is \(\xi \) defined on \({A_1 \cap A_2}\) s.t. \({\varPhi \vdash {\varphi \supset \xi }}\) and \({\varPsi \vdash {\xi \supset \psi }}\). The formula \(\xi \) is called a split interpolant.
In general, \(\mathsf {CIP}\), \(\mathsf {S}\mathsf {CIP} \), and \(\mathsf {SIP}\) are not equivalent (having one does not imply having the others). Equivalence depends on the particularities of the logical connectives under consideration and on logical consequence satisfying properties such as compactness, deduction, etc. Logics known to have all three different versions of interpolation are, for example, \(\mathsf {CPL}\), IPL, and the modal logics \(\mathsf {K}\), \(\mathsf {S5}\) and \(\mathsf {H}(\mathsf {A},\downarrow )\) with local and global consequence. For a discussion regarding equivalence of interpolation in these logics see [3, 4]. We take a particular interest in \(\mathsf {SIP}\): as an interpolation result in its own right, given its widespread applicability, and as a step towards obtaining Beth definability in a standard way [28].
3.2 Interpolation in Default Logics
We explore what the natural formulations of \(\mathsf {CIP}\), \(\mathsf {S}\mathsf {CIP} \), and \(\mathsf {SIP}\), look like for default consequence in default logics.
Definition 14
We say that default consequence in a default logic \(\mathscr {D}\mathfrak {L}\) has the Default Craig Interpolation Property, notation \(\mathscr {D}\mathsf {CIP} \), iff whenever  , there is \(\xi \) defined on
, there is \(\xi \) defined on  , s.t.
, s.t.  and
and  .
.
Proposition 5
For any default logic \(\mathscr {D}\mathfrak {L}= \langle \mathfrak {L}, \mathscr {E}\rangle \); if consequence in \(\mathfrak {L}\) has \(\mathsf {CIP}\), then, default consequence in \(\mathscr {D}\mathfrak {L}\) has \(\mathscr {D}\mathsf {CIP} \).
The proof of Proposition 5 is direct from the definition of a default logic and \(\mathsf {CIP}\) for \(\vdash \) in \(\mathfrak {L}\). \(\mathscr {D}\mathsf {CIP} \) is rather trivial as it involves only reasoning from empty default theories, thus reducing default consequences to consequences in the underlying logic. Let us consider the more interesting case of \(\mathscr {D}\mathsf {S}\mathsf {CIP} \), the \(\mathsf {S}\mathsf {CIP} \) version of interpolation for Default Logics, which makes use of non-empty default theories.
Definition 15
We say that default consequence in a default logic \(\mathscr {D}\mathfrak {L}\) has the Default Strong Craig Interpolation Property, notation \(\mathscr {D}\mathsf {S}\mathsf {CIP} \), iff whenever  , there is \(\xi \) defined on
, there is \(\xi \) defined on  , s.t.
, s.t.  and
and  .
.
Proposition 6
For any default logic \(\mathscr {D}\mathfrak {L}= \langle \mathfrak {L}, \mathscr {E}\rangle \); if consequence in \(\mathfrak {L}\) has \(\mathsf {S}\mathsf {CIP} \), then, default consequence in \(\mathscr {D}\mathfrak {L}\) has \(\mathscr {D}\mathsf {S}\mathsf {CIP} \).
Proof (by cases)
Let \(\Theta \) be a default theory; if \(\mathscr {E}(\Theta ) = \emptyset \),  and
and  . The result follows trivially from these facts. If \(\mathscr {E}(\Theta ) \ne \emptyset \):
. The result follows trivially from these facts. If \(\mathscr {E}(\Theta ) \ne \emptyset \):
- (
 ):
): -
Let
 ; then, there is \({E \in \mathscr {E}(\Theta )}\) s.t. \({E \vdash {\varphi \supset \psi }}\). From \(\mathsf {S}\mathsf {CIP} \), there is \(\xi \) defined on
; then, there is \({E \in \mathscr {E}(\Theta )}\) s.t. \({E \vdash {\varphi \supset \psi }}\). From \(\mathsf {S}\mathsf {CIP} \), there is \(\xi \) defined on  s.t. \({E \vdash {\varphi \supset \xi }}\) and \({E \vdash {\xi \supset \psi }}\). So,
s.t. \({E \vdash {\varphi \supset \xi }}\) and \({E \vdash {\xi \supset \psi }}\). So,  and
and  , with
, with  .
. - (
 ):
): -
Let
 , and \(\varGamma = \bigcap {\mathscr {E}(\Theta )}\); then, \(\varGamma \vdash {\varphi \supset \psi }\). From \(\mathsf {S}\mathsf {CIP} \), there is \(\xi \) defined on
, and \(\varGamma = \bigcap {\mathscr {E}(\Theta )}\); then, \(\varGamma \vdash {\varphi \supset \psi }\). From \(\mathsf {S}\mathsf {CIP} \), there is \(\xi \) defined on  s.t. \(\varGamma \vdash {\varphi \supset \xi }\) and \(\varGamma \vdash {\xi \supset \psi }\). Thus,
s.t. \(\varGamma \vdash {\varphi \supset \xi }\) and \(\varGamma \vdash {\xi \supset \psi }\). Thus,  and
and  , with
, with  .
.
The result follows from ( ) and (
) and ( ).
).
We now turn our attention to what does \(\mathsf {SIP}\) look like for default consequence.
Remark 2
For default theories \(\Theta _i\), define  .
.
Definition 16
We say that default consequence in a default logic \(\mathscr {D}\mathfrak {L}\) has the Default Split Interpolation Property, notation \(\mathscr {D}\mathsf {SIP} \), iff for all \(\Theta _1\) and \(\varphi \) defined on an alphabet \(A_1\), and \(\Theta _2\) and \(\psi \) defined on an alphabet \(A_2\), if  , there is \(\xi \) defined on \({A_1 \cap A_2}\), s.t.
, there is \(\xi \) defined on \({A_1 \cap A_2}\), s.t.  and
and  .
.
For \(\mathscr {D}\mathsf {SIP} \) we obtain a negative result in the following form.
Proposition 7
For any traditional default logic \(\mathscr {D}\mathfrak {L}\) built on a logic extending Classical Propositional Logic, default consequence in \(\mathscr {D}\mathfrak {L}\) does not have \(\mathscr {D}\mathsf {SIP} \).
Proof
W.l.o.g. let \(\mathfrak {L}\) be \(\mathsf {CPL}\), and  and
and  , it follows that:
, it follows that:
-
(1)
for all \(E_1 \in \mathscr {E}(\Theta _1)\),
 .
. -
(2)
for all \(E_2 \in \mathscr {E}(\Theta _2)\),
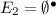 .
. -
(3)
for all \(E \in \mathscr {E}(\Theta _1 \sqcup \Theta _2)\),
 .
.
From (3),  . Immediately,
. Immediately,  , and
, and  . Then, any formula \(\xi \) defined on
. Then, any formula \(\xi \) defined on  is equivalent to \(\top \), \(\bot \), q, or \(\lnot q\). If we fix \(\xi \) to any of these formulas, either from (1),
is equivalent to \(\top \), \(\bot \), q, or \(\lnot q\). If we fix \(\xi \) to any of these formulas, either from (1),  ; or from (2),
; or from (2),  .
.
We explored some natural formulations of \(\mathsf {CIP}\), \(\mathsf {S}\mathsf {CIP} \), and \(\mathsf {SIP}\) for default consequence in a default logic. We have shown positive transfer results for \(\mathscr {D}\mathsf {CIP} \) and \(\mathscr {D}\mathsf {S}\mathsf {CIP} \). We highlight the generality of these results: not only they concern traditional logics, but all default logics. This level of generality, i.e., proofs depending on extensions and not their construction, is achieved thanks to the abstract presentation of what is a default logic. We have also shown a negative transfer result for \(\mathscr {D}\mathsf {SIP} \). In this case the counter-example is much more concrete, but still sufficiently general to cover all traditional default logics. Lack of \(\mathscr {D}\mathsf {SIP} \) is a set back for Beth definability, as we are now pre-empted to use the standard argument for establishing the latter from the former [28]. Nonetheless, we show that Beth definability can still be obtained in some form for some default logics.
3.3 Definability
Beth definability is commonly regarded as a sign of a well behaved logic. We adapt our definition of this property from [22].
Definition 17
Let \(\mathfrak {L}\) be any logic, \(\varPhi \) be a set of formulas s.t.  , and \(q \notin A\); we say that consequence in \(\mathfrak {L}\) has the Beth Definability Property (\(\mathsf {BDP}\)) iff whenever
, and \(q \notin A\); we say that consequence in \(\mathfrak {L}\) has the Beth Definability Property (\(\mathsf {BDP}\)) iff whenever

there is \(\varepsilon \) defined on an alphabet \(A_0 = {A \setminus \{p\}}\) s.t.
Equation (1) expresses that \(\varPhi \) implicitly defines p; whereas Eq. (2) is the explicit definition of p from \(\varPhi \).
In general, \(\mathsf {BDP}\) can be obtained from \(\mathsf {SIP}\) through a standard argument [28]. Let us remark that failure of \(\mathsf {SIP}\) does not necessarily imply failure of \(\mathsf {BDP}\). The latter property may still be obtained through other means.
3.4 Definability in Default Logics
Definition 18 introduces a natural formulation of Beth definability for default logics.
Definition 18
Let \(\mathscr {D}\mathfrak {L}\) be a default logic, \(\Theta \) a default theory s.t.  , and \(q \notin A\); we say that default consequence in \(\mathscr {D}\mathfrak {L}\) has the Default Beth definability property (\(\mathscr {D}\mathsf {BDP} \)) iff whenever
, and \(q \notin A\); we say that default consequence in \(\mathscr {D}\mathfrak {L}\) has the Default Beth definability property (\(\mathscr {D}\mathsf {BDP} \)) iff whenever

there is \(\varepsilon \) defined on an alphabet \(A_0 = {A \setminus \{p\}}\) s.t.

Equation (3) expresses that \(\Theta \) implicitly defines p; whereas \(\varepsilon \) in Eq. (4) is the explicit definition of p from \(\Theta \).
Proving Beth definability for default consequence in default logics requires some additional definitions and lemmas (the proofs of which are in Appendix A). First, it needs a condition on stability, see Definition 19. This condition states that the extensions of a default theory are in harmony with the extensions of its extended default theory under substitution.
Definition 19
We say that a default logic \({\mathscr {D}\mathfrak {L}= \langle \mathfrak {L}, \mathscr {E}\rangle }\) is stable iff for all default theories \(\Theta \) defined on an alphabet A, if \(q \notin A\), it follows that for all \({E \in \mathscr {E}(\Theta )}\), there is  s.t.
s.t.  .
.
Lemma 1 shows that the condition of being stable is rather natural, in the sense that it is satisfied by a non-trivial class of default logics, i.e., those that are strongly saturated and, in particular, by traditional default logics.
Lemma 1
Any strongly saturated default logic \(\mathscr {D}\mathfrak {L}\) is stable.
Lemma 2 establishes that the notion coherence for the extensions of a given default theory is preserved if we augment the default theory by substitution.
Lemma 2
Let \(\mathscr {D}\mathfrak {L}\) be a default logic; for all default theories \(\Theta \) and all  , if \(\varDelta \) is self coherent in \(\Theta \), then,
, if \(\varDelta \) is self coherent in \(\Theta \), then,  is self coherent in
is self coherent in  .
.
The following lemma, simplifies a key step in the proof of Proposition 8.
Lemma 3
Let  be a set of sets of formulas s.t. for all \(i \in I\),
be a set of sets of formulas s.t. for all \(i \in I\),  and
and  ; if consequence in \(\mathfrak {L}\) has \(\mathsf {SIP}\), \(q \notin A\), and
; if consequence in \(\mathfrak {L}\) has \(\mathsf {SIP}\), \(q \notin A\), and  , then
, then  .
.
Proposition 8
For any default logic \(\mathscr {D}\mathfrak {L}= \langle \mathfrak {L}, \mathscr {E}\rangle \); if \(\mathscr {D}\mathfrak {L}\) is stable and consequence in \(\mathfrak {L}\) has \(\mathsf {SIP}\), then, sceptical default consequence in \(\mathscr {D}\mathfrak {L}\) has \(\mathscr {D}\mathsf {BDP} \).
Proof
(by cases). Let \(\Theta \) be any default theory defined on alphabet A, and \(q \notin A\); if  , the result holds trivially from the fact that \(\mathscr {D}\mathfrak {L}\) is stable. Otherwise, i..e, if
, the result holds trivially from the fact that \(\mathscr {D}\mathfrak {L}\) is stable. Otherwise, i..e, if  , let
, let  ; from the fact that \(\mathscr {D}\mathfrak {L}\) is stable,
; from the fact that \(\mathscr {D}\mathfrak {L}\) is stable,  . From Lemma 3,
. From Lemma 3,  . From \(\mathsf {SIP}\), there is \(\xi \) defined on \(A \setminus \{p\}\) s.t.
. From \(\mathsf {SIP}\), there is \(\xi \) defined on \(A \setminus \{p\}\) s.t.  and (\(\dagger \))
and (\(\dagger \))  . Substituting p for q in (\(\dagger \)) we obtain
. Substituting p for q in (\(\dagger \)) we obtain  . Therefore, there is \(\xi \) defined on \(A \setminus \{p\}\) s.t.
. Therefore, there is \(\xi \) defined on \(A \setminus \{p\}\) s.t.  and
and  .
.
Corollary 1
For all traditional default logics built on a logic \(\mathfrak {L}\); if \(\mathfrak {L}\) has \(\mathsf {SIP}\), then sceptical consequence has \(\mathscr {D}\mathsf {BDP} \).
For credulous default consequence we obtain the following negative result.
Proposition 9
For all traditional default logic \(\mathscr {D}\mathfrak {L}\) built on a logic extending \(\mathsf {CPL}\), credulous default consequence in \(\mathscr {D}\mathfrak {L}\) does not have \(\mathscr {D}\mathsf {SIP} \).
Proof
W.l.o.g. let \(\mathfrak {L}\) be CPL; consider a default theory \({\Theta = ( \emptyset , \{ \delta _1, \delta _2 \} )}\), where

Trivially, we get  . Moreover:
. Moreover:
-
(1)
In classical, justified, constrained, and rational default logic on \(\mathfrak {L}\), it follows that,
 where:
where:  ; and
; and  .
. -
(2)
In justified, constrained, and rational default logic on \(\mathfrak {L}\), it follows that, for all \(E \in \mathscr {E}(\Theta )\),
 .
. -
(3)
In classical default logic on \(\mathfrak {L}\), it follows that, \(\mathscr {E}(\Theta ) = \emptyset \).
Clearly,  . From (1),
. From (1),  and
and  . To see why, note that
. To see why, note that  and
and  are both in
are both in  . Immediately,
. Immediately,  , and also
, and also  . In justified, constrained, and rational default logic on \(\mathfrak {L}\), there is no \(\xi \) defined on
. In justified, constrained, and rational default logic on \(\mathfrak {L}\), there is no \(\xi \) defined on  for which
for which  and
and  . To see why, note from (2) that every \(E \in \mathscr {E}(\Theta )\) is equal to
. To see why, note from (2) that every \(E \in \mathscr {E}(\Theta )\) is equal to  . Let E be any such extension, it is easy to see that there are models \(\mathfrak {M}_1\) and \(\mathfrak {M}_2\) of E s.t. \(\mathfrak {M}_1 \Vdash p\) and \(\mathfrak {M}_1 \Vdash \lnot p\). This establishes failure of \(\mathscr {D}\mathsf {BDP} \) for justified, constrained, and rational default logic on \(\mathfrak {L}\). In classical default logic on \(\mathfrak {L}\), there is no \(\xi \) defined on
. Let E be any such extension, it is easy to see that there are models \(\mathfrak {M}_1\) and \(\mathfrak {M}_2\) of E s.t. \(\mathfrak {M}_1 \Vdash p\) and \(\mathfrak {M}_1 \Vdash \lnot p\). This establishes failure of \(\mathscr {D}\mathsf {BDP} \) for justified, constrained, and rational default logic on \(\mathfrak {L}\). In classical default logic on \(\mathfrak {L}\), there is no \(\xi \) defined on  for which
for which  and
and  simply because \(\mathscr {E}(\Theta ) = \emptyset \). This establishes failure of \(\mathscr {D}\mathsf {BDP} \) for classical default logic on \(\mathfrak {L}\). In summary, the default theory \(\Theta \) defined above exhibits a counter-example for \(\mathscr {D}\mathsf {BDP} \) for credulous default consequence in any traditional default logic built on a logic extending \(\mathsf {CPL}\).
simply because \(\mathscr {E}(\Theta ) = \emptyset \). This establishes failure of \(\mathscr {D}\mathsf {BDP} \) for classical default logic on \(\mathfrak {L}\). In summary, the default theory \(\Theta \) defined above exhibits a counter-example for \(\mathscr {D}\mathsf {BDP} \) for credulous default consequence in any traditional default logic built on a logic extending \(\mathsf {CPL}\).
Even though \(\mathscr {D}\mathsf {SIP} \) fails for default logics, we showed that under certain conditions, \(\mathscr {D}\mathsf {BDP} \) can be still obtained for the sceptical default consequence.
4 Final Remarks
Interpolation and Beth definability are recognized as important properties of the meta-theory of a logic. However, few authors have explored these properties in the field of Non-monotonic Logic, and in default logics in particular. A pioneering work in this area is [1]. Therein the author studies interpolation for circumscription, default logic, and logic programs with the stable models semantics. The version of interpolation presented in [1] is different from the ones investigated here, and is proven for sceptical default consequence in what we would call classical default logic over \(\mathsf {CPL}\) (with finite vocabularies). The author also formulates a version of split interpolation and proves it for credulous consequence in the same context. However, the proof of this property requires the alphabet of the consequences of one default theory to be disjoint from the alphabet of the prerequisites and justifications of the defaults in other default theory. Thus the result applies to a restricted set of cases. In contrast, our results hold for a richer collection of default logics and generalize some of those introduced in [1]. Another interesting interpolation result in the field of Non-monotonic is [20]. This work studies interpolation in equilibrium logic; presenting a technique to obtain interpolation results by relying on the fact that the version of non-monotonic consequence in question can be defined via some minimally (axiomatically) defined models in some monotonic logic. This technique does not directly apply in default logics, since minimal sets of models of the base logics are not immediately connected to extensions. But this deserves a deeper investigation. We are, to the best of our knowledge, unaware of investigations of Beth definability in default logics.
We investigated interpolation and Beth definability in default logics. To this end, we started with a presentation of a general frawework for defining a default logic \(\mathscr {D}\mathfrak {L}\) from a basic monotonic logic \(\mathfrak {L}\). This framework covers well-known traditional default logics found in the literature, but encompasses a much richer family of default logics. Then, we defined suitable versions of interpolation and Beth definability for Default Logics, and studied their statuses. Given the generality of our definition of a default logic, the discussed results hold (or fail to hold) for several versions of default logics. In particular, we showed that \(\mathsf {CIP}\) and \(\mathsf {S}\mathsf {CIP} \) (two versions of the so-called Craig Interpolation Property) transfers from \(\mathfrak {L}\) to \(\mathscr {D}\mathfrak {L}\), but Split Interpolation \(\mathsf {SIP}\) fails for default logics extending \(\mathsf {CPL}\), even if \(\mathfrak {L}\) has it. When considered as a step towards Beth definability, this negative result is a set back. However, we showed that the sceptical default consequence in a \(\mathscr {D}\mathfrak {L}\) has Beth definability (\(\mathscr {D}\mathsf {BDP} \)) if \(\mathscr {D}\mathfrak {L}\) is stable (i.e., the extensions of a default theory are in harmony with those of its augmented default theory under substitution) and \(\mathfrak {L}\) has \(\mathsf {SIP}\). Different is the case for credulous default consequence, in which \(\mathscr {D}\mathsf {BDP} \) fails for any \(\mathscr {D}\mathfrak {L}\) built on a logic extending \(\mathsf {CPL}\).
We view this work as a first step towards a better understanding of the meta-theory of default logics in general. As future work, it would be interesting to apply similar ideas to study proof calculi for default logics that are parameterized on the underlying logic. Moreover, it would be interesting to see whether the methods for constructing interpolants in the underlying proof calculi transfer to the default version (see e.g. [8]).
References
Amir, E.: Interpolation theorems for nonmonotonic reasoning systems. In: Flesca, S., Greco, S., Ianni, G., Leone, N. (eds.) JELIA 2002. LNCS (LNAI), vol. 2424, pp. 233–244. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45757-7_20
Antoniou, G., Wang, K.: Default logic. In: Gabbay, D., Woods, J. (eds.) The Many Valued and Nonmonotonic Turn in Logic. Handbook of the History of Logic, vol. 8, pp. 517–555. North-Holland (2007)
Areces, C., Blackburn, P., Marx, M.: Hybrid logics: characterization, interpolation and complexity. J. Symb. Logic 66(3), 977–1010 (2001)
Areces, C., de Rijke, M.: Interpolation and bisimulation in temporal logic. In: Workshop on Logic, Language, Information and Computation (WoLLIC 1998), pp. 15–21 (1998)
Areces, C., ten Cate, B.: Hybrid logics. In: Blackburn, P., van Benthem, J., Wolter, F. (eds.) Handbook of Modal Logic, pp. 821–868. Elsevier (2006)
Bicarregui, J., Dimitrakos, T., Gabbay, D., Maibaum, T.: Interpolation in practical formal development. Logic J. IGPL 9(2), 231–244 (2001)
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge University Press, Cambridge (2001)
Blackburn, P., Marx, M.: Constructive interpolation in hybrid logic. J. Symb. Logic 68(2), 463–480 (2003)
Cassano, V., Areces, C., Castro, P.: Reasoning about prescription and description using prioritized default rules. In: Barthe, G., Sutcliffe, G., Veanes, M. (eds.) 22nd International Conference on Logic for Programming, Artificial Intelligence and Reasoning (LPAR-22). EPiC Series in Computing, vol. 57, pp. 196–213. EasyChair (2018)
Chellas, B.: Modal Logic: An Introduction. Cambridge University Press, Cambridge (1980)
Craig, W.: Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory. J. Symb. Logic 22, 269–285 (1957)
Delgrande, J., Schaub, T.: Expressing default logic variants in default logic. J. Logic Comput. 15(5), 593–621 (2005)
Delgrande, J., Schaub, T., Jackson, W.: Alternative approaches to default logic. Artif. Intell. 70(1–2), 167–237 (1994)
Diaconescu, R., Goguen, J., Stefaneas, P.: Logical support for modularisation. Papers Presented at the 2nd Annual Workshop on Logical Environments, pp. 83–130. Cambridge University Press, Cambridge (1993)
Enderton, H.: A Mathematical Introduction to Logic, 2nd edn. Academic Press, Cambridge (2001)
Font, J.: Abstract Algebraic Logic. An Introductory Textbook, 1st edn. College Publications (2016)
Froidevaux, C., Mengin, J.: A framework for default logics. In: Pearce, D., Wagner, G. (eds.) JELIA 1992. LNCS, vol. 633, pp. 154–173. Springer, Heidelberg (1992). https://doi.org/10.1007/BFb0023427
Froidevaux, C., Mengin, J.: Default logics: a unified view. Comput. Intell. 10, 331–369 (1994)
Gabbay, D., Maksimova, L.: Interpolation and Definability: Modal and Intuitionistic Logic. Oxford University Press, Oxford (2005)
Gabbay, D., Pearce, D., Valverde, A.: Interpolable formulas in equilibrium logic and answer set programming. J. Artif. Intell. Res. 42, 917–943 (2011)
Hintikka, J.: Knowledge and Belief. Cornell University Press, Ithaca (1962)
Hoogland, E.: Definability and Interpolation. Ph.D. thesis, Institute for Logic, Language and Computation Universiteit van Amsterdam (2001)
Kontchakov, R., Wolter, F., Zakharyaschev, M.: Can you tell the difference between DL-Lite ontologies? In: 11th International Conference on Principles of Knowledge Representation and Reasoning (KR 2008), pp. 285–295. AAAI Press (2008)
Łukaszewicz, W.: Considerations on default logic: an alternative approach. Comput. Intell. 4, 1–16 (1988)
Maibaum, T., Sadler, M.: Axiomatizing specification theory. In: 3rd Workshop on Theory and Applications of ADTs (WADT 1984). Informatik-Fachberichte, vol. 116, pp. 171–177. Springer, Heidelberg (1984)
McMillan, K.L.: Applications of craig interpolants in model checking. In: Halbwachs, N., Zuck, L.D. (eds.) TACAS 2005. LNCS, vol. 3440, pp. 1–12. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31980-1_1
Mikitiuk, A., Truszczynski, M.: Constrained and rational default logics. In: 14th International Joint Conference on Artificial Intelligence (IJCAI 1995), pp. 1509–1517 (1995)
Parikh, R.: Beth definability, interpolation and language splitting. Synthese 179(2), 211–221 (2011)
Reiter, R.: A logic for default reasoning. AI 13(1–2), 81–132 (1980)
Schaub, T.: On constrained default theories. In: 11th European Conference on Artificial Intelligence (ECAI 1992), pp. 304–308 (1992)
Shoenfield, J.: Mathematical Logic. Addison-Wesley, Boston (1967)
Suppes, P.: Axiomatic Set Theory. Dover Books on Mathematics. Dover Publications, Mineola (1972)
van Dalen, D.: Logic and structure, 5th edn. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-85108-0
Veloso, P., Maibaum, T.: On the modularization theorem for logical specifications. Inf. Process. Lett. 53(5), 287–293 (1995)
Von Wright, G.H.: Deontic logic. Mind 60, 1–15 (1951)
Ackowledgements
This work was partially supported by ANPCyT-PICTs-2017-1130 and 2016-0215, MinCyT Córdoba, SeCyT-UNC, the Laboratoire International Associé INFINIS and the European Union’s Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement No. 690974 for the project MIREL: MIning and REasoning with Legal texts.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Selected Proofs
A Selected Proofs
Remark 3
Let \(\mathfrak {L}\) be any logic, and \(\varPhi \) and \(\varPsi \) be sets of sentences; we say that \(\varPsi \) is a conservative extension of \(\varPhi \), notation \(\varPsi \ge \varPhi \), iff  and
and  .
.
Lemma 4
Let \(\mathfrak {L}\) be any logic, \(\varPhi \) be a set of sentences defined on an alphabet A, and \(q \notin A\); if consequence in \(\mathfrak {L}\) has \(\mathsf {SIP}\),  and
and  .
.
Proof
Trivially,  . In turn, let
. In turn, let  ; then,
; then,  , alt.,
, alt.,  . From \(\mathsf {SIP}\), there is \(\varepsilon \) defined on \(A \setminus \{p\}\) s.t.
. From \(\mathsf {SIP}\), there is \(\varepsilon \) defined on \(A \setminus \{p\}\) s.t.  and
and  . Since
. Since  ,
,  results in
results in  . Then,
. Then,  and
and  ; and so,
; and so,  , alt.,
, alt.,  . Therefore,
. Therefore,  .
.
Lemma 1
Any strongly saturated default logic \(\mathscr {D}\mathfrak {L}\) is stable.
Proof
Let \(\Theta \) be a default theory defined on an alphabet A, and and \(q \notin A\). In addition, let \(E \in \mathscr {E}(\Theta )\) be s.t.  for some
for some  . Since \(\mathscr {D}\mathfrak {L}\) is strongly saturated, \(\varDelta \) is saturated in \(\Theta \). The result follows immediately if
. Since \(\mathscr {D}\mathfrak {L}\) is strongly saturated, \(\varDelta \) is saturated in \(\Theta \). The result follows immediately if  is saturated in
is saturated in  ; as
; as  is our extension. The proof proceeds by contradiction. Let
is our extension. The proof proceeds by contradiction. Let  be not saturated in
be not saturated in  ; w.l.o.g. there is a default
; w.l.o.g. there is a default  s.t. \(\delta \) is detached by
s.t. \(\delta \) is detached by  . Clearly,
. Clearly,  or
or  for some
for some  . If
. If  , from Lemma 4, \(\delta \) is detached by \(\varDelta \); and so \(\varDelta \) is not saturated. This yields a contradiction. If
, from Lemma 4, \(\delta \) is detached by \(\varDelta \); and so \(\varDelta \) is not saturated. This yields a contradiction. If  for some
for some  , from Lemma 4,
, from Lemma 4,  is detached by
is detached by  ; and so
; and so  is not saturated. But by substitution, \(\delta '\) is detached by \(\varDelta \), and so \(\varDelta \) is not saturated. This also yields a contradiction. Thus,
is not saturated. But by substitution, \(\delta '\) is detached by \(\varDelta \), and so \(\varDelta \) is not saturated. This also yields a contradiction. Thus,  is saturated in
is saturated in  .
.
Lemma 2
Let \(\mathscr {D}\mathfrak {L}\) be a default logic; for all default theories \(\Theta \) and all  , if \(\varDelta \) is self coherent in \(\Theta \), then,
, if \(\varDelta \) is self coherent in \(\Theta \), then,  is self coherent in
is self coherent in  .
.
Proof
Similar to that of Lemma 1.
Lemma 3
Let  be a set of sets of formulas s.t. for all \(i \in I\),
be a set of sets of formulas s.t. for all \(i \in I\),  and
and  ; if consequence in \(\mathfrak {L}\) has \(\mathsf {SIP}\), \(q \notin A\), and
; if consequence in \(\mathfrak {L}\) has \(\mathsf {SIP}\), \(q \notin A\), and  , then
, then  .
.
Proof
(by contradiction). Let us assume that  ; by definition, it follows that all (\(*\))
; by definition, it follows that all (\(*\))  . At the same time, let
. At the same time, let  ; then, for all \(\xi \) defined on \({A \setminus \{p\}}\), either (\(\dagger \))
; then, for all \(\xi \) defined on \({A \setminus \{p\}}\), either (\(\dagger \))  or (\(\ddagger \))
or (\(\ddagger \))  . From (\(\dagger \)), there is
. From (\(\dagger \)), there is  ; and from Lemma 4, (\(\S \))
; and from Lemma 4, (\(\S \))  . But (\(\S \)) leads to a contradiction; since from (\(*\))
. But (\(\S \)) leads to a contradiction; since from (\(*\))  , by \(\mathsf {SIP}\), there is in fact \(\xi \) defined on \(A \setminus \{p\}\) s.t.
, by \(\mathsf {SIP}\), there is in fact \(\xi \) defined on \(A \setminus \{p\}\) s.t.  ! Similarly, we obtain a contradiction from (\(\ddagger \)). Thus,
! Similarly, we obtain a contradiction from (\(\ddagger \)). Thus,  .
.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Cassano, V., Fervari, R., Areces, C., Castro, P.F. (2019). Interpolation and Beth Definability in Default Logics. In: Calimeri, F., Leone, N., Manna, M. (eds) Logics in Artificial Intelligence. JELIA 2019. Lecture Notes in Computer Science(), vol 11468. Springer, Cham. https://doi.org/10.1007/978-3-030-19570-0_44
Download citation
DOI: https://doi.org/10.1007/978-3-030-19570-0_44
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-19569-4
Online ISBN: 978-3-030-19570-0
eBook Packages: Computer ScienceComputer Science (R0)





 is consistent.
is consistent. is consistent.
is consistent. is consistent.
is consistent.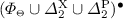 is consistent.
is consistent. ):
): ; then, there is
; then, there is  s.t.
s.t.  and
and  , with
, with  .
. ):
): , and
, and  s.t.
s.t.  and
and  , with
, with  .
. .
.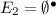 .
. .
. where:
where:  ; and
; and  .
. .
.