Symmetries and Integrals

Abstract

In these lectures, I want to illustrate an application of symmetry ideas to integration of differential equations. Basically, we will consider only differential equations of finite type, i.e. equations with finite-dimensional space Sol of (local) solutions. Ordinary differential equations make up one of the main examples of such equations.

3.1 Preface

In these lectures, I want to illustrate an application of symmetry ideas to integration of differential equations. Basically, we will consider only differential equations of finite type, i.e. equations with finite-dimensional space Sol of (local) solutions. Ordinary differential equations make up one of the main examples of such equations. The symmetry Lie algebra Sym induces an action on manifold Sol. In the case when this action is transitive, we expect to get more detailed information on solutions. Here, we are going to realize this expectation; namely, we will show that in the case when the Lie algebra Sym is solvable, integration of the differential equation can be done by quadratures due to the Lie–Bianchi theorem (see, for example, [4] or [6]). In the case when the Lie algebra Sym contains simple subalgebras, integration shall use quadratures (for radical of the Lie algebra) and integration of some differential equations, which we will call model equations [6, 10]. The model equations depend on the type of the simple Lie subalgebras and are natural generalizations of the well-known Riccati differential equations. They possess nonlinear Lie superposition, and all their solutions could be obtained by nonlinear superposition of a finite set of solutions (the so-called fundamental solutions). Once more, the form of this superposition and the number of fundamental solutions are dictated by the symmetry Lie algebra. In order to give a more “practical” reader a feeling of the power of the geometrical approach to differential equations, we included in these lectures a number of examples on the formula level.

The paper is organized as follows. First, we consider symmetries of two types of distributions: Cartan distributions and completely integrable distributions. We show how to integrate completely integrable distributions possessing a symmetry Lie algebra that acts in a transitive way on the space of (local) integral manifolds. We begin with the most trivial (but also the more applicable) case of a commutative symmetry Lie algebra and show how to get quadratures. As an example of application of this case, we discuss the famous Liouville–Arnold theorem on integrable Hamilton systems. We propose also the general reduction principle that allows to split integration for pair $\left ( \mathcal {J}\text{,}\mathrm {Sym} \right ),$ where $\mathcal {J} \subset \mathrm {Sym}$ is an ideal in the symmetry Lie algebra, into two separate cases with symmetry algebra $\mathcal {J}$ and $\mathrm {Sym}/\mathcal {J}$. Application of this principle to solvable Lie algebras gives us the Lie–Bianchi theorem (together with a constructive method of finding quadratures), as well as integration of cases with general symmetry algebra Sym by means of model equations. We conclude these lectures by showing applications to ordinary differential equations and especially to the “toy” case of Schrödinger type equations: We show that (nontrivial) geometries on the line are hidden in these equations and how symmetries allow us to write explicit solutions of these equations.

I consider these lectures as an invitation to the wonderful world of symmetries and differential equations. More details, results, and methods can be found in more advanced expositions (see, for example, the cited books at the end of the lectures).

3.2 Distributions

Let M be an (n + m)-dimensional smooth manifold, and let τ : TM → M be the tangent bundle. Then, a distribution P on M is a smooth field

$$\displaystyle \begin{aligned} P:a\in M\longmapsto P\left( a\right) \subset T_{a}M \end{aligned}$$

of m-dimensional subspaces of the tangent spaces. The number m is called the dimension of the distribution, $m=\dim P$, and the number n is called a codimension of P, n = codimP.

The statement that P is a smooth family could be formulated in two different ways:

• 1. For any point a ∈ M, there are vector fields $\left \langle X_1,\ldots ,X_m \right \rangle$ defined in a neighborhood O of a such that the vectors X _i,b ∈ T _b M, i = 1, …, m belong to and form a basis in P(b) for every b ∈ O.

• 2. There are differential 1-forms $\left \langle \omega _{1},..,\omega _{n}\right \rangle$, such that

  $$\displaystyle \begin{aligned} P\left( b\right) =\ker \omega _{1,b}\cap \cdots \cap \ker \omega _{n,b} \end{aligned}$$

  in the neighborhood O.

For the first definition, let us introduce $C^{\infty }\left ( M\right )$ -module

$$\displaystyle \begin{aligned} D(P)=\{X\in \mathrm{Vect}(M),X_{a}\in P\left( a\right) ,\forall a\in M\} \end{aligned}$$

of all smooth vector fields lying in (or tangent to) the distribution P.

Then, $\left ( 1\right )$ states that this module is locally free (=projective) and that the sets $\left \langle X_{1},\ldots ,X_{m}\right \rangle$ give us local bases for D(P). In a similar way, let us introduce another $C^{\infty }\left ( M\right )$-module

$$\displaystyle \begin{aligned} \mathrm{Ann}\left( P\right) =\left\{ \omega \in \varOmega ^{1}\left( M\right) ,\omega \left( X\right) =0,\forall X\in D\left( P\right) \right\} \end{aligned}$$

of all smooth differential 1-forms vanishing on vector fields from P. Then, $\left ( 2\right )$ states that this module is also locally free and that the sets $\left \langle \omega _{1},..,\omega _{n}\right \rangle$ are local bases for this module.

Example 3.1

Consider $M=\mathbb {R}^{3}$ with coordinates $\left ( x,y,z\right )$, and let ω = dz − ydx. This form does not vanish at any point of M and therefore defines a distribution P on M of dimension 2 and codimension 1. The vector fields

$$\displaystyle \begin{aligned} X_{1}=\frac{\partial }{\partial y},\quad X_{2}=\frac{\partial }{\partial x}+y\frac{ \partial }{\partial z} {} \end{aligned} $$

(3.1)

give us a basis in the module D(P).

A submanifold N ⊂ M is said to be integral for the distribution P if

$$\displaystyle \begin{aligned} T_{a}N\subset P\left( a\right) , {} \end{aligned} $$

(3.2)

for all a ∈ N. This condition is better to formulate in terms of the differential 1-forms $\left \langle \omega _{1},..,\omega _{n}\right \rangle$. Then, N is integrable if their restrictions to N are equal to zero:

$$\displaystyle \begin{aligned} \left. \omega _{i}\right\vert {}_{N}=0,\ i=1,\ldots,n. \end{aligned}$$

An integral manifold is maximal if it is not contained in an integral manifold of greater dimension.

Example 3.2

The distribution (3.1) has 1-dimensional integral submanifolds. Namely, assume that x is a coordinate on N, i.e.

$$\displaystyle \begin{aligned} N=\left\{ z=A(x) ,\, y=B(x) \right\} , \end{aligned}$$

for some smooth functions A and B. Then,

and N is integral if and only if and

(3.3)

On the other hand, if N is a 2-dimensional integral manifold, then the vector field ∂∕∂z is not tangent to N, because $\partial /\partial z\notin D\left ( P\right ).$ Therefore, we can represent

$$\displaystyle \begin{aligned} N=\left\{ z=A\left( x,y\right) \right\} . \end{aligned}$$

Then, $\left . \omega \right \vert { }_{N}=dA-ydx=\left ( A_{x}-y\right ) dx+A_{y}dy=0$ if and only if

$$\displaystyle \begin{aligned} A_{x}=y,\, A_{y}=0, {} \end{aligned} $$

(3.4)

which is impossible.

Two observations should be made from this example: (1) maximal integral manifolds can have dimension less than $\dim P$ and (2) finding of integral manifolds is equivalent to finding of solutions of some differential equations.

A distribution is said to be completely integrable if the dimension of every maximal integral manifold is exactly the dimension of the distribution itself, and if for any point of M, there is a maximal integral manifold containing this point. For such distributions, the entire manifold can be presented as the disjoint union of maximal integral manifolds of the distribution, which are the leaves of a foliation, so that the notion of a completely integrable distribution is equivalent to that of a foliation.

Theorem 3.1 (Frobenius)

A distribution P is completely integrable if and only if the module $D\left ( P\right )$ is closed with respect to commutator of vector fields

(3.5)

Moreover, if the distribution P is completely integrable, and if N ₁ and N ₂ are integral submanifolds of P, passing through a point a ∈ N ₁ ∩ N ₂ , then N ₁ = N ₂ in a neighborhood of the point.

Example 3.3

Consider the distribution given by (3.1). As we have seen, the maximal integral manifolds for this distribution have dimension 1, and therefore this distribution is not completely integrable. On the other hand, the module $D\left ( P\right )$ for this distribution is generated by the vector fields

$$\displaystyle \begin{aligned} X_{1}=\frac{\partial }{\partial y},\quad X_{2}=\frac{\partial }{\partial x}+y\frac{ \partial }{\partial z}, \end{aligned}$$

and we have

The condition (3.5) can be reformulated in terms of differential forms generating the module $\mathrm {Ann}\left ( P\right ) .$ Namely, using the formula

we get

for all $X,Y\in D\left ( P\right )$ and $\omega \in \mathrm {Ann}\left ( P\right ) .$ Therefore, the condition (3.5) is equivalent to

$$\displaystyle \begin{aligned} d\omega \left( X,Y\right) =0, \end{aligned}$$

for all $X,Y\in D\left ( P\right )$. In other words, the restriction of the differential 2-form $\left . d\omega \right \vert { }_{P}$ on the distribution P vanishes for all forms $\omega \in \mathrm {Ann}\left ( P\right ) .$

In terms of local bases $\left \langle X_{1},\ldots ,X_{m}\right \rangle$ for the module $D\left ( P\right )$ or $\left \langle \omega _{1},..,\omega _{n}\right \rangle$ for the module $\mathrm {Ann}\left ( P\right )$, the conditions for complete integrability can be reformulated in the following equivalent forms:

• 1.
  

  (3.6)

  for all i, j = 1, …., m and some smooth functions $c_{ij}^{k}.$

• 2.
  $$\displaystyle \begin{aligned} d\omega _{i}=\sum_{j}\gamma _{ij}\wedge \omega _{j}, {} \end{aligned} $$

  (3.7)

  for all i, j = 1, …., n and some differential 1-forms γ _ij.

3.3 Distributions and Differential Equations

3.3.1 Cartan Distributions (ODEs)

Let J ^k be the space of all k-jets of functions in one variable x. Then, the k-jet of a smooth function f(x) at point $a\in \mathbb {R}$, denoted by $[f]_{a}^{k}$, is given by its set of derivatives:

We denote by $\left ( x,u_{0},u_{1},\ldots ,u_{k}\right )$ the coordinates on J ^k satisfying

$$\displaystyle \begin{aligned} u_{i}\left( [f]_{a}^{k}\right) =f^{\left( i\right) }\left( a\right) , \end{aligned}$$

for all i = 0, 1, …k, and $x\left ( [f]_{a}^{k}\right ) =a.$

The differential 1-forms

$$\displaystyle \begin{aligned} \omega _{i}=du_{i}-u_{i+1}dx, {} \end{aligned} $$

(3.8)

on J ^k, where i = 0, …, k − 1, we call Cartan forms, and the distribution

$$\displaystyle \begin{aligned} C_{k}=\ker \omega _{0}\cap \cdots \cap \ker \omega _{k-1} \end{aligned}$$

we call the Cartan distribution on the jet-space.

We have $\dim {\mathbf {J}}^{k}=k+2$, codim C _k = k, and therefore $\dim C_{k}=2,$ i.e. C _k is a distribution of planes.

It is easy to see that a basis in the module $D\left ( C_{k}\right )$ of vector fields tangent to C _k is formed by vector fields

$$\displaystyle \begin{aligned} \begin{array}{rcl} X_{1} & =&\displaystyle \frac{\partial }{\partial u_{k}}, {} \\ X_{2} & =&\displaystyle \frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}}+\cdots +u_{k}\frac{\partial }{\partial u_{k-1}}, \end{array} \end{aligned} $$

(3.9)

and

$$\displaystyle \begin{aligned}{}[X_{1},X_{2}]=\frac{\partial }{\partial u_{k-1}}\notin D\left( C_{k}\right) . \end{aligned}$$

Therefore, C _k is a non-integrable distribution, and its maximal integral manifolds have dimension 1.

To find these curves, we remark that trajectories of the vector field X ₁ are integral curves for C _k and, similarly to (3.1), integral curves N on which x is a coordinate have the special form

By an ordinary differential equation (ODE) of order k, we mean a relation that connects components of k-jets $[f]_{a}^{k}$ of unknown functions $f\left ( x\right ),$ i.e. a relation of the form

$$\displaystyle \begin{aligned} F\left( x,u_{0},\ldots,u_{k}\right) =0, {} \end{aligned} $$

(3.10)

which is valid when u _i are coordinates of solutions.

Geometrically, it means that we consider a submanifold (possibly with singularities)

$$\displaystyle \begin{aligned} \mathcal{E}_{F}=\left\{ F\left( x,u_{0},\ldots,u_{k}\right) =0\right\} \subset {\mathbf{J}}^{k}, \end{aligned}$$

and solutions are curves

$$\displaystyle \begin{aligned} L_{A}^{\left( k\right) }\subset \mathcal{E}_{F}. \end{aligned}$$

Assuming that $\mathcal {E}_{F}$ is a smooth submanifold of J ^k, we say that solutions of the ODE $\mathcal {E}_{F}$ are integral curves of the Cartan distribution C _k lying in $\mathcal {E}_{F},$ or, in other words, they are integral curves of the restriction of the distribution C _k on $\mathcal {E}_{F}$:

$$\displaystyle \begin{aligned} C_{F}:a\in \mathcal{E}_{F}\rightarrow C_{k}\left( a\right) \cap T_{a}\left( \mathcal{E}_{F}\right) . \end{aligned}$$

Remark that $\dim C_{F}\left ( a\right ) =1$ if $C_{k}\left ( a\right )$ is not a subspace of $T_{a}\left ( \mathcal {E}_{F}\right )$ and that $\dim C_{F}\left ( a\right ) =2$ if $C_{k}\left ( a\right ) \ \subset \ T_{a}\left ( \mathcal {E}_{F}\right ) .$ In the last case, we say that point $a\in \mathcal {E}_{F}$ is a singular point.

Therefore, on the complement , we have a 1-dimensional distribution C _F. This is obviously a completely integrable distribution, and its integral curves are smooth solutions of the equation if and only if function x is a coordinate on L.

To find a basis X in the module $D\left ( C_{F}\right )$, we write down vector field X in the form

$$\displaystyle \begin{aligned} X=a(x) X_{1}+b(x) X_{2}, \end{aligned}$$

where X ₁ and X ₂ form basis in C _k. Then, $X\in D\left ( C_{F}\right )$ if and only if X is tangent to $\mathcal {E}_{F}$ or if

$$\displaystyle \begin{aligned} X\left( F\right) =0, \end{aligned}$$

on $\mathcal {E}_{F}.$ Thus,

$$\displaystyle \begin{aligned} a\frac{\partial F}{\partial u_{k}}+bD_{k}\left( F\right) =0 \end{aligned}$$

on $\mathcal {E}_{F}.$ Here, we denoted by

$$\displaystyle \begin{aligned} D_{k}=\frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}} +\cdots +u_{k}\frac{\partial }{\partial u_{k-1}} {} \end{aligned} $$

(3.11)

the vector field X ₂ in (3.9).

Remark that $\mathrm {Sing}\left ( \mathcal {E}_{F}\right )$ is given by equations

$$\displaystyle \begin{aligned} \frac{\partial F}{\partial u_{k}}=0,\, D_{k}\left( F\right) =0,\, F=0 \end{aligned}$$

and in general defines a submanifold $\mathrm {Sing}\left ( \mathcal {E}_{F}\right ) \subset \mathcal {E}_{F}$ of codimension 2.

Equations $\mathcal {E}_{F},$ where $\frac {\partial F}{\partial u_{k}}\neq 0,$ are called equations of principal type, and for such equations, a basis in $D\left ( C_{F}\right )$ has the form

$$\displaystyle \begin{aligned} D=\frac{\partial F}{\partial u_{k}}D_{k}-D_{k}\left( F\right) \frac{ \partial }{\partial u_{k}}, \end{aligned}$$

and x is a coordinate on integral curves.

Thus, for principal type equations, solutions are smooth functions, and in all other cases, they are singular and multivalued functions (see [7] for more such examples).

To simplify the formulae in what follows, we will consider only principal type equations of the form

$$\displaystyle \begin{aligned} u_{k}=F\left( x,u_{0},\ldots,u_{k-1}\right) . {} \end{aligned} $$

(3.12)

Then, $\mathcal {E}_{F}$ is diffeomorphic to J ^k−1, $\left ( x,u_{0},\ldots ,u_{k-1}\right )$ are coordinates on $\mathcal {E}_{F}$, and the basic vector field in $D\left ( C_{F}\right )$ has the form

$$\displaystyle \begin{aligned} D_{k}=\frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}} +\cdots +F\frac{\partial }{\partial u_{k-1}}. \end{aligned}$$

The distribution C _F can also be defined by the following Cartan forms:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \omega _{0} & =&\displaystyle du_{0}-u_{1}dx, {} \\ & &\displaystyle .............. \notag \\ \omega _{k-2} & =&\displaystyle du_{k-2}-u_{k-1}dx, \\ \omega _{k-1} & =&\displaystyle du_{k-1}-Fdx. \end{array} \end{aligned} $$

(3.13)

When working with algebraic equations, we use different algebraic manipulations in order to simplify them. For differential equations, the class of possible manipulations can be essentially extended by adding the operation of differentiation or prolongation.

Take, for example, system (3.4)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial A}{\partial x} & =&\displaystyle y, \\ \frac{\partial A}{\partial y} & =&\displaystyle 0, \end{array} \end{aligned} $$

which we investigated above. Then, by differentiating, the first and second equations in x and y, we get the following system:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial A}{\partial x} & =&\displaystyle y,\, \frac{\partial ^{2}A}{\partial x^{2}}=0,\, \frac{\partial ^{2}A}{\partial x\partial y}=1, \\ \frac{\partial A}{\partial y} & =&\displaystyle 0,\, \frac{\partial ^{2}A}{\partial x\partial y }=0,\, \frac{\partial ^{2}A}{\partial y^{2}}=0, \end{array} \end{aligned} $$

which is obviously contradictory and therefore has no solutions.

To apply the prolongation procedure to the ordinary differential equations, we introduce the formal derivation (the total derivative in x)

$$\displaystyle \begin{aligned} D=\frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}}+\cdots +u_{k}\frac{\partial }{\partial u_{k-1}}+u_{k+1}\frac{\partial }{\partial u_{k}}+\cdots . \end{aligned}$$

Then, the prolongation of Eq. (3.10) is the following system $\mathcal {E}_{F}^{\left ( 1\right ) }\subset {\mathbf {J}}^{k+1}:$

$$\displaystyle \begin{aligned} \begin{array}{rcl} & &\displaystyle F\left(x,u_{0}, \ldots,u_{k}\right) =0, \\ & &\displaystyle D\left( F\right) =D_{k}\left( F\right) +u_{k+1}\frac{\partial F}{\partial u_{k}}=0. \end{array} \end{aligned} $$

Applying in series this procedure, we get l-th prolongations $\mathcal {E} _{F}^{\left ( l\right ) }\subset {\mathbf {J}}^{k+l}$ given by relations

$$\displaystyle \begin{aligned} F=0,\, D\left( F\right) =0,\, D^{2}\left( F\right) =0, \ldots,\, D^{l}\left( F\right) =0. {} \end{aligned} $$

(3.14)

The advantage of using prolongations $\mathcal {E}_{F}^{\left ( l\right ) }$ and their inverse limit $\mathcal {E}_{F}^{\left ( \infty \right ) }\subset \mathbf { J}^{\infty }$ comes from the fact that these equations contain information on all derivatives of solutions up to order l or ∞.

It is easy to see that the Cartan distributions C on the prolongations are still 1-dimensional at regular points and generated by the restrictions of the total derivative D on $\mathcal {E}_{F}^{\left ( l\right ) }.$

3.3.2 Cartan Distributions (PDEs)

For the case of functions of n variables $x=\left ( x_{1},\ldots ,x_{n}\right )$, and corresponding partial differential equations, the above constructions can be repeated, practically word by word.

Namely, denote by ${\mathbf {J}}^{k}\left ( n\right )$ the space of all k-jets of functions in n variables. Then, the k-jet $[f]_{a}^{k}$ of a smooth function f(x ₁, …, x _n) at a point $a\in \mathbb {R}^{n}$ is given by the values of its derivatives

$$\displaystyle \begin{aligned} \frac{\partial ^{\sigma }f}{\partial x^{\sigma }}\left( a\right) \end{aligned}$$

at the point. Here, $\sigma =\left ( \sigma _{1},\ldots ,\sigma _{n}\right )$ are multi-indices of order $0\leqslant \left \vert \sigma \right \vert \leqslant k,$ where $\left \vert \sigma \right \vert =\sigma _{1}+\cdots +\sigma _{n}.$

Denote by $\left ( x,u_{\sigma },0\leqslant \left \vert \sigma \right \vert \leqslant k\right )$ the standard coordinates on ${\mathbf {J}}^{k}\left ( n\right )$, where

$$\displaystyle \begin{aligned} u_{\sigma }\left( [f]_{a}^{k}\right) =\frac{\partial ^{\sigma }f}{\partial x^{\sigma }}\left( a\right) . \end{aligned}$$

Define also the Cartan forms

$$\displaystyle \begin{aligned} \omega _{\sigma }=du_{\sigma }-\sum_{i}u_{\sigma +1_{i}}dx_{i} \end{aligned}$$

and the Cartan distribution

We have $\dim {\mathbf {J}}^{k}=n+\binom {n+k}{k}$, $\mathrm {codim}\, C_{k}=\binom {n+k-1}{k-1},$ and therefore $\dim C_{k}=n+\binom {n+k-1}{k}.$

The following vector fields make up a basis in the module $D\left ( C_{k}\right )$:

$$\displaystyle \begin{aligned} \begin{array}{rcl} X_{\sigma } & =&\displaystyle \frac{\partial }{\partial u_{\sigma }},\left\vert \sigma \right\vert =k, \\ Y_{i} & =&\displaystyle \frac{\partial }{\partial x_{i}}+\sum_{\left\vert \sigma \right\vert \leqslant k-1}u_{\sigma +1_{i}}\frac{\partial }{\partial u_{\sigma }}. \end{array} \end{aligned} $$

We have $[X_{\sigma },Y_{i}]=\frac {\partial }{\partial u_{\sigma -1_{i}}} \notin D\left ( C_{k}\right )$ if $\sigma _{i}\geqslant 1,$ and therefore the Cartan distribution is not completely integrable.

Similarly to the 1-dimensional case, this distribution has two types maximal integral manifolds:

• 1.
  $$\displaystyle \begin{aligned} L_{A}^{\left( k\right) }=\left\{ u_{0}=A(x) ,\, u_{\sigma }=\frac{ \partial ^{\left\vert \sigma \right\vert }A}{\partial x^{\sigma }}\right\} , \end{aligned}$$

  where A(x) is a smooth function, and

• 2. integral manifolds of the completely integrable distribution generated by all vector fields X _σ.

Remark that the dimension of the first type of integral manifolds equals n, while the dimension for the second type of integral manifolds equals $\binom {n+k-1}{k},$ and $\binom {n+k-1}{k}>n$ if $n\geqslant 1$ and $k\geqslant 2.$ For the complete description of various maximal integral manifolds (and their dimensions) for the Cartan distributions, see [11].

As above, we will consider differential equations (PDEs in this case) as submanifolds

$$\displaystyle \begin{aligned} \mathcal{E}_{F}=\left\{ F\left( x,u_{\sigma }\right) =0\right\} \subset {\mathbf{J}}^{k}\left( n\right) \end{aligned}$$

and their smooth solutions as submanifolds $L_{A}^{\left ( k\right ) }\subset \mathcal {E}_{F}.$

In the more general case, we will by solution mean any such n-dimensional submanifold L of the Cartan distribution that $L\subset \mathcal {E}_{F},$ i.e. n-dimensional integral submanifold L of the restriction of the Cartan distribution on $\mathcal {E}_{F}.$

By using the total derivations

$$\displaystyle \begin{aligned} D_{i}=\frac{\partial }{\partial x_{i}}+\sum u_{\sigma +1_{i}}\frac{\partial }{\partial u_{\sigma }}, \end{aligned}$$

where i = 1, .., n, we define prolongations

$$\displaystyle \begin{aligned} \mathcal{E}_{F}^{\left( l\right) }=\left\{ F\left( x,u_{\sigma }\right) =0,\, D^{\sigma }\left( F\right) =0,\, \left\vert \sigma \right\vert \leqslant l\right\} \subset {\mathbf{J}}^{k+l}\left( n\right) , \end{aligned}$$

which contains all information about (k + l)-jets of solutions.

3.4 Symmetry

By a (finite) symmetry of the distribution P on the manifold M, we understand a (possibly local) diffeomorphism ϕ : M → M, which takes P into itself, i.e. such that $\phi _{\ast }\left ( P_{a}\right ) =P_{\phi \left ( a\right ) },$ for all points a ∈ M, or, in short, $\phi _{\ast }\left ( P\right ) =P.$

A vector field X is said to be (an infinitesimal) symmetry of the distribution if the flow generated by X consists of finite symmetries.

The infinitesimal approach turns out to be much more constructive and more algebraic than its finite counterpart, so in what follows the word symmetry will always mean infinitesimal symmetry unless otherwise explicitly specified.

Assume that distribution P is generated by differential 1-forms ω ₁, …, ω _m, where m = codim P. We write $P=\left \langle \omega _{1},\ldots ,\omega _{m}\right \rangle$. Then, the condition $\phi _{\ast }\left ( P\right ) =P$ means that the differential 1-forms $\phi ^{\ast }\left ( \omega _{1}\right ) ,\ldots ,\phi ^{\ast }\left ( \omega _{m}\right )$ determine the same distribution P and therefore can be expressed in terms of the basis forms

$$\displaystyle \begin{aligned} \begin{array}{rcl} \phi ^{\ast }\left( \omega _{1}\right) & =&\displaystyle a_{11}\omega _{1}+\cdots + a_{1m}\omega _{m}, \\ & &\displaystyle .................. \\ \phi ^{\ast }\left( \omega _{m}\right) & =&\displaystyle a_{m1}\omega _{1}+\cdots + a_{mm}\omega _{m}, \end{array} \end{aligned} $$

for some smooth functions a _ij, or in the equivalent form

$$\displaystyle \begin{aligned} \phi ^{\ast }\left( \omega _{1}\right) \wedge \omega _{1} \wedge \cdots \wedge \omega _{m}=0,\; \ldots, \; \phi ^{\ast }\left( \omega _{m}\right) \wedge \omega _{1} \wedge \cdots \wedge \omega _{m}=0. {} \end{aligned} $$

(3.15)

These conditions take the form

$$\displaystyle \begin{aligned} \begin{array}{rcl} L_{X}\left( \omega _{1}\right) & =&\displaystyle a_{11}\omega _{1}+\cdots + a_{1m}\omega _{m}, \\ & &\displaystyle .................... \\ L_{X}\left( \omega _{m}\right) & =&\displaystyle a_{m1}\omega _{1}+\cdots + a_{mm}\omega _{m}, \end{array} \end{aligned} $$

or

$$\displaystyle \begin{aligned} L_{X}\left( \omega _{1}\right) \wedge \omega _{1}\cdots \wedge \omega _{m}=0,\; \ldots, \; L_{X}\left( \omega _{m}\right) \wedge \omega _{1}\cdots \wedge \omega _{m}=0, {} \end{aligned} $$

(3.16)

for infinitesimal symmetries X.

Let us denote by $\mathrm {Sym}\left ( P\right )$ the set of all infinitesimal symmetries of the distribution P. Then, the above formulae show that the following conditions are equivalent:

• $X\in \mathrm {Sym}\left ( P\right ) ,$

• 

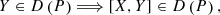
• $\omega \in \mathrm {Ann}\left ( P\right ) \Longrightarrow L_{X}\left ( \omega \right ) \in \mathrm {Ann}\left ( P\right ).$

It follows that $\mathrm {Sym}\left ( P\right )$ is a Lie algebra over $\mathbb {R}$ with respect to the commutator of vector fields.

3.4.1 Symmetries of the Cartan Distributions

Let us now consider symmetries of the Cartan distributions first on J ^k.

Lemma 3.1

We have

$$\displaystyle \begin{aligned} df=D_{k}\left( f\right) dx+\frac{\partial f}{\partial u_{k}}du_{k}\mod \left\langle \omega _{0},\ldots,\omega _{k-1}\right\rangle , \end{aligned}$$

for any smooth function f on J ^k.

Proof

Indeed, we have

$$\displaystyle \begin{aligned} du_{i}=u_{i+1}dx+\omega _{i}, \end{aligned}$$

for all i = 0, …, k − 1. Therefore,

$$\displaystyle \begin{aligned} \begin{array}{rcl} df & =&\displaystyle \frac{\partial f}{\partial x}dx+\sum_{i=0}^{k}\frac{\partial f}{ \partial u_{i}}du_{i}=\frac{\partial f}{\partial x}dx+\sum_{i=0}^{k-1}u_{i+1} \frac{\partial f}{\partial u_{i}}dx+\frac{\partial f}{\partial u_{k}} du_{k}+\sum_{i=0}^{k-1}\frac{\partial f}{\partial u_{i}}\omega _{i} \\ & =&\displaystyle D_{k}\left( f\right) dx+\frac{\partial f}{\partial u_{k}}du_{k}\mod \left\langle \omega _{0},\ldots,\omega _{k-1}\right\rangle . \end{array} \end{aligned} $$

□

Now, let $X\in \mathrm {Sym}\left ( C_{k}\right )$ and

$$\displaystyle \begin{aligned} X=a\frac{\partial }{\partial x}+\sum_{i=0}^{k}A_{i}\frac{\partial }{\partial u_{i}}, \end{aligned}$$

where a and A _i are smooth functions on J ^k. Then, by using the above lemma, we get

$$\displaystyle \begin{gathered} L_{X}\left( \omega _{i}\right) =dA_{i}-u_{i+1}da-A_{i+1}dx= \\ \left( D_{k}\left( A_{i}\right) {-}u_{i{+}1}D_{k}\left( a\right) {-}A_{i{+}1}\right) dx{+}\left( \frac{\partial A_{i}}{\partial u_{k}}{-}u_{i+1}\frac{ \partial a}{\partial u_{k}}\right) du_{k}\!\mod\left\langle \omega _{0},\ldots,\omega _{k-1}\right\rangle , \end{gathered} $$

for i = 0, …, k − 1. Therefore,

$$\displaystyle \begin{aligned} \begin{array}{rcl} & &\displaystyle A_{i+1}=D_{k}\left( A_{i}\right) -u_{i+1}D_{k}\left( a\right) , {} \\ & &\displaystyle \frac{\partial A_{i}}{\partial u_{k}}-u_{i+1}\frac{\partial a}{\partial u_{k}}=0, \end{array} \end{aligned} $$

(3.17)

for $i\leqslant k-1.$

Let us introduce the functions

$$\displaystyle \begin{aligned} \phi _{i}=A_{i}-u_{i+1}a, \end{aligned}$$

for all $i\leqslant k-1.$ Then, the system (3.17) takes the form:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \phi _{i+1} & =&\displaystyle D_{k}\left( \phi _{i}\right) , \\ \frac{\partial \phi _{i}}{\partial u_{k}} & =&\displaystyle 0, \end{array} \end{aligned} $$

for $i\leqslant k-2,$ and

$$\displaystyle \begin{aligned} \begin{array}{rcl} A_{k} & =&\displaystyle D_{k}\left( \phi _{k-1}\right) , \\ a & =&\displaystyle -\frac{\partial \phi _{k-1}}{\partial u_{k}}. \end{array} \end{aligned} $$

Therefore,

$$\displaystyle \begin{aligned} \phi _{i}=D_{k}^{i}\left( \phi _{0}\right), \end{aligned}$$

for $i\leqslant k-2,$ and the condition $\frac {\partial \phi _{k-2}}{\partial u_{k}}=0$ implies that $\phi _{0}=\phi \left ( x,u_{0},u_{1}\right ) ,$ and

$$\displaystyle \begin{aligned} a=-\frac{\partial \phi _{k-1}}{\partial u_{k}}=-\frac{\partial \phi }{ \partial u_{1}}. \end{aligned}$$

Moreover,

$$\displaystyle \begin{aligned} A_{i}=D_{k}^{i}\left( \phi \right) +\frac{\partial \phi }{\partial u_{1}} u_{i+1}, \end{aligned}$$

for $i\leqslant k-1,$ and

$$\displaystyle \begin{aligned} A_{k}=D_{k}^{k}\left( \phi \right) . \end{aligned}$$

Summarizing, we get the following description of symmetries of the Cartan distribution.

Theorem 3.2 (Bäcklund–Lie)

Any symmetry $X\in \mathrm {Sym}\left ( C_{k}\right )$ has the form

$$\displaystyle \begin{aligned} X=\sum_{i=0}^{k}D_{k}^{i}\left( \phi \right) \frac{\partial }{\partial u_{i}} -\frac{\partial \phi }{\partial u_{1}}D_{k}, {} \end{aligned} $$

(3.18)

for some smooth function $\phi =\phi \left ( x,u_{0},u_{1}\right ).$

Remark 3.1

• 1. We call the function ϕ, which defines the symmetry, the generating function, and the corresponding vector field X will be denoted by X _ϕ. Thus,

  $$\displaystyle \begin{aligned} \phi =\omega _{0}\left( X_{\phi }\right) . \end{aligned}$$

• 2. The commutator of two symmetries X _ϕ and X _ψ is also a symmetry. Denote its generating function by [ϕ, ψ], then

  

  and the bracket [ϕ, ψ] (called the Lagrange bracket) defines a Lie algebra structure on $C^{\infty }\left ( {\mathbf {J}}^{1}\right ) .$

  Moreover, a straightforward computation shows that

  

  (3.19)

• 3. The Cartan distribution C ₁ defines the contact structure on J ¹. The elements of $\mathrm {Sym}\left ( C_{1}\right )$ are called contact vector fields, and they also have form (3.18)

  $$\displaystyle \begin{aligned} X_{\phi }=\phi \frac{\partial }{\partial u_{0}}+D_{1}\left( \phi \right) \frac{\partial }{\partial u_{1}}-\frac{\partial \phi }{\partial u_{1}}D_{1}, {} \end{aligned} $$

  (3.20)

  where

  $$\displaystyle \begin{aligned} D_{1}=\frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}}. \end{aligned}$$

• 4. Vector fields (3.18) are prolongations of (3.20).

Similar results are valid for symmetries of Cartan distributions in the jet spaces ${\mathbf {J}}^{k}\left ( n\right ).$

Theorem 3.3 (Lie–Bäcklund)

Any symmetry $X\in \mathrm {Sym}\left ( C_{k}\right )$ on $\mathbf {J} ^{k}\left ( n\right )$ has the form

$$\displaystyle \begin{aligned} X_{\phi }=\sum_{\left\vert \sigma \right\vert \leqslant k}D_{k}^{\sigma }\left( \phi \right) \frac{\partial }{\partial u_{\sigma }}-\sum_{i=1}^{n}\frac{ \partial \phi }{\partial u_{i}}D_{i,k}, {} \end{aligned} $$

(3.21)

where $\phi \left ( x_{1},\ldots ,x_{n},u_{0},u_{1},\ldots ,u_{n}\right ) =\omega _{0}\left ( X_{\phi }\right )$ is the generating function, and

$$\displaystyle \begin{aligned} \begin{array}{rcl} D_{i,k} & =&\displaystyle \frac{\partial }{\partial x_{i}}+u_{i}\frac{\partial }{\partial u_{0}}+\cdots +u_{\sigma +1_{i}}\frac{\partial }{\partial u_{\sigma }} +\cdots ,\left\vert \sigma \right\vert \leqslant k-1, \\ D_{k}^{\sigma } & =&\displaystyle D_{1,k}^{\sigma _{1}}\circ \cdots \circ D_{n,k}^{\sigma _{n}}. \end{array} \end{aligned} $$

The Lagrange bracket $\left [ \phi ,\psi \right ] =X_{\phi }\left ( \psi \right ) -X_{1}\left ( \phi \right ) \psi$ defines the Lie algebra structure on $C^{\infty }\left ( {\mathbf {J}}^{1}\left ( n\right ) \right ) ,$ and, as above, $[\phi ,\psi ]=\omega _{0}\left ( [X_{\phi },X_{\psi }]\right ) .$

3.4.2 Symmetries of Completely Integrable Distributions

Let $X\in \mathrm {Sym}\left ( P\right )$ be a symmetry of a completely integrable distribution P, and let A _t : M → M be the corresponding flow. Then, for any integral manifold L ⊂ M, the submanifolds $A_{t}\left ( L\right )$ are also integral.

In other words, a symmetry X generates a flow on the set $\mathrm {Sol} \left ( P\right )$ of all maximal integral manifolds. There is, however, a distinguished class of symmetries (they are called characteristic symmetries) which generate trivial flows, i.e. they leave invariant every integral manifold. Namely, we have [D(P), D(P)] ⊂ D(P), because P is a completely integrable distribution, and therefore $D(P)\subset \mathrm {Sym}\left ( P\right )$.

Moreover, the vector fields X ∈ D(P) are tangent to any maximal integral manifold of P and therefore generate the trivial flow on $\mathrm {Sol} \left ( P\right )$. The relation $[\mathrm {Sym}\left ( P\right ) ,D(P)]\subset D(P)$ shows that D(P) is an ideal in the Lie algebra $\mathrm { Sym}\left ( P\right )$. We call elements of the quotient Lie algebra

$$\displaystyle \begin{aligned} \mathrm{Shuf}\left( P\right) =\mathrm{Sym}\left( P\right) /D\left( P\right) \end{aligned}$$

shuffling symmetries of the distribution P.

The name reflects the fact that flows on $\mathrm {Sol}\left ( P\right )$ corresponding to different representatives of a class $X\mod D\left ( P\right )$ rearrange, or shuffle, the set of maximal integral manifolds of P in the some way.

3.5 The Lie–Bianchi Theorem

Let P be a completely integrable distribution, codim P = m, generated by the differential 1-forms ω ₁, …, ω _m, and let $\mathfrak {g} \subset \mathrm {Shuf}\left ( P\right )$ be a Lie subalgebra with $\dim \mathfrak {g}=m$. Let $\overline {X}_{1},\ldots ,\overline {X}_{m}$ be a basis of $\mathfrak g$, where $\overline {X}_{i}=X_{i}\mod D\left ( P\right )$ for $X_{i}\in \mathrm { Sym}\left ( P\right ), i=1,\ldots ,m)$.

Suppose that $\mathfrak {g}$ is transversal to the distribution in the sense that the natural mappings

$$\displaystyle \begin{aligned} \mathfrak{g\rightarrow }T_{a}\left( M\right) /P_{a}\end{aligned} $$

are isomorphisms for all points a ∈ M.

The problem of integration of a distribution consists of describing its maximal integral manifolds. For completely integrable distributions, this is equivalent to finding a complete set of first integrals.

A function $H\in C^{\infty }\left ( M\right )$ is called a first integral of the distribution P if every integral manifold of P lies entirely in some level surface $M_{c}=H^{-1}\left ( c\right )$ or, equivalently, if $Z\left ( H\right ) =0$ for every vector field $Z\in D\left ( P\right )$ or, equivalently, if $dH\in \mathrm {Ann}\left ( P\right ) .$

A complete set of first integrals of the distribution P is a set of functions H ₁, …, H _m with the property that

$$\displaystyle \begin{aligned} M_{c_{1},\ldots,c_{m}}=H_{1}^{-1}\left( c_{1}\right) \cap \cdots \cap H_{m}^{-1}\left( c_{m}\right)\end{aligned} $$

represent the set of all maximal integral manifolds of P in some dense domain of M. In this section, we discuss a method to find such integrals when we have a transversal shuffling algebra of symmetries.

3.5.1 Commutative Lie Algebra Symmetries

Assume that the transversal shuffling algebra of symmetries $\mathfrak {g}$ is commutative. The matrix

is nondegenerate: $\det \left ( \varXi \right ) \neq 0.$

Let us choose another basis in the module Ann(P) such that

(3.22)

Indeed, we have relations

where the matrix $A=\left \Vert a_{ij}\right \Vert$ is also nondegenerate.

The condition (3.22) is equivalent to AΞ = 1, or A = Ξ ⁻¹. In other words, the differential forms where

satisfy condition (3.22). To simplify notation, let us assume that the basis ω ₁, .., ω _m is normalized from the very beginning, i.e. satisfies condition (3.22).

Then, we have

$$\displaystyle \begin{aligned} d\omega _{i}\left( X_{k},X_{l}\right) =X_{k}\left( \omega _{i}\left( X_{l}\right) \right) -X_{l}\left( \omega _{i}\left( X_{k}\right) \right) -\omega _{i}\left( [X_{k},X_{l}]\right) =0, \end{aligned}$$

because of the commutativity of Lie algebra $\mathfrak {g}$ and condition (3.22).

We also have

$$\displaystyle \begin{aligned} d\omega _{i}\left( X_{k},Z\right) =X_{k}\left( \omega _{i}\left( Z\right) \right) -Z\left( \omega _{i}\left( X_{k}\right) \right) -\omega _{i}\left( [X_{k},Z]\right) =0, \end{aligned}$$

for all vector fields $Z\in D\left ( P\right ) ,$ because $\omega _{i}\left ( Z\right ) =0$ and $[X_{k},Z]\in D\left ( P\right ) .$

And finally

$$\displaystyle \begin{aligned} d\omega _{i}\left( Z_{1},Z_{2}\right) =Z_{1}\left( \omega _{i}\left( Z_{2}\right) \right) -Z_{2}\left( \omega _{i}\left( Z_{1}\right) \right) -\omega _{i}\left( [Z_{1},Z_{2}]\right) =0, \end{aligned}$$

for all pairs of vector fields $Z_{1},Z_{2}\in D\left ( P\right )$ because of complete integrability P, $[Z_{1},Z_{2}]\in D\left ( P\right )$.

Theorem 3.4

Let $\mathfrak {g=}\left \langle \overline {X}_{1},\ldots , \overline {X}_{m}\right \rangle$ be a transversal commutative Lie algebra of shuffling symmetries, and let $\left \langle \omega _{1},..,\omega _{m}\right \rangle$ be a normalized basis in $\mathrm {Ann}\left ( P\right ).$ Then, all differential 1-forms ω _i are closed:

$$\displaystyle \begin{aligned} d\omega _{i}=0, \end{aligned}$$

for i = 1, …, m.

Corollary 3.1

Under conditions of the above theorem and $H^{1}\left ( M,\mathbb {R}\right ) =0$ , the complete set of first integrals can be found by quadratures:

$$\displaystyle \begin{aligned} H_{1}=\int \omega _{1},\ldots,H_{m}=\int \omega _{m}.\end{aligned} $$

Example 3.4

Example (Distributions of Codimension 1) Let $P=\ker \omega$ be a completely integrable distribution of codimension one, and let X be a transversal symmetry of P, i.e. $\omega \left ( X\right ) \neq 0.$ Then, the differential 1-form

$$\displaystyle \begin{aligned} \frac{\omega }{\omega \left( X\right) }\end{aligned} $$

is closed, and

$$\displaystyle \begin{aligned} \int \frac{\omega }{\omega \left( X\right) }\end{aligned} $$

is a first integral.

Example 3.5

Let $M=\mathbb {R}\times \mathbb {R}\times \left ( 0,2\pi \right ) ,\$with coordinates $x\in \mathbb {R},$ $y\in \mathbb {R},$ ϕ ∈ (0, 2π). The 1-form

$$\displaystyle \begin{aligned} \omega =2\sin ^{2}\frac{\phi }{2}\ dx+\sin \phi \ dy-y\ d\phi\end{aligned} $$

defines the so-called oricycle distribution, and the vector field

$$\displaystyle \begin{aligned} X=\frac{\partial }{\partial x}\end{aligned} $$

is a shuffling symmetry. The 1-form

$$\displaystyle \begin{aligned} \overline{\omega }=\frac{\omega }{\omega \left( X\right) }=dx+\frac{\sin \phi }{1-\cos \phi }dy-\frac{y}{1-\cos \phi }d\phi \end{aligned}$$

is closed, and the function

$$\displaystyle \begin{aligned} H=\int \overline{\omega }=x+y\ \cot \frac{\phi }{2} \end{aligned}$$

is a first integral.

Example 3.6

(Liouville–Arnold) Let $\left ( M^{2n},\varOmega \right )$ be 2n-dimensional symplectic manifold with structure 2-form Ω, and let the functions $\left ( H_{1},..,H_{n}\right )$ be independent and in involution, i.e.

$$\displaystyle \begin{aligned} dH_{1}\wedge \cdots \wedge dH_{n}\neq 0, \end{aligned}$$

and the Poisson brackets vanish: [H _i, H _j] = 0 for i, j = 1, …, n.

Then, the level surfaces

$$\displaystyle \begin{aligned} L^{c}=\left\{ H_{1}=c_{1},\ldots,H_{n}=c_{n}\right\} \subset M^{2n} \end{aligned}$$

are Lagrangian submanifolds, and the Hamiltonian vector fields $X_{H_{i}}$, i = 1, …, n are tangent to L ^c.

These vector fields are independent, and the involutivity conditions mean that they commute. We have $\dim L^{c}=n$ and, as we have seen, there exist such differential 1-forms $\omega _{1}^{c},..,\omega _{n}^{c}$ that $\omega _{i}^{c}\left ( X_{H_{j}}\right ) =\delta _{ij},$ which are closed. Then, integrals $F_{i}^{c}=\int _{L^{c}}\omega _{i}^{c}$ give us (multivalued) functions on L ^c with linearly independent differentials. The submanifolds L ^c give us a foliation of M, and we define functions F _i, i = 1, …, n on M by the requirement that their restrictions on L ^c equal $F_{i}^{c}.$

Differentials of the functions H ₁, …, H _n, F ₁, …, F _n are linearly Independent, and therefore, in simply connected domains, they are coordinates.

We have [H _i, H _j] = 0, and [H _i, F _j] = δ _ij, and the flows along Hamiltonian vector fields $X_{H_{i}}$ in these coordinates take the form

$$\displaystyle \begin{aligned} \overset{\cdot }{H}_{j}=0,\;\overset{\cdot }{F}_{j}=\delta _{ij}. \end{aligned}$$

Therefore, the equations for flows of Hamiltonian vector fields $X_{H_{i}}$ are integrated in quadratures.

3.5.2 Symmetry Reduction

Let P be a completely integrable distribution, $\mathfrak {g} \subset \mathrm {Sym}\left ( P\right )$ a Lie algebra of shuffling symmetries, and $\mathfrak {j\subset g}$ an ideal in the Lie algebra. For any point a ∈ M, define a subspace $P_{\mathfrak {j}}\left ( a\right ) \subset T_{a}M$ formed by the space $P\left ( a\right )$ and the space generated by values of vector fields from $\mathfrak {j}$ at the point. Assume that $\dim P_{\mathfrak {j} }\left ( a\right )$ is constant, so that $P_{\mathfrak {j}}\supset P$ is a distribution. Then, the following result is valid.

Theorem 3.5

• 1. The distribution $P_{\mathfrak {j}}\supset P$ is completely integrable, and

• 2. the quotient Lie algebra $\mathfrak {g\diagup j}$ is a shuffling symmetry Lie algebra of the distribution $P_{\mathfrak {j}}.$

Proof

We have

• $[D\left ( P\right ) ,D\left ( P\right ) ]\subset D\left ( P\right ) ,$ because P is completely integrable.

• $[\mathfrak {j},D\left ( P\right ) ]\subset D\left ( P\right ) ,$ because $\mathfrak {j}$ is symmetry ideal.

• $[\mathfrak {j},\mathfrak {j}]\subset \mathfrak {j},$ because $\mathfrak {j }$ is an ideal.

• Therefore, $[D\left ( P_{\mathfrak {j}}\right ) ,D\left ( P_{\mathfrak {j} }\right ) ]\subset D\left ( P_{\mathfrak {j}}\right )$ and $P_{\mathfrak {j}}$ is completely integrable.

• $[\mathfrak {g,}D\left ( P\right ) ]\subset D\left ( P\right )$ and $[ \mathfrak {g,j}]\subset \mathfrak {j.}$ Therefore, $\mathfrak {g}$ is a symmetry algebra of $P_{\mathfrak {j}},$ and $\mathfrak {g\diagup j}$ is a shuffling symmetry algebra.

□

Remark 3.2

This theorem shows that integration of P with symmetry algebra $\mathfrak {g }$ could be done in two steps:

• 1. Integration of the completely integrable distribution with symmetry algebra $\mathfrak {g\diagup j}$.

• 2. Integration of the restrictions of distribution P on integral manifolds of distribution $P_{\mathfrak {j}}$ by symmetry algebra $\mathfrak { j.}$

Assume now that algebra $\mathfrak {g\diagup j}$ is commutative. Then, the first step could be done by quadratures due to theorem (3.4). The next step involves integration of distributions with symmetry algebra $\mathfrak {j}$, and if this algebra possesses an ideal $\mathfrak {j} _{2}\subset \mathfrak {j}_{1}=\mathfrak {j,}$ such that $\mathfrak {j} _{1}\diagup \mathfrak {j}_{2}$ is commutative, we could reduce it by quadratures. There is a special class of Lie algebras that can be exhausted by this procedure.

Let $\mathfrak {g}$ be a Lie algebra. A Lie algebra $\mathfrak {g}$ is said to be solvable if there is chain of subalgebras $\mathfrak {j}_{i}$

$$\displaystyle \begin{aligned} \mathfrak{g\supset j}_{1}\mathfrak{\supset \cdots \supset j}_{i}\mathfrak{ \supset j}_{i+1}\mathfrak{\supset \cdots \supset j}_{k}=0, \end{aligned}$$

such that $\mathfrak {j}_{i+1}$ is an ideal in $\mathfrak {j}_{i}$ and the quotient Lie algebra $\mathfrak {j}_{i}\mathfrak {\diagup j}_{i+1}$ is commutative for every i.

A more constructive, but equivalent, definition uses the chain of derived subalgebras. Namely, the derived Lie algebra $\mathfrak {g} ^{\left ( 1\right ) }=[\mathfrak {g,g}]$ is the subalgebra of $\mathfrak {g}$ that consists of all linear combinations of Lie brackets of pairs of elements of $\mathfrak {g,}$ and derived series of the Lie algebra is given by $\mathfrak {g}^{\left ( i\right ) }=[\mathfrak {g}^{\left ( i-1\right ) }\mathfrak {,g}^{\left ( i-1\right ) }],$ for i = 1, 2, ….

We have chain of Lie subalgebras

$$\displaystyle \begin{aligned} \mathfrak{g}\supset \mathfrak{g}^{\left( 1\right) }\supset \cdots \supset \mathfrak{g}^{\left( i\right) }\supset \mathfrak{g}^{\left( i+1\right) }\supset \cdots , \end{aligned}$$

with commutative Lie algebras $\mathfrak {g}^{\left ( i\right ) }\diagup \mathfrak {g}^{\left (i+1\right ) },$ and the Lie algebra $\mathfrak {g}$ is solvable if $\mathfrak {g}^{\left ( k\right ) }=0,$ for some k.

Assume now that $\mathfrak {g}$ is a solvable Lie algebra of shuffling symmetries which is transversal to the completely integrable distribution P. Let $\mathfrak {g}^{\left ( 1\right ) }$ be the first derived subalgebra and let $l=\mathrm {codim}_{\mathfrak {g}}\mathfrak {g}^{\left (1\right ) }>0.$ We choose a basis X ₁, …, X _l, …, X _m in the Lie algebra $\mathfrak {g}$ in such a way that $X_{1},\ldots ,X_{l}\notin \mathfrak {g }^{\left ( 1\right ) }$, but $X_{i}\in \mathfrak {g}^{\left ( 1\right ) },$ for $i\geqslant l+1$. We also choose a basis ω ₁, …, ω _m in $\mathrm {Ann}\left ( P\right )$ such that $\omega _{i}\left ( X_{j}\right ) =\delta _{ij}.$ Then,

$$\displaystyle \begin{aligned} d\omega _{i}\left( X_{s},X_{t}\right) =-\omega _{i}\left( [X_{s},X_{t}]\right) =0 \end{aligned}$$

for all i = 1, …, l and s, t = 1, …, m.

Therefore, the differential 1-forms $\omega _{i},i\leqslant l,$ are closed and

$$\displaystyle \begin{aligned} H_{i}=\int \omega _{i} \end{aligned}$$

are (in general multivalued) first integrals of the distribution P.

Moreover, the submanifolds

$$\displaystyle \begin{aligned} M_{c}=H_{1}^{-1}\left( c_{1}\right) \cap \cdots \cap H_{l}^{-1}\left( c_{l}\right) \end{aligned}$$

are $\mathfrak {g}^{\left ( 1\right ) }$-invariant because

$$\displaystyle \begin{aligned} X_{i}\left( H_{j}\right) =dH_{j}\left( X_{i}\right) =\omega _{j}\left( X_{i}\right) =0, \end{aligned}$$

if $j\leqslant l,i\geqslant l+1.$

Let P _c be the restriction of distribution P on the submanifold M _c. Then, P _c is a completely integrable distribution of the same dimension $\dim P$ and codimension $\dim \mathfrak {g}^{\left ( 1\right ) }.$ Applying the above procedure in series to derived subalgebras $\mathfrak { \mathfrak {g}^{\left ( i\right ) }}$, we find the complete sequence of first integrals by integration of closed differential 1-forms, and the integral manifolds of P are given by quadratures: $H_{1}^{-1}\left ( c_{1}\right ) \cap \cdots \cap H_{m}^{-1}\left ( c_{m}\right )$.

Theorem 3.6 (Lie–Bianchi)

Let P be a completely integrable distribution, and let $\mathfrak { \mathfrak {g}}$ be a solvable symmetry Lie algebra transversal to P, $\dim \mathfrak {g}=\mathrm {codim}\,P$ . Then, the distribution P is integrable by quadratures.

3.5.3 Quadratures and Model Equations

In this section, we consider in more detail the case when the symmetry Lie algebra $\mathfrak {g} \subset \mathrm {Sym}\left ( P\right )$ of a completely integrable distribution P acts in a transitive way on the set $\mathrm {Sol}\left ( P\right )$ of all maximal integral manifolds of P. In general, this set has very complicated structure, which is why we restrict ourselves to only consider the set $\mathrm {Sol}_{\text{loc}}\left ( P\right )$ of local maximal integral submanifolds or (better to say) germs. In a small neighborhood of a point a ∈ M, this set is an open domain in $\mathbb {R}^{m},$ where m = codim P.

So, we assume that $\dim \mathfrak {g} \geqslant m$, and the value maps ξ _a :  $\mathfrak {g\rightarrow }T_{a}M\diagup P_{a}$ are surjections. The case when ξ _a are isomorphisms and $\mathfrak { \mathfrak {g}}$ is a solvable Lie algebra is completely covered by the Lie–Bianchi theorem.

To proceed with the general case, we take a homogeneous space $G\diagup H$ of a simply connected Lie group G, where $\mathrm {Lie}(G)=\mathfrak { \mathfrak {g}}$ and $\mathrm {Lie}(H)=\ker \xi _{a}.$ The left action of the Lie group G on the homogeneous space $G\diagup H$ gives us the embedding λ of the Lie algebra $\mathfrak {g}$ into Lie algebra $\mathrm {Vect}\left ( G\diagup H\right )$ of vector fields on $G\diagup H.$

Let us consider a distribution $\widehat {P}$ on $M\times G\diagup H$ generated at point $\left ( a,b\right ) \in M\times G\diagup H$ by vectors of P _a and vectors $X_{a}+\lambda \left ( X\right ) _{b},$ where $X\in \mathfrak {g}.$ In other words, the module $D(\widehat {P})$ is generated by $D\left ( P\right )$ and vector fields of the form $X+\lambda \left ( X\right ) ,$ where $X\in \mathfrak {g}.$

This distribution is completely integrable, because $[D\left ( P\right ) ,D\left ( P\right ) ]\subset D\left ( P\right )$ and $[\mathfrak {g} ,D\left ( P\right ) ]\subset D\left ( P\right ).$ Moreover, $\mathrm {codim}\, \widehat {P}=\dim G\diagup H$ and maximal integral manifolds of $\widehat {P}$ are graphs of some maps $h:M\rightarrow G\diagup H$, which we call integral.

Assume that we have an integral map h. Then, the tangent space to the graph at a point $\left ( a,h\left ( a\right ) \right )$ equals to $\widehat {P}_{\left ( a,h\left ( a\right ) \right ) },$ the image of differential h _∗,a at a point a ∈ M, $\mathrm {Im}\, h_{\ast ,a}=T_{h\left ( a\right ) }\left ( G\diagup H\right ) ,$ and therefore h _∗,a is a surjection. Consider a submanifold $M_{b}=h^{-1}\left ( b\right ) \subset M,$ $b\in G\diagup H.$ Then, $\mathrm {codim}\, M_{b}=\dim G\diagup H=\mathrm {codim}\, P$ and TM _b ⊂ P. Therefore, M _b are maximal integral manifolds of P and to find them, if the integral map h is known, we should solve functional equations h(x) = b.

To construct an integral map h, we will use the following lifting method. Assume that the value of h at a point a ₀ ∈ M is fixed, $h\left ( a_{0}\right ) =b_{0},$ and M is a connected manifold. Then, to find value $h\left ( a_{1}\right )$ at a point a ₁ ∈ M, we take a path $\alpha \left ( t\right ),$ with α(t ₀) = a ₀, α(t ₁) = a ₁, and lift it to a path $\overline {\alpha }(t)$ on $M\times G\diagup H$ in such a way that the curve $\overline {\alpha }(t)$ is an integral curve for the distribution $\widehat {P}$. Assume that the tangents $\overset {\cdot }{\alpha }\left ( t\right )$ to the curve do not lie in the distribution P. Then, we can present them as linear combinations of values of vector fields in $\mathfrak {g},$ say

$$\displaystyle \begin{aligned} \overset{\cdot }{\alpha }\left( t\right) =q_{1}(t)\ X_{1,\alpha \left( t\right) }+\cdots +q_{k}(t)\ X_{k,\alpha \left( t\right) }, {} \end{aligned} $$

(3.23)

for some functions q ₁(t), …, q _k(t), where X ₁, …, X _k is a basis in the Lie algebra $\mathfrak {g}.$

The path $\overline {\alpha }(t)$ on $M \times G\diagup H$ is a lift of the path α(t) on M, and integral curve for distribution $\widehat {P}$, if and only if $\overline {\alpha }(t)$ satisfies the following equation, similar to (3.23):

$$\displaystyle \begin{aligned} \overset{\cdot }{\overline{\alpha }}\left( t\right) =q_{1}(t)\ \lambda (X_{1})_{\overline{\alpha }(t)}+\cdots +q_{k}(t)\ \lambda (X_{k})_{\overline{ \alpha }(t)}. {} \end{aligned} $$

(3.24)

In other words, in order to lift the path α(t) to the path $\overline {\alpha }(t)$, we have to find integral curves of a vector field of the form

$$\displaystyle \begin{aligned} \frac{\partial }{\partial t}+\sum_{i=1}^{k}q_{i}\left( t\right) \lambda \left( X_{i}\right) {} \end{aligned} $$

(3.25)

on $\mathbb {R} \times G\diagup H$, which correspond to paths $X(t) =\sum _{i=1}^{k}q_{i}\left ( t\right ) X_{i}$ on the Lie algebra $\mathfrak { \mathfrak {g.}}$ We call equations of form (3.24) model differential equations.

Summarizing, we get the following generalization of the Lie–Bianchi theorem.

Theorem 3.7

Let $\mathfrak {g}$ be a symmetry Lie algebra of a completely integrable distribution P on a connected manifold M such that the value maps ξ _a :  $\mathfrak {g\rightarrow }T_{a}M\diagup P_{a}$ are surjective. Then, integration of the distribution can be done by using solutions of model differential equations, corresponding to the Lie algebra symmetry, and solutions of a number of functional equations.

We begin with the main properties of the model differential equations.

Theorem 3.8

For any system of model ordinary differential equations associated with a path X _t on the Lie algebra $\mathfrak { \mathfrak {g}}$ and the vector field

$$\displaystyle \begin{aligned} Z=\frac{\partial }{\partial t}+\lambda \left( X_{t}\right) , \end{aligned}$$

there is a path g(t) on the group G with g(0) = e, such that any trajectory y(t) of Z has the form

$$\displaystyle \begin{aligned} y(t) =g(t) y(0) . {} \end{aligned} $$

(3.26)

Moreover, this property defines the class of model equations completely.

Proof

If the path g(t) is given, then the path X _t is defined as follows:

$$\displaystyle \begin{aligned} X_{t}=g_{\ast }\left( t\right) ^{-1}\left( \overset{\cdot }{g}\left( t\right) \right) , {} \end{aligned} $$

(3.27)

and from (3.26), we get $\overset {\cdot }{y}\left ( t\right ) =\lambda \left ( X_{t}\right )$. On the other hand, if the path X _t is given, then the path g(t) is found from equation (3.27). □

Let us analyze one-dimensional models.

Theorem 3.9 (Lie)

Let a finite-dimensional Lie algebra $\mathfrak {g}$ act on $\mathbb {R}$ in a transitive way. Then, $\dim \mathfrak {g}\leqslant 3$ , and locally the action is one of the following:

• 1. $\dim \mathfrak {g}=1$, $\mathfrak {g}= \left \langle \frac {\partial }{\partial x}\right \rangle ,$

• 2. $\dim \mathfrak {g}=2$, $\mathfrak {g}= \left \langle \frac {\partial }{\partial x},x\frac {\partial }{\partial x} \right \rangle ,$ and

• 3. $\dim \mathfrak {g}=3$, $\mathfrak {g}= \left \langle \frac {\partial }{\partial x},x\frac {\partial }{\partial x},x^{2} \frac {\partial }{\partial x}\right \rangle .$

A proof of this theorem can be found, for example, in [6]. The theorem shows that vector fields for model equations in the 1-dimensional case have the following forms:

• 1. $\frac {\partial }{\partial t}+a\left ( t\right ) \frac {\partial }{ \partial x},$

• 2. $\frac {\partial }{\partial t}+a\left ( t\right ) \frac {\partial }{ \partial x}+b\left ( t\right ) x\frac {\partial }{\partial x},$ and

• 3. $\frac {\partial }{\partial t}+a\left ( t\right ) \frac {\partial }{ \partial x}+b\left ( t\right ) x\frac {\partial }{\partial x}+c\left ( t\right ) x^{2}\frac {\partial }{\partial x}.$

The corresponding model equations are

• 1. $\overset {\cdot }{x}\left ( t\right ) =a\left ( t\right ) ,$

• 2. $\overset {\cdot }{x}\left ( t\right ) =a\left ( t\right ) +b\left ( t\right ) \ x\left ( t\right ) ,$ and

• 3. $\overset {\cdot }{x}\left ( t\right ) =a\left ( t\right ) +b\left ( t\right ) \ x\left ( t\right ) +c\left ( t\right ) \ x\left ( t\right ) ^{2}.$

Let functions a(t) and b(t) be given. To find solutions of model equations of types 1 and 2, we should add to our set of functions

• 1. the function $\int a(t) dt$ and

• 2. the functions $\exp \left (\int b(t)dt\right )$ and $\int a(t)\exp \left ( -\int b(t)dt\right ) dt$,

respectively.

This observation explains the idea of Liouville (1833) to introduce the field of elementary functions as the result of a series of Liouvillian extensions of the field of rational functions, i.e. extension by adding integrals and exponents of integrals, in other words, by adding solutions of model equations of the first and second types.

Model equations of the type 3 are known as Riccati equations and, as we will see later, they are related to linear ordinary equations of the second order as well as projective structures on the line.

More information on model equations corresponding to simple Lie groups can be found in [6].

3.5.4 The Lie Superposition Principle

Here, we use Theorem 3.8 to get more information about solutions of model equations.

As we have seen, finding solution y(t) of the model equation is equivalent to finding a path g(t) on the Lie group G, and y(t) = g(t)y(0). Assume that we know k solutions, say y ₁(t), …, y _k(t), then y _i(t) = g(t)y _i(0), for all i = 1, …, k.

From a geometrical point of view, this means that points $\left ( y_{1}(t) ,\ldots ,y_{k}(t) \right ) \in \left ( G\diagup H\right ) ^{k}=\left ( G\diagup H\right ) \times \cdots \times \left ( G\diagup H\right )$ and $\left ( y_{1}(0) ,\ldots ,y_{k}(0) \right ) \in \left ( G\diagup H\right ) ^{k}$ can be transformed by a single transformation g(t) ∈ G, for any k = 1, 2, ….

To analyze this situation, consider diagonal G-actions on direct products $( G\diagup H)^{k}$, $g:a=\left ( a_{1},\ldots ,a_{k}\right ) \rightarrow ga=\left ( ga_{1},\ldots ,ga_{k}\right ).$ Then, the stationary group G _a is the intersection $G_{a_{1}}\cap \cdots \cap G_{a_{k}}$ of stationary subgroups $G_{a_{i}}$ of points $a_{i}\in G\diagup H.$

By the stiffness of a homogeneous manifold, we mean a number k such that the stationary groups G _a for general points $a=\left ( a_{1},\ldots ,a_{k}\right ) \in \left ( G\diagup H\right ) ^{k}$ are trivial. We call such points regular. Given two regular points $a,b\in \left ( G\diagup H\right ) ^{k}$, there is a unique element $\gamma \left ( a,b\right ) \in G$ such that $a=\gamma \left ( a,b\right ) b.$

A set of solutions $\left ( y_{1}(t) ,\ldots ,y_{k}(t) \right )$ is said to be fundamental solution of the model equation if k is the stiffness of $G\diagup H$ and $\left ( y_{1}(0) ,\ldots ,y_{k}(0)\right )$ is a regular point. Then, we define the path g(t) as

$$\displaystyle \begin{aligned} g\left( t\right) =\gamma \left( (y_{1}(t) ,\ldots,y_{k}(t) ),(y_{1}(0) ,\ldots,y_{k}(0) )\right) , \end{aligned}$$

and all solutions of the model equation have the form

$$\displaystyle \begin{aligned} y(t) =\gamma \left( (y_{1}(t) ,\ldots,y_{k}(t) ),(y_{1}(0) ,\ldots,y_{k}(0)\right) \ y(0). {} \end{aligned} $$

(3.28)

The last formula is called the Lie superposition principle.

Example 3.7

Example (1D model equations)

• 1. Consider the case $G\diagup H=\mathbb {R},$ $\mathfrak {g}=\left \langle \frac { \partial }{\partial x}\right \rangle .$ Then, $\gamma \left ( a,b\right ) =a-b.$ The fundamental solution is a solution of equation $\overset {\cdot }{y} (t) =A(t)$, and the superposition principle says that all solutions of the equation $\overset {\cdot }{x}(t) =A(t)$ have the form

  $$\displaystyle \begin{aligned} x(t) =x(0) +\left( y(t) -y(0) \right) . \end{aligned}$$

• 2. Let $G\diagup H=\mathbb {R},$ $\mathfrak {g}=\left \langle \frac { \partial }{\partial x},x\frac {\partial }{\partial x}\right \rangle$ and G be the group of all affine transformations of the line. The stiffness is k = 2 and

  $$\displaystyle \begin{aligned} \gamma \left( \left( a_{1},a_{2}\right) ,\left( b_{1},b_{2}\right) \right) \ x=\frac{\left( x-b_{2}\right) a_{1}-\left( x-b_{1}\right) a_{2}}{b_{1}-b_{2}} . \end{aligned}$$

  The fundamental solution of the model equation $\overset {\cdot }{x}(t) =A(t) +B(t) x(t)$ is pair of solutions y ₁(t), y ₂(t) such that y ₁(0) ≠ y ₂(0), and the superposition principle says that the general solution has the form

  $$\displaystyle \begin{aligned} x(t) =\frac{\left( x(0) -y_{2}(0) \right) y_{1}(t) -\left( x(0) -y_{1}(0) \right) y_{2}(t) }{y_{1}(0) -y_{2}(0) }. \end{aligned}$$

• 3. Consider $G\diagup H=\mathbb {R}{\mathbf {P}}^{1},\mathfrak {g}= \left \langle \frac {\partial }{\partial x},x\frac {\partial }{\partial x},x^{2} \frac {\partial }{\partial x}\right \rangle$ with the group $G=\mathbf {SL}_{2}\left ( \mathbb {R}\right )$ of projective transformations

  $$\displaystyle \begin{aligned} A:x\rightarrow \frac{a_{11}x+a_{12}}{a_{21}x+a_{22}}, \end{aligned}$$

  where $A=\left \Vert a_{ij}\right \Vert \in \mathbf {SL}_{2}\left ( \mathbb {R} \right )$. It is known that any projective transformation of the projective line is completely determined by images of three distinct points. Therefore, the stiffness of $\mathbb {R}{\mathbf {P}}^{1}$ equals 3. It is also known that the cross-ratio

  $$\displaystyle \begin{aligned} \frac{x-a_{1}}{x-a_{2}}\frac{a_{3}-a_{2}}{a_{3}-a_{1}} \end{aligned}$$

  is a projective invariant. Therefore, the element $\gamma \left ( a,b\right ) \in \mathbf {SL}_{2}\left ( \mathbb {R}\right )$ such that $y=\gamma \left ( \left ( x_{1},x_{2},x_{3}\right ) ,\left ( y_{1},y_{2},y_{3}\right ) \right ) x$ can be found from the equation:

  $$\displaystyle \begin{aligned} \frac{y-y_{1}}{y-y_{2}}\frac{y_{3}-y_{2}}{y_{3}-y_{1}}=\frac{x-x_{1}}{x-x_{2} }\frac{x_{3}-x_{2}}{x_{3}-x_{1}}. \end{aligned}$$

  Thus, a fundamental solution for the Riccati equation $\overset {\cdot }{x} (t)=A(t) +B(t) x(t) +C(t) x(t) ^{2}$ is a triple of solutions $\left ( y_{1}(t),y_{2}(t) ,y_{3}(t)\right )$ with distinct initial values y ₁(0), y ₂(0), y ₃(0), and the general solution y(t) can be found from the equation

  $$\displaystyle \begin{aligned} \frac{y(0) -y_{1}(0) }{y(0) -y_{2}(0) }\frac{y_{3}(0) -y_{2}(0) }{y_{3}(0) -y_{1}(0) }=\frac{y(t) -y_{1}(t) }{y(t) -y_{2}(t) }\frac{y_{3}(t) -y_{2}(t) }{y_{3}(t) -y_{1}(t) } . \end{aligned}$$

3.6 Ordinary Differential Equations

As we have seen above, the ordinary differential equation

(3.29)

of order k, for functions y(x) in one variable x, is represented as a submanifold $\mathcal {E}_{F}$ in the space of k-jets J ^k:

$$\displaystyle \begin{aligned} \mathcal{E}_{F}=\left\{ F\left( x,u_{0},u_{1},\ldots,u_{k}\right) =0\right\} \subset {\mathbf{J}}^{k}. \end{aligned}$$

Its solutions y(x) are represented by curves

These curves are integral for the restriction C _F of the Cartan distribution

$$\displaystyle \begin{aligned} C_{k}=\ker \omega _{0}\cap \cdots \cap \ker \omega _{k-1} \end{aligned}$$

on $\mathcal {E}_{F}$. Here,

$$\displaystyle \begin{aligned} \omega _{i}=du_{i}-u_{i+1}dx \end{aligned}$$

are the Cartan forms.

As we have seen, the Cartan distribution C _k has dimension 2, and therefore the spaces of the distribution C _F are intersections

$$\displaystyle \begin{aligned} T\mathcal{E}_{F}\cap C_{k}=\ker dF\cap \ker \omega _{0}\cap \cdots \cap \ker \omega _{k-1}, \end{aligned}$$

which are of dimension 2 or 1. The points $x_{k}\in \mathcal {E}_{F}$ where the intersection has dimension 2 we call singular and the points where the dimension equals 1 we call regular.

Since we have

$$\displaystyle \begin{aligned} dF=D_{k}\left( F\right) dx+\frac{\partial F}{\partial u_{k}}du_{k}\ \mod C_{k}, \end{aligned}$$

where

$$\displaystyle \begin{aligned} D_{k}=\frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}} +\cdots +u_{k}\frac{\partial }{\partial u_{k-1}}, \end{aligned}$$

points are singular if and only if

$$\displaystyle \begin{aligned} D_{k}\left( F\right) =0,\; \frac{\partial F}{\partial u_{k}}=0. {} \end{aligned} $$

(3.30)

At regular points, we have $\dim C_{F}=1$ and the vector field

$$\displaystyle \begin{aligned} Z_{F}=\frac{\partial F}{\partial u_{k}}D_{k}-D_{k}\left( F\right) \frac{ \partial }{\partial u_{k}} {} \end{aligned} $$

(3.31)

is a basis in the distribution.

Thus, solutions L _y of (3.29) are trajectories of Z _F. However, there are trajectories of Z _F, which does not have the form L _y since the function x, in general, is not a coordinate on the trajectory. This situation appears every time when $\frac {\partial F}{\partial u_{k}}=0$ on the trajectory.

Thus, we have two alternatives. Either we continue to consider solutions of (3.29) as smooth functions on the line, or we start to consider solutions as integral curves of distribution C _F. We shall follow the second alternative, and then we get solvability of our equation at regular points for free. Also, if $L\subset \mathcal {E}_{F}$ is an integral curve of C _F, then we can remove from L the points where $\frac {\partial F}{\partial u_{k}}=0$. Then, we get

where each curve L _i has the form

$$\displaystyle \begin{aligned} L_{i}=L_{y_{i}(x) }, \end{aligned}$$

for some functions y _i(x), each defined on its own interval. In this case, we call integral curves L multivalued solutions of ( 3.29).

There are also exceptional cases, when $\frac {\partial F}{\partial u_{k}}=0$ at all points of L. Then, L has the form

$$\displaystyle \begin{aligned} L=\left\{ x=\mathrm{const},u_{0}=\mathrm{const}_{0},\ldots,u_{k-1}= \mathrm{const}_{k-1}\right\} , \end{aligned}$$

where constants are chosen in such a way that

$$\displaystyle \begin{aligned} F\left( \mathrm{const},\mathrm{const}_{0},\ldots,\mathrm{const}_{k-1},u_{k}\right) =0. \end{aligned}$$

Example 3.8

Consider the Lissajous equation (see [7]):

(3.32)

where a ≠ 0 and b ≠ 0 are some constants. Here,

$$\displaystyle \begin{aligned} F=\left( 1-x^{2}\right) u_{2}-xu_{1}+\frac{a^{2}}{b^{2}}u_{0}, \end{aligned}$$

and

$$\displaystyle \begin{aligned} \mathcal{E}_{F}=\left\{ u_{0}=\frac{\left( x^{2}-1\right) u_{2}+xu_{1}}{a^{2} }b^{2}\right\} \subset {\mathbf{J}}^{2} \end{aligned}$$

is a smooth 3-dimensional submanifold in J ² with coordinates $\left ( x,u_{1},u_{2}\right ) .$

We have

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial F}{\partial u_{2}} & =&\displaystyle 1-x^{2}, \\ D_{2}\left( F\right) & =&\displaystyle -3xu_{2}+\frac{a^{2}-b^{2}}{b^{2}}u_{1}, \end{array} \end{aligned} $$

and therefore the two curves

$$\displaystyle \begin{aligned} x=\pm 1,\, u_{1}=\pm \frac{a^{2}}{b^{2}}u_{0},\, u_{2}=\frac{a^{2}\left( a^{2}-b^{2}\right) }{3b^{4}}u_{0} \end{aligned}$$

consist of singular points of the equation.

Also, $\frac {\partial F}{\partial u_{2}}=1-x^{2}$, which implies that all integral curves that contain points $\left ( x=\pm 1,u_{0},u_{1},u_{2}\right )$ are multivalued solutions. To find these solutions, we represent them in parametric forms

$$\displaystyle \begin{aligned} \begin{array}{rcl} x & =&\displaystyle \cos \left( bt\right) , \\ y & =&\displaystyle f\left( t\right) , \end{array} \end{aligned} $$

for − 1 < x < 1, and in the form

$$\displaystyle \begin{aligned} \begin{array}{rcl} x & =&\displaystyle \pm \cosh \left( bt\right) , \\ y & =&\displaystyle g\left( t\right) , \end{array} \end{aligned} $$

for x > 1 or x < −1. Then, our equation in the first case takes the form

and the form

in the second case. Therefore, the solutions have the form

$$\displaystyle \begin{aligned} \begin{array}{rcl} x & =&\displaystyle \cos \left( bt\right) , \\ y & =&\displaystyle c_{1}\cos \left( at\right) +c_{2}\sin \left( at\right) , \end{array} \end{aligned} $$

on intervals |x| < 1 and

$$\displaystyle \begin{aligned} \begin{array}{rcl} x & =&\displaystyle \pm \cosh \left( bt\right) , \\ y & =&\displaystyle c_{1}\cosh \left( at\right) +c_{2}\sinh \left( at\right) , \end{array} \end{aligned} $$

on intervals $\left \vert x\right \vert >1$. We plot the first type of solutions for c ₁ = 0 and c ₂ = 1 in the cases where $\frac {a}{b}=\frac {3}{5}$ and $\frac {a}{b}=\frac {3}{5 \pi }$, respectively. The first picture (Fig. 3.1) gives exactly what we expect from multivalued solutions, but the second one (Fig. 3.2) is very far from the standard image.

Fig. 3.1

The solution to (3.32) given by $x=\cos {}(5t)$ and $y=\sin {}(3t)$

Fig. 3.2

The solution to (3.32) given by $x=\cos {}(5\pi t)$ and $y=\sin {}(3t)$

3.7 ODE Symmetries

To simplify our exposition, we will assume that Eq. (3.29) is resolved with respect to the highest derivative and therefore has the form

$$\displaystyle \begin{aligned} \mathcal{E}=\left\{ u_{k}=F\left( x,u_{0},..,u_{k-1}\right) \right\} . {} \end{aligned} $$

(3.33)

Then, functions $\left ( x,u_{0},..,u_{k-1}\right )$ are coordinates on $\mathcal {E}$, and the Cartan distribution $C_{\mathcal {E}}$ on $\mathcal {E}$ is given by forms

$$\displaystyle \begin{aligned} \omega _{0}=du_{0}-u_{1}dx,\ldots.,\,\omega _{k-2}=du_{k-2}-u_{k-1}dx,\,\omega _{k-1}=du_{k-1}-Fdx \end{aligned}$$

and generated by the truncated total derivative

$$\displaystyle \begin{aligned} D=\frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}}+\cdots +u_{k-1}\frac{\partial }{\partial u_{k-2}}+F\frac{\partial }{\partial u_{k-1} }. \end{aligned}$$

Similarly to what we had in the general case, we have now the following expression for differentials of functions on $\mathcal {E}$ modulo the Cartan forms:

$$\displaystyle \begin{aligned} df=D\left( f\right) ~dx~\mod\left\langle \omega _{0},..,\omega _{k-1}\right\rangle , \end{aligned}$$

where f = f(x, u ₀, .., u _k−1).

We have $\dim C_{\mathcal {E}}=1$, and therefore this distribution is completely integrable, and the vector field D is obviously characteristic. We present shuffling symmetries in the form

$$\displaystyle \begin{aligned} X=a_{0}\frac{\partial }{\partial u_{0}}+\cdots +a_{k-1}\frac{\partial }{ \partial u_{k-1}}, \end{aligned}$$

where a _i are functions on $\mathcal {E}.$

This vector field is a symmetry of $C_{\mathcal {E}}$, or of $\mathcal {E}$, if

$$\displaystyle \begin{aligned} L_{X}\left( \omega _{i}\right) =0\mod\left\langle \omega _{0},\ldots,\omega _{k-1}\right\rangle , \end{aligned}$$

for all i = 0, …, k − 1.

We have

$$\displaystyle \begin{aligned} L_{X}\left( \omega _{i}\right) =da_{i}-a_{i+1}dx=\left( D\left( a_{i}\right) -a_{i+1}\right) dx\mod\left\langle \omega _{0},\ldots,\omega _{k-1}\right\rangle , {} \end{aligned} $$

(3.34)

for i = 0, …, k − 2, and

$$\displaystyle \begin{aligned} L_{X}\left( \omega _{k-1}\right) =da_{k-1}-X\left( F\right) dx=\left( D\left( a_{k-1}\right) -X\left( F\right) \right) dx\mod\left\langle \omega _{0},\ldots,\omega _{k-1}\right\rangle . {}\end{aligned} $$

(3.35)

Therefore, if we put $a_{0}=\phi \left ( x,u_{0},..,u_{k-1}\right )$, then the formulae (3.34) and (3.35) give us

$$\displaystyle \begin{aligned} a_{i}=D^{i}\left( \phi \right) , \end{aligned}$$

for i = 0, …, k − 1 and

$$\displaystyle \begin{aligned} D^{k}\left( \phi \right) -X\left( F\right) =0. \end{aligned}$$

Therefore,

$$\displaystyle \begin{aligned} X=X_{\phi }=\phi \frac{\partial }{\partial u_{0}}+D\left( \phi \right) \frac{ \partial }{\partial u_{1}}\cdots +D^{k-1}\left( \phi \right) \frac{\partial }{\partial u_{k-1}}, {} \end{aligned} $$

(3.36)

and the last formula gives us condition on ϕ (Lie equation):

$$\displaystyle \begin{aligned} D^{k}\left( \phi \right) -\frac{\partial F}{\partial u_{k-1}}D^{k-1}\left( \phi \right)-\cdots -\frac{\partial F}{ \partial u_{1}}D\left( \phi \right) -\frac{\partial F}{\partial u_{0}}\phi =0. {} \end{aligned} $$

(3.37)

Summarizing, we get the following result.

Theorem 3.10

Let $\mathrm {Sym}\left ( \mathcal {E}\right )$ be the Lie algebra of shuffling symmetries of ODE (3.33). Then, formula (3.36) gives the isomorphism of this Lie algebra with the space of smooth solutions to the Lie equation (3.37). The Lie algebra structure in $\mathrm {Sym}\left ( \mathcal {E}\right )$ in terms of solutions (3.37), we call them generating functions, has the following form:

where

(3.38)

Proof

To prove (3.38), we remark that $\phi =X_{\phi }\left ( u_{0}\right ) .$

Therefore,

□

Remark 3.3

• 1. If we compare formula (3.36) with description of symmetries of the general Cartan distribution, we see that when the generating function has the form $\phi =\phi \left ( x,u_{0},u_{1}\right )$, then the symmetries X _ϕ are restrictions of the contact symmetry of C _k on our differential equation. Moreover, symmetries with generating function ϕ, depending on u ₂, ..u _k−1, are not anymore classical contact symmetries, and this can happen only when the order of the differential equation $k\geqslant 3.$

• 2. Contact symmetries with generating functions $\phi =b\left ( x,u_{0}\right ) +a\left ( x,u_{0}\right ) u_{1}$ are called point symmetries. They correspond to transformations given by vector fields

  $$\displaystyle \begin{aligned} -a\frac{\partial }{\partial x}+b\frac{\partial }{\partial u_{0}} \end{aligned}$$

  on the plane J ⁰ of the 0-jets (see [6] for more details).

• 3. Point symmetries, with generating functions $\phi =b(x)u_{0}+a\left ( x\right ) u_{1},$ correspond to transformations, which are linear automorphisms of the line bundle $\pi _{0}:{\mathbf {J}}^{0}\rightarrow \mathbb { R}.$ We call them linear symmetries.

3.7.1 Integration of ODEs with Commutative Symmetry Algebras

In this section, we will discuss an application of symmetries to integration of ODEs.

Assume that Eq. (3.33) has k linearly independent (in some domain) commuting symmetries $X_{\phi _{0}},\ldots ,X_{\phi _{k-1}},[\phi _{i},\phi _{j}]=0.$

Remark that all symmetries $X_{\phi _{i}}$ preserve the Cartan distribution, and therefore

for some functions λ _i, i = 0, …, k − 1.

Applying both sides of this relation to the function x and using the relations $X_{\phi _{i}}(x) =0$, D(x) = 1, we get λ _i = 0, i.e. k + 1 vector fields $D,X_{\phi _{0}},\ldots ,X_{\phi _{k-1}}$ commute and are linearly independent.

Consider differential forms

$$\displaystyle \begin{aligned} \omega _{-1}=dx,\omega _{0},\ldots,\omega _{k-1} \end{aligned}$$

on $\mathcal {E}$, then $\omega _{-1}\left ( D\right ) =1,$ $\omega _{i}\left ( D\right ) =0,$ for $i\geqslant 0,$ and $\omega _{i}\left ( X_{\phi _{j}}\right ) =D^{i}\left ( \phi _{j}\right ),$ for $i,j\geqslant 0.$

Therefore, the matrix Ξ that we used in Sect. 3.5.1 has the form

where

Therefore, the differential forms

where

(3.39)

give us the dual coframe: $\theta _{i}\left ( X_{\phi _{i}}\right ) =\delta _{ij}$, and they are closed dθ _i = 0.

Let

$$\displaystyle \begin{aligned} f_{i}=\int \theta _{i}, {} \end{aligned} $$

(3.40)

then the functions $\left ( x,f_{0},..,f_{k-1}\right )$ are coordinates on $\mathcal {E}$ and since

$$\displaystyle \begin{aligned} D\left( f_{i}\right) =\theta _{i}\left( D\right) =0, \end{aligned}$$

they are first integrals. In other words, solutions of $\mathcal {E}$ are given by relations

$$\displaystyle \begin{aligned} f_{0}\left( x,u_{0},\ldots,u_{k-1}\right) =\mathrm{const}_{0},\ldots.,f_{k-1}\left( x,u_{0},\ldots,u_{k-1}\right) =\mathrm{const}_{k-1}, {} \end{aligned} $$

(3.41)

and the explicit dependency u ₀ on x could be found by the elimination u ₁, …, u _k−1 from the above equations.

Theorem 3.11

Solutions of ODE (3.33) of order k with k linearly independent commuting symmetries $X_{\phi _{0}},\ldots ,X_{\phi _{k-1}}$ can be found by quadrature (3.39, 3.40, 3.41).

Example 3.9

Example (k = 1) Consider the first-order ODE

Its symmetries have the form

$$\displaystyle \begin{aligned} X_{\phi }=\phi \left( x,u_{0}\right) \frac{\partial }{\partial u_{0}}, \end{aligned}$$

where the function ϕ is a solution of the Lie equation

$$\displaystyle \begin{aligned} D\left( \phi \right) -F_{u_{0}}\phi =\phi _{x}+F\phi _{u_{0}}-F_{u_{0}}\phi =0, \end{aligned}$$

and

$$\displaystyle \begin{aligned} \theta =\frac{\omega _{0}}{\omega _{0}\left( X_{\phi }\right) }=\frac{ du_{0}-Fdx}{\phi }. \end{aligned}$$

If we consider the Lie equation as equation on F given ϕ, we get

$$\displaystyle \begin{aligned} F=\phi \left( x,u_{0}\right) \left( h(x) +\int \frac{\phi _{x}}{ \phi ^{2}}du_{0}\right) , \end{aligned}$$

and

$$\displaystyle \begin{aligned} \theta =\frac{du_{0}}{\phi }-\left( h(x) +\int \frac{\phi _{x}}{ \phi ^{2}}du_{0}\right) dx, \end{aligned}$$

for arbitrary functions h(x) and $\phi \left ( x,u_{0}\right ) .$

Example 3.10

Example (k = 2) Consider the second-order ODE

Symmetries of this equation are vector fields of the form

$$\displaystyle \begin{aligned} X_{\phi }=\phi \frac{\partial }{\partial u_{0}}+\left( \phi _{x}+u_{1}\phi _{u_{0}}+F\phi _{u_{1}}\right) \frac{\partial }{\partial u_{1}}, \end{aligned}$$

where generating function $\phi =\phi \left ( x,u_{0},u_{1}\right )$ satisfies the Lie equation

$$\displaystyle \begin{aligned} D^{2}\phi -\frac{\partial F}{\partial u_{1}}D\left( \phi \right) -\frac{ \partial F}{\partial u_{0}}\phi =0, \end{aligned}$$

with

$$\displaystyle \begin{aligned} D=\frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}}+F\left( u_{0},u_{1}\right) \frac{\partial }{\partial u_{1}}. \end{aligned}$$

Remark that the equation is invariant with respect to translations in x, and therefore ϕ = u ₁ is a solution of the Lie equation. In order to get a commutative algebra of symmetries, we assume that the generating function for the second symmetry is of the form $\phi \left ( u_{0}\right )$. For this type of symmetry, the Lie equation takes the form

$$\displaystyle \begin{aligned} \phi _{u_{0}u_{0}}u_{1}^{2}-\phi F_{u_{0}}-\phi _{u_{0}}\left( u_{1}F_{u_{1}}-F\right) =0. \end{aligned}$$

For example, equations with function F quadratic in u ₁ have the form

$$\displaystyle \begin{aligned} F\left( u_{0},u_{1}\right) =\frac{\phi _{u_{0}}+c_{1}}{\phi } u_{1}^{2}+c_{2}u_{1}+c_{3}\phi , {} \end{aligned} $$

(3.42)

and $\phi =\phi \left ( u_{0}\right )$ is the symmetry of the equation.

Let us take the representative with $c_{1}=0,c_{2}=0,c_{3}=1,\phi =\exp \left ( u_{0}\right )$:

$$\displaystyle \begin{aligned} u_{2}=u_{1}^{2}+\exp (u_{0}). \end{aligned}$$

It has commutative symmetry algebra $\left ( \phi _{1}=u_{1},\phi _{2}=\exp (u_{0})\right )$. Then,

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} \theta _{1} & =&\displaystyle -u_{1}\exp \left( -u_{0}\right) \omega _{0}+\exp \left( -u_{0}\right) \omega _{1} \\ \theta _{2} & =&\displaystyle \exp \left( -2u_{0}\right) \left( u_{1}^{2}+u_{0}\right) \omega _{0}-u_{1}\exp \left( -2u_{0}\right) \omega _{1} \end{array} \end{aligned} $$

are closed 1-forms. We have

$$\displaystyle \begin{aligned} \theta _{1}=dH_{1}, \qquad \theta _{2}=dH_{2}, \end{aligned}$$

where

$$\displaystyle \begin{aligned} \begin{array}{rcl} H_{1} & =&\displaystyle -x+\exp \left( -u_{0}\right) u_{1}+c_{1}, \\ H_{2} & =&\displaystyle -\frac{1}{2}u_{1}^{2}\exp \left( -2u_{0}\right) -\exp \left( -u_{0}\right) +c_{2}, \end{array} \end{aligned} $$

and solutions of the equation are given by

$$\displaystyle \begin{aligned} y(x)=\ln \left( \frac{2}{2c_{2}-c_{1}^{2}-x^{2}+2c_{1}x}\right) , \end{aligned}$$

where c ₁ and c ₂ are constants.

3.8 Schrödinger Type Equations

3.8.1 Actions of Diffeomorphisms on Schrödinger Type Equations

In this part, we consider linear second-order equations of the form

(3.43)

with the potential W(x), and we study the cases when W is integrable, i.e. the Eq. (3.43) can be solved by quadratures. Because of linearity (3.43), we will restrict ourselves to linear symmetries ϕ = a(x)u ₀ + b(x)u ₁.

Then, the Lie equation takes the form

$$\displaystyle \begin{aligned} D^{2}\left( \phi \right) +W(x) \phi =0, {} \end{aligned} $$

(3.44)

where

$$\displaystyle \begin{aligned} D=\frac{\partial }{\partial x}+u_{1}\frac{\partial }{\partial u_{0}} -W(x)u_{0}\frac{\partial }{\partial u_{1}}, \end{aligned}$$

or

in explicit form. Therefore,

where the function b(x) satisfies the following third-order differential equation:

(3.45)

To understand the meaning of this equation, consider the action of point transformations on equations of type (3.43). If these transformations preserve the class of linear equations, they have to be of the following form:

$$\displaystyle \begin{aligned} T:\left( x,u_{0}\right) \rightarrow \left( y=Y(x) ,A(x)u_{0}\right) .\end{aligned} $$

Then, the image of (3.43) under this transformation is the following equation:

$$\displaystyle \begin{aligned} K_{2}u_{2}+K_{1}u_{1}+K_{0}u_{0}=0,\end{aligned} $$

where

Therefore, to get transformations preserving the class of Schrödinger type equations, we should require that K ₁ = 0, and this requirement gives us the following class of transformations (up to a constant scaling of u ₀):

(3.46)

Then, Eq. (3.43) will be transformed to the same type of equation with potential $\widetilde {W}$ equal to

(3.47)

Notice that if we consider symmetric differential forms

$$\displaystyle \begin{aligned} g_{W}=Wdy^{2}, \end{aligned}$$

then the last equation takes the following form:

$$\displaystyle \begin{aligned} g_{\widetilde{W}}=Y^{\ast }\left( g_{W}\right) -S\left( Y\right) , \end{aligned}$$

where

is the Schwarzian derivative.

It is easy to check that $S\left ( Y\right ) =0$ if and only if Y  is a projective transformation:

$$\displaystyle \begin{aligned} Y(x) =\frac{ax+b}{cx+d}, \end{aligned}$$

where

Therefore, the $\mathbf {SL}_{2}\left ( \mathbb {R}\right )$-action on the set of Schrödinger equations is equivalent to the $\mathbf {SL}_{2}\left ( \mathbb {R}\right )$-action on the space of quadratic differential forms.

3.8.2 Actions of the Diffeomorphism Group on Tensors

To understand the geometrical meaning of solutions of Schrödinger type equations, we reconsider actions of the diffeomorphism group on tensors.

Let M and N be manifolds, and let ϕ : M → N be a diffeomorphism. We define action ϕ _∗ of ϕ on tensors in such a way that

$$\displaystyle \begin{aligned} \left( \psi \circ \phi \right) _{\ast }=\psi _{\ast }\circ \phi _{\ast }, \qquad \left( \phi _{\ast }\right) ^{-1}=\left( \phi ^{-1}\right) _{\ast }. {} \end{aligned} $$

(3.48)

Functions :

For $f\in C^{\infty }\left ( M\right )$, we define $\phi _{\ast }\left ( f\right ) \in C^{\infty }\left ( N\right )$ as follows:

$$\displaystyle \begin{aligned} \phi _{\ast }\left( f\right) =f\circ \phi ^{-1}. \end{aligned}$$

Remark that the difference of $\phi _{\ast }\left ( f\right )$ from the more standard $\phi ^{\ast }\left ( h\right ) =h\circ \phi$, where $h\in C^{\infty }\left ( N\right )$ and $\phi ^{\ast }\left ( h\right ) \in C^{\infty } \left ( M\right )$, is the following:

• We define $\phi _{\ast }\left ( f\right )$ for diffeomorphisms ϕ only but $\phi ^{\ast }\left ( h\right )$ defined for all smooth mappings ϕ.

• Since we have $\left ( \phi \circ \psi \right ) ^{\ast }=\psi ^{\ast }\circ \phi ^{\ast }$, instead of (3.48), the correspondence ϕ↦ϕ ^∗ is not a group homomorphism, but ϕ↦ϕ _∗ is.

Vector fields :

Let $V\in \mathrm {Vect}\left ( M\right )$ be a vector field on M, we define $\phi _{\ast }\left ( V\right )$ by

$$\displaystyle \begin{aligned} \phi _{\ast }\left( V\right) \left( h\right) =\phi _{\ast }\left( V\left( \phi _{\ast }^{-1}\left( h\right) \right) \right) , \end{aligned}$$

where $h\in C^{\infty }\left ( N\right )$ or, in operator form,

$$\displaystyle \begin{aligned} \phi _{\ast }\left( V\right) =\phi _{\ast }\circ V\circ \phi _{\ast }^{-1}. \end{aligned}$$

Then, once more, we have property (3.48), and

$$\displaystyle \begin{aligned} \phi _{\ast }\left( fV\right) =\phi _{\ast }\left( f\right) \phi _{\ast }\left( V\right) , \end{aligned}$$

for all $f\in C^{\infty }\left ( M\right ) .$

Differential Forms :

Let $\omega \in \varOmega ^{1}\left ( M\right )$ be a differential 1-form on M, and then we define $\phi _{\ast }\left ( \omega \right ) \in \varOmega ^{1}\left ( N\right )$ as follows:

$$\displaystyle \begin{aligned} \left\langle \phi _{\ast }\left( \omega \right) ,Z\right\rangle =\phi _{\ast }\left\langle \omega ,\phi _{\ast }^{-1}\left( Z\right) \right\rangle , \end{aligned}$$

for all vector fields $Z\in \mathrm {Vect}\left ( N\right )$. For exterior differential forms of higher degree, we define

$$\displaystyle \begin{aligned} \phi _{\ast }\left( \omega _{1}\wedge \cdots \wedge \omega _{k}\right) =\phi _{\ast }\left( \omega _{1}\right) \wedge \cdots \wedge \phi _{\ast }\left( \omega _{k}\right) , \end{aligned}$$

where $\omega _{1}\in \varOmega ^{1}\left ( M\right ) ,\ldots ,\omega _{k}\in \varOmega ^{1}\left ( M\right )$ and $\omega _{1}\wedge \cdots \wedge \omega _{k}\in \varOmega ^{k}\left ( M\right ) .$ In a similar way, we define images of the symmetric differential forms and general tensors.

Once more, we have property (3.48) for maps of differential forms and tensors.

Coordinates :

Let $x=\left ( x_{1},..,x_{n}\right )$ be local coordinates on M and let $y=\left ( y_{1},..,y_{n}\right )$ be local coordinates on N. Assume that diffeomorphism ϕ has the following form in these coordinates:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \phi & :&\displaystyle x\rightarrow y=Y(x) , \\ \phi ^{-1} & :&\displaystyle y\rightarrow x=X\left( y\right) . \end{array} \end{aligned} $$

Then,

$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x) & \Longrightarrow &\displaystyle \phi _{\ast }\left( f\right) \left( y\right) =f\left( X\left( y\right) \right) , \\ h\left( y\right) & \Longrightarrow &\displaystyle \phi _{\ast }^{-1}\left( h\right) \left( x\right) =h\left( Y(x) \right) . \end{array} \end{aligned} $$

Let $V=\frac {\partial }{\partial x_i}\in \mathrm {Vect}\left ( M\right )$. Then, $\phi _{\ast }\left ( V\right ) \in \mathrm {Vect}\left ( N\right )$ has the form

$$\displaystyle \begin{aligned} \phi _{\ast }\left( V\right) =\sum_{j=1}^{n}a_{j}\left( y\right) \frac{ \partial }{\partial y_{j}}, \end{aligned}$$

and

$$\displaystyle \begin{aligned} a_{j}\left( y\right) &=\phi _{\ast }\left( V\right) \left( y_{j}\right) =\phi _{\ast }\left( V\left( \phi _{\ast }^{-1}\left( y_{j}\right) \right) \right) \\&=\phi _{\ast }\left( V\left( Y_{j}(x) \right) \right) =\phi _{\ast }\left( \frac{\partial Y_{j}}{\partial x_{i}}\right) =\frac{\partial Y_{j}}{\partial x_{i}}\left( X\left( y\right) \right) .\end{aligned} $$

Therefore,

$$\displaystyle \begin{aligned} \phi _{\ast }\left( \frac{\partial }{\partial x_{i}}\right) =\sum_{j=1}^{n} \frac{\partial Y_{j}}{\partial x_{i}}\left( X\left( y\right) \right) \frac{ \partial }{\partial y_{j}}. \end{aligned} $$

(3.49)

Let $\omega =dx_{i}\in \varOmega ^{1}\left ( M\right )$ be a differential 1 -form. Then,

$$\displaystyle \begin{aligned} \phi _{\ast }\left( dx_{i}\right) =\sum_{j=1}^{n}b_{j}\left( y\right) \ dy_{j}, \end{aligned}$$

and

$$\displaystyle \begin{aligned} b_{j}\left( y\right) =\phi _{\ast }\left( \left\langle dx_{i},\phi _{\ast }^{-1}\left( \frac{\partial }{\partial y_{j}}\right) \right\rangle \right) = \frac{\partial X_{i}}{\partial y_{j}}\left( X\left( y\right) \right) . \end{aligned}$$

Therefore,

$$\displaystyle \begin{aligned} \phi _{\ast }\left( dx_{i}\right) =\sum_{j=1}^{n}\frac{\partial X_{i}}{ \partial y_{j}}\left( X\left( y\right) \right) \ dy_{j}. \end{aligned}$$

Solutions :

As we have seen, the natural type of transformations for solutions of Eq. (3.43) is very similar to transformation of vector fields, with only one difference: instead of the multiplier $\frac { \partial Y}{\partial x}$ that we used for transformations of vector fields, we have to use multiplier $\sqrt {\frac {\partial Y}{\partial x}},$ i.e. solutions of the Schrödinger type equations behave like “$\frac {1}{2}-$ vector fields.” To check this hypothesis, we substitute square b(x) = y(x)² of a solution y(x) of equation (3.43) in symmetry Eq. (3.45) and get zero.

Therefore, any product of solutions b(x) = y ₁(x)y ₂(x) of the Schrödinger equation also satisfies equation (3.45). In other words, if $\left \langle y_{1}\left ( x\right ) ,y_{2}(x) \right \rangle$ is a fundamental set of solutions of Eq. (3.43), then $\left \langle y_{1}(x) ^{2},2y_{1}(x) y_{2}(x) ,y_{2}^{2}(x) \right \rangle$ is a fundamental set of solutions of Eq. (3.45 ).

These functions represent vector fields

$$\displaystyle \begin{aligned} A=y_{1}(x) ^{2}\frac{\partial }{\partial x},\ H=2y_{1}\left( x\right) y_{2}(x) \frac{\partial }{\partial x},\ B=y_{2}(x)^2 \frac{\partial }{\partial x}. \end{aligned}$$

Assume that the Wronskian of y ₁ and y ₂ equals 1. Then,

i.e. these vector fields satisfy the structure equations of the Lie algebra $\mathfrak {sl}\left ( 2,\mathbb {R}\right )$.

To summarize, we have the following result.

Theorem 3.12

• 1. The solution space of Eq.(3.45) is formed by pairwise products of solutions of Eq.(3.43), i.e. Eq.(3.45) is a symmetric square of Eq.(3.43).

• 2. The solution space of Eq.(3.45) is the $\mathfrak {sl} \left ( 2,\mathbb {R}\right )$ Lie algebra with respect to bracket

• 3. The Lie equation on symmetries of Schrödinger equation (3.43 ) defines a projective structure on the line: $\mathfrak {sl}\left ( 2,\mathbb { R}\right ) \subset \mathrm {Vect}\left ( \mathbb {R}\right ) .$

Remark 3.4

By a projective structure on $\mathbb {R}$, we mean a covering $\mathbb {R}$ by intervals $\left ( U_{\alpha },t_{\alpha }\right )$ with coordinates t _α such that on intersections U _α ∩ U _β, these coordinates are connected by projective transformations

$$\displaystyle \begin{aligned} t_{\beta }=\frac{a_{11}^{\beta \alpha }t_{\alpha }+a_{12}^{\beta \alpha }}{ a_{21}^{\beta \alpha }t_{\alpha }+a_{22}^{\beta \alpha }}, {} \end{aligned} $$

(3.50)

where

(3.51)

It is easy to check with formula (3.47) that locally any Schr ödinger equation (3.43) could be transformed to the equation The Lie algebra, corresponding to this equation, has the form

$$\displaystyle \begin{aligned} \mathfrak{sl}\left( 2,\mathbb{R}\right) =\left\langle \frac{\partial }{ \partial x},x\frac{\partial }{\partial x},x^{2}\frac{\partial }{\partial x} \right\rangle . {} \end{aligned} $$

(3.52)

In particular, any realization $\mathfrak {sl}\left ( 2,\mathbb {R}\right ) \subset \mathrm {Vect}\left ( \mathbb {R}\right )$ is locally equivalent to model (3.52), and any two such realizations are connected by a projective transformation (3.50).

In other words, to define a projective structure on $\mathbb {R}$ is equivalent to have a representation of Lie algebra $\mathfrak {sl}\left ( 2, \mathbb {R}\right )$ in Lie algebra of vector fields $\mathrm {Vect}\left ( \mathbb {R}\right )$, and it is also equivalent to have a Schrödinger equation (3.43).

Example 3.11

To the Schrödinger equation, corresponds the Lie algebra

$$\displaystyle \begin{aligned} \mathfrak{sl}\left( 2,\mathbb{R}\right) =\left\langle \sin ^{2}\left( \omega x\right) \frac{\partial }{\partial x},\sin\left( 2\omega x\right) \frac{ \partial }{\partial x},\cos ^{2}\left(\omega x\right) \frac{\partial }{ \partial x}\right\rangle , {} \end{aligned} $$

(3.53)

which is not equivalent to (3.52) on $\mathbb {R}$ because any nonvanishing vector field in (3.53) has an infinite number of zeroes, while those in (3.52) have not more than two.

3.8.3 Integration of Schrödinger Type Equations with Integrable Potentials

As we have seen, the Schrödinger type equations (3.43) have linear symmetries of the form ϕ ₀ = u ₀ and , where the function b = b(x) is a solution of the Lie equation

They do commute $\left [ \phi _{0},\phi _{b}\right ] =0$, and therefore the Schr ödinger equation can be integrated in quadratures if we know a nontrivial symmetry ϕ _b. In this case, we call potential W integrable.

Moreover, integrating the Lie equation with respect to W with given function b, we get the relation

(3.54)

where c _b is a constant.

Remark that the solution space of the Lie equation is a Lie algebra, which is isomorphic to $\mathfrak {sl}_{2}$, and the constant c _b is proportional to the value of the Killing form on $\mathfrak {sl}_{2}$ on the vector $b\in \mathfrak {sl}_{2}.$

The relation (3.54) shows that if two potentials W and $\widetilde {W }$ have the same symmetry ϕ _b, then

$$\displaystyle \begin{aligned} \widetilde{W}-W=\frac{c}{b^{2}},\end{aligned} $$

for some constant c.

This observation can also be used in the opposite way: if W is an integrable potential with symmetry ϕ _b, then the potential $W+\frac {c}{b^{2}}$ is also integrable with the same symmetry ϕ _b.

Example 3.12

The potentials

$$\displaystyle \begin{aligned} \frac{c}{\left( c_{2}x^{2}+2c_{1}x+c_{0}\right) ^{2}},\end{aligned} $$

$$\displaystyle \begin{aligned} \omega ^{2}+\frac{c}{\left( c_{1}\sin \left( 2\omega x\right) +c_{2}\cos \left( 2\omega x\right) +c_{0}\right) ^{2}}, \end{aligned}$$

and

$$\displaystyle \begin{aligned} 1+\frac{1}{\left( \sin \left( 2x\right) +1\right) ^{2}} \end{aligned}$$

are integrable (Figs. 3.3 and 3.4).

Fig. 3.3

$w= \frac {1}{ \left ( x^{2}+1 \right )^{2}}$

Fig. 3.4

$w=1+ \frac {1}{ \left ( \sin ^{2} \left ( 2x \right ) +1 \right ) ^{2}}$

3.8.3.1 Integration by Symmetries

To integrate the Schrödinger equation with given symmetry ϕ _b, we will use the following observation:

Lemma 3.2

Let ϕ and ψ be symmetries of the Schrödinger equation. Then, the function

$$\displaystyle \begin{aligned} H=\phi D\left( \psi \right) -\psi D\left( \phi \right) \end{aligned}$$

is a first integral.

Proof

The conditions that ψ and ϕ are symmetries mean that $D^{2}\left ( \psi \right ) +W\psi =0$ and $D^{2}\left ( \phi \right ) +W\phi =0$. Therefore,

$$\displaystyle \begin{aligned} D\left( H\right) =D\left( \phi \right) D\left( \psi \right) -D\left( \psi \right) D\left( \phi \right) =0. \end{aligned}$$

□

By applying this lemma to the symmetries ψ = ϕ ₀ = u ₀ and ϕ = ϕ _b, we get that

$$\displaystyle \begin{aligned} H=\frac{c_{b}}{b}\phi _{0}^{2}+\frac{1}{b}\phi _{b}^{2} \end{aligned}$$

is a first integral of the equation.

Assume that $c_{b}=c_{0}^{2}>0,$ and let y be a solution. Let

$$\displaystyle \begin{aligned} z=\frac{y}{\sqrt{\left\vert b\right\vert }}, \end{aligned}$$

then

Let

for some function γ. Then,

and therefore solutions y have the form

$$\displaystyle \begin{aligned} y=\frac{c}{c_{0}}\sqrt{\left\vert b\right\vert }\sin \left( c_{0}\int \frac{ dx}{b}\right) . \end{aligned}$$

In a similar way, we get

$$\displaystyle \begin{aligned} y=\frac{c}{c_{0}}\sqrt{\left\vert b\right\vert }\sinh \left( c_{0}\int \frac{ dx}{b}\right) \end{aligned}$$

for the case $c_{b}=-c_{0}^{2}<0,$ and

$$\displaystyle \begin{aligned} y=c\sqrt{\left\vert b\right\vert }\int \frac{dx}{b} \end{aligned}$$

for the case c _b = 0.

Finally, we conclude that knowledge of a single nontrivial linear symmetry ϕ _b gives us

• Potential function

  

• Fundamental solution (if $c_{b}=c_{0}^{2}>0$ )

  $$\displaystyle \begin{aligned} y_{1}=\sqrt{\left\vert b\right\vert }\sin \left( c_{0}\int \frac{dx}{b} \right) ,y_{2}=\sqrt{\left\vert b\right\vert }\cos \left( c_{0}\int \frac{dx }{b}\right) . \end{aligned}$$

• Linear symmetries

  $$\displaystyle \begin{aligned} b_{1}=b,b_{2}=b\sin \left( 2c_{0}\int \frac{dx}{b}\right) ,b_{3}=b\cos \left( 2c_{0}\int \frac{dx}{b}\right). \end{aligned}$$

• Integrable potentials

  $$\displaystyle \begin{aligned} W+\sum_{i}\frac{k_{i}}{\left( c_{1i}b_{1}+c_{2i}b_{2}+c_{i3}b_{3}\right) ^{2} },\ \ \text{etc.} \end{aligned}$$

Example 3.13

For the case

$$\displaystyle \begin{aligned} W=1+\frac{2}{\left( 2+\sin 2x\right) ^{2}},\; b=2+\sin 2x,\;c_{b}=5, \end{aligned}$$

we have (Fig. 3.5)

$$\displaystyle \begin{aligned} \begin{array}{rcl} y_{1} & =&\displaystyle \sqrt{2+\sin 2x}\sin \left( \frac{2}{\sqrt{3}}\arctan \left( \frac{ 2\tan x+1}{\sqrt{3}}\right) \right) , \\ y_{2} & =&\displaystyle \sqrt{2+\sin 2x}\cos \left( \frac{2}{\sqrt{3}}\arctan \left( \frac{ 2\tan x+1}{\sqrt{3}}\right) \right) . \end{array} \end{aligned} $$

Fig. 3.5

$w=1+ \frac {2}{ \left ( 2+\sin 2x \right ) ^{2}}$

3.8.3.2 Lame Equation

Let us consider the case when the potential function W generates linear symmetry for the corresponding Schrödinger equation.

In other words, the lift of the vector field

$$\displaystyle \begin{aligned} W(x) \frac{\partial }{\partial x} \end{aligned}$$

in the bundle of $\frac {1}{2}$-vector fields is a symmetry of the Schrö dinger equation.

Putting b = W in the Lie equation gives us differential equation for potential:

or

for some constant c ₁. Therefore,

for some constant c ₂, and

$$\displaystyle \begin{aligned} W=-2\wp , \end{aligned}$$

where ℘ is the Weierstrass p-function with invariants g ₂ = −c ₁ and g ₃ = c ₂∕2.

Therefore, the Lame equation

has linear symmetry

with constant c _℘ = −g ₃.

The fundamental solution (in the case, g ₃ < 0) has the form

$$\displaystyle \begin{aligned} y_{1}=\sqrt{\left\vert \wp \right\vert }\sin \left( \sqrt{-g_{3}}\int \frac{ dx}{\wp }\right) ,y_{2}=\sqrt{\left\vert \wp \right\vert }\cos \left( \sqrt{ -g_{3}}\int \frac{dx}{\wp }\right) , \end{aligned}$$

and all linear symmetries are generated by

$$\displaystyle \begin{aligned} b_{1}=\wp ,b_{2}=\wp \sin \left( 2\sqrt{-g_{3}}\int \frac{dx}{b}\right) ,b_{3}=\wp \cos \left( 2\sqrt{-g_{3}}\int \frac{dx}{b}\right) , \end{aligned}$$

and the potentials

$$\displaystyle \begin{aligned} -2\wp +\sum_{i}\frac{k_{i}}{\wp ^{2}\left( c_{1i}+c_{2i}\sin \left( 2\sqrt{ -g_{3}}\int \frac{dx}{b}\right) +c_{i3}\cos \left( 2\sqrt{-g_{3}}\int \frac{ dx}{b}\right) \right) ^{2}} \end{aligned}$$

are integrable.

3.8.3.3 Eigenvalue Problem

Here, we consider equations of the form

(3.55)

At first, we consider equations that have symmetries that are linear in λ:

$$\displaystyle \begin{aligned} b=b_{0}+\lambda b_{1}. \end{aligned}$$

Collecting terms with λ ², λ, and λ ⁰, we get the following relations: $b_{1}=\mathrm {const},b_{0}=-\frac {W}{2}$, and b ₀ is a symmetry of W. Therefore, we get the discussed case of the Lame equation:

with symmetry

$$\displaystyle \begin{aligned} b=\lambda +\wp . \end{aligned}$$

Then, the functions

$$\displaystyle \begin{aligned} y=C_{1}\sqrt{\left\vert \wp +\lambda \right\vert }\sin \left( \sqrt{-g_{3}} \int \frac{dx}{\wp +\lambda }\right) +C_{2}\sqrt{\left\vert \wp +\lambda \right\vert }\cos \left( \sqrt{-g_{3}}\int \frac{dx}{\wp +\lambda }\right) \end{aligned}$$

satisfy equation (3.55).

Assume that we are looking for eigenvalues for the boundary value problem $y\left ( a\right ) =y\left ( b\right ) =0$ on the interval [a, b], where the function ℘ has no singularities.

Then, the boundary value problem gives us a linear system for the coefficients C ₁ and C ₂ of the solution

$$\displaystyle \begin{aligned} &y(x) =C_{1}\sqrt{\left\vert \wp (x) +\lambda \right\vert }\sin \left( \sqrt{-g_{3}}\int_{a}^{x}\frac{dx}{\wp +\lambda } \right) \\ &+C_{2}\sqrt{\left\vert \wp (x) +\lambda \right\vert } \cos \left( \sqrt{-g_{3}}\int_{a}^{x}\frac{dx}{\wp +\lambda }\right) . \end{aligned} $$

We have

$$\displaystyle \begin{aligned} C_{2}\sqrt{\left\vert \wp \left( a\right) +\lambda \right\vert }=0, \end{aligned}$$

at the point x = a and

$$\displaystyle \begin{aligned} C_{1}\sqrt{\left\vert \wp \left( b\right) +\lambda \right\vert }\sin \left( \sqrt{-g_{3}}\int_{a}^{b}\frac{dx}{\wp +\lambda }\right) +C_{2}\sqrt{ \left\vert \wp \left( b\right) +\lambda \right\vert }\cos \left( \sqrt{-g_{3} }\int_{a}^{b}\frac{dx}{\wp +\lambda }\right) =0 \end{aligned}$$

at the point x = b.

Therefore, solutions of the equation

$$\displaystyle \begin{aligned} \sqrt{\left\vert \wp \left( a\right) +\lambda \right\vert }\sqrt{\left\vert \wp \left( b\right) +\lambda \right\vert }\sin \left( \sqrt{-g_{3}} \int_{a}^{b}\frac{dx}{\wp +\lambda }\right) =0 \end{aligned}$$

are eigenvalues for given boundary problem, or

$$\displaystyle \begin{aligned} \begin{array}{rcl} \lambda & =&\displaystyle -\wp \left( a\right) ,\lambda =-\wp \left( b\right) , \\ \int_{a}^{b}\frac{dx}{\wp +\lambda } & =&\displaystyle \frac{\pi k}{\sqrt{-g_{3}}},k=0,\pm 1,\pm 2,\ldots. \end{array} \end{aligned} $$

are the eigenvalues.

Similar results are valid for eigenvalue problems with symmetries that are polynomial in λ (see [8]).